| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Модуляция потока воздуха
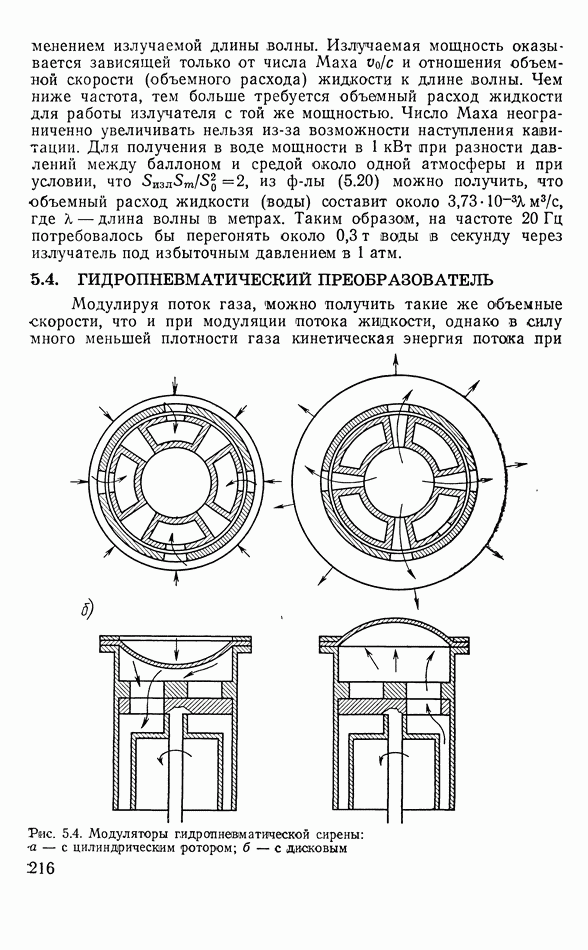
Рассмотрим схему рис. 5.1. Из резервуара большого объема через патрубок с заслонкой воздух поступает в излучающий рупор. Заслонка при помощи какого-либо механизма изменяет проходное сечение патрубка по закону


Рис. 6.1. Схема модуляции воздушного потока колеблющимся вентилем
Для протекающей по патрубку струи газа, пренебрегая его сжимаемостью, можно записать уравнение сил в виде 

где  скорость газа в струйке на пути в вентиле;
скорость газа в струйке на пути в вентиле;
I — длина пути газа в вентиле;  скорость и давление в газе, подтекающем к вентилю;
скорость и давление в газе, подтекающем к вентилю;  то же, для газа, вытекающего из вентиля.
то же, для газа, вытекающего из вентиля.
Уравнение (5.2) отражает тот факт, что газ ускоряется в вентиле под действием разности полных гидродинамических напоров по обе стороны рассматриваемого участка. Так как в резервуаре газ покоится, то 
За вентилем имеется лишь короткий патрубок, и в предельном случае отсутствия нагрузки со стороны рупора  атмосферное давление, а скорость в патрубке по всей его длине одинакова, так как сжимаемостью газа на малой длине I пренебрегли. Тогда (5.1) принимает (вид:
атмосферное давление, а скорость в патрубке по всей его длине одинакова, так как сжимаемостью газа на малой длине I пренебрегли. Тогда (5.1) принимает (вид:

где  разность давлений между резервуаром и атмосферой.
разность давлений между резервуаром и атмосферой.
Если вентиль внезапно открыть, то накопившийся в патрубке газ будет разгоняться по закону:

Справедливость этого решения проверяется подстановкой его в (5.3). Кроме того, оно удовлетворяет начальному условию  при
при  Это соответствует тому, что в момент открытия заслонки газ покоится.
Это соответствует тому, что в момент открытия заслонки газ покоится.
Даже при очень небольшой разности давлений  достигает десятков метров в секунду, так что на длине патрубка вентиля, скажем, в
достигает десятков метров в секунду, так что на длине патрубка вентиля, скажем, в  постоянная
постоянная  составит
составит 
При больших разностях давлений влияние инерции частиц на линейную скорость в вентиле будет еще меньше. Главными сопротивлениями, которые должно преодолевать давление газа в баллоне, будут динамический напор и сопротивления излучения звука в рупоре и в резервуаре. При периодическом синусоидальном изменении сечения щели 5 вентиля со стороны резервуара на вентиль будет действовать не полное давление, а уменьшенное на величину акустической реакции  об, где
об, где  акустическое сопротивление излучения волн в резервуар,
акустическое сопротивление излучения волн в резервуар,  переменная составляющая объемной скорости воздуха, вытекающего из баллона. Аналогично этому со стороны рупора у вентиля будет давление, увеличенное на
переменная составляющая объемной скорости воздуха, вытекающего из баллона. Аналогично этому со стороны рупора у вентиля будет давление, увеличенное на  по сравнению с атмосферным, где
по сравнению с атмосферным, где  акустическое сопротивление рупора.
акустическое сопротивление рупора.
Если в районе вентиля по-прежнему будем считать воздух несжимаемым, а разность давлений между резервуаром и атмосферой небольшой, так что разность средних плотностей газа в резервуаре и в рупоре можно не учитывать, то, пренебрегая инерцией газа в вентиле и вводя акустические реакции резервуара и рупора, вместо (5.2) получим

Для определения  следует связать
следует связать  с законом модуляции и между собой еще одним соотношением. Так как в (5.5) пренебрежено изменением средней плотности газа, то объемную
с законом модуляции и между собой еще одним соотношением. Так как в (5.5) пренебрежено изменением средней плотности газа, то объемную
скорость газа в устройстве как перед модулятором, так и в горле рупора можно считать одинаковой.
В первом приближении линейная скорость газа мало изменяется по сравнению с  и можно положить:
и можно положить:

Тогда

Объемную скорость получим умножением (5.1) на (5.6):

Здесь член  отброшен с целью линеаризировать и упростить задачу. Если модуляция сечения не (велика, т. е.
отброшен с целью линеаризировать и упростить задачу. Если модуляция сечения не (велика, т. е.  то точность выражения (5.8) не хуже, чем (5.7). Подставив (5.7) и (5.8) в (5.5), получим возможность определить
то точность выражения (5.8) не хуже, чем (5.7). Подставив (5.7) и (5.8) в (5.5), получим возможность определить  через постоянную составляющую линейной скорости
через постоянную составляющую линейной скорости  и амплитуду модуляции сечения
и амплитуду модуляции сечения  В общем случае
В общем случае  и
и  имеют как активную, так и реактивную составляющие.
имеют как активную, так и реактивную составляющие.
Обозначим  и запишем после подстановок (5.7) и (5.8) переменную часть линеаризованного равенства (5.5) в комплексной форме:
и запишем после подстановок (5.7) и (5.8) переменную часть линеаризованного равенства (5.5) в комплексной форме:

Тогда, разделяя вещественную и мнимую части (5.9), получим два уравнения для определения  из которых легко получить:
из которых легко получить:

Полная пневматическая мощность, протекающая через клапан, в принятом приближении составит

Полная акустическая мощность

Пневмоакустический кпд найдем, поделив (5.12) на (5.11):

Найденный таким образом кпд максимален при условии 

Если реактивные сопротивления компенсированы, а критическая частота рупора ниже излучаемой, тагк что активную часть акустического сопротивления можно принять равной  то из условия
то из условия
 легко получить, что разность давлений, при которой
легко получить, что разность давлений, при которой  равна примерно 0,7 атм:
равна примерно 0,7 атм:

Этот результат неточен, так как при таких разностях давлений следует уже учитывать сжимаемость воздуха. Однако качественно результат верен: пневматический излучатель имеет максимальный кпд при вполне определенной разности давлений. При учете сжимаемости и инерции воздуха в клапане расчеты становятся более громоздкими. Исходные уравнения принимают вид:

Здесь  скорость потока в патрубке;
скорость потока в патрубке;  скорость потока в щели клапана;
скорость потока в щели клапана;  ее постоянная составляющая;
ее постоянная составляющая;  - статистические давления в баллоне и в атмосфере соответственно;
- статистические давления в баллоне и в атмосфере соответственно;  акустические реакции
акустические реакции  патрубок со стороны баллона и рупора соответственно;
патрубок со стороны баллона и рупора соответственно;  и
и  — плотности воздуха в баллоне и атмосфере; у— показатель адиабаты; I — длина патрубка.
— плотности воздуха в баллоне и атмосфере; у— показатель адиабаты; I — длина патрубка.
С помощью того же приема линеаризации, как и в упрощенном случае, можно получить выражения для мощности и кпд:

Здесь  — частота;
— частота;  скорости звука в баллоне и в рупоре;
скорости звука в баллоне и в рупоре;  сечение патрубка;
сечение патрубка;  среднее сечение щели;
среднее сечение щели;  коэффициент модуляции сечения щели, так что
коэффициент модуляции сечения щели, так что  амплитуда изменения сечения щели;
амплитуда изменения сечения щели;  сечение горла рупора;
сечение горла рупора; 
Если  много меньше единицы, то
много меньше единицы, то

При  эта формула дает те же условия для
эта формула дает те же условия для  что и упрощенная. На практике
что и упрощенная. На практике  всегда меньше единицы и оптимальная разность давлений соответствует
всегда меньше единицы и оптимальная разность давлений соответствует  т. е. меньше 0,7. Практически она лежит около
т. е. меньше 0,7. Практически она лежит около  атм.
атм.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
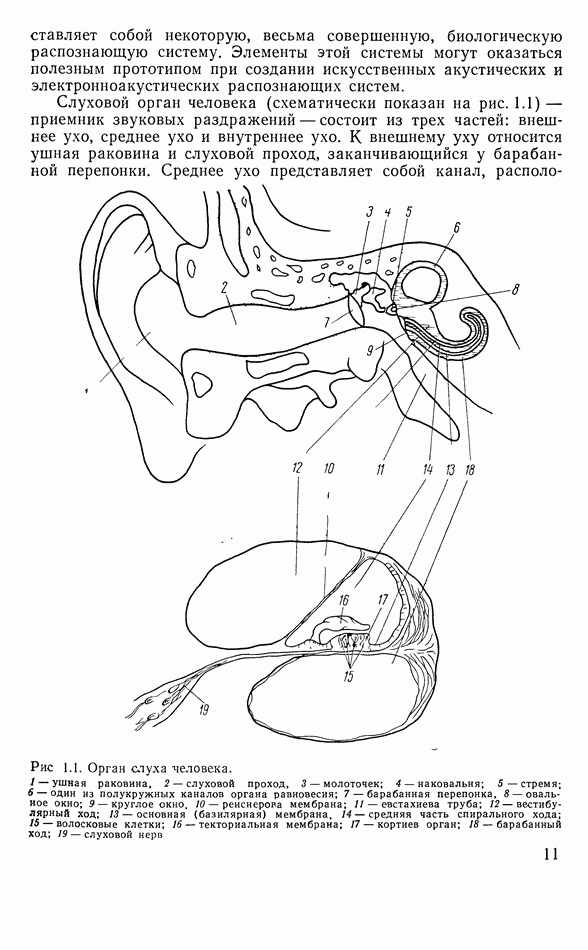
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
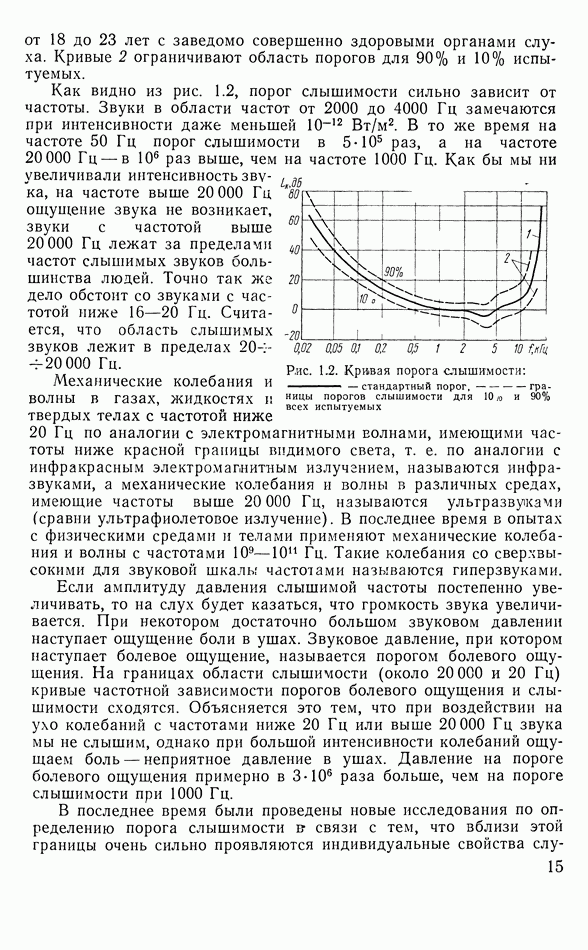
- 1.4. ПОРОГ СЛЫШИМОСТИ
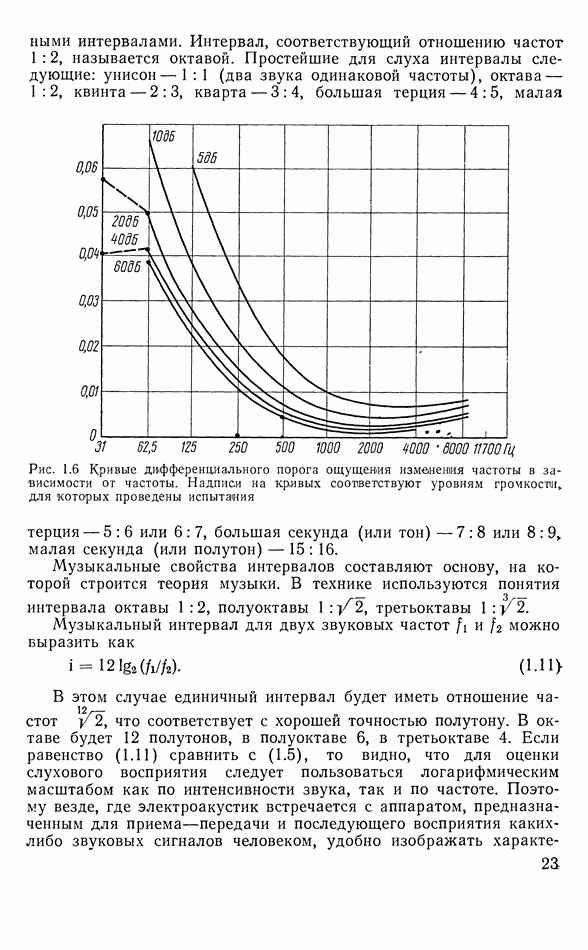
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
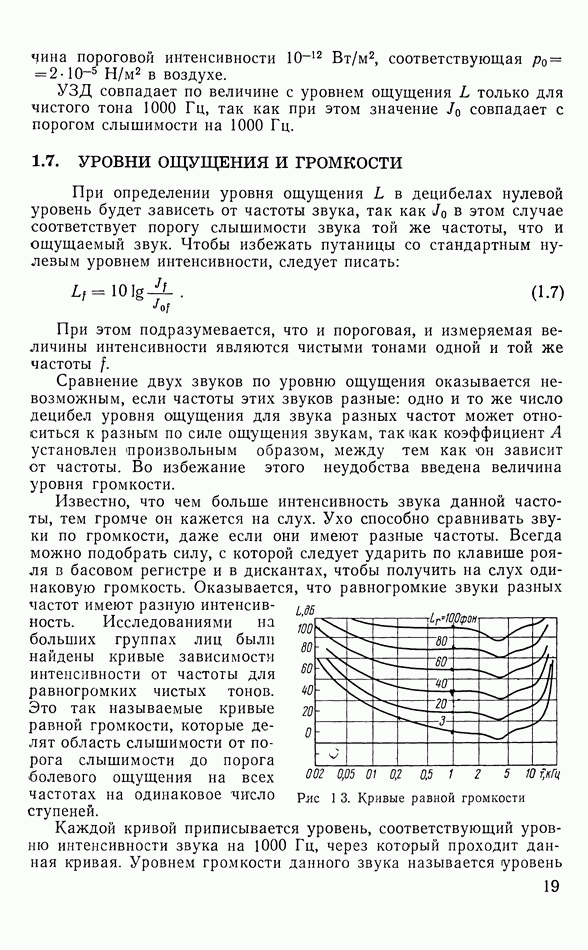
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
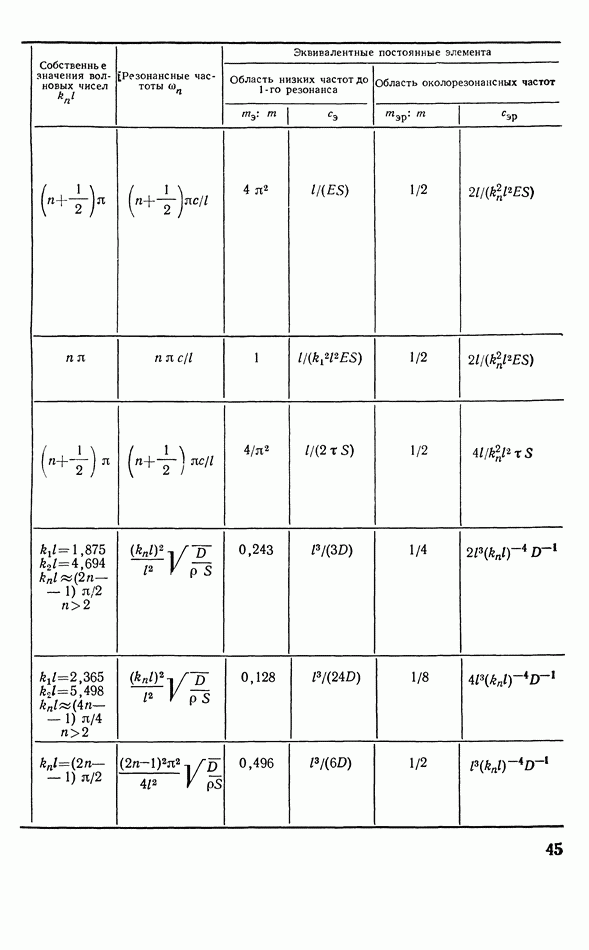
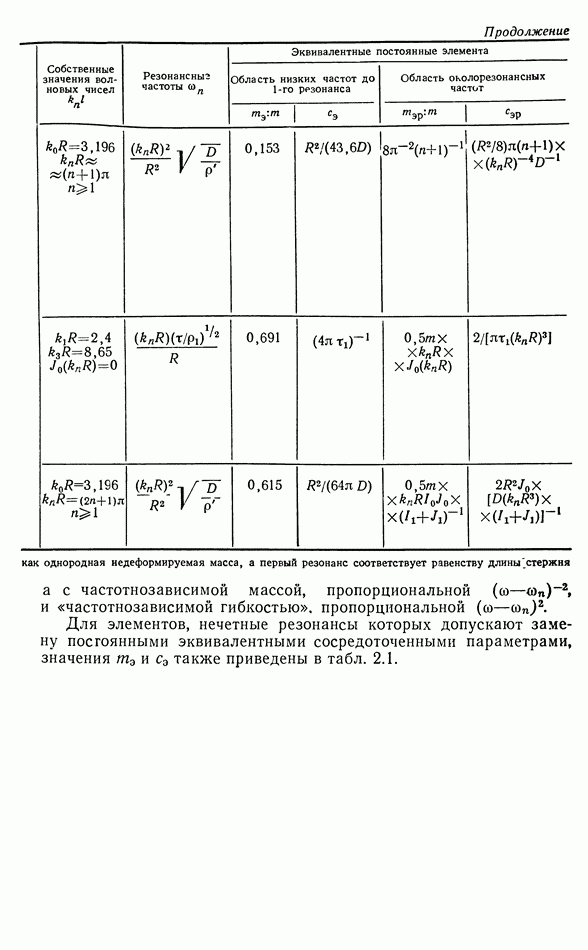
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
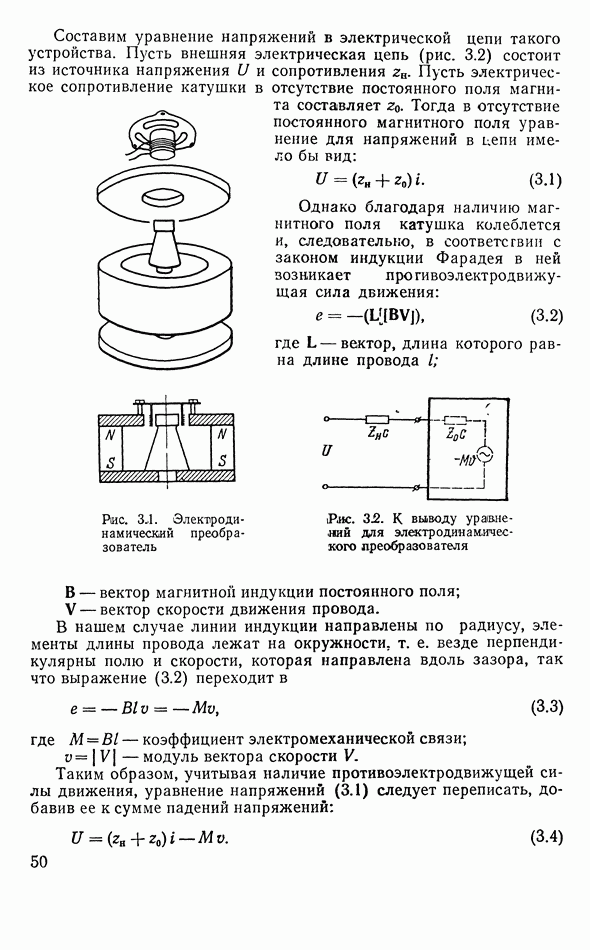
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
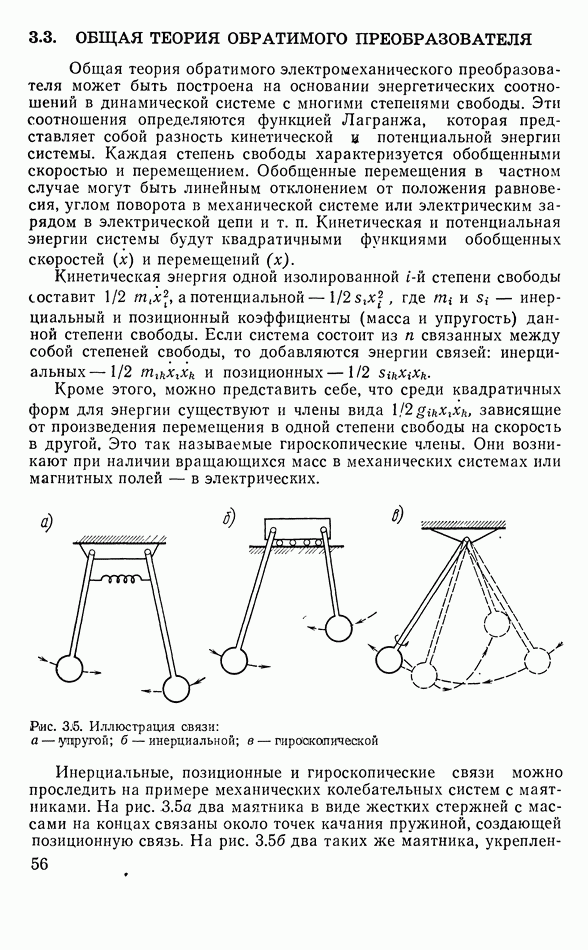
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
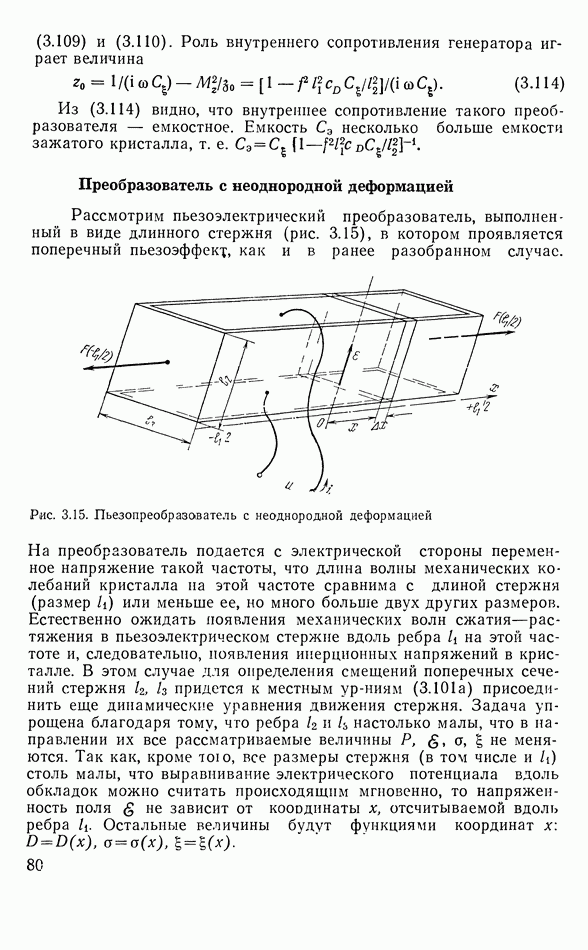
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
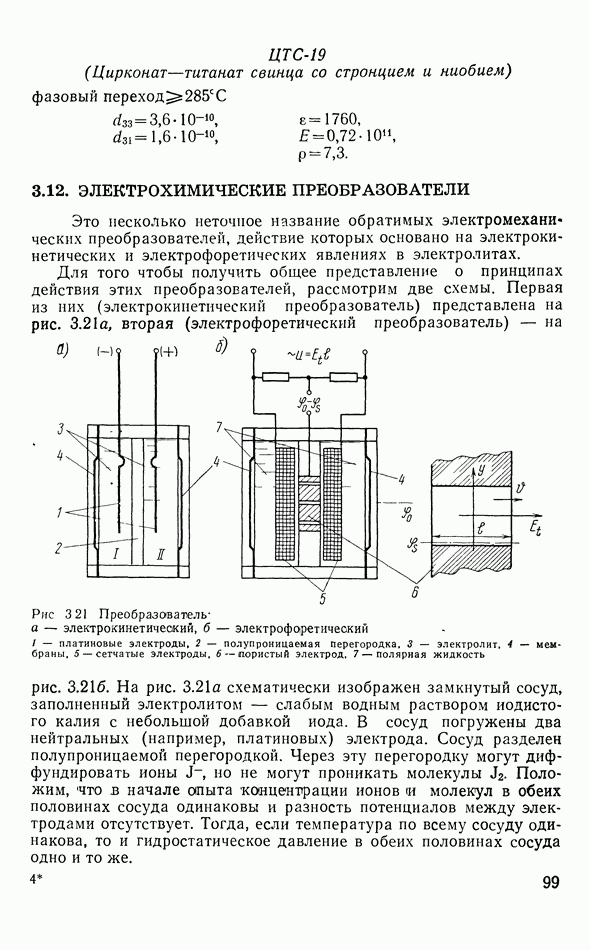
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
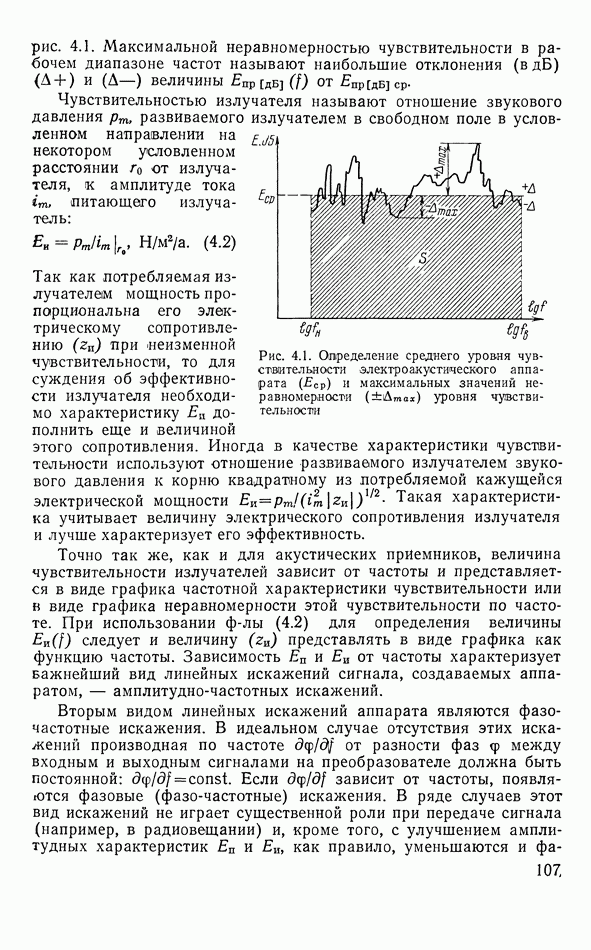
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
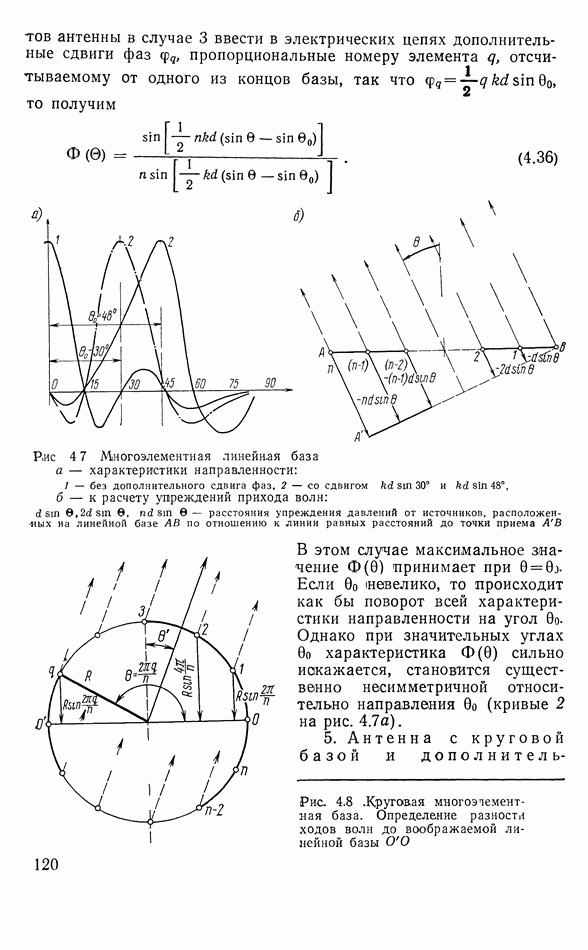
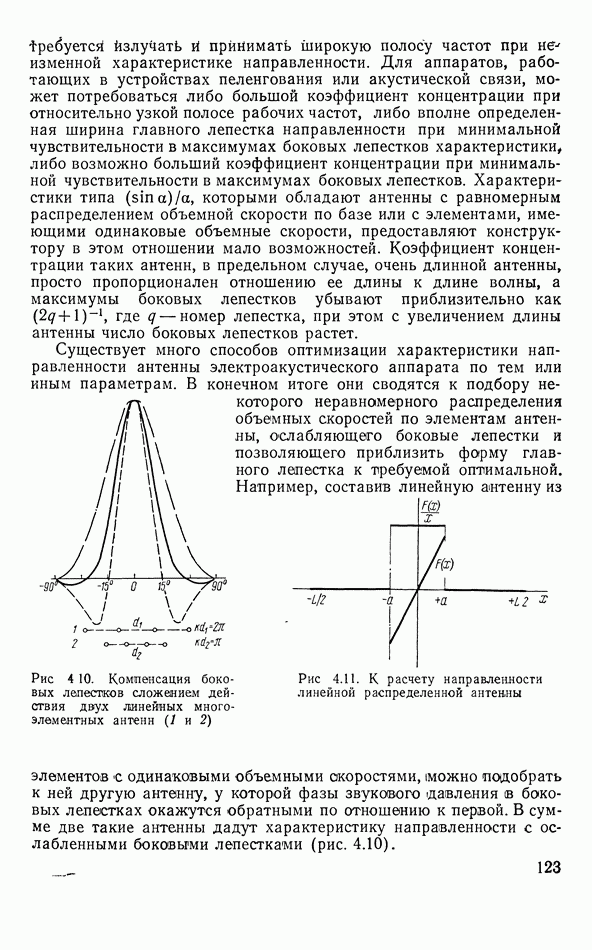
- Оптимизация характеристики направленности антенны
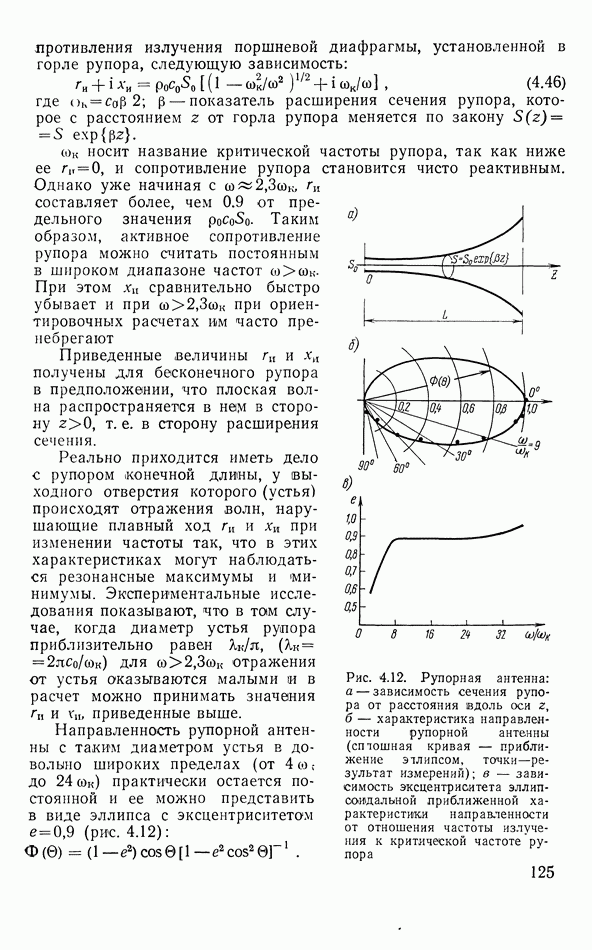
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
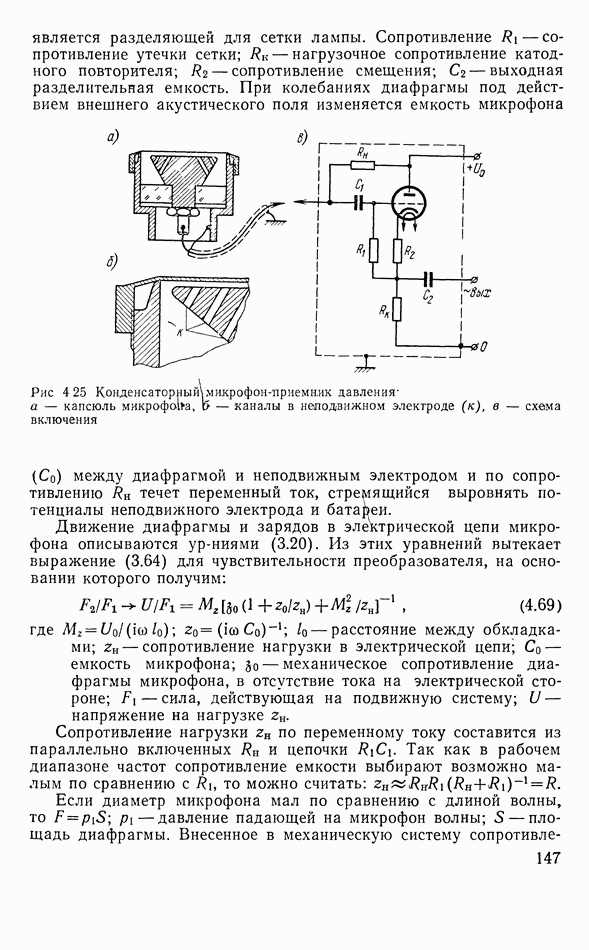
- Ненаправленный микрофон-приемник давления
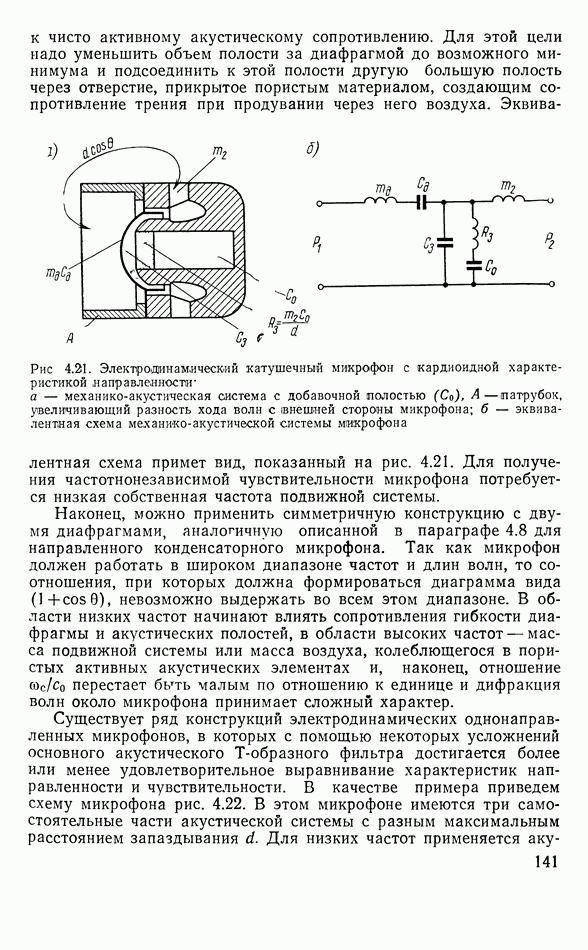
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
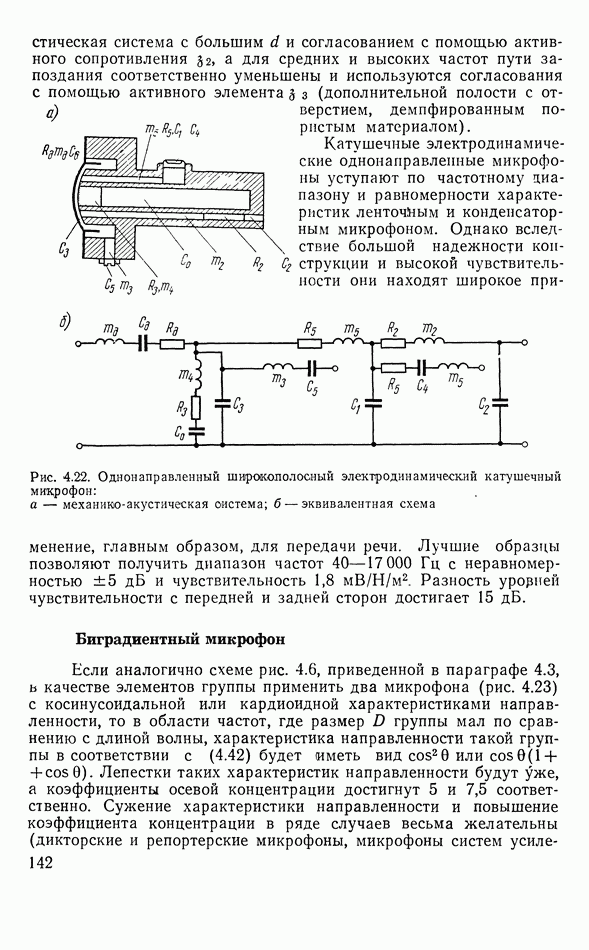
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
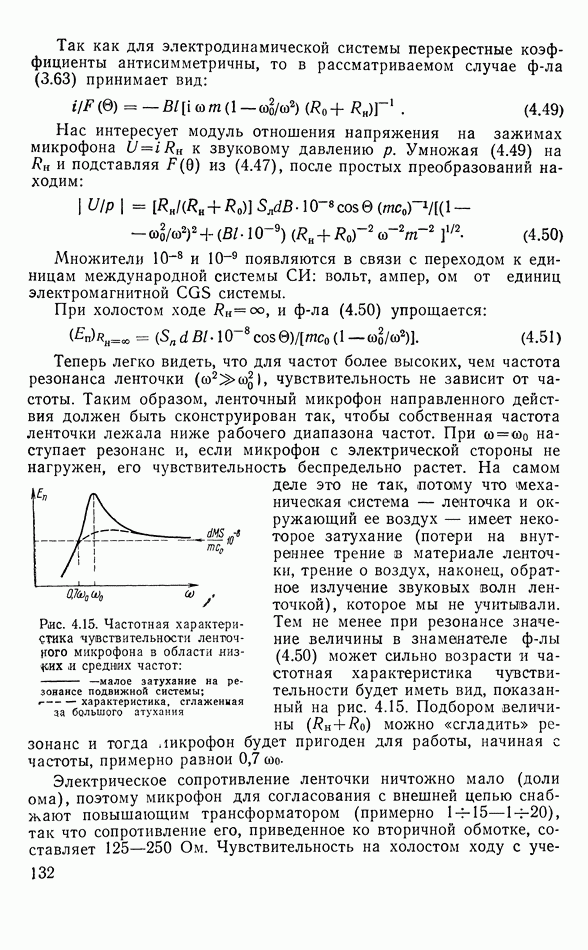
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
- Головки записи и воспроизведения
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы