| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
Общая теория обратимого электромеханического преобразователя может быть построена на основании энергетических соотношений в динамической системе с многими степенями свободы. Эти соотношения определяются функцией Лагранжа, которая представляет собой разность кинетической  потенциальной энергии системы. Каждая степень свободы характеризуется обобщенными скоростью и перемещением. Обобщенные перемещения в частном случае могут быть линейным отклонением от положения равновесия, углом поворота в механической системе или электрическим зарядом в электрической цепи и т. п. Кинетическая и потенциальная энергии системы будут квадратичными функциями обобщенных скоростей
потенциальной энергии системы. Каждая степень свободы характеризуется обобщенными скоростью и перемещением. Обобщенные перемещения в частном случае могут быть линейным отклонением от положения равновесия, углом поворота в механической системе или электрическим зарядом в электрической цепи и т. п. Кинетическая и потенциальная энергии системы будут квадратичными функциями обобщенных скоростей  и перемещений
и перемещений 
Кинетическая энергия одной изолированной  степени свободы составит 1/2 а потенциальной -
степени свободы составит 1/2 а потенциальной -  , где
, где  и
и  инерциальный и позиционный коэффициенты (масса и упругость) данной степени свободы. Если система состоит из
инерциальный и позиционный коэффициенты (масса и упругость) данной степени свободы. Если система состоит из  связанных между собой степеней свободы, то добавляются энергии связей: инерциальных —1/2 тгихгхк и позиционных -
связанных между собой степеней свободы, то добавляются энергии связей: инерциальных —1/2 тгихгхк и позиционных -  .
.
Кроме этого, можно представить себе, что среди квадратичных форм для энергии существуют и члены вида  зависящие от произведения перемещения в одной степени свободы на скорость в другой. Это так называемые гироскопические члены. Они возникают при наличии вращающихся масс в механических системах или магнитных полей — в электрических.
зависящие от произведения перемещения в одной степени свободы на скорость в другой. Это так называемые гироскопические члены. Они возникают при наличии вращающихся масс в механических системах или магнитных полей — в электрических.

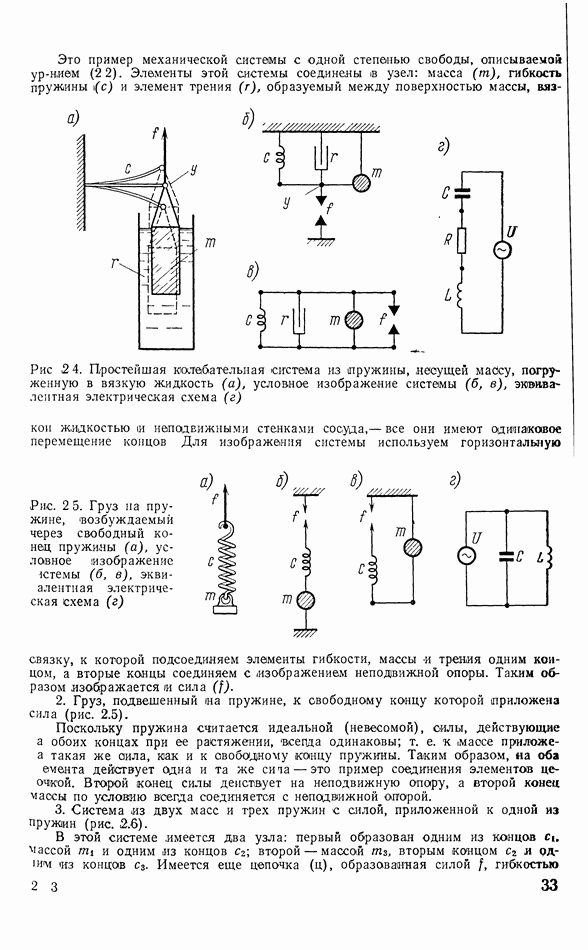
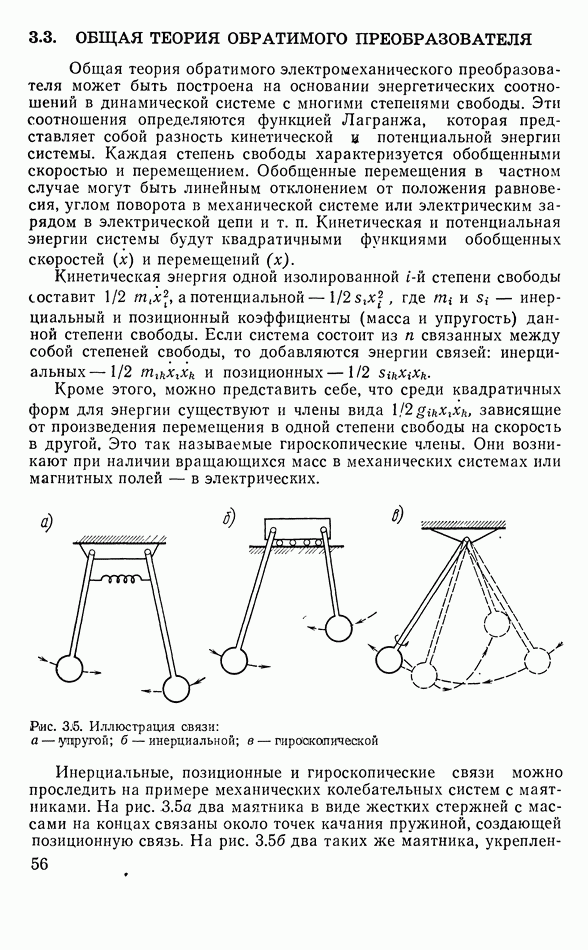
Рис. 3.5. Иллюстрация связи: а — ущругой; б - инерциальной; в — гироскопической
Инерциальные, позиционные и гироскопические связи можно проследить на примере механических колебательных систем с маятниками. На рис. 3.5 а два маятника в виде жестких стержней с массами на концах связаны около точек качания пружиной, создающей позиционную связь. На рис. 3.56 два таких же маятника,
укрепленных на массивной опоре, которая может свободно скользить по основанию, связаны инерциальной связью.
На рис. 3.5в изображен такой же маятник, который может качаться в двух направлениях: в плоскости чертежа и перпендикулярно ей. Это тоже один из видов систем с двумя степенями свободы. Гироскопическая связь в такой системе осуществляется, если массивному шару маятника сообщить момент количества движения  направленный вдоль стержня маятника. В силу закона сохранения момента количества движения, при отклонении маятника в плоскости чертежа возникнет гироскопический эффект: маятник станет двигаться также и в плоскости, перпендикулярной чертежу. Это объясняется появлением компенсирующего момента количества движения
направленный вдоль стержня маятника. В силу закона сохранения момента количества движения, при отклонении маятника в плоскости чертежа возникнет гироскопический эффект: маятник станет двигаться также и в плоскости, перпендикулярной чертежу. Это объясняется появлением компенсирующего момента количества движения  такого, что в сумме с моментом
такого, что в сумме с моментом  отклоненного маятника первоначально заданный вдоль вертикали момент
отклоненного маятника первоначально заданный вдоль вертикали момент  сохраняется. Характерно, что в первых двух случаях связи осуществляются по общей линии движения, а в третьем — по взаимно перпендикулярным линиям. Сложив кинетические энергии всех степеней свободы системы, включая и энергии связи, получим полную кинетическую энергию системы
сохраняется. Характерно, что в первых двух случаях связи осуществляются по общей линии движения, а в третьем — по взаимно перпендикулярным линиям. Сложив кинетические энергии всех степеней свободы системы, включая и энергии связи, получим полную кинетическую энергию системы  и потенциальную
и потенциальную 
Из подробного рассмотрения связи между направлениями компенсирующих моментов количества движения и поворотов маятника в его двух плоскостях качания вытекает, что коэффициенты  равны по абсолютной величине и противоположны по знаку -
равны по абсолютной величине и противоположны по знаку -  В то же время очевидно, что если инерциальные и позиционные связи отличны от нуля, то суммы коэффициентов
В то же время очевидно, что если инерциальные и позиционные связи отличны от нуля, то суммы коэффициентов  должны быть отличны от нуля, так как в выражениях для
должны быть отличны от нуля, так как в выражениях для  члены вида тгкхгхк и ткгхрхг всегда встречаются в паре друг с другом. Но тогда соответствующим выбором всегда можно сделать
члены вида тгкхгхк и ткгхрхг всегда встречаются в паре друг с другом. Но тогда соответствующим выбором всегда можно сделать  Эти свойства симметрии коэффициентов
Эти свойства симметрии коэффициентов  и антисимметрии
и антисимметрии  являются основными для теории преобразователя. Можно всегда перенормировать величины этих коэффициентов, чтобы не было необходимости писать множитель 1/2 перед двойными суммами. Тогда окончательно функция Лагранжа запишется так:
являются основными для теории преобразователя. Можно всегда перенормировать величины этих коэффициентов, чтобы не было необходимости писать множитель 1/2 перед двойными суммами. Тогда окончательно функция Лагранжа запишется так:

Если в системе имеется рассеяние энергии, то для описания ее, кроме функции  следует использовать еще функцию рассеяния:
следует использовать еще функцию рассеяния:

определяющую убыль полного запаса энергии системы в единицу времени. Наконец, если на систему действуют внешние силы, то для полного описания системы необходимо присоединить условие равенства внешних сил силам реакции со стороны системы. Найдя частные производные по координатам  от потенциальных членов, можно найти позиционные реакции, а определив скорость изменения
от потенциальных членов, можно найти позиционные реакции, а определив скорость изменения  импульсов (т. е. частных производных инерциальных членов по скоростям
импульсов (т. е. частных производных инерциальных членов по скоростям  с обратными знаками, — реакции ускорения. Все эти действия могут быть записаны с помощью одного дифференциального оператора
с обратными знаками, — реакции ускорения. Все эти действия могут быть записаны с помощью одного дифференциального оператора 
Полученная система сил реакций должна уравновешиваться внешними силами  Если в системе имеется рассеяние энергии, то частично внешние силы работают против сил, обусловленных рассеянием. Эти последние находят при помощи
Если в системе имеется рассеяние энергии, то частично внешние силы работают против сил, обусловленных рассеянием. Эти последние находят при помощи  дифференцированием по скорости
дифференцированием по скорости  В результате известные уравнения Лагранжа записываются:
В результате известные уравнения Лагранжа записываются:

Эти уравнения остаются формально правильными не только, когда введенные величины  имеют размерности механических перемещений сил, масс, упругостей и коэффициентов линейного трения, но и во всех случаях, когда
имеют размерности механических перемещений сил, масс, упругостей и коэффициентов линейного трения, но и во всех случаях, когда  имеет размерность энергии,
имеет размерность энергии,  мощности,
мощности,  и описывают соответственно внешние воздействия и положения некоторых избранных независимых величин, характеризующих систему. Поэтому
и описывают соответственно внешние воздействия и положения некоторых избранных независимых величин, характеризующих систему. Поэтому  носят название «обобщенных» сил и координат соответственно.
носят название «обобщенных» сил и координат соответственно.
Подставив (3.23) и (3.24) в (3.25), получим 

где
Ограничиваясь случаем периодического синусоидального движения и полагая  имеем:
имеем:  Тогда из (3.27) получим
Тогда из (3.27) получим  уравнений вида:
уравнений вида: 

где 
Коэффициенты  распадаются на суммы симметричных слагаемых:
распадаются на суммы симметричных слагаемых:

а антисимметричных:

Динамическая система может быть весьма сложной — обладать большим числом степеней свободы. Однако при рассмотрении свойств преобразователя нас, как правило, интересуют только две из всех независимых степеней свободы системы: это те, к которым прикладываются внешние воздействия или реакции других систем. Все остальные степени свободы преобразователя являются внутренними — к ним не прикладываются воздействия извне. Тогда вся система  уравнений будет состоять из
уравнений будет состоять из  однородных уравнений (для которых
однородных уравнений (для которых  и двух уравнений с правой частью:
и двух уравнений с правой частью:

Путем исключения  из интересующих нас скоростей
из интересующих нас скоростей  система (3.30) может быть сведена к системе двух уравнений:
система (3.30) может быть сведена к системе двух уравнений:

Новые коэффициенты  выражаются через
выражаются через  системы (3.30). При этом можно показать, что в силу соотношений (3.29) для
системы (3.30). При этом можно показать, что в силу соотношений (3.29) для  сохраняется аналогичное свойство:
сохраняется аналогичное свойство:

В дальнейшем будем интересоваться только системой (3.31), поэтому для удобства записи опустим штрихи у коэффициентов этой новой системы.
Система ур-ний (3.31) содержит основные соотношения, на которых базируется теория двустороннего линейного обратимого преобразователя. Она показывает, что обобщенная сила, приложенная к одной из сторон преобразователя, линейно связана с обобщенными скоростями на обеих сторонах его. Зная коэффициенты  можно определить, какие силы
можно определить, какие силы  должны действовать на преобразователь, чтобы получить желаемые обобщенные скорости
должны действовать на преобразователь, чтобы получить желаемые обобщенные скорости 
Из системы ур-ний (3.31) следует, что не обязательно знать конкретное устройство преобразователя — его схему. Достаточно измерить коэффициенты  чтобы полностью определить его поведение.
чтобы полностью определить его поведение.
Если необходимо определить скорости  по заданным силам, то систему (3.31) следует разрешить относительно
по заданным силам, то систему (3.31) следует разрешить относительно 

Общие правила решения линейных уравнений позволяют найти у

Из рассмотрения общих свойств динамической системы, внутри которой нет собственных источников энергии, можно получить, что  всегда положительно. Соотношения (3.34) приводят к тому, что так же, как и в системе (3.31), в новой системе (3.33) соблюдается соотношение:
всегда положительно. Соотношения (3.34) приводят к тому, что так же, как и в системе (3.31), в новой системе (3.33) соблюдается соотношение:

Системы ур-ний (3.31) и (3.33) являются основными для теории двустороннего преобразователя. Свойства перекрестных коэффициентов (3.32) и (3.36) в этих уравнениях объясняют, почему в преобразователях различных систем могут появиться коэффициенты связи симметричные и антисимметричные. Если в системе нет гироскопических связей  то
то  Если, наоборот, связь только гироскопическая, то
Если, наоборот, связь только гироскопическая, то  Последний случай соответствует таким электромеханическим преобразователям, в которых связь осуществляется через магнитные поля, где силы взаимодействия направлены по нормали к движению зарядов и к магнитным силовым линиям, а первый случай
Последний случай соответствует таким электромеханическим преобразователям, в которых связь осуществляется через магнитные поля, где силы взаимодействия направлены по нормали к движению зарядов и к магнитным силовым линиям, а первый случай  преобразователям со связью через электрическое поле, где силы взаимодействия направлены по движению зарядов и по направлению поля.
преобразователям со связью через электрическое поле, где силы взаимодействия направлены по движению зарядов и по направлению поля.
Отметим, что общее выражение для коэффициентов  показывает, что возможен такой преобразователь, который работает только «в одну сторону». Если, например,
показывает, что возможен такой преобразователь, который работает только «в одну сторону». Если, например,  то
то  Сила
Сила  приложенная на «первой» стороне, вызывает скорость
приложенная на «первой» стороне, вызывает скорость  но не вызывает скорости
но не вызывает скорости  «на второй», а сила
«на второй», а сила  вызывает как скорость
вызывает как скорость  на своей стороне, так и на другой —
на своей стороне, так и на другой —  Очевидно, что можно осуществить такую систему, комбинируя электростатический и электродинамический преобразователи.
Очевидно, что можно осуществить такую систему, комбинируя электростатический и электродинамический преобразователи.
На практике всегда приходится иметь дело либо со случаем симметрии  либо антисимметрии
либо антисимметрии  в электромеханическом преобразователе, поэтому далее будем считать, что в системе (3.31) или (3.33) только три коэффициента независимы, например
в электромеханическом преобразователе, поэтому далее будем считать, что в системе (3.31) или (3.33) только три коэффициента независимы, например 
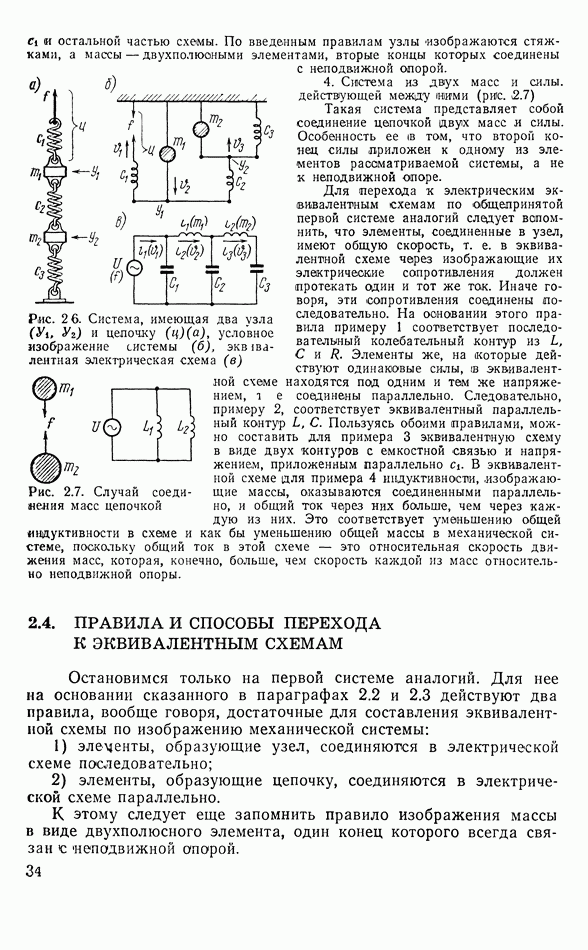
Двусторонняя механическая система условно изображена на рис. 3.6. Сама система изображается в виде «ящика», из которого выступают два стержня (I и II).

Рис. 3 6 Условное изображение двусторонней механической системы

Рис. 3.7. Электрический четырехполюсник
Стержни могут перемещаться, колеблясь вдоль себя. Внешняя сила, приложенная к стержню  изображена стрелкой
изображена стрелкой  и скорость на этой же стороне — стрелкой Аналогичные обозначения имеются для стержня
и скорость на этой же стороне — стрелкой Аналогичные обозначения имеются для стержня  Стержни
Стержни  и II связаны с какой-то динамической системой внутри ящика так, что при действии, например, силы
и II связаны с какой-то динамической системой внутри ящика так, что при действии, например, силы  возникает движение как стержня I, так и стержня II. Таким образом, энергия колебаний со стороны
возникает движение как стержня I, так и стержня II. Таким образом, энергия колебаний со стороны  может передаваться на сторону II и обратно.
может передаваться на сторону II и обратно.
Уравнения (3.31) и (3.33) на основании сказанного выше о свойствах обобщенных координат и скоростей остаются в силе и для электрической двусторонней системы. Изображение такой электрической системы представлено на рис. 3.7. Здесь роль сил и скоростей играют напряжения  и токи
и токи  В электронике и теории электрической связи такое устройство называется четырехполюсником.
В электронике и теории электрической связи такое устройство называется четырехполюсником.
Коэффициенты  или
или  могут быть получены из опыта. Например, освободим систему на стороне II (рис. 3.6), т. е. сделаем
могут быть получены из опыта. Например, освободим систему на стороне II (рис. 3.6), т. е. сделаем  и приложим известную силу на стороне
и приложим известную силу на стороне  Тогда, измерив и
Тогда, измерив и  на основании (3.33) получим:
на основании (3.33) получим:

Приложив теперь силу с другой стороны, найдем:

Точно так же, используя системы ур-ний (3.31), можно определить:

Условие  означает, что соответствующая сторожа системы заторможена. В случае электрической системы опыты для определения коэффициентов у потребуют короткого замыкания зажимов одной стороны, а для определения коэффициентов
означает, что соответствующая сторожа системы заторможена. В случае электрической системы опыты для определения коэффициентов у потребуют короткого замыкания зажимов одной стороны, а для определения коэффициентов  холостого хода на одной стороне.
холостого хода на одной стороне.

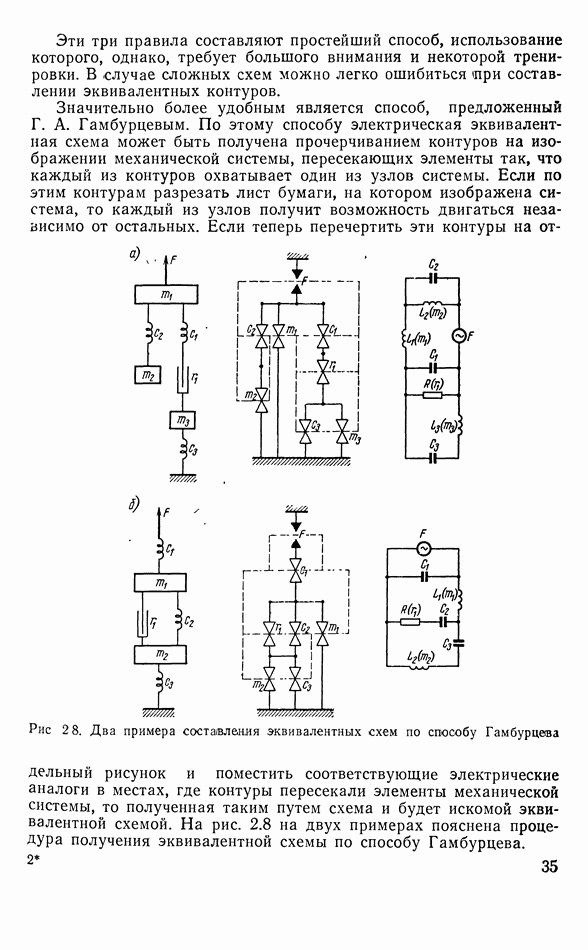
Рис. 3.8. Смешанная система (двусторонний преобразователь)
Наиболее интересным случаем является смешанная система, в которой одна сторона электрическая, а другая — механическая. Такая система и является двусторонним электромеханическим преобразователем. Она условно изображается так, как показано на рис. 3.8.
Приведем еще некоторые важные формы уравнений двусторонней системы:
Форма а. Предположим, что известен режим системы на стороне II, т. е., зная величины  надо найти величины и
надо найти величины и  Тогда уравнения системы удобно записать так:
Тогда уравнения системы удобно записать так:

Коэффициенты  можно выразить через
можно выразить через 

По условию  и тогда из (3.40) следует
и тогда из (3.40) следует

Итак, форма а обладает следующим свойством: определитель, составленный из коэффициентов а, равен отрицательной единице.
Если известен режим на стороне I, т. е. задана  то удобно использовать форму
то удобно использовать форму  уравнений двусторонней системы:
уравнений двусторонней системы:

Переход к форме  от формы а выполняется так же, как и переход от формы
от формы а выполняется так же, как и переход от формы  к форме у:
к форме у:

При помощи форм  можно рассчитать поведение преобразователя в различных режимах нагрузки его сторон.
можно рассчитать поведение преобразователя в различных режимах нагрузки его сторон.
Подчеркнем, что все полученные ф-лы (3.31) - (3.43) относятся к преобразователю, не имеющему внутри источников энергии, к так называемому пассивному линейному обратимому двустороннему преобразователю.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
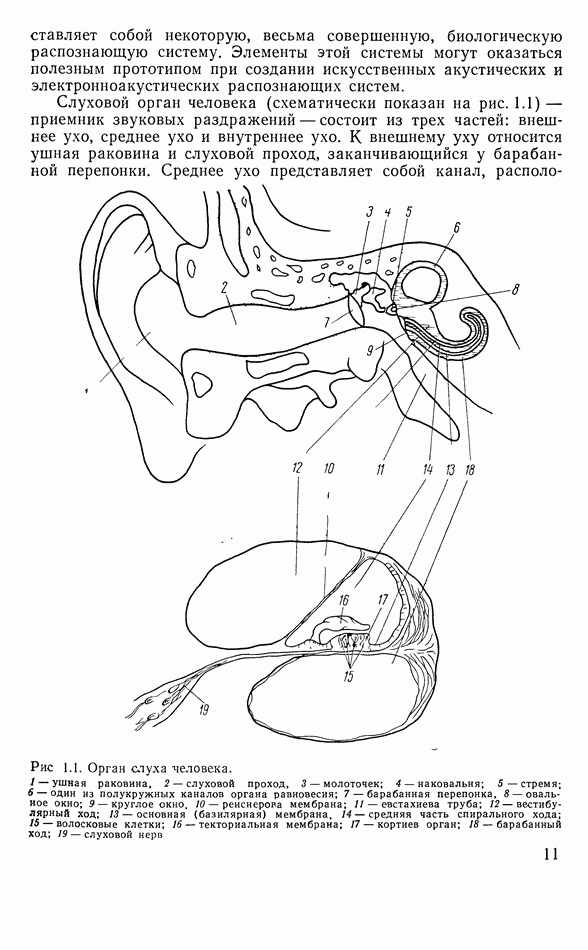
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
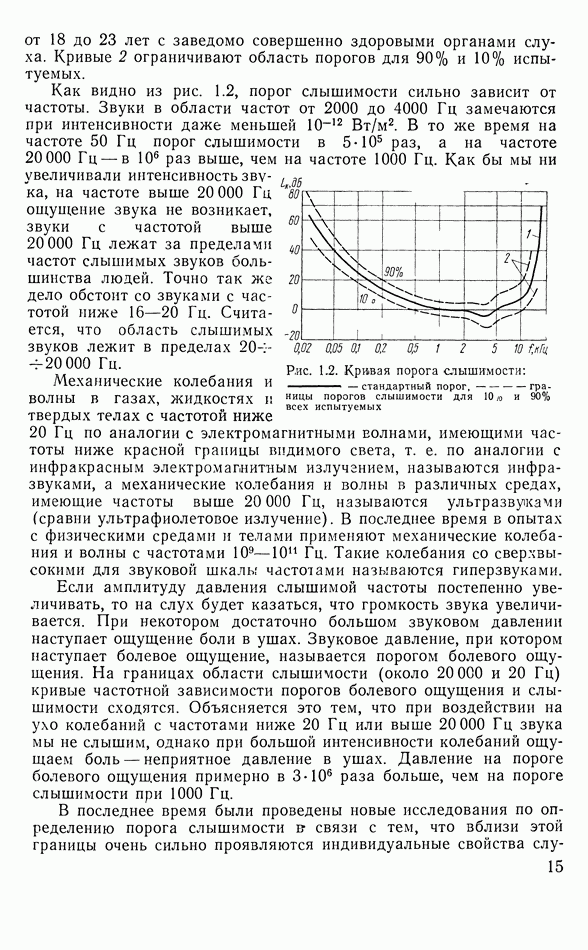
- 1.4. ПОРОГ СЛЫШИМОСТИ
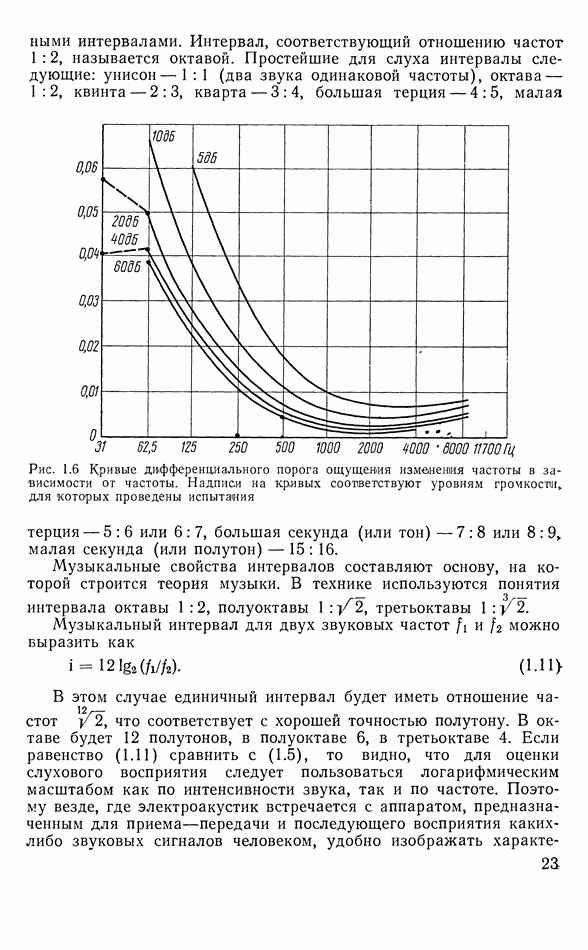
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
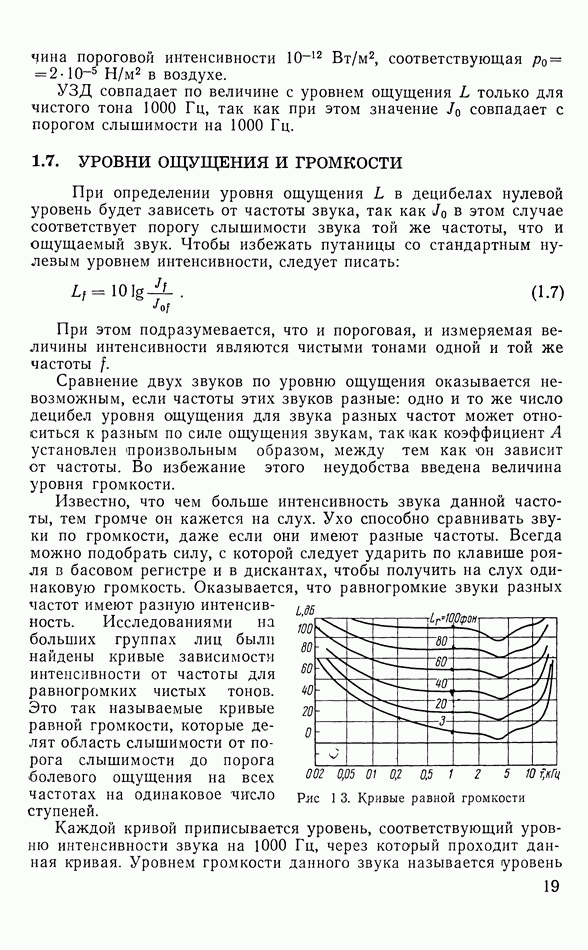
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
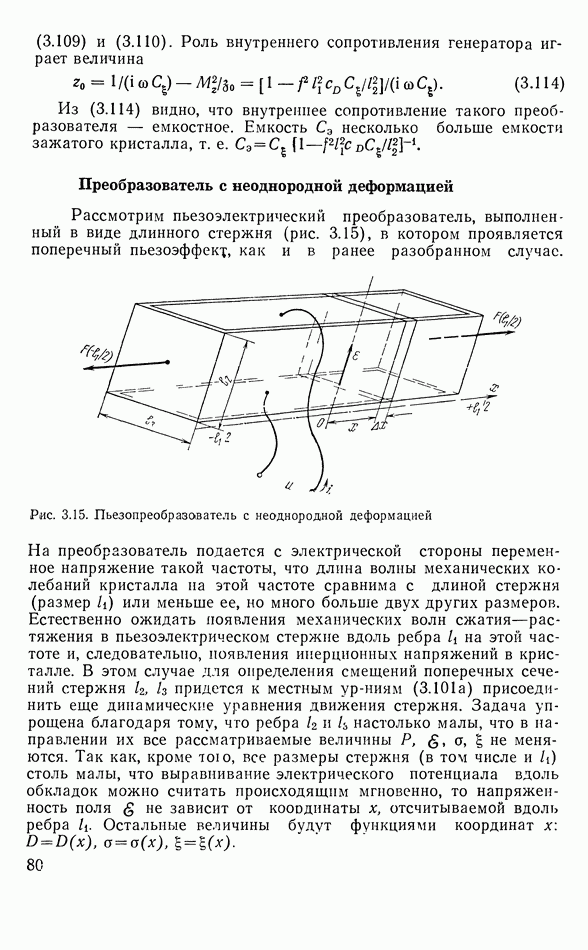
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
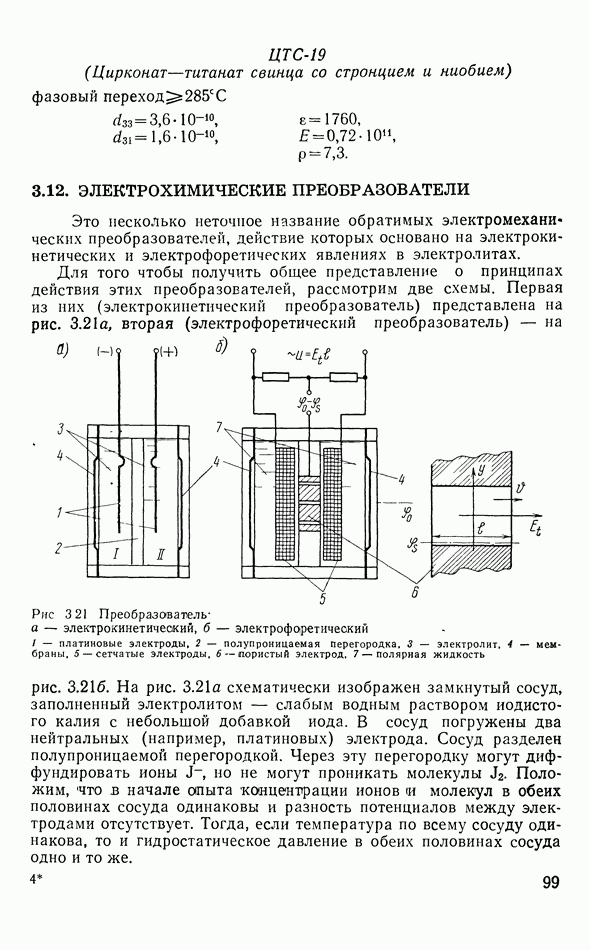
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
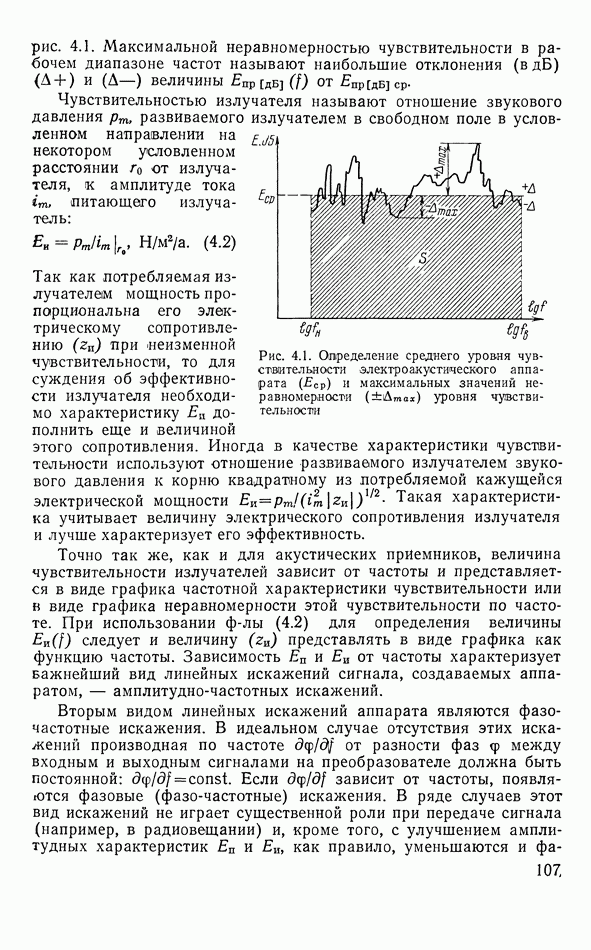
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
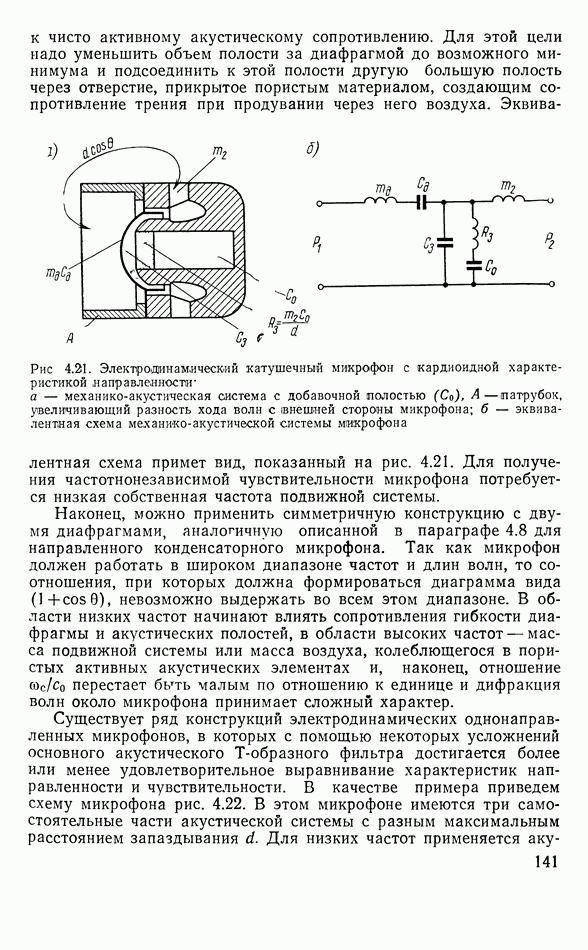
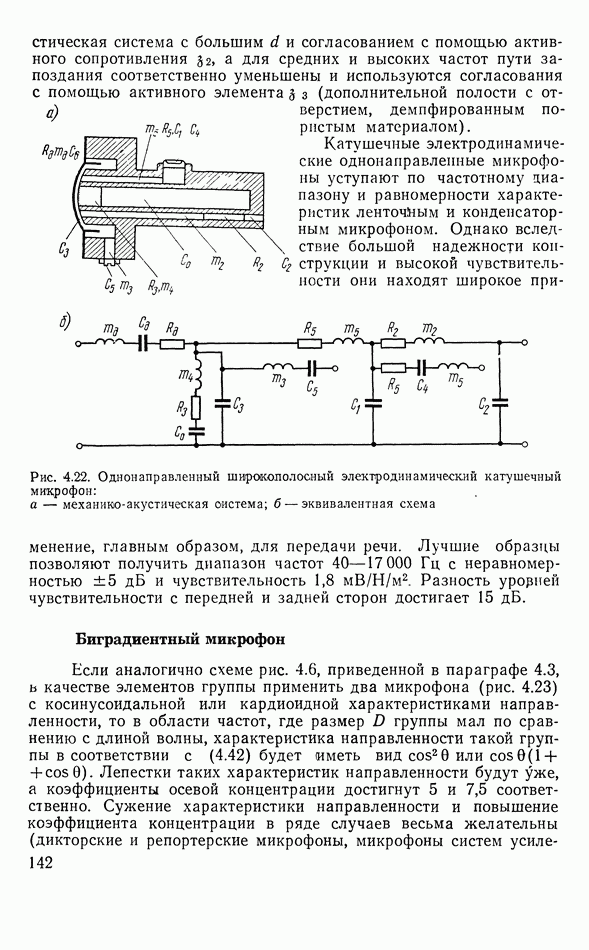
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
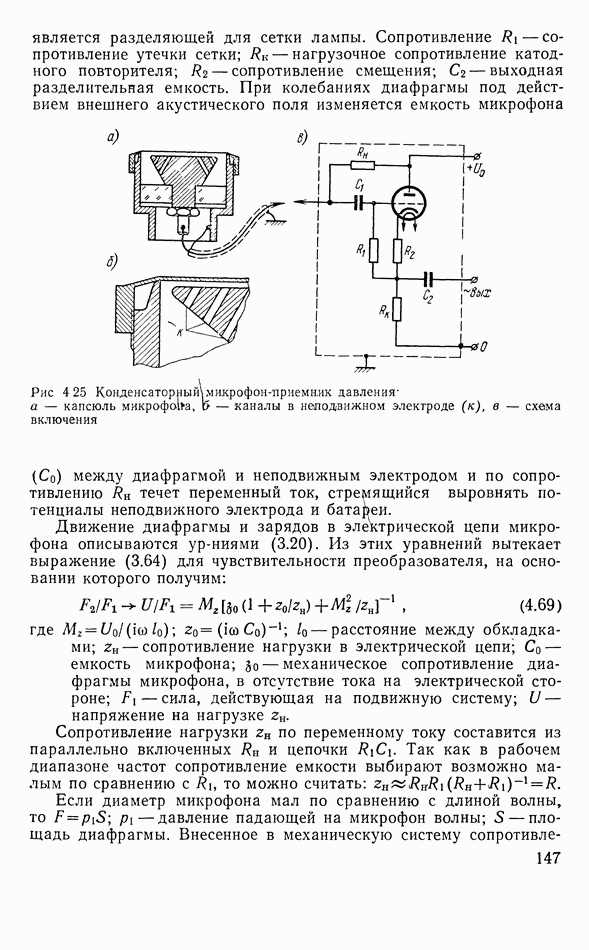
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
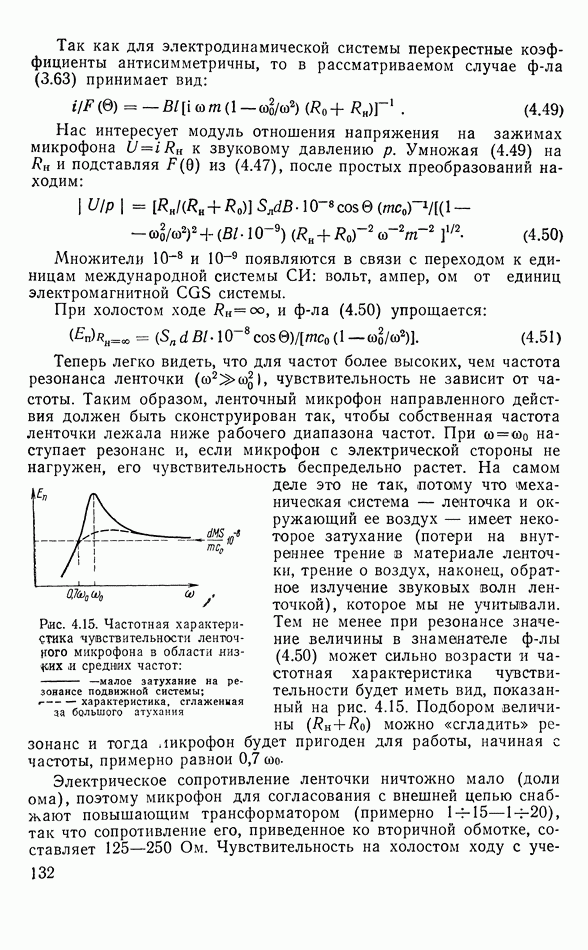
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
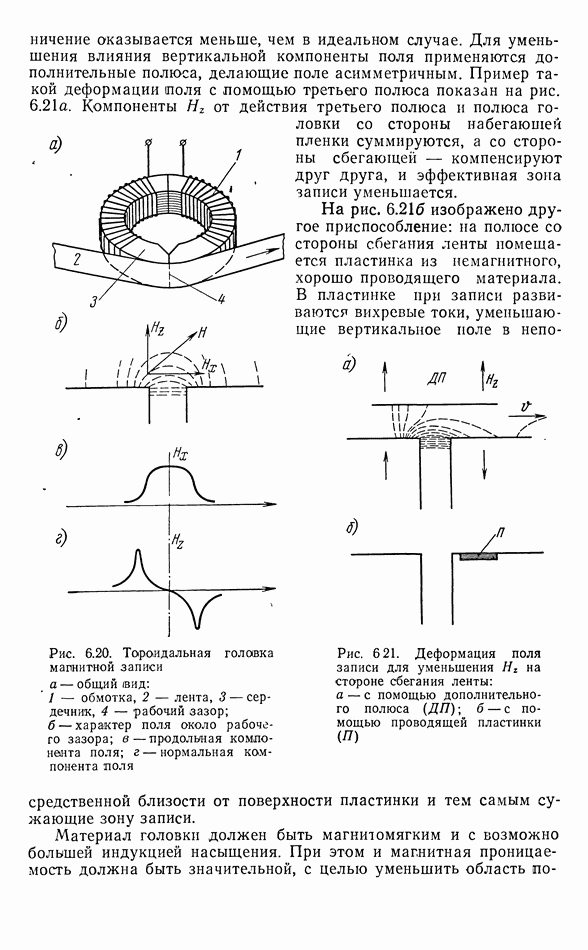
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
- Головки записи и воспроизведения
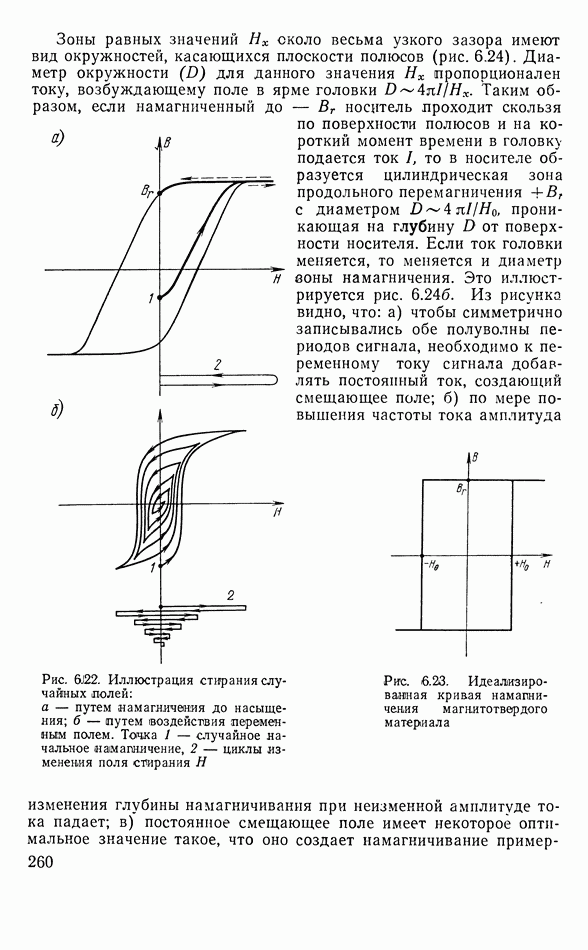
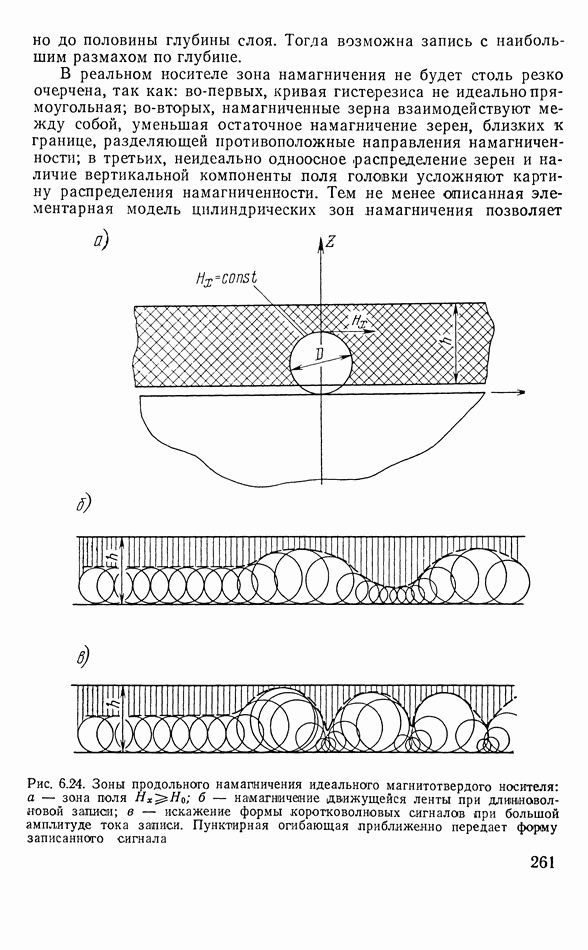
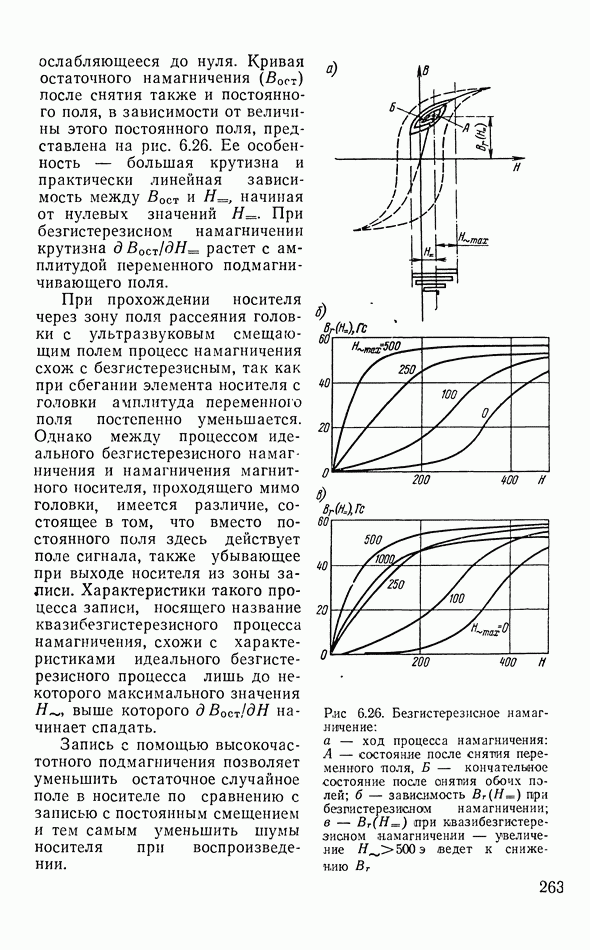
- Процесс намагничения магнитной ленты полем головки
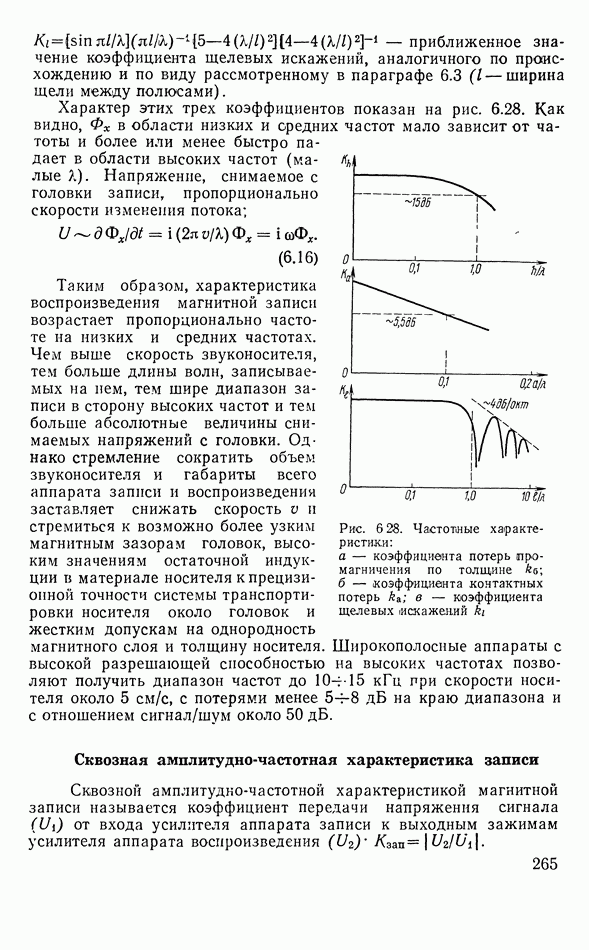
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
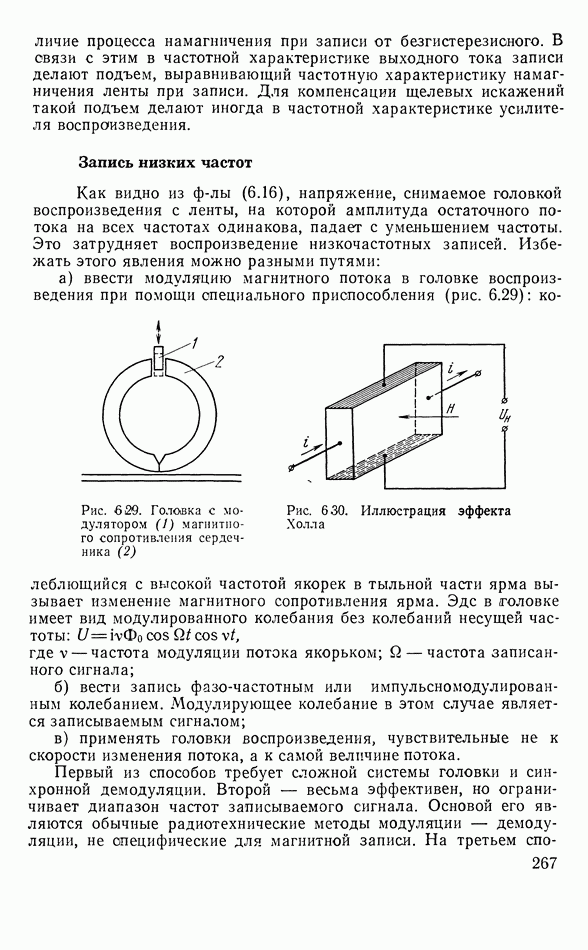
- Запись низких частот
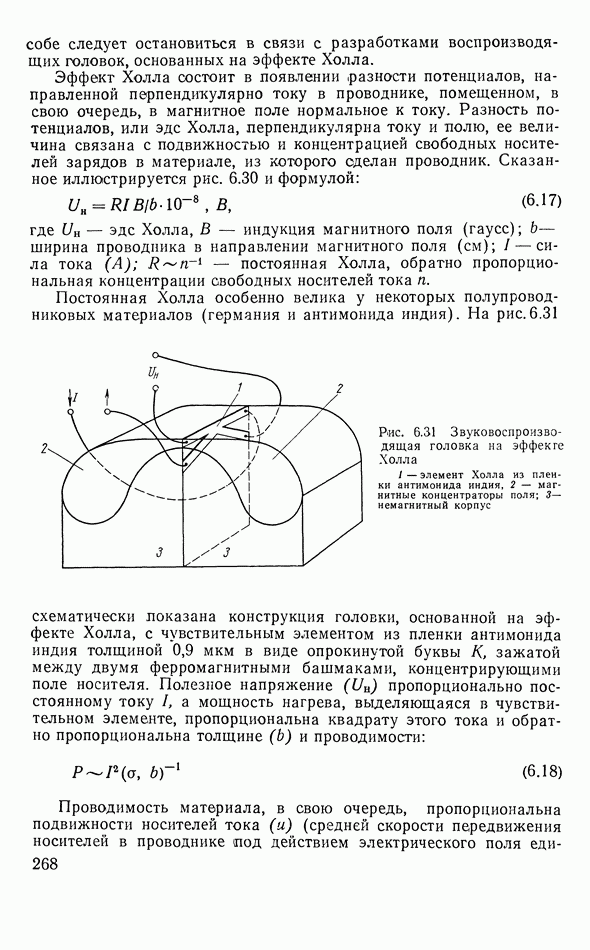
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы