| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Сопротивление излучения антенны
Сопротивление излучения антенны в общем случае имеет комплексный характер  Его активная составляющая позволяет вычислить излучаемую антенной мощность, если известна скорость опорной точки
Его активная составляющая позволяет вычислить излучаемую антенной мощность, если известна скорость опорной точки 

С другой стороны, мощность излучения антенны на основании (4.15) и (4.16) может быть представлена как

где  давление на оси антенны на расстоянии
давление на оси антенны на расстоянии 
Сравнивая (4.24) и (4.25), получим:

Это выражение дает связь между сопротивлением излучения, коэффициентом концентрации и чувствительностью антенны как излучателя.
Активное сопротивление излучения антенны может быть в ряде случаев вычислено довольно простым способом. Если известно звуковое давление, которое развивает в заданной точке пространства «элементарный» источник, расположенный на поверхности антенны, то можно подсчитать полное давление, развиваемое всей антенной в любой точке пространства. Под элементарным источником понимаем излучатель малой поверхности  в пределах которой колебательная скорость
в пределах которой колебательная скорость  на поверхности антенны однородна. Давление, развиваемое таким источником при единичной объемной скорости
на поверхности антенны однородна. Давление, развиваемое таким источником при единичной объемной скорости  — так называемая функция источника, зависит от координат точки на поверхности, обозначенных нами для простоты через
— так называемая функция источника, зависит от координат точки на поверхности, обозначенных нами для простоты через  , и координат точки поля
, и координат точки поля  отсчитываемых от центра антенны. Тогда:
отсчитываемых от центра антенны. Тогда:

В ряде случаев функция источника  оказывается очень простым выражением. Так, если антенна представляет собой часть бесконечной плоскости, остальная поверхность которой — жесткий неподвижный экран, так что излучение антенны происходит в полупространство, то
оказывается очень простым выражением. Так, если антенна представляет собой часть бесконечной плоскости, остальная поверхность которой — жесткий неподвижный экран, так что излучение антенны происходит в полупространство, то

где  модуль радиуса вектора с началом в точке
модуль радиуса вектора с началом в точке  антенны и концом в точке поля
антенны и концом в точке поля 
Для точек пространства, весьма удаленных от излучателя  при вычислении интеграла (4.27) можно считать, что модуль
при вычислении интеграла (4.27) можно считать, что модуль  стоящий в знаменателе (4.28), не зависит от
стоящий в знаменателе (4.28), не зависит от  и просто равен
и просто равен  расстоянию центра антенны от точки поля
расстоянию центра антенны от точки поля  и что все
и что все  параллельны
параллельны  Тогда в этом частном случае, опуская временной множитель, получим:
Тогда в этом частном случае, опуская временной множитель, получим:

В этой удаленной точке интенсивность излучения может быть принята равной  а полная мощность излучения
а полная мощность излучения

где интеграл берется по полусфере с центром в определяющей точке антенны. На основании (4.24) и (4.30) можно теперь вычис лить  При помощи (4.29) и (4.30) можно также найти характеристику направленности и коэффициент концентрации соответст венно.
При помощи (4.29) и (4.30) можно также найти характеристику направленности и коэффициент концентрации соответст венно.
Реактивную составляющую сопротивления излучения в ряде случаев можно определить, рассматривая течение среды, образующееся около антенны так, как если бы эта среда была
несжимаемой. Однако такой подход возможен лишь тогда, когда размеры антенны заведомо малы по сравнению с длиной волны. В общем случае требуется решить задачу о распространении волн в среде при заданных условиях на границе антенны. Наконец, если известно выражение для  то с помощью (4.27) можно найти
то с помощью (4.27) можно найти  давление на самой антенне. Тогда, интегрируя
давление на самой антенне. Тогда, интегрируя  в пределах площади антенны, можно получить полную силу реакции поля
в пределах площади антенны, можно получить полную силу реакции поля  Отсюда следует:
Отсюда следует:

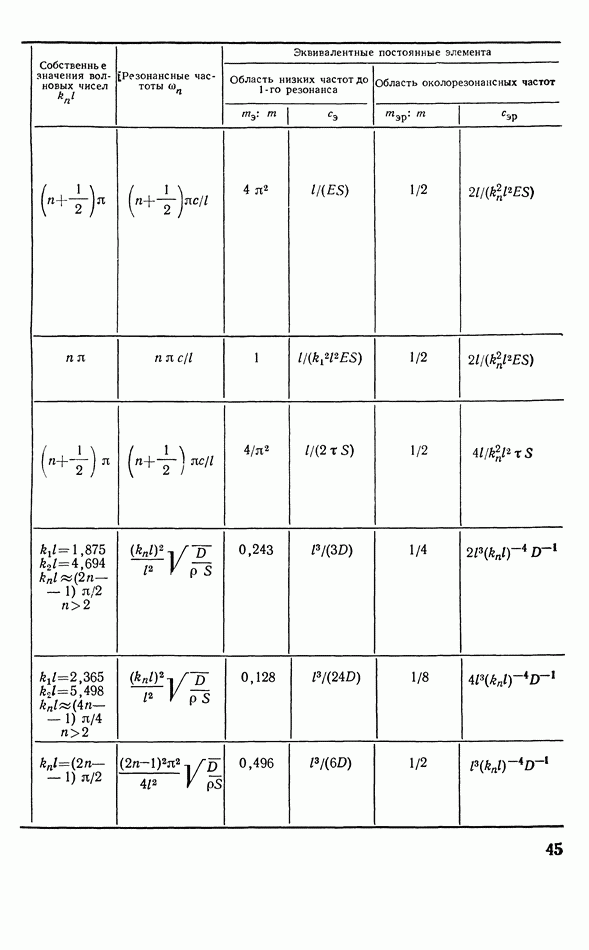
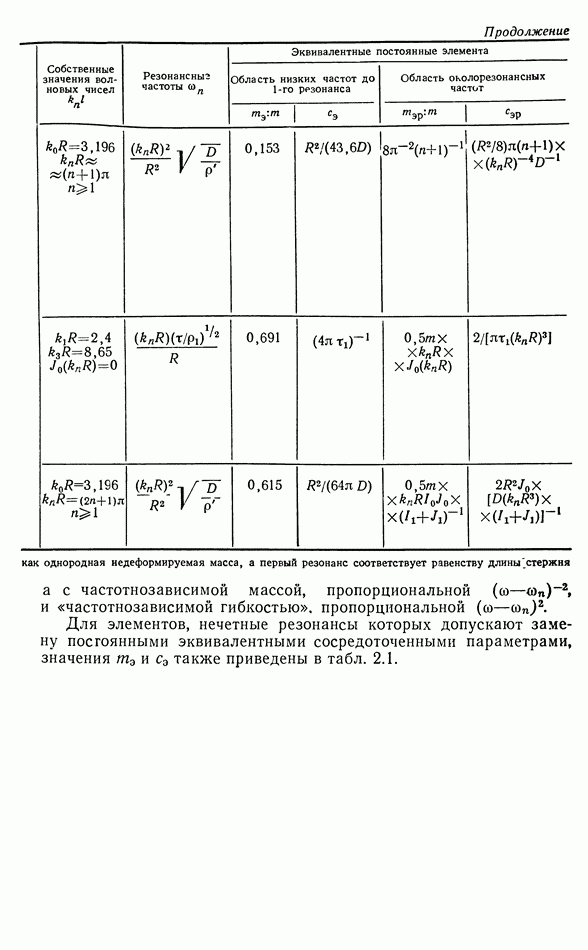
Указать универсальную простую процедуру для нахождения полного сопротивления излучения антенны невозможно. Приведем ниже сводку сопротивлений излучения некоторых простых антенн, часто используемых в инженерных расчетах. В сводке даны удельные коэффициенты сопротивления излучения на единицу излучающей площади антенны. Для перехода к механическому сопротивлению коэффициенты, данные в сводке, следует умножить на  волновое сопротивление среды, в которую излучает антенна, 5 — площадь антенны. Коэффициенты даны как функции произведения волнового числа и характерных размеров антенны:
волновое сопротивление среды, в которую излучает антенна, 5 — площадь антенны. Коэффициенты даны как функции произведения волнового числа и характерных размеров антенны:
1. Сферическая пульсирующая антенна радиуса 

2. Сферическая осциллирующая антенна радиуса 

3. Пульсирующая антенна, линейные размеры которой малы по сравнению с длиной волны:

4. Плоский круглый поршень, находящийся в неподвижном плоском экране:

 функции Бесселя и Струве первого порядка, а — радиус поршня.
функции Бесселя и Струве первого порядка, а — радиус поршня.
5. Малый круглый поршень, колеблющийся без экрана:

 площадь поршня.
площадь поршня.
6. Малый круглый поршень, колеблющийся без экрана, но только одной своей стороной:

7. Антенна из двух противофазно пульсирующих антенн малых линейных размеров и находящихся на малом расстоянии друг от друга по сравнению с длиной волны:

d - расстояние между антеннами,  см.
см. 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
- 1.4. ПОРОГ СЛЫШИМОСТИ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
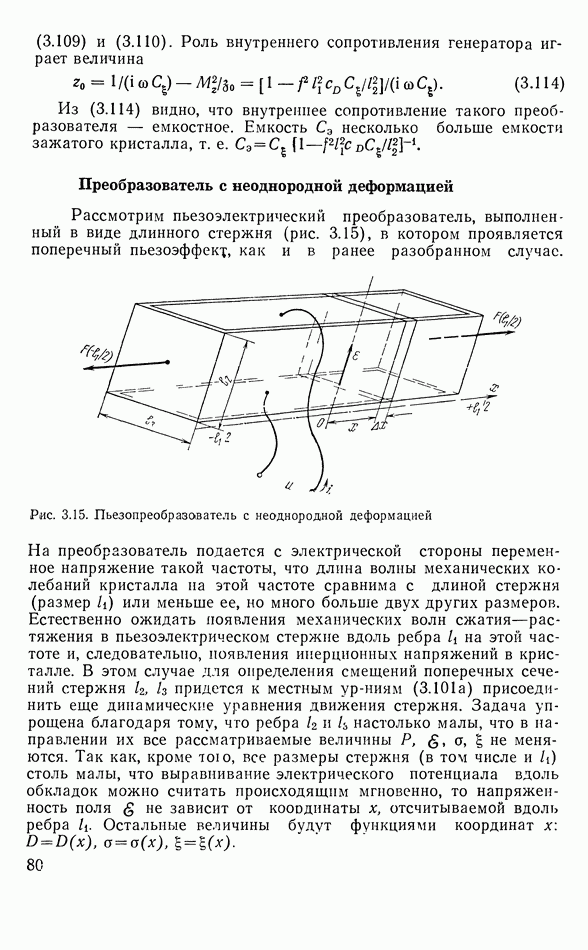
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
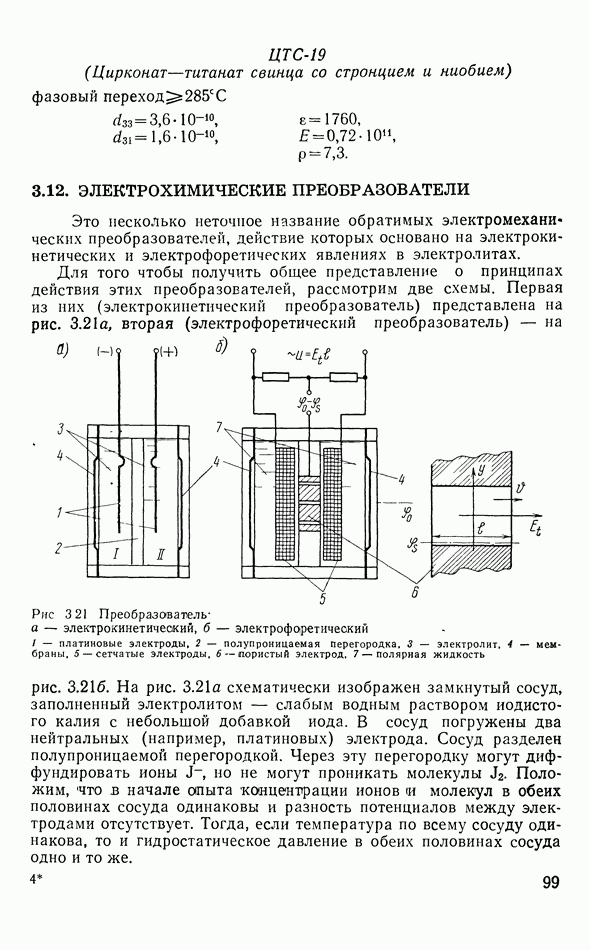
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
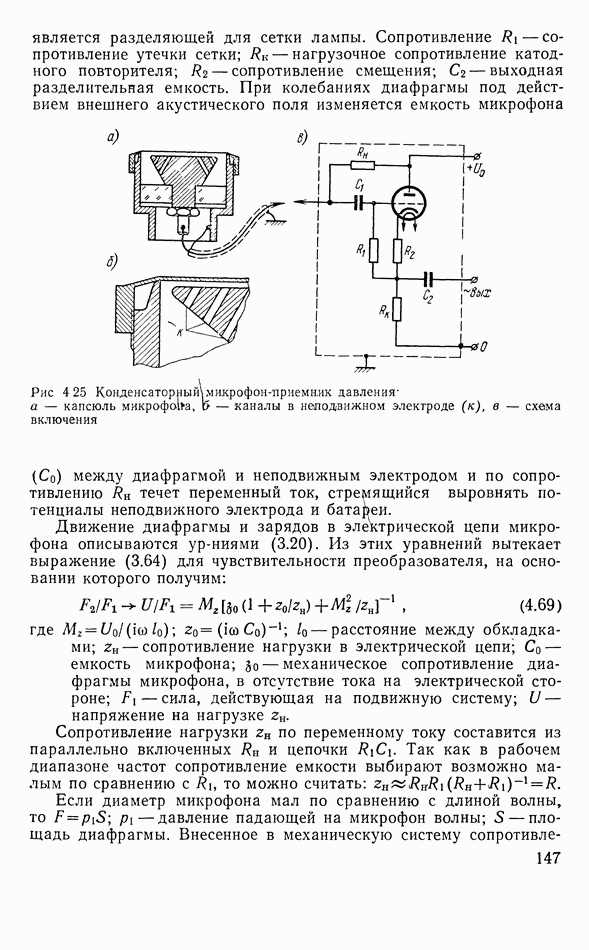
- Ненаправленный микрофон-приемник давления
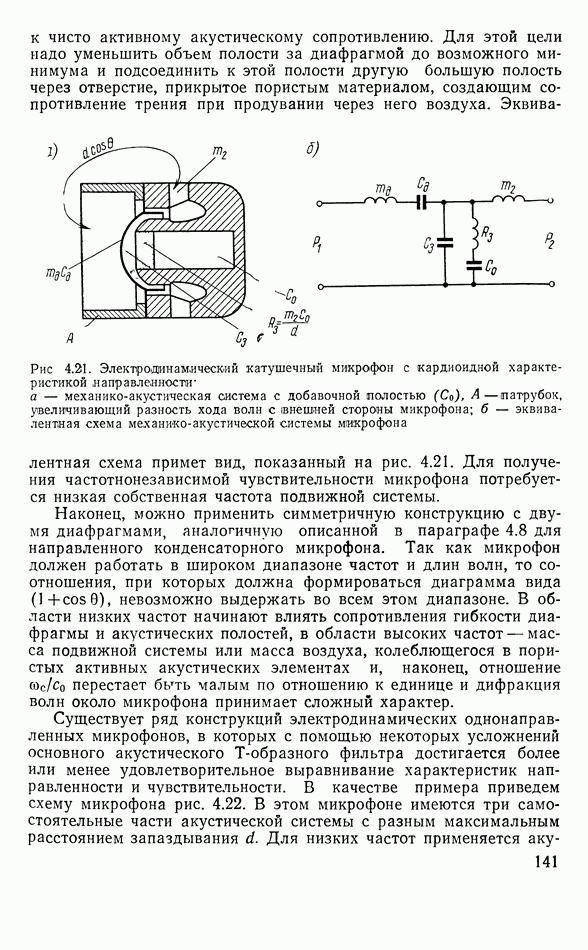
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
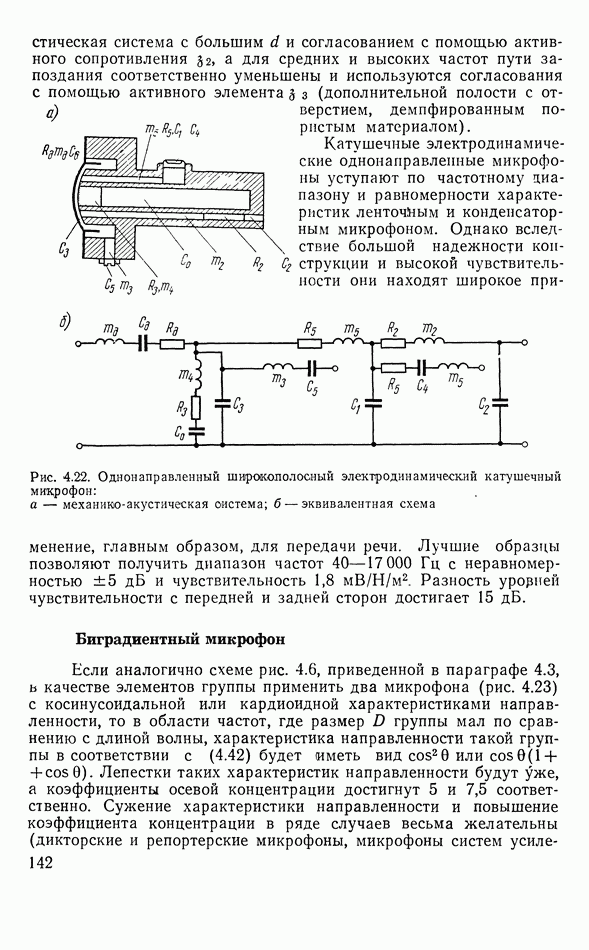
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
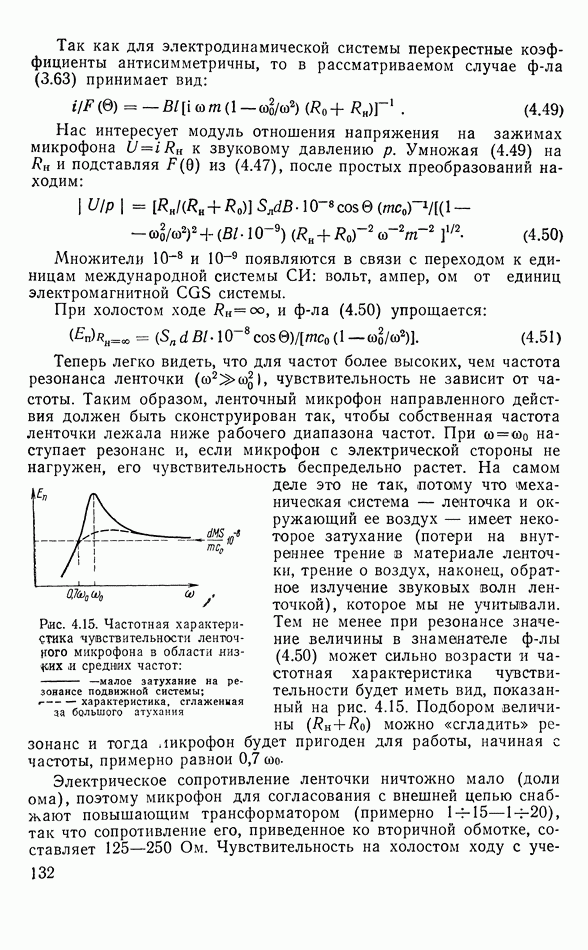
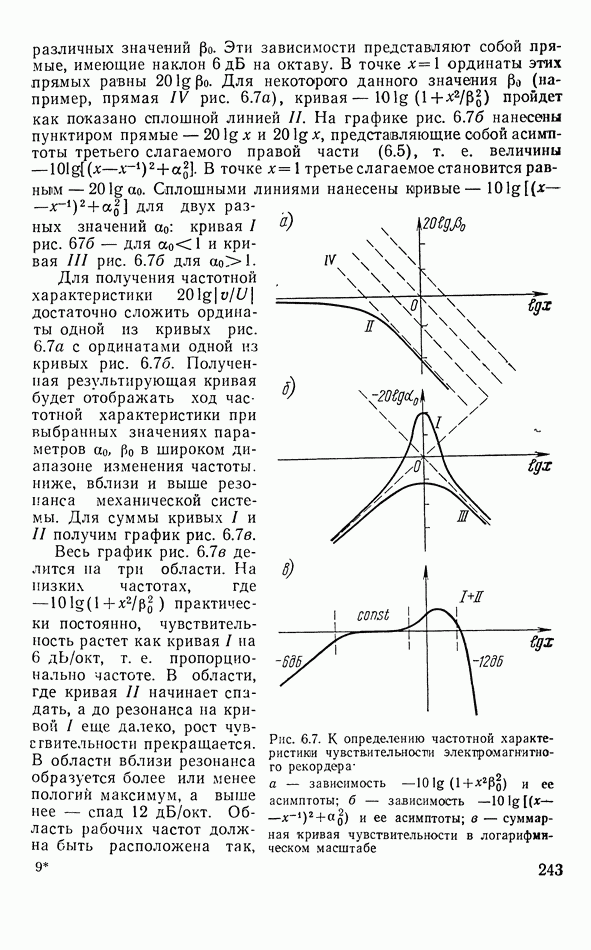
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
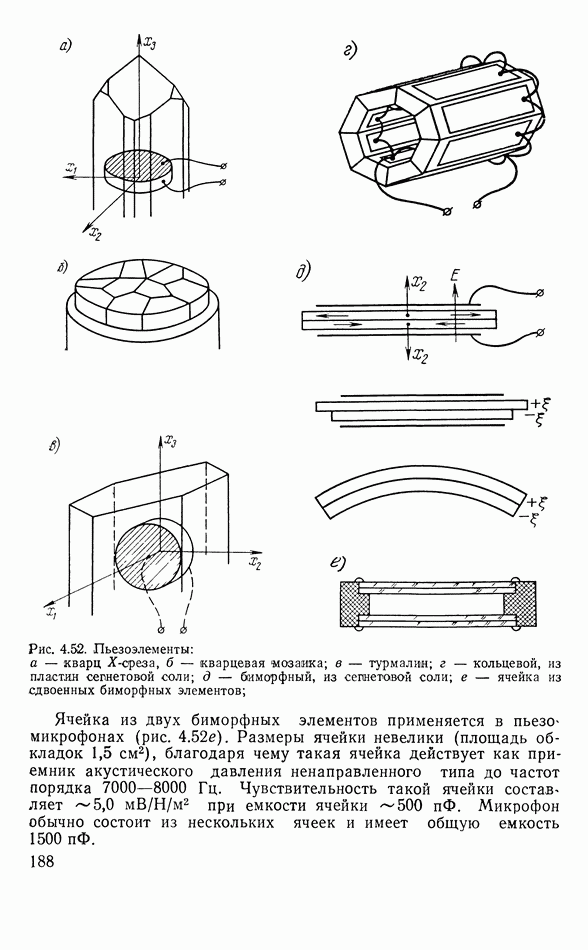
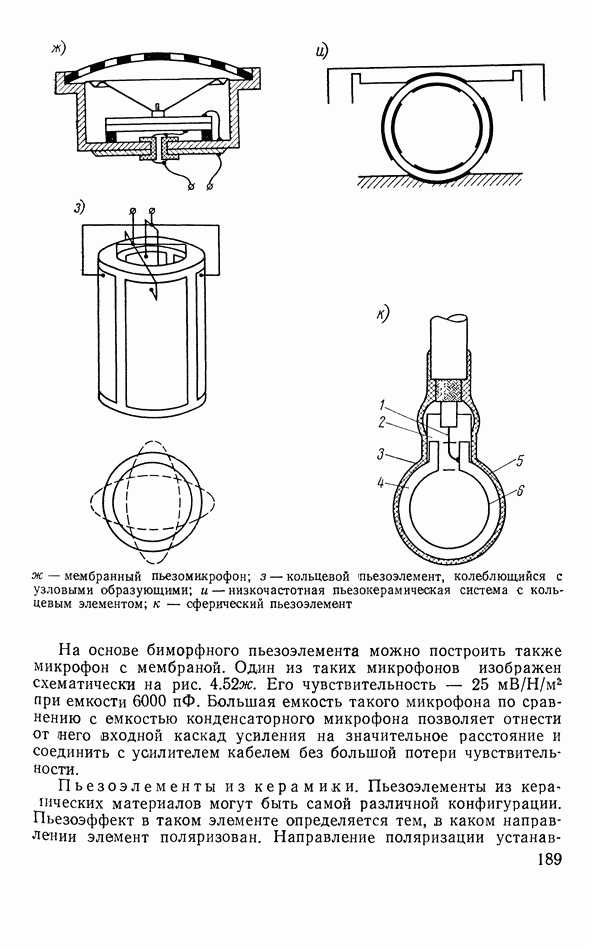
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
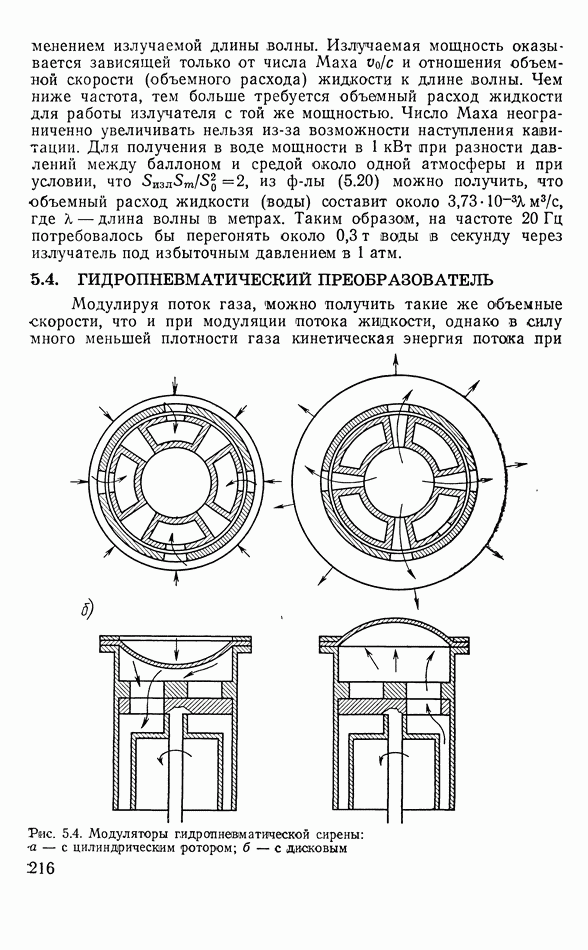
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
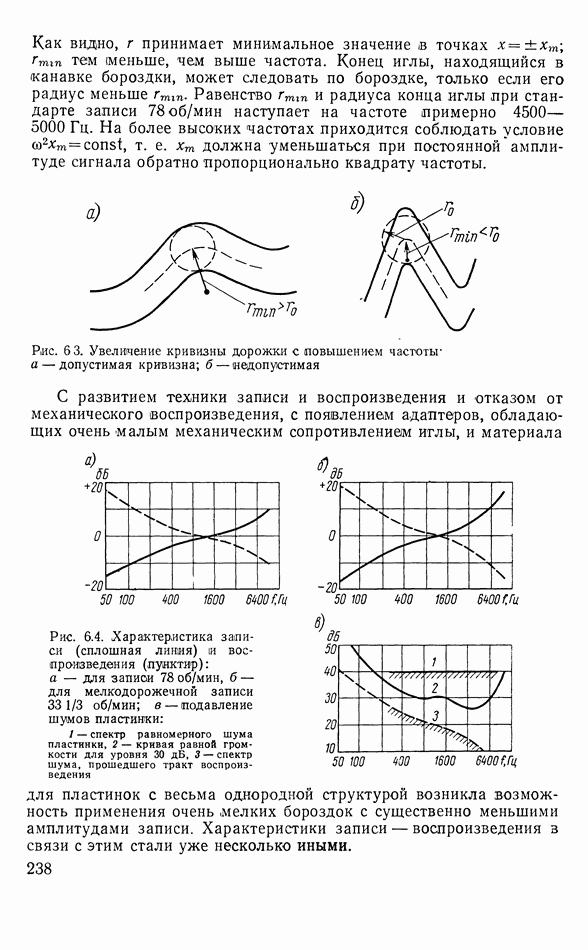
- Краткие сведения о звукоснимателях
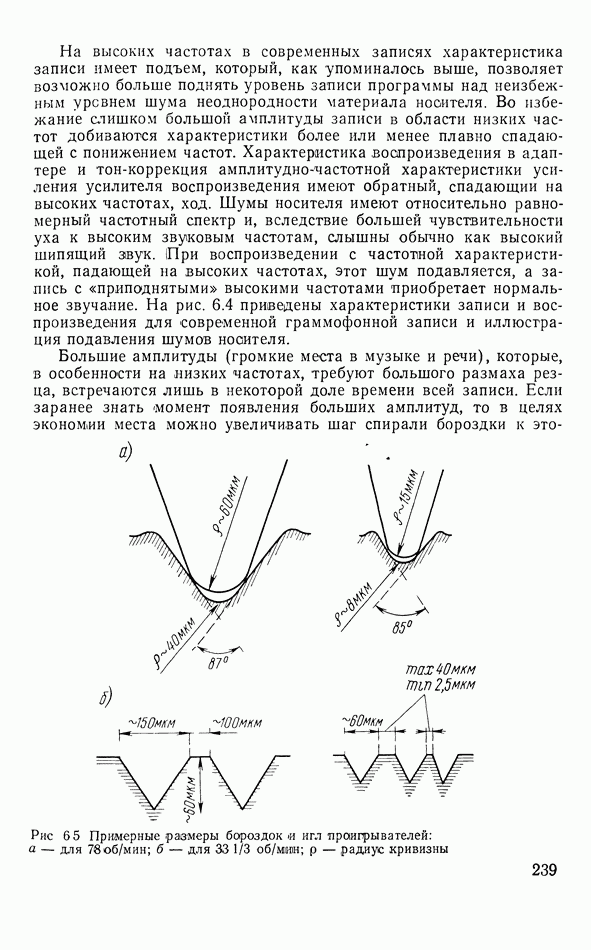
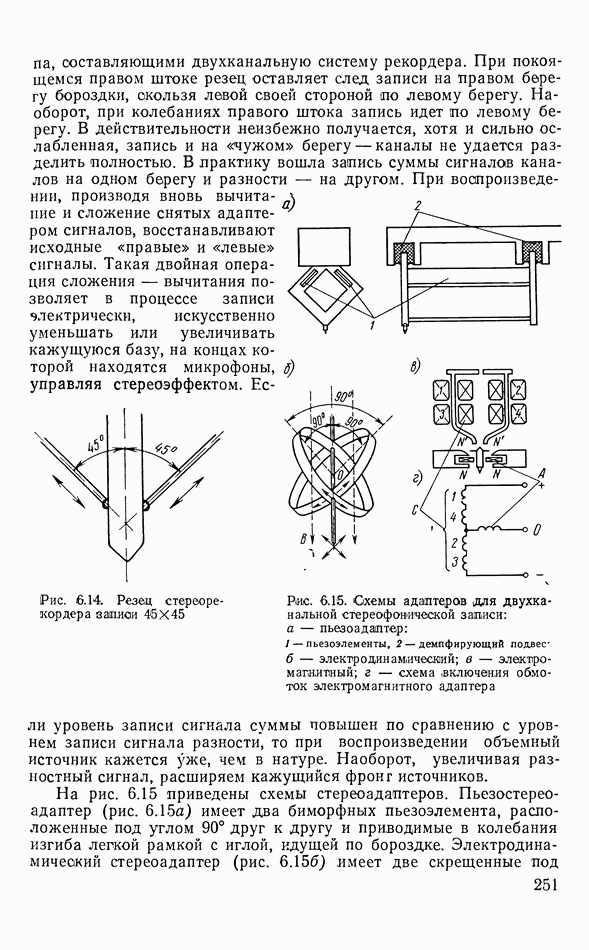
- Стереограммофонная запись
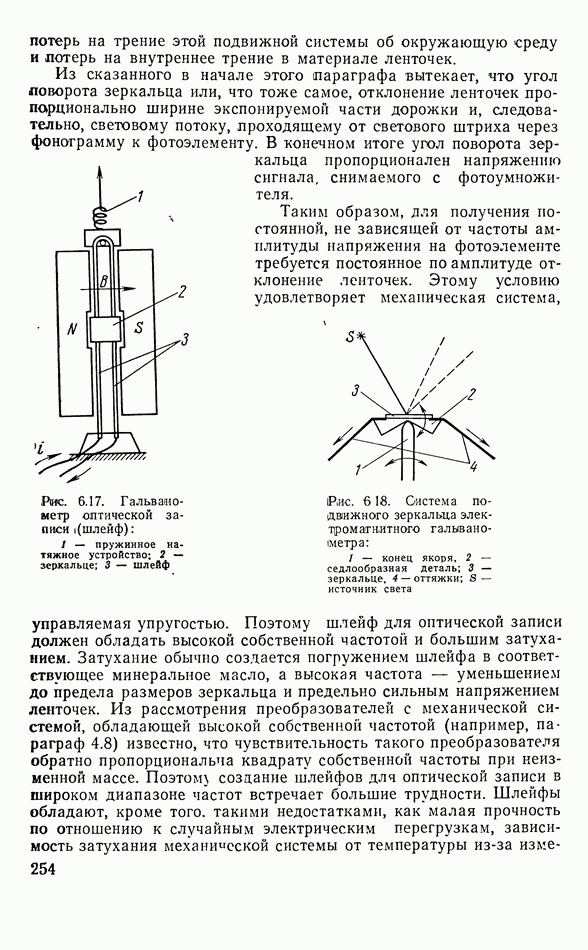
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
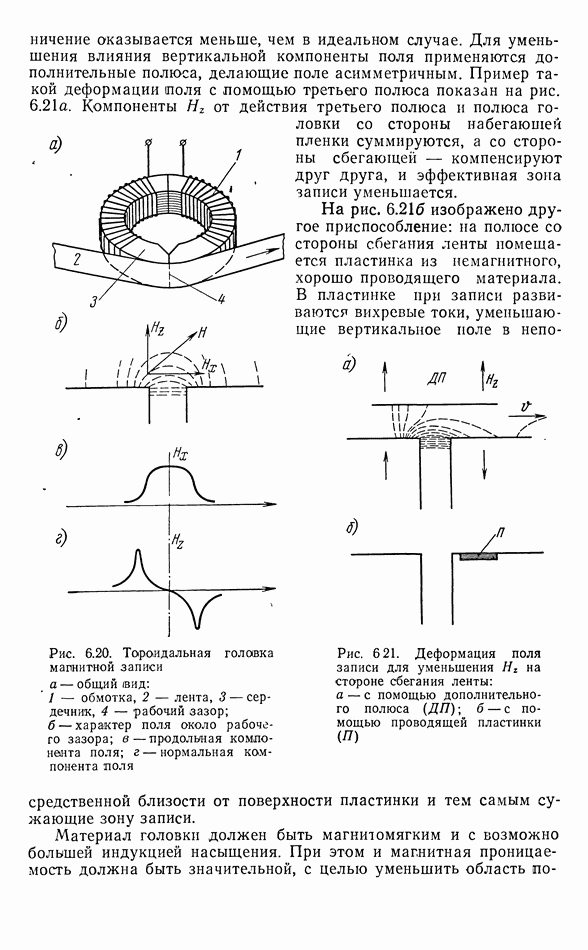
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
- Головки записи и воспроизведения
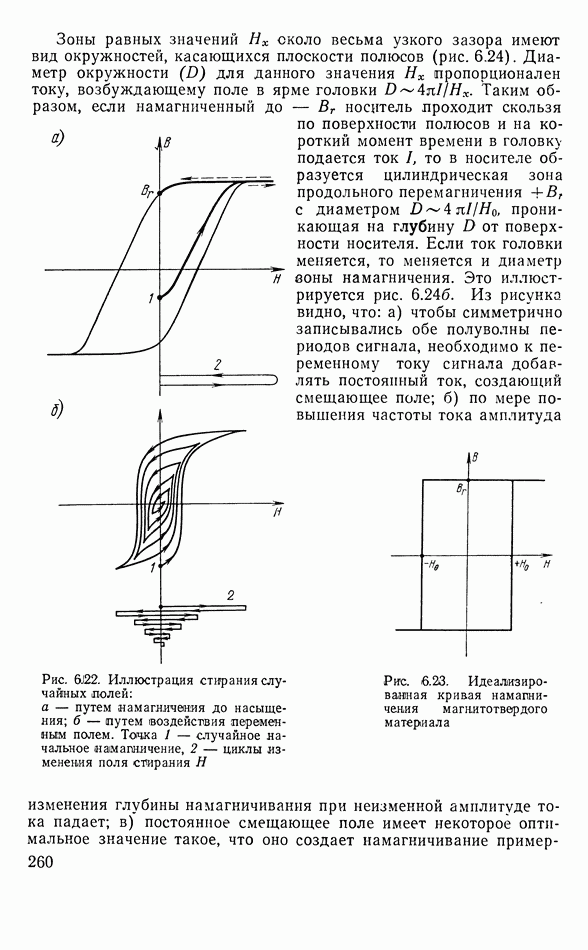
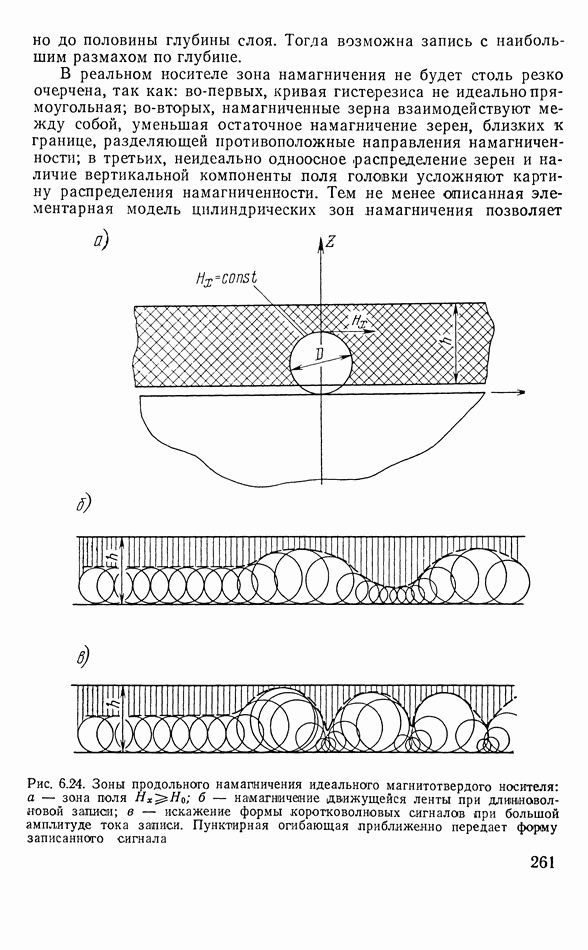
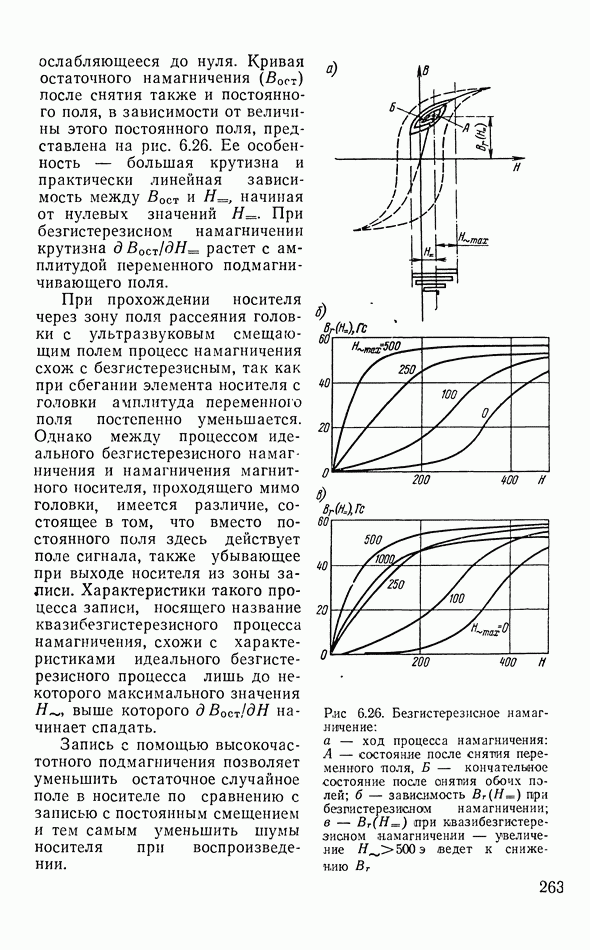
- Процесс намагничения магнитной ленты полем головки
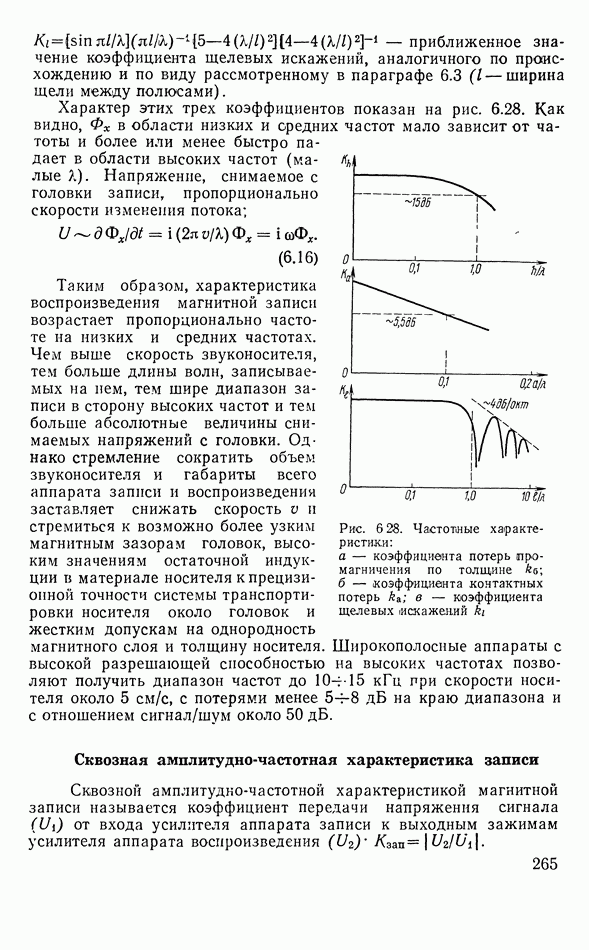
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
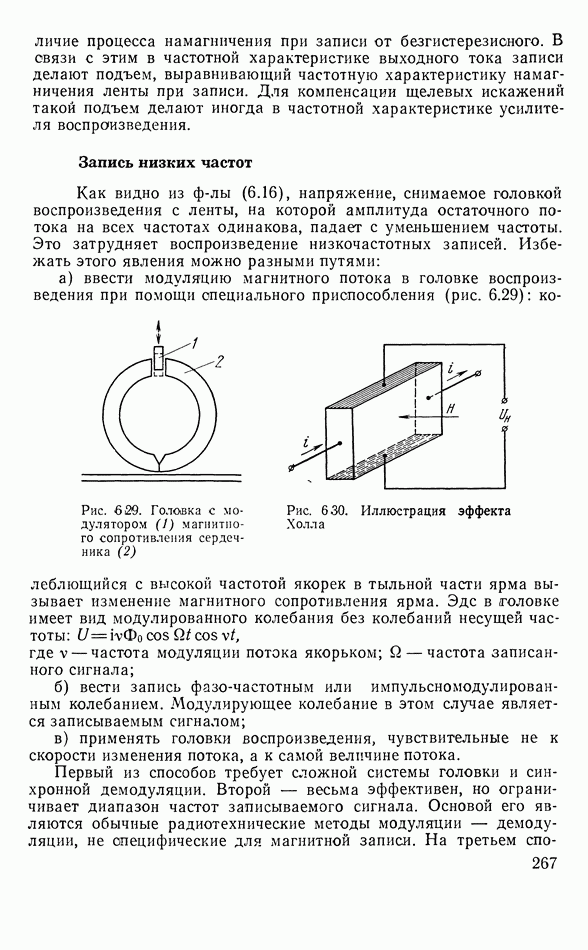
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы