| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
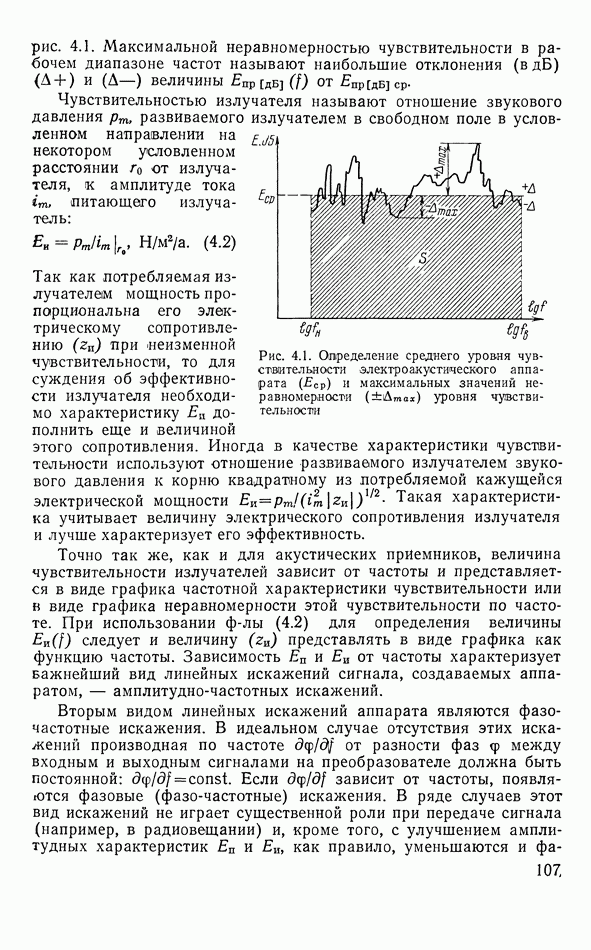
Выбор среза кристалла при изготовлении пьезоэлементов
Пьезоэлементом называют пластинку или брусок, вырезанные из кристалла определенным образом относительно кристаллографических осей. В общем случае ребра такого бруска или пластинки могут и не совпадать с направлением кристаллографических осей
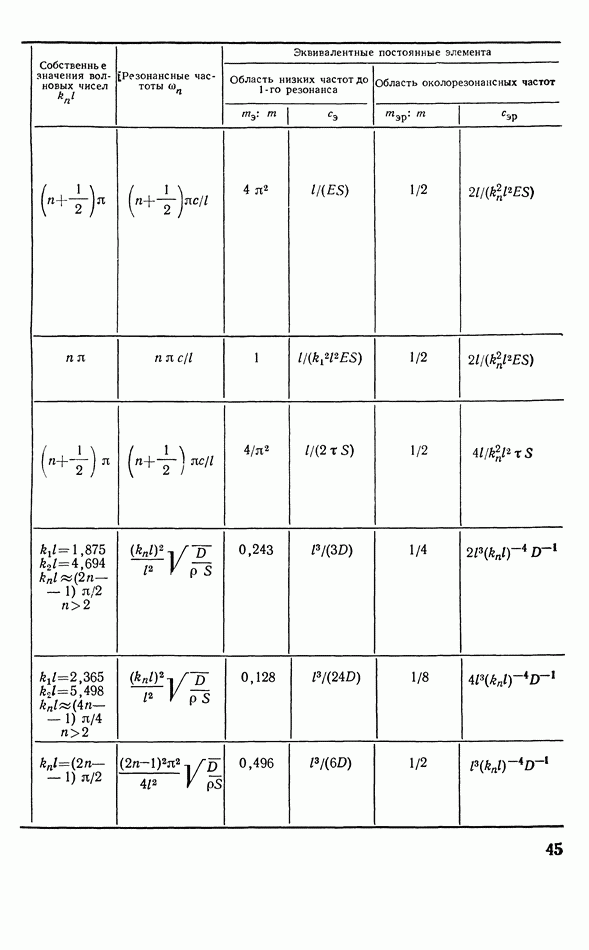
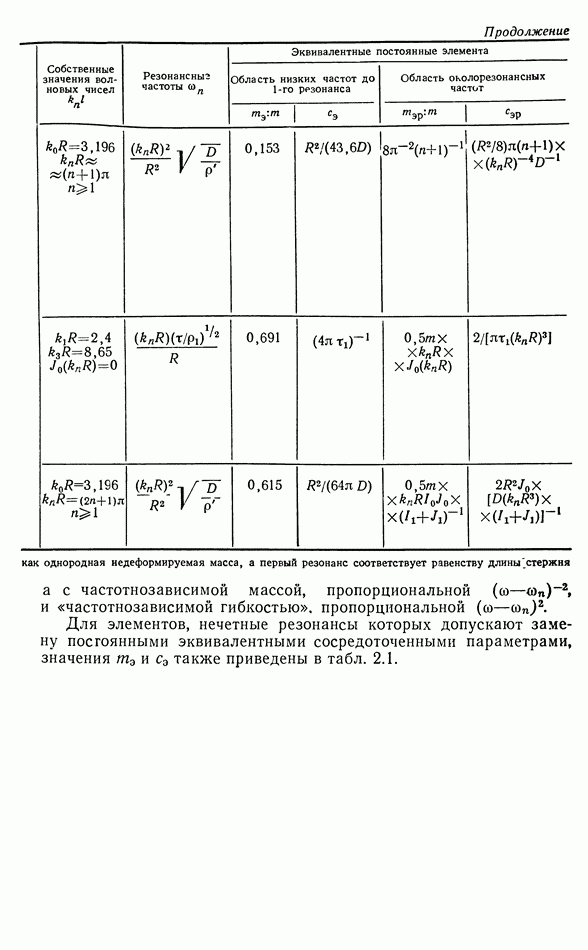
данного кристалла и соответственно плоскости его — с координатными плоскостями этой системы осей. Как будет себя вести такой элемент под действием электрического поля, приложенного вдоль какого-либо из его ребер? Как он будет поляризоваться при определенной деформации? Из рассмотрения приведенных выше значений  ничего сразу об этом сказать нельзя, если только направления поляризации или деформации (т. е. ребра пьезоэлемента) не совпадают с направлениями составляющих, для которых эти значения даны. Для ответа на поставленные вопросы необходимо перейти к новой системе координат, совпадающей с направлениями ребер и граней пьезоэлемента, т. е. надо произвести поворот координатной системы и найти составляющие
ничего сразу об этом сказать нельзя, если только направления поляризации или деформации (т. е. ребра пьезоэлемента) не совпадают с направлениями составляющих, для которых эти значения даны. Для ответа на поставленные вопросы необходимо перейти к новой системе координат, совпадающей с направлениями ребер и граней пьезоэлемента, т. е. надо произвести поворот координатной системы и найти составляющие  по новым осям.
по новым осям.

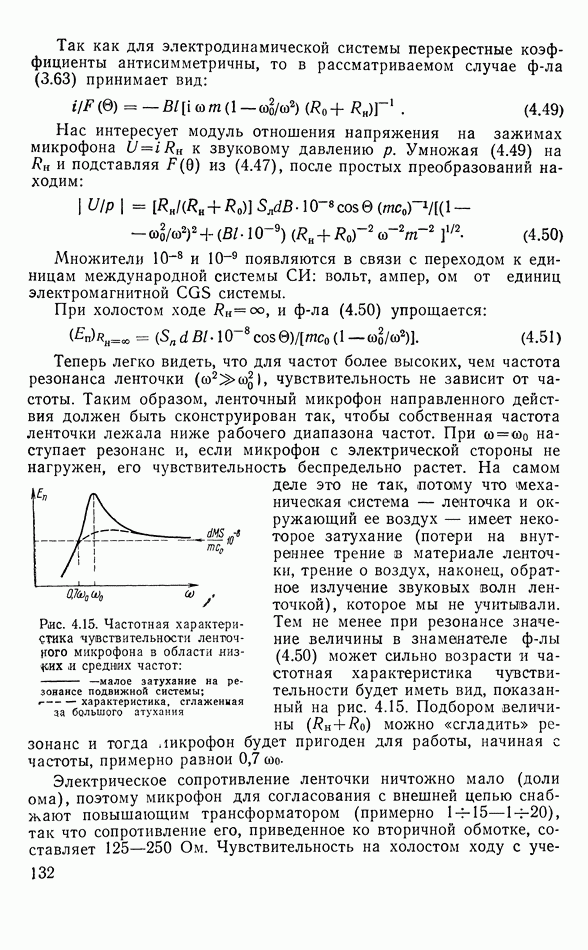
Рис. 320. К определению направления среза кристалла
Эта операция — переход к новой системе координат — представляет собой классический прием тензорного исчисления. Правила такого перехода разработаны и позволяют аналитическим путем установить поведение пьезоэлемента при любой ориентации относительно главных осей. Этим способом пользуются при теоретическом исследовании вопроса о расположении пьезоэлемента или, как говорят, о выборе «среза кристалла» для получения оптимального пьезоэффекта. Формулы перехода довольно громоздки, хотя, по существу, не сложны. На примере сегнетовой соли, без обращения к этим общим формулам, проиллюстрируем, как можно представить себе поведение пьезоэлемента, вырезанного не в направлении кристаллографических осей. Составляющие тензора пьезомодуля для сегнетовой соли имеют вид:

Пьезомодуль  превосходит
превосходит  во много раз. Поэтому для получения эффективного пьезоэлемента стремятся использовать модуль
во много раз. Поэтому для получения эффективного пьезоэлемента стремятся использовать модуль  Из приведенного расположения составляющих пьезомодуля видно, что при приложении электрического поля вдоль осей
Из приведенного расположения составляющих пьезомодуля видно, что при приложении электрического поля вдоль осей  наибольший пьезоэффект проявляется в виде деформаций
наибольший пьезоэффект проявляется в виде деформаций
 Эти деформации согласно данным табл. 3.1 соответствуют чистому сдвигу, который не всегда удобен для использования в преобразователях. Рассмотрим, какую деформацию испытывает квадратная пластинка
Эти деформации согласно данным табл. 3.1 соответствуют чистому сдвигу, который не всегда удобен для использования в преобразователях. Рассмотрим, какую деформацию испытывает квадратная пластинка  (рис. 3.20) с ребрами единичной длины, расположенная в плоскости
(рис. 3.20) с ребрами единичной длины, расположенная в плоскости  так, что ребро
так, что ребро  составляет угол
составляет угол  с осью
с осью  а электрическое поле приложено в направлении
а электрическое поле приложено в направлении  Из геометрических построений на рисунке можно легко найти:
Из геометрических построений на рисунке можно легко найти:

Тогда продольная деформация отрезка  которая обозначена
которая обозначена  для новых осей, повернутых относительно
для новых осей, повернутых относительно  на угол
на угол  составит:
составит:

Здесь отброшены величины порядка малости  Заменив в (3.148)
Заменив в (3.148)  на
на  получим продольную деформацию ребра
получим продольную деформацию ребра  (вдоль новой оси
(вдоль новой оси 

Наконец, взяв разность углов поворотов или, пользуясь малостью углов  разность тангенсов углов поворотов отрезков
разность тангенсов углов поворотов отрезков  и
и  найдем деформацию сдвига:
найдем деформацию сдвига:

Деформации и можно записать в виде:

Сопоставляя эту запись с (3.149) и (3.150) и имея в виду, что  можем записать составляющие пьезомодулей относительно новых осей
можем записать составляющие пьезомодулей относительно новых осей  для поля, действующего в направлении
для поля, действующего в направлении 

Отсюда видно, что поворот на угол  обращает
обращает  в нуль, а
в нуль, а  делает по абсолютной величине максимальными, равными
делает по абсолютной величине максимальными, равными 
Следовательно, пластинка сегпетовой соли, вырезанная под углом 45° к кристаллографическим осям испытывает чистое растяжение — сжатие при действии поля вдоль оси  Это известный
Это известный  весьма часто используемый в пьезопреобразователях из сегнетовой соли, в которых необходимы пьезоэлементы, работающие на растяжение — сжатие.
весьма часто используемый в пьезопреобразователях из сегнетовой соли, в которых необходимы пьезоэлементы, работающие на растяжение — сжатие.
В задачу разработчиков пьезоматериалов для преобразователей обычно входит подробное исследование тензора  и отыскание на основании общих правил трансформации координат, составляющих
и отыскание на основании общих правил трансформации координат, составляющих  удобных для практического использования. При этом приходится учитывать и свойства анизотропии диэлектрической проницаемости (тензора
удобных для практического использования. При этом приходится учитывать и свойства анизотропии диэлектрической проницаемости (тензора  поскольку чувствительность преобразователей-приемников зависит от константы Харкевича
поскольку чувствительность преобразователей-приемников зависит от константы Харкевича  являющейся частным от деления
являющейся частным от деления  а излучателей — от константы
а излучателей — от константы  Мэсона, в которую входит и модуль упругости пьезокристалла. Наконец, кроме задачи изучения среза, дающего максимальную чувствительность, есть еще задача получения стабильных преобразователей, чувствительность которых возможно меньше зависит от температуры. Поэтому исследуют также зависимости
Мэсона, в которую входит и модуль упругости пьезокристалла. Наконец, кроме задачи изучения среза, дающего максимальную чувствительность, есть еще задача получения стабильных преобразователей, чувствительность которых возможно меньше зависит от температуры. Поэтому исследуют также зависимости  от температуры и коэффициенты температурного расширения кристалла с целью отыскания таких срезов, при которых температурная зависимость чувствительности пьезоэлемента или его резонансной частоты была бы минимальной.
от температуры и коэффициенты температурного расширения кристалла с целью отыскания таких срезов, при которых температурная зависимость чувствительности пьезоэлемента или его резонансной частоты была бы минимальной.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
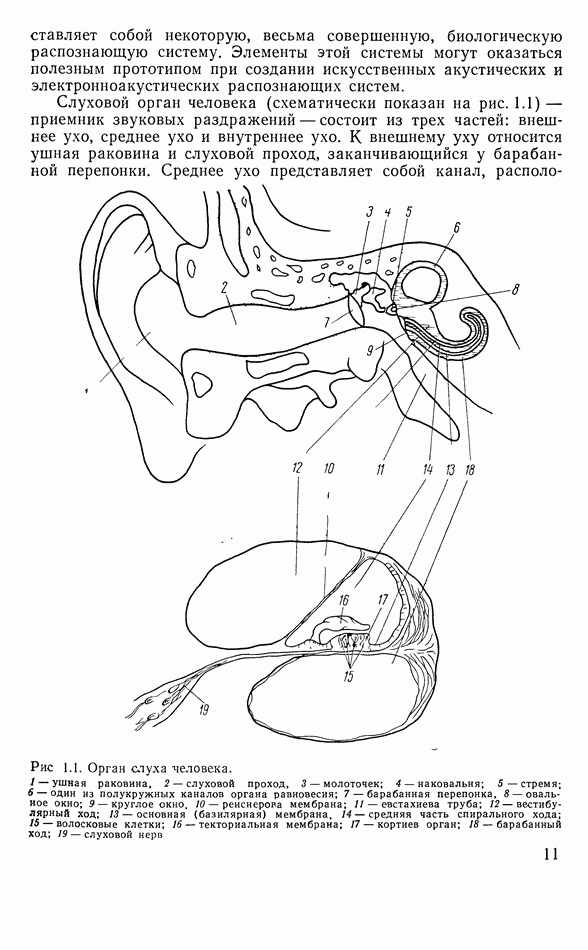
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
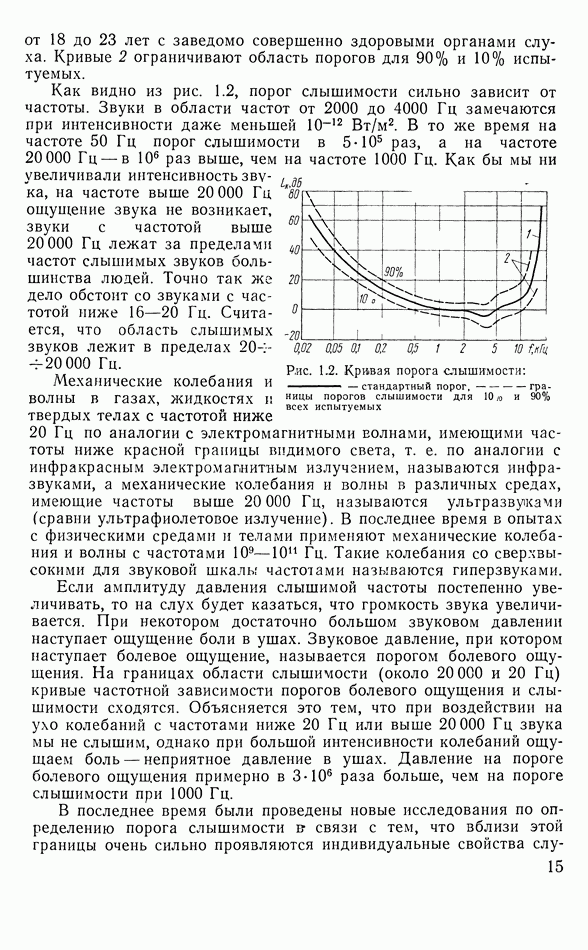
- 1.4. ПОРОГ СЛЫШИМОСТИ
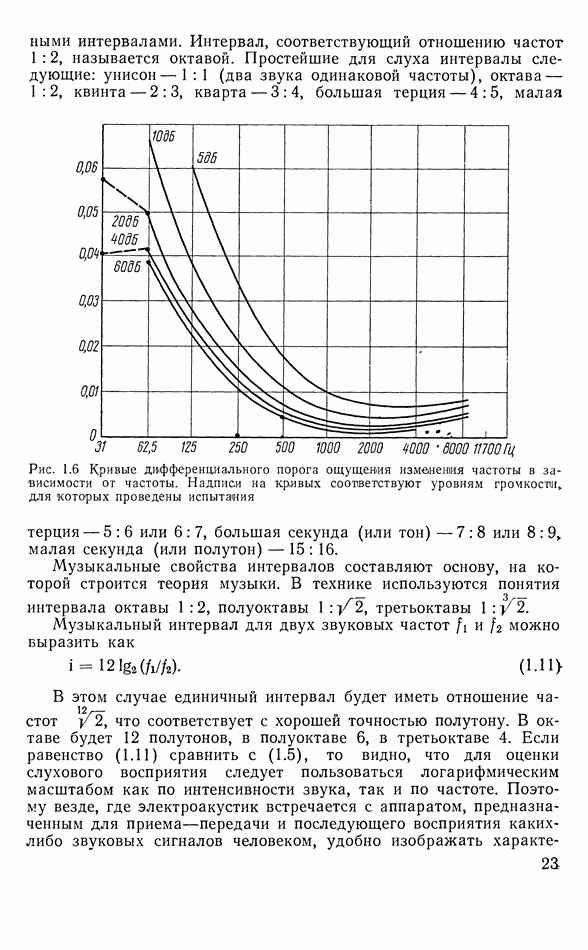
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
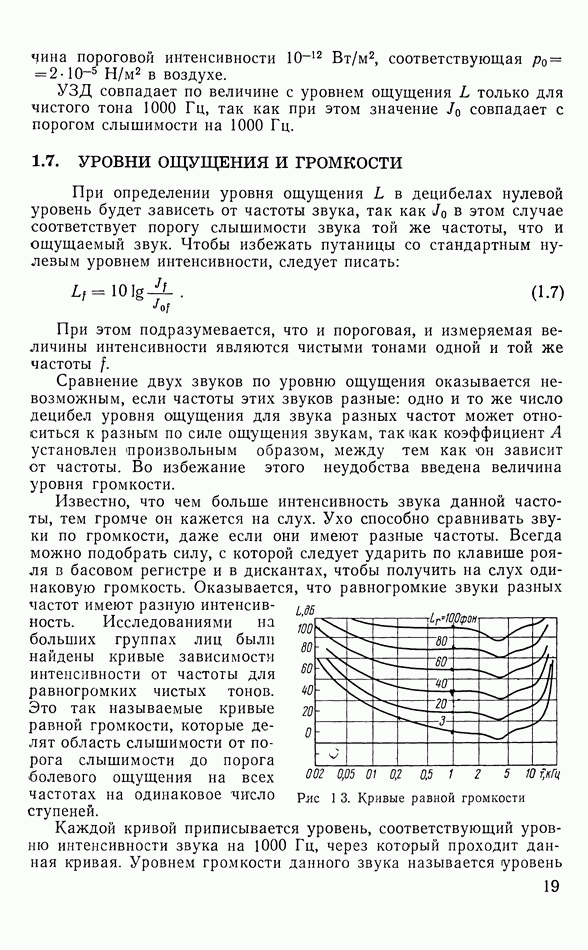
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
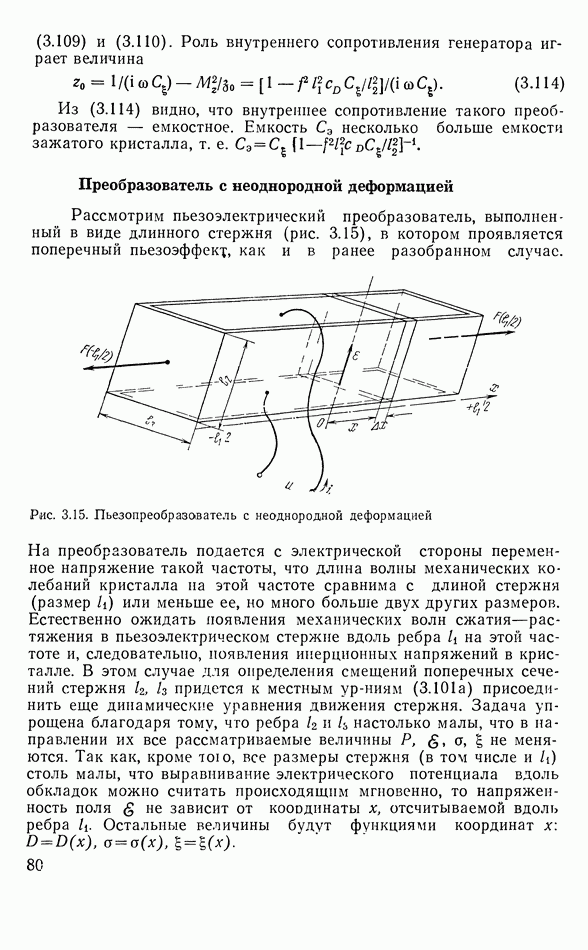
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
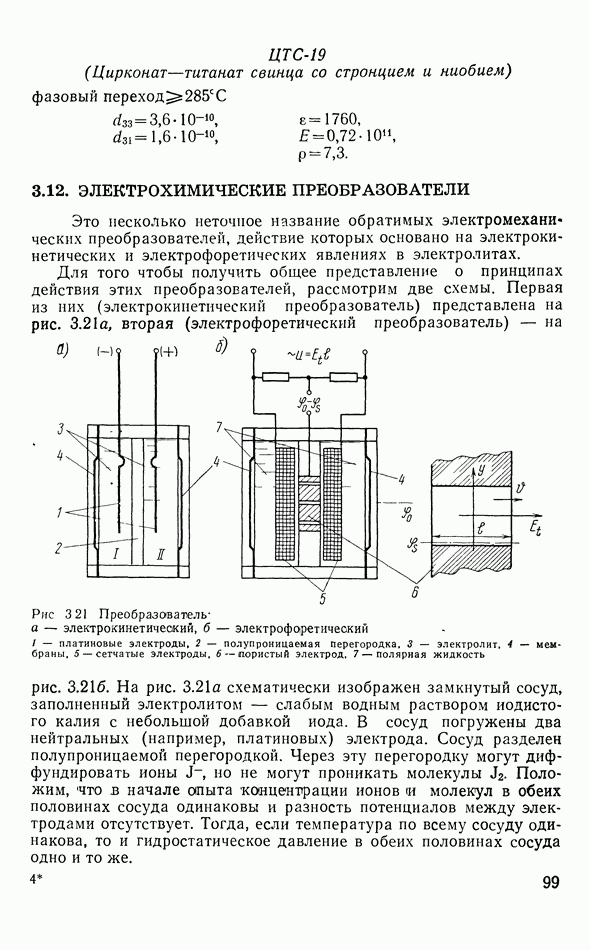
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
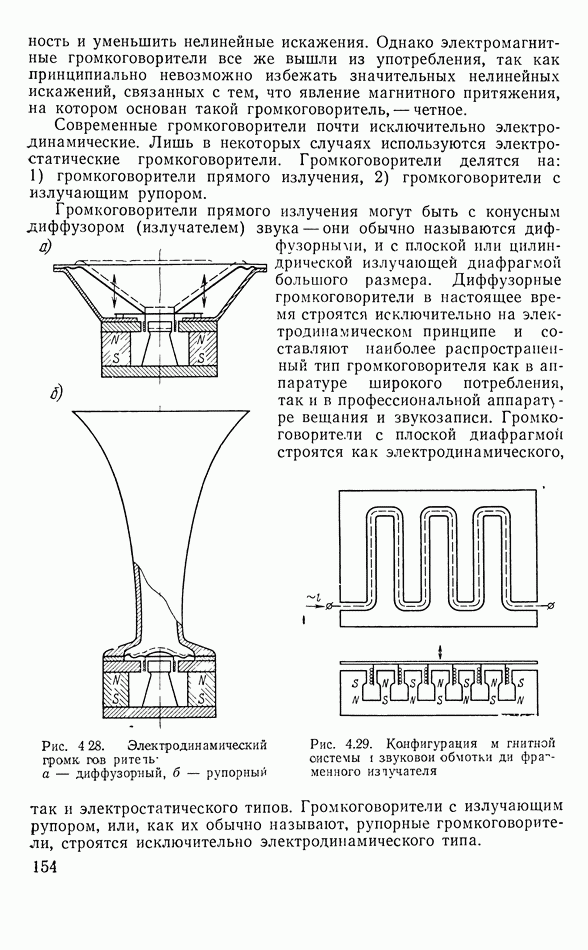
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
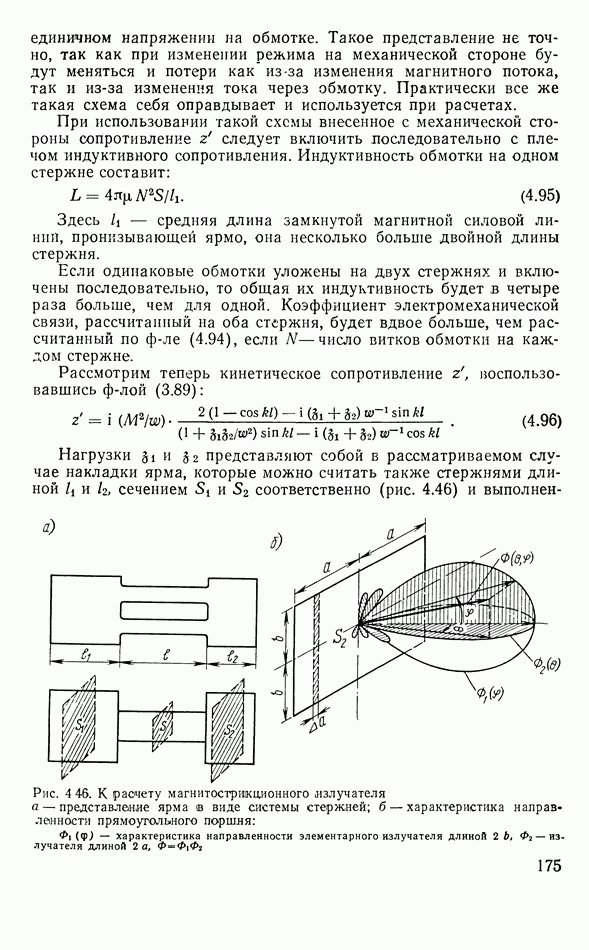
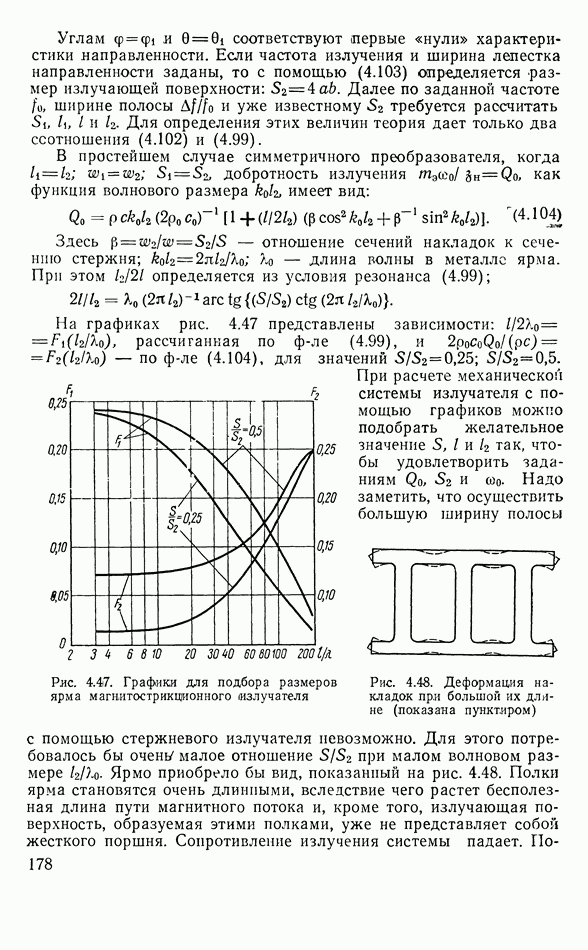
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
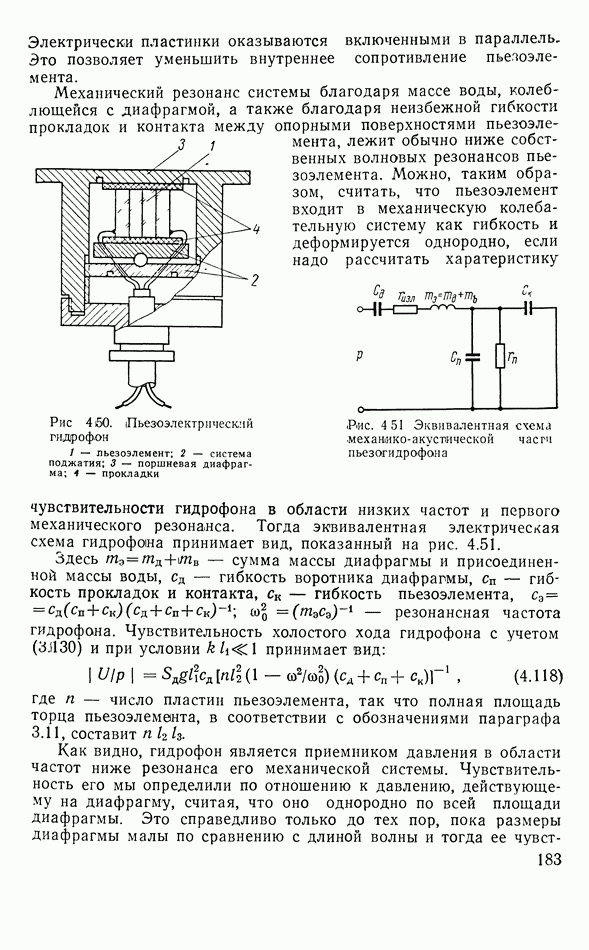
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
- Головки записи и воспроизведения
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы