| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
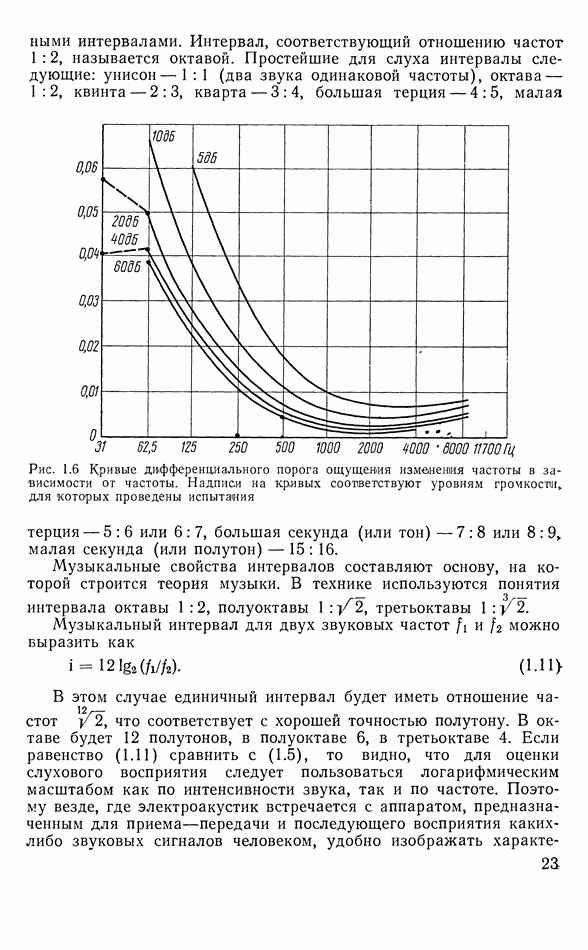
1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
Минимальная различимая на слух разность интенсивности двух звуков одной и той же частоты определяет так называемый дифференциальный порог слышимости по интенсивности звука, а минимальная различимая на слух разность частот двух звуков одинаковой интенсивности — дифференциальный порог различимости звука по частоте.
Вебером (1846 г.) было установлено весьма общее психофизиологическое соотношение, состоящее в том, что минимальный различимый прирост раздражителя составляет около 10% от первоначальной интенсивности раздражителя, действовавшего перед тем, как интенсивность его возросла. Это условие может быть записано так:

где  прирост интенсивности, который следует дать звуку интенсивности
прирост интенсивности, который следует дать звуку интенсивности  чтобы стала заметна разница в громкости между звуками
чтобы стала заметна разница в громкости между звуками  Величина
Величина  составляет примерно 10%. Подчеркнем еще раз, что это соотношение связано со свойствами нервной системы и наблюдается не только при звуковых раздражителях, но и при зрительных, осязательных и др., почему оно и носит название всеобщего физиологического закона. Если считать, что
составляет примерно 10%. Подчеркнем еще раз, что это соотношение связано со свойствами нервной системы и наблюдается не только при звуковых раздражителях, но и при зрительных, осязательных и др., почему оно и носит название всеобщего физиологического закона. Если считать, что  величина очень малая, для удобства математической трактовки можно выражение (1.1) записать так:
величина очень малая, для удобства математической трактовки можно выражение (1.1) записать так:

где  - (принятая за бесконечно малую) величина прироста интенсивности,
- (принятая за бесконечно малую) величина прироста интенсивности,  соответственно «бесконечно малый прирост величины нашего ощущения» и А — коэффициент пропорциональности, который можно определить, условившись относительно единиц измерения величины
соответственно «бесконечно малый прирост величины нашего ощущения» и А — коэффициент пропорциональности, который можно определить, условившись относительно единиц измерения величины 
Интегрируя выражение (1.2), получим:

где С — постоянная интегрирования.
Так как при некоторой интенсивности звука  соответствующей порогу слышимости, ощущение звука пропадает, т. е.
соответствующей порогу слышимости, ощущение звука пропадает, т. е.  становится равным нулю, то (1.3) можно переписать так:
становится равным нулю, то (1.3) можно переписать так:

Выбрав коэффициент  получим равенство:
получим равенство:

Величина  носит название уровня ощущения звука. Равенства (1.3) и (1.4) показывают, что уровень ощущения пропорционален логарифму интенсивности звука. Эта математическая формулировка соотношения, найденного Вебером, принадлежит Фехнеру (1860 г.) и носит название психофизиологического закона Вебера-Фехнера. Выбранное значение коэффициента
носит название уровня ощущения звука. Равенства (1.3) и (1.4) показывают, что уровень ощущения пропорционален логарифму интенсивности звука. Эта математическая формулировка соотношения, найденного Вебером, принадлежит Фехнеру (1860 г.) и носит название психофизиологического закона Вебера-Фехнера. Выбранное значение коэффициента  вообще говоря, произвольно, однако оказывается удачным, так как десятичные логарифмы общеупотребительны, 10 — удобное целое число и при этом величина прироста интенсивности 12,5%, близкая к минимально различимой на слух, даст согласно
вообще говоря, произвольно, однако оказывается удачным, так как десятичные логарифмы общеупотребительны, 10 — удобное целое число и при этом величина прироста интенсивности 12,5%, близкая к минимально различимой на слух, даст согласно  величину
величину 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
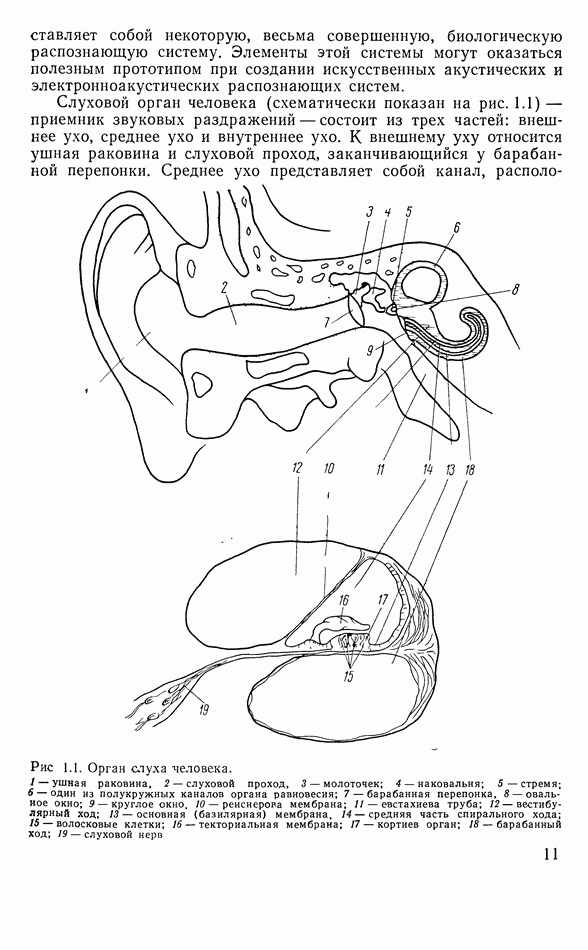
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
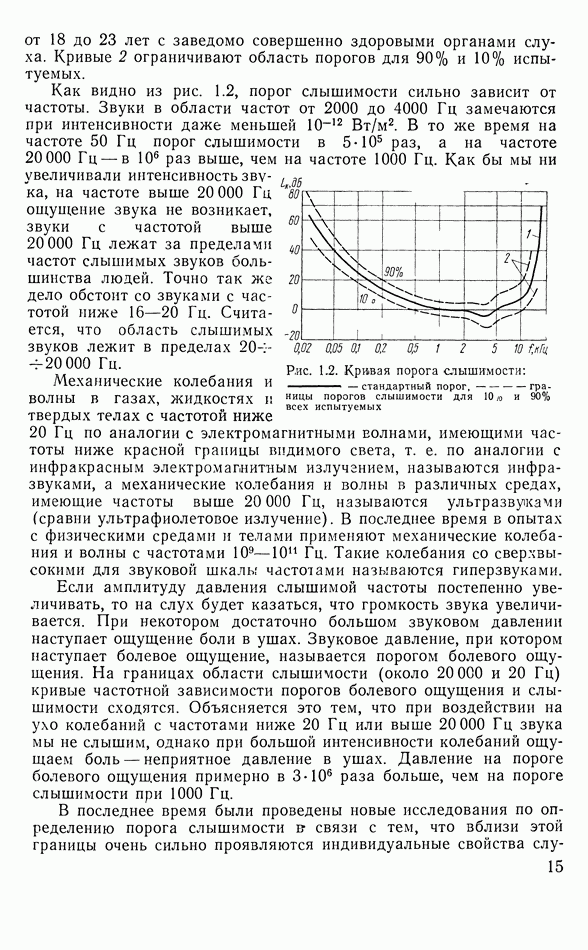
- 1.4. ПОРОГ СЛЫШИМОСТИ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
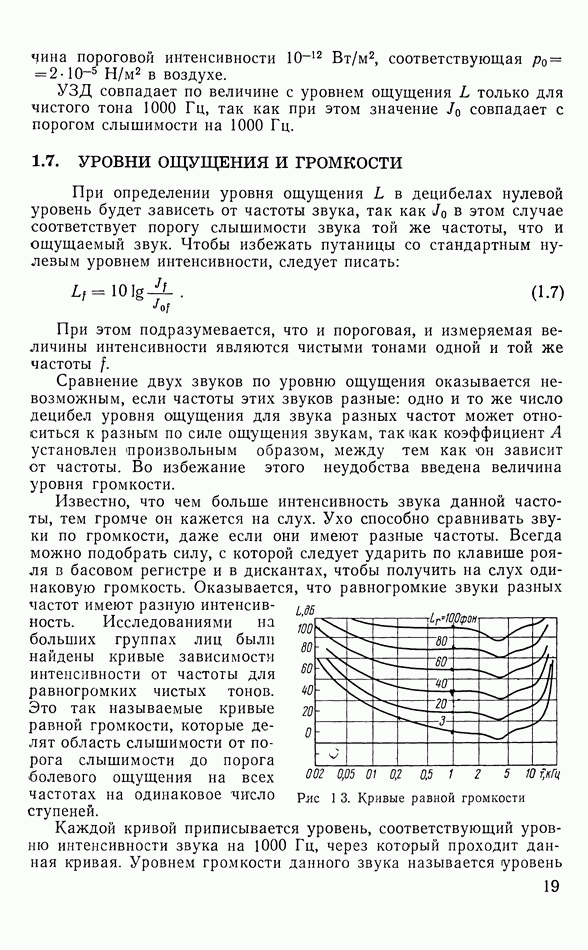
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
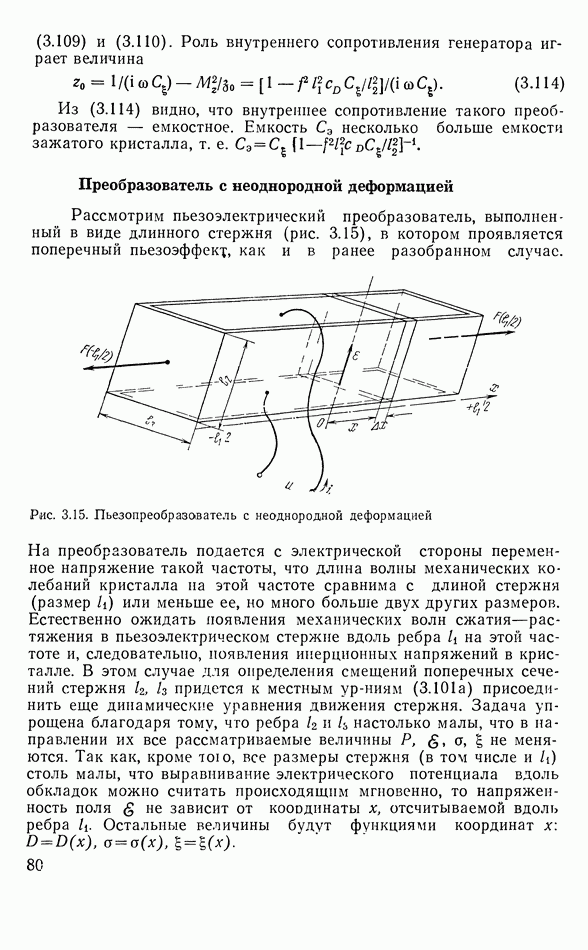
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
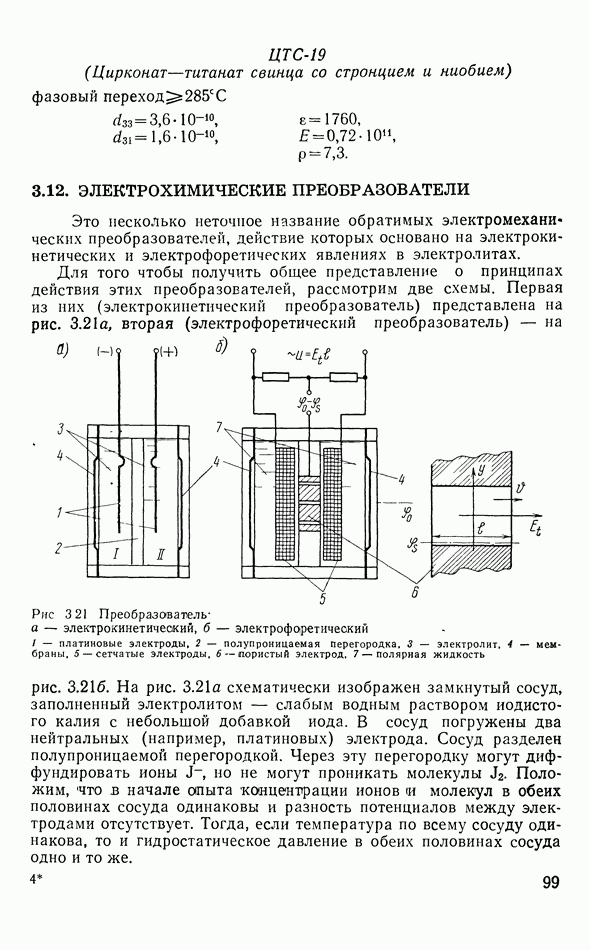
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
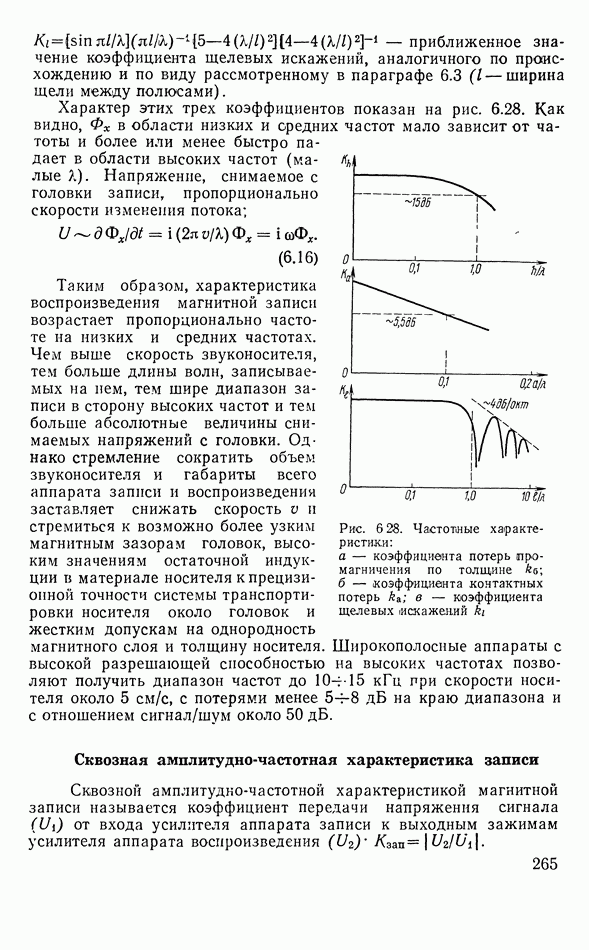
- Головки записи и воспроизведения
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
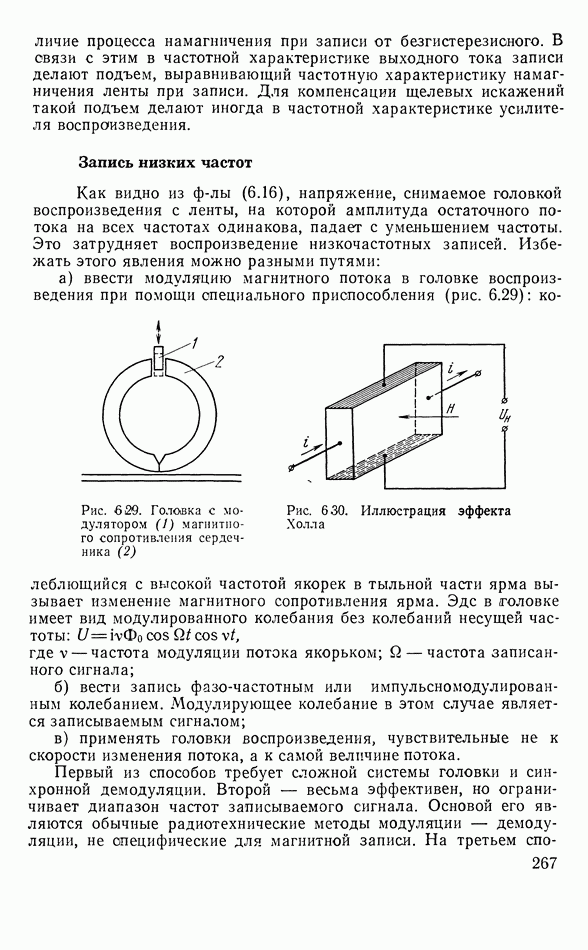
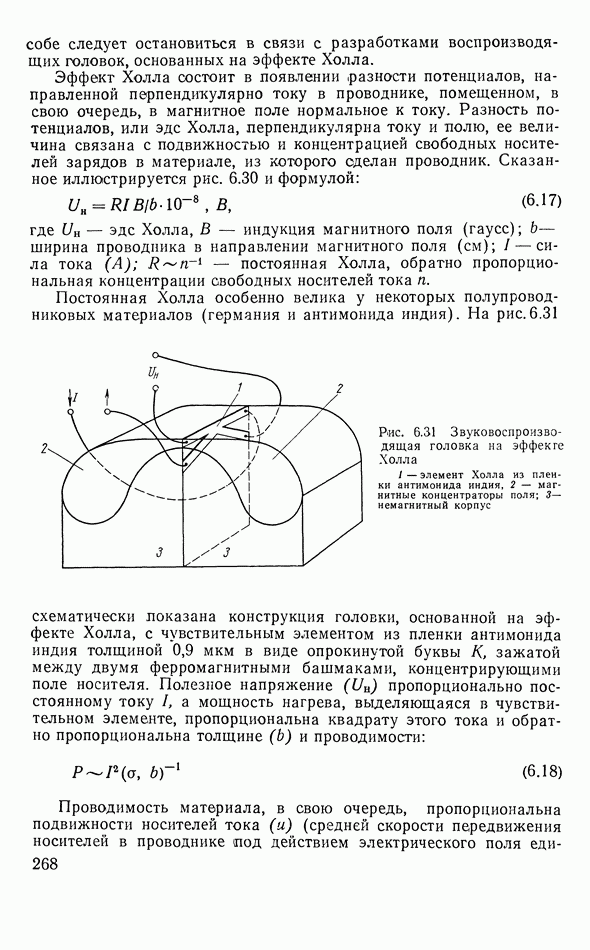
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы