| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
При расчете механических систем электроакустических аппаратов удобнее пользоваться эквивалентными электрическими схемами с сосредоточенными параметрами, чем схемами с распределенными параметрами. Процесс расчета и результат его оказываются тогда много проще и нагляднее. В действительности, конструктивные элементы аппарата не являются в точности «сосредоточенными». Например, в качестве гибкого пружинящего элемента часто используют стержень (балочку), зажатый одним концом. Детальное рассмотрение колебаний изгиба стержня показывает, что такая балочка имеет бесконечный ряд собственных частот.
В зависимости от соотношения частоты возбуждающей силы и частот резонансов она может оказывать либо гибкое, либо инерциальное сопротивление. Это справедливо и для конструктивных элементов, выполняемых в виде стержней, работающих на сжатие—растяжение, поперечно колеблющихся мембран, пластин, цилиндрических оболочек.
Акустические элементы системы: трубопроводы, газовые объемы, сопротивления излучения для акустических антенн в общем случае также представляют собой сопротивления, сложным образом зависящие от частоты. Для того чтобы упростить расчет,
элементы колебательной системы аппарата по возможности заменяют так называемыми «эквивалентными сосредоточенными параметрами». Условия эквивалентности, или, иначе говоря, степень приближения, с которой такие сосредоточенные параметры отражают поведение действительной конструкции, должна быть установлена на основании теоретического рассмотрения — с одной стороны и требований практики — с другой.
Любой электроакустический аппарат рассчитывается для работы в некотором заданном диапазоне частот. Отсюда вытекает требование полного или приближенного (с заданной погрешностью) совпадения характеристик эквивалентной схемы с сосредоточенными параметрами с характеристиками реальной конструкции в рабочем диапазоне частот. Большое число собственных частот каждого элемента в рабочем диапазоне ведет к чрезмерному усложнению частотных характеристик аппарата и затрудняет управление ими путем подбора конструктивных размеров. Поэтому, как правило, стремятся конструкцию аппарата выбрать такой, чтобы отдельные ее элементы обладали не более чем одной собственной частотой в рабочем диапазоне или недалеко за его пределами. Тогда каждый элемент можно рассматривать как простейшую колебательную систему с одной эквивалентной массой, одной эквивалентной гибкостью и, если это необходимо по условиям расчета, одним эквивалентом активного механического сопротивления.
В случаях, когда такое упрощение не удается сделать, элемент системы либо вводят в эквивалентную схему без упрощений, либо во внимание принимают несколько его резонансов, которые неизбежно попадают в рабочий диапазон частот.
Рассмотрим условия эквивалентности, которые необходимо соблюсти при замене конструктивных элементов системой с одной степенью свободы. Интерес представляют два случая: 1) собственная частота элемента лежит на верхнем краю частотного диапазона или выше его; 2) собственная частота элемента лежит в середине рабочего диапазона. Третий случай — низкая собственная частота — сводится к первым двум путем замены одного элемента двумя: одним гибким и одним массивным, собственные частоты которых лежат выше рабочего диапазона или в середине его.
Для случаев 1 и 2 естественно, прежде всего, потребовать, чтобы собственные частоты конструктивных элементов, ближайшие к рабочему диапазону, совпадали с собственными частотами эквивалентной системы с сосредоточенными параметрами:

где  эквивалентная масса системы с сосредоточенными параметрами;
эквивалентная масса системы с сосредоточенными параметрами;  эквивалентная гибкость этой же системы;
эквивалентная гибкость этой же системы;  ближайшая к рабочему диапазону собственная частота действительного конструктивного элемента механической системы.
ближайшая к рабочему диапазону собственная частота действительного конструктивного элемента механической системы.
Вторым требованием будет требование равенства механического сопротивления эквивалентной системы с сосредоточенными параметрами механическому сопротивлению конструктивного элемента. В случае 1 конструктивный элемент на нижнем краю диапазозона частот действительно становится сосредоточенным и представляет собой либо практически недеформируемую массу, либо практически не обладающую инерцией гибкость. Проще всего потребовать, чтобы точное равенство сопротивлений достигалось при нулевой частоте:

где  сопротивление эквивалентной системы с сосредоточенными параметрами;
сопротивление эквивалентной системы с сосредоточенными параметрами;  сопротивление конструктивного элемента.
сопротивление конструктивного элемента.
Эквивалентная система с одной степенью свободы без затухания состоит из двух элементов, поэтому условия (2.15) и (2.16) полностью определяют их. Если три  то, очевидно,
то, очевидно,  и для такого конструктивного элемента получим систему эквивалентных параметров:
и для такого конструктивного элемента получим систему эквивалентных параметров:

Если при  то
то  и система эквивалентных параметров имеет вид
и система эквивалентных параметров имеет вид

При таком выборе эквивалентов скорость колебаний точки приложения силы в эквивалентной системе будет совпадать со скоростью колебаний точки приложения силы к конструктивному элементу, который заменяется эквивалентными сосредоточенными параметрами, при 
В ряде случаев на конструктивный элемент аппарата действует не сосредоточенная сила, а равномерно распределенное колебательное давление со стороны акустической системы. Например, при работе телефона или микрофона на мембрану действует звуковое давление.
При расчете такого конструктивного элемента следует выбрать «точку приведения», т. е. ту точку элемента, движение которой нам необходимо знать для дальнейшего расчета аппарата. Это может быть, например, точка мембраны, к которой механически подсоединен какой-либо другой элемент аппарата или около которой в мембрану входит магнитный поток электромагнитного устройства телефона и т. п. В этом случае механическое сопротивление конструктивного элемента надо определить как отношение полной силы, создаваемой звуковым давлением  на площадь элемента (5) к скорости
на площадь элемента (5) к скорости  точки приведения:
точки приведения:

Определив  из выражения (2.19), можно найти по ф-лам (2.17) и (2.18) элементы
из выражения (2.19), можно найти по ф-лам (2.17) и (2.18) элементы 
Обратимся теперь к случаю 2 — резонансная частота конструктивного элемента находится в середине рабочего диапазона. Этот случай характерен для аппаратов, работающих в узкой полосе частот вблизи резонанса этого конструктивного элемента. Тогда следует подобрать структуру эквивалентной схемы так, чтобы она хорошо воспроизводила частотную зависимость механического сопротивления конструктивного элемента именно вблизи резонанса. Условие (2.15) оставим прежним, а вместо (2.16) рассмотрим поведение вблизи резонанса. Если  разложить в ряд по со около резонанса:
разложить в ряд по со около резонанса:

то, так как  в первом приближении получим
в первом приближении получим

Значит, выбрав второе условие так, чтобы

получим с точностью до членов второго порядка совпадение хода  вблизи резонанса.
вблизи резонанса.
Сопротивление эквивалентной системы с сосредоточенными параметрами имеет вид  тогда
тогда

Приравнивая абсолютное значение  нашего конструктивного элемента величине
нашего конструктивного элемента величине  найдем искомый эквивалентный параметр для области вблизи резонанса:
найдем искомый эквивалентный параметр для области вблизи резонанса:

По  рассчитывают конструктивный элемент, работающий около резонанса сил, при котором
рассчитывают конструктивный элемент, работающий около резонанса сил, при котором  Если область работы аппарата лежит вблизи резонанса скоростей конструктивного элемента, то
Если область работы аппарата лежит вблизи резонанса скоростей конструктивного элемента, то  и для расчетов надо пользоваться сравнением обратных величин, так называемых податливостей 3—1 реальной и эквивалентной систем элемента. В этом случае условие эквивалентности имеет вид:
и для расчетов надо пользоваться сравнением обратных величин, так называемых податливостей 3—1 реальной и эквивалентной систем элемента. В этом случае условие эквивалентности имеет вид:  при
при 
Рассуждая аналогичным путем относительно податливости около резонанса скоростей и выбирая эквивалентную схему в виде параллельного контура, получим значение эквивалентной сосредоточенной гибкости:

Формулы (2.15) — (2.22) позволяют найти эквивалентные сосредоточенные параметры конструктивного элемента, если известны расположение его резонанса, ближайшего к рабочему диапазону
частот, и частотная характеристика точного значения сопротивления этого элемента.
Рассмотрим подробно процедуру нахождения  для конструктивного элемента в виде консольной балочки (стержня, зажатого одним концом), к свободному концу которой приложена сила. Движение свободного конца входит в расчет аппарата.
для конструктивного элемента в виде консольной балочки (стержня, зажатого одним концом), к свободному концу которой приложена сила. Движение свободного конца входит в расчет аппарата.
Теория поперечных колебаний тонкого стержня дает точное значение сопротивления:

где  полная масса балочки; I — ее длина;
полная масса балочки; I — ее длина;  погонная масса;
погонная масса;  модуль упругости;
модуль упругости;  плоский момент инерции поперечного сечения балочки.
плоский момент инерции поперечного сечения балочки.
Резонансы сил  наблюдаются при условии:
наблюдаются при условии:

Из этого уравнения можно найти  ;
; 

Найдем  для случая, когда первый резонанс балочки лежит в верхней части рабочего диапазона. Условие (2.15) принимает вид
для случая, когда первый резонанс балочки лежит в верхней части рабочего диапазона. Условие (2.15) принимает вид

а условие (2.16)

Теперь легко найти 

Итак, консольную балочку вплоть до первой резонансной частоты (и даже несколько выше) можно заменить простой колебательной системой с массой, составляющей 0,243 от массы балочки, и гибкостью  Величина
Величина  соответствует статическому прогибу балочки тех же размеров под действием единичной силы — это статическая гибкость балочки.
соответствует статическому прогибу балочки тех же размеров под действием единичной силы — это статическая гибкость балочки.
Рассмотрим теперь работу балочки вблизи ее резонанса. В этом случае определим  с помощью (2.23), подставив затем в полученное выражение условие резонанса (2.24). Полагая
с помощью (2.23), подставив затем в полученное выражение условие резонанса (2.24). Полагая  где
где 
 находим
находим  Подставляя из
Подставляя из  получаем:
получаем:

Продифференцировав и подставив в полученное выражение значение  найдем:
найдем:

Окончательно искомое соотношение для  в соответствии с (2.21) будет
в соответствии с (2.21) будет  т. е. вблизи любого из резонансов балочки ее эквивалентную массу удобно принимать равной одной четверти полной массы. Гибкость следует рассчитывать для каждой резонансной частоты в соответствии с (2.25):
т. е. вблизи любого из резонансов балочки ее эквивалентную массу удобно принимать равной одной четверти полной массы. Гибкость следует рассчитывать для каждой резонансной частоты в соответствии с (2.25):

Как видно, эквиваленты  для области около первого резонанса очень мало отличаются от «низкочастотных», определяемых по ф-лам (2.28) и (2.29).
для области около первого резонанса очень мало отличаются от «низкочастотных», определяемых по ф-лам (2.28) и (2.29).
При работе консольной балки вблизи резонанса скоростей  резонансные частоты следует искать из условия равенства нулю знаменателя выражения
резонансные частоты следует искать из условия равенства нулю знаменателя выражения 

Если не считать нулевого корня этого уравнения  который соответствует статической деформации балки, следующие корни располагаются при значениях
который соответствует статической деформации балки, следующие корни располагаются при значениях  Так как
Так как  отличается от единицы менее чем на 0,003 для
отличается от единицы менее чем на 0,003 для  то (2.32) можно заменить простым соотношением:
то (2.32) можно заменить простым соотношением:  Подстановка (2.32) в (2.22) и вычисление производной дают:
Подстановка (2.32) в (2.22) и вычисление производной дают:

Так как  то с большой точностью можно пользоваться приближенными соотношениями:
то с большой точностью можно пользоваться приближенными соотношениями:

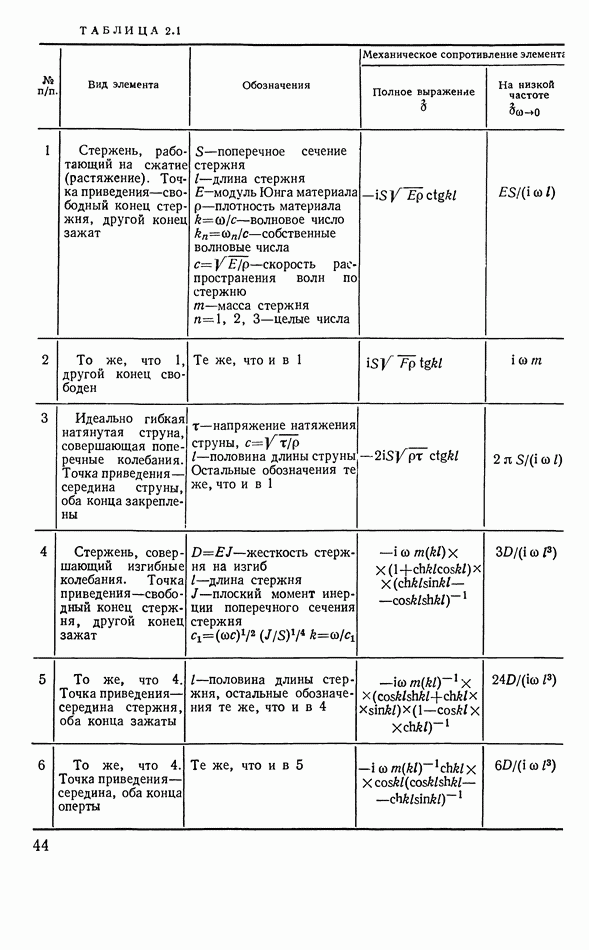
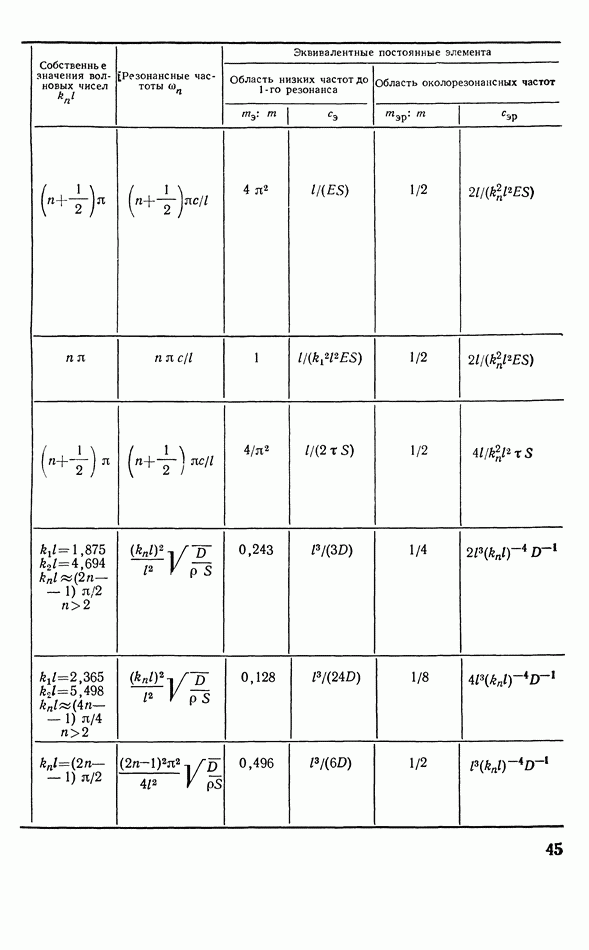
В табл. 2.1 приведены некоторые важнейшие формулы для расчета эквивалентных постоянных по отношению к сосредоточенным силам, для резонансов сил и скоростей в области низких частот и резонансов.
(см. скан)
(см. скан)
(см. скан)
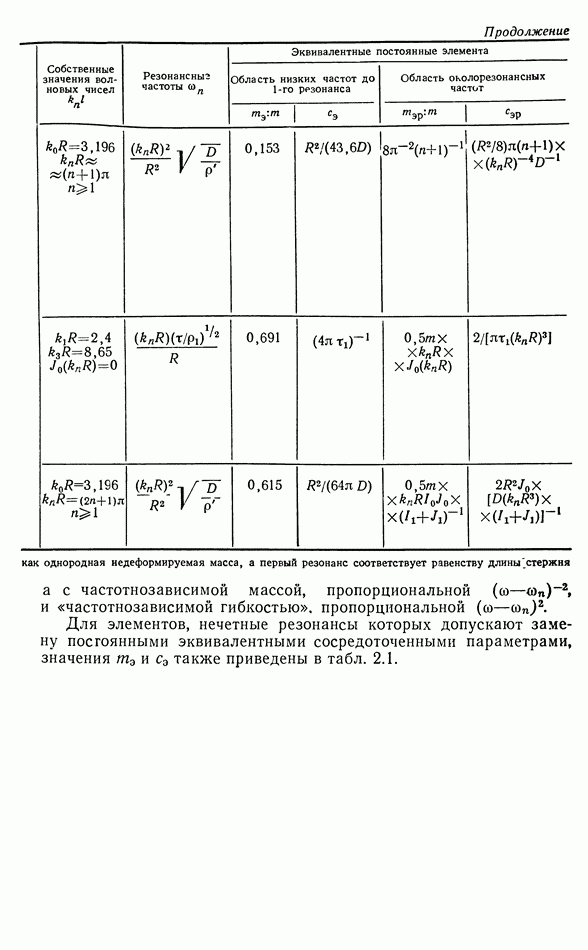
Если эквивалентные параметры рассчитаны по отношению к распределенным силам, то полной аналогии с эквивалентами, имеющими одну степень свободы около резонансов исходного элемента, не получается. Это объясняется следующим. Выбирая в качестве точки приведения одну из точек конструктивного элемента, можно столкнуться с таким случаем, когда эта точка ни при каких значениях частоты не затормаживается — нет явления антирезонанса. В результате сопротивление такого элемента, около его резонансов, проходя через нулевое значение, меняется поочередно с гибкого на инерциальное и с инерциального на гибкое. Для области резонансов, в которых сопротивление изменяется с гибкого на инерциальное, можно подыскать эквивалентные параметры сосредоточенной системы; для другой части резонансов это не удается сделать, так как потребовалось бы иметь дело не с постоянной,
Продолжение (см. скан)
а с частотнозависимой массой, пропорциональной  и «частотнозависимой гибкостью», пропорциональной
и «частотнозависимой гибкостью», пропорциональной 
Для элементов, нечетные резонансы которых допускают замену постоянными эквивалентными сосредоточенными параметрами, значения  также приведены в табл. 2.1.
также приведены в табл. 2.1.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
- 1.4. ПОРОГ СЛЫШИМОСТИ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
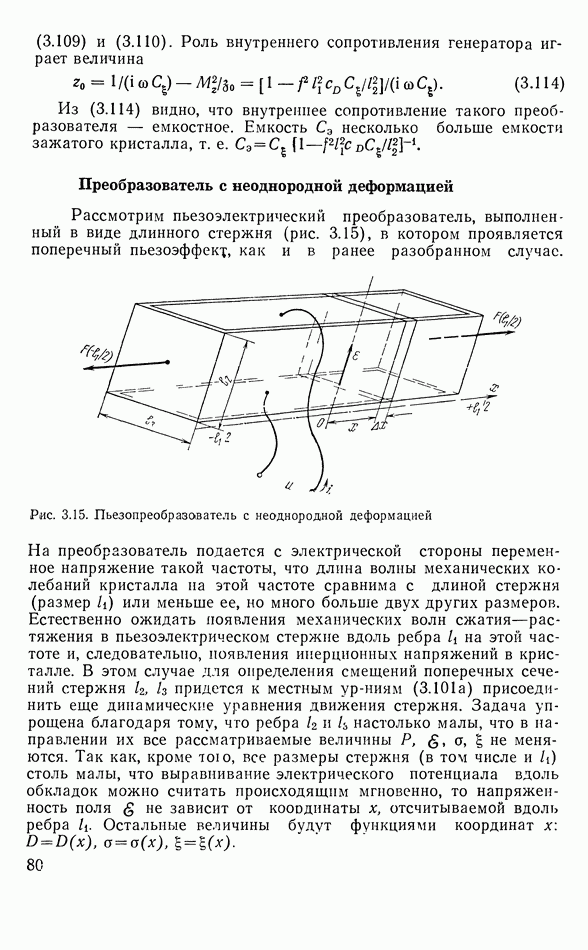
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
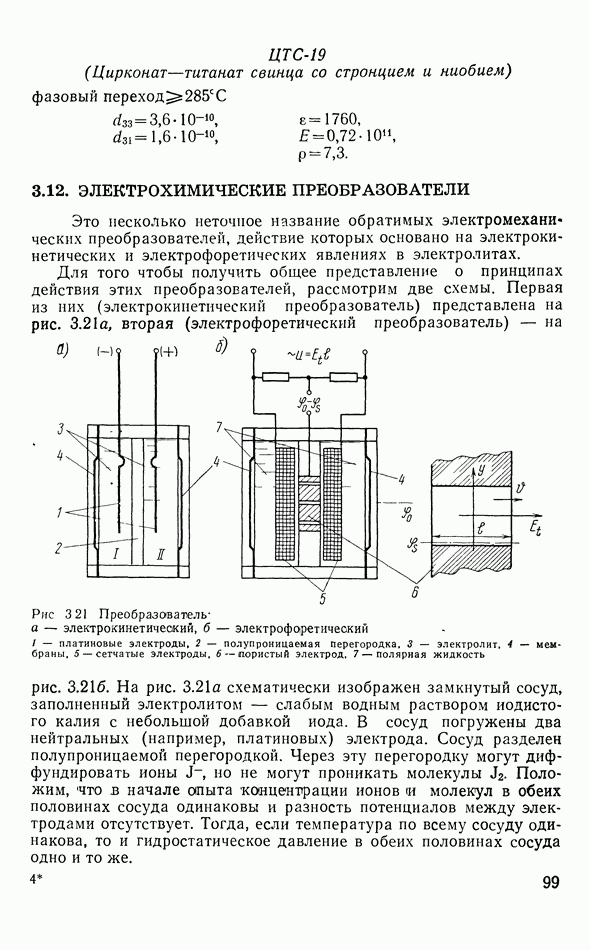
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
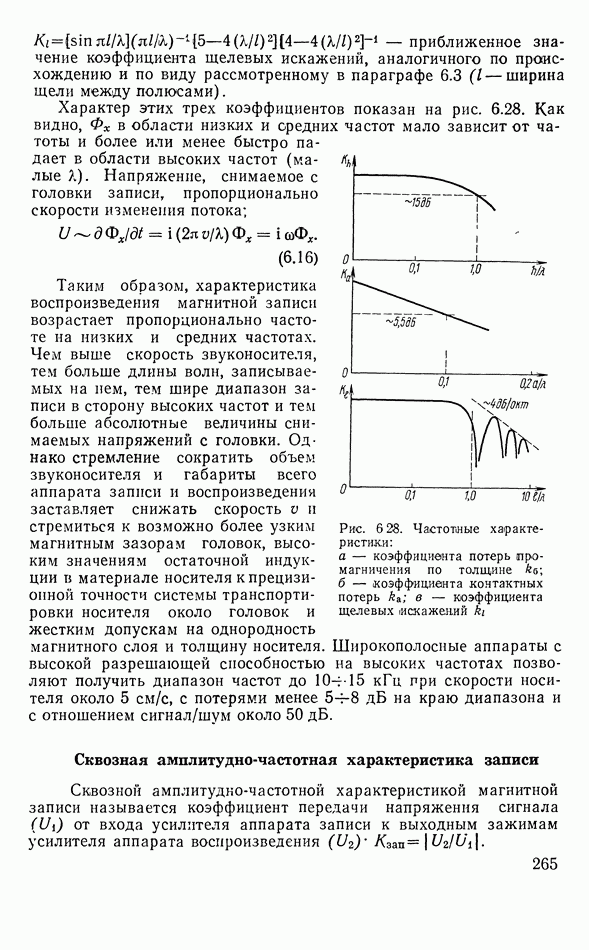
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
- Головки записи и воспроизведения
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
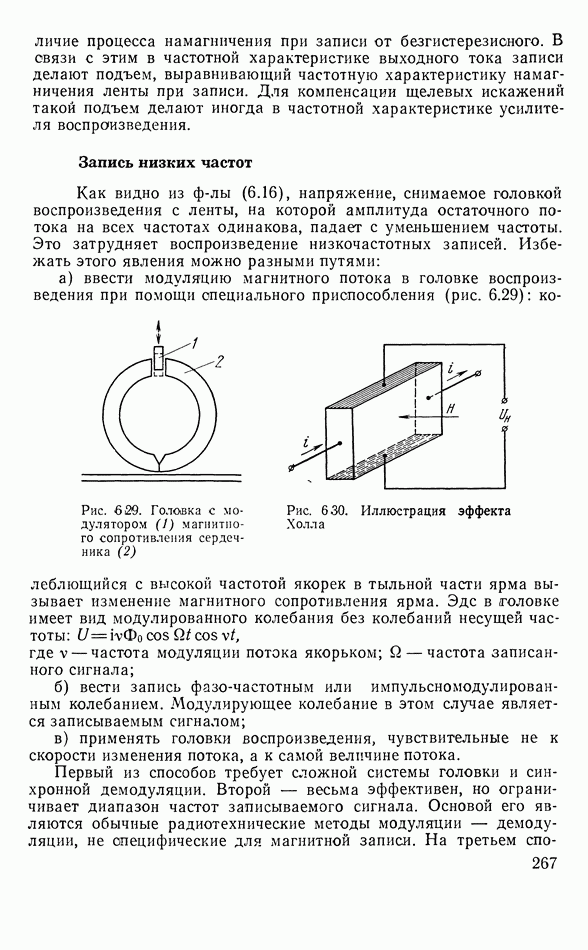
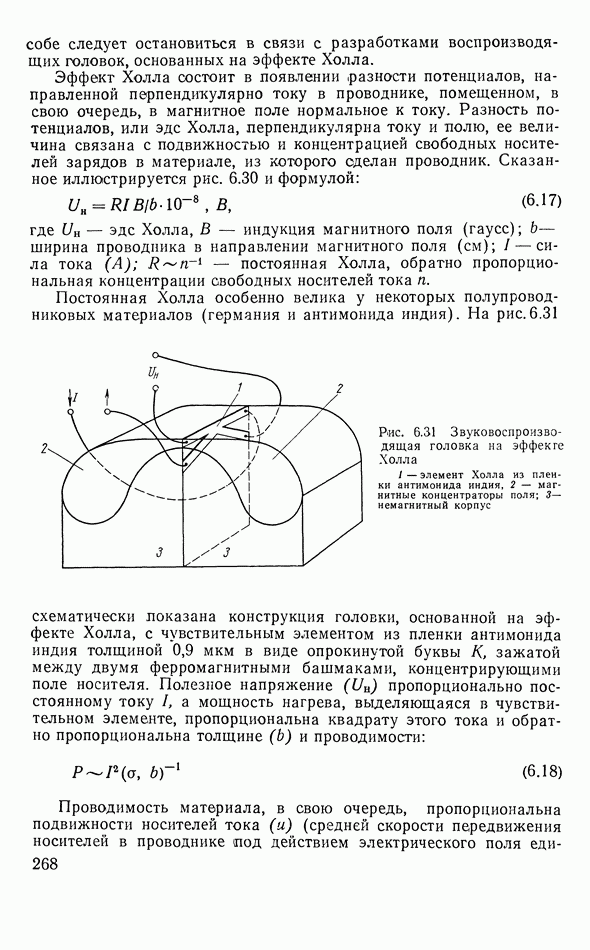
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы