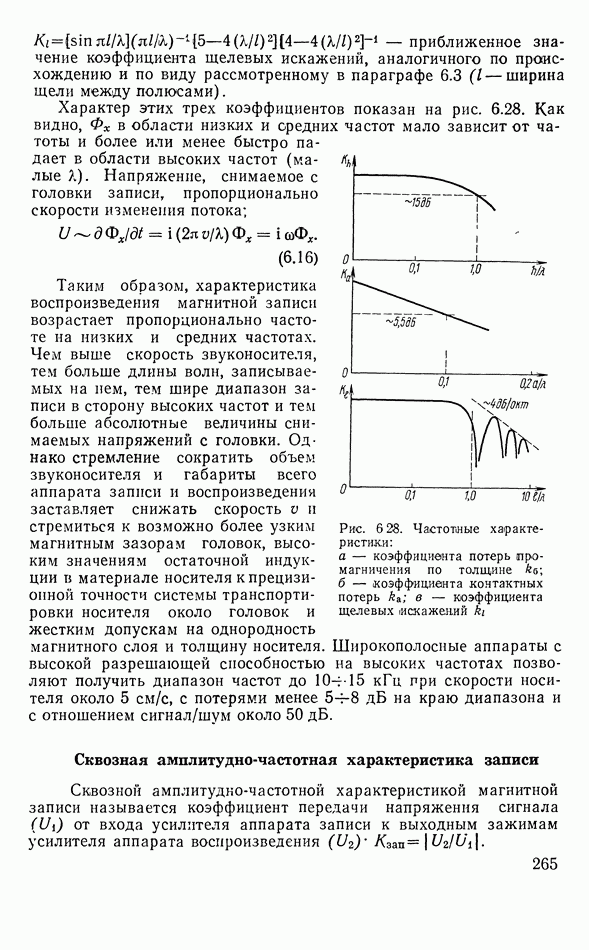
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
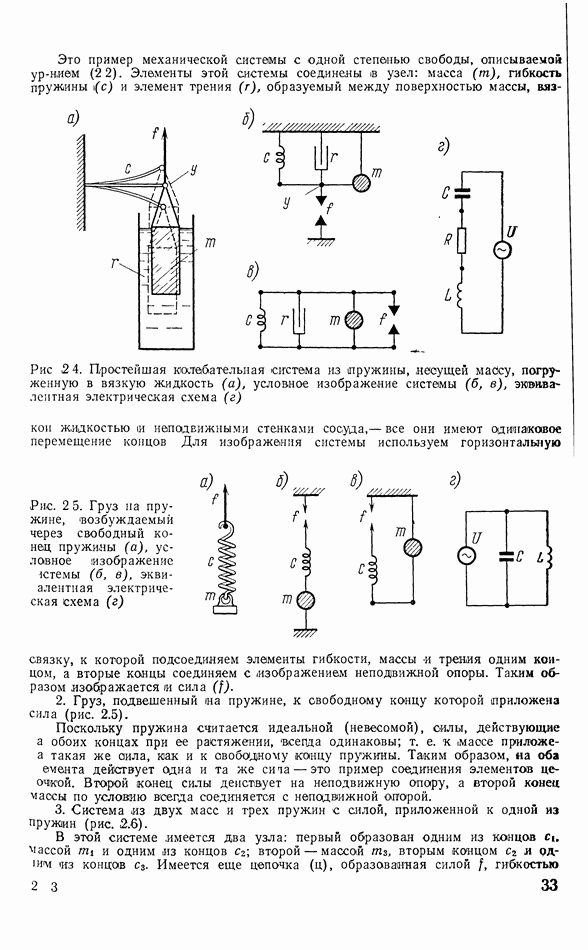
Преобразователь с неоднородной деформацией
Рассмотрим пьезоэлектрический преобразователь, выполненный в виде длинного стержня (рис. 3.15), в котором проявляется поперечный пьезоэффект, как и в ранее разобранном случае.

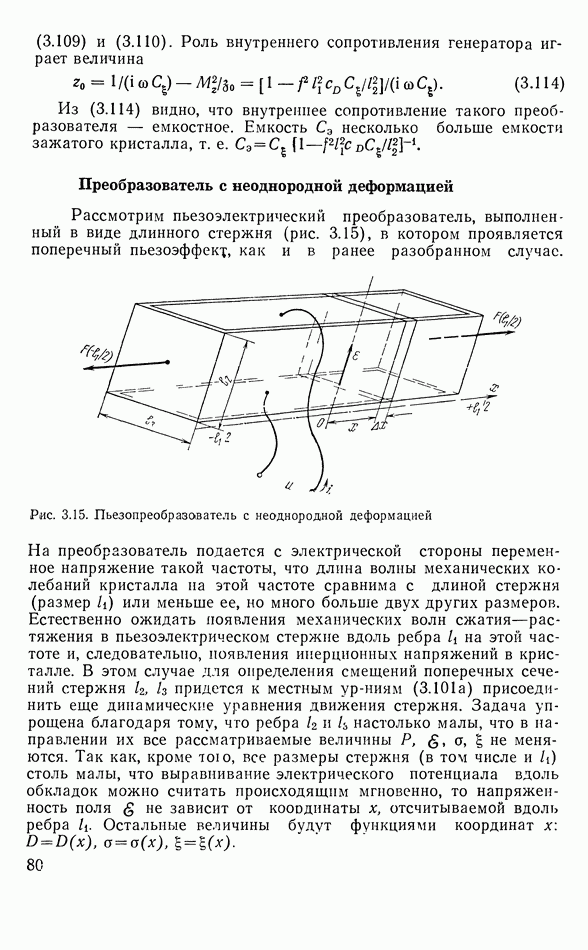
Рис. 3.15. Пьезопреобразователь с неоднородной деформацией
На преобразователь подается с электрической стороны переменное напряжение такой частоты, что длина волны механических колебаний кристалла на этой частоте сравнима с длиной стержня (размер  или меньше ее, но много больше двух других размеров. Естественно ожидать появления механических волн сжатия—растяжения в пьезоэлектрическом стержне вдоль ребра
или меньше ее, но много больше двух других размеров. Естественно ожидать появления механических волн сжатия—растяжения в пьезоэлектрическом стержне вдоль ребра  на этой частоте и, следовательно, появления инерционных напряжений в кристалле. В этом случае для определения смещений поперечных сечений стержня
на этой частоте и, следовательно, появления инерционных напряжений в кристалле. В этом случае для определения смещений поперечных сечений стержня  придется к местным ур-ниям (3.101а) присоединить еще динамические уравнения движения стержня. Задача упрощена благодаря тому, что ребра
придется к местным ур-ниям (3.101а) присоединить еще динамические уравнения движения стержня. Задача упрощена благодаря тому, что ребра  настолько малы, что в направлении их все рассматриваемые величины
настолько малы, что в направлении их все рассматриваемые величины  не меняются. Так как, кроме тою, все размеры стержня (в том числе и
не меняются. Так как, кроме тою, все размеры стержня (в том числе и  столь малы, что выравнивание электрического потенциала вдоль обкладок можно считать происходящим мгновенно, то напряженность поля
столь малы, что выравнивание электрического потенциала вдоль обкладок можно считать происходящим мгновенно, то напряженность поля  не зависит от кооодинаты х, отсчитываемой вдоль ребра
не зависит от кооодинаты х, отсчитываемой вдоль ребра  Остальные величины будут функциями координат
Остальные величины будут функциями координат 
Если смещение поперечного сечения стержня в точке  обозначить
обозначить  то деформация элемента
то деформация элемента  стержня, очевидно, составит
стержня, очевидно, составит

Разность механических напряжений  по сторонам элемента
по сторонам элемента  должна уравновесить силу инерции и внешнюю силу, действующие на элемент стержня. Для простоты будем считать, что внешняя объемная сила отсутствует. Тогда уравнение движения запишется так:
должна уравновесить силу инерции и внешнюю силу, действующие на элемент стержня. Для простоты будем считать, что внешняя объемная сила отсутствует. Тогда уравнение движения запишется так:

где  плотность материала стержня.
плотность материала стержня.
Уравнение (3.116) надо решить совместно с ур-ниями (3.101) или (3.101а), чтобы найти вид колебаний  Величина тока, текущего через обкладки преобразователя, определится с помощью поляризации:
Величина тока, текущего через обкладки преобразователя, определится с помощью поляризации:

Воспользуемся вторым из ур-ний (3.101) и продифференцируем его по х, помня, что  не зависит от
не зависит от  в данном случае. Тогда получим:
в данном случае. Тогда получим:

Далее, воспользовавшись (3.115), подставим  из (3.118) в (3.116):
из (3.118) в (3.116):

Так как нас интересуют установившиеся синусоидальные колебания стержня под действием синусоидального электрического поля  то естественно, попытаться найти колебание у в виде синусоидальной волны
то естественно, попытаться найти колебание у в виде синусоидальной волны 
Уравнение (3.119) удовлетворяется, если взять

где  произвольные постоянные, зависящие от условий на границах (торцах) стержня, а
произвольные постоянные, зависящие от условий на границах (торцах) стержня, а  Из второго ур-ния (3.101) и соотношений (3.115) и (3.120) найдем механическое напряжение
Из второго ур-ния (3.101) и соотношений (3.115) и (3.120) найдем механическое напряжение 

Теперь с помощью первого ур-ния (3.101) и (3.117) найдем:

Задаваясь условиями на концах стержня  легко найти
легко найти  и полностью определить все параметры преобразователя.
и полностью определить все параметры преобразователя.
Рассмотрим пьезоэлектрический стержневой преобразователь со свободным концом  второй его конец
второй его конец  будем
будем
считать механическим выходом. Перемещение  этого конца и действующая на него сила
этого конца и действующая на него сила  будут, следовательно, определять режим механического выхода. Тогда, очевидно,
будут, следовательно, определять режим механического выхода. Тогда, очевидно,  что даст на основании (3.121) два уравнения для нахождения величин
что даст на основании (3.121) два уравнения для нахождения величин 

Найдя с помощью  и подставив в (3.120) и (3.122), получим искомые уравнения пьезоэлектрического преобразователя, выполненного в виде стержня из пьезоэлектрического материала, работающего на поперечном пьезоэффекте, с одним свободным концом и вторым нагруженным:
и подставив в (3.120) и (3.122), получим искомые уравнения пьезоэлектрического преобразователя, выполненного в виде стержня из пьезоэлектрического материала, работающего на поперечном пьезоэффекте, с одним свободным концом и вторым нагруженным:

где  площадь торца стержня, к которому приложена сила
площадь торца стержня, к которому приложена сила  скорость конца стержня;
скорость конца стержня;  емкость свободного от напряжений стержня;
емкость свободного от напряжений стержня;  ток;
ток;  напряжение на электрической стороне пьезопреобразователя.
напряжение на электрической стороне пьезопреобразователя.
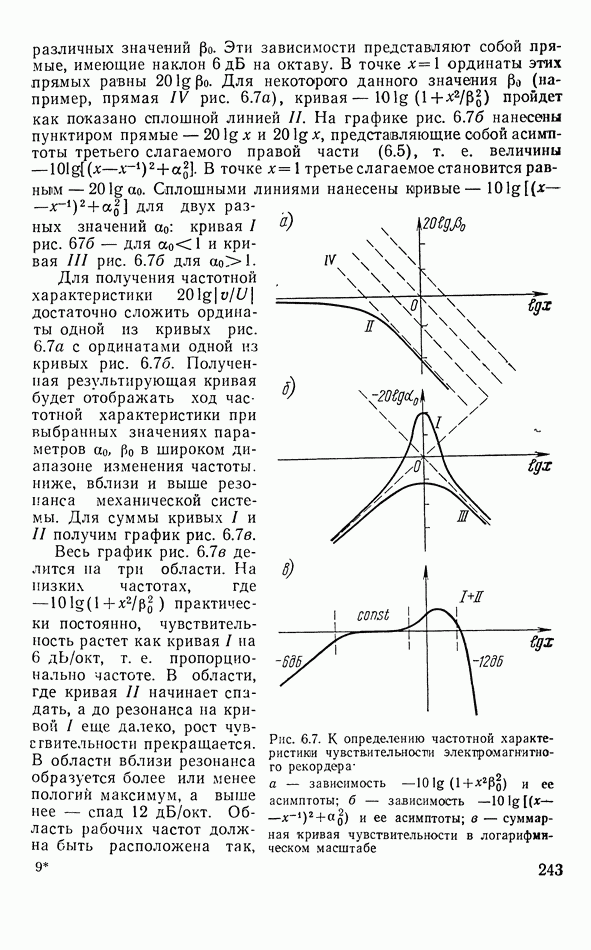
Уравнения написаны в форме у. Коэффициент преобразования рассматриваемого преобразователя  как видно, сложным образом зависит от частоты. Это связано с механическими резонансными свойствами стержня. Величина механической податливости преобразователя в отсутствие электрического напряжения (т. е. когда обкладки преобразователя замкнуты накоротко)
как видно, сложным образом зависит от частоты. Это связано с механическими резонансными свойствами стержня. Величина механической податливости преобразователя в отсутствие электрического напряжения (т. е. когда обкладки преобразователя замкнуты накоротко)  показывает, что в условиях
показывает, что в условиях  при возбуждении силой
при возбуждении силой  стержень ведет себя как обычная механическая линия, по которой распространяются продольные волны сжатия. Если, например, длина стержня значительно меньше длины волны, то
стержень ведет себя как обычная механическая линия, по которой распространяются продольные волны сжатия. Если, например, длина стержня значительно меньше длины волны, то

Так как  масса стержня, то, как и следовало ожидать, в этом случае (т. е. на низкой частоте) стержень под действием силы
масса стержня, то, как и следовало ожидать, в этом случае (т. е. на низкой частоте) стержень под действием силы  движется как сосредоточенная масса. Резонансы сил и скоростей чередуются по мере повышения частоты как обычно:
движется как сосредоточенная масса. Резонансы сил и скоростей чередуются по мере повышения частоты как обычно:  резонансы сил и
резонансы сил и  резонансы скоростей.
резонансы скоростей.
Рассмотрим теперь наш преобразователь при отсутствии нагрузки на механической стороне  Тогда в соответствии со вторым из ур-ний (3.124) ток. текущий через преобразователь, может быть представлен суммой двух токов:
Тогда в соответствии со вторым из ур-ний (3.124) ток. текущий через преобразователь, может быть представлен суммой двух токов:

Первое слагаемое правой части (3.125) представляет собой ток емкости обкладок стержня в отсутствие механических деформаций, второе слагаемое — ток некоторой эквивалентной разомкнутой на конце электрической длинной линии, в которой резонансы токов и напряжений соответствуют механическим резонансам скоростей и сил стержня. При низких частотах, когда  переходит в
переходит в


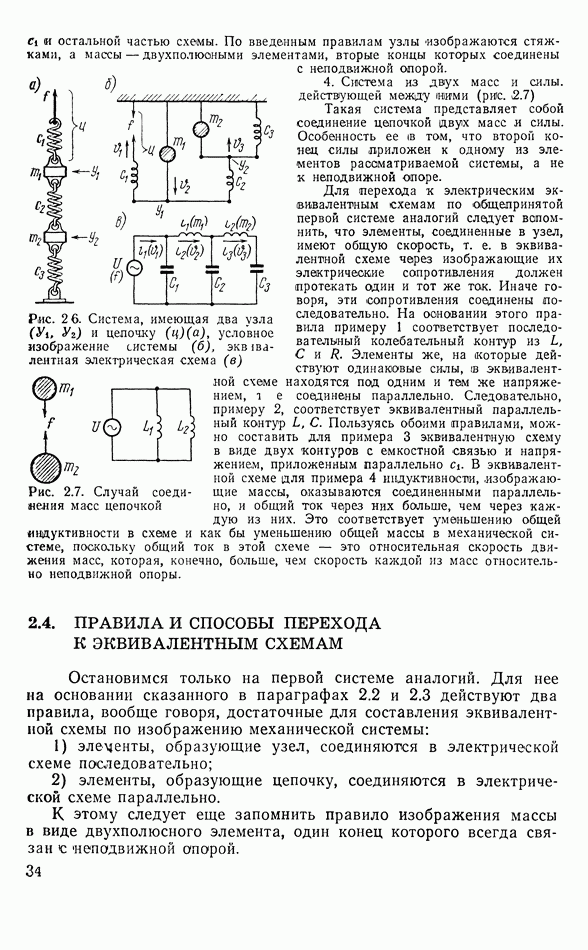
Рис. 3.16. Пьезопреобразователь-двигатель а — эквивалентная схема; б - составляющие тока преобразователя, в — эквивалентные схемы преобразователя вблизи механических резонансов сил и скоростей
На низких частотах, если оба конца стержня свободны, электрическое сопротивление преобразователя соответствует емкости  в отсутствие механических напряжений. Вблизи
в отсутствие механических напряжений. Вблизи  второе слагаемое в правой части (3.125) резко возрастает по абсолютной величине и, проходя через бесконечность, меняет знак, точно так же, как в идеальном электрическом контуре вблизи резонанса напряжений. Тот же ход тока наблюдается при
второе слагаемое в правой части (3.125) резко возрастает по абсолютной величине и, проходя через бесконечность, меняет знак, точно так же, как в идеальном электрическом контуре вблизи резонанса напряжений. Тот же ход тока наблюдается при  пп. На рис. 3.166 изображены зависимости тока
пп. На рис. 3.166 изображены зависимости тока  и его слагаемых от частоты. Под ними на рис. 3.16в изображены эквивалентные электрические схемы преобразователя вблизи механических резонансов сил и скоростей.
и его слагаемых от частоты. Под ними на рис. 3.16в изображены эквивалентные электрические схемы преобразователя вблизи механических резонансов сил и скоростей.
Уравнения (3.124), разрешенные относительно  будут иметь вид
будут иметь вид

где  масса пьезоэлемента.
масса пьезоэлемента.
С помощью этих уравнений можно найти, например, чувствительность холостого хода для приемника механического ускорения (акселерометра):  .
.
Из второго ур-ния (3.127) получим

При  эта величина постоянна и равна
эта величина постоянна и равна  т. е. пропорциональна константе Харкевича и погонной массе кристалла.
т. е. пропорциональна константе Харкевича и погонной массе кристалла.
Легко также показать, что при  ур-ния (3.127) переходят в (3.105). При
ур-ния (3.127) переходят в (3.105). При  чувствительность акселерометра падает в
чувствительность акселерометра падает в  раз, при
раз, при  т. е. когда
т. е. когда  близок к нулю
близок к нулю  чувствительность благодаря механическому резонансу неограниченно возрастает.
чувствительность благодаря механическому резонансу неограниченно возрастает.

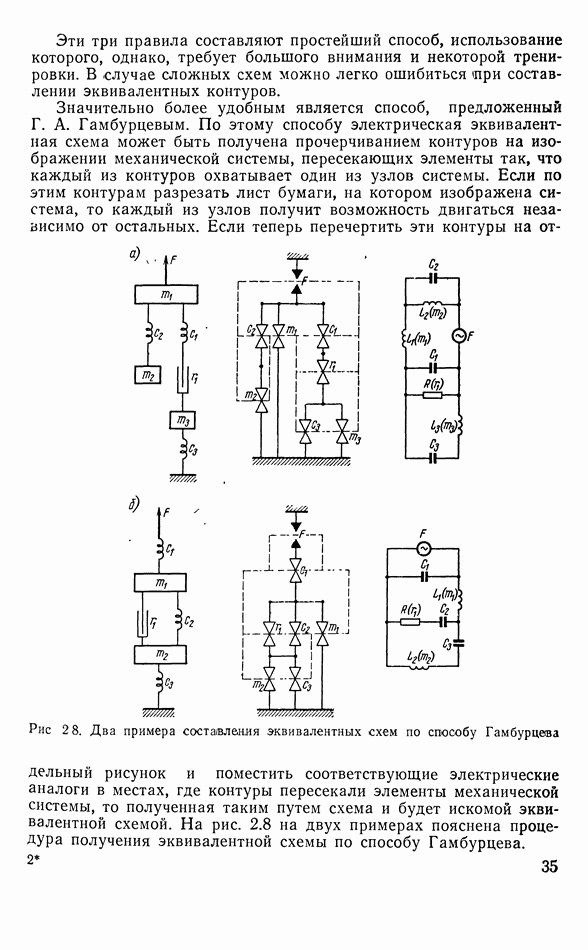
Рис. 3.17. Чувствительность пьезоакселерсметра в зависимости от частоты
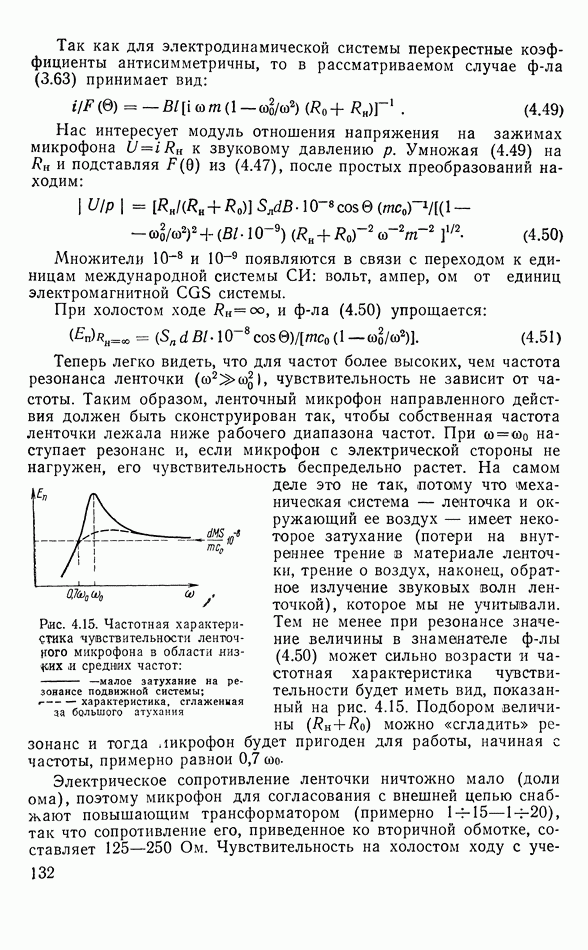
В действительности, вследствие затухания звука в кристалле, наблюдается резонансный пик (рис. 3.17).
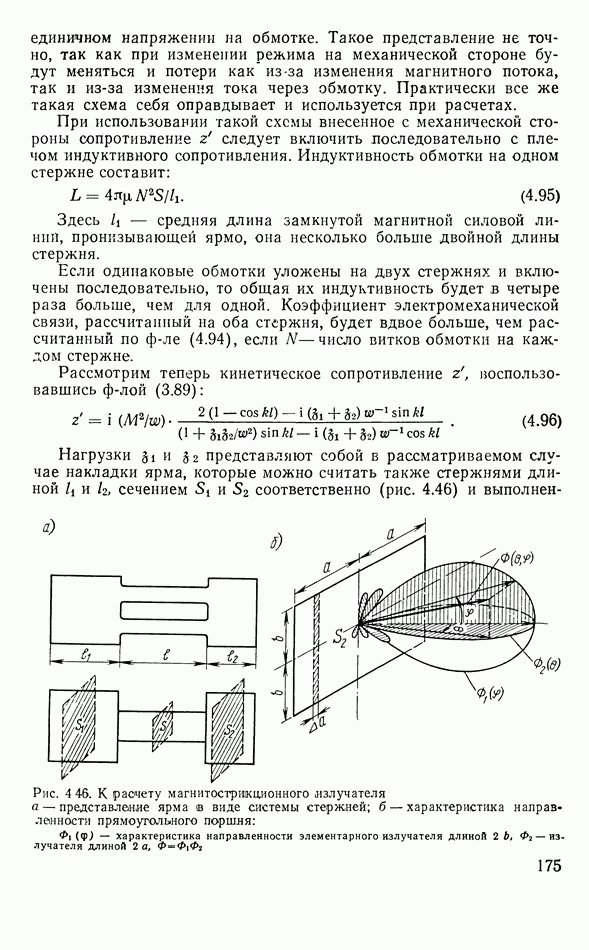
При использовании такого пьезоэлемента как полуволновый излучатель  его чувствительность при излучении плоской волны на основании первого из ур-ний (3.127) и соотношения для нагрузки излучения
его чувствительность при излучении плоской волны на основании первого из ур-ний (3.127) и соотношения для нагрузки излучения  составит:
составит:

где  отношение волновых сопротивлений среды
отношение волновых сопротивлений среды  и кристалла
и кристалла 
Такой пьезоэлемент представляет интерес и как четвертьволновой излучатель, при  Точное условие резонанса:
Точное условие резонанса:  Коэффициенты при
Коэффициенты при  в первом из уравнений (3.127) при этом беапредельно возрастают и отношение
в первом из уравнений (3.127) при этом беапредельно возрастают и отношение  можно получить разделив коэффициент при
можно получить разделив коэффициент при  на коэффициент при
на коэффициент при  Умножив это отношение на волновое сопротивление среды и положив
Умножив это отношение на волновое сопротивление среды и положив  (получим искомую чувствительность
(получим искомую чувствительность  Расчет дает величину отличающуюся от чувствительности полуволнового излучателя в и раз. Если волновое сопротивление среды больше чем у кристалла
Расчет дает величину отличающуюся от чувствительности полуволнового излучателя в и раз. Если волновое сопротивление среды больше чем у кристалла  то четвертьволновой излучатель эффективнее.
то четвертьволновой излучатель эффективнее.
Аналогичным путем можно найти уравнение для пьезоэлемента, который с одной стороны укреплен неподвижно и находится под воздействием силы с другой стороны:

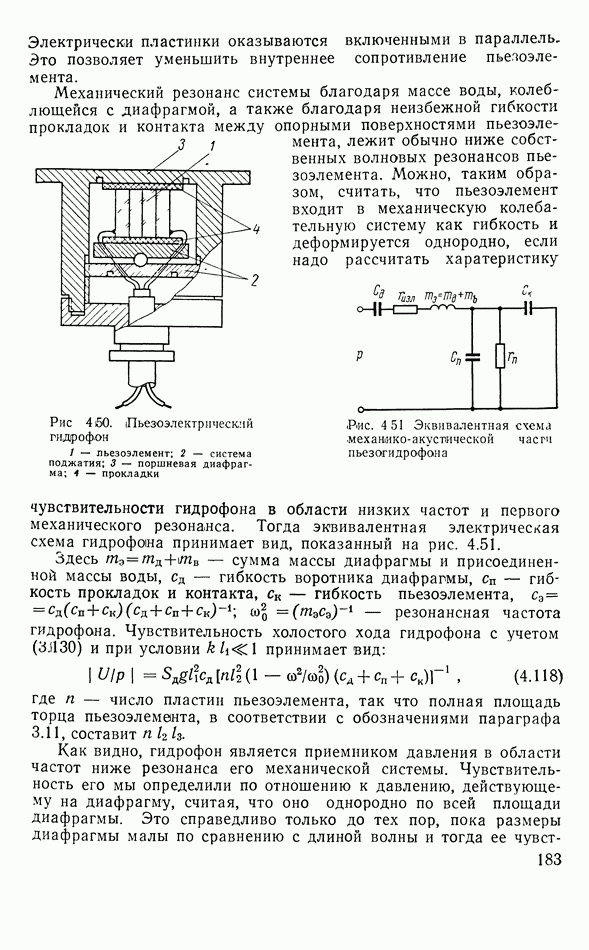
Чувствительность такого пьезоэлемента, как приемника давления, имеет вид:

При  имеем
имеем  как и следовало ожидать. При
как и следовало ожидать. При  наступает первый резонанс. При грубом приближении
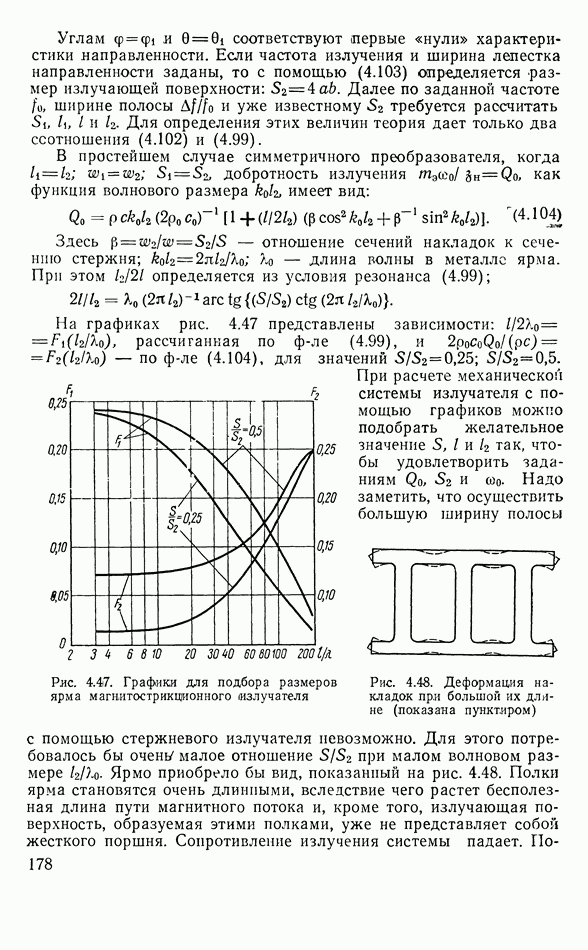
наступает первый резонанс. При грубом приближении  с увеличением частоты чувствительность в среднем падает как
с увеличением частоты чувствительность в среднем падает как  (наблюдаются резонансные выбросы чувствительности, а при
(наблюдаются резонансные выбросы чувствительности, а при  минимумы.
минимумы.

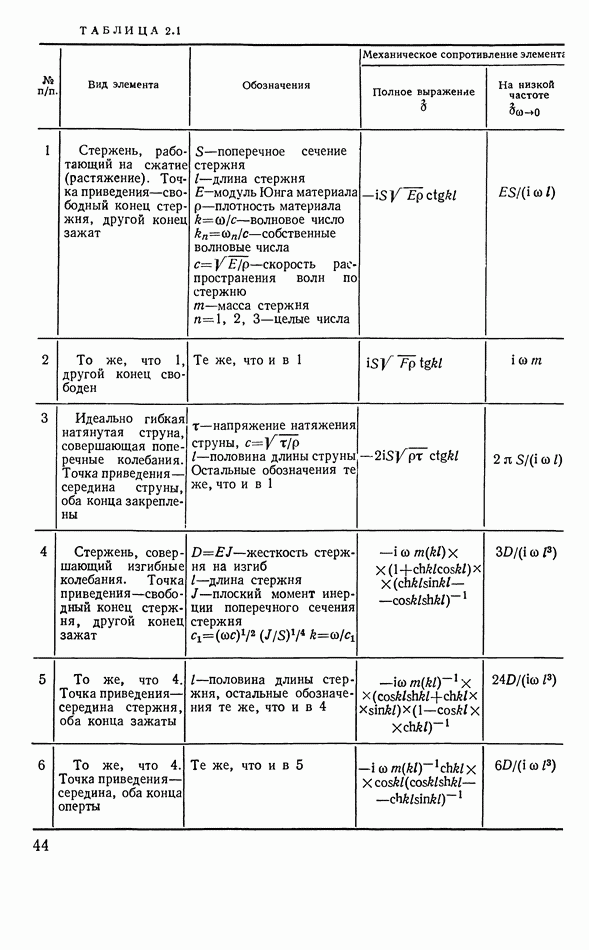
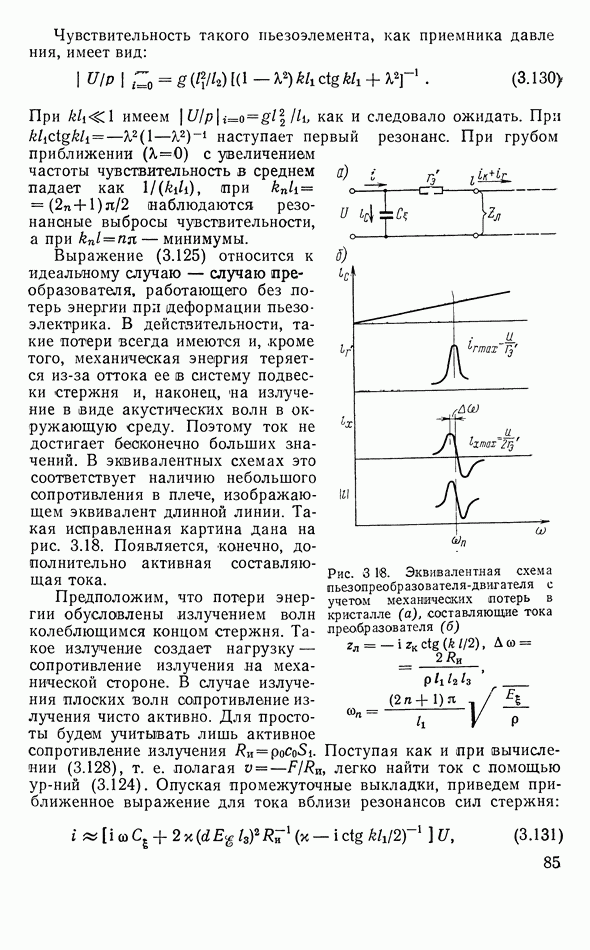
Рис. 3 18. Эквивалентная схема пьезопреобразователя-двигателя с учетом механических потерь в кристалле  составляющие тока преобразователя
составляющие тока преобразователя  .
.
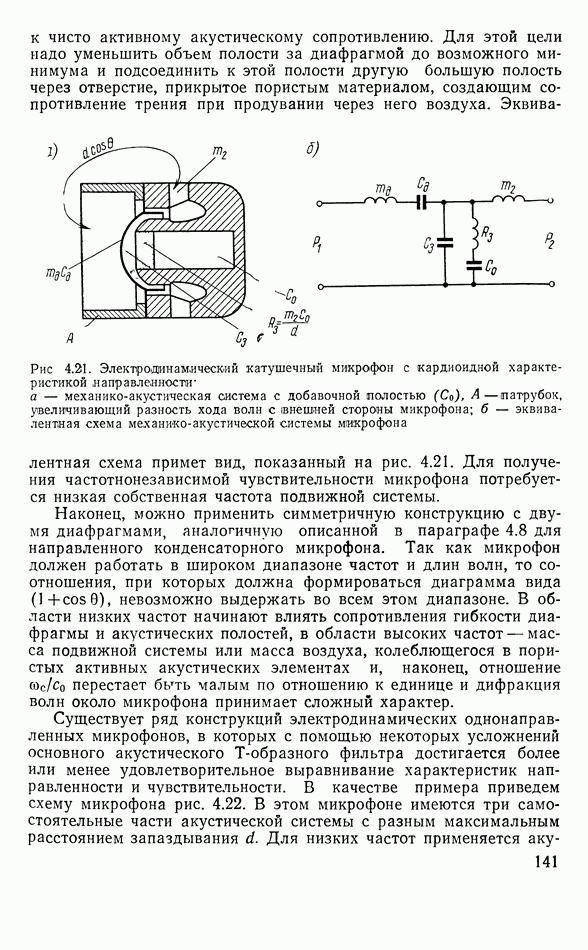
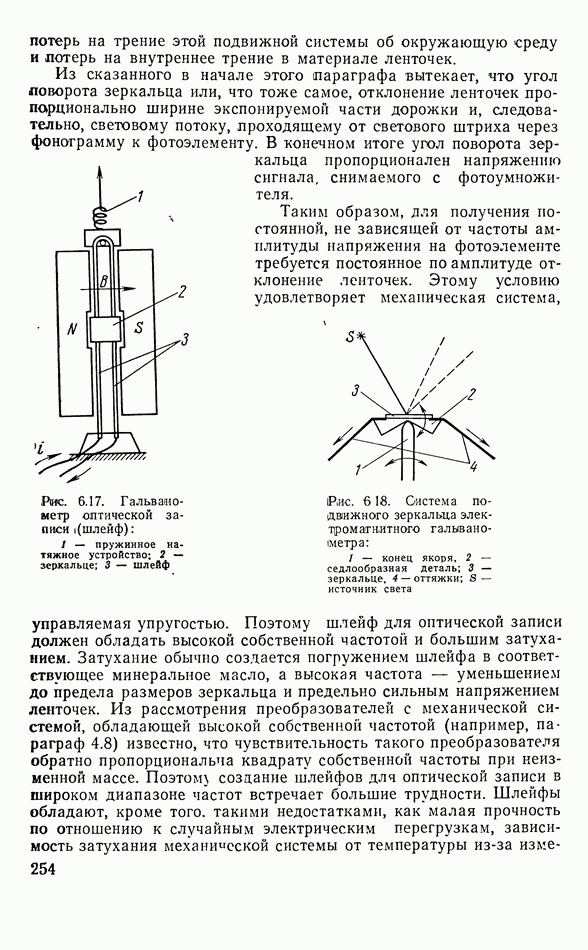
Выражение (3.125) относится к идеальному случаю — случаю преобразователя, работающего без потерь энергии при деформации пьезоэлектрика. В действительности, такие потери всегда имеются и, кроме того, механическая энергия теряется из-за оттока ее в систему подвески стержня и, наконец, на излучение в виде акустических волн в окружающую среду. Поэтому ток не достигает бесконечно больших значений. В эквивалентных схемах это соответствует наличию небольшого сопротивления в плече, изображающем эквивалент длинной линии. Такая исправленная картина дана на рис. 3.18. Появляется, конечно, дополнительно активная составляющая тока.
Предположим, что потери энергии обусловлены излучением волн колеблющимся концом стержня. Такое излучение создает нагрузку — сопротивление излучения на механической стороне. В случае излучения плоских волн сопротивление излучения чисто активно. Для простоты будем учитывать лишь активное сопротивление излучения  Поступая как и при вычислении (3.128), т. е. полагая
Поступая как и при вычислении (3.128), т. е. полагая  легко найти ток с помощью ур-ний (3.124). Опуская промежуточные выкладки, приведем приближенное выражение для тока вблизи резонансов сил стержня:
легко найти ток с помощью ур-ний (3.124). Опуская промежуточные выкладки, приведем приближенное выражение для тока вблизи резонансов сил стержня:

где  отношение акустического сопротивления излучения к волновому механическому сопротивлению пьезоэлектрического стержня.
отношение акустического сопротивления излучения к волновому механическому сопротивлению пьезоэлектрического стержня.
Перепишем (3.131) несколько иначе

Теперь видно, что эквивалентная электрическая схема преобразователя должна быть составлена из двух параллельных ветвей (см. рис. 3.18). Первая из них, как и раньше, — емкость зажатого кристалла, а вторая — длинная разомкнутая на конце линия, включенная последовательно с активным сопротивлением. Величина эквивалентного сопротивления определяется выражением 
Величина волнового сопротивления линии  Разделив вещественную и мнимую составляющие тока во втором слагаемом правой части (3.131), получим следующее выражение для тока на входе преобразователя:
Разделив вещественную и мнимую составляющие тока во втором слагаемом правой части (3.131), получим следующее выражение для тока на входе преобразователя:

где 

На рис. 3.186 изображены все три составляющие тока преобразователя и модуль суммарного тока вблизи первого резонанса сил.
Если механические параметры преобразователя привести к его механическому выходу, то вблизи резонанса его можно заменить эквивалентной массой  гибкостью
гибкостью  и активным сопротивлением Внесенные в электрическую цепь эквиваленты соответственно представляются в виде:
и активным сопротивлением Внесенные в электрическую цепь эквиваленты соответственно представляются в виде:

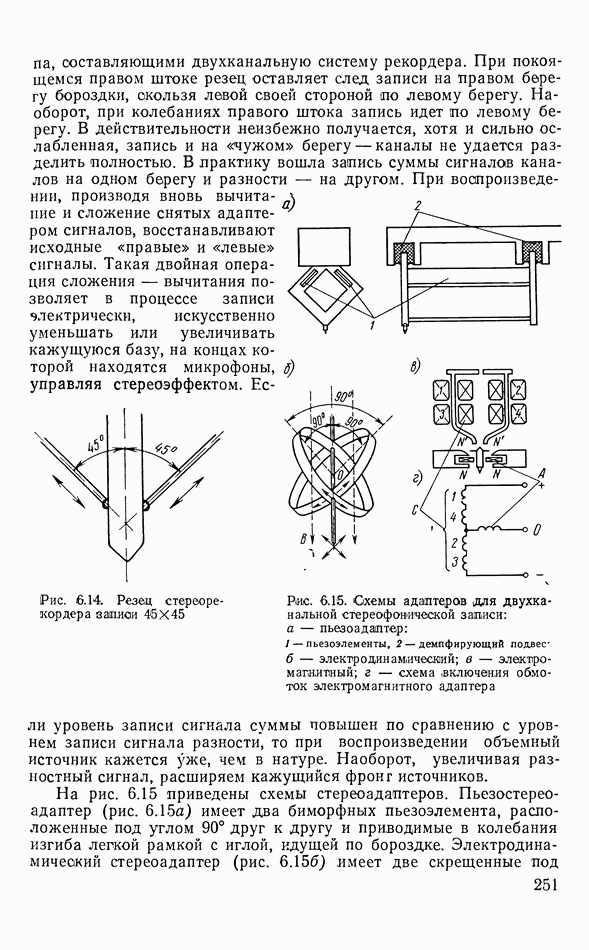
Рассмотренный случай соответствует пьезопреобразователю с неоднородной деформацией при поперечном пьезоэффекте. Аналогичное рассмотрение можно провести и при продольном пьезоэффекте. В этой случае направления электрического поля и механической деформации совпадают. Так как деформация неоднородна, то и напряженность поля будет функцией расстояния вдоль
стержня  Зато поляризация
Зато поляризация  очевидно, в любом поперечном сечении, перпендикулярном оси х, одинакова. Тогда для составления уравнений преобразователя удобнее пользоваться местными уравнениями в форме
очевидно, в любом поперечном сечении, перпендикулярном оси х, одинакова. Тогда для составления уравнений преобразователя удобнее пользоваться местными уравнениями в форме  откуда вследствие
откуда вследствие  следует
следует  и равенство (3.119) примет вид:
и равенство (3.119) примет вид:

Теперь, как видно, скорость распространения механической волны определяется модулем упругости в отсутствие поляризации  Дальнейший ход выкладок аналогичен предыдущему примеру, однако, отыскивать придется не ток
Дальнейший ход выкладок аналогичен предыдущему примеру, однако, отыскивать придется не ток  (который теперь прямо определяется через поляризацию
(который теперь прямо определяется через поляризацию  а напряжение на обкладках
а напряжение на обкладках  с помощью второго из ур-ния (3.101а) и ур-ния (3.133). Для пьезопреобразователя с продольным пьезоэффектом, у которого один конец пьезоэлемента свободен, получим уравнения:
с помощью второго из ур-ния (3.101а) и ур-ния (3.133). Для пьезопреобразователя с продольным пьезоэффектом, у которого один конец пьезоэлемента свободен, получим уравнения:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
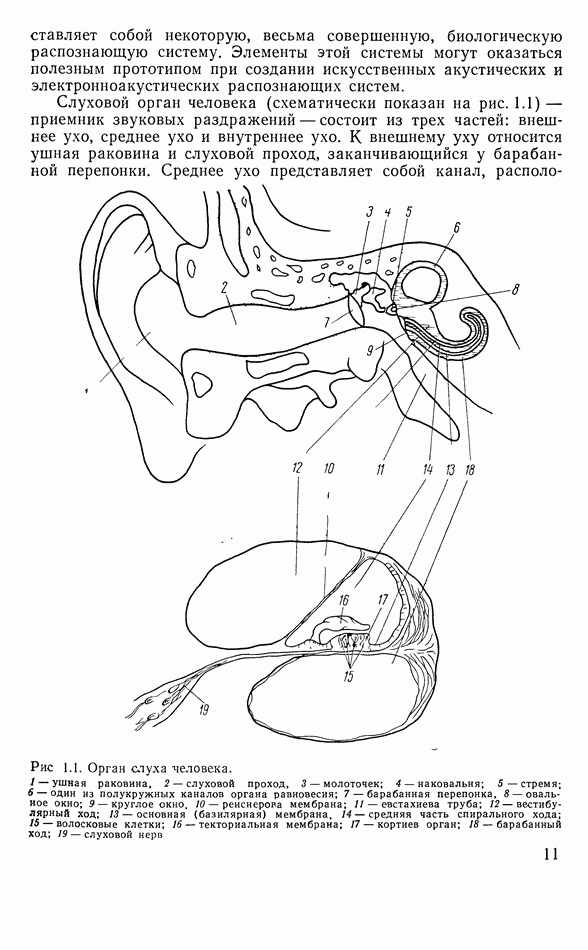
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
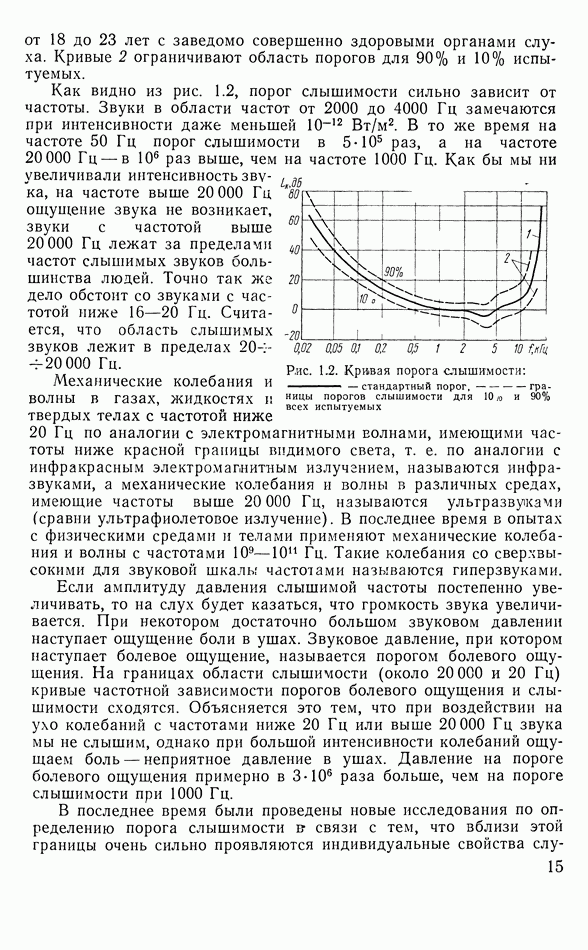
- 1.4. ПОРОГ СЛЫШИМОСТИ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
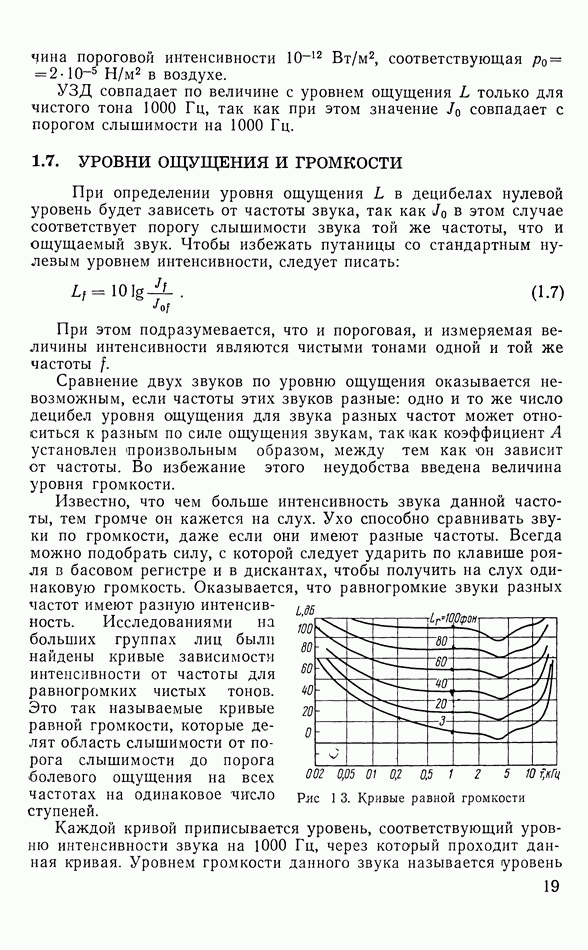
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
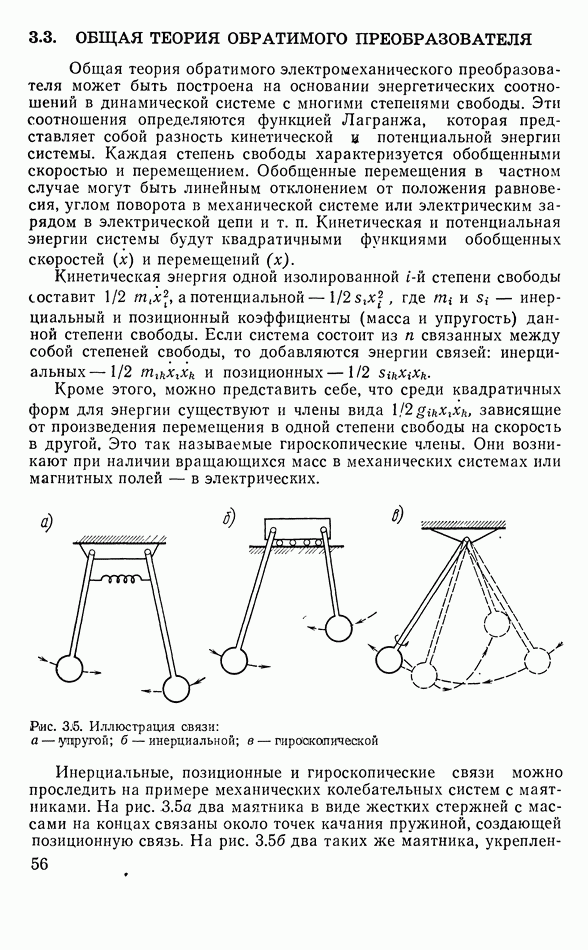
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
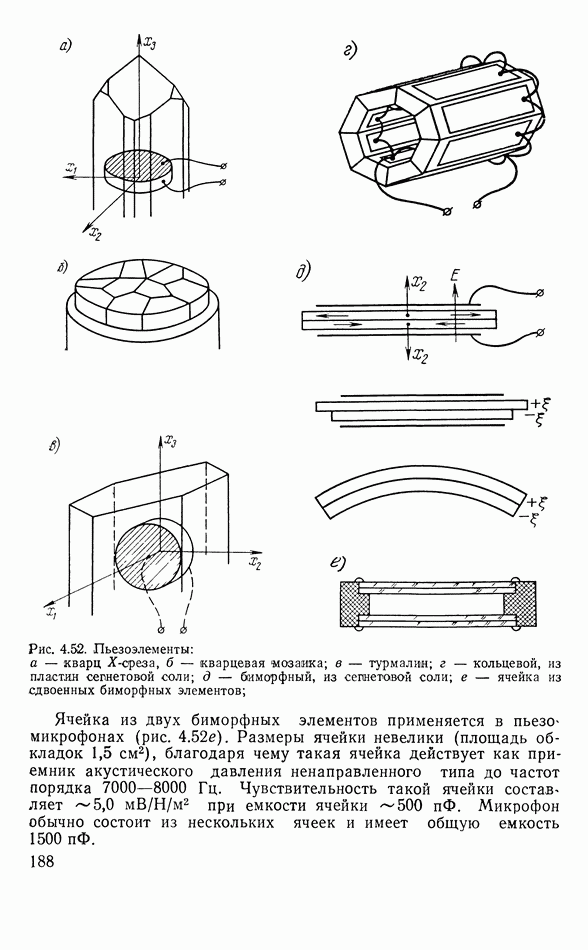
- Преобразователь с однородной деформацией
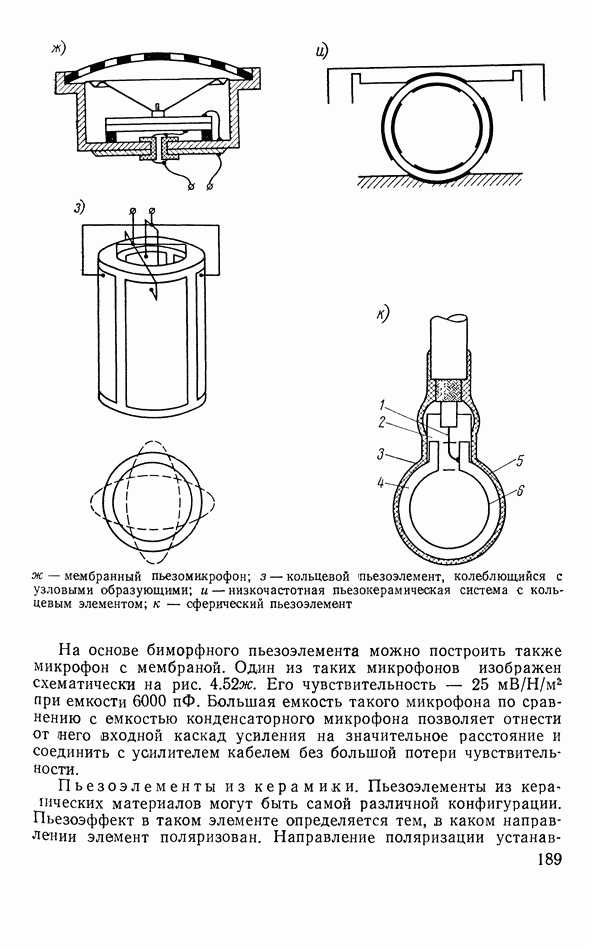
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
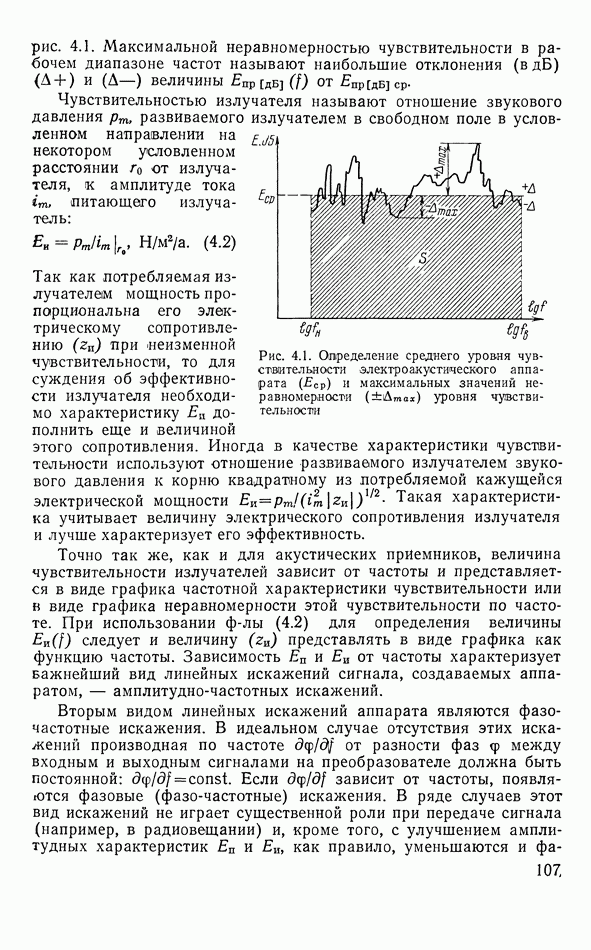
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
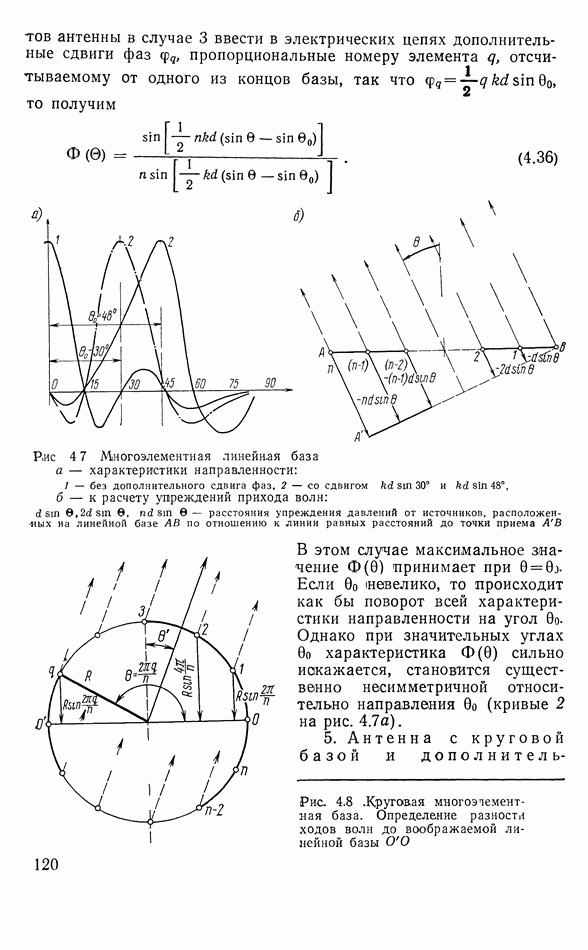
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
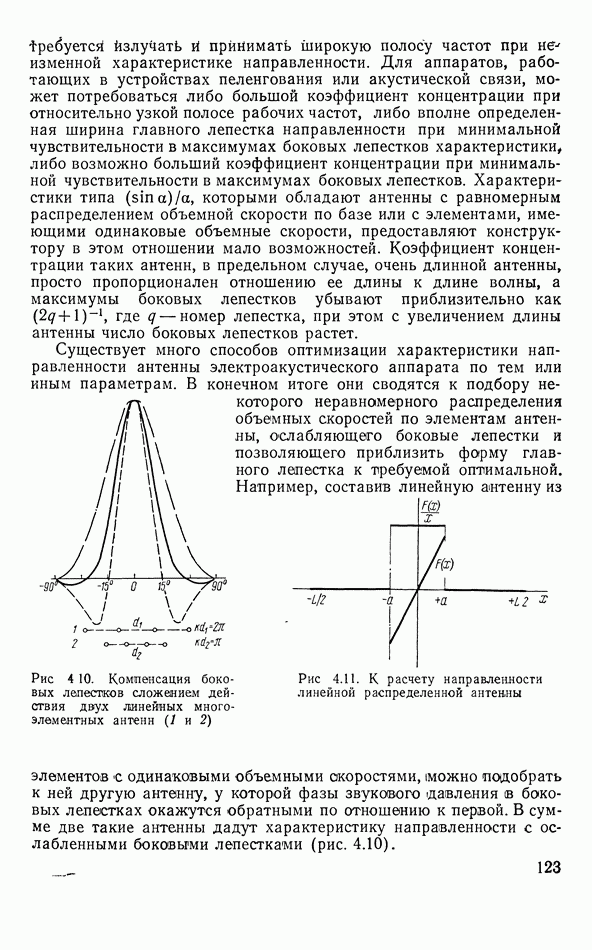
- Оптимизация характеристики направленности антенны
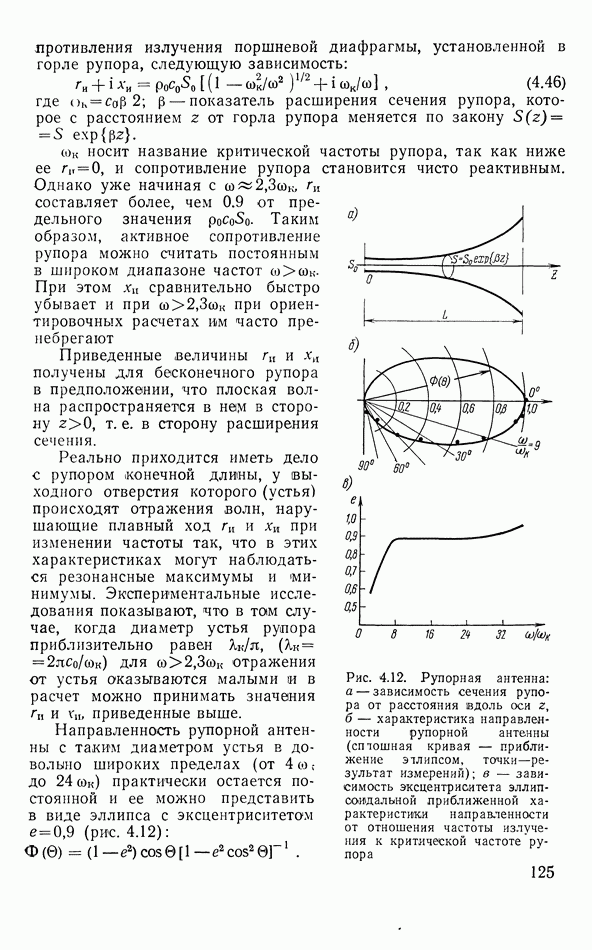
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
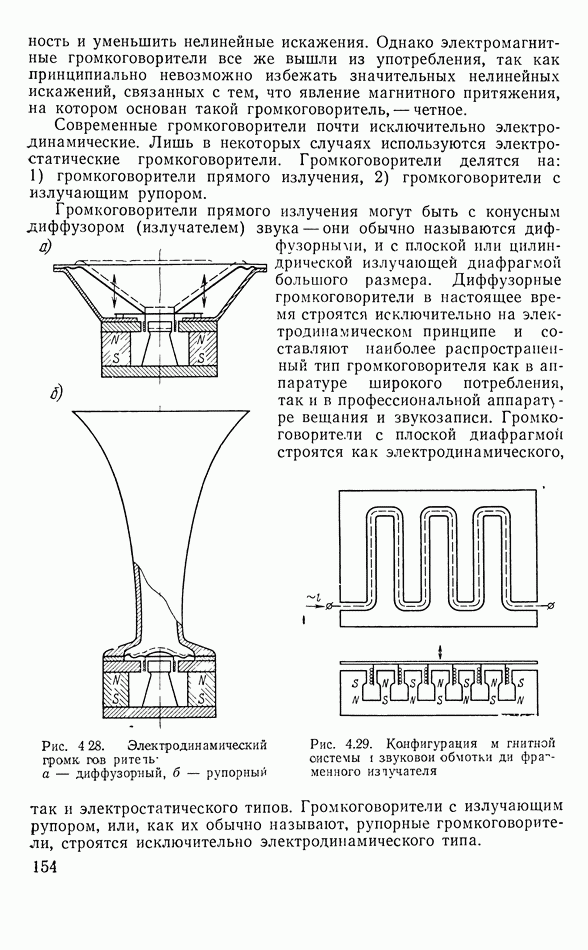
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
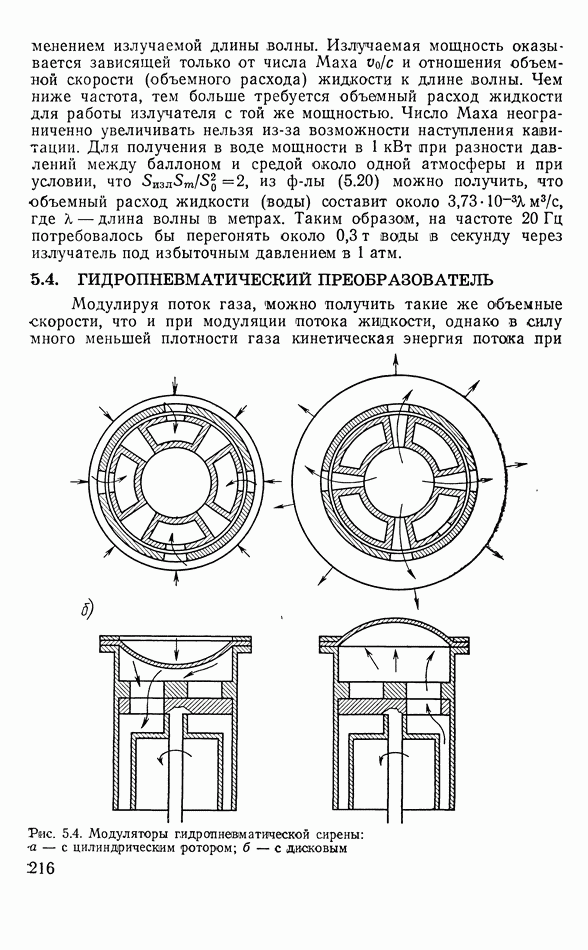
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
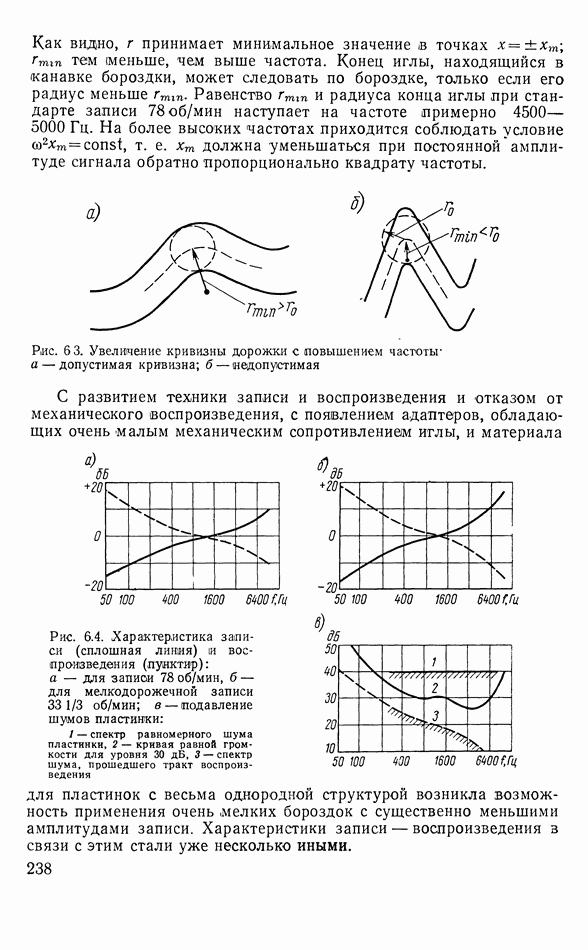
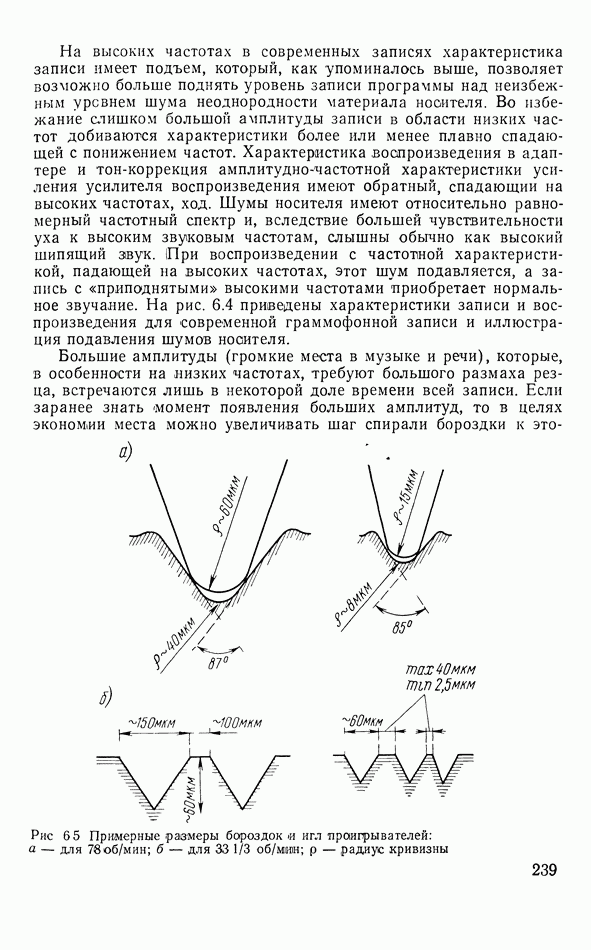
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
- Головки записи и воспроизведения
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
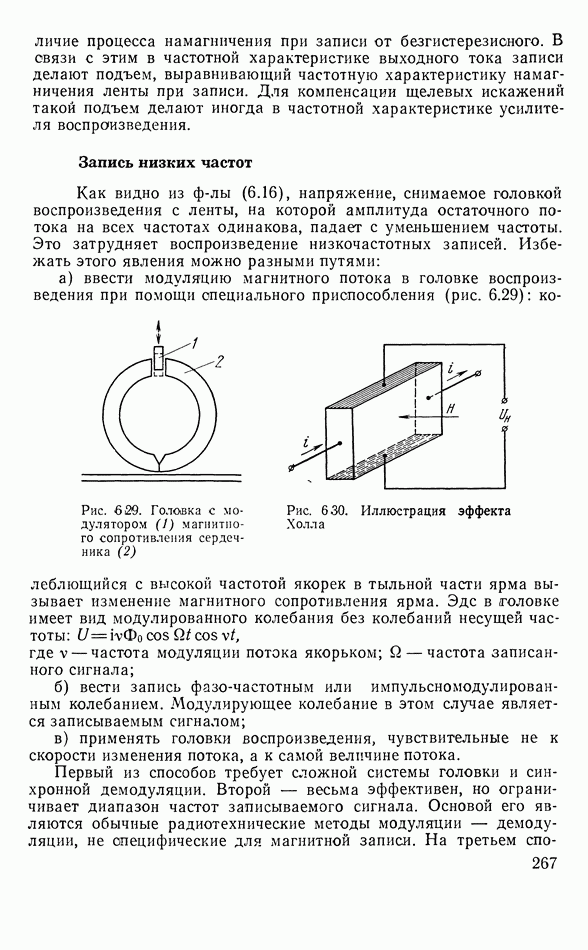
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы