| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5.2. Конструктивные алгоритмы
Предшественником конструктивных алгоритмов можно считать методику обучения многослойных нейронных сетей, включающую в себя следующие шаги:
ШАГ 1. Выбор начального числа нейронов в скрытых слоях.
ШАГ 2. Инициализация сети, заключающаяся в присваивании синаптическим весам и смещениям сети случайных значений из заданного диапазона.
ШАГ 3. Обучение сети по заданной выборке.
ШАГ 4. Завершение в случае успешного обучения. Если сеть обучить не удалось, то число нейронов увеличивается и повторяются шаги со второго по четвертый.
В конструктивных алгоритмах число нейронов в скрытых слоях также изначально мало и постепенно увеличивается В отличие от этой методики, в конструктивных алгоритмах сохраняются навыки, приобретенные сетью до увеличения числа нейронов.
Конструктивные алгоритмы различаются правилами задания значений параметров в новых, добавленных в сеть, нейронах:
• значения параметров являются случайными числами из заданного диапазона;
• значения синаптических весов нового нейрона определяются путем расщепления (splitting) одного из старых нейронов
Первое правило не требует значительных вычислений, однако его использование приводит к некоторому увеличению значения функции ошибки после каждого добавления нового нейрона. В результате случайного задания значений параметров новых нейронов может появиться избыточность в числе нейронов скрытого слоя Расщепление нейронов лишено двух указанных недостатков Суть алгоритма расщепления проиллюстрирована на рис 1 7
На этом рисунке показан вектор весов нейрона скрытого слоя на некотором шаге обучения и векторы изменения весов, соответствующие отдельным обучающим примерам. Векторы изменений имеют два преимущественных направления и образуют в пространстве область, существенно отличающуюся от сферической. Суть алгоритма заключается в выявлении и расщеплении таких нейронов В результате расщепления вместо одного исходного в сети оказывается два нейрона. Первый из этих нейронов имеет вектор весов, представляющий из себя сумму вектора весов исходного нейрона и векторов изменений весов одного из

Рис. 1.7. Вектор весов нейрона скрытого слоя и изменения, соответствующие отдельным обучающим примерам
преимущественных направлений. В результате суммирования векторов изменений весов другого преимущественного направления и вектора весов исходного нейрона получают синаптические веса второго нового нейрона.
Расщеплять нейроны, векторы изменений которых имеют два преимущественных направления, необходимо потому, что наличие таких нейронов приводит к осцилляциям при обучении методом обратного распространения. При обучении методом с интегральной функцией ошибки наличие таких нейронов приводит к попаданию в локальный минимум с большим значением ошибки.
Алгоритм расщепления включает в себя:
• построение ковариационной матрицы векторов изменений синаптических весов;
• вычисление собственных векторов и собственных значений полученной матрицы с помощью итерационного алгоритма  в соответствии с которым выполняется стохастический градиентный подъем и ортогонализация Грамма-Шмидта.
в соответствии с которым выполняется стохастический градиентный подъем и ортогонализация Грамма-Шмидта.
Недостатком алгоритма является экспоненциальный рост времени вычислений при увеличении размерности сети.
Для преодоления указанного недостатка предложен упрощенный алгоритм расщепления, который не требует значительных вычислений. Общее число нейронов в сети, построенной с помощью этого алгоритма по заданной обучающей выборке, может быть несколько больше, чем у сети, построенной с помощью исходного алгоритма.
В упрощенном алгоритме для расщепления выбирается нейрон с наибольшим значением функционала:

где  вектор изменений синаптических весов нейрона;
вектор изменений синаптических весов нейрона;  - номер нейрона;
- номер нейрона;  число нейронов; к - номер обучающего примера;
число нейронов; к - номер обучающего примера;  число примеров в обучающей выборке.
число примеров в обучающей выборке.
Таким образом, в качестве критерия выбора нейрона для расщепления используется отношение суммы длин векторов изменений синаптических весов нейрона, соответствующих различным обучающим примерам, к длине суммы этих векторов.
В результате расщепления вместо исходного нейрона в сеть вводятся два новых нейрона. Значение каждого синаптического веса нового нейрона есть значение соответствующего веса старого нейрона плюс некоторый небольшой шум. Величины весов связей выходов новых нейронов и нейронов следующего слоя равны половине величин весов связей исходного нейрона с соответствующими весами следующего слоя. Упрощенный алгоритм, как и исходный, гарантирует, что функция ошибки после расщепления увеличиваться не будет.
Кроме описанных способов выбора нейронов для расщепления, может быть использован анализ чувствительности, в процессе которого строятся матрицы Гессе для вторых производных функции ошибки по параметрам сети. По величине модуля второй производной судят о важности значения данного параметра для решения задачи. Параметры с малыми значениями вторых производных обнуляют. Анализ чувствительности требует больших вычислительных ресурсов.
Дополнительная информация об алгоритмах обучения приведена в приложении.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
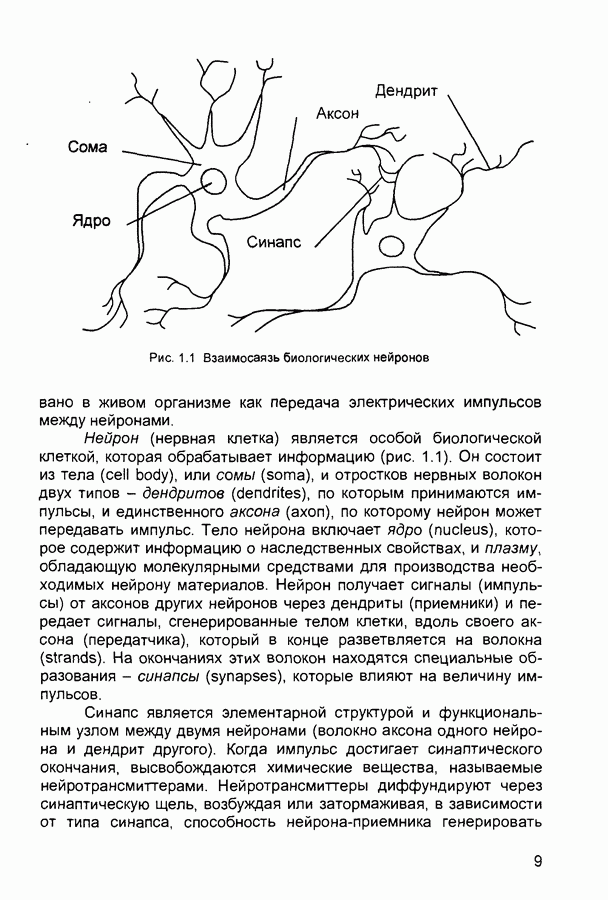
- 1.1. Биологический нейрон
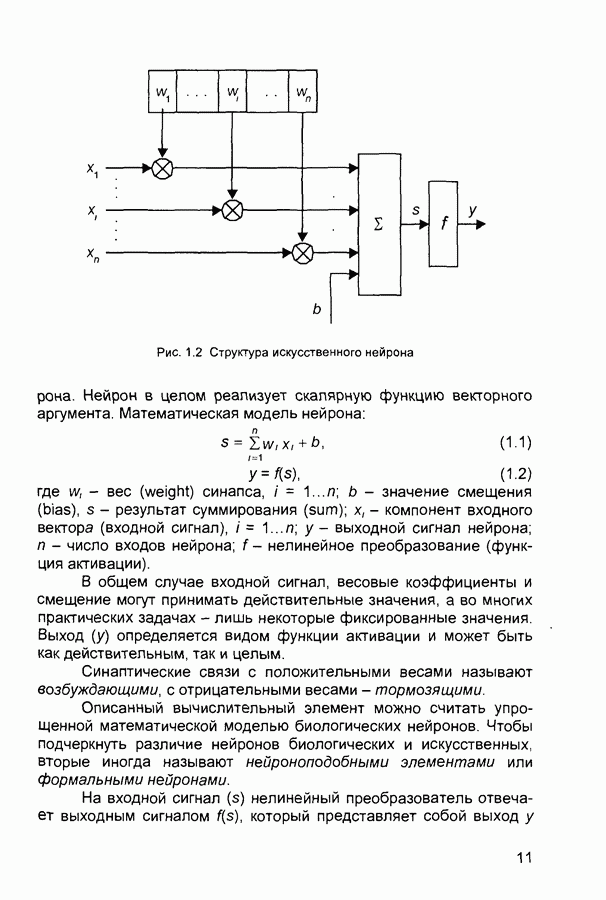
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
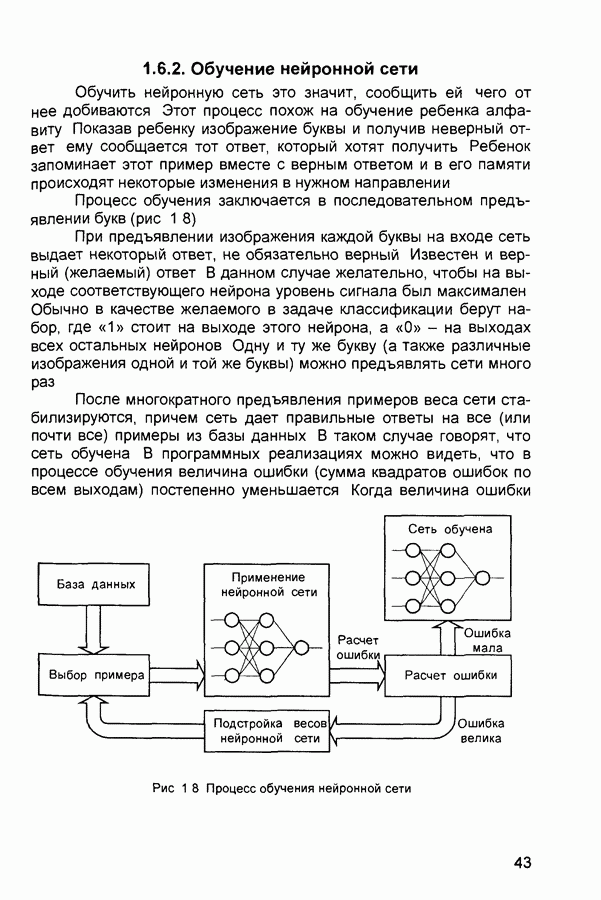
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
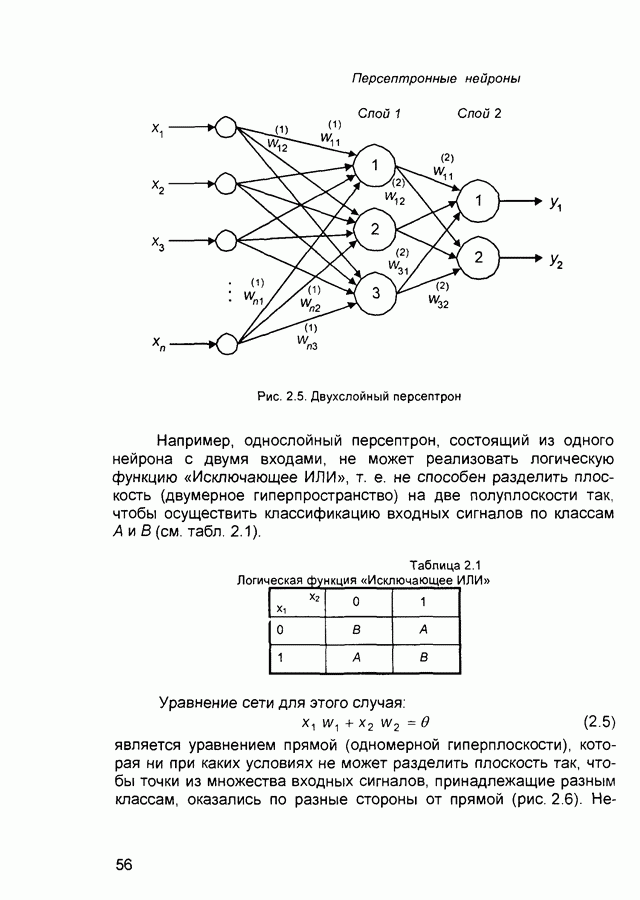
- 2.2. Персептроны
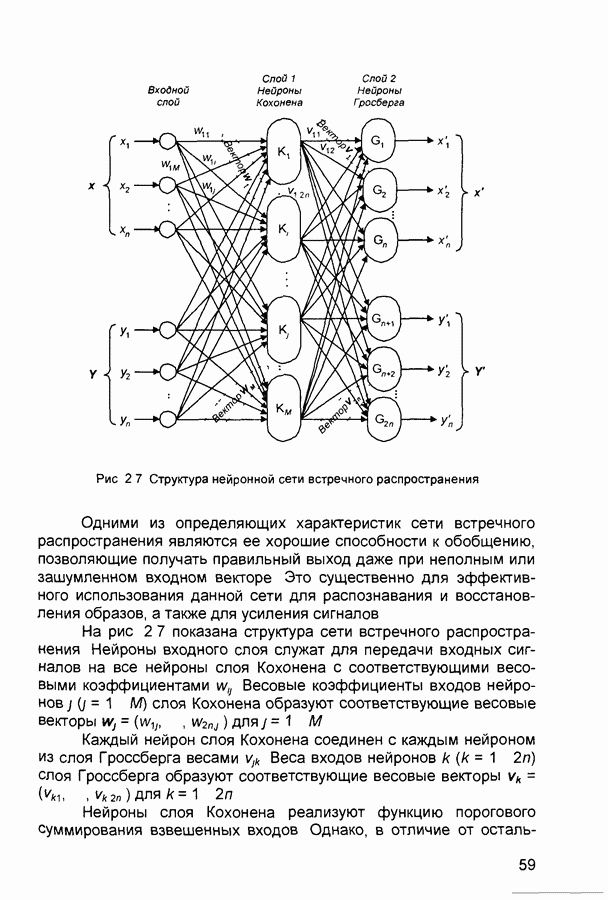
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
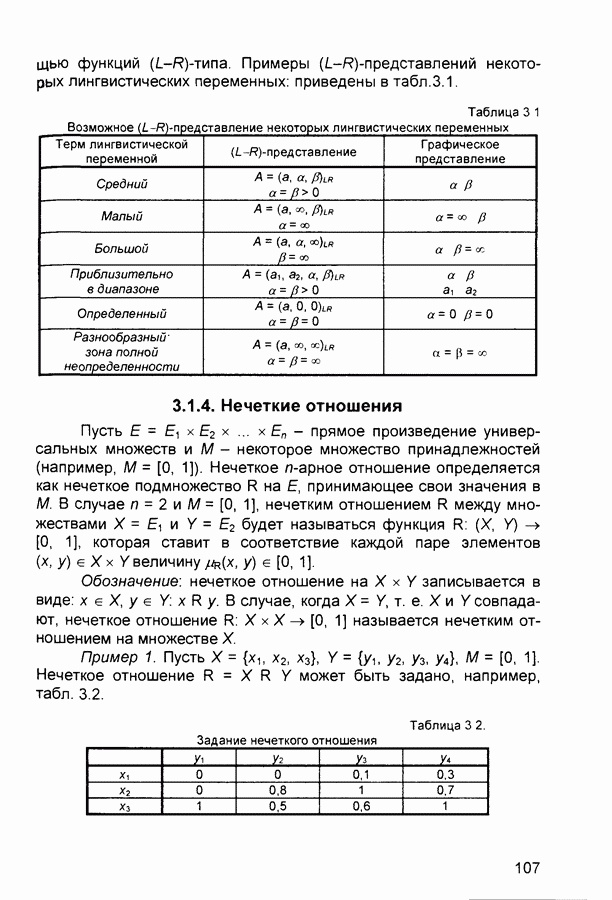
- 3.1.4. Нечеткие отношения
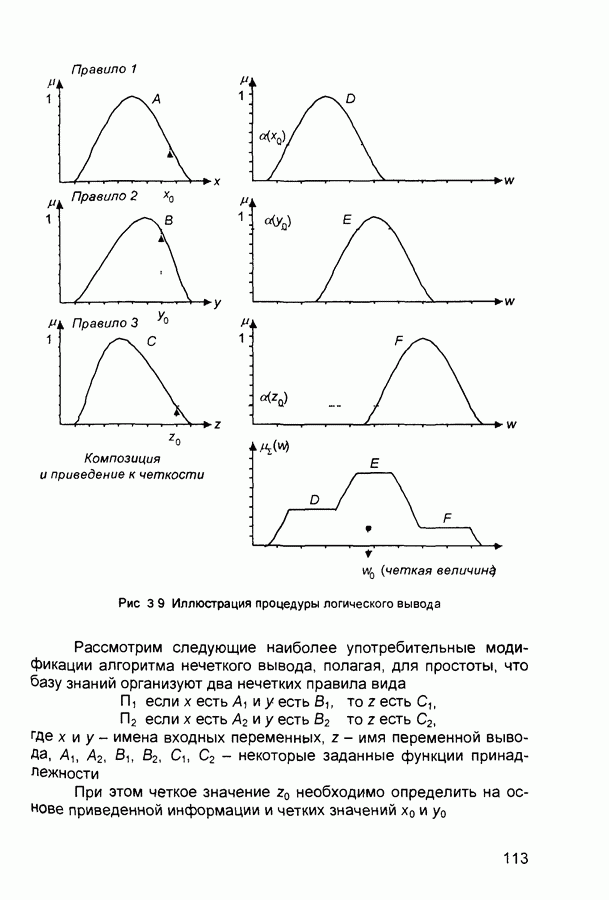
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
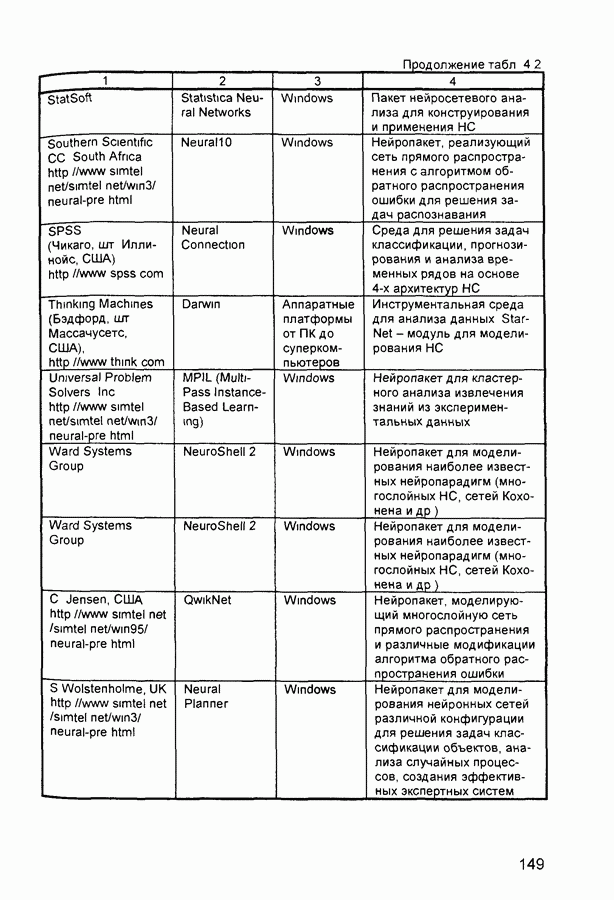
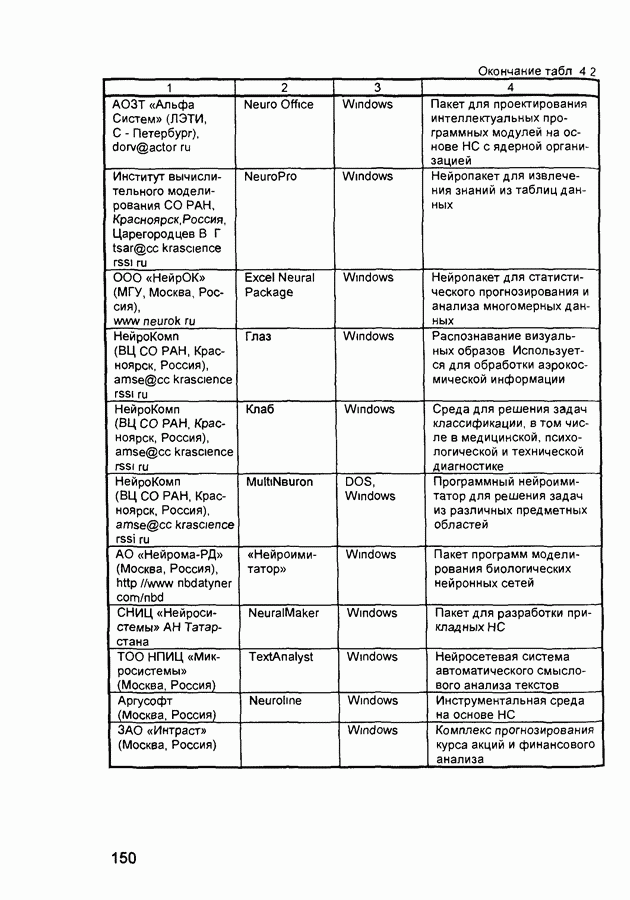
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
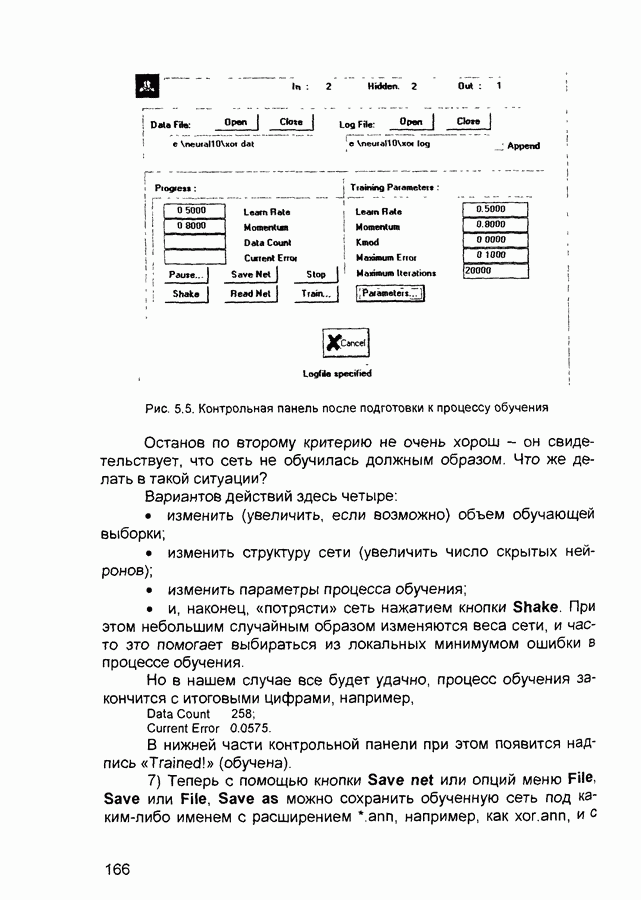
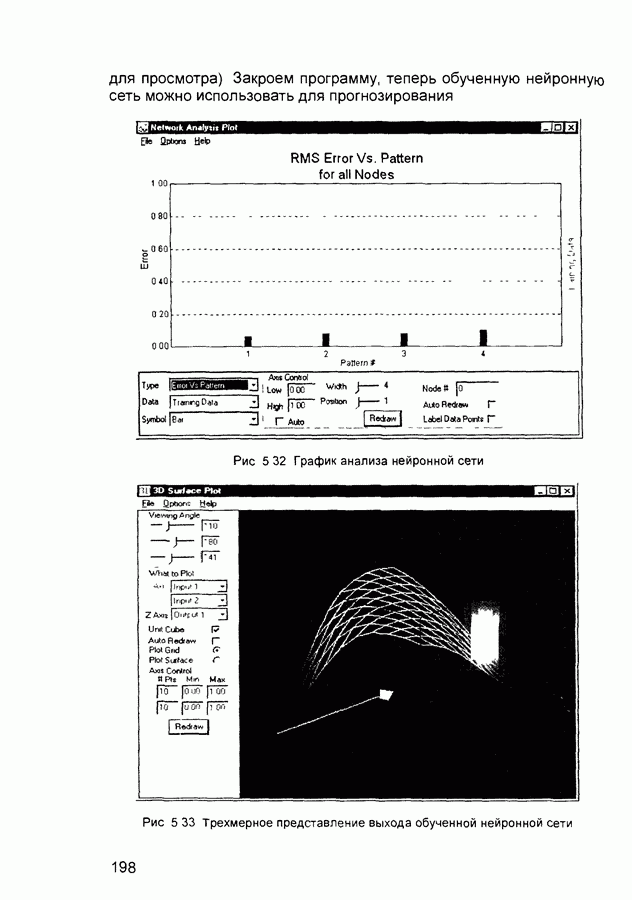
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
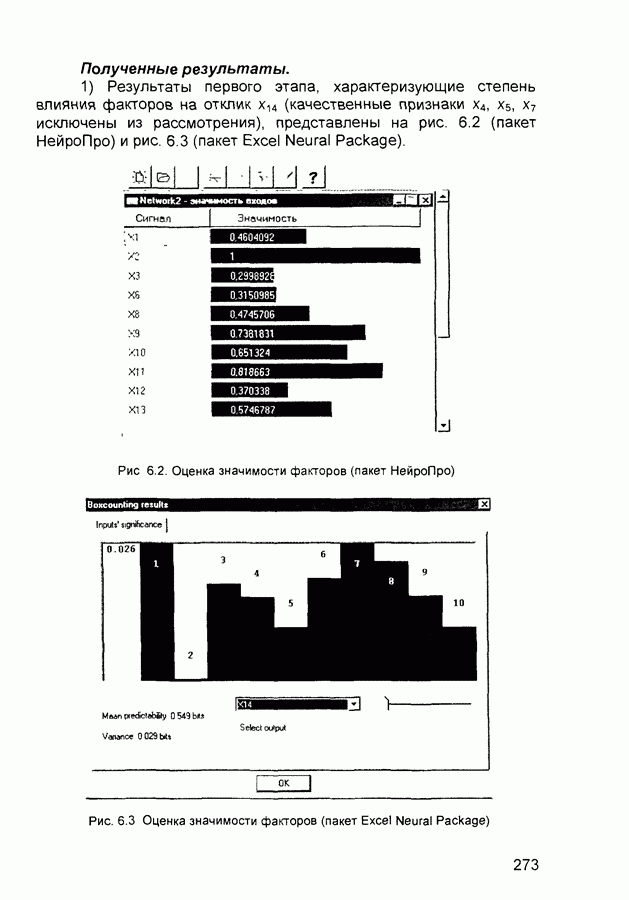
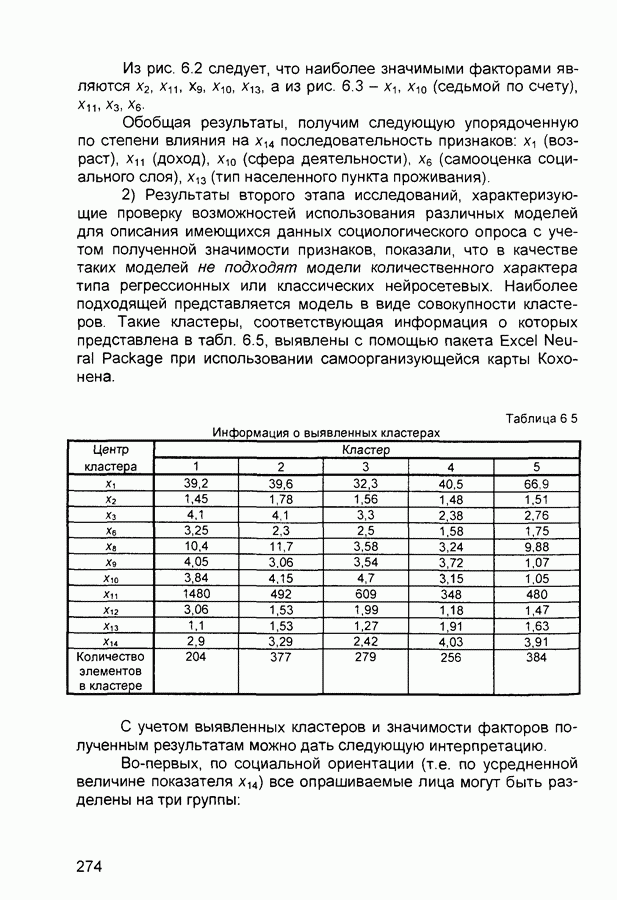
- 6.2. Анализ данных социологического опроса
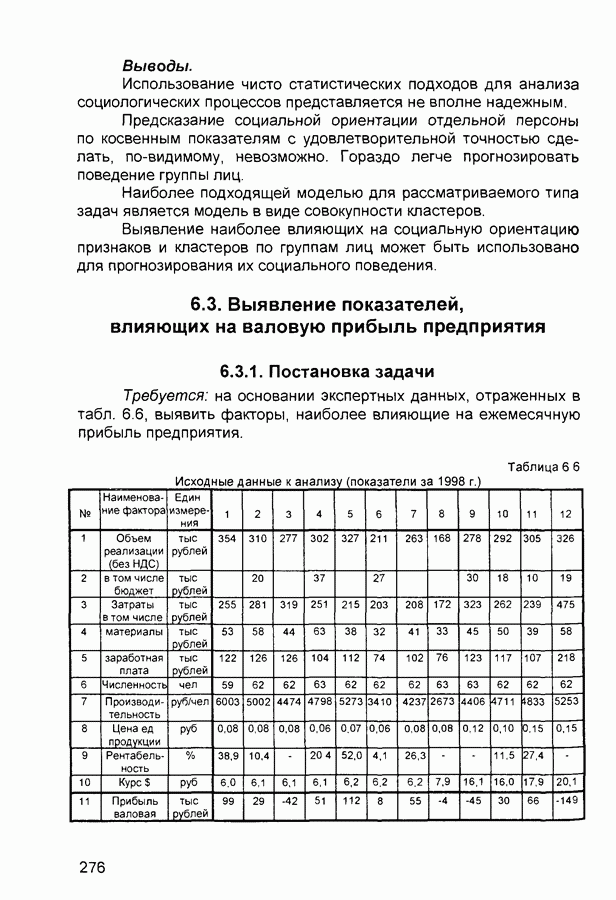
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
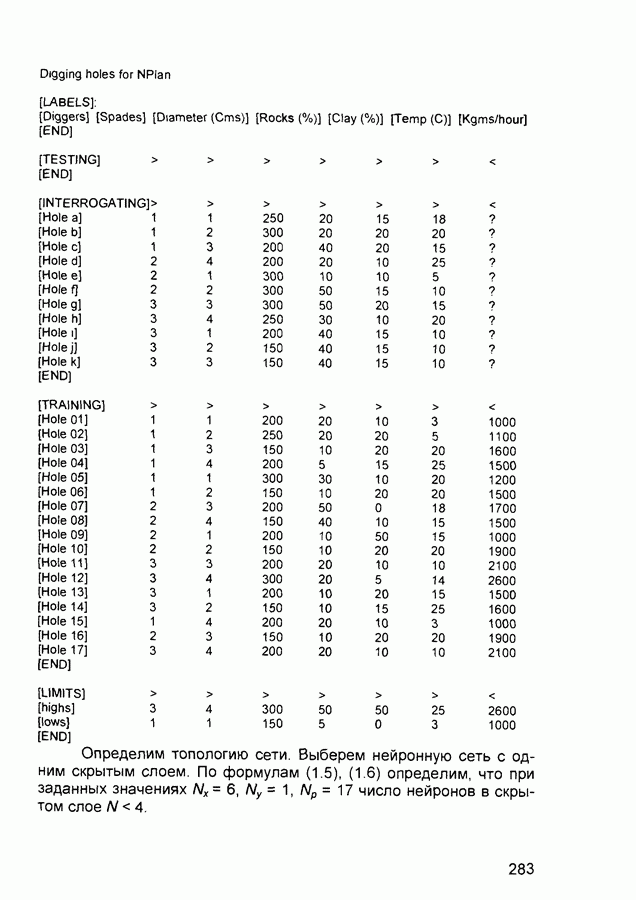
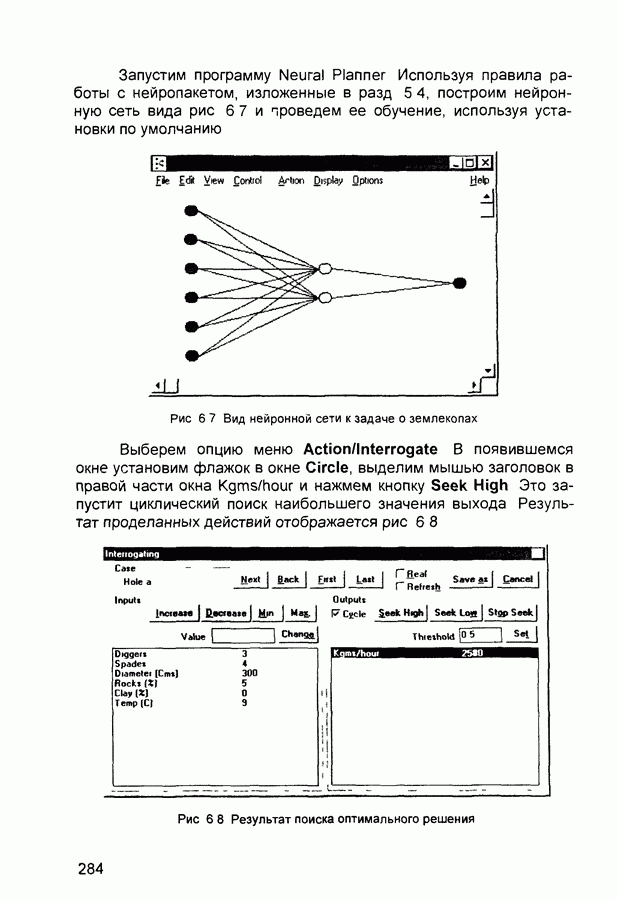
- 6.5. Задача о землекопах
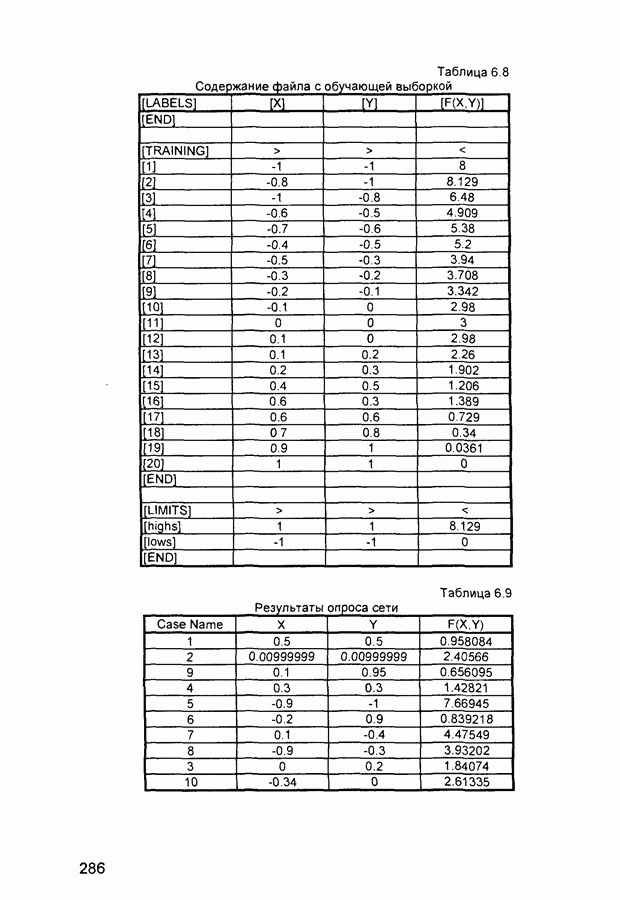
- 6.6. Аппроксимация функции
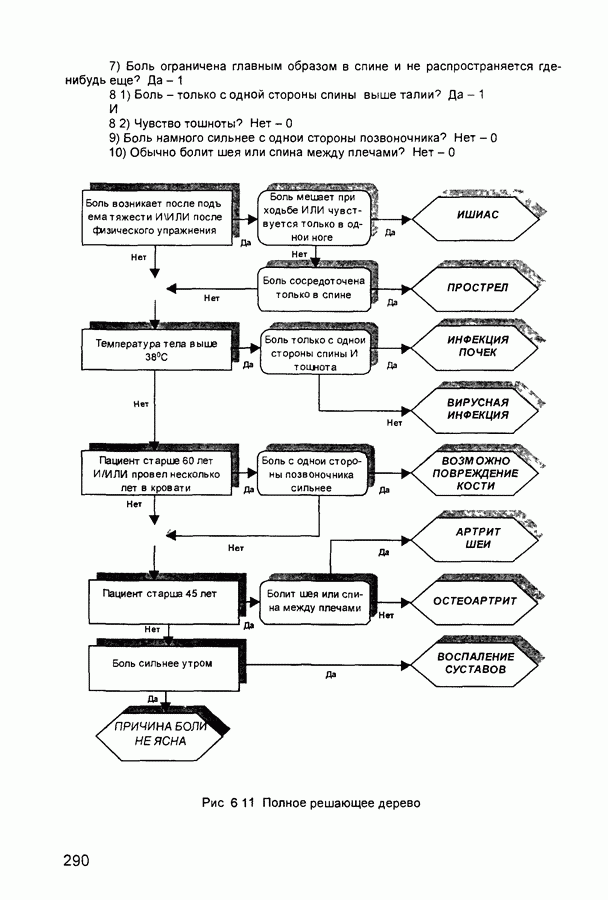
- 6.7. Нейросетевая экспертная система
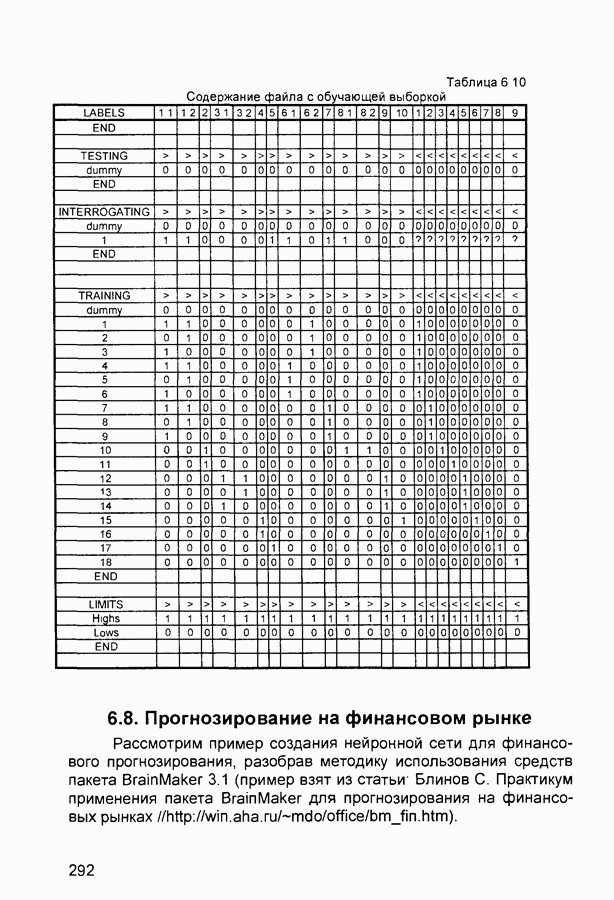
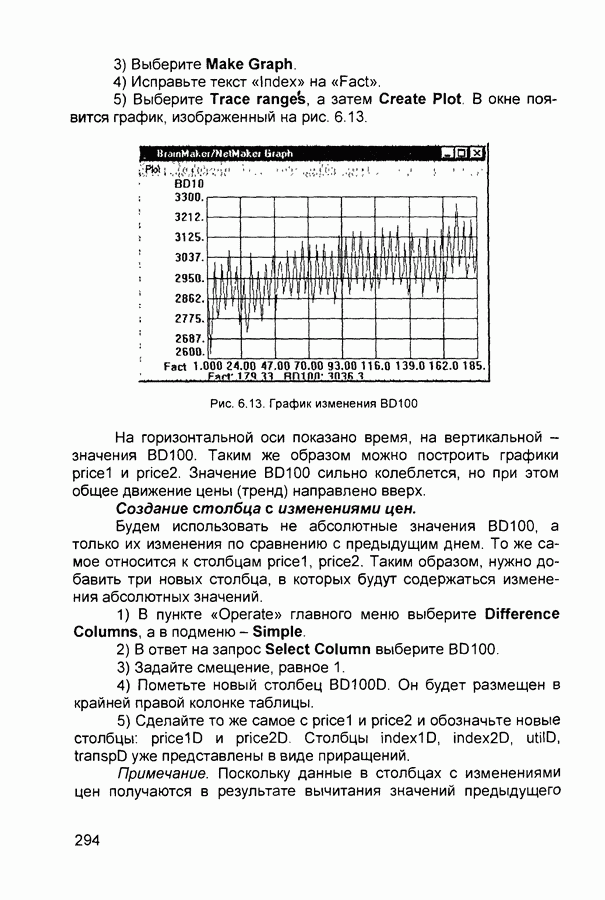
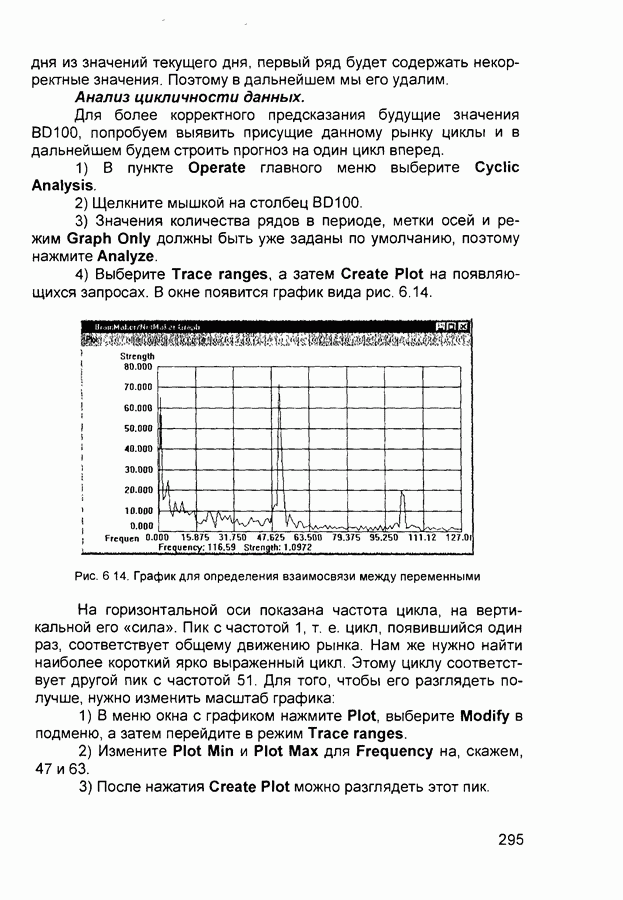
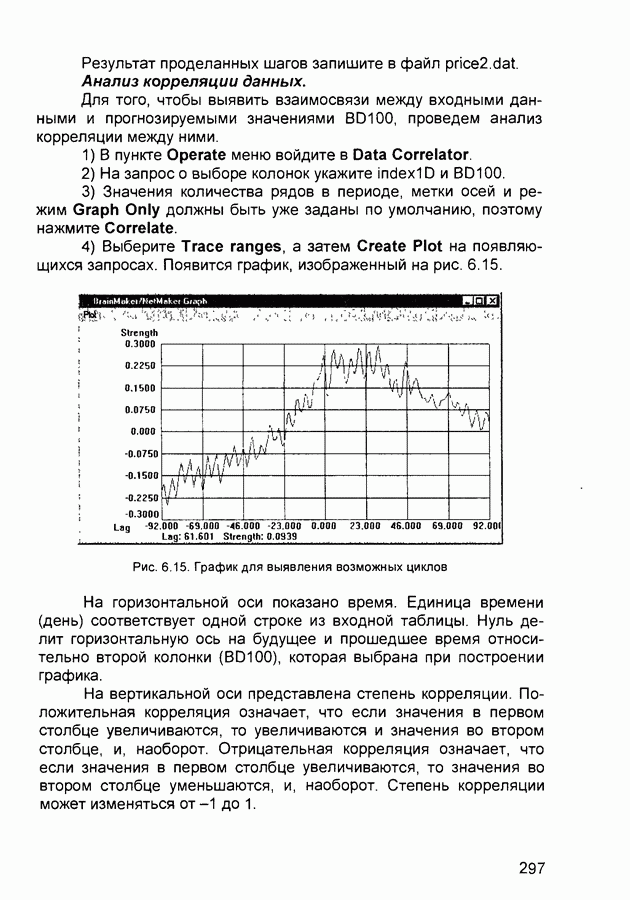
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
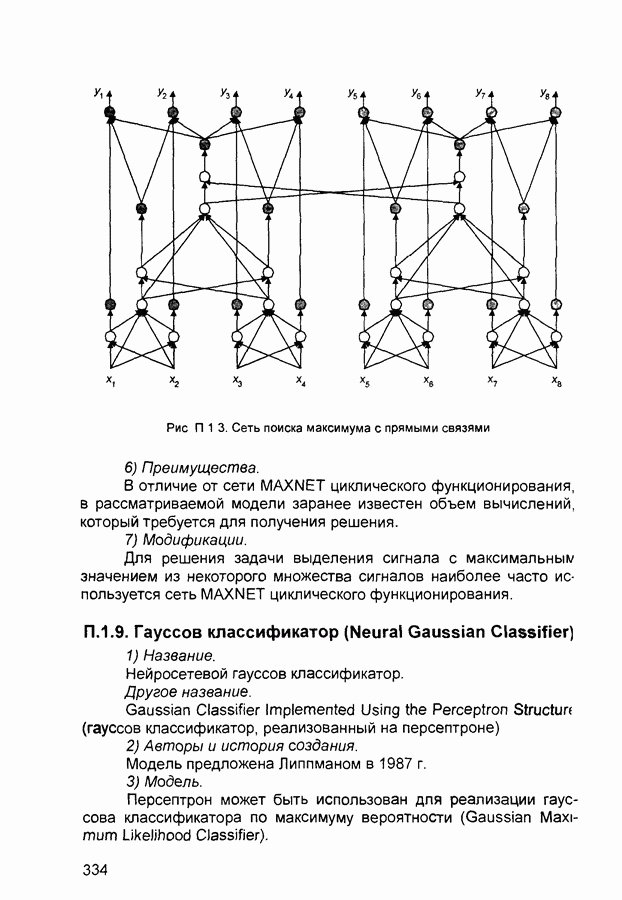
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы