| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
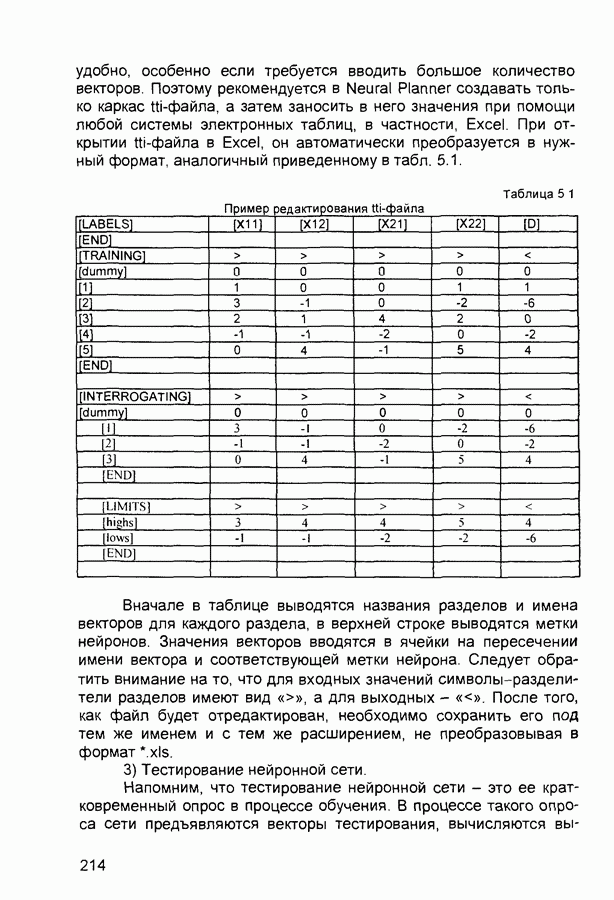
3.1.2. Операции над нечеткими множествами
Логические операции
Включение
Пусть А и  - нечеткие множества на универсальном множестве Е Тогда А содержится в В, если
- нечеткие множества на универсальном множестве Е Тогда А содержится в В, если  Обозначение
Обозначение 
Иногда используют термин «доминирование», т. е. в случае когда  , говорят, что В доминирует А.
, говорят, что В доминирует А.
Равенство
А и  равны, если
равны, если 
Обозначение. А = В.
Дополнение
Пусть  и
и  - нечеткие множества, заданные на Е. А и
- нечеткие множества, заданные на Е. А и  дополняют друг друга, если
дополняют друг друга, если

Обозначение.  или
или 
Очевидно, что  (дополнение определено для
(дополнение определено для 
1], но очевидно, что его можно определить для любого упорядоченного М).
Пересечение
А Г) В - наибольшее нечеткое подмножество, содержащееся одновременно в А и 

Объединение
 - наименьшее нечеткое подмножество, включающее как А, так и
- наименьшее нечеткое подмножество, включающее как А, так и  с функцией принадлежности:
с функцией принадлежности:

Разность
 с функцией принадлежности:
с функцией принадлежности:

Дизъюнктивная сумма
 с функцией принадлежности:
с функцией принадлежности:

Наглядное представление логических операций над нечеткими множествами
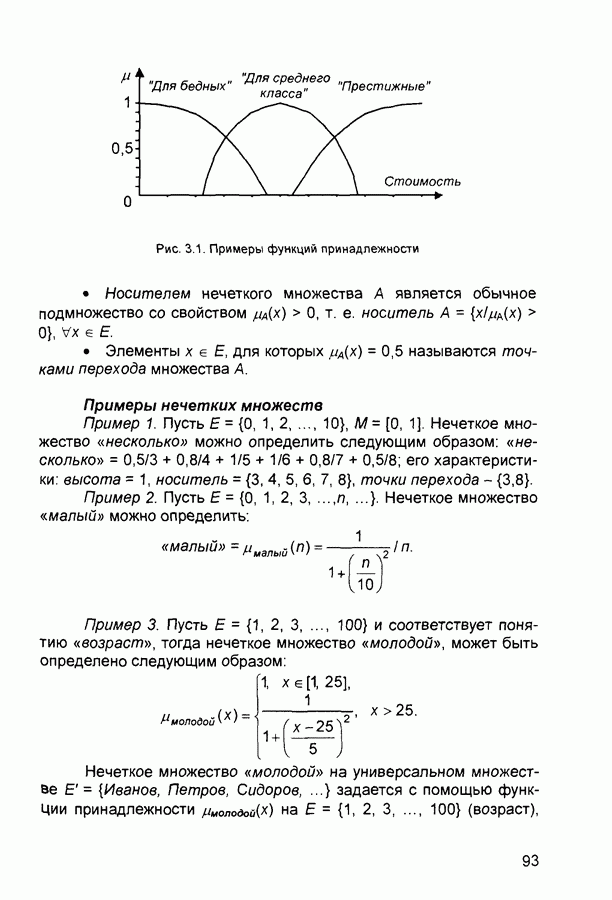
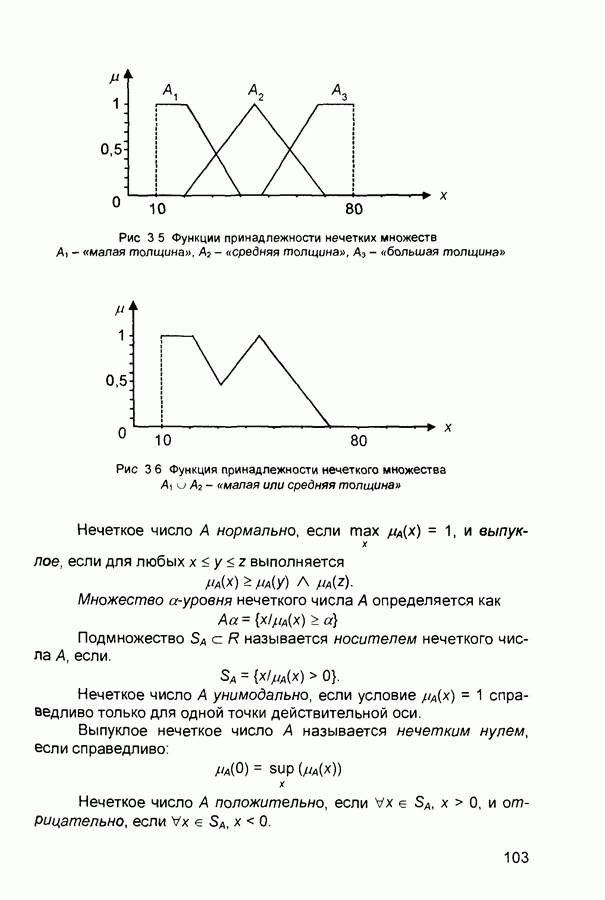
Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значения  на оси абсцисс в произвольном порядке расположены элементы Е. Если Е по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые логические операции над нечеткими множествами (рис. 3.3).
на оси абсцисс в произвольном порядке расположены элементы Е. Если Е по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые логические операции над нечеткими множествами (рис. 3.3).

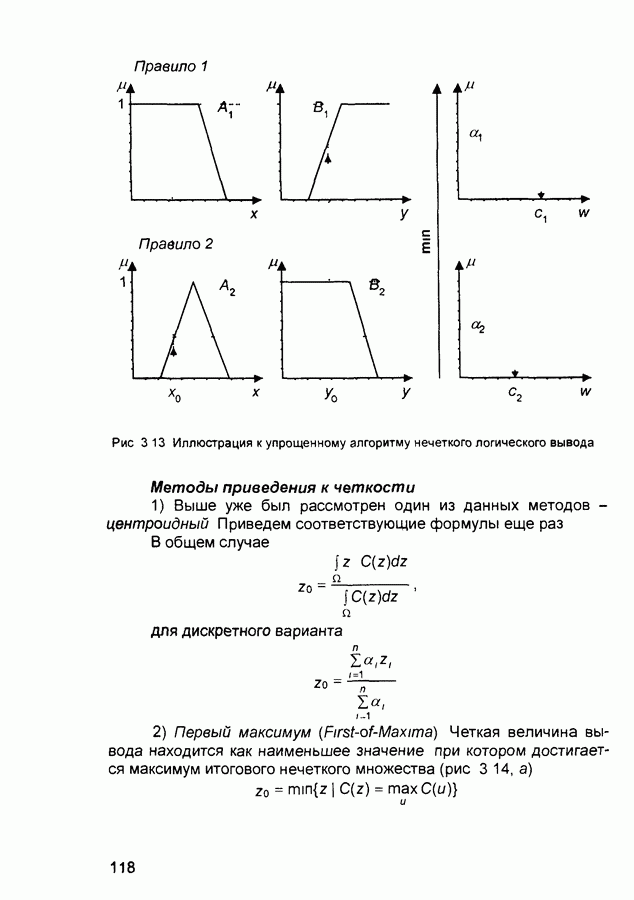
Рис. 3.3 Графическая интерпретация нечетких логических операций: а - нечеткое множество 
Свойства операций объединения и пересечения
Пусть А, В, С - нечеткие множества, тогда выполняются следующие свойства:
(см. скан)
В отличие от четких множеств, для нечетких множеств в общем случае:

Замечание. Введенные выше операции над нечеткими множествами основаны на использовании операций max и min В теории нечетких множеств рассмотрены вопросы построения обобщенных, параметризованных операторов пересечения, объединения и дополнения, позволяющих учесть разнообразные смысловые оттенки соответствующих им связок «И», «ИЛИ», «НЕ».
Один из подходов к обобщению операторов пересечения и объединения заключается в их определении в классе треугольных норм и конорм.
Треугольной нормой ( -нормой) называется двуместная действительная функция
-нормой) называется двуместная действительная функция  удовлетворяющая следующим условиям:
удовлетворяющая следующим условиям:
(см. скан)
Примеры t-норм:

Треугольной конормой ( -конормой) называется двуместная действительная функция
-конормой) называется двуместная действительная функция  , со свойствами:
, со свойствами:
 ограниченность;
ограниченность;
 если на
если на  - монотонность,
- монотонность,
 - коммутативность,
- коммутативность,
 - ассоциативность.
- ассоциативность.
Примеры  -конорм.
-конорм.

Алгебраические операции над нечеткими множествами
Алгебраическое произведение А и  обозначается
обозначается  и формируется следующим образом:
и формируется следующим образом:

Алгебраическая сумма этих множеств обозначается  и определяется как:
и определяется как:

Для операций  справедливы следующие свойства:
справедливы следующие свойства:

Не выполняются:

При совместном использовании операций  справедливы свойства:
справедливы свойства:

На основе операции алгебраического произведения определена операция возведения в степень а нечеткого множества А, где  - положительное число. Нечеткое множество
- положительное число. Нечеткое множество  определяется функцией принадлежности
определяется функцией принадлежности  Частным случаем возведения в степень являются:
Частным случаем возведения в степень являются:
 - операция концентрирования (уплотнения),
- операция концентрирования (уплотнения),
 - операция растяжения,
- операция растяжения,
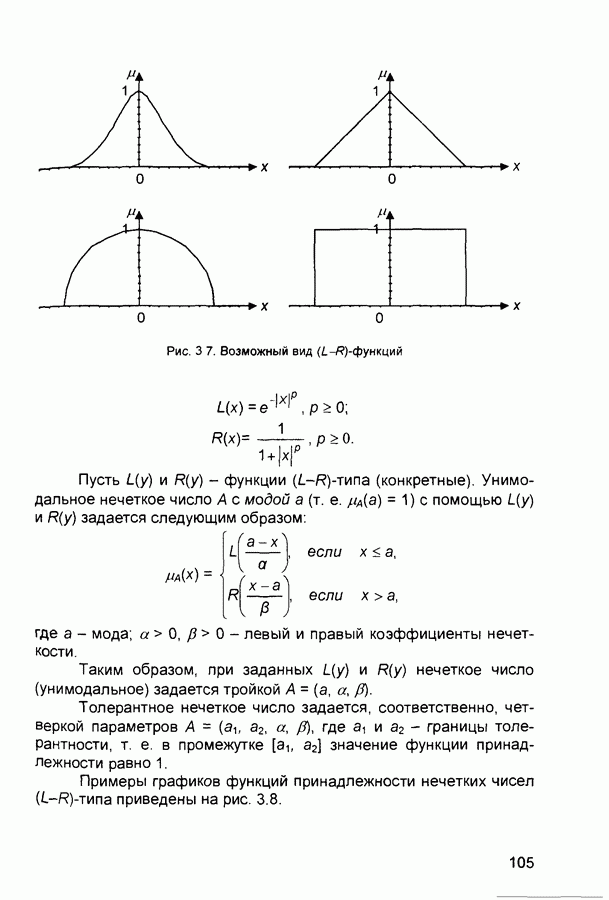
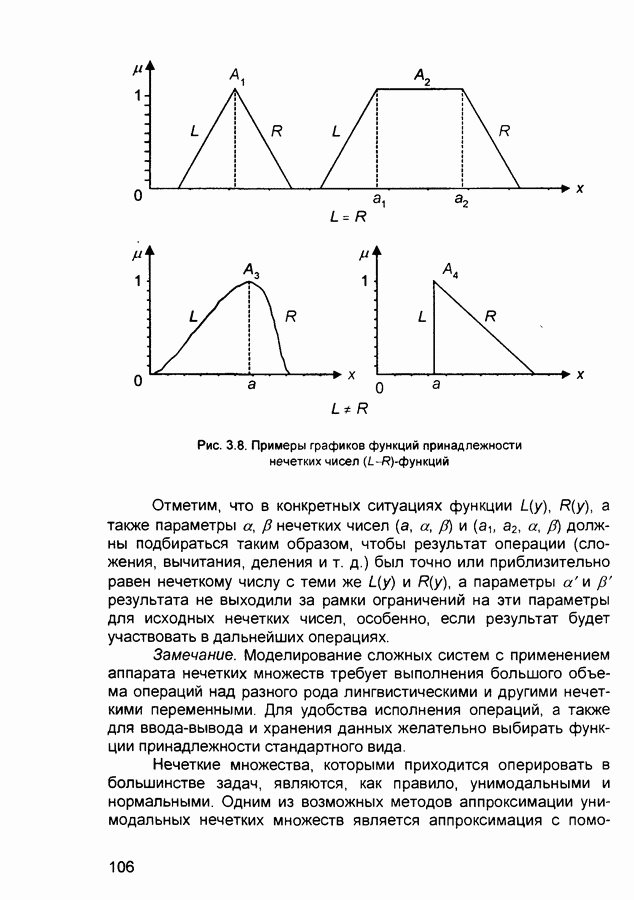
которые используются при работе с лингвистическими неопределенностями (рис. 3.4).

Рис. 3.4 Операции концентрирования (уплотнения) и растяжения
Умножение на число. Если  - положительное число, такое, что
- положительное число, такое, что  то нечеткое множество
то нечеткое множество  имеет функцию принадлежности:
имеет функцию принадлежности:

Выпуклая комбинация нечетких множеств. Пусть  - нечеткие множества универсального множества Е, а
- нечеткие множества универсального множества Е, а  неотрицательные числа, сумма которых равна 1.
неотрицательные числа, сумма которых равна 1.
Выпуклой комбинацией  называется нечеткое множество А с функцией принадлежности:
называется нечеткое множество А с функцией принадлежности:

Декартово (прямое) произведение нечетких множеств. Пусть  - нечеткие подмножества универсальных множеств
- нечеткие подмножества универсальных множеств  соответственно. Декартово или прямое произведение
соответственно. Декартово или прямое произведение  является нечетким подмножеством множества
является нечетким подмножеством множества  с функцией принадлежности:
с функцией принадлежности:

Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества.
Пусть А - нечеткое множество, Е - универсальное множество и для всех  определены нечеткие множества
определены нечеткие множества  Совокупность всех
Совокупность всех  называется ядром оператора увеличения нечеткости Н. Результатом действия оператора Н на нечеткое множество А является нечеткое множество вида:
называется ядром оператора увеличения нечеткости Н. Результатом действия оператора Н на нечеткое множество А является нечеткое множество вида:

где  - произведение числа на нечеткое множество.
- произведение числа на нечеткое множество.
Пример. Пусть 
Тогда 
Четкое множество  -уровня (или уровня а). Множеством
-уровня (или уровня а). Множеством  -уровня нечеткого множества А универсального множества Е называется четкое подмножество
-уровня нечеткого множества А универсального множества Е называется четкое подмножество  универсального множества Е, определяемое в виде:
универсального множества Е, определяемое в виде:

Пример. Пусть  Тогда
Тогда 
Свойство множества  -уровня: если
-уровня: если  то
то 
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
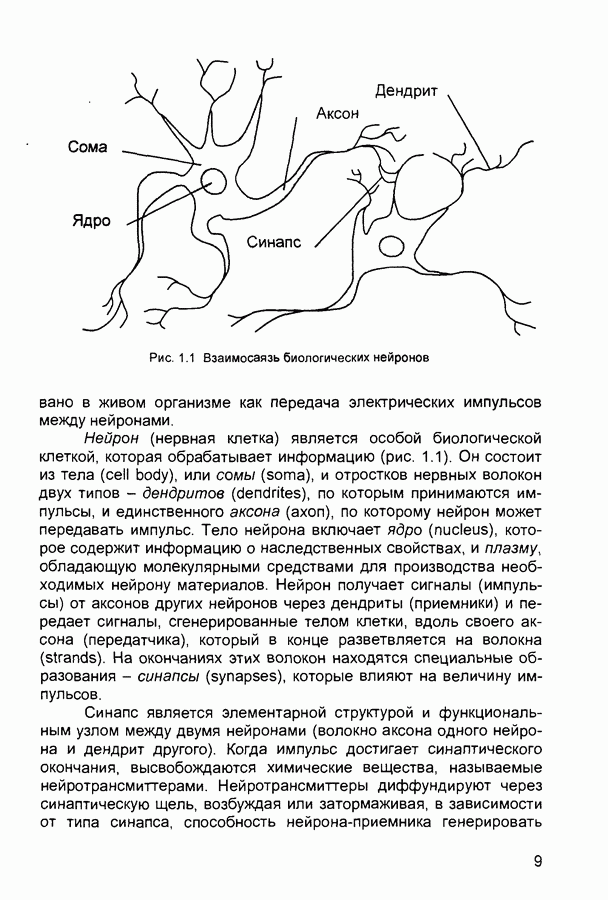
- 1.1. Биологический нейрон
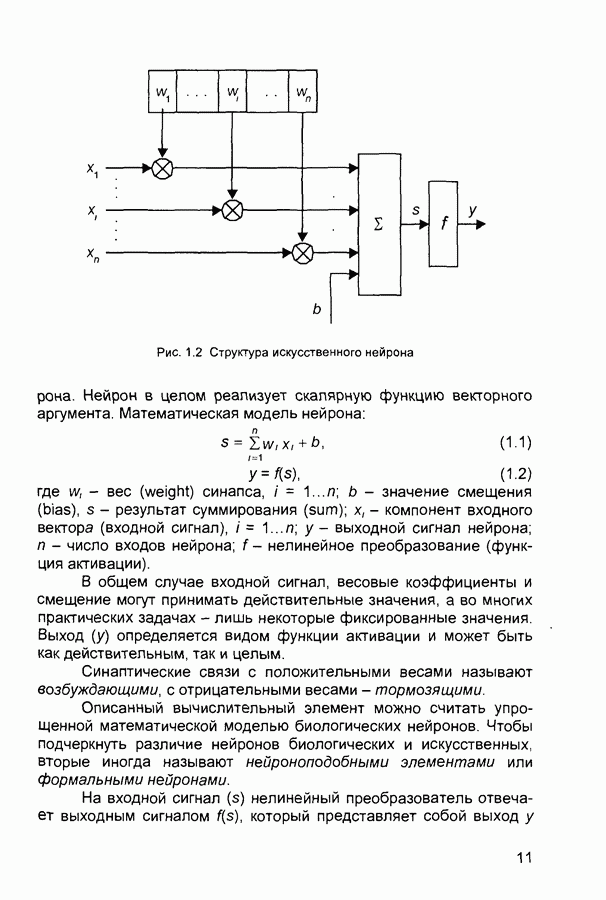
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
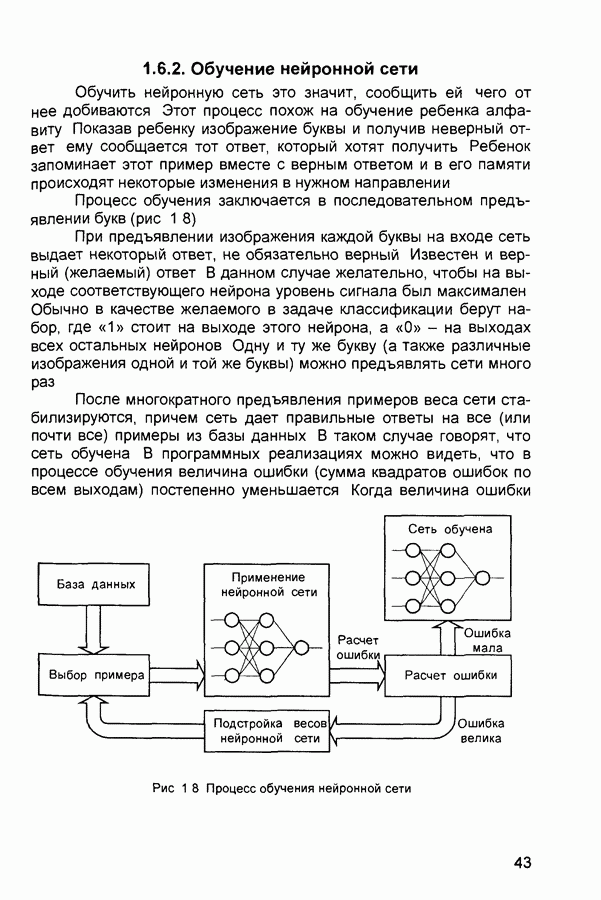
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
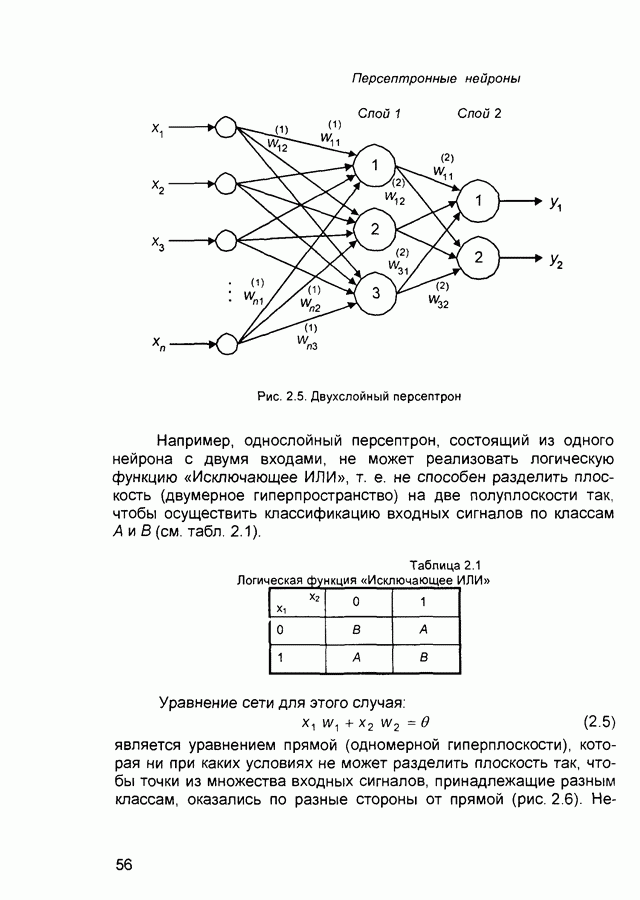
- 2.2. Персептроны
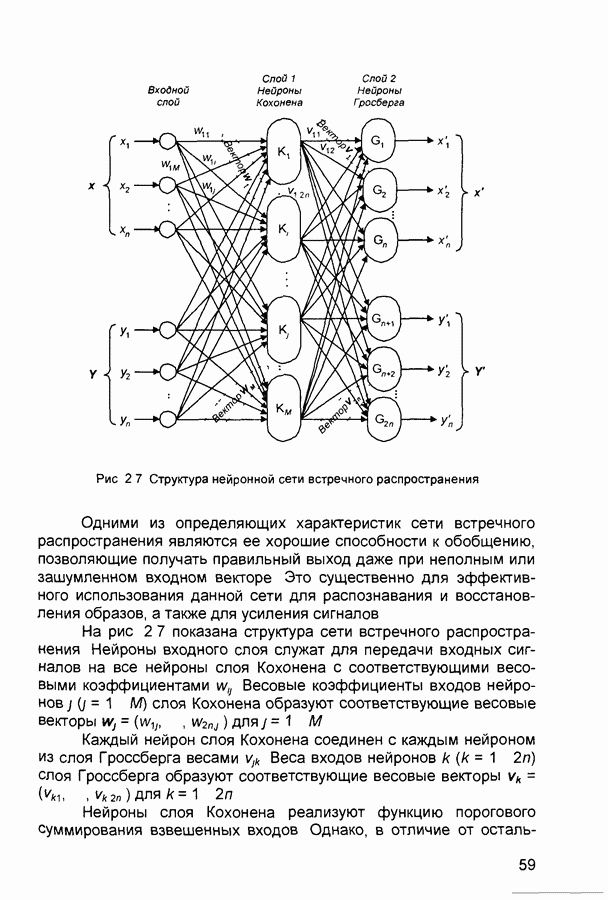
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
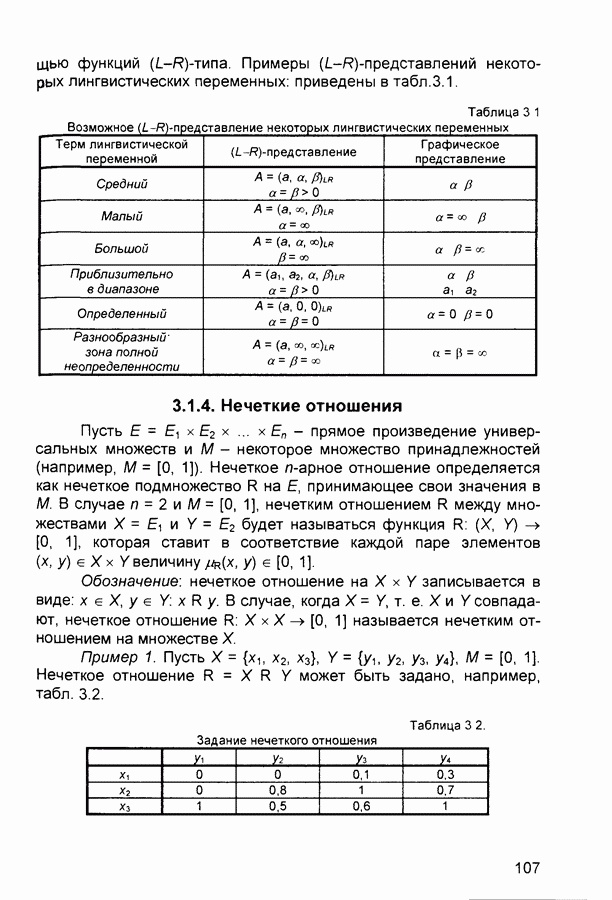
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
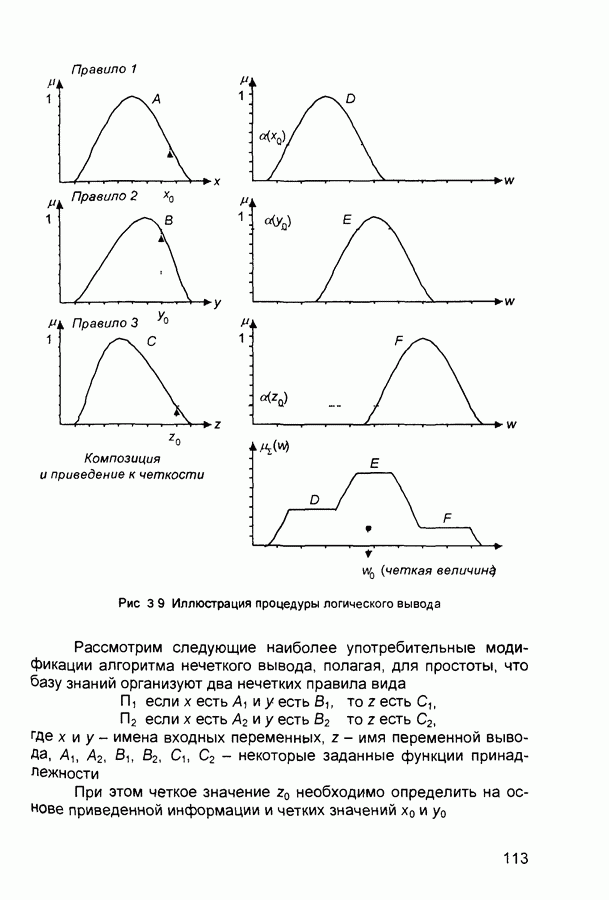
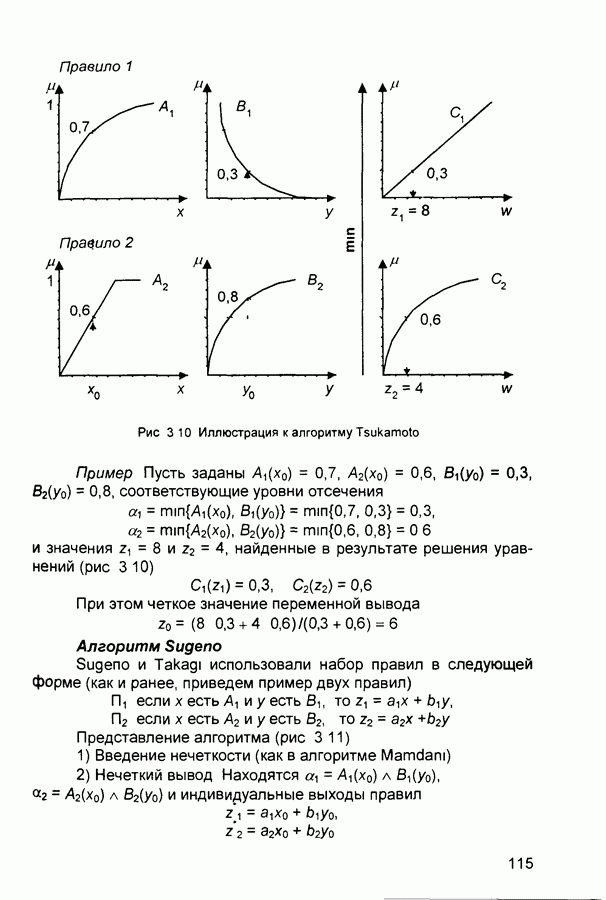
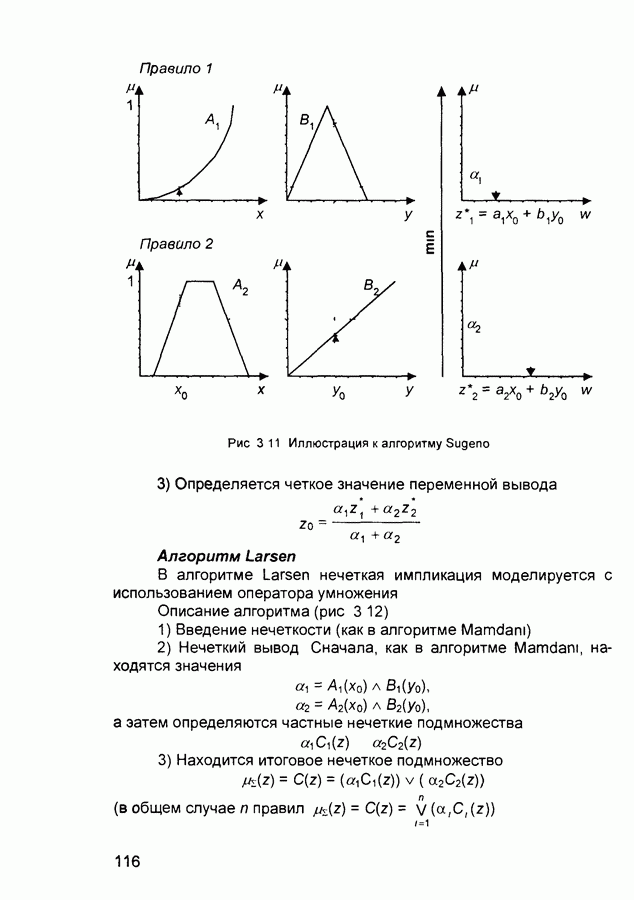
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
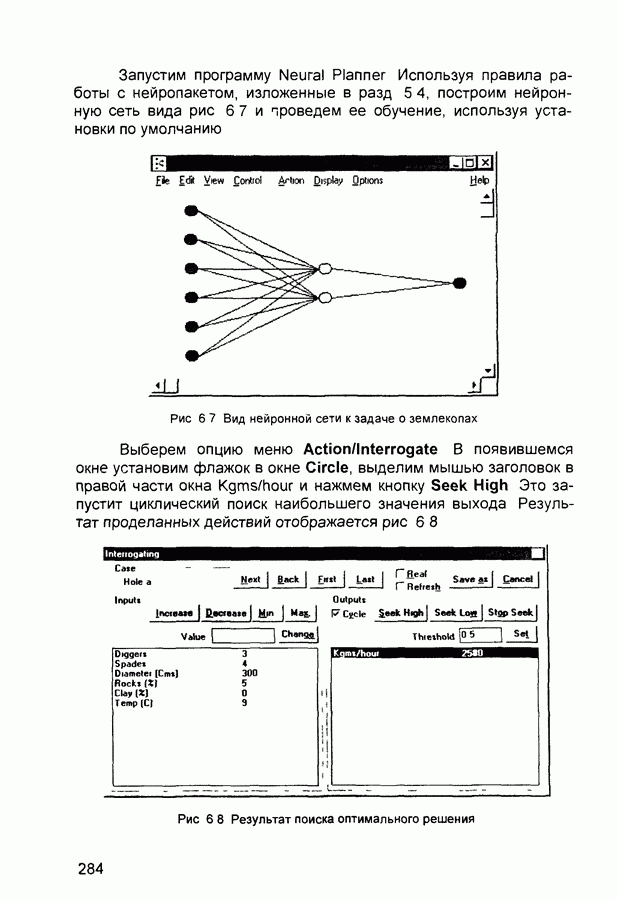
- 6.5. Задача о землекопах
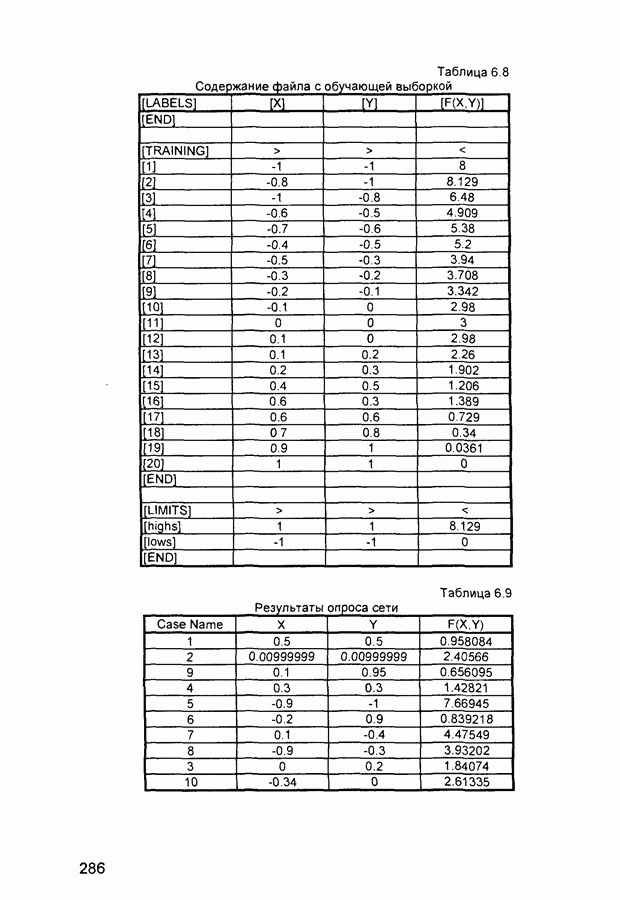
- 6.6. Аппроксимация функции
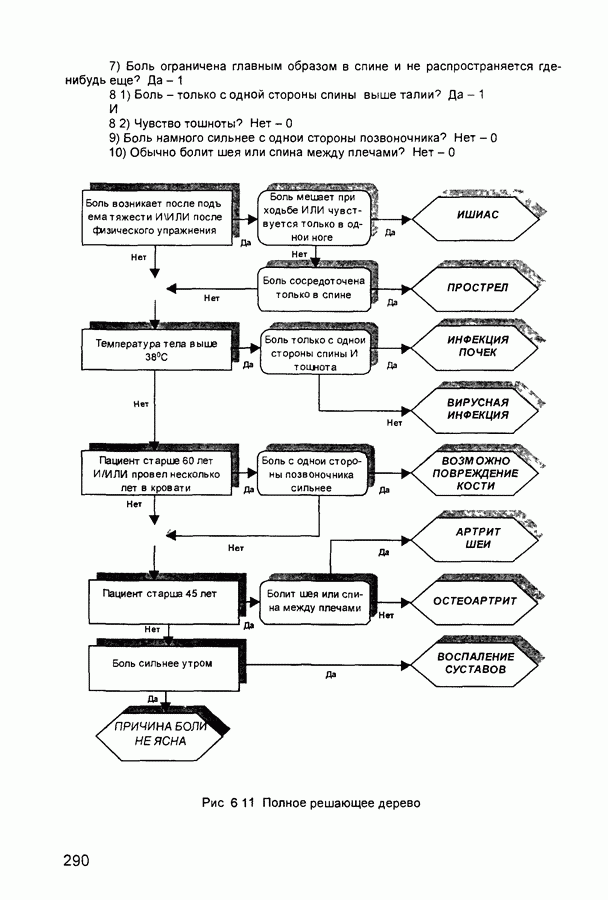
- 6.7. Нейросетевая экспертная система
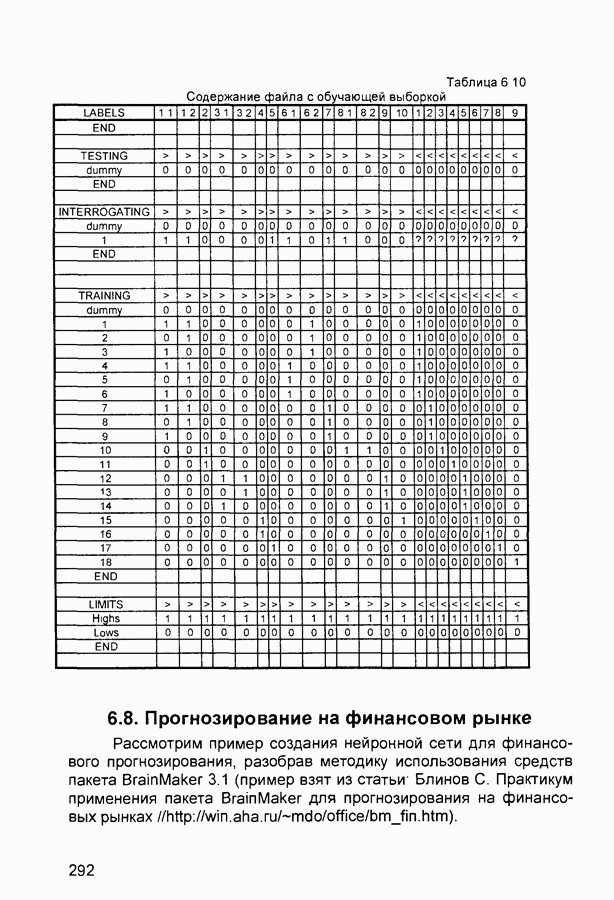
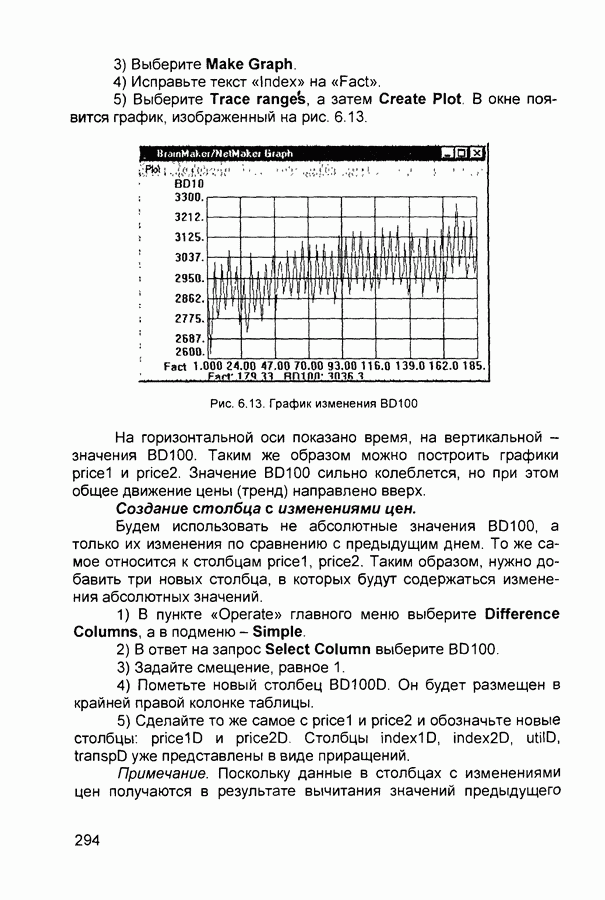
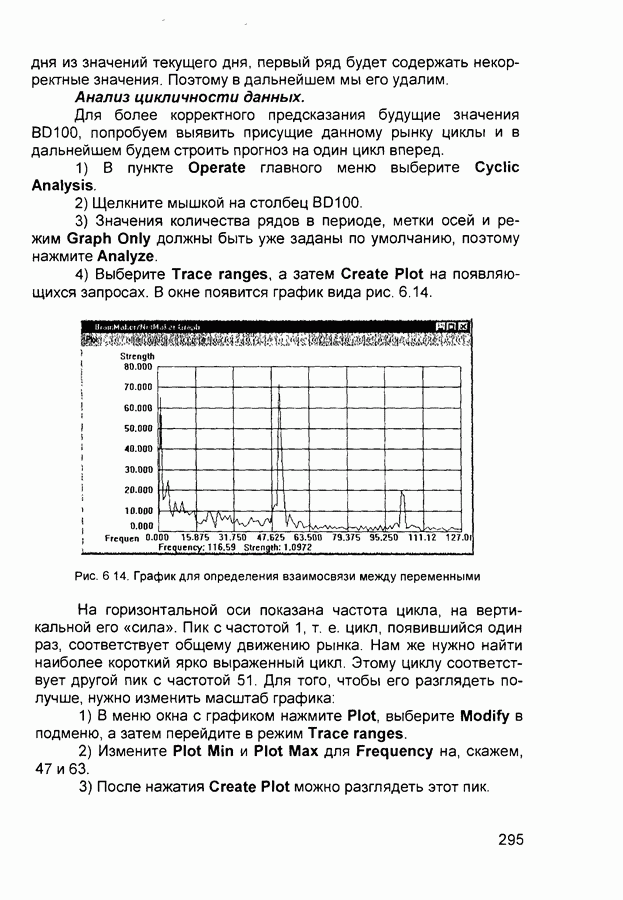
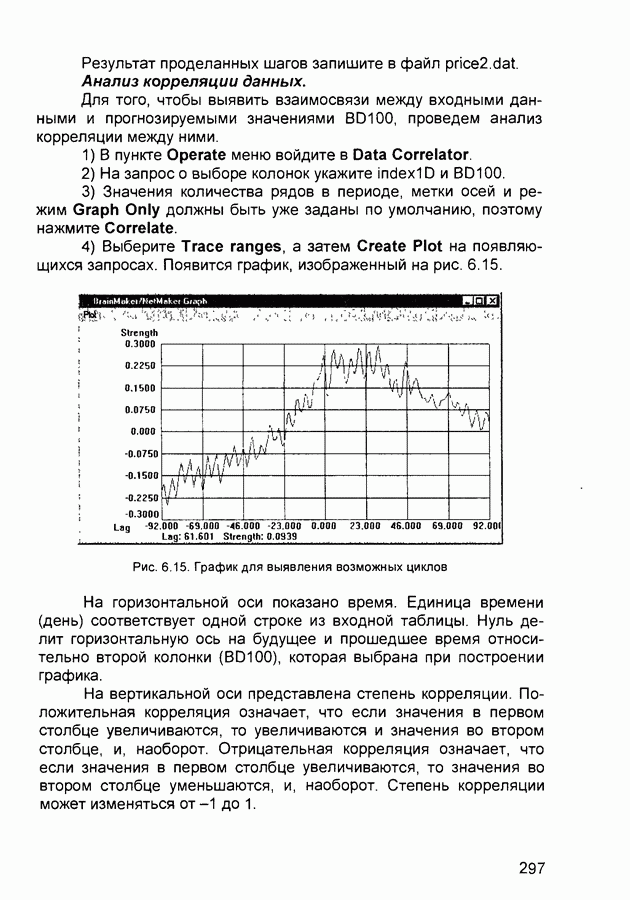
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
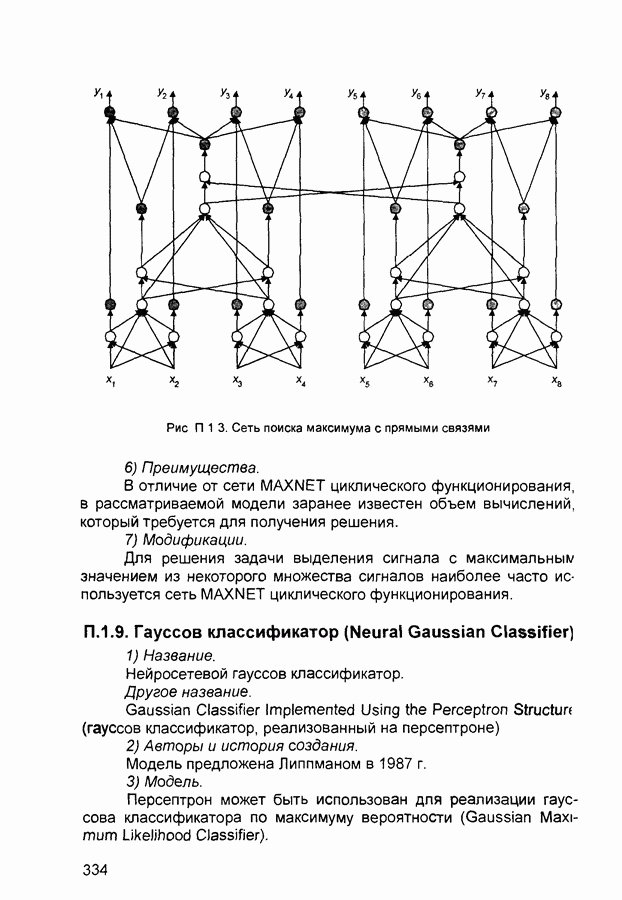
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы