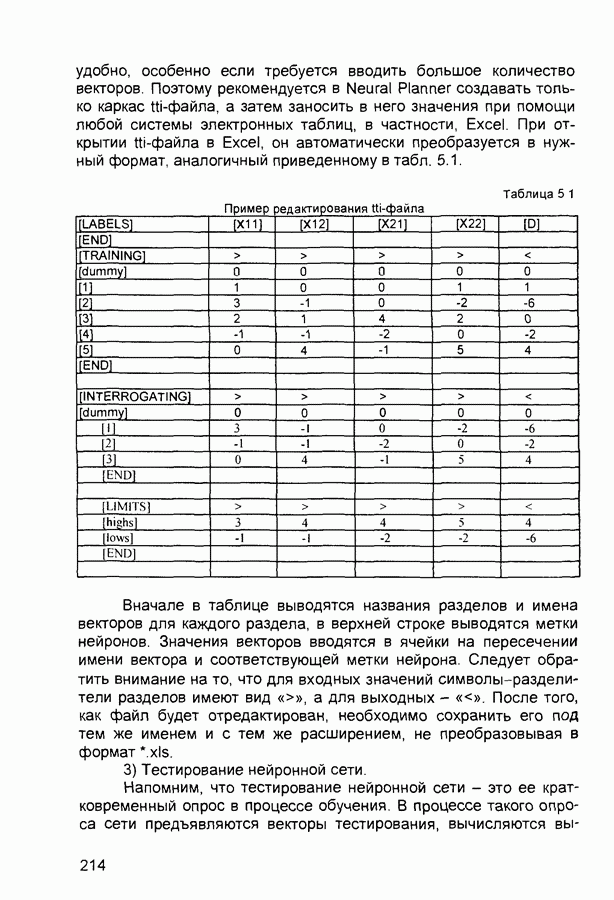
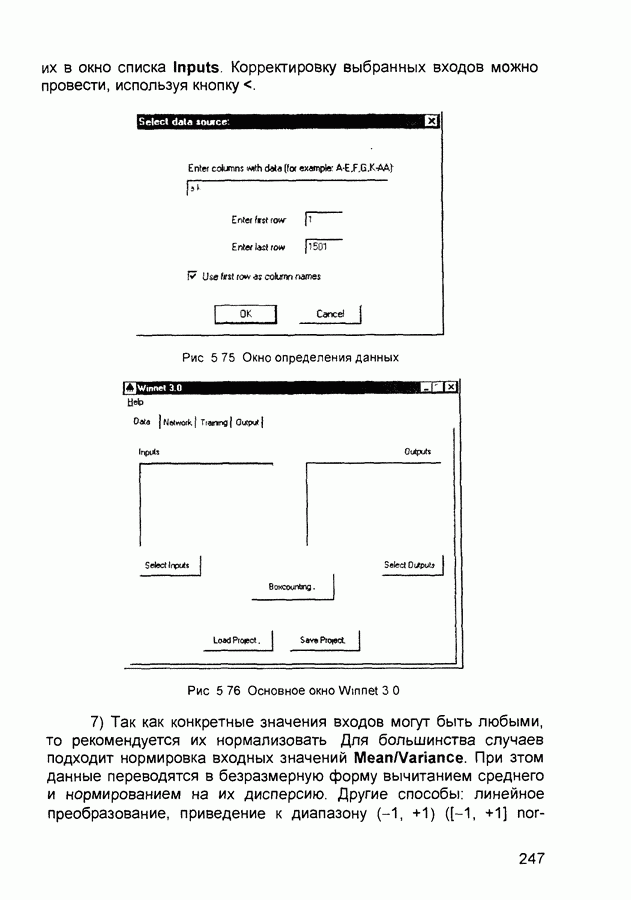
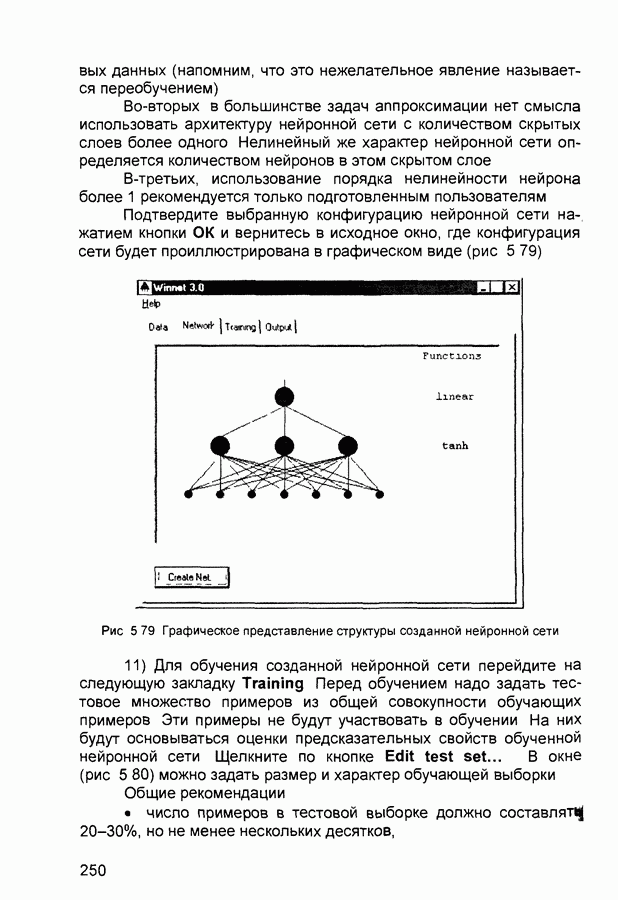
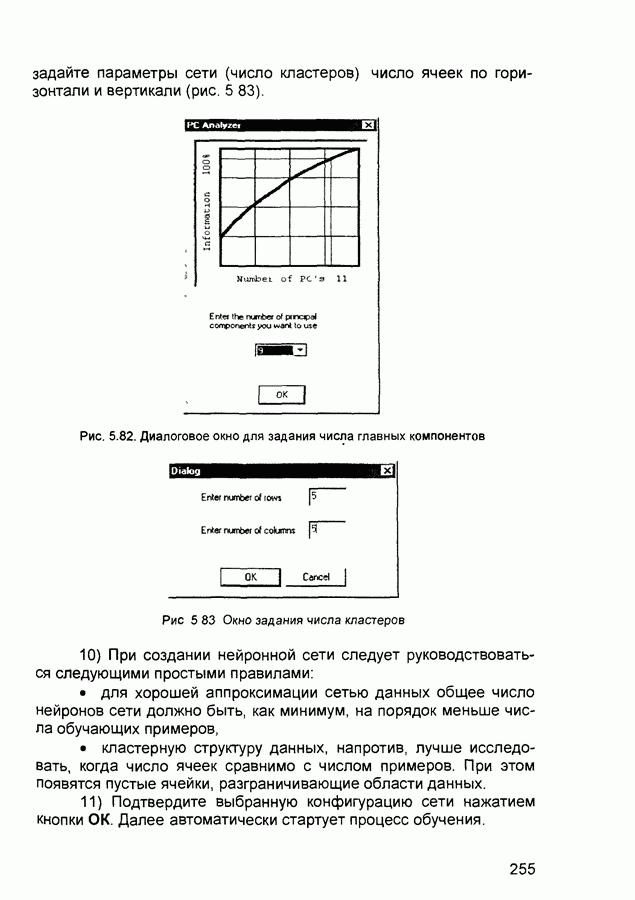
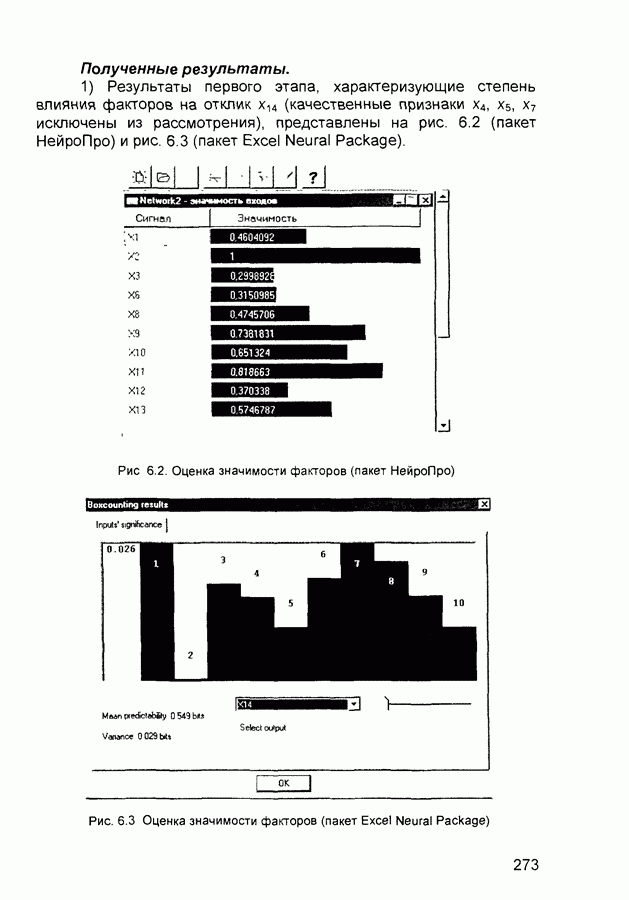
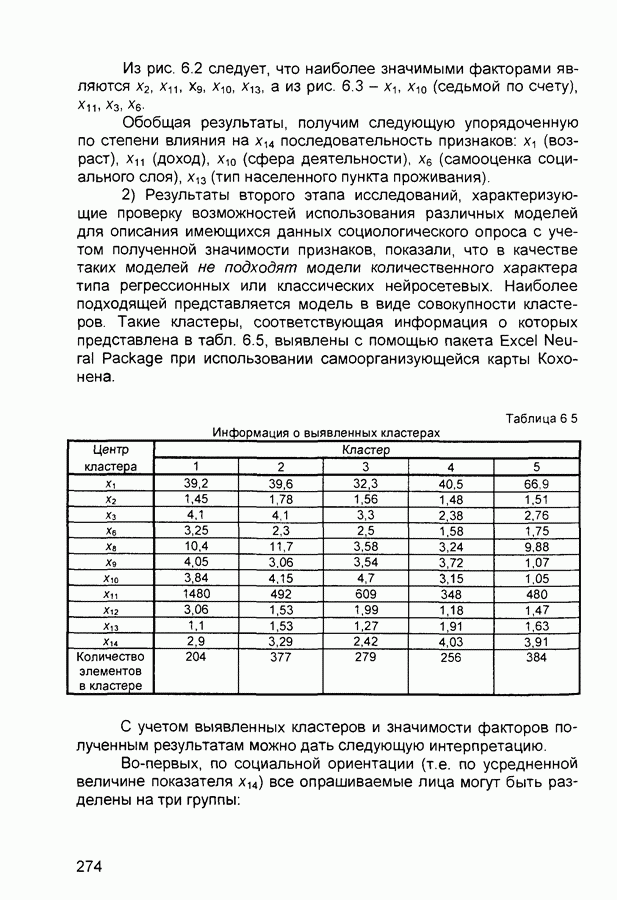
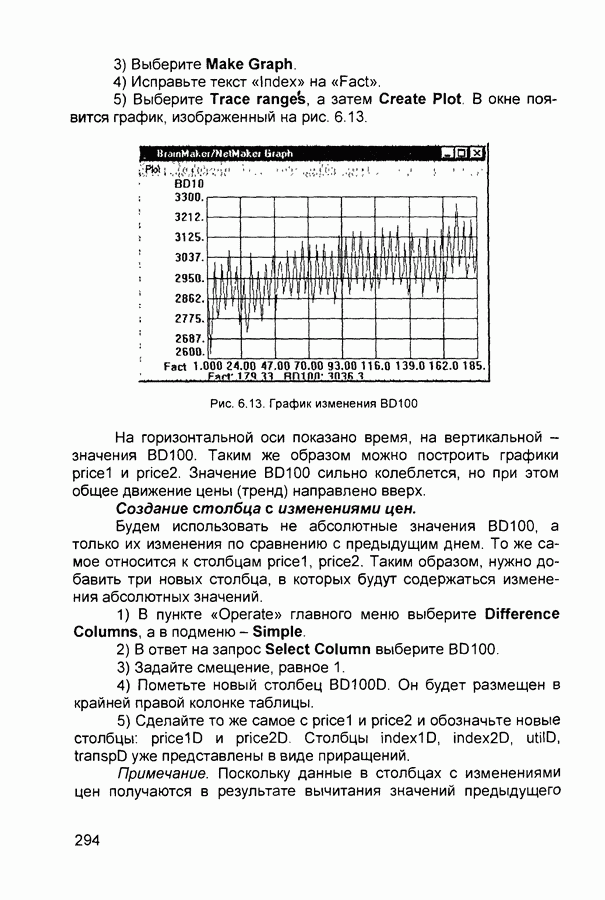
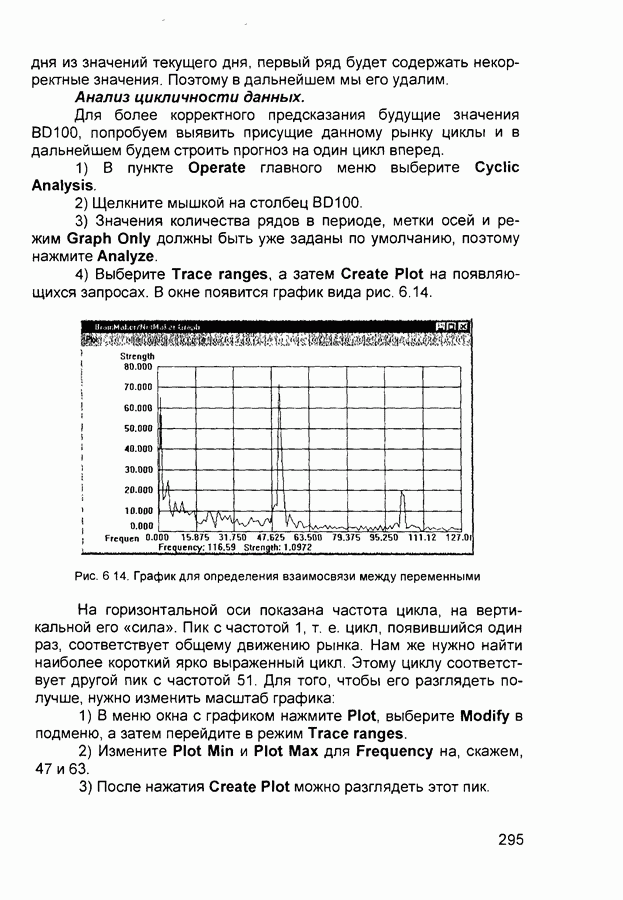
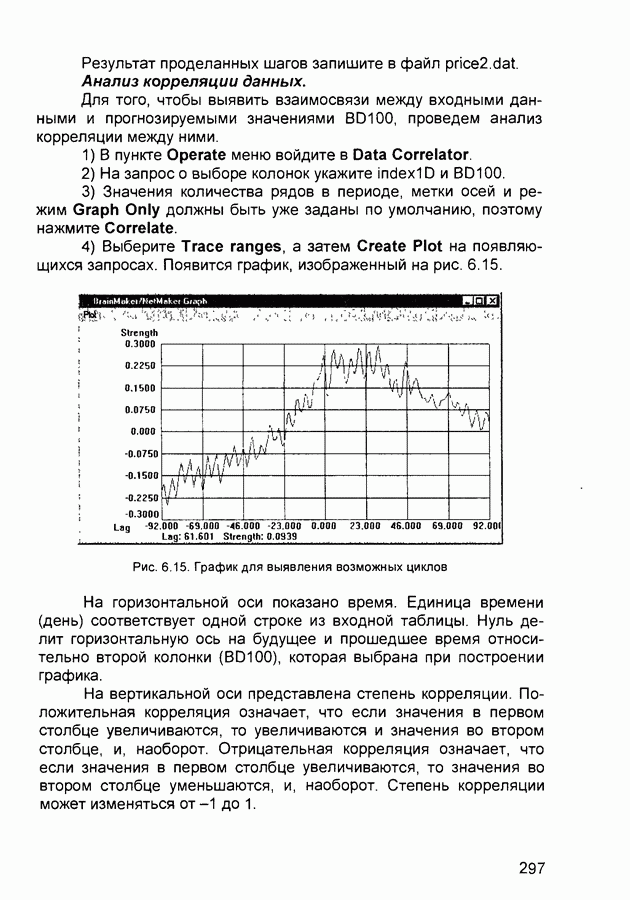
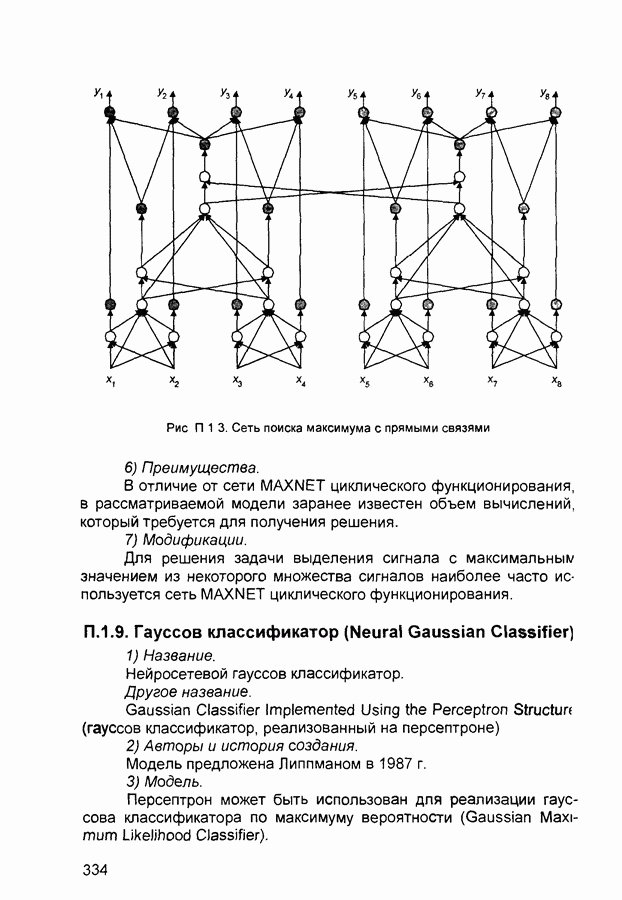
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.1. Общие сведения о программах моделирования нейронных сетей
Программу моделирования нейронной сети обычно называют программой-имитатором или нейропакетом, понимая под этим программную оболочку, эмулирующую для пользователя среду нейрокомпьютера на обычном компьютере.
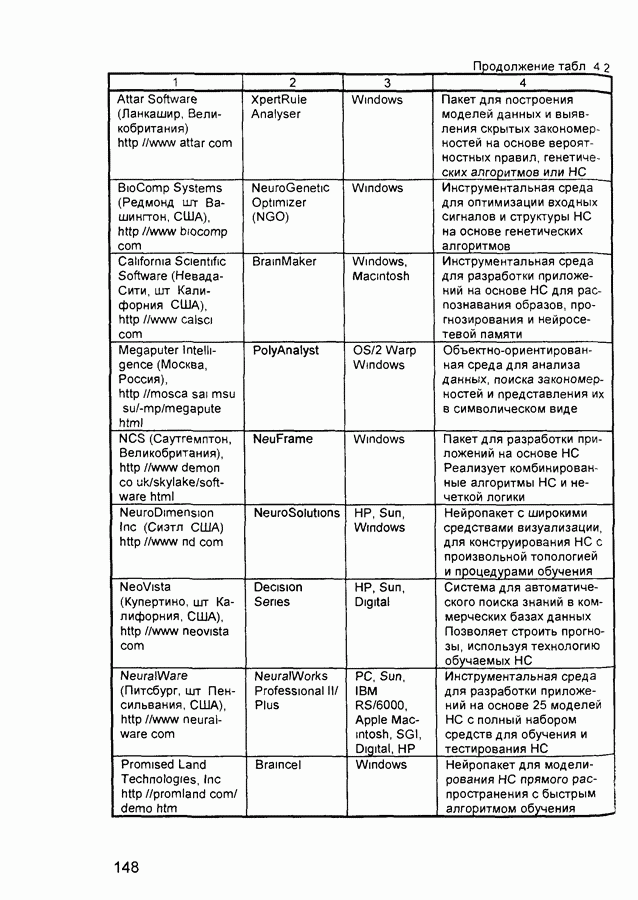
В настоящее время на рынке программного обеспечения имеется множество самых разнообразных программ для моделирования нейронных сетей. Можно выделить несколько основных функций, которые реализованы во всех этих программах.
Формирование (создание) нейронной сети
Для решения разных практических задач требуются различные модели нейронных сетей. Модель нейронной сети определяется моделями нейронов и структурой связей сети.
Программы-имитаторы в зависимости от структуры связей реализуют следующие группы нейронных сетей.
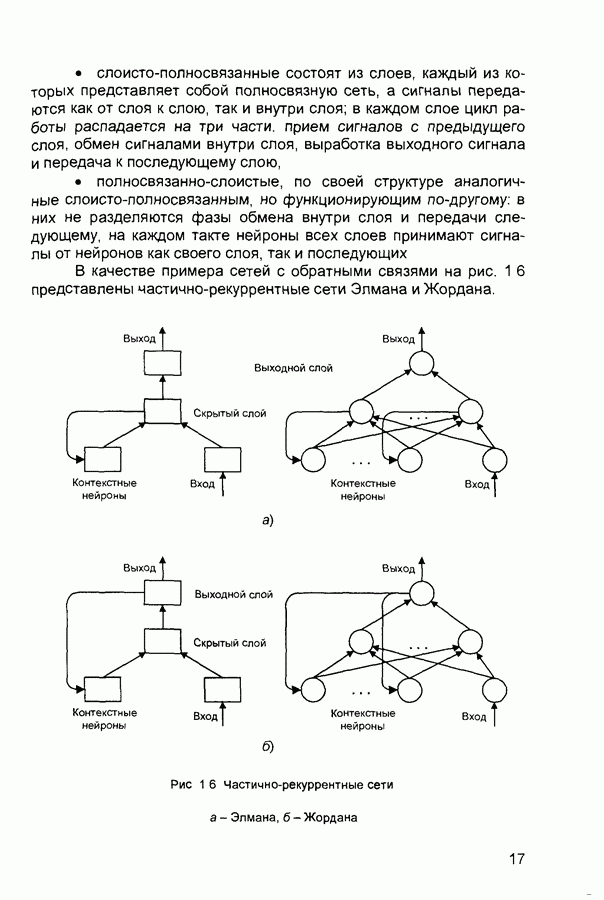
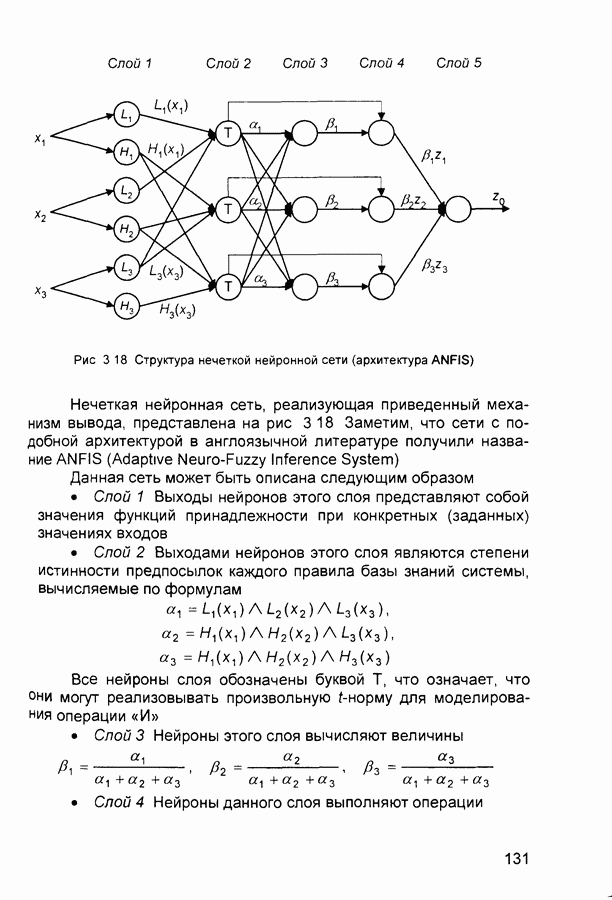
• Многослойные нейронные сети. Нейроны в таких сетях делятся на группы с общим входным сигналом - слои. Различают несколько типов связей между слоями с номерами q и (q + р):
• последовательные р = 1);
• прямые (р > 1);
• обратные р < 0).
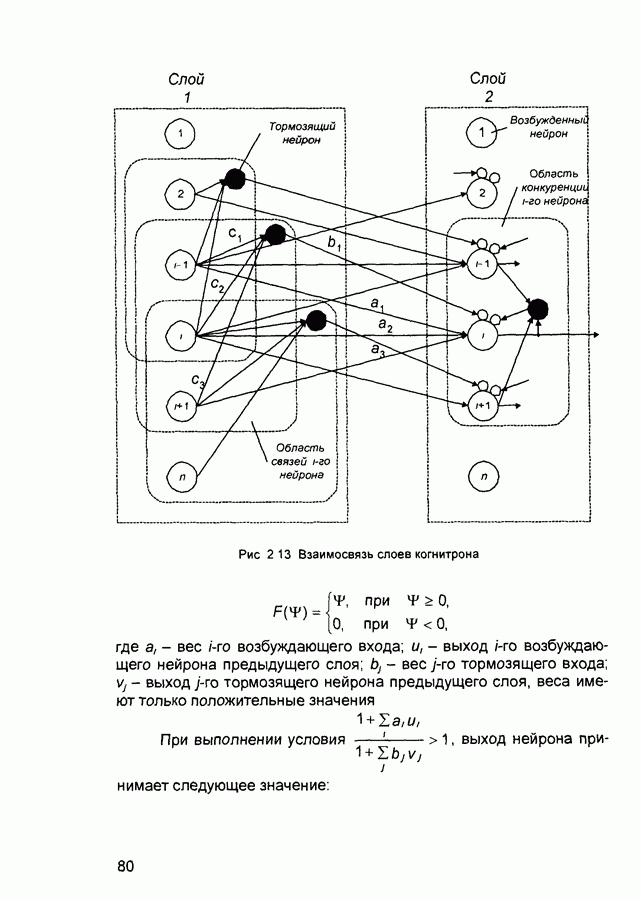
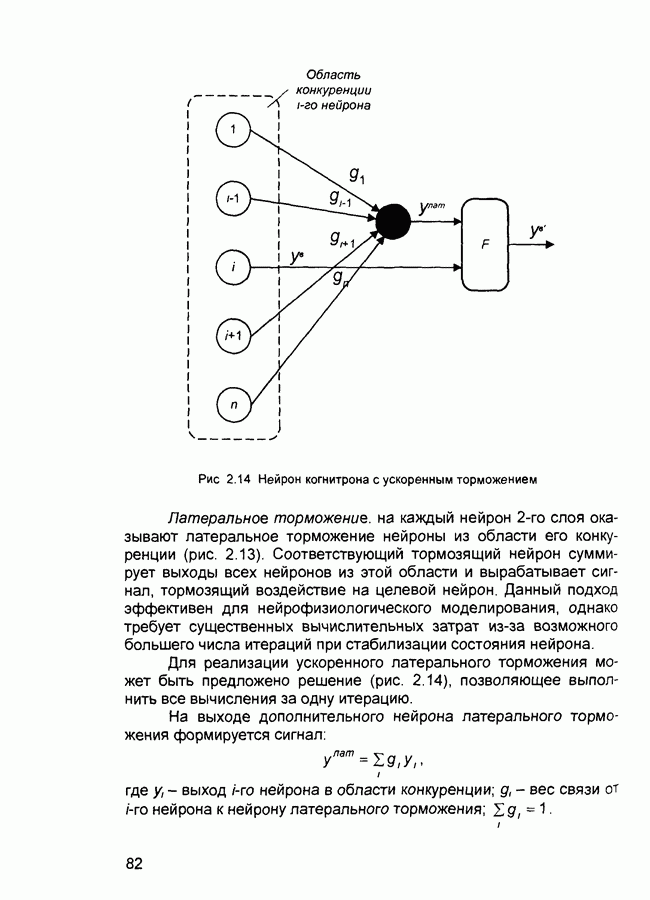
Связи между нейронами одного слоя называют латеральными (боковыми).
• Полносвязные нейронные сети. Каждый нейрон в полносвязных сетях связан со всеми остальными. На каждом такте функционирования сети на входы нейронов подается внешний входной сигнал и выходы нейронов предыдущего такта.
• Нейронные сети с локальными связями. Нейроны в таких сетях располагаются в узлах прямоугольной или гексагональной решетки. Каждый нейрон связан с небольшим числом (4, 6 или 8) своих топологических соседей.
• Неструктурированные нейронные сети. К этой группе относятся все модели нейронных сетей, которые нельзя отнести ни к одной из предыдущих групп.
Модели реализуемых программами-имитаторами нейронов чрезвычайно разнообразны. В простейшем случае нейроны первого порядка выполняет взвешенное суммирование компонентов входного вектора и нелинейное преобразование результата суммирования. Нейроны более высоких порядков осуществляют перемножение двумерных матриц и многомерных тензоров.
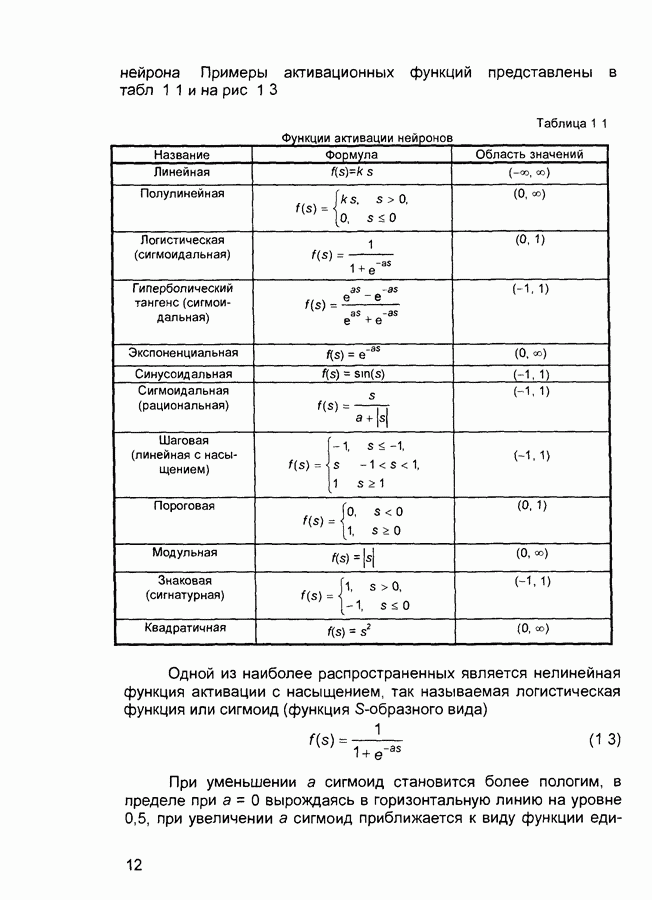
В моделях нейронов используются различные варианты нелинейных преобразований. Наиболее часто используются сигмоидальные, кусочно-линейные и жесткие пороговые функции активации. В сети все нейроны могут иметь как одинаковые (гомогенная сеть), так и различные функции активации (гетерогенная сеть).
Для построения нейронной сети, ориентированной на решение конкретной задачи, используются процедуры формирования нейронных сетей, которые обеспечивают ввод указанных характеристик моделей нейронов и структур нейронных сетей.
Каждая группа моделей нейронных сетей может быть использована для решения лишь некоторого ограниченного класса практических задач. Так, многослойные и полносвязные нейронные сети с сигмоидальными передаточными функциями используются для распознавания образов и адаптивного управления; нейронные сети с локальными связями - для обработки изображений и некоторых других частных задач. Для решения задач линейной алгебры используются многослойные сети с особыми передаточными функциями.
Лишь для небольшого числа моделей нейронных сетей существует строгое математическое обоснование возможности их применения для решения конкретных практических задач. В наибольшей степени теоретически проработаны двухслойные нейронные сети с сигмоидальными передаточными функциями. На основе приведенной в гл. 1 теоремы Колмогорова-Арнольда доказано, что такие сети могут реализовывать любые отображения входного сигнала в выходной. К построению многопараметрических отображений сводится большинство задач распознавания, управления, идентификации.
Обучение нейронной сети
В большинстве программ-имитаторов предлагаются стандартные процедуры обучения нейронных сетей, ориентированные на конкретные нейропарадигмы.
Как правило, в нейропакетах реализуется возможность задания различных типов данных и различных размерностей входных и
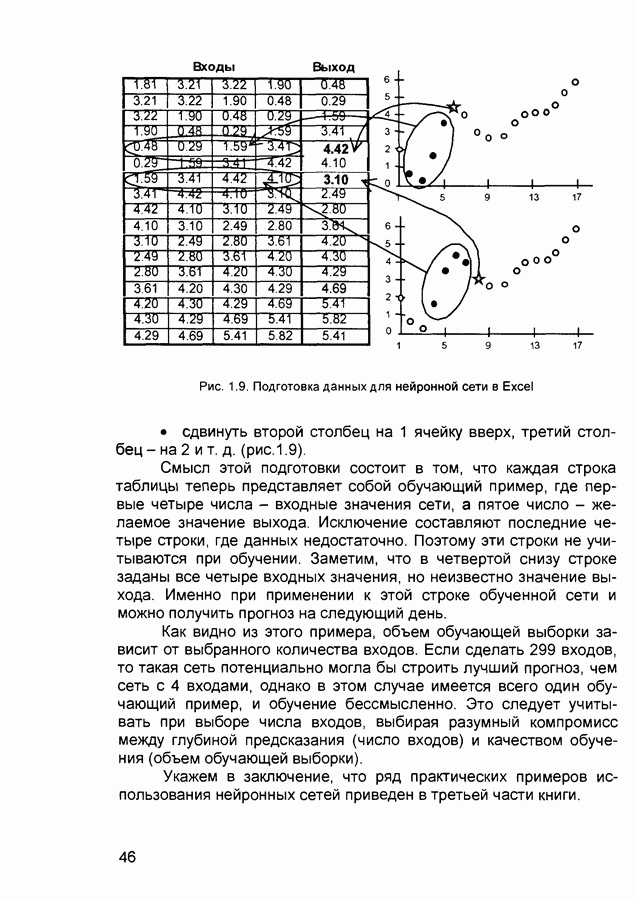
выходных сигналов в зависимости от решаемой задачи В качестве входных данных в обучающей выборке могут использоваться растровые изображения, таблицы чисел, распределения Типы входных данных - бинарные (0 и 1), биполярные (-1 и +1) числа, целые или действительные числа из некоторого диапазона Выходные сигналы сети - векторы целых или действительных чисел
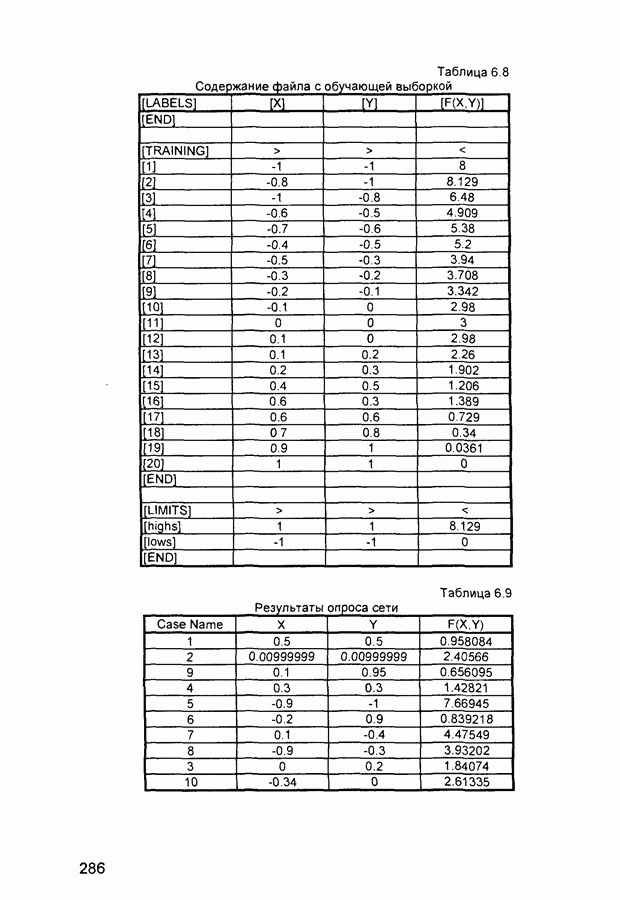
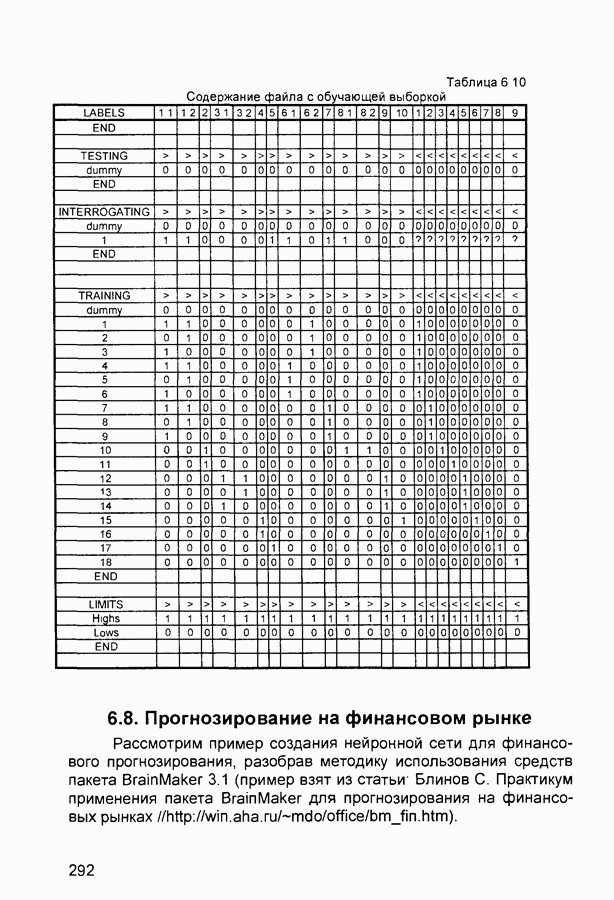
Для решения практических задач часто требуются обучающие выборки большого объема Поэтому в ряде нейропакетов предусмотрены средства, облегчающие процесс формирования и использования обучающих примеров Однако в настоящее время отсутствует универсальная методика построения обучающих выборок и набор обучающих примеров, как правило, формируется индивидуально для каждой решаемой задачи
В качестве функции ошибки, численно определяющей сходство всех текущих выходных сигналов сети и соответствующих требуемых выходных сигналов обучающей выборки, в большинстве случаев используется среднеквадратичное отклонение Однако в ряде нейроимитаторов существует либо возможность выбора, либо задания своей функции ошибки
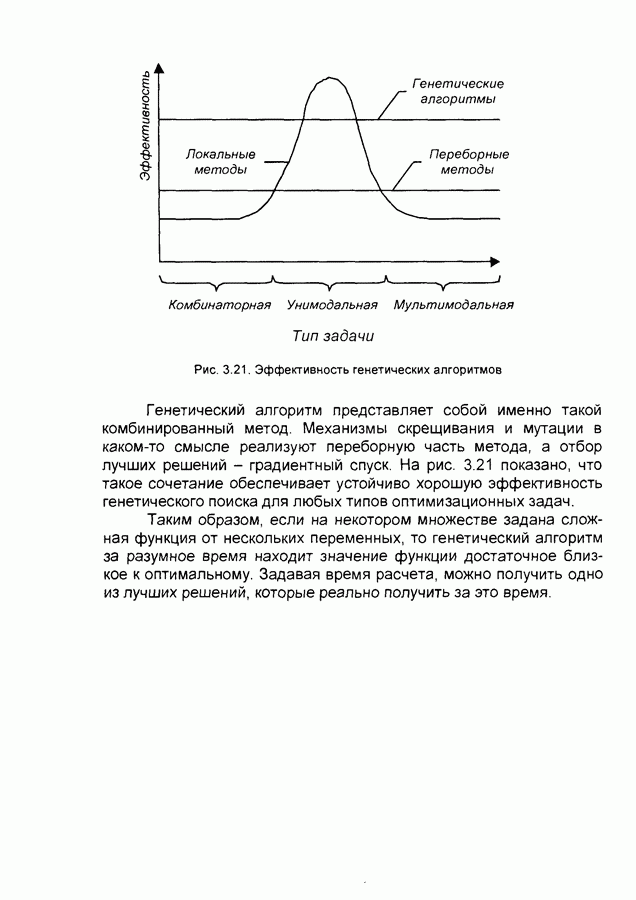
Реализуемые в нейропакетах алгоритмы обучения нейронных сетей можно разделить на три группы градиентные, стохастические, генетические Градиентные алгоритмы (первого и второго порядков) основаны на вычислении частных производных функции ошибки по параметрам сети В стохастических алгоритмах поиск минимума функции ошибки ведется случайным образом Генетические алгоритмы комбинируют свойства стохастических и градиентных алгоритмов на основе аналога генетического наследования реализуют перебор вариантов, а на основе аналога естественного отбора - градиентный спуск
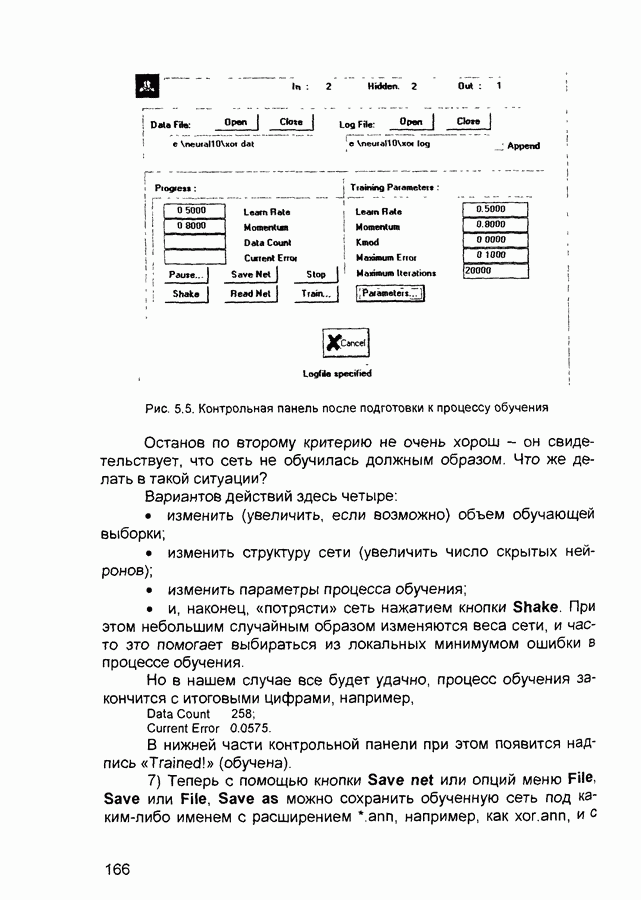
При обучении нейронных сетей, как правило, используются следующие критерии останова
• при достижении некоторого малого значения функции ошибки,
• в случае успешного решения всех примеров обучающей выборки (при неизменности выходных сигналов сети)
В нейроимитаторах предусмотрено наличие специальных процедур инициализации перед обучением сети, т. е. присваивания параметрам сети некоторых малых случайных значений
Обучение представляет собой итерационную процедуру, которая при реализации на персональных компьютерах требует значительного времени Скорость сходимости алгоритма обучения является одной из самых важных характеристик программ для моделирования нейронных сетей
Тестирование обученной нейронной сети
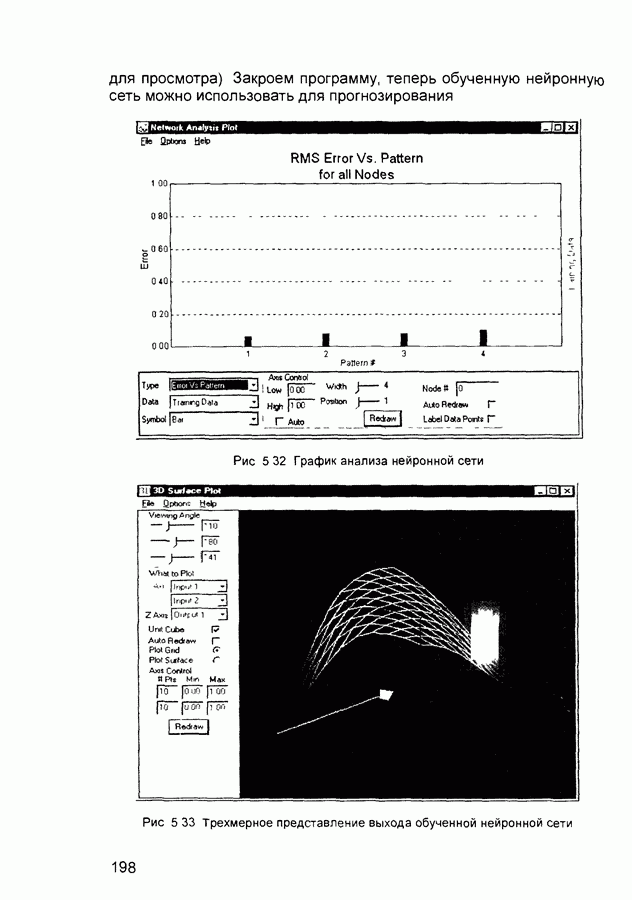
Для проверки правильности обучения построенной нейронной сети в нейроимитаторах предусмотрены специальные средства ее тестирования В сеть вводится некоторый сигнал который, как правило, не совпадает ни с одним из входных сигналов примеров обучающей выборки Далее анализируется получившийся выходной сигнал сети
Тестирование обученной сети может проводиться либо на одиночных входных сигналах, либо на тестовой выборке, которая имеет структуру, аналогичную обучающей выборке, и также состоит из пар (<вход>, <требуемый выход>) Обычно, обучающая и тестовая выборки не пересекаются Тестовая выборка строится индивидуально для каждой решаемой задачи
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
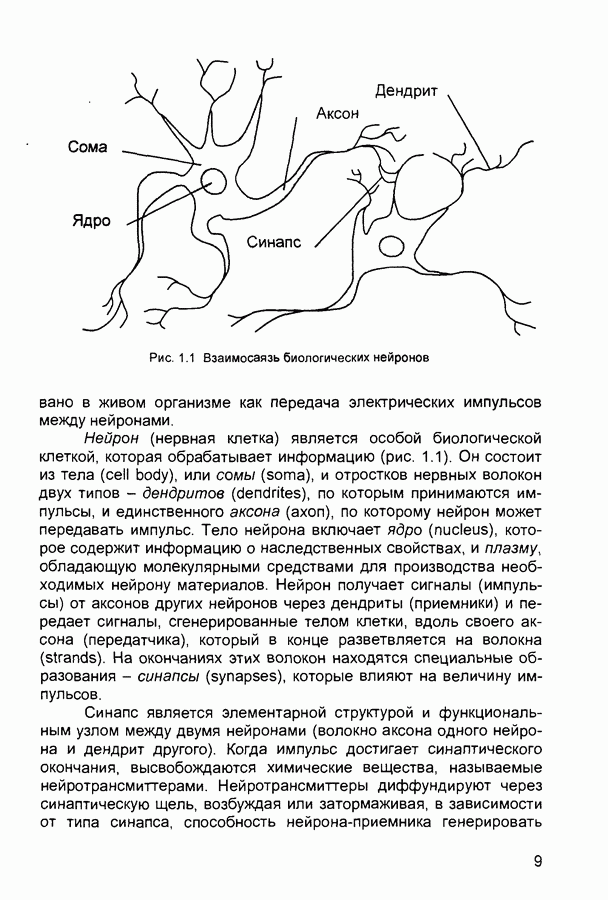
- 1.1. Биологический нейрон
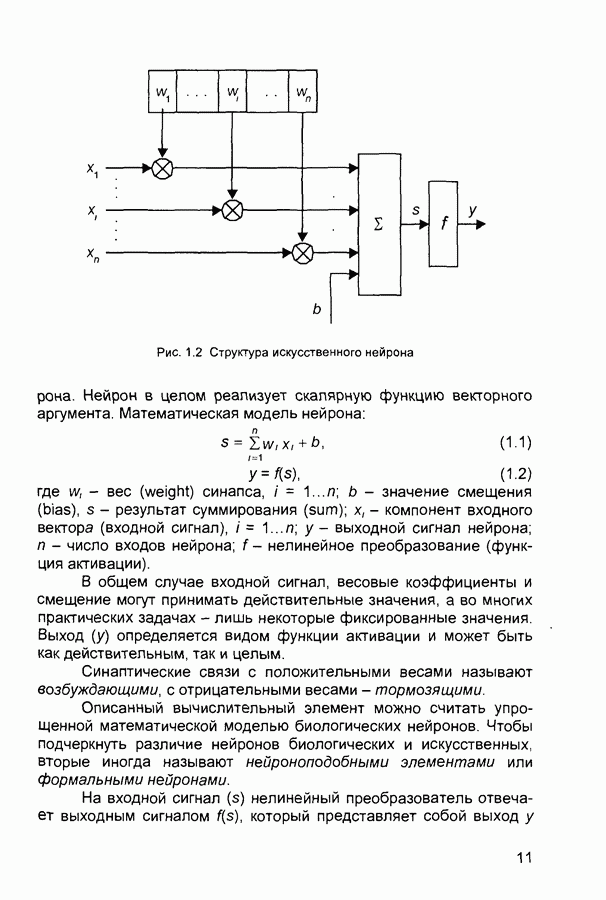
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
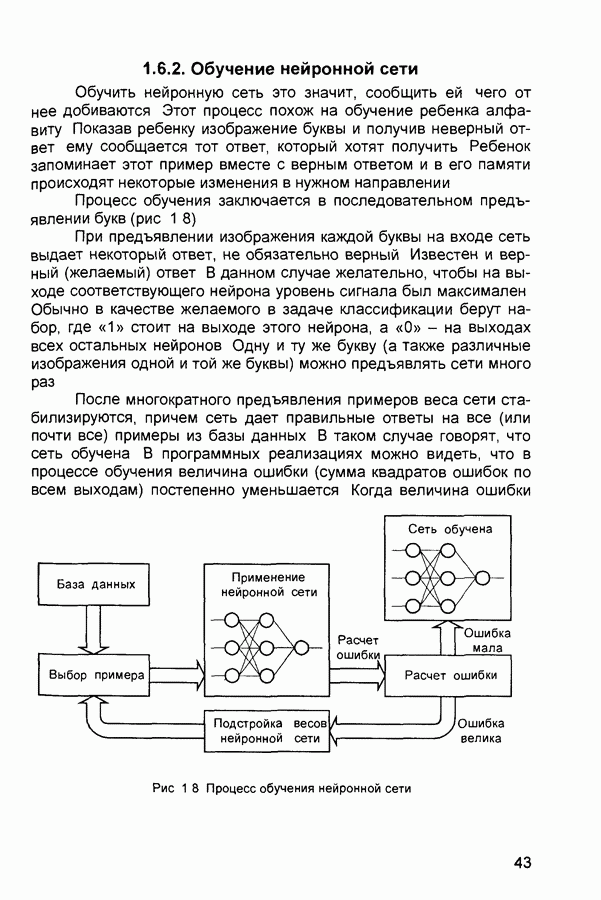
- 1.6. Краткое обобщение материалов главы
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
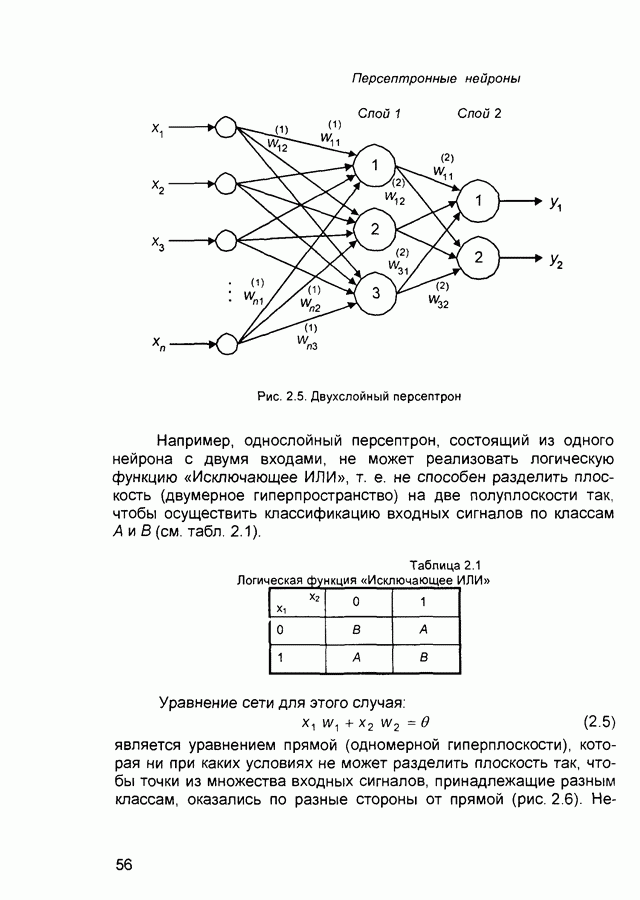
- 2.2. Персептроны
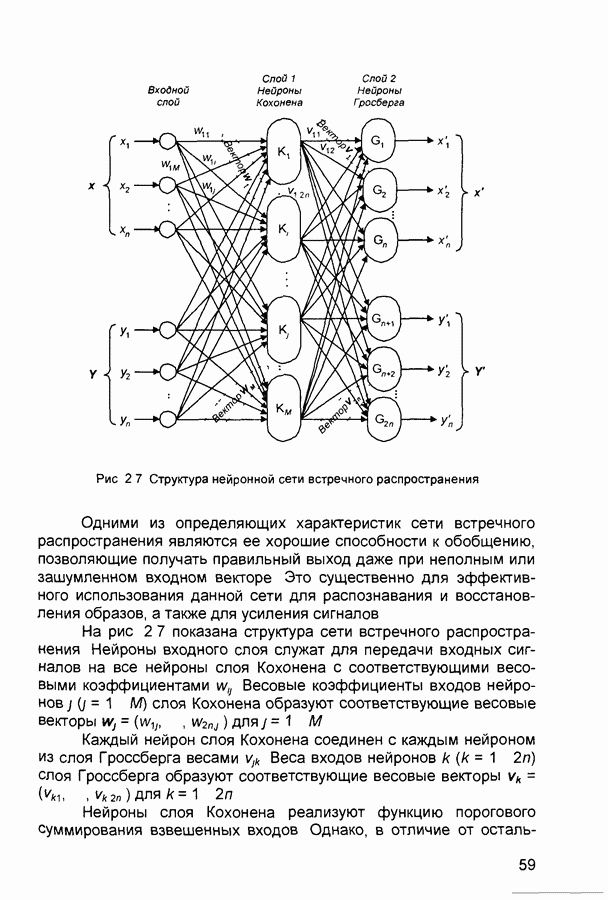
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
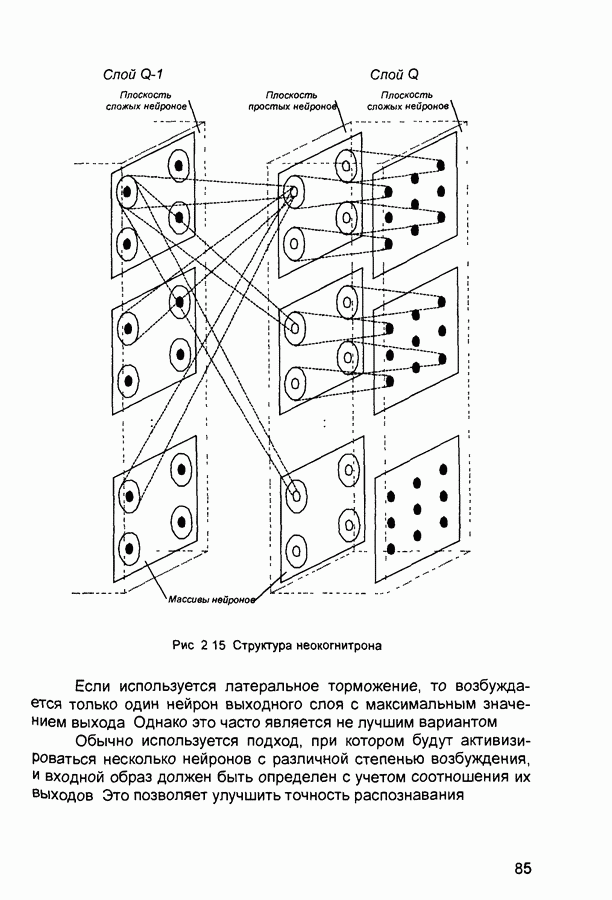
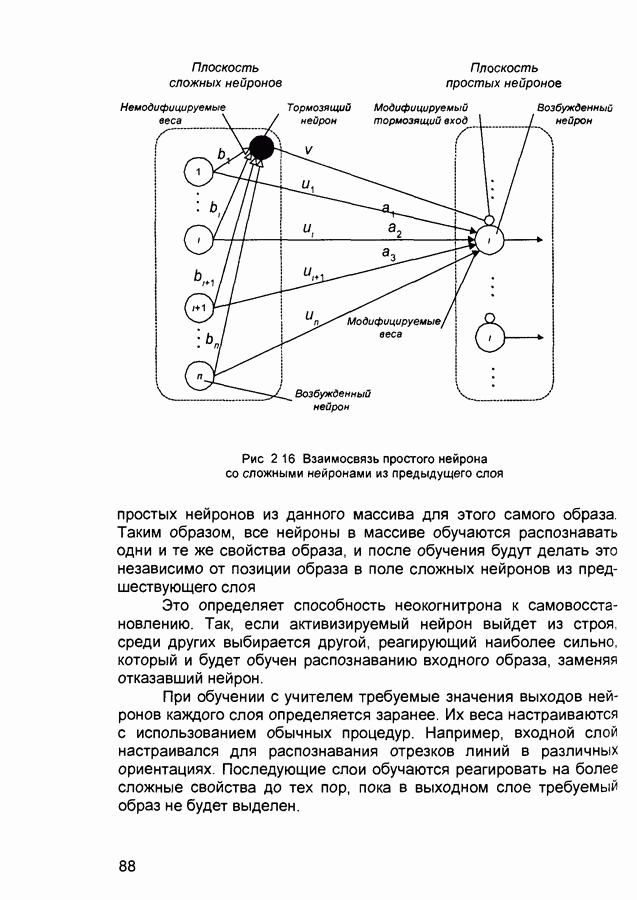
- 2.8. Неокогнитрон
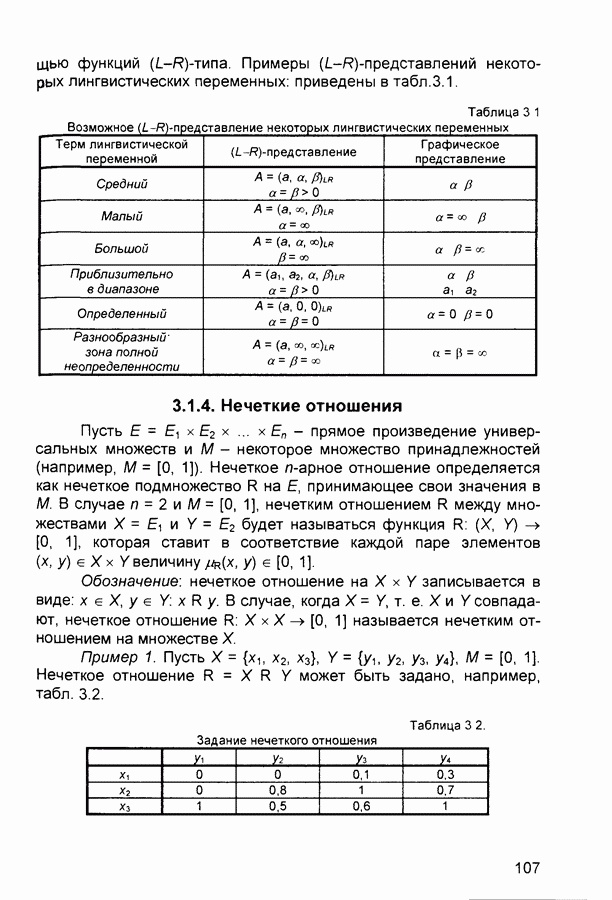
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
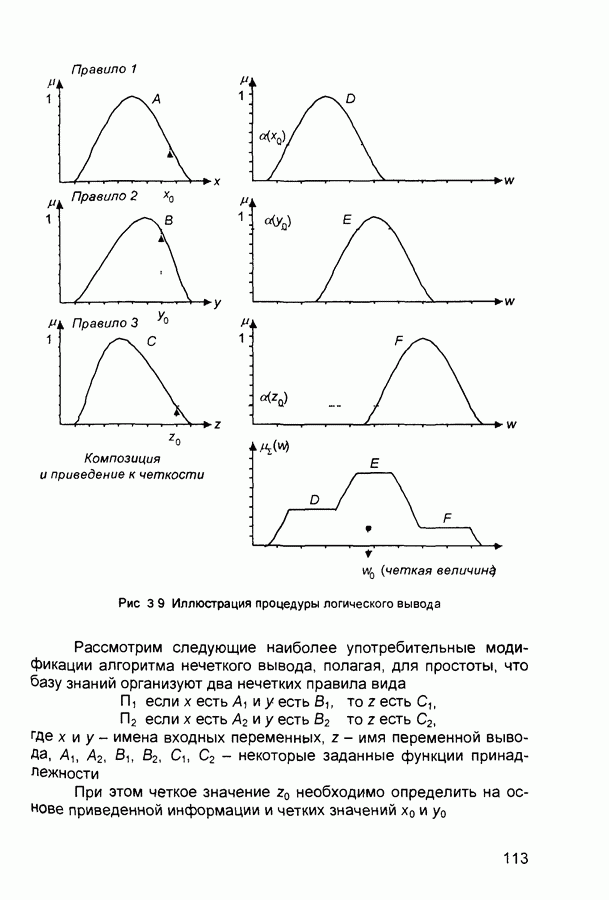
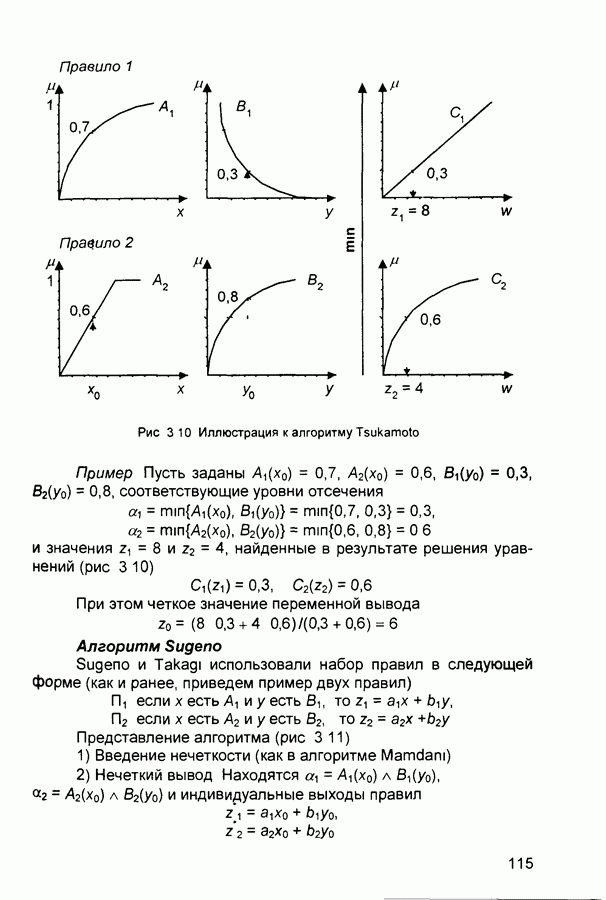
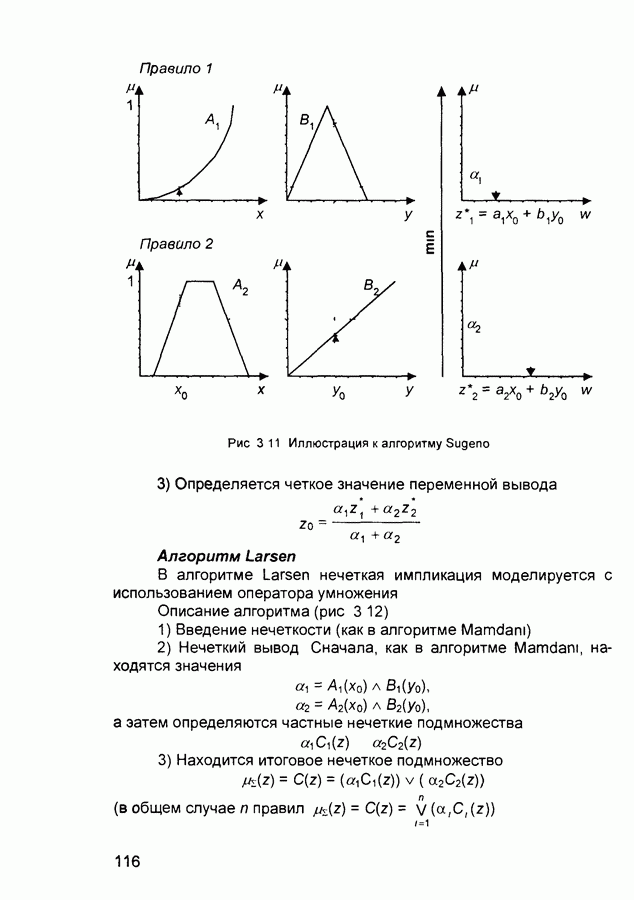
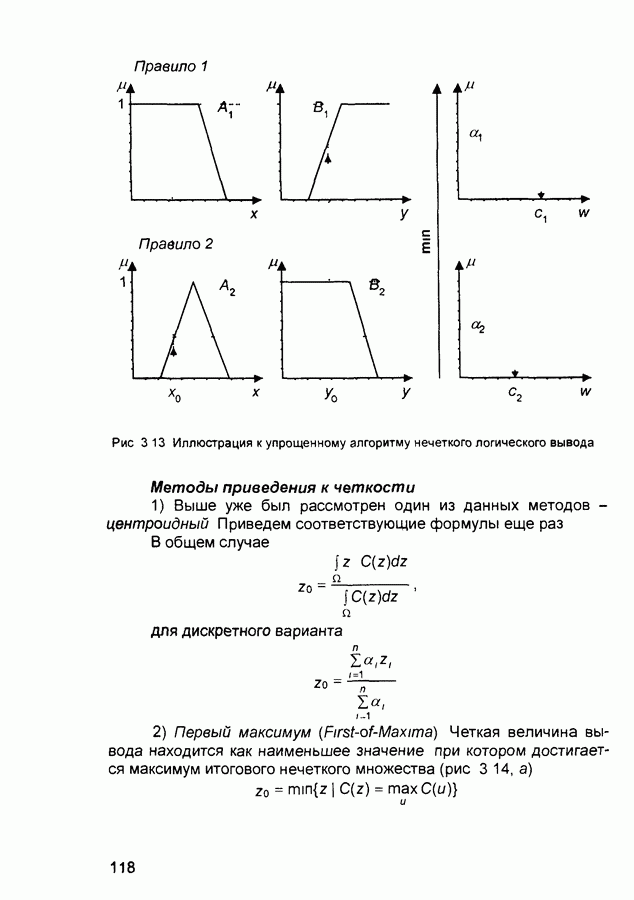
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
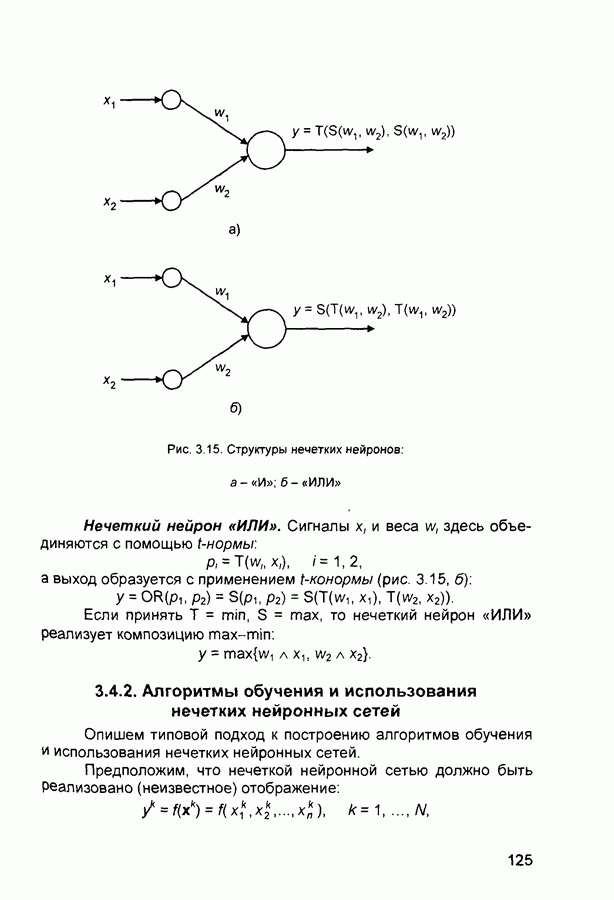
- 3.4. Синтез нечетких нейронных сетей
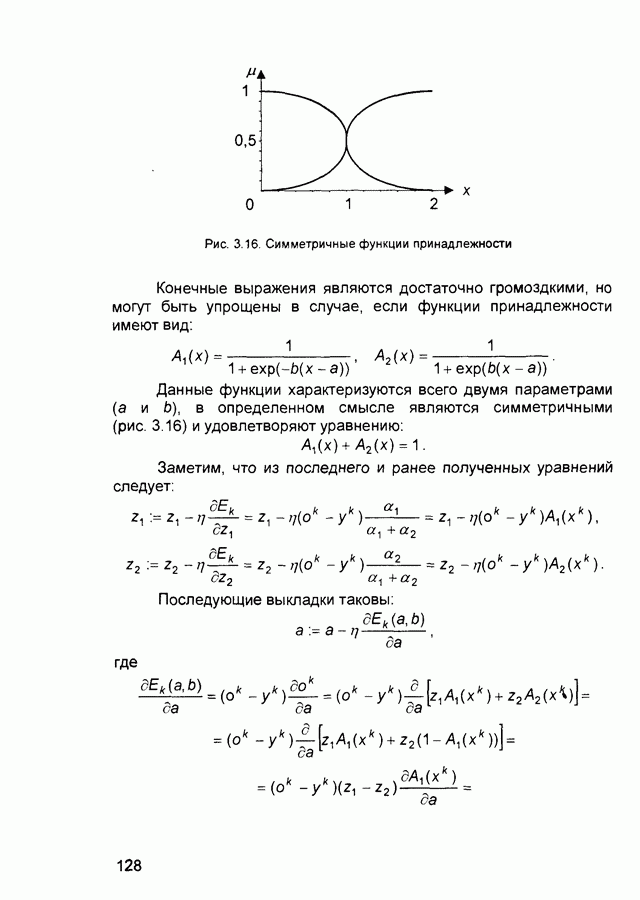
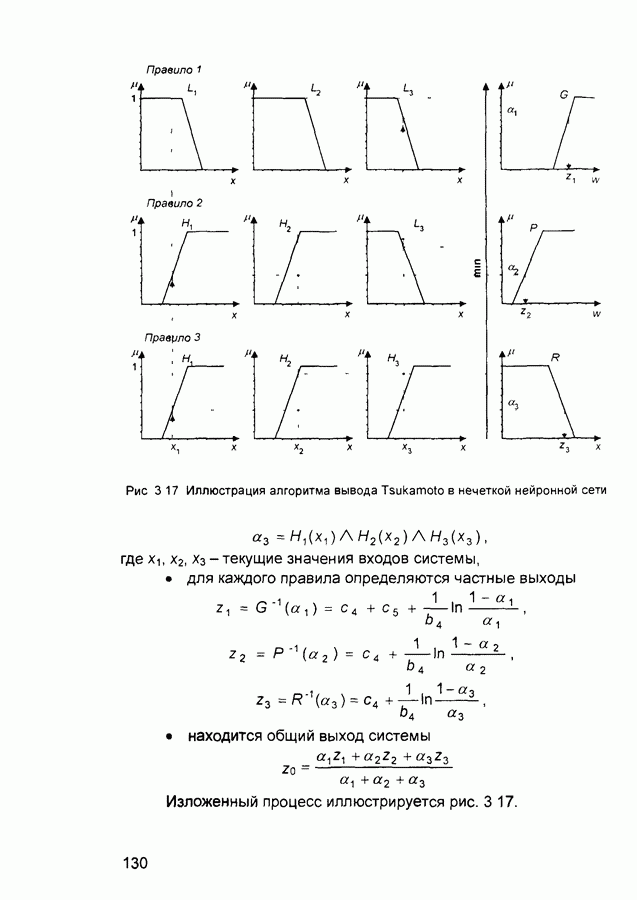
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
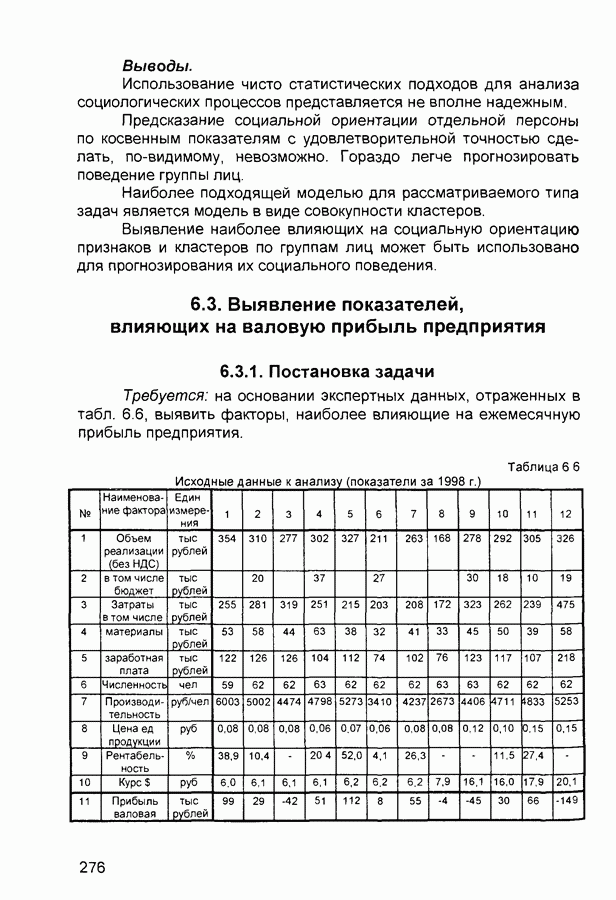
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
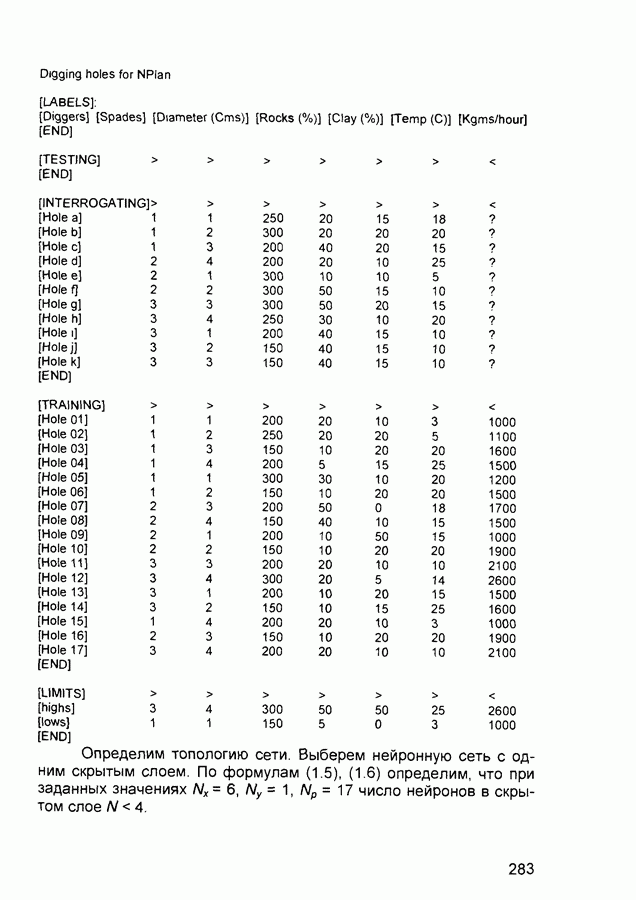
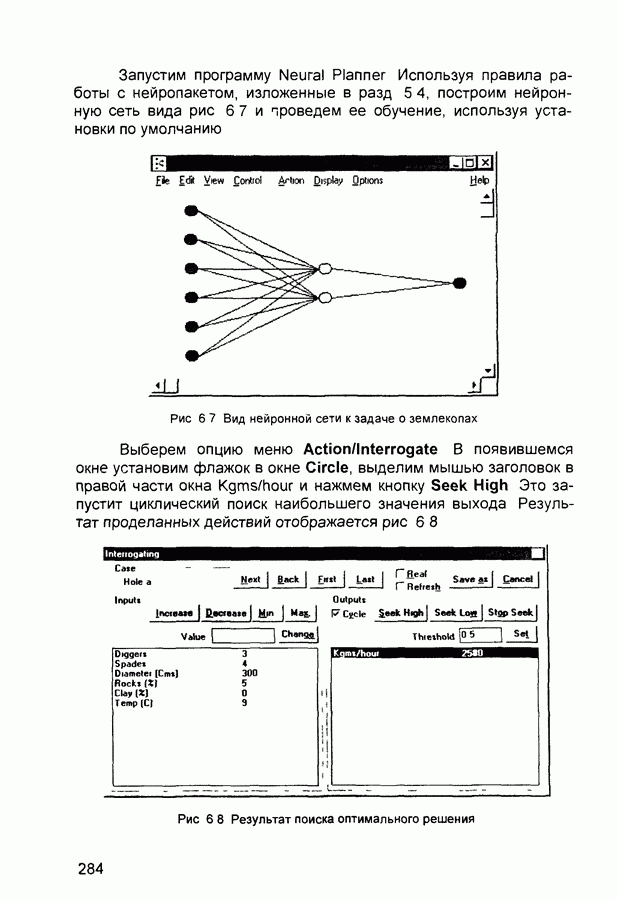
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
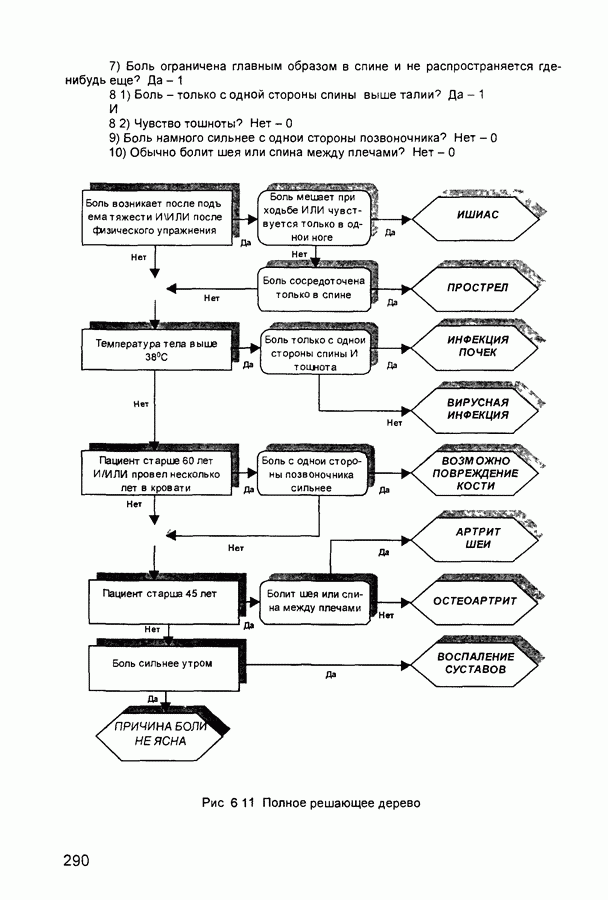
- 6.7. Нейросетевая экспертная система
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы