| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4.2. Нейронные сети Хэмминга
В случае, если необходимо определить номер эталона, ближайший к предъявленному входному вектору, может быть использована сеть Хэмминга. Преимуществами этой сети по сравнению с сетью Хопфилда являются меньшие затраты на память и объем вычислений.
Нейронная сеть Хэмминга (рис. 2.9) состоит из входного, скрытого и выходного слоев нейронов. Скрытый и выходной слои содержат по К нейронов, где К - число эталонов. Нейроны

Рис. 2.9. Структура нейронной сети Хэмминга
скрытого слоя  синапсами соединены с выходами нейронов входного слоя сети. Выходы нейронов выходного слоя связаны со входами остальных нейронов этого слоя отрицательными обратными (ингибиторными) связями. Единственная положительная обратная связь подается с выхода для каждого нейрона выходного слоя на его же вход.
синапсами соединены с выходами нейронов входного слоя сети. Выходы нейронов выходного слоя связаны со входами остальных нейронов этого слоя отрицательными обратными (ингибиторными) связями. Единственная положительная обратная связь подается с выхода для каждого нейрона выходного слоя на его же вход.
Сеть выбирает эталон с минимальным хэмминговым расстоянием от предъявленного входного вектора путем активизации только одного выхода сети (нейрона выходного слоя), соответствующего этому эталону.
Хэммингово расстояние представляет собой пример меры сходства или, вернее, различия, первоначально введенной для бинарных функций в диадном пространстве. Она применима для сравнения любых упорядоченных наборов, принимающих дискретные значения и, вероятно, является наилучшей из известных мер сходства между цифровыми кодами. Для бинарных последовательностей  хэммингово расстояние можно определить:
хэммингово расстояние можно определить:

Здесь функция  определяется как число элементов набора
определяется как число элементов набора  принимающих значение логической «1».
принимающих значение логической «1».
На этапе настройки сети Хэмминга устанавливаются следующие значения весов нейронов скрытого слоя и порога их активационной функции:

где  компонент
компонент  эталона;
эталона; 
Коэффициенты отрицательных обратных связей нейронов выходного слоя задают равными некоторой величине из интервала  а коэффициенты положительной обратной связи -
а коэффициенты положительной обратной связи - 
Рассмотрим алгоритм функционирования сети Хэмминга.
ШАГ 1. На нейроны входного слоя подается вектор 
На их выходах формируются следующие значения (верхний индекс указывает номер слоя):

В соответствии с этим устанавливаются значения на выходах нейронов выходного слоя:

ШАГ 2. В результате новой  итерации определяются новые состояния нейронов выходного слоя:
итерации определяются новые состояния нейронов выходного слоя:

Активационная функция  имеет вид порога (рис. 1.3, б), причем величина «ступеньки» должна быть достаточно большой, чтобы возможные значения
имеет вид порога (рис. 1.3, б), причем величина «ступеньки» должна быть достаточно большой, чтобы возможные значения  не приводили к насыщению.
не приводили к насыщению.
ШАГ 3. Проверка изменения состояний нейронов выходного слоя за последнюю итерацию. И переход к шагу 2 в случае, если наблюдались изменения. Иначе - окончание процедуры.
Роль нейронов входного слоя весьма условна: воспользовавшись один раз на шаге 1 значениями его весовых коэффициентов, сеть больше не обращается к нему, поэтому этот слой может быть вообще исключен из сети (заменен на матрицу весовых коэффициентов).
В заключении можно сделать следующее обобщение. Сети Хопфилда и Хэмминга позволяют просто и эффективно решить
задачу автоассоциативной памяти: воссоздания образов по неполной и искаженной информации. Невысокая емкость сетей (число запоминаемых образов) объясняется тем, что сети не просто запоминают образы, а позволяют проводить их обобщение, например, с помощью сети Хэмминга возможна классификация по критерию максимального правдоподобия. Вместе с тем, легкость построения программных и аппаратных моделей делают эти сети привлекательными для многих практических применений.
В случае, если необходимо определить эталон, ближайший к предъявленному входному вектору (например, на основе хэммингова расстояния), часто возникают проблемы, связанные с различием длин или с ограничениями на длину последовательностей или количество компонентов в наборах.
Отметим один важный аспект проблемы сравнения векторов различной длины. Так, последовательность большей длины может представлять собой функцию в пространстве с числом измерений большим, чем число измерений другой функции на разницу числа параметров в длинах последовательностей. Это определяет возможность перехода к оценке не только количественного, но и качественного сходства векторов, к оперированию в терминах вероятности, нечетких оценок, отнесению вектора к какому-либо классу.
Эти различия и ограничения сравнения векторов различной длины можно устранить различными способами, например, с помощью меры сходства Танимото.
Авторами предложены модели оптимизирующих нейронных сетей, реализующие восстановление по искаженному (зашумленному) образу ближайший к нему эталонный, позволяющие снять ограничения на различия и ограничения длин сравниваемых векторов с сохранением высокой достоверности распознавания.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
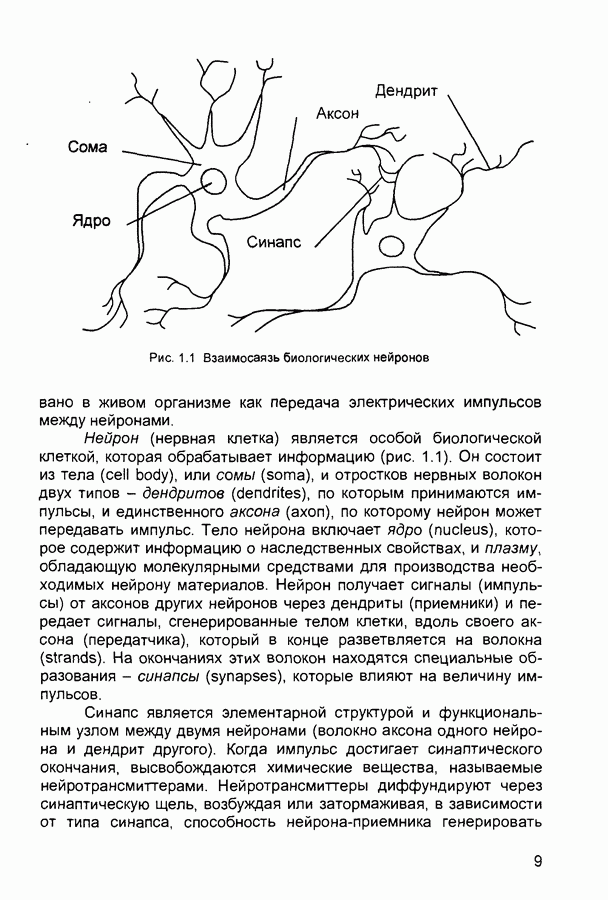
- 1.1. Биологический нейрон
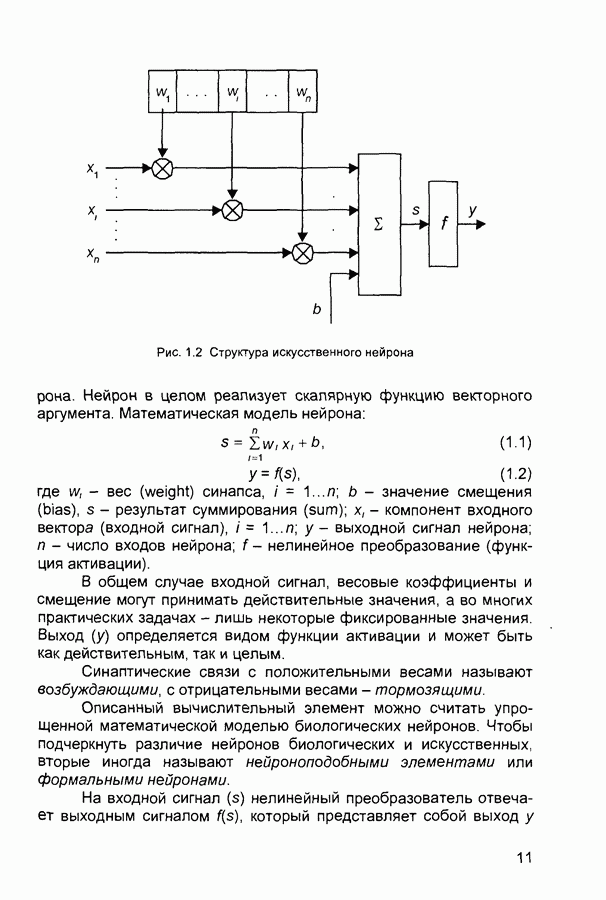
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
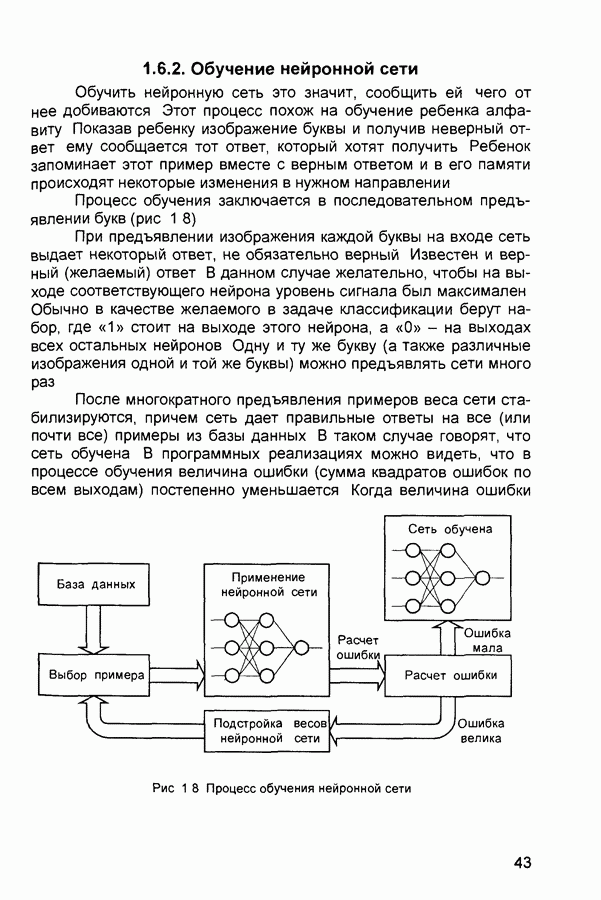
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
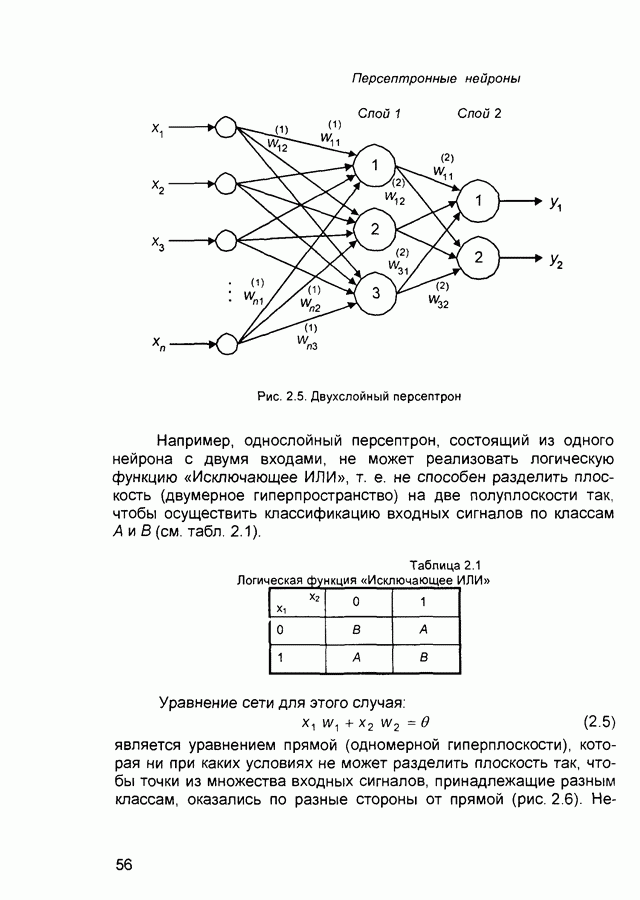
- 2.2. Персептроны
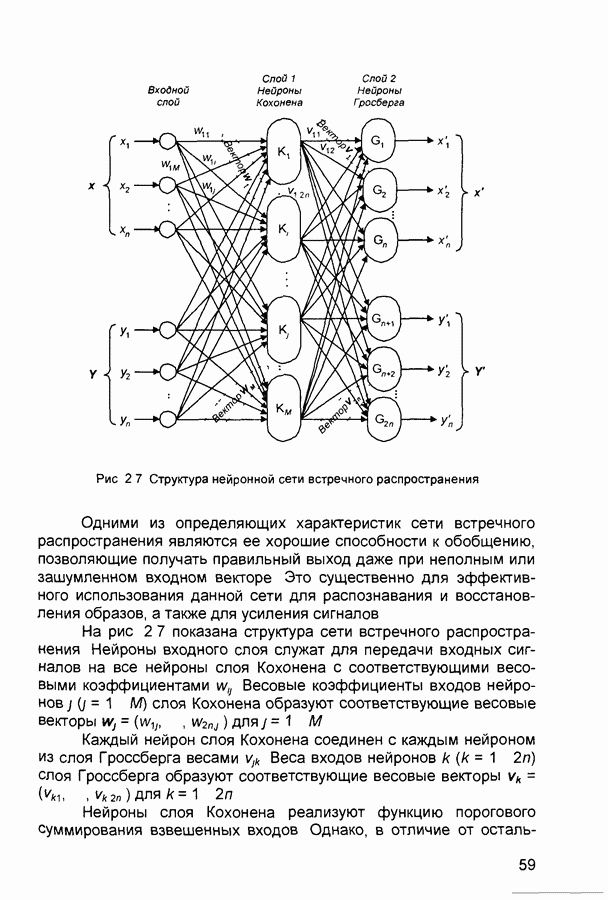
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
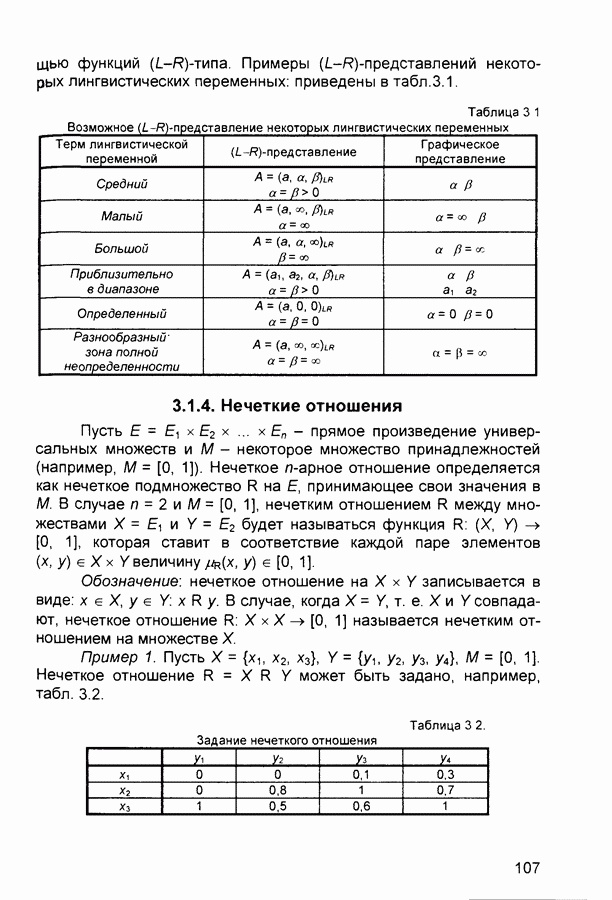
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
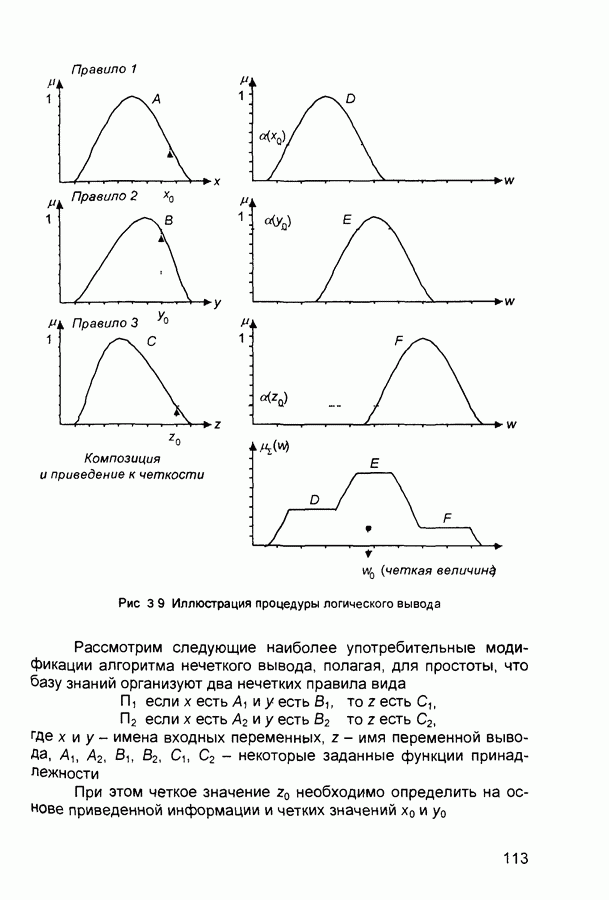
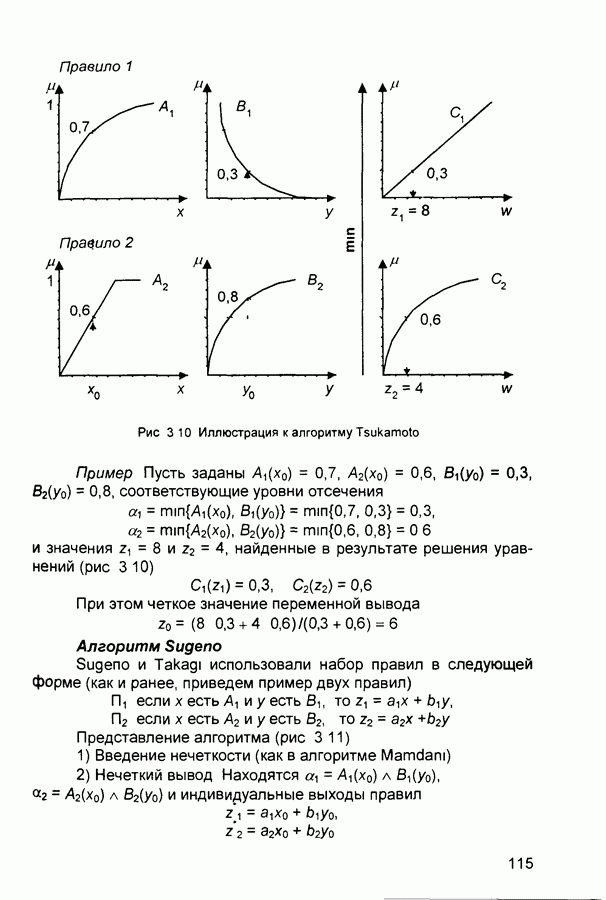
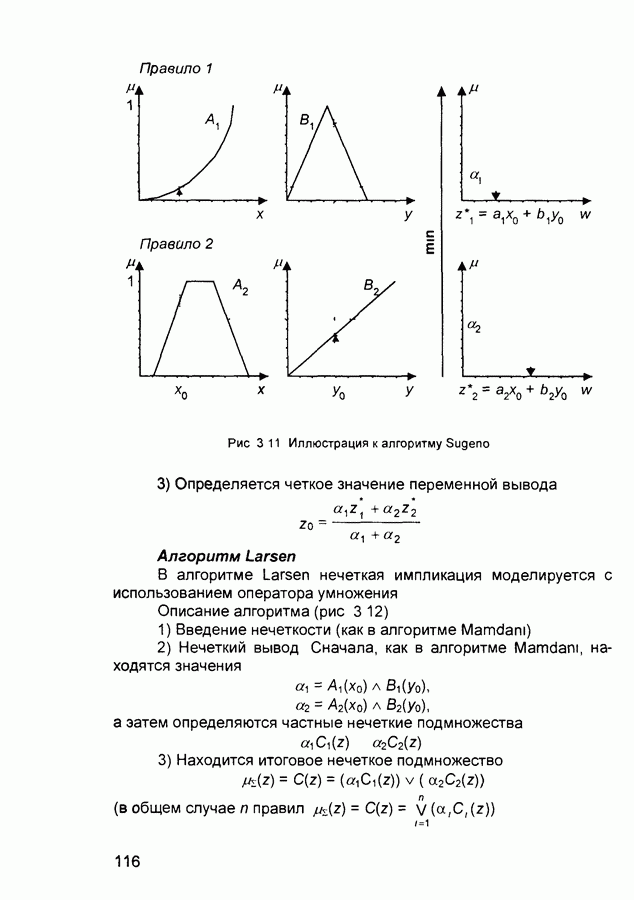
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
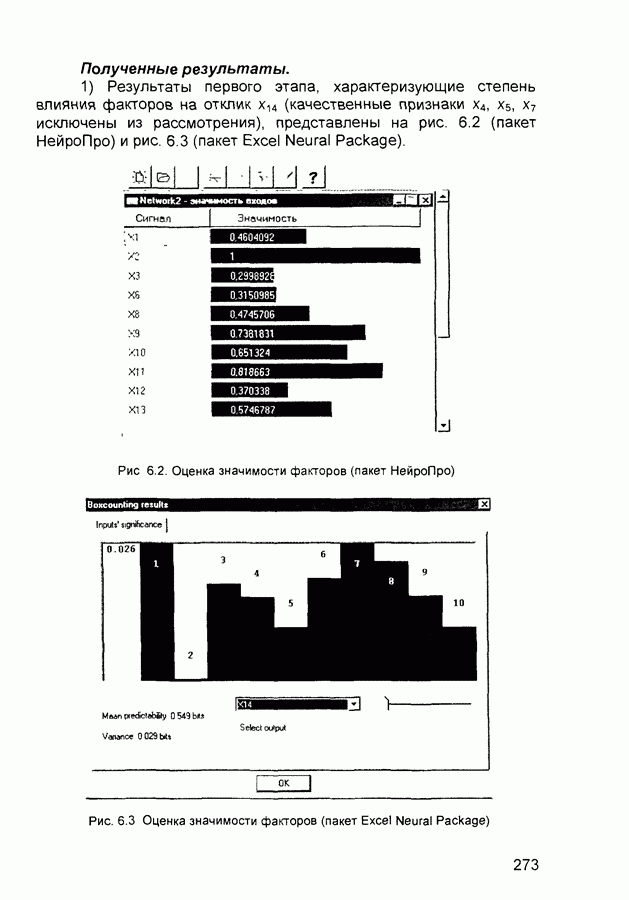
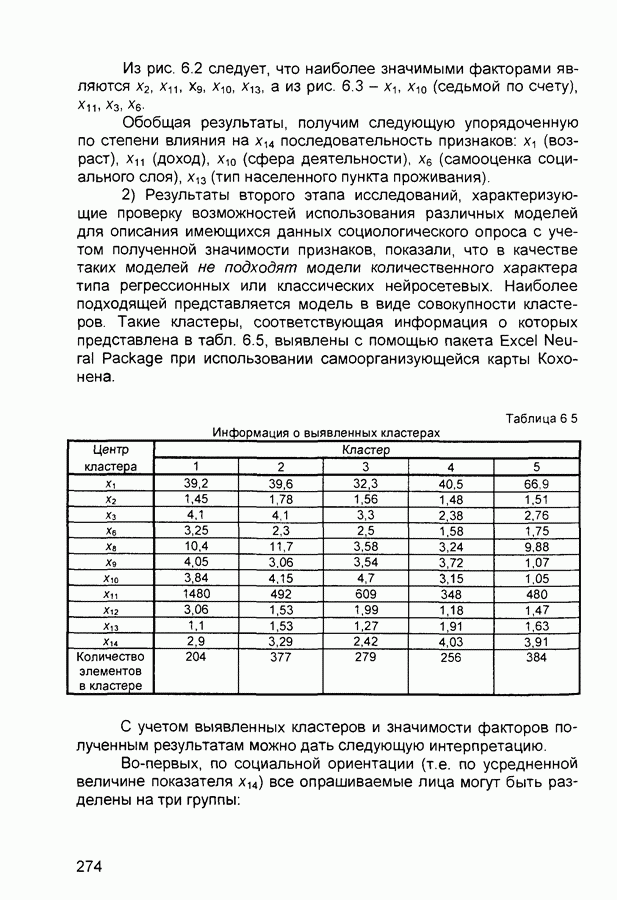
- 6.2. Анализ данных социологического опроса
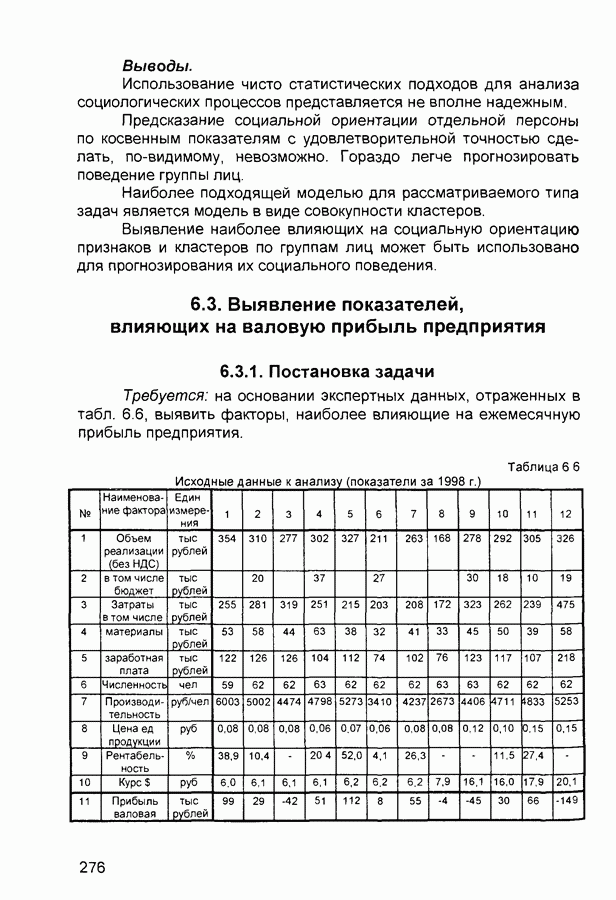
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
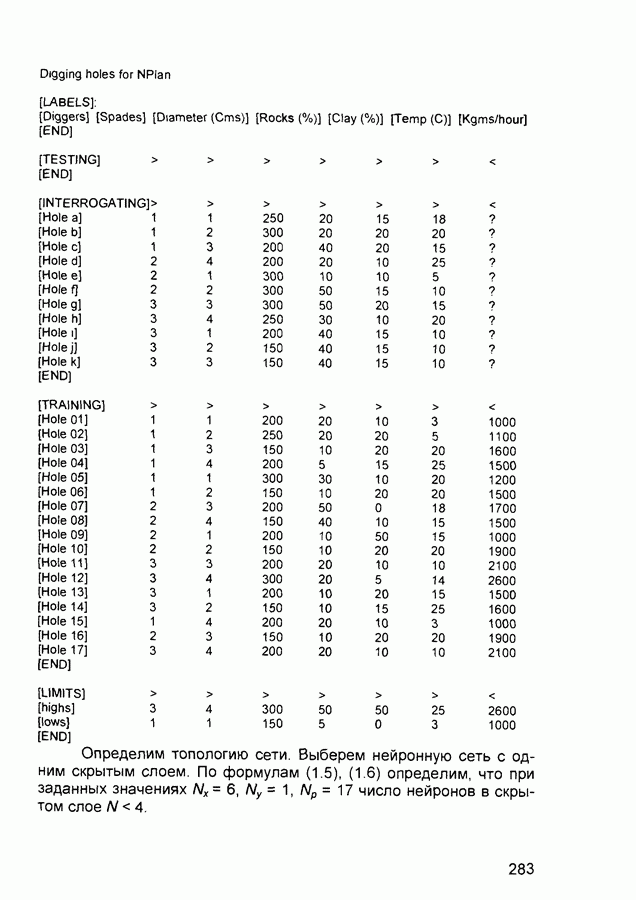
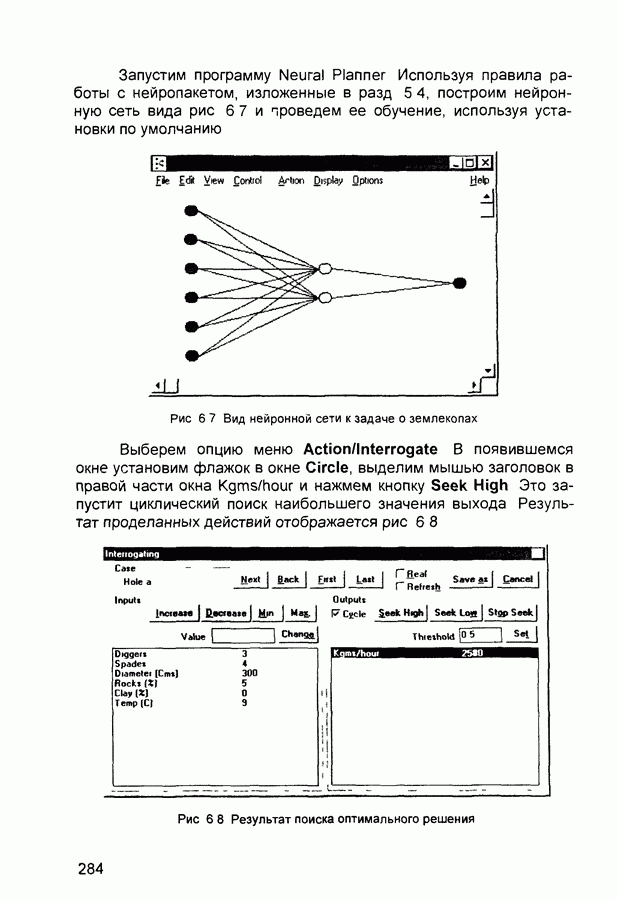
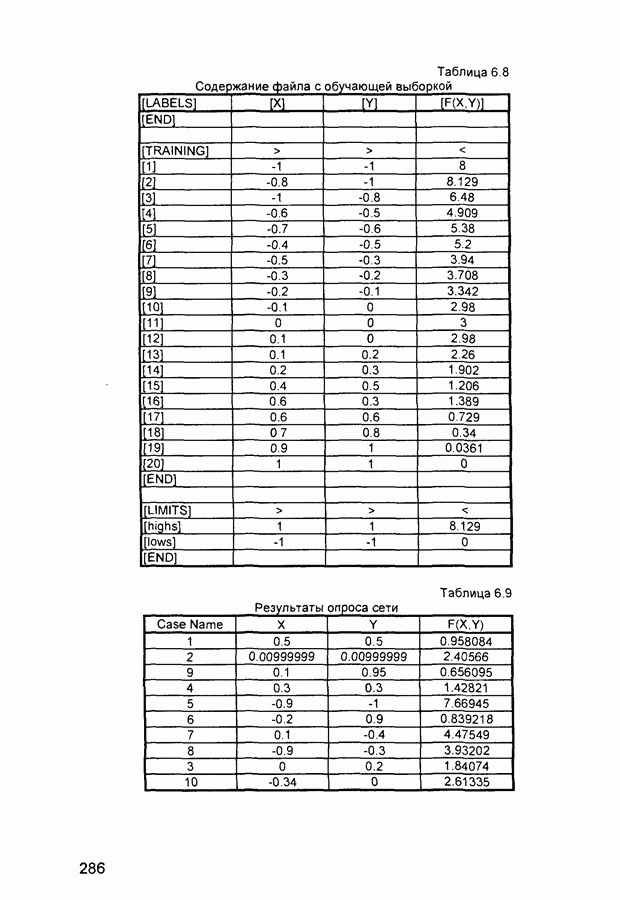
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
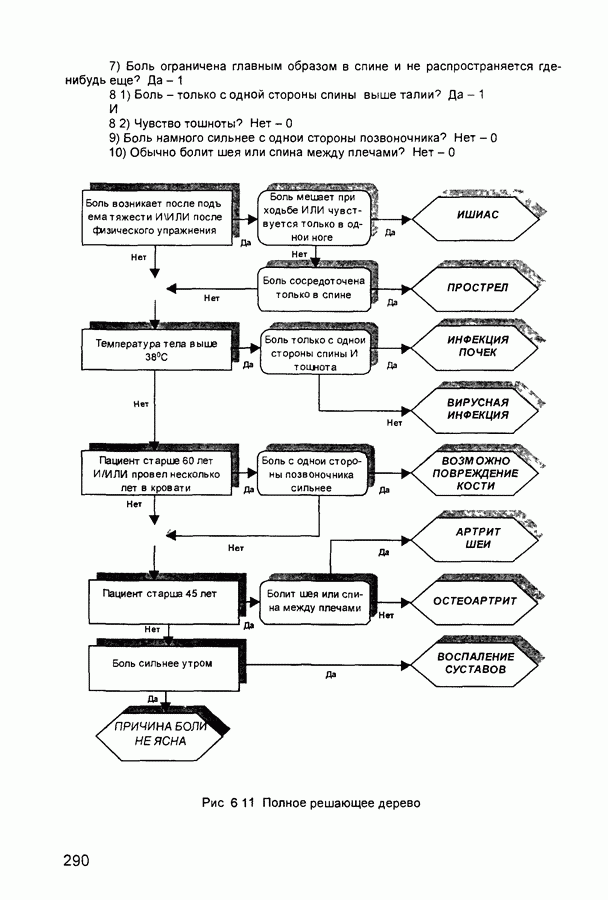
- 6.7. Нейросетевая экспертная система
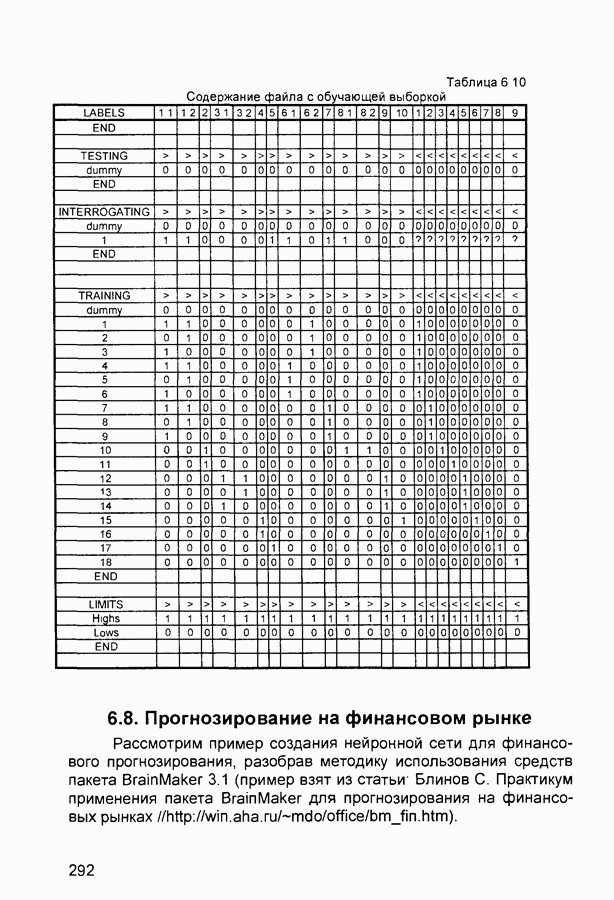
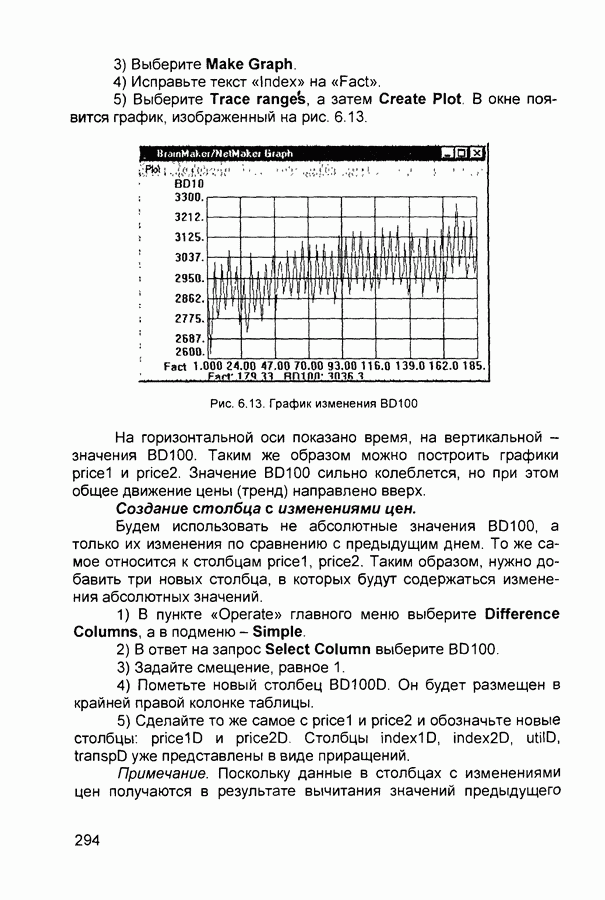
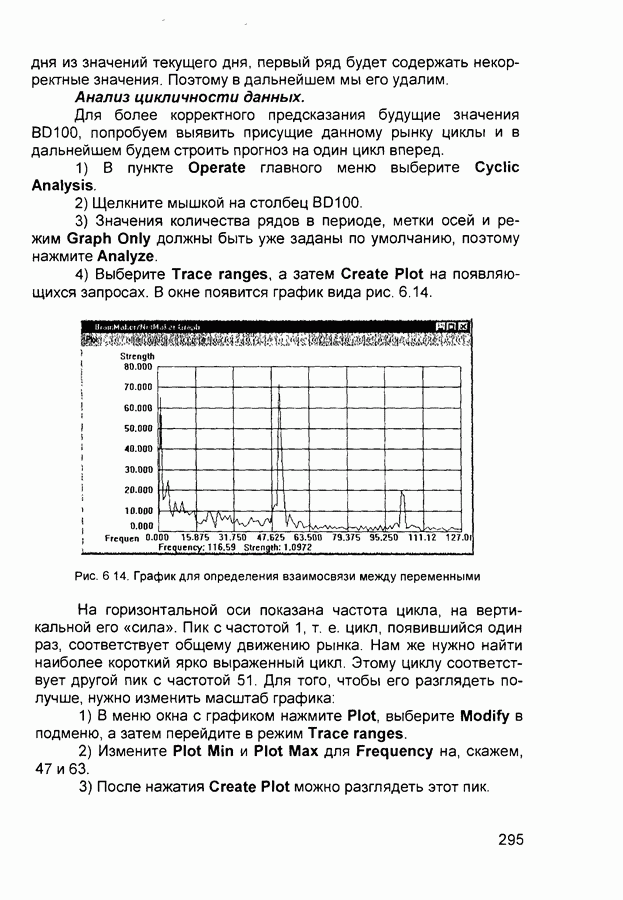
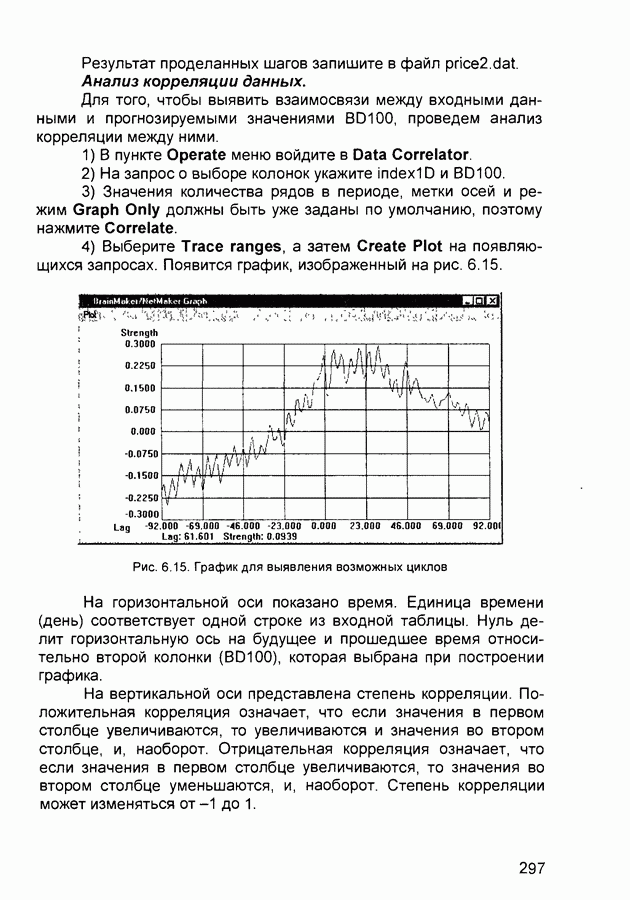
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
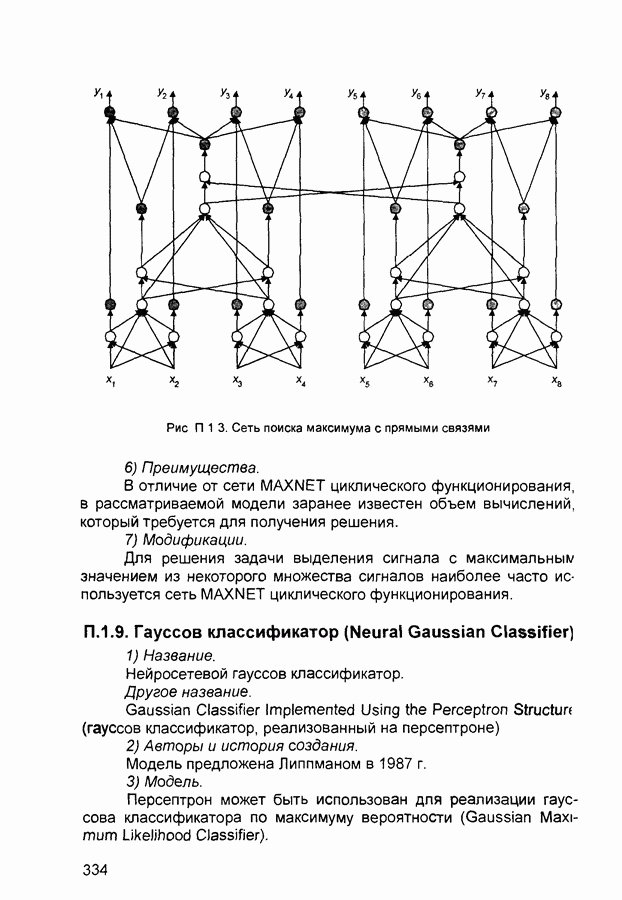
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы