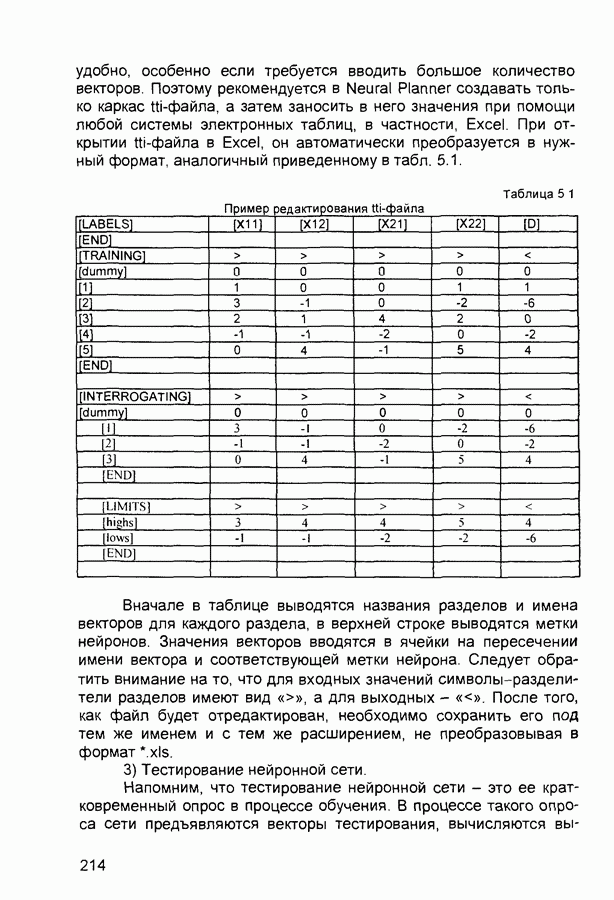
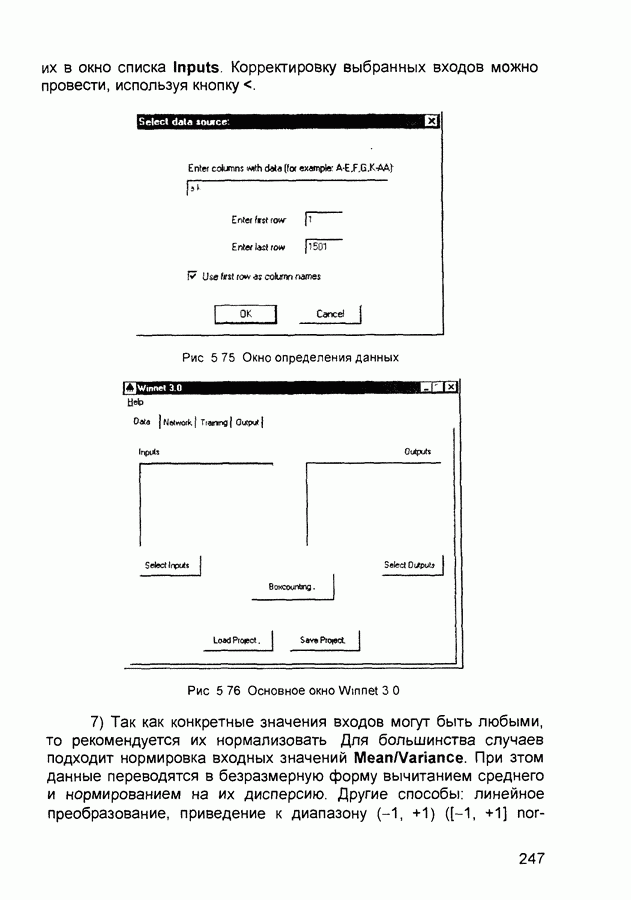
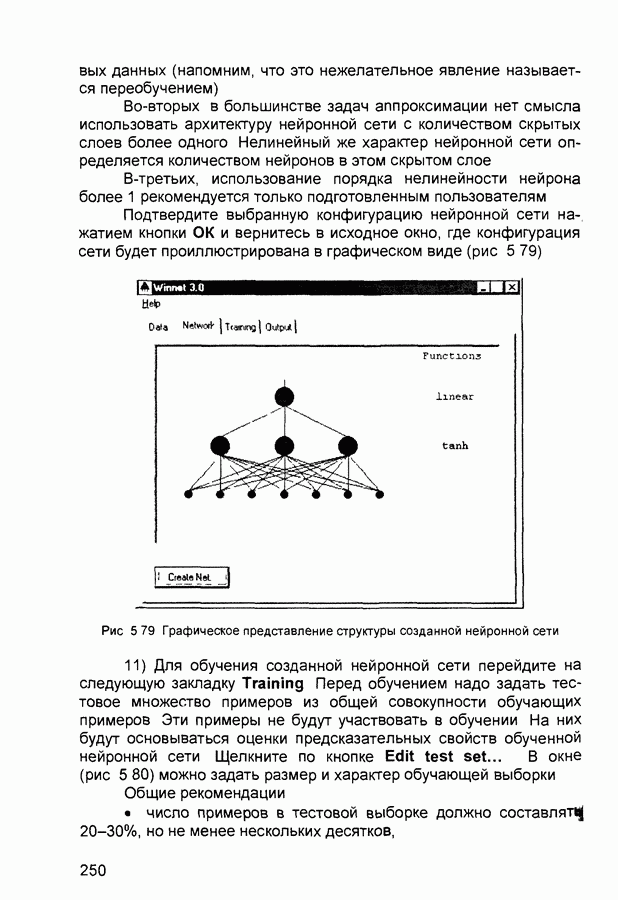
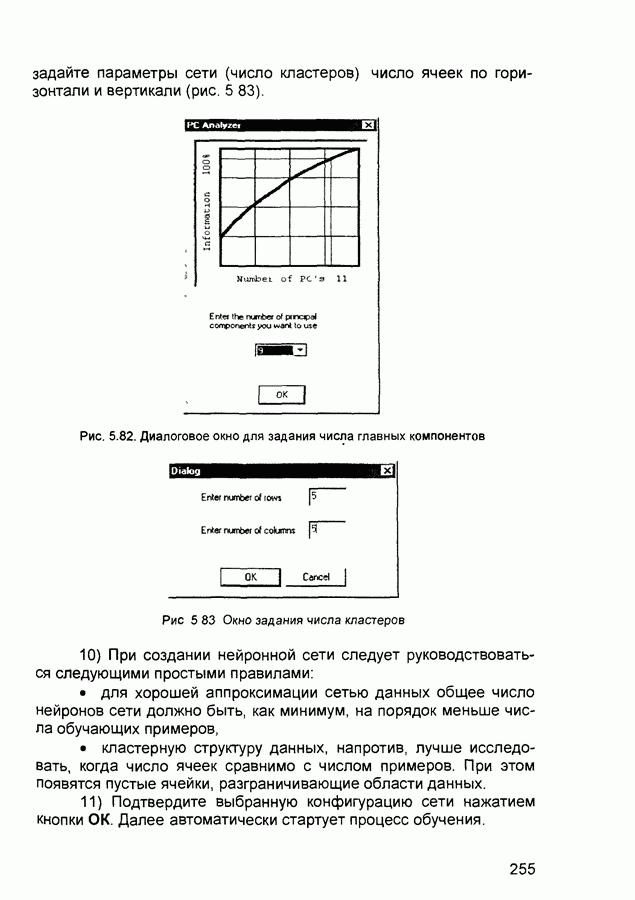
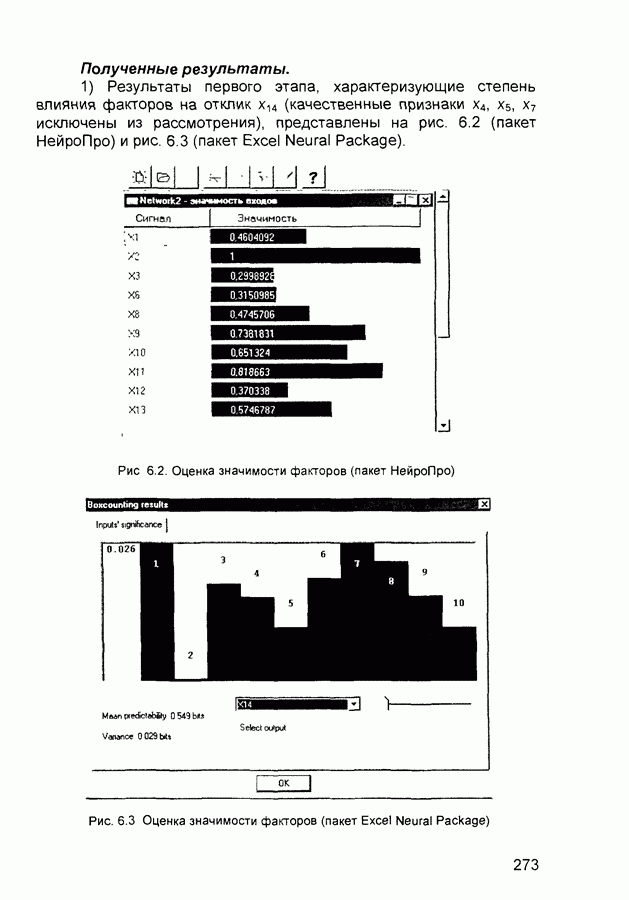
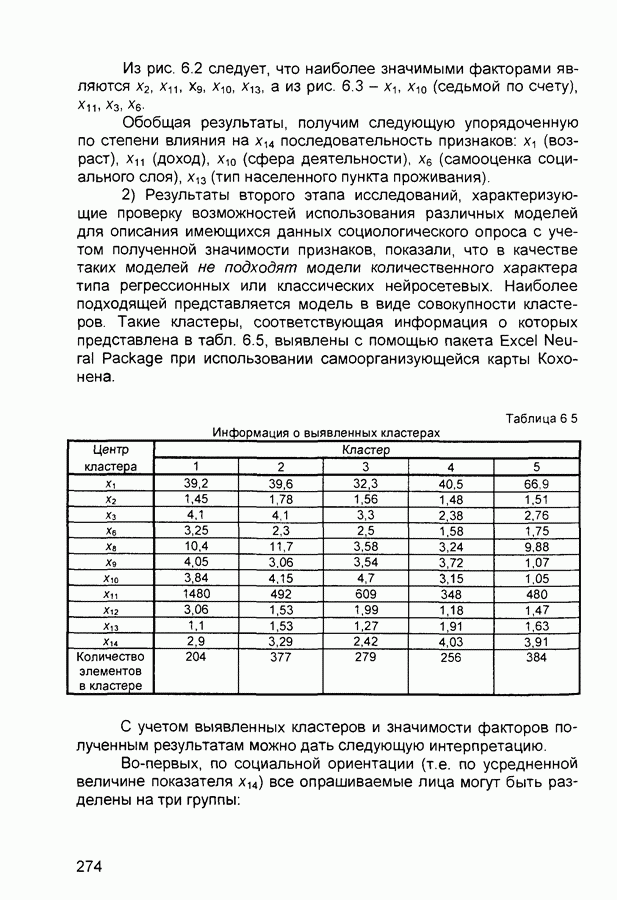
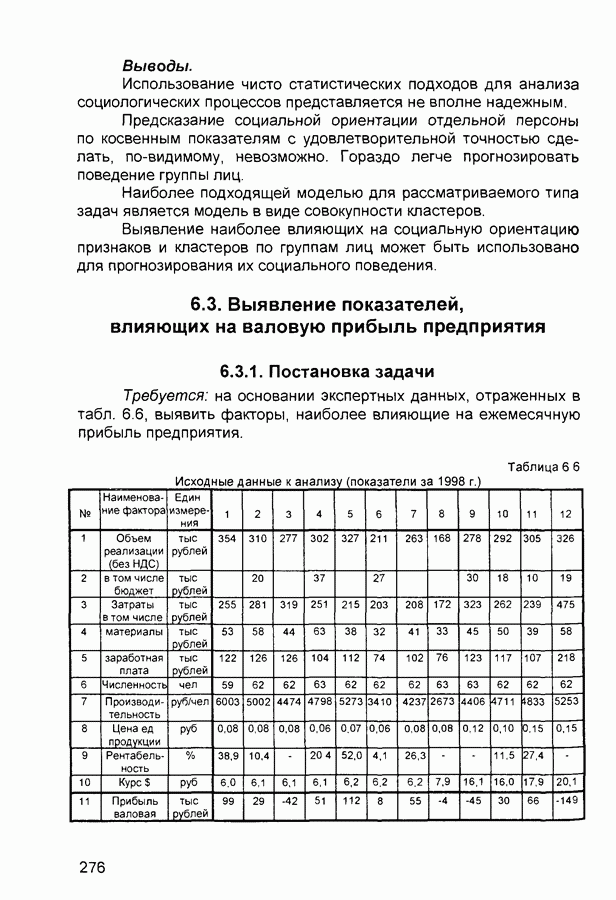
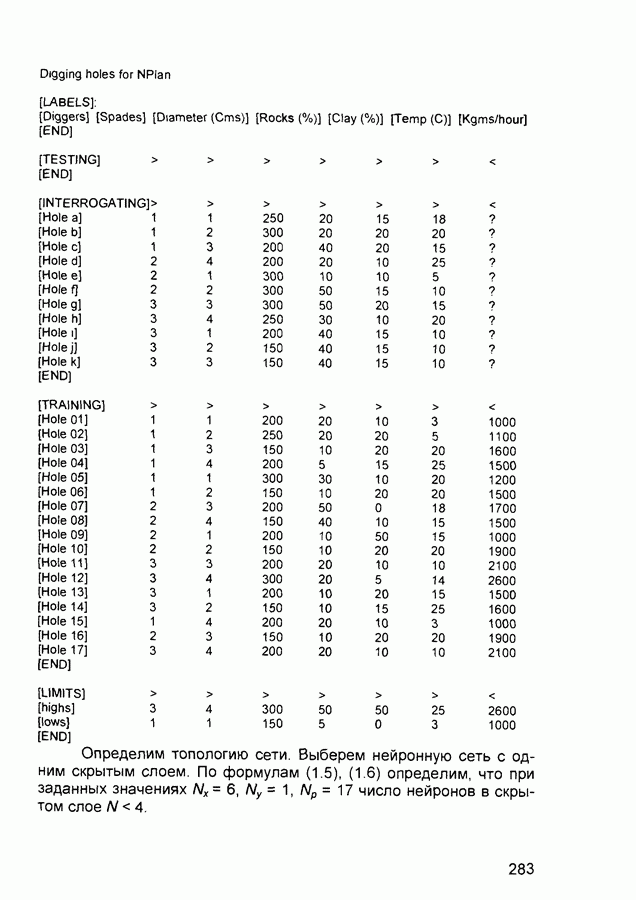
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
Опишем типовой подход к построению алгоритмов обучения и использования нечетких нейронных сетей.
Предположим, что нечеткой нейронной сетью должно быть реализовано (неизвестное) отображение:

при наличии обучающего множества:

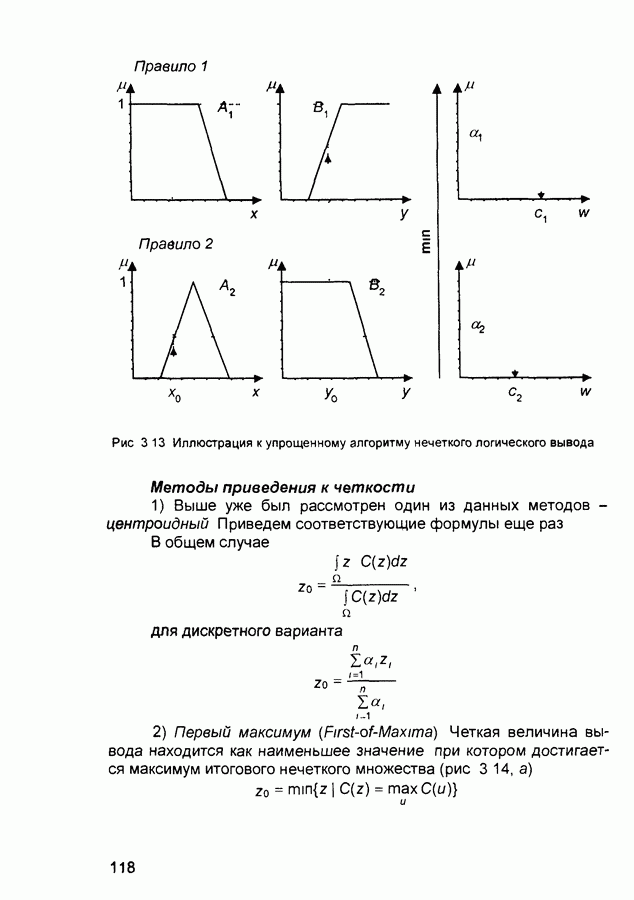
Для моделирования неизвестного отображения  используем упрощенный алгоритм нечеткого вывода (см. разд. 3.2), применяя следующую форму записи предикатных правил:
используем упрощенный алгоритм нечеткого вывода (см. разд. 3.2), применяя следующую форму записи предикатных правил:

где  - нечеткие числа треугольной формы,
- нечеткие числа треугольной формы,  - вещественные числа
- вещественные числа
Степень истинности  правила определяется с помощью операции умножения (Larsen):
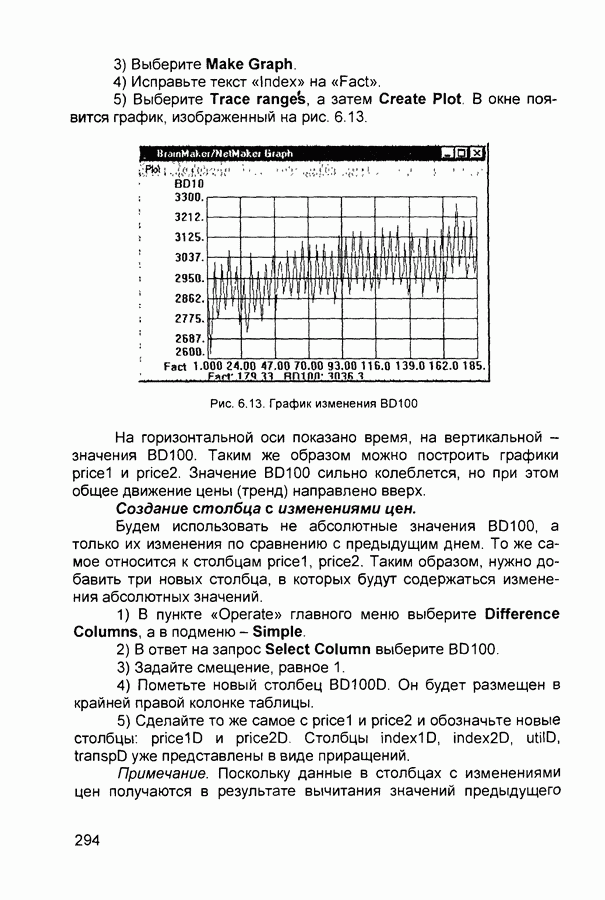
правила определяется с помощью операции умножения (Larsen):

(можно использовать и другие представления для моделирования логического оператора 
Выход нечеткой системы определяется в соответствии с центроидным методом (дискретный вариант):

Введение функции ошибки для  предъявленного образца
предъявленного образца

позволяет, далее, как в обычных нейронных сетях использовать градиентный метод для подстройки параметров заданных предикатных правил. Так, величины  можно корректировать по соотношению:
можно корректировать по соотношению:

где  - константа, характеризующая скорость обучения.
- константа, характеризующая скорость обучения.
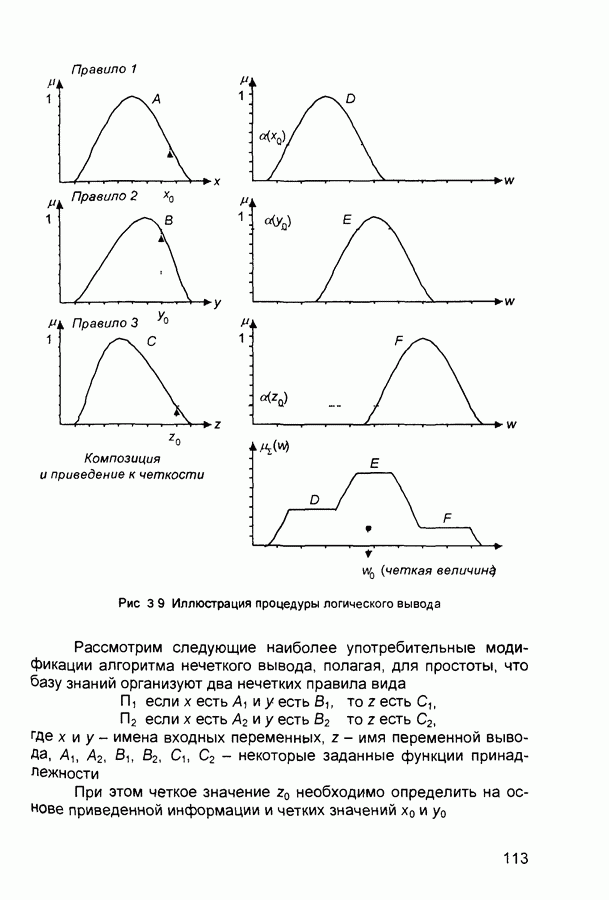
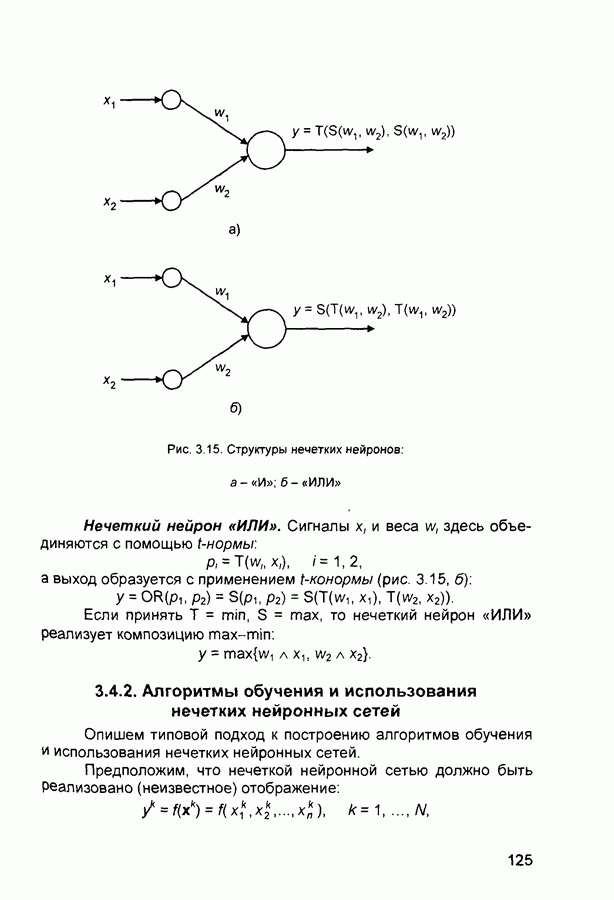
Более детально алгоритм настройки рассмотрим на примере системы, включающей два правила:

при этом предполагается, что нечеткие понятия А, («малый») и  («большой») имеют сигмоидные функции принадлежности:
(«большой») имеют сигмоидные функции принадлежности:

характеризующиеся параметрами 
Степени истинности правил определяются в данном случае соотношениями:

а выход системы - выражением:

Предположим, что имеется обучающее множество  отображающее неизвестную функцию
отображающее неизвестную функцию 
Требуется: осуществить такую настройку параметров системы  при которой обеспечивается наилучшая аппроксимация данной функции.
при которой обеспечивается наилучшая аппроксимация данной функции.
Решение. Для данного случая функция ошибки может быть записана в форме:

Используя далее тот же подход, как и при выводе алгоритма обратного распространения ошибки (см. разд. 1.4), запишем:

Аналогичным образом могут быть получены выражения для коррекции коэффициентов  Исходные соотношения таковы:
Исходные соотношения таковы:


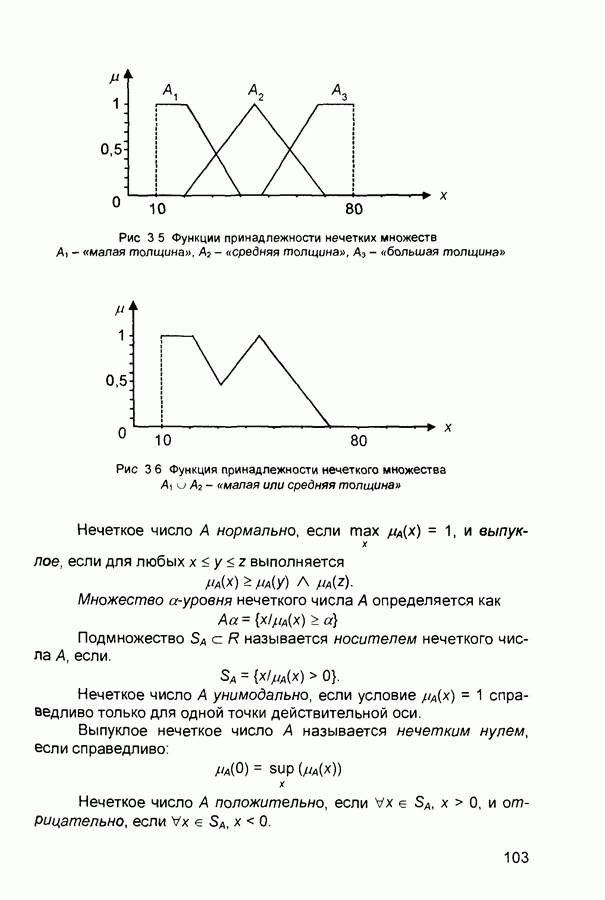
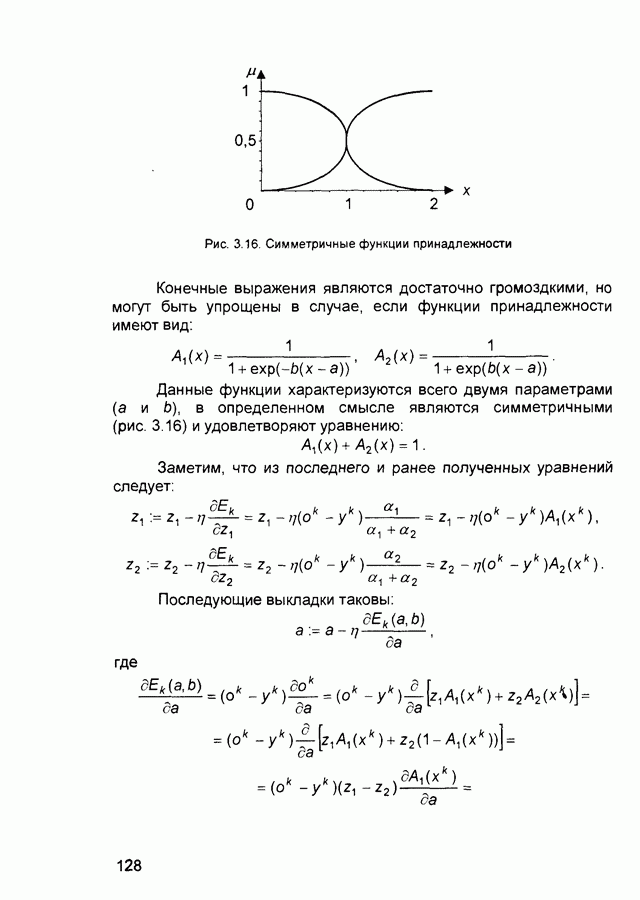
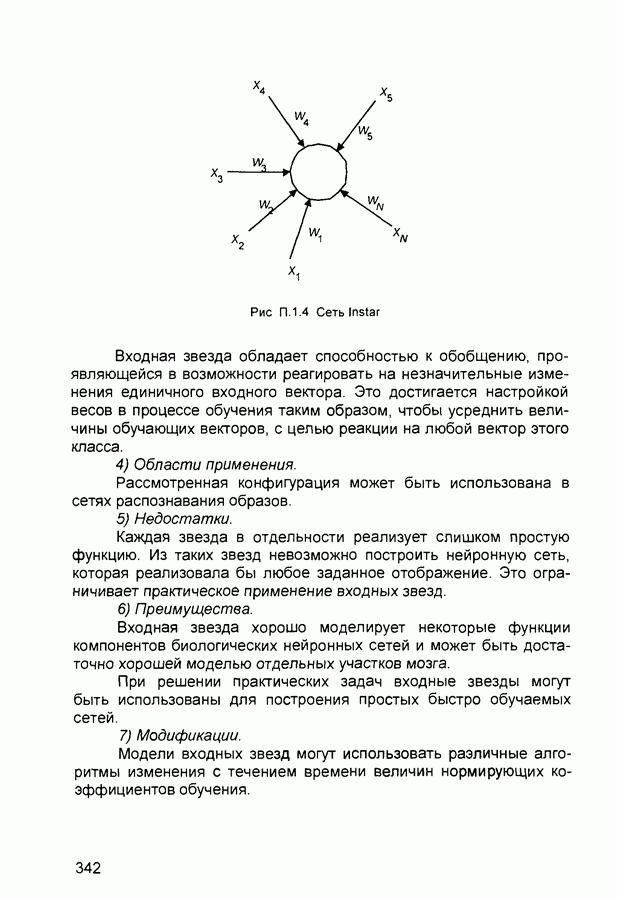
Рис. 3.16. Симметричные функции принадлежности
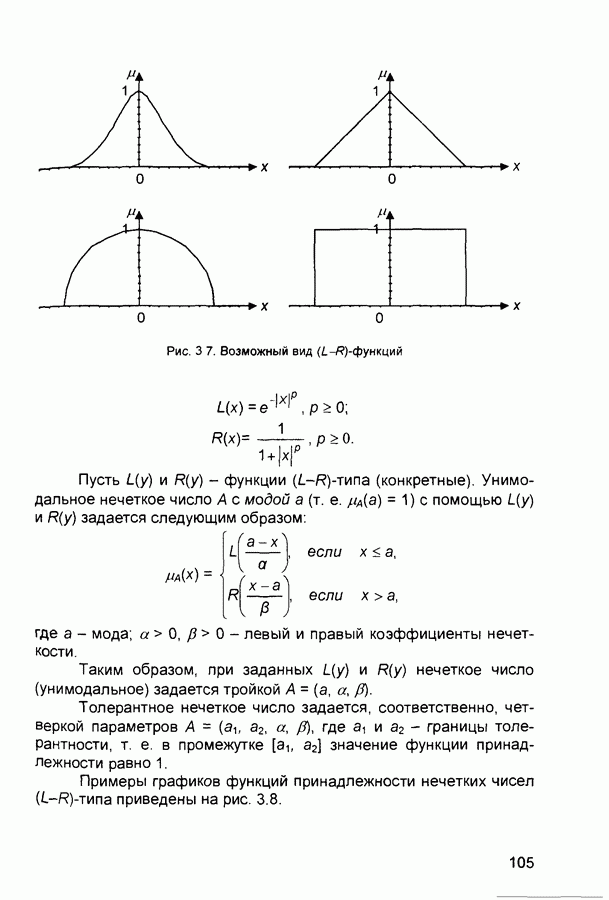
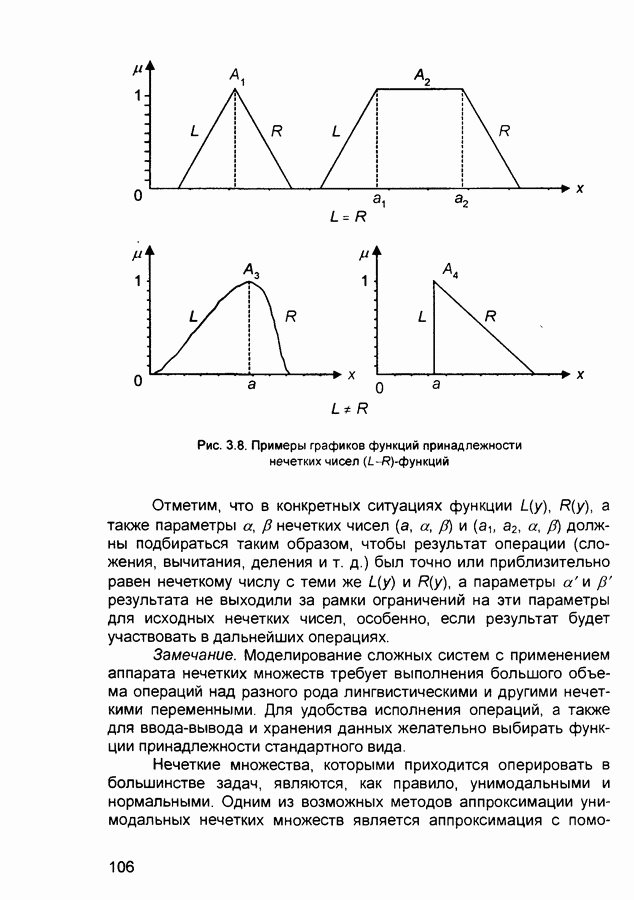
Конечные выражения являются достаточно громоздкими, но могут быть упрощены в случае, если функции принадлежности имеют вид:

Данные функции характеризуются всего двумя параметрами (а и Ь), в определенном смысле являются симметричными (рис. 3.16) и удовлетворяют уравнению:

Заметим, что из последнего и ранее полученных уравнений следует:

Последующие выкладки таковы:

где


и

где

Приведенные выкладки, как представляется, полностью иллюстрируют идеи алгоритмов обучения и использования нечеткой нейронной сети.
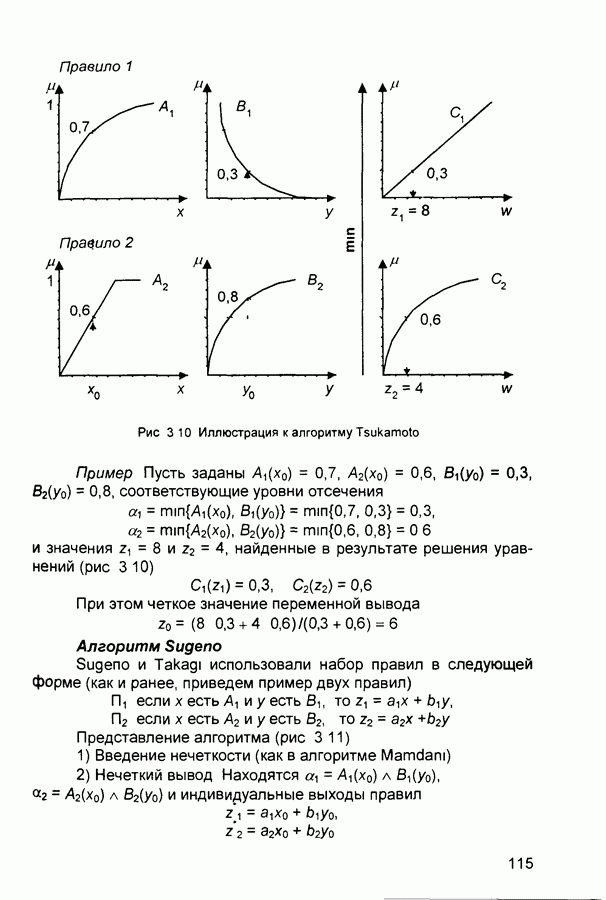
Рассмотрим другой пример нечеткой системы, имеющей следующую базу знаний:

где  - входные переменные, у - выход системы,
- входные переменные, у - выход системы,  - некоторые нечеткие множества с функциями принадлежности сигмоидного типа:
- некоторые нечеткие множества с функциями принадлежности сигмоидного типа:

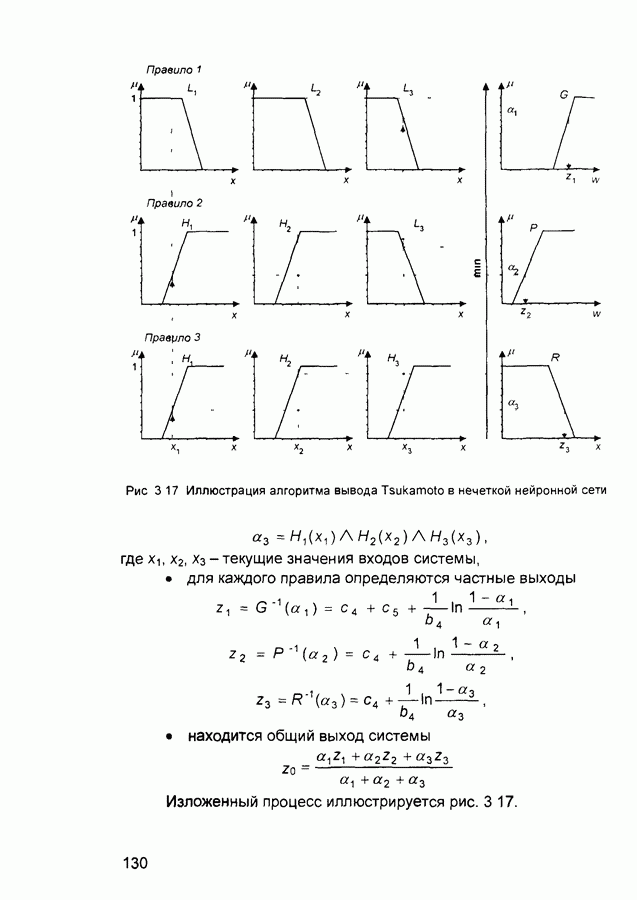
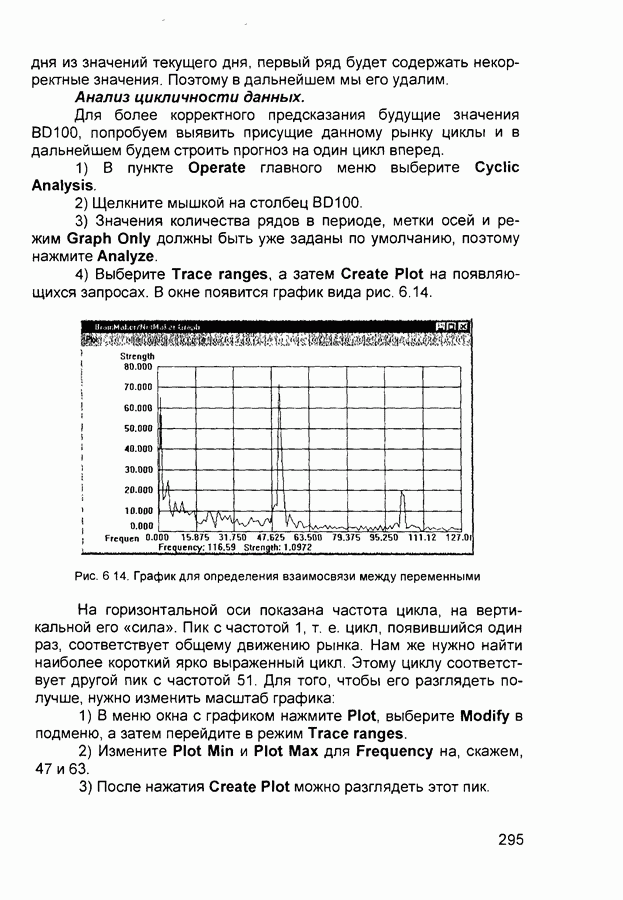
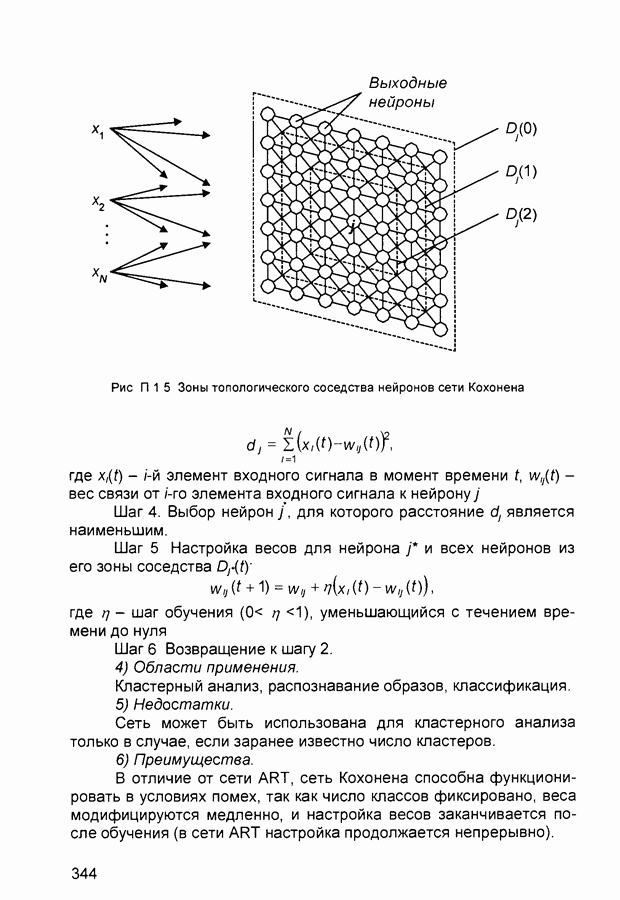
Для определения выходной переменной используется алгоритм вывода Tsukamoto (см. разд. 3.2), в соответствии с которым:
• подсчитываются значения истинности предпосылок для каждого правила:


Рис. 3.17 Иллюстрация алгоритма вывода Tsukamoto в нечеткой нейронной сети

где  - текущие значения входов системы,
- текущие значения входов системы,
• для каждого правила определяются частные выходы

• находится общий выход системы

Изложенный процесс иллюстрируется рис. 3 17.

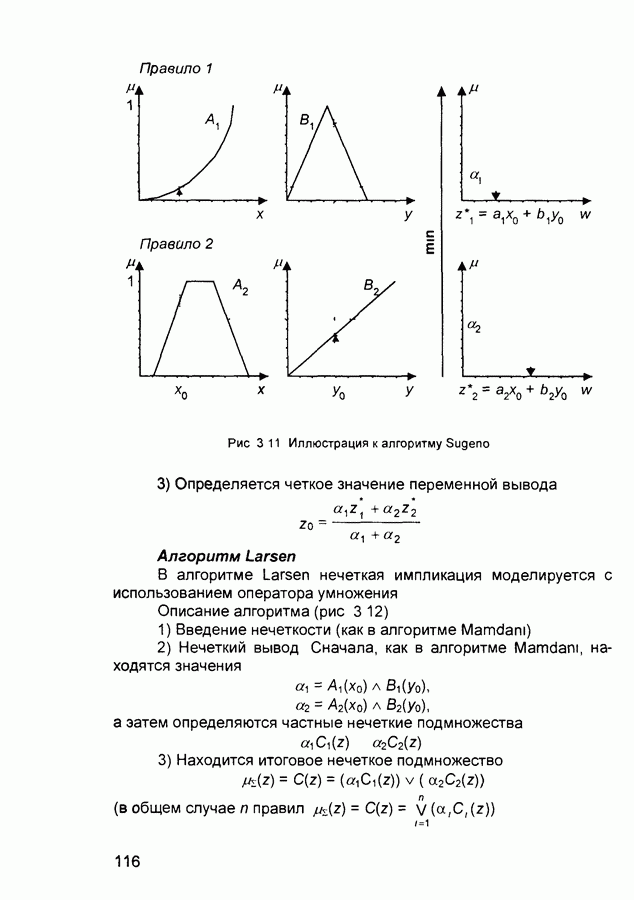
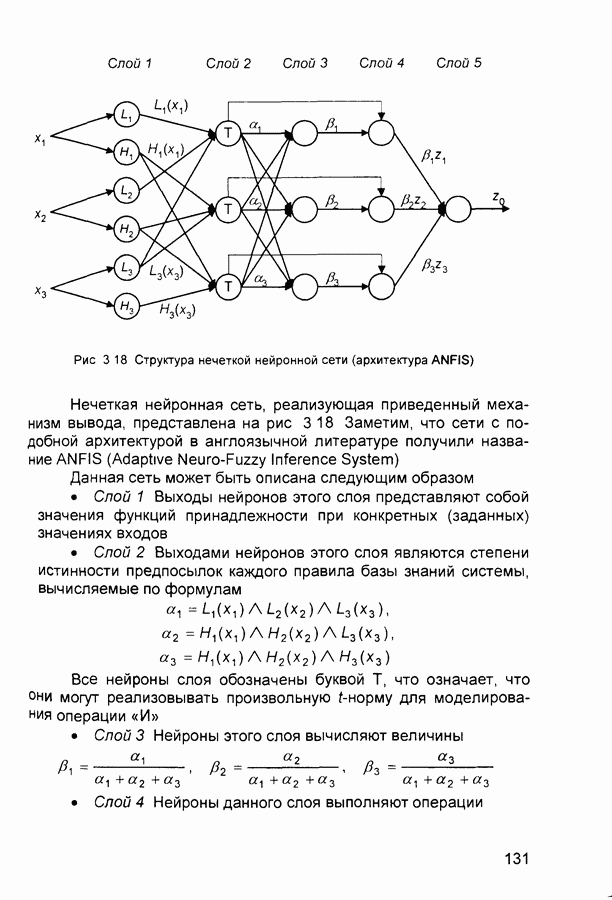
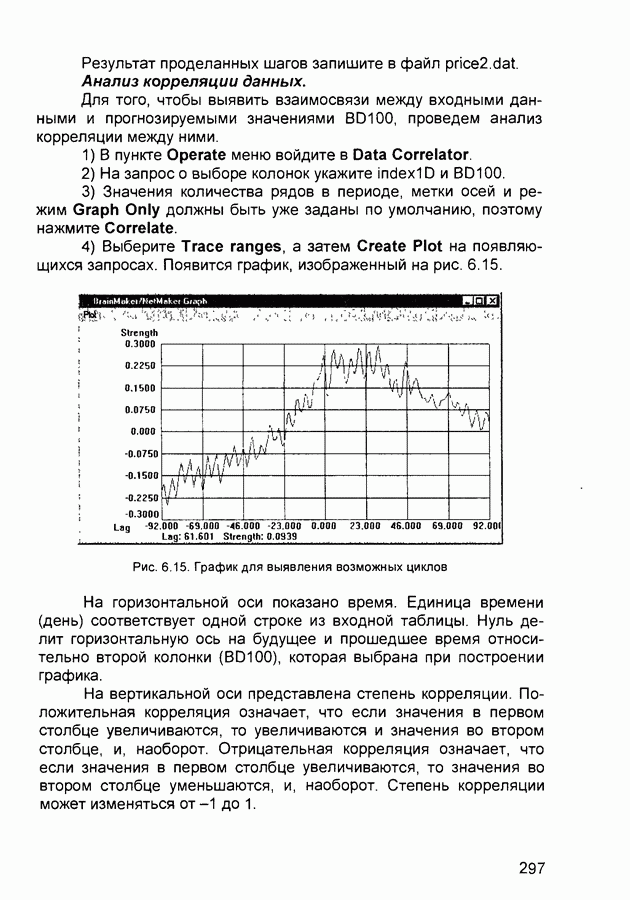
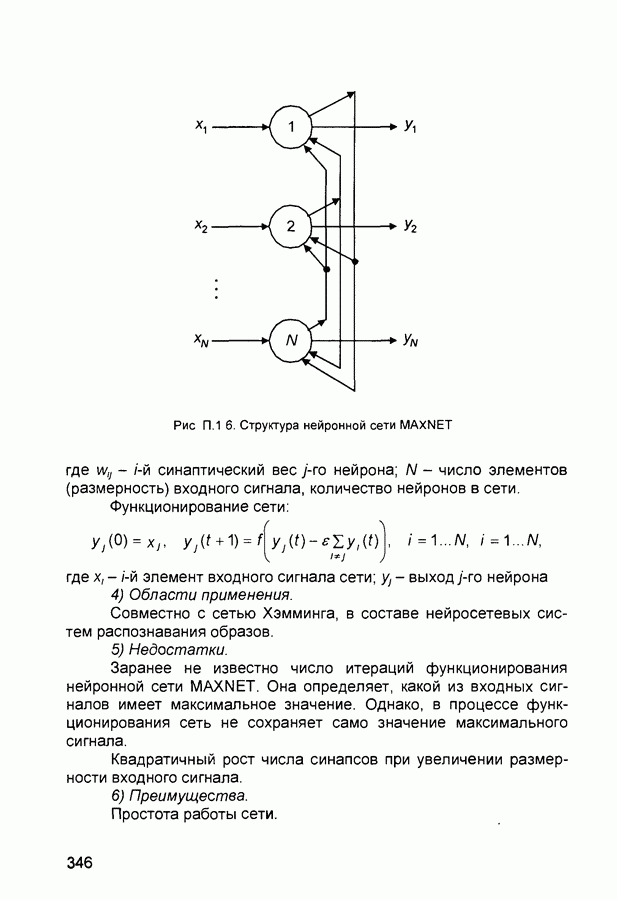
Рис. 3.18 Структура нечеткой нейронной сети (архитектура ANFIS)
Нечеткая нейронная сеть, реализующая приведенный механизм вывода, представлена на рис 3 18 Заметим, что сети с подобной архитектурой в англоязычной литературе получили название ANFIS (Adaptive Neuro-Fuzzy Inference System)
Данная сеть может быть описана следующим образом
• Слой 1 Выходы нейронов этого слоя представляют собой значения функций принадлежности при конкретных (заданных) значениях входов
• Слой 2 Выходами нейронов этого слоя являются степени истинности предпосылок каждого правила базы знаний системы, вычисляемые по формулам

Все нейроны слоя обозначены буквой Т, что означает, что они могут реализовывать произвольную  -норму для моделирования операции «И»
-норму для моделирования операции «И»
• Слой 3 Нейроны этого слоя вычисляют величины

• Слой 4 Нейроны данного слоя выполняют операции

• Слой 5. Единственный нейрон этого слоя вычисляет выход сети:

Корректировка параметров системы для функций принадлежности  и
и  производится в соответствии с ранее рассмотренным подходом Так, например, настройка коэффициентов для функций принадлежности
производится в соответствии с ранее рассмотренным подходом Так, например, настройка коэффициентов для функций принадлежности  осуществляется по формулам.
осуществляется по формулам.

где 
Соответствующие выражения могут быть получены и для остальных коэффициентов:  и
и  .
.
Генерация нечетких правил
Можно выделить два подхода к модификации топологии нечеткой нейронной сети на этапах обучения и использования. Первый, традиционный подход основан на введении дополнительных продукционных правил в базу знаний системы. При этом следует учитывать непротиворечивость ее пополнения.
Другой подход предполагает генерацию новых продукционных правил, не противоречащих правилам из базы знаний системы, исходя из анализа экспериментальных данных об объекте на основе предложенной одним из авторов книги процедуры, которая рассмотрена ниже.
Предположим, что исследуемый объект имеет  входов (иначе, векторный вход
входов (иначе, векторный вход  и один выход у и имеет «истинное» (неизвестное) описание:
и один выход у и имеет «истинное» (неизвестное) описание:

где  - функция неизвестного вида,
- функция неизвестного вида,  - случайная аддитивная помеха (отражающая действие не учитываемых факторов) с нулевым средним значением и произвольным (неизвестным) распределением на
- случайная аддитивная помеха (отражающая действие не учитываемых факторов) с нулевым средним значением и произвольным (неизвестным) распределением на 
Предположим далее, что на объекте может быть реализован эксперимент, заключающийся в регистрации  пар значений
пар значений
 при этом величины (векторы) х, измеряются без ошибок, значение
при этом величины (векторы) х, измеряются без ошибок, значение  при необходимости допускает модификацию.
при необходимости допускает модификацию.
Алгоритм построения системы может быть теперь описан следующим образом.
ШАГ 1. Из  произвольных значений
произвольных значений  составляется начальная база знаний модели, отображаемая матрицей
составляется начальная база знаний модели, отображаемая матрицей  со строками вида
со строками вида 
Такое представление, очевидно, эквивалентно набору продукционных правил вида:

ШАГ 2. Для каждой новой экспериментальной точки  рассчитывается прогнозируемое значение по формуле, соответствующей рассмотренному центроидному методу:
рассчитывается прогнозируемое значение по формуле, соответствующей рассмотренному центроидному методу:

где  - функция колоколообразной или экспоненциальной формы.
- функция колоколообразной или экспоненциальной формы.

Л - параметр функций.
ШАГ 3. Проверяется неравенство:

где  - заданная константа, определяющая погрешность аппроксимации.
- заданная константа, определяющая погрешность аппроксимации.
При выполнении неравенства база знаний системы пополняется путем расширения матрицы  (добавлением строки
(добавлением строки  В противном случае матрица
В противном случае матрица  остается без изменений.
остается без изменений.
ШАГ 4. Проверяется правило останова. В данном варианте алгоритма построение модели считается законченным, если в соответствии с шагами 2 и 3 перебраны все  экспериментальных точек (без учета значений начальной базы знаний).
экспериментальных точек (без учета значений начальной базы знаний).
Если не все экспериментальные точки использованы, то осуществляется переход к шагу 2, в противном случае - останов.
В процессе реализации алгоритма параметры  считаются априори заданными.
считаются априори заданными.

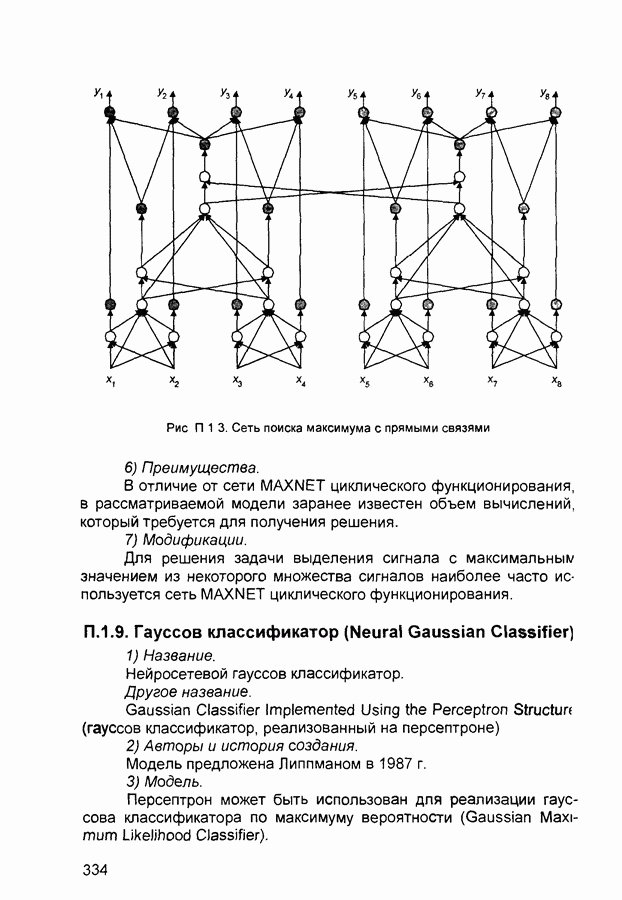
Рис. 3.19 Нечеткая нейронная сеть для решения задач классификации
При использовании системы заданными считаются матрица  (на этапе использования модели она не изменяется), отмеченные параметры
(на этапе использования модели она не изменяется), отмеченные параметры  и расчет у производится в соответствии с шагом 2 приведенного алгоритма.
и расчет у производится в соответствии с шагом 2 приведенного алгоритма.
Нетрудно видеть, что описанный алгоритм, в сущности, соответствует упрощенному алгоритму нечеткого логического вывода (см. разд. 3.2), но отличается от последнего тем, что база знаний не остается фиксированной, а модернизируется по мере поступления экспериментальных данных Причем непротиворечивость нового продукционного правила относительно набора правил из базы знаний гарантируется предложенной процедурой ее пополнения.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
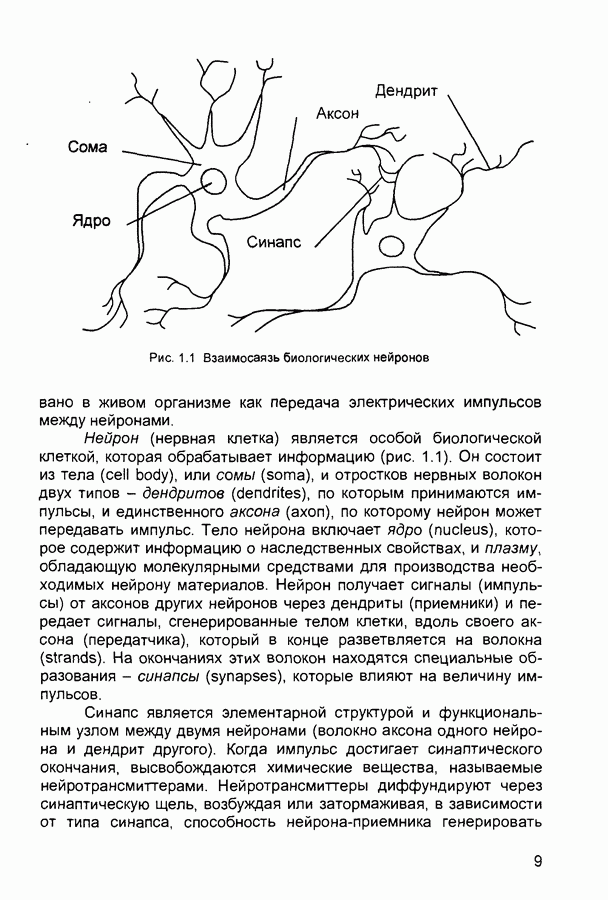
- 1.1. Биологический нейрон
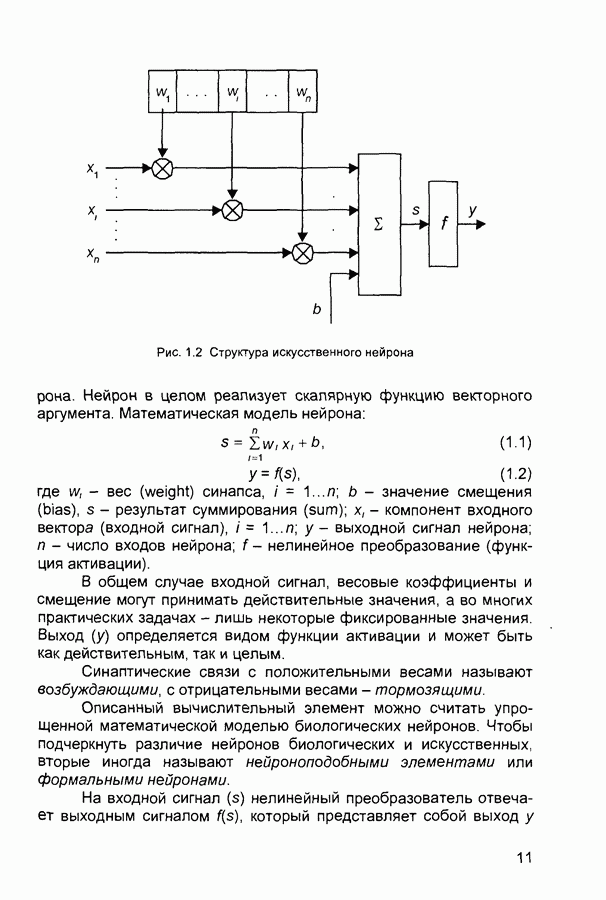
- 1.2. Структура и свойства искусственного нейрона
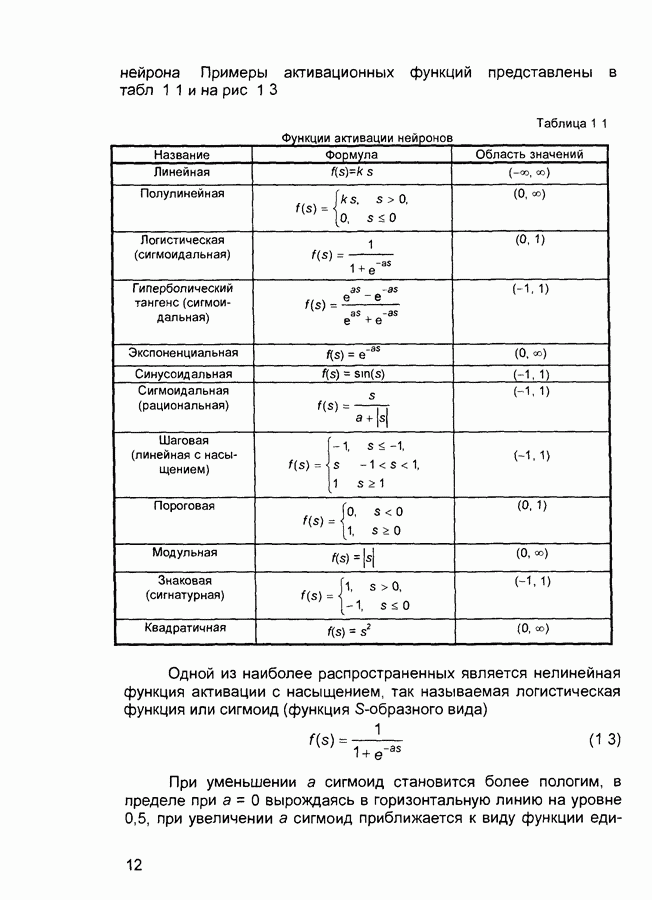
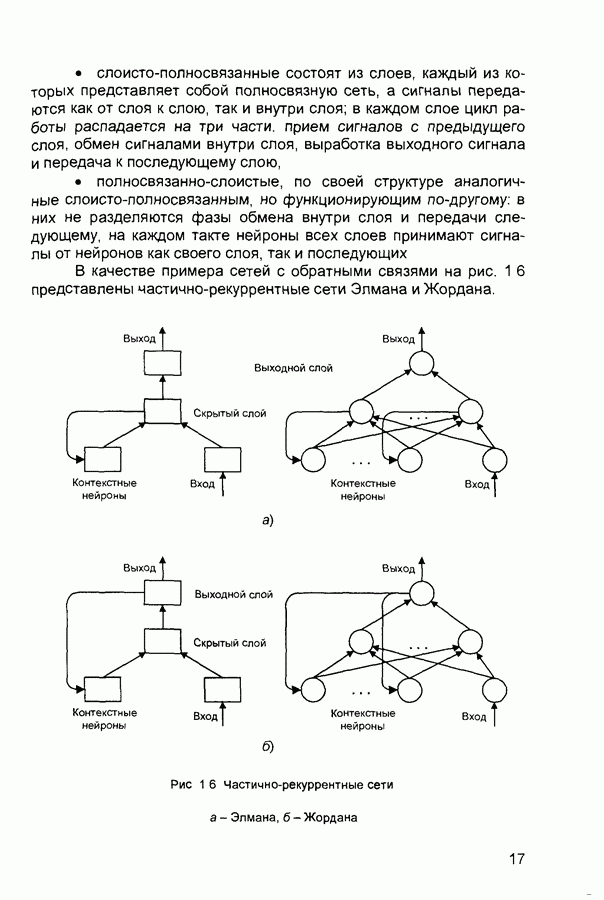
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
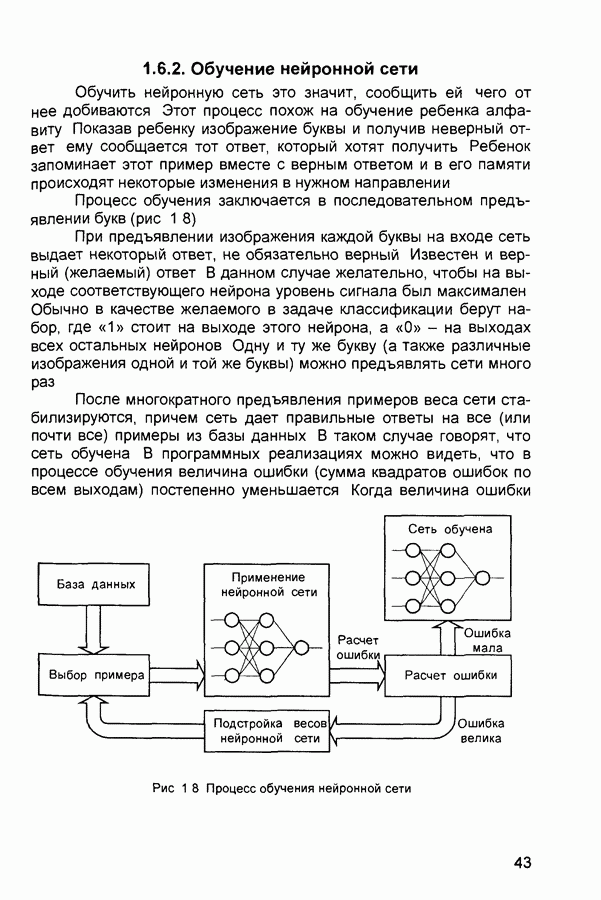
- 1.6.2. Обучение нейронной сети
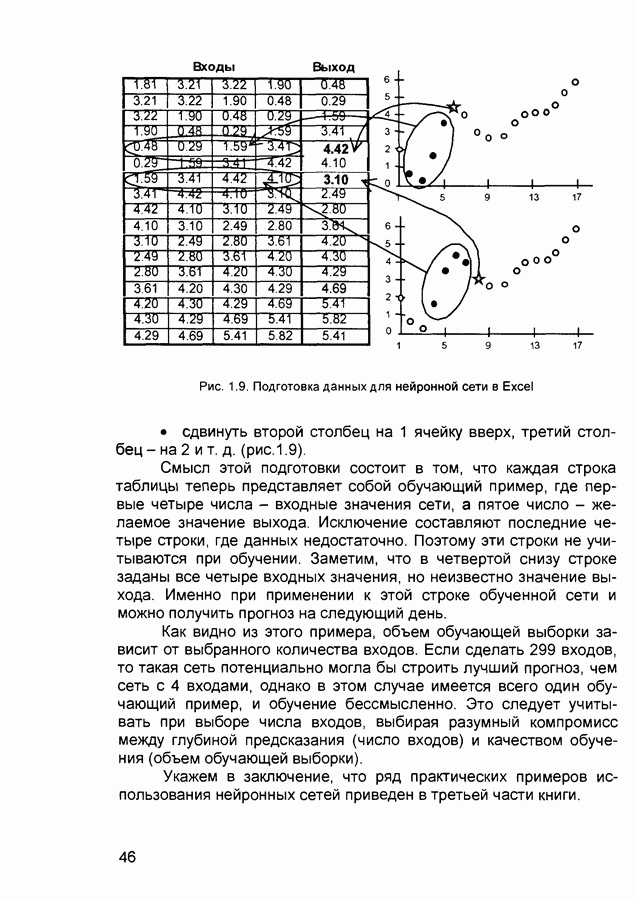
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
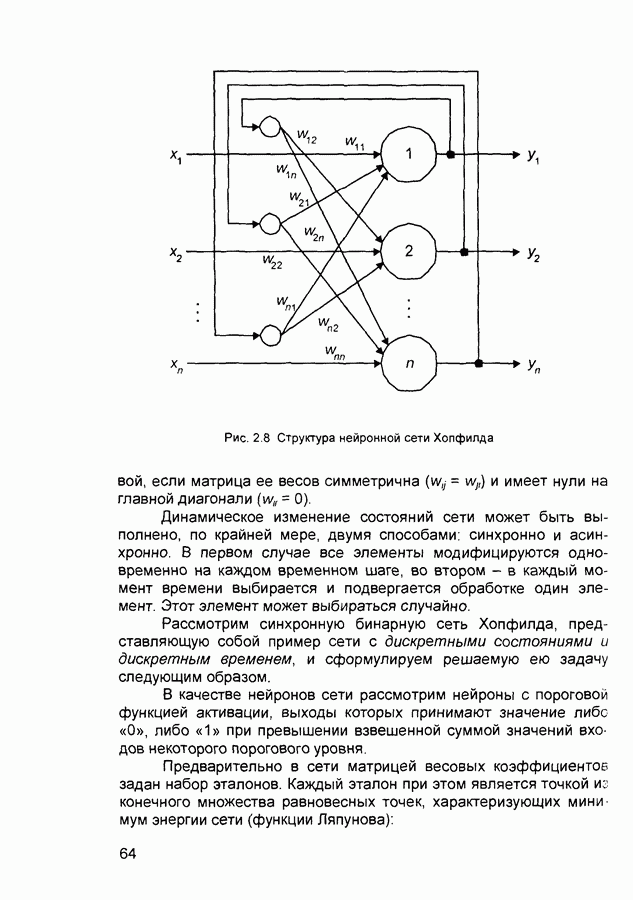
- 2.1. Ассоциативная память нейронных сетей
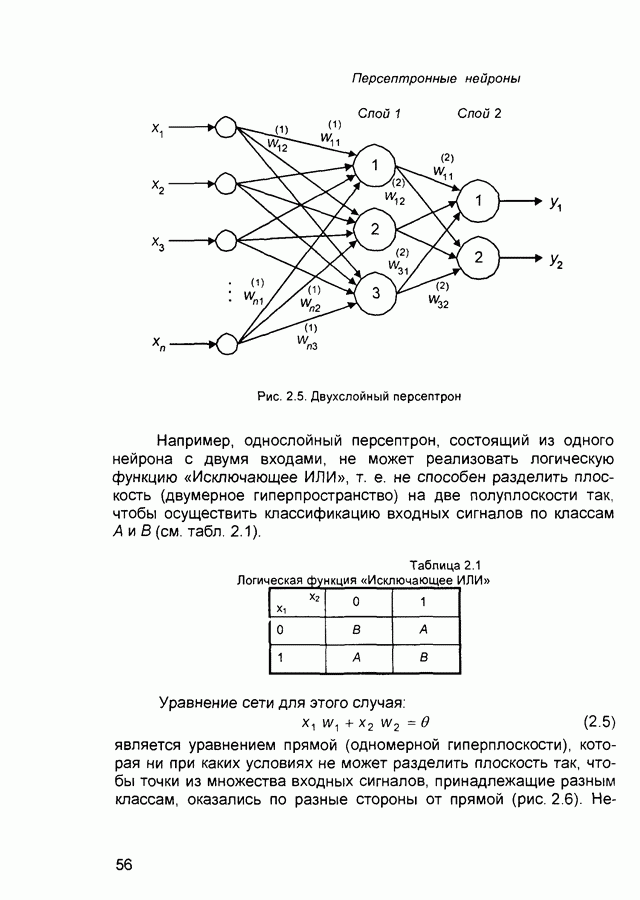
- 2.2. Персептроны
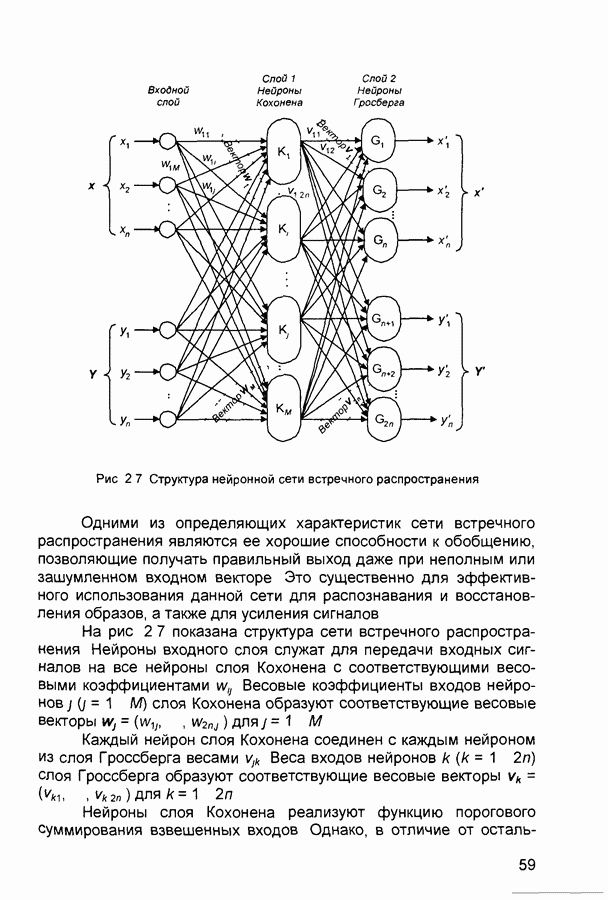
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
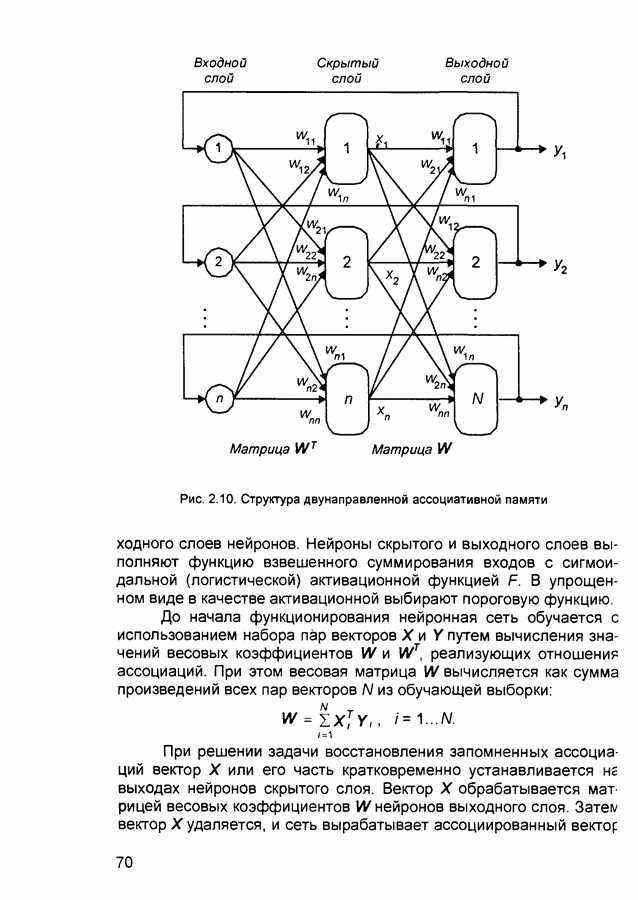
- 2.5. Двунаправленная ассоциативная память
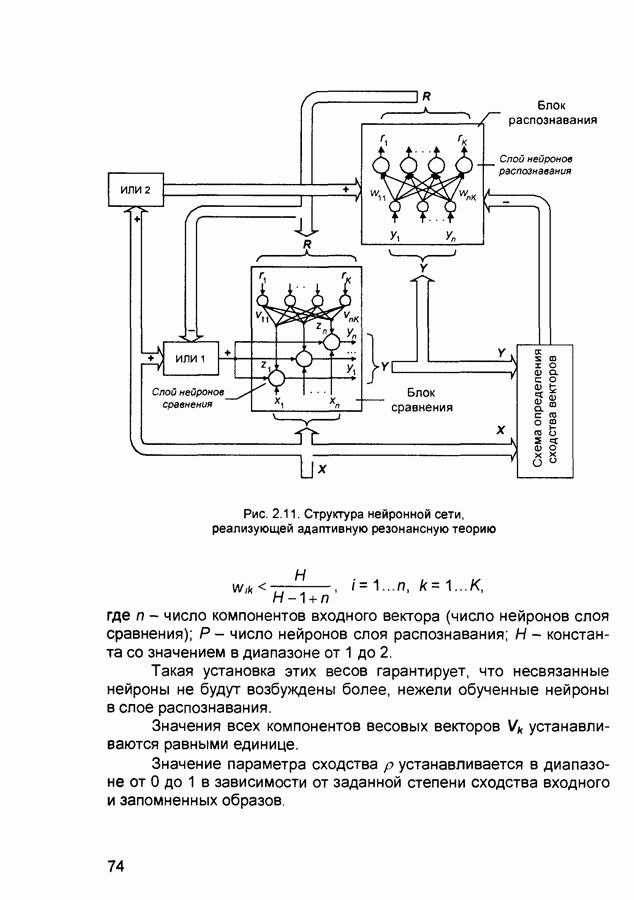
- 2.6. Сети адаптивной резонансной теории
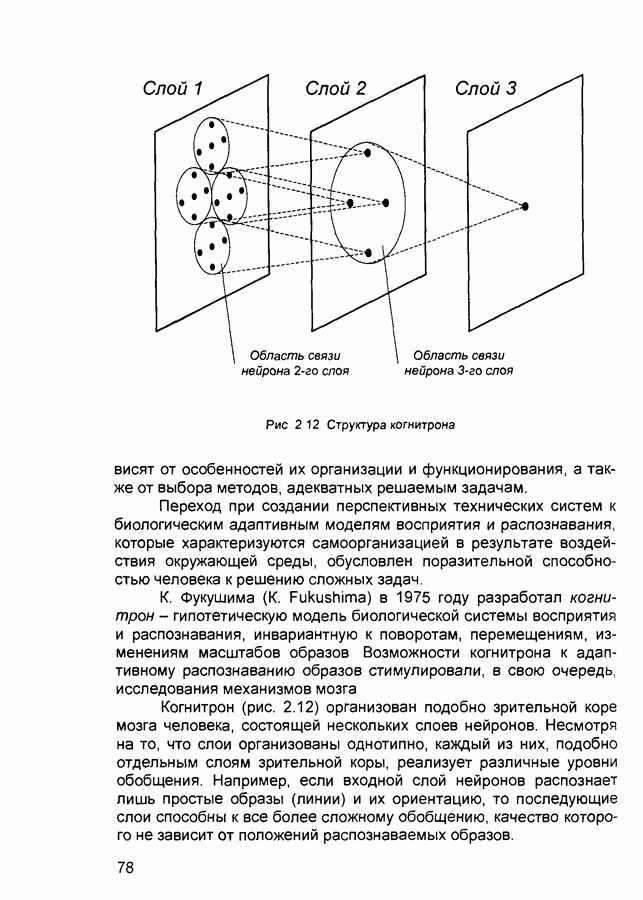
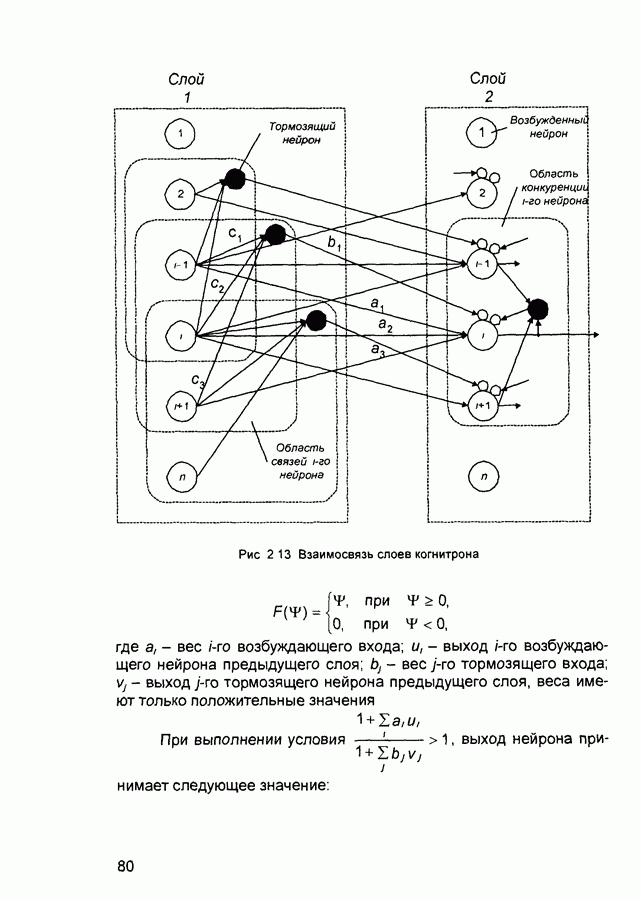
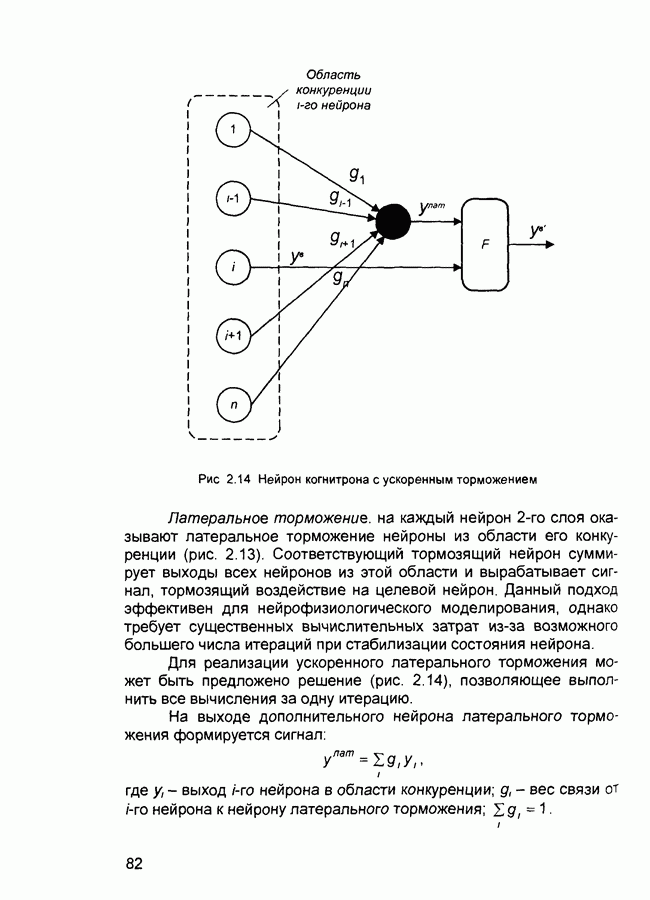
- 2.7. Когнитрон
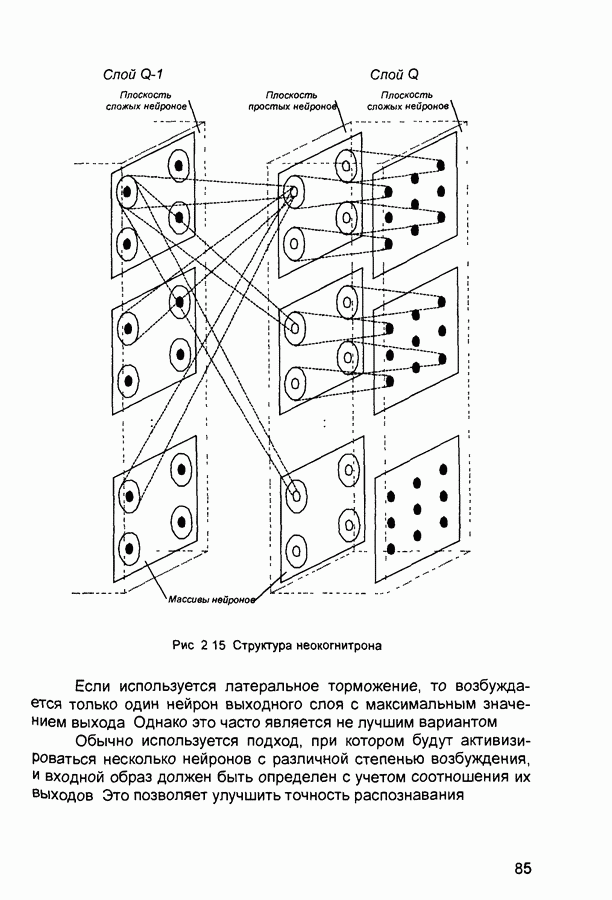
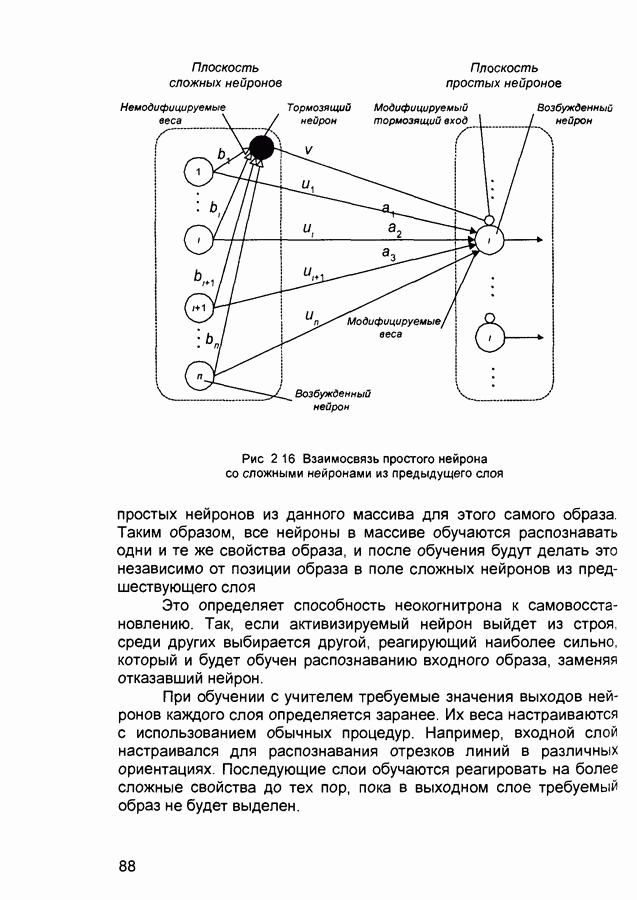
- 2.8. Неокогнитрон
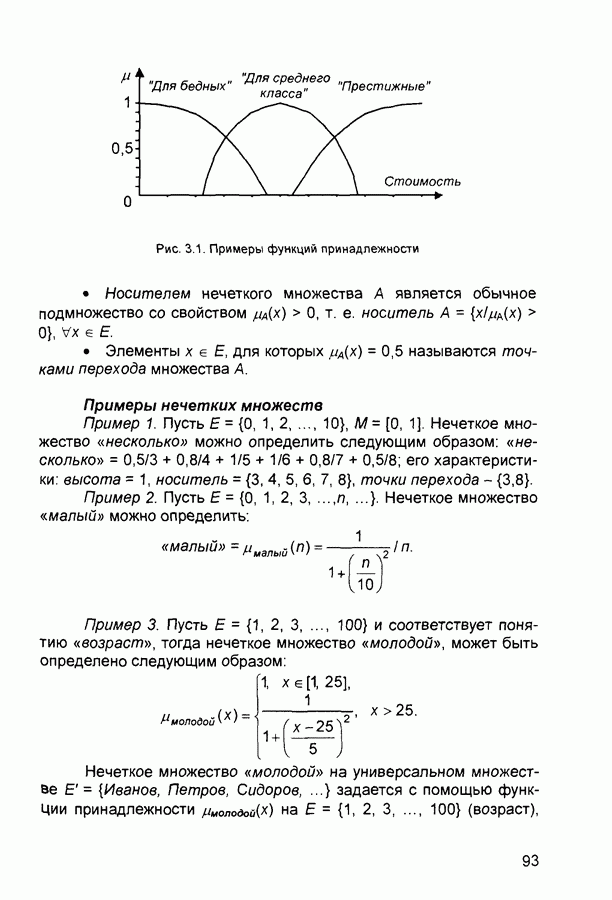
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
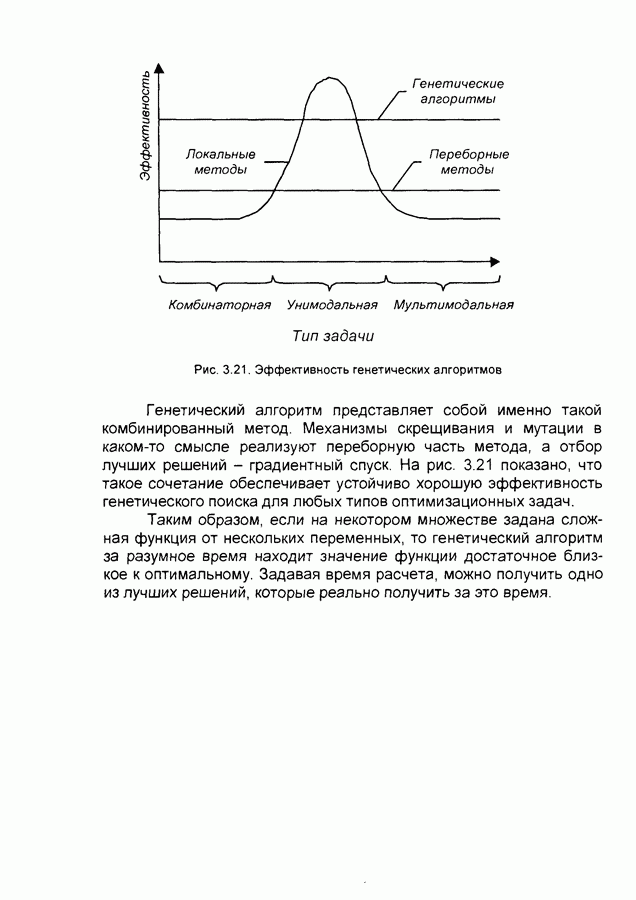
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
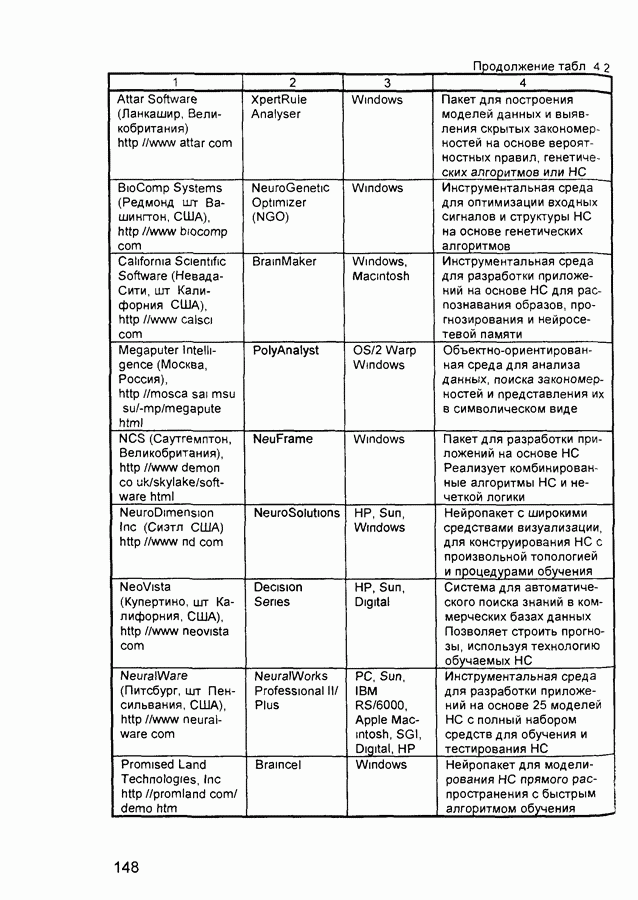
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
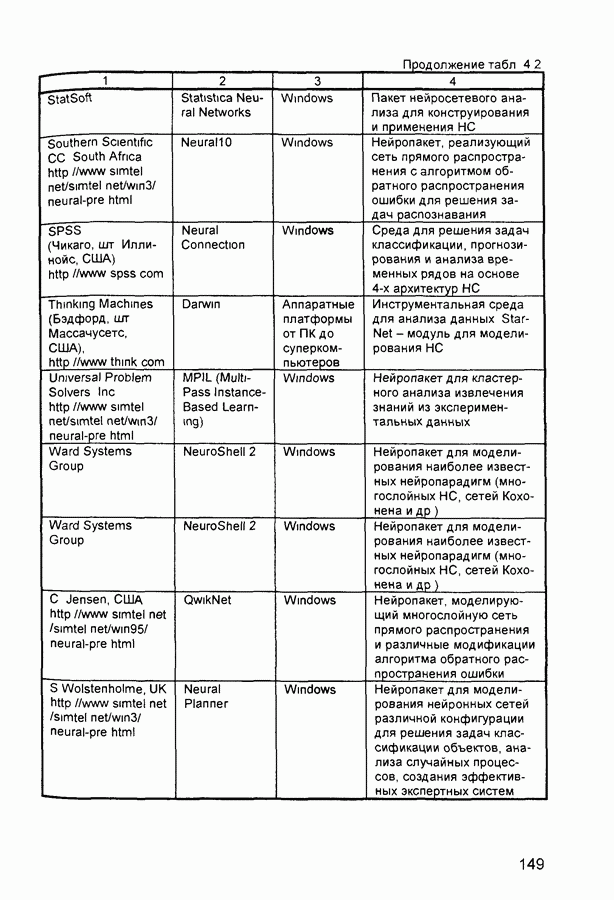
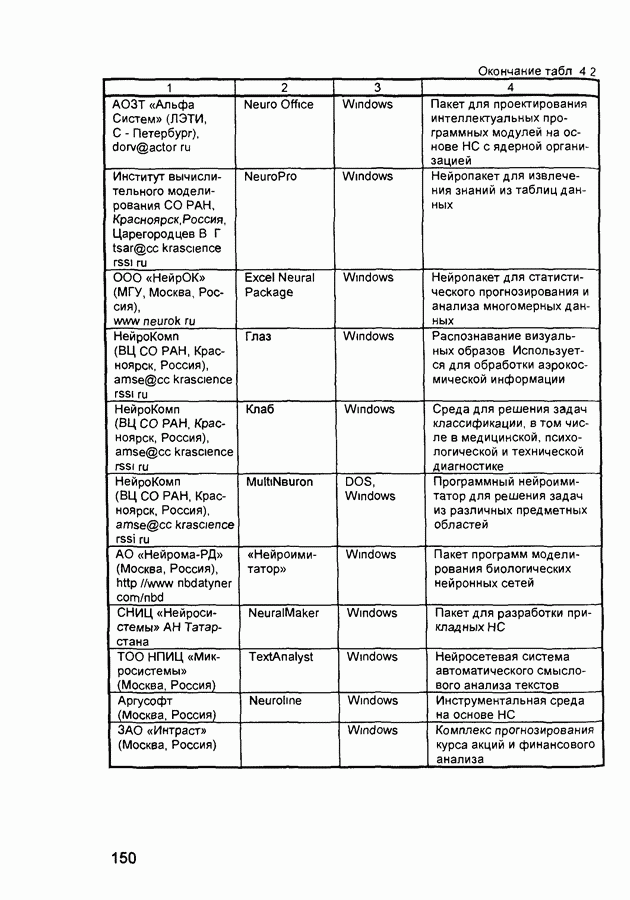
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
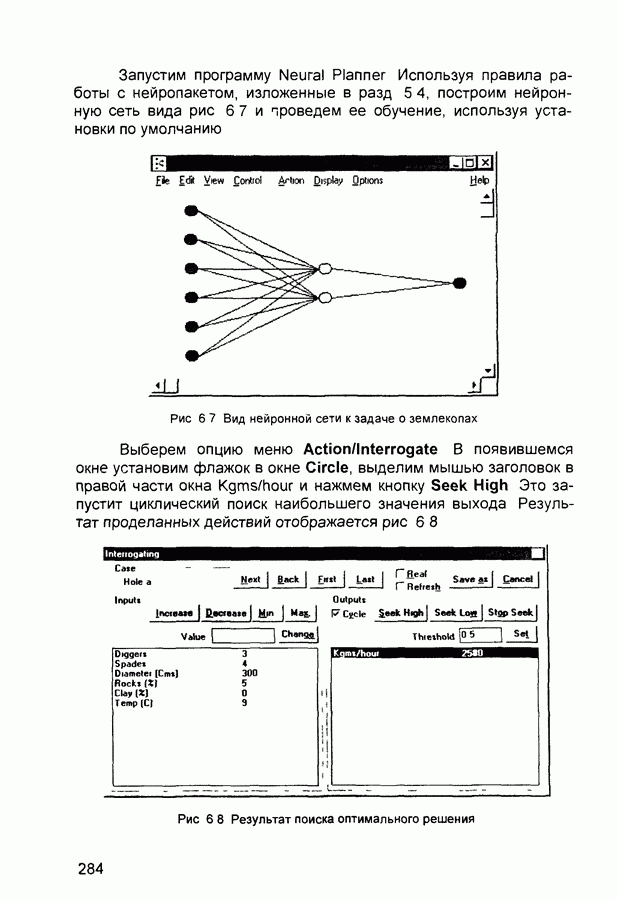
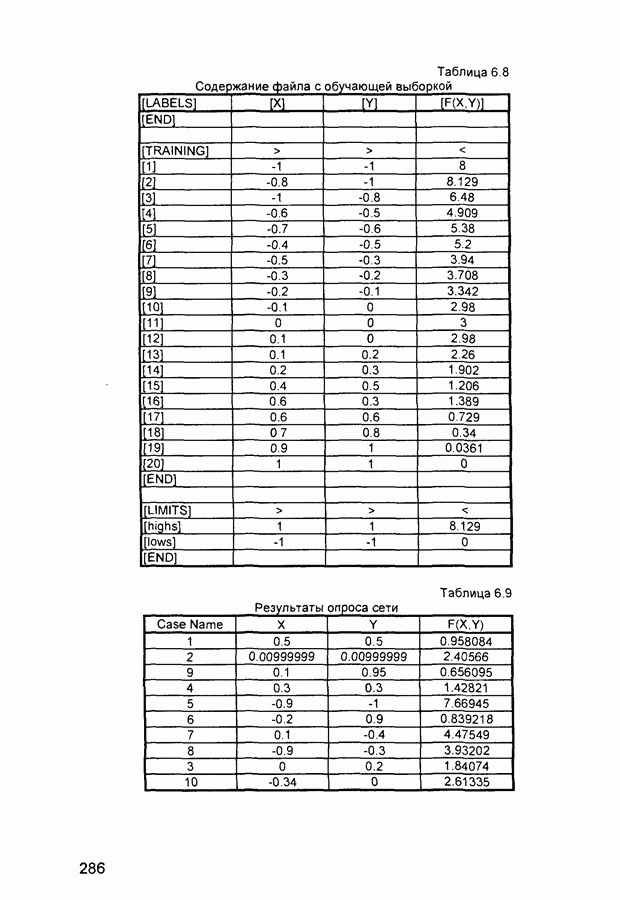
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
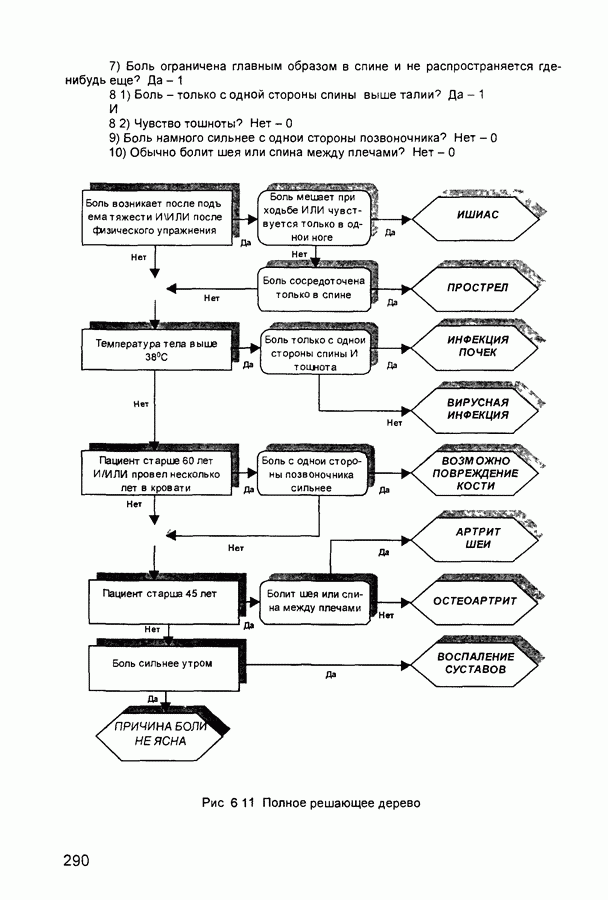
- 6.7. Нейросетевая экспертная система
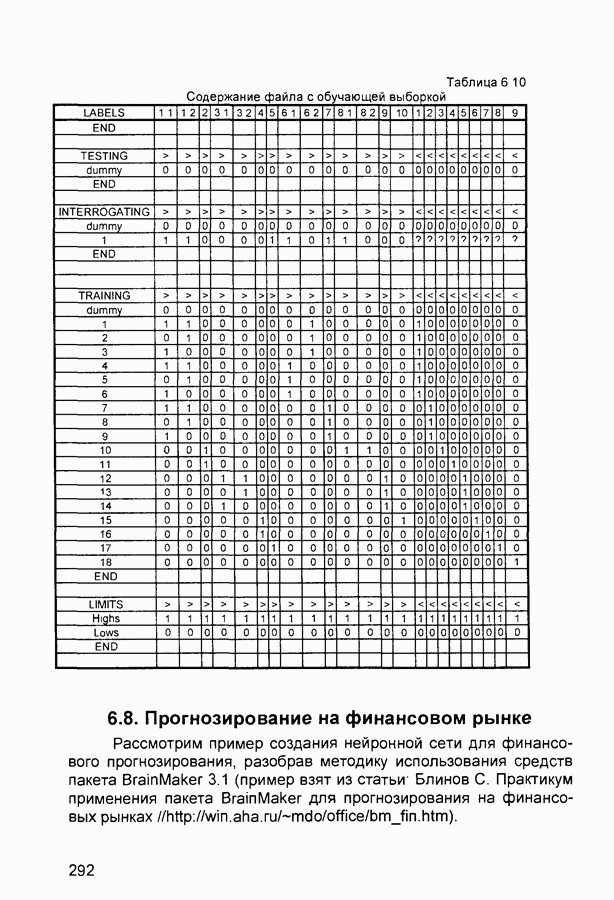
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы