| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.1.3. Нечеткие и лингвистические переменные
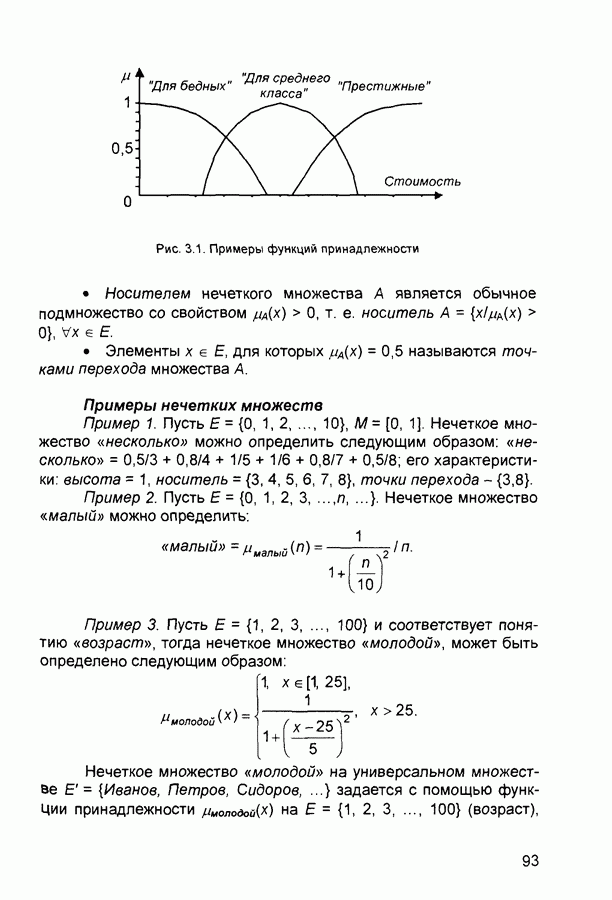
Понятия нечеткой и лингвистической переменных используются при описании объектов и явлений с помощью нечетких множеств.
Нечеткая переменная характеризуется тройкой параметров  где
где
а - наименование переменной,
X - универсальное множество (область определения а),
А - нечеткое множество на X, описывающее ограничения (т. е.  на значения нечеткой переменной а.
на значения нечеткой переменной а.
Лингвистическая переменная  характеризуется набором параметров
характеризуется набором параметров  где
где
 - наименование лингвистической переменной;
- наименование лингвистической переменной;
Т - множество ее значений (терм-множество), представляющих наименования нечетких переменных, областью определения каждой из которых является множество X. Множество Т называется базовым терм-множеством лингвистической переменной;
 - синтаксическая процедура, позволяющая оперировать элементами терм-множества Г, в частности, генерировать новые термы (значения). Множество
- синтаксическая процедура, позволяющая оперировать элементами терм-множества Г, в частности, генерировать новые термы (значения). Множество  где
где  - множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной;
- множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной;
М - семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой  в нечеткую переменную, т. е. сформировать соответствующее нечеткое множество.
в нечеткую переменную, т. е. сформировать соответствующее нечеткое множество.
Замечание. Для избежания большого количества символов:
• символ  используют как для названия самой переменной, так и для обозначения всех ее значений;
используют как для названия самой переменной, так и для обозначения всех ее значений;
• один и тот же символ используется для обозначения нечеткого множества и его названия, например, терм «молодой», являющийся значением лингвистической переменной  одновременно есть и нечеткое множество М («молодой»).
одновременно есть и нечеткое множество М («молодой»).
Присвоение нескольких значений символам предполагает возможность решения неопределенностей с помощью контекста
Пример. Пусть эксперт определяет толщину выпускаемого изделия с помощью понятий «малая толщина», «средняя толщина» и «большая толщина», при зтом минимальная толщина равна 10 мм, а максимальная - 80 мм.
Формализация такого описания может быть проведена с помощью следующей лингвистической переменной  где
где
 толщина изделия;
толщина изделия;
 толщина», «средняя толщина», «большая
толщина», «средняя толщина», «большая 

 - процедура образования новых термов с помощью связок
- процедура образования новых термов с помощью связок  «или» и модификаторов типа «очень», «не», «слегка». Например - «малая или средняя толщина», «очень малая
«или» и модификаторов типа «очень», «не», «слегка». Например - «малая или средняя толщина», «очень малая  - процедура задания на
- процедура задания на  нечетких подмножеств
нечетких подмножеств  «малая толщина»,
«малая толщина»,  «средняя толщина»,
«средняя толщина»,  «большая толщина», а также нечетких множеств для термов из
«большая толщина», а также нечетких множеств для термов из  в соответствии с правилами трансляции нечетких связок и модификаторов
в соответствии с правилами трансляции нечетких связок и модификаторов  «или», «не», «очень», «слегка» и др. над нечеткими множествами вида:
«или», «не», «очень», «слегка» и др. над нечеткими множествами вида: 
Замечание. Наряду с рассмотренными выше базовыми значениями лингвистической переменной «толщина»  толщина», «средняя толщина», «большая
толщина», «средняя толщина», «большая  возможны значения, зависящие от области определения X. В данном случае значения лингвистической переменной «толщина изделия» могут быть определены как «около 20 мм», «около 50 мм», «около 70 мм», т. е. в виде нечетких чисел.
возможны значения, зависящие от области определения X. В данном случае значения лингвистической переменной «толщина изделия» могут быть определены как «около 20 мм», «около 50 мм», «около 70 мм», т. е. в виде нечетких чисел.
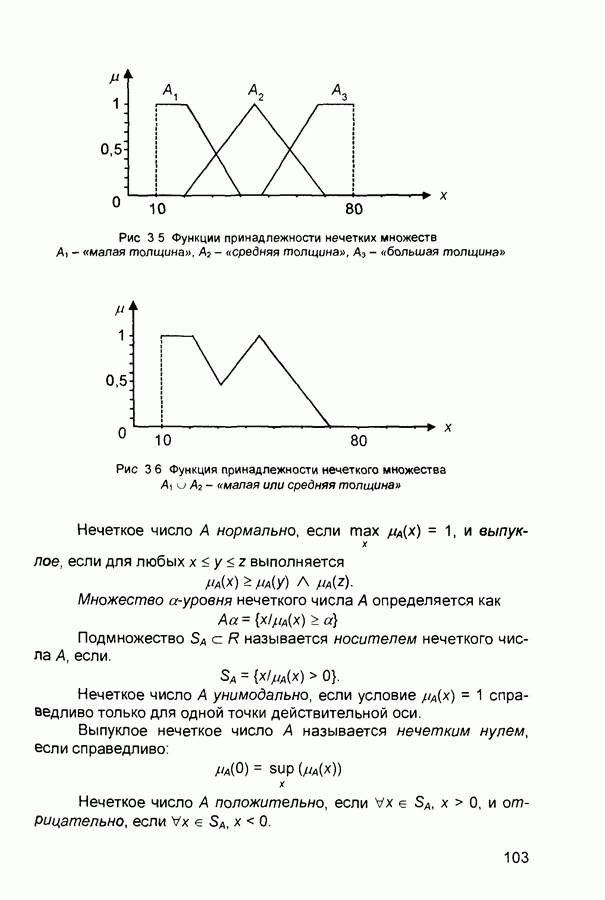
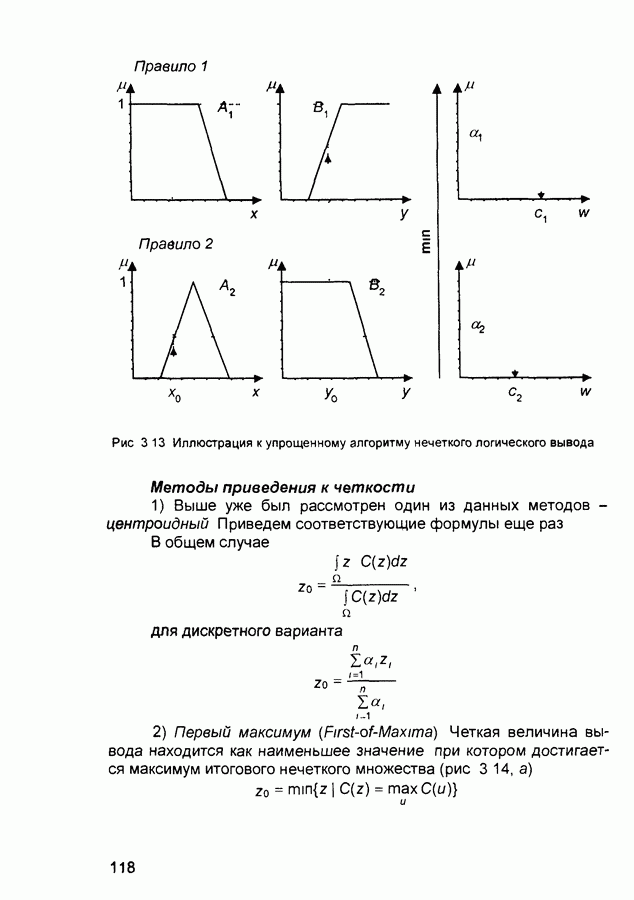
Терм-множество и расширенное терм-множество в условиях примера можно характеризовать функциями принадлежности, приведенными на рис. 3 5 и рис. 3 6.
Нечеткие числа
Нечеткие числа - нечеткие переменные, определенные на числовой оси, т. е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел  с функцией принадлежности
с функцией принадлежности  , где
, где 

Рис. 3.5 Функции принадлежности нечетких множеств  - «малая толщина»,
- «малая толщина»,  - «средняя толщина»,
- «средняя толщина»,  - «большая толщина»
- «большая толщина»

Рис. 3.6 Функция принадлежности нечеткого множества  - «малая или средняя толщина»
- «малая или средняя толщина»
Нечеткое число А нормально, если  и выпуклое, если для любых
и выпуклое, если для любых  выполняется
выполняется

Множество  -уровня нечеткого числа А определяется как
-уровня нечеткого числа А определяется как

Подмножество  с
с  называется носителем нечеткого числа А, если.
называется носителем нечеткого числа А, если.

Нечеткое число А унимодально, если условие  справедливо только для одной точки действительной оси.
справедливо только для одной точки действительной оси.
Выпуклое нечеткое число А называется нечетким нулем, если справедливо:

Нечеткое число А положительно, если  и отрицательно, если
и отрицательно, если 
Операции над нечеткими числами
Расширенные бинарные арифметические операции (сложение, умножение и др.) для нечетких чисел определяются через соответствующие операции для четких чисел с использованием принципа обобщения следующим образом.
Пусть А и В - нечеткие числа, и - нечеткая операция, соответствующая операции над обычными числами. Тогда (используя здесь и в дальнейшем обозначения V вместо  вместо
вместо  можно записать:
можно записать:

Отсюда:

Нечеткие числа (L-R)-типа
Нечеткие числа  - это разновидность нечетких чисел специального вида, задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними.
- это разновидность нечетких чисел специального вида, задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними.
Функции принадлежности нечетких чисел  задаются с помощью не возрастающих на множестве неотрицательных действительных чисел функций действительного переменного
задаются с помощью не возрастающих на множестве неотрицательных действительных чисел функций действительного переменного  удовлетворяющих свойствам: а)
удовлетворяющих свойствам: а) 
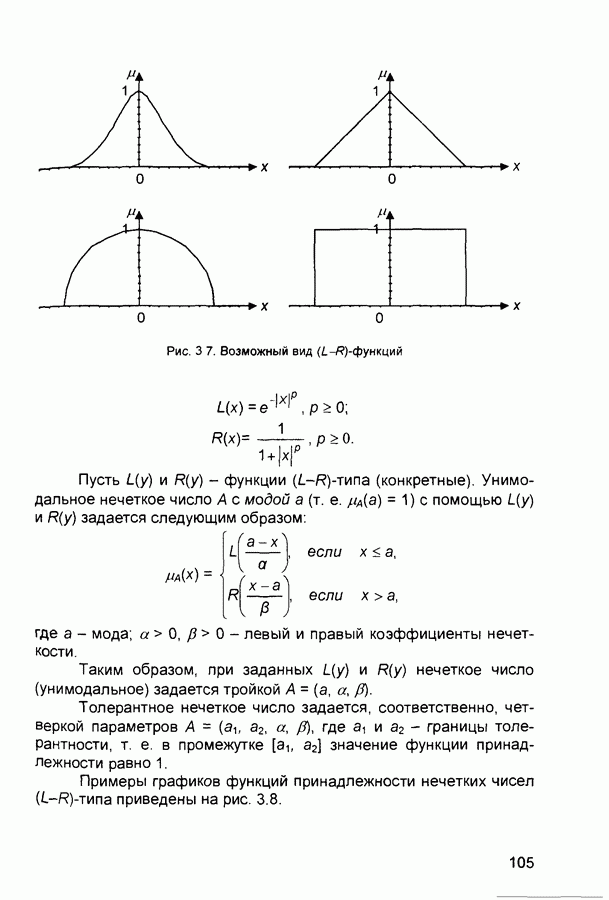
Очевидно, что к классу  относятся функции, графики которых имеют вид, представленный на рис. 3.7.
относятся функции, графики которых имеют вид, представленный на рис. 3.7.
Примерами аналитического задания  могут быть функции:
могут быть функции:

Рис. 3 7. Возможный вид  -функций
-функций

Пусть  - функции
- функции  (конкретные). Унимодальное нечеткое число А с модой а (т. е.
(конкретные). Унимодальное нечеткое число А с модой а (т. е.  ) с помощью
) с помощью  задается следующим образом:
задается следующим образом:

где  - мода;
- мода;  - левый и правый коэффициенты нечеткости.
- левый и правый коэффициенты нечеткости.
Таким образом, при заданных  нечеткое число (унимодальное) задается тройкой
нечеткое число (унимодальное) задается тройкой  .
.
Толерантное нечеткое число задается, соответственно, четверкой параметров  где
где  - границы толерантности, т. е. в промежутке
- границы толерантности, т. е. в промежутке  значение функции принадлежности равно 1.
значение функции принадлежности равно 1.
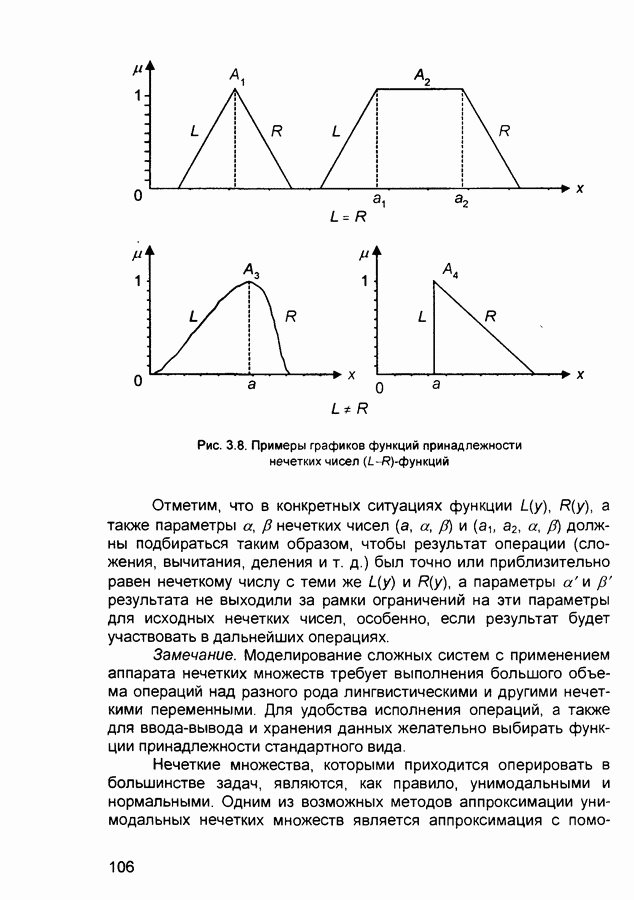
Примеры графиков функций принадлежности нечетких чисел  приведены на рис. 3.8.
приведены на рис. 3.8.

Рис. 3.8. Примеры графиков функций принадлежности нечетких чисел 
Отметим, что в конкретных ситуациях функции  а также параметры
а также параметры  нечетких чисел
нечетких чисел  должны подбираться таким образом, чтобы результат операции (сложения, вычитания, деления и т. д.) был точно или приблизительно равен нечеткому числу с теми же
должны подбираться таким образом, чтобы результат операции (сложения, вычитания, деления и т. д.) был точно или приблизительно равен нечеткому числу с теми же  а параметры
а параметры  результата не выходили за рамки ограничений на эти параметры для исходных нечетких чисел, особенно, если результат будет участвовать в дальнейших операциях.
результата не выходили за рамки ограничений на эти параметры для исходных нечетких чисел, особенно, если результат будет участвовать в дальнейших операциях.
Замечание. Моделирование сложных систем с применением аппарата нечетких множеств требует выполнения большого объема операций над разного рода лингвистическими и другими нечеткими переменными. Для удобства исполнения операций, а также для ввода-вывода и хранения данных желательно выбирать функции принадлежности стандартного вида.
Нечеткие множества, которыми приходится оперировать в большинстве задач, являются, как правило, унимодальными и нормальными. Одним из возможных методов аппроксимации унимодальных нечетких множеств является аппроксимация с
помощью функций  -типа. Примеры
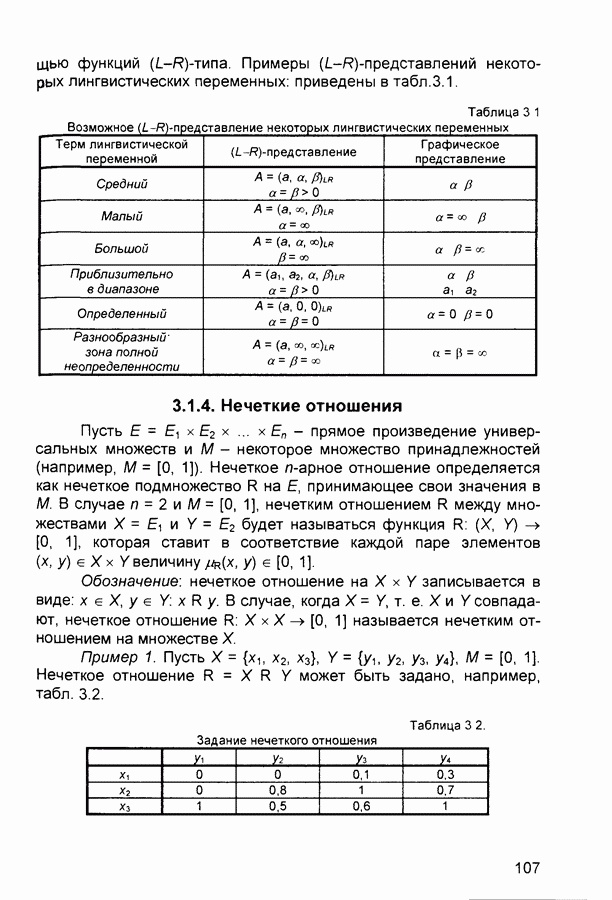
-типа. Примеры  -представлений некоторых лингвистических переменных: приведены в
-представлений некоторых лингвистических переменных: приведены в 
Таблица 3.1 (см. скан) Возможное  -представление некоторых лингвистических переменных
-представление некоторых лингвистических переменных
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
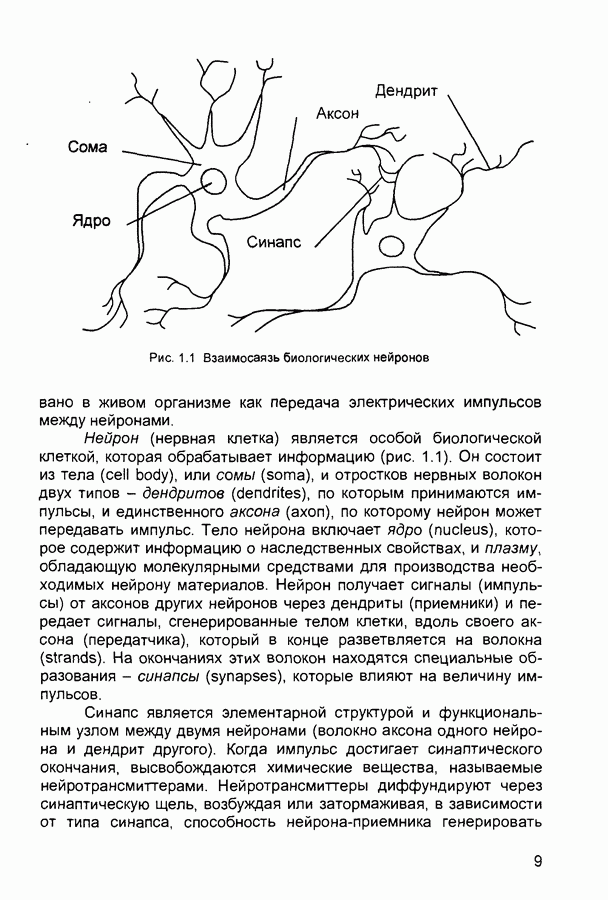
- 1.1. Биологический нейрон
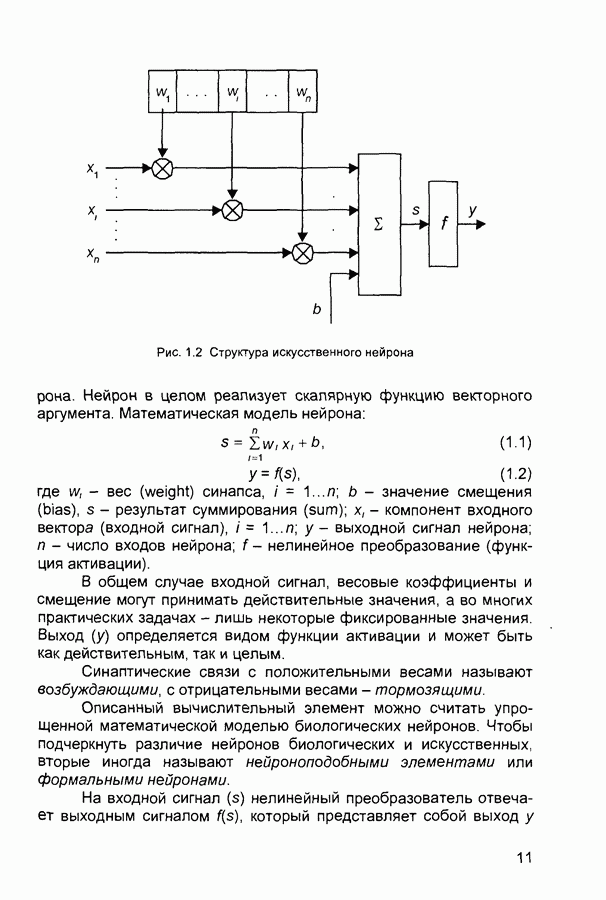
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
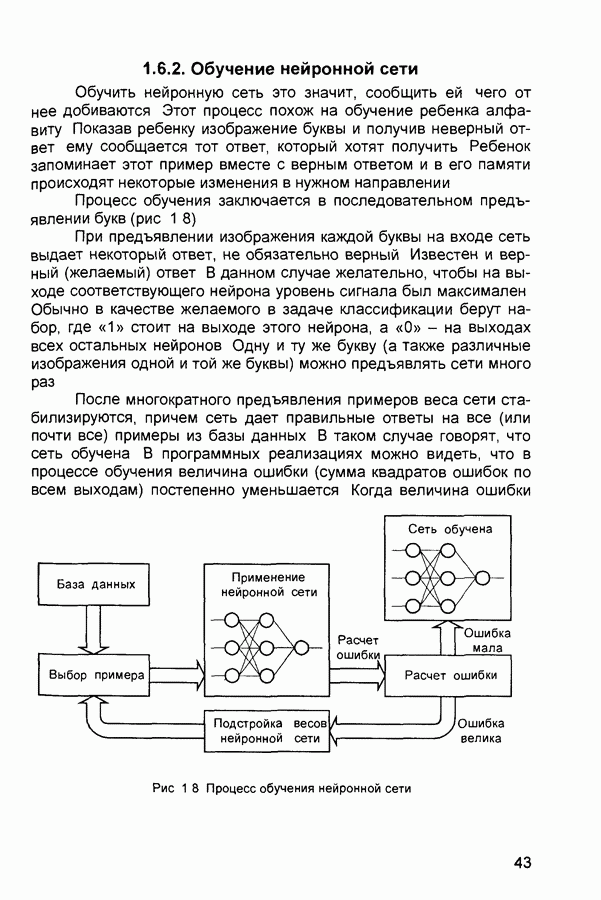
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
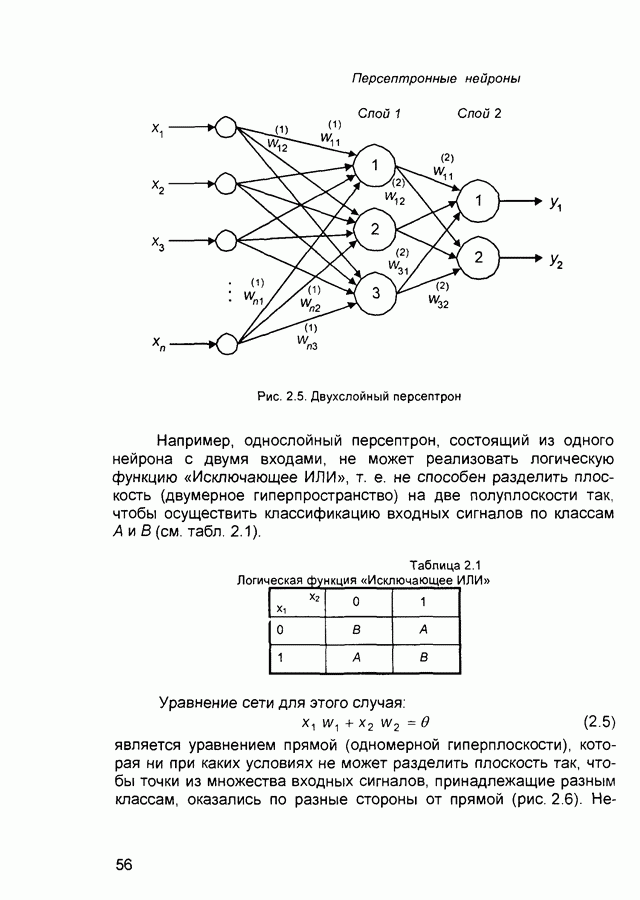
- 2.2. Персептроны
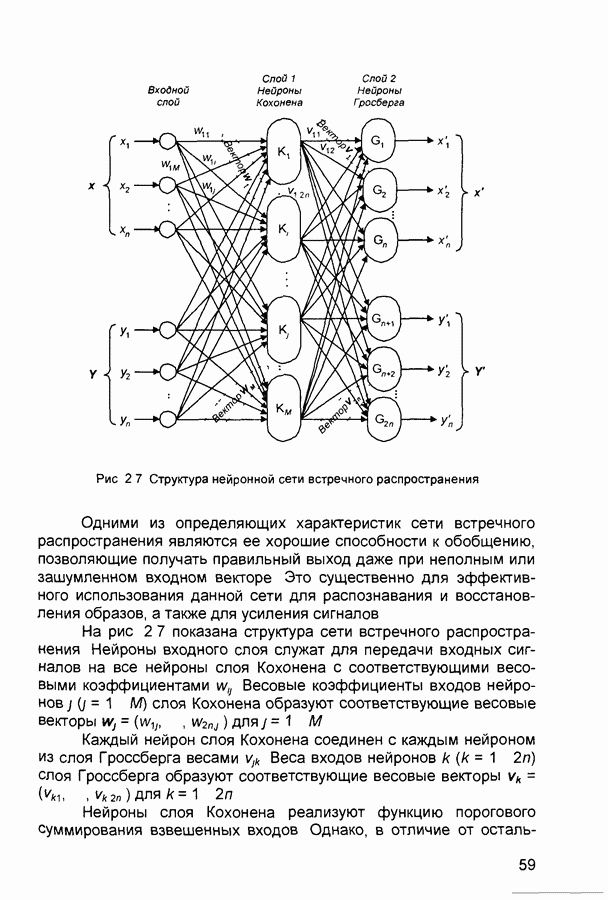
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
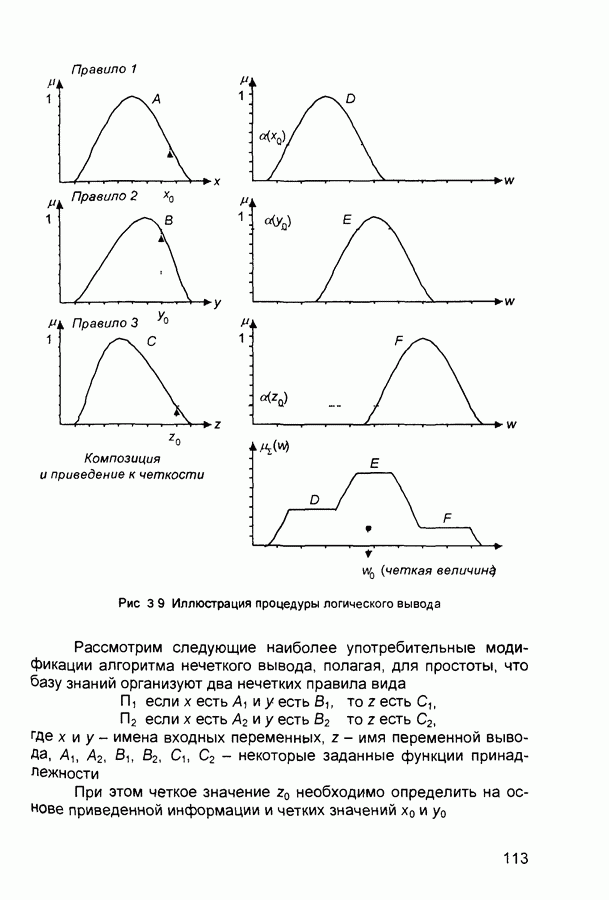
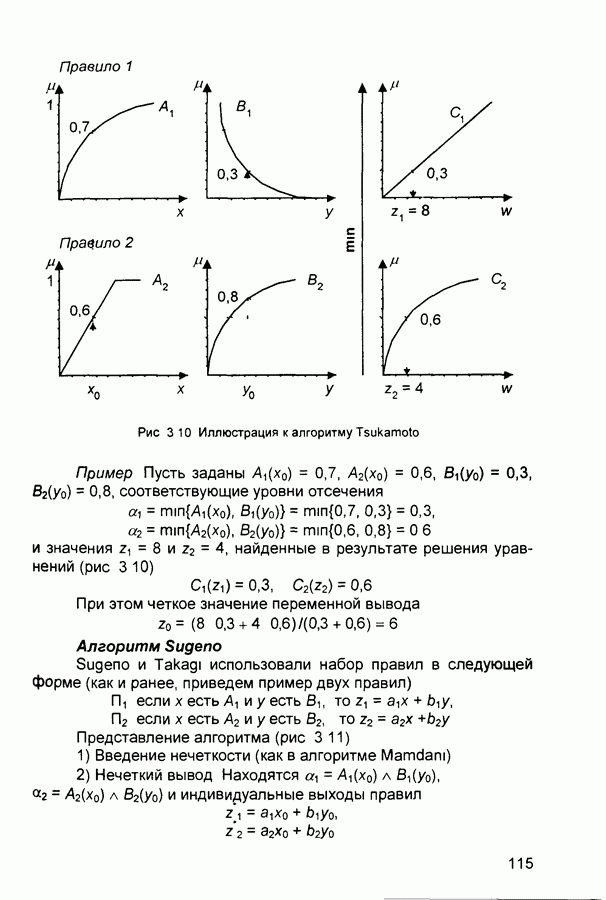
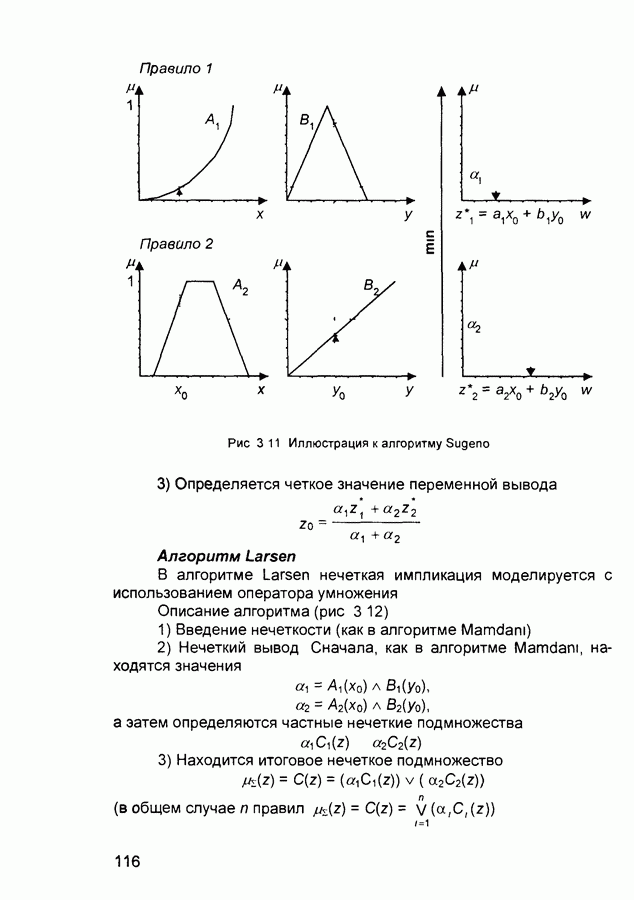
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
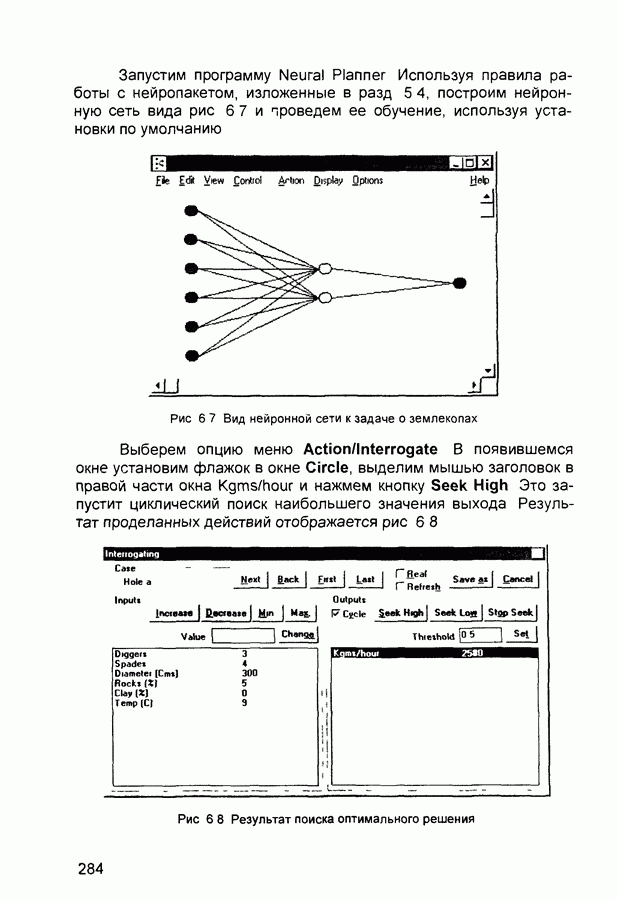
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
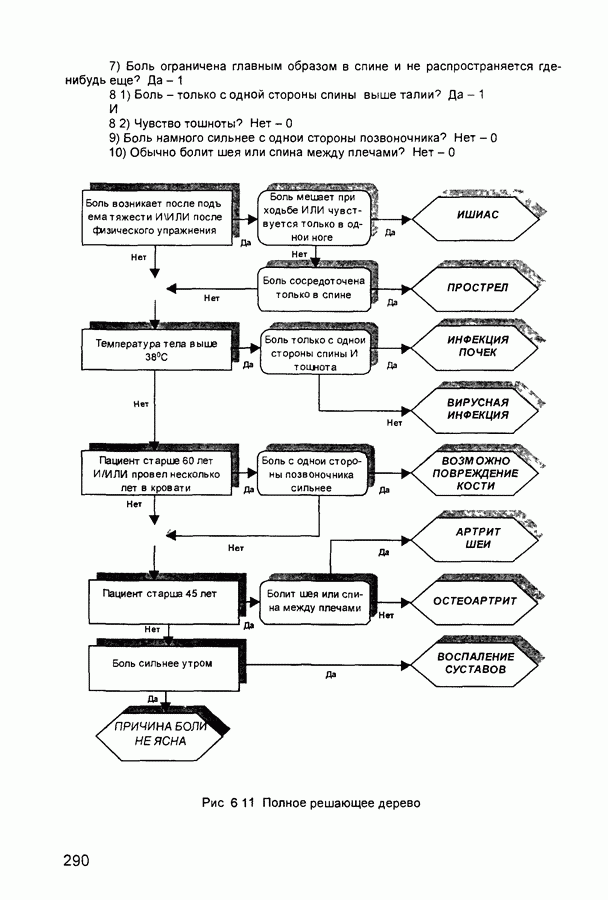
- 6.7. Нейросетевая экспертная система
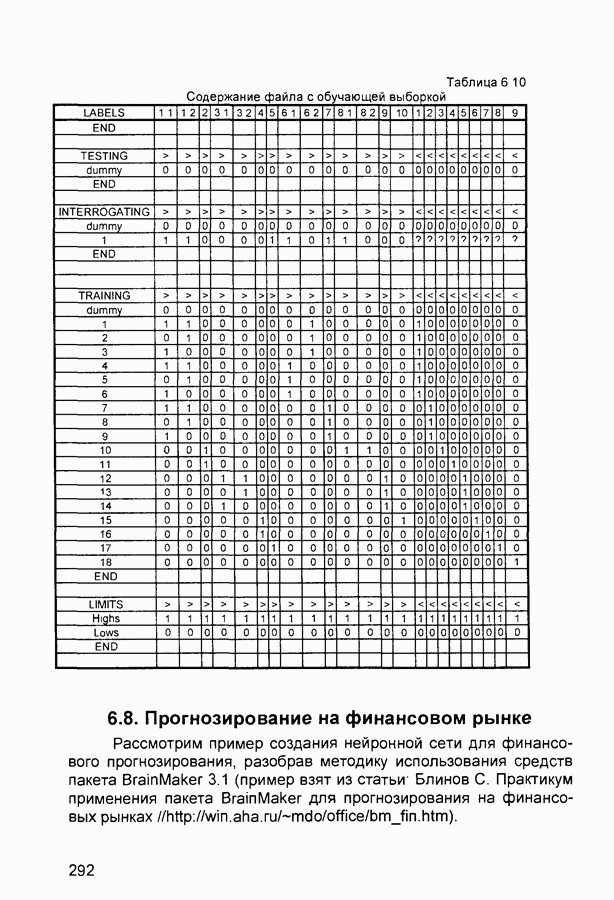
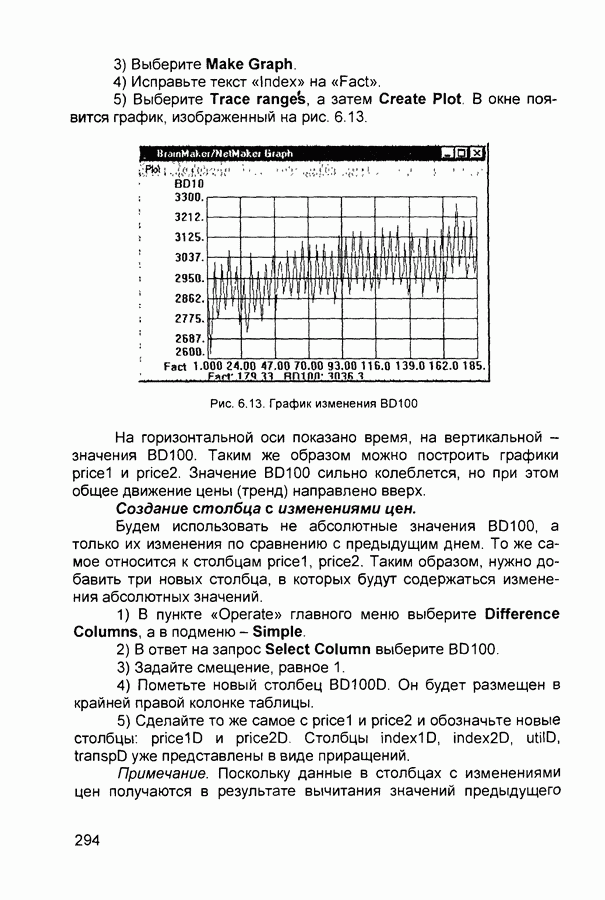
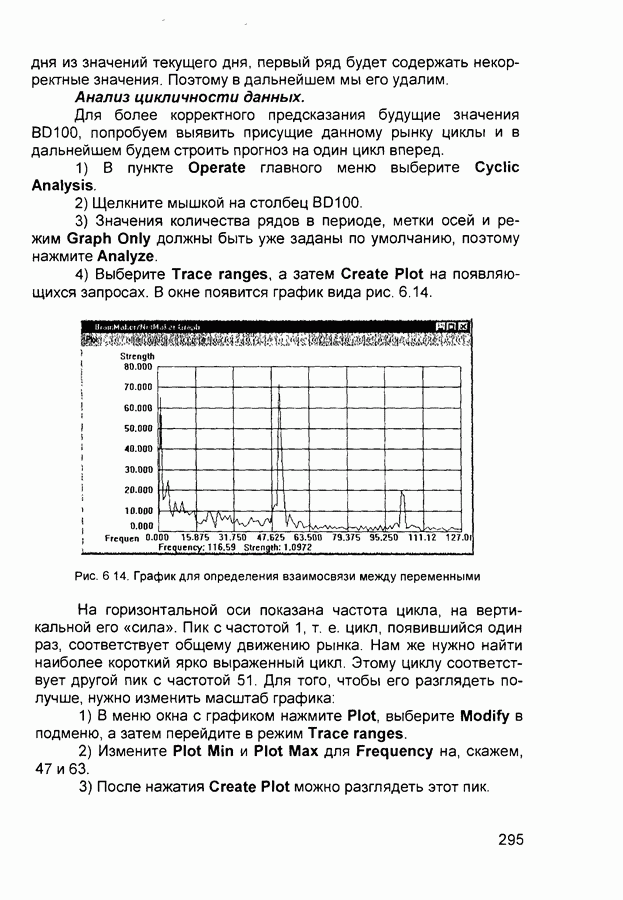
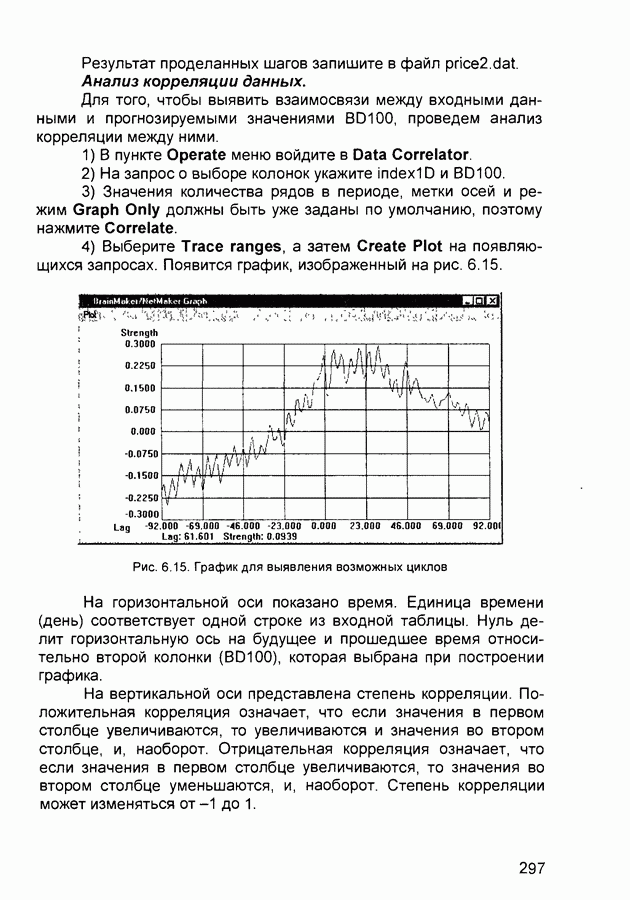
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
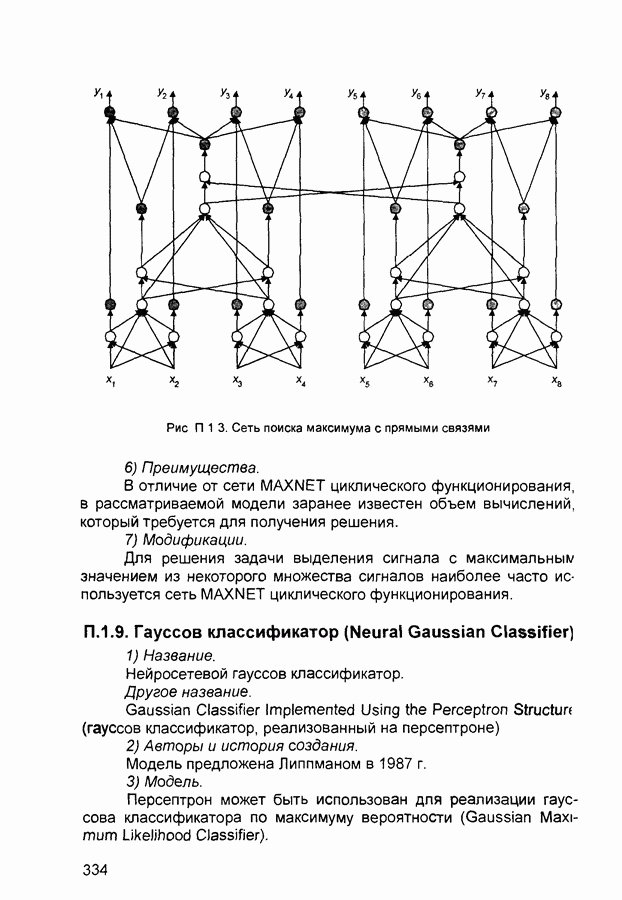
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы