| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
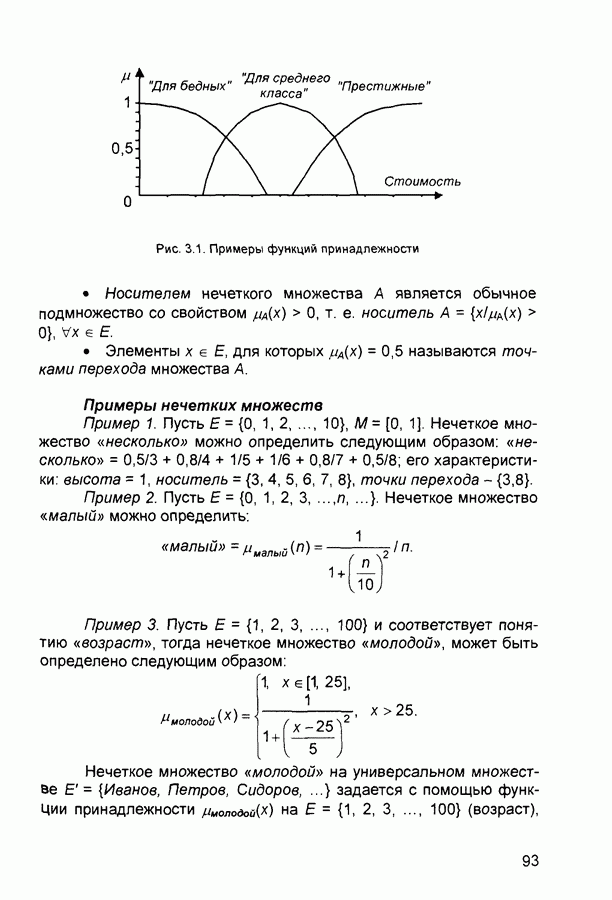
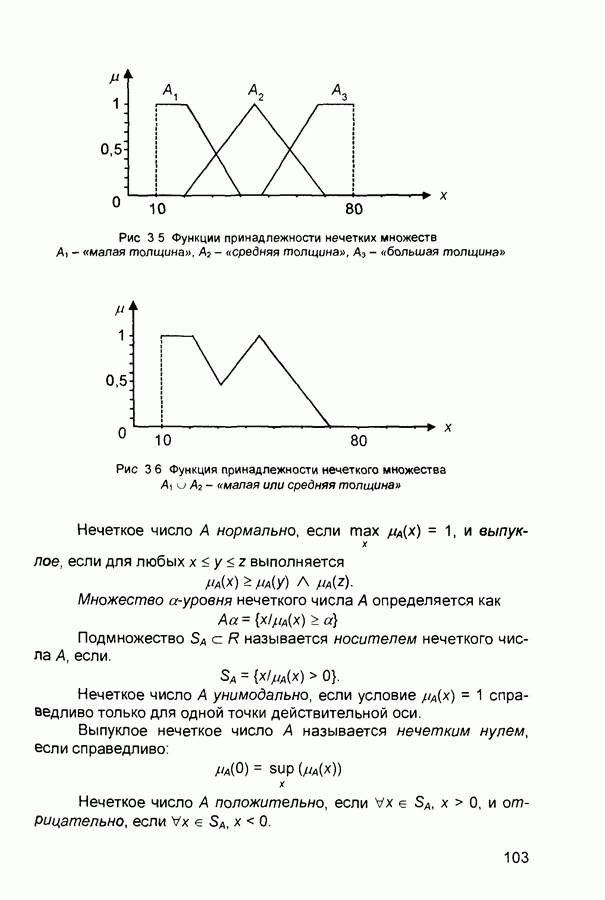
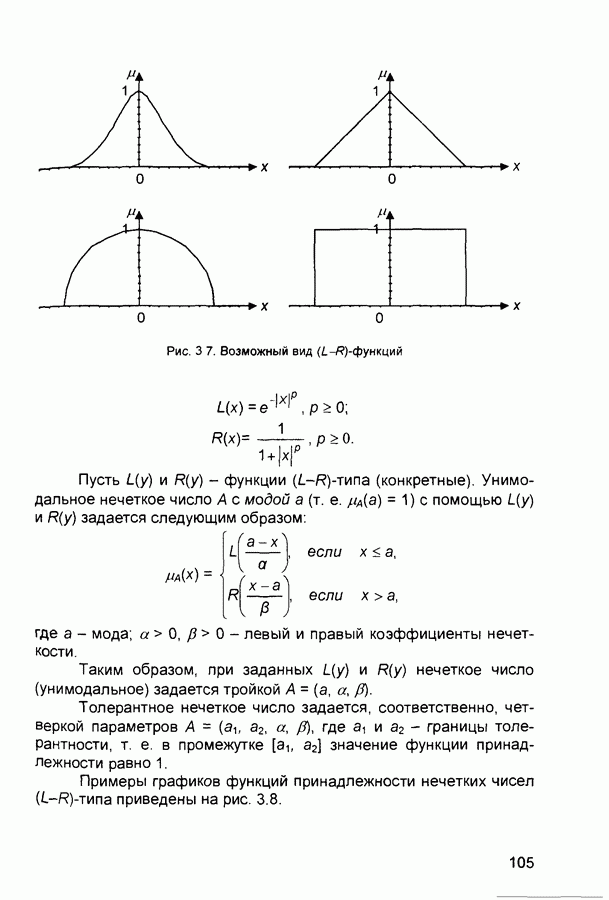
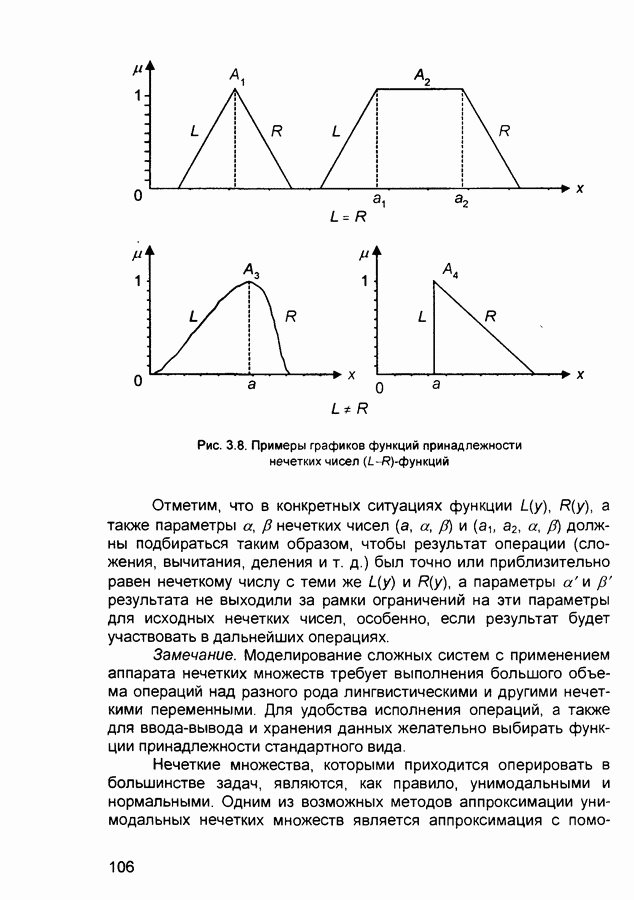
2.3. Нейронные сети встречного распространения
Объединение разнотипных нейронных структур в единой архитектуре зачастую приводит к свойствам, которых нет у них по отдельности Причем именно каскадные соединения нейронных структур, специализирующихся на решении различных задач, по зволяют решить проблему комплексно
Нейронные сети встречного распространения, состоящие и входного слоя нейронов и слоев нейронов Кохонена и Гроссберга по своим характеристикам существенно превосходят возможности сетей с одним скрытым слоем нейронов Так, время их обучения задачам распознавания и кластеризации более, чем в сто раз меньше времени обучения аналогичным задачам сетей с обратным распространением ошибки Это может быть полезно в тех приложениях, где долгая обучающая процедура невозможна

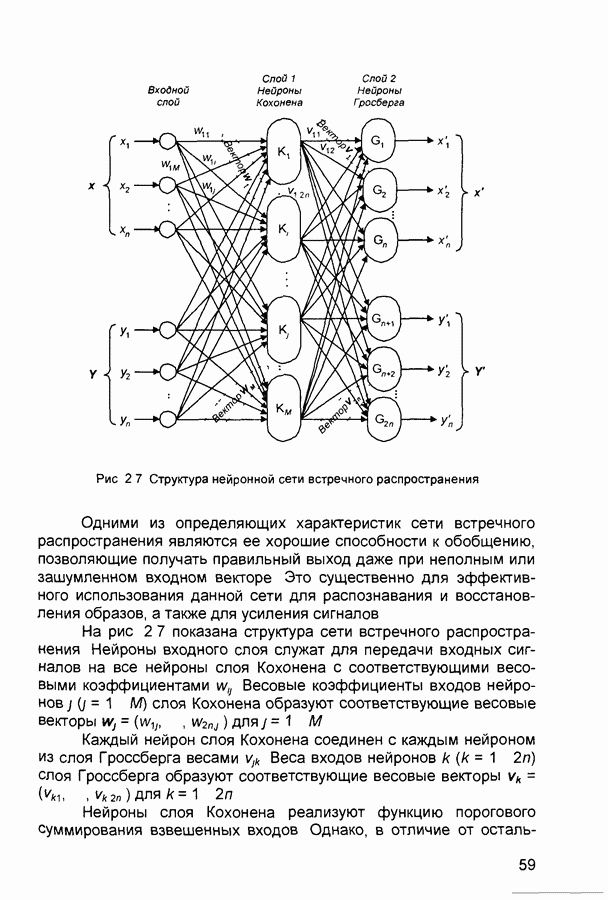
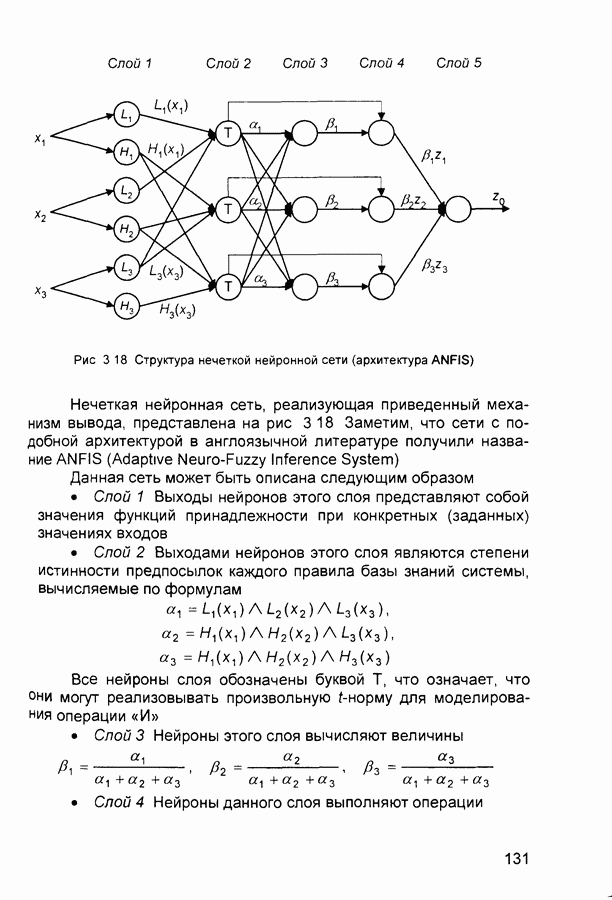
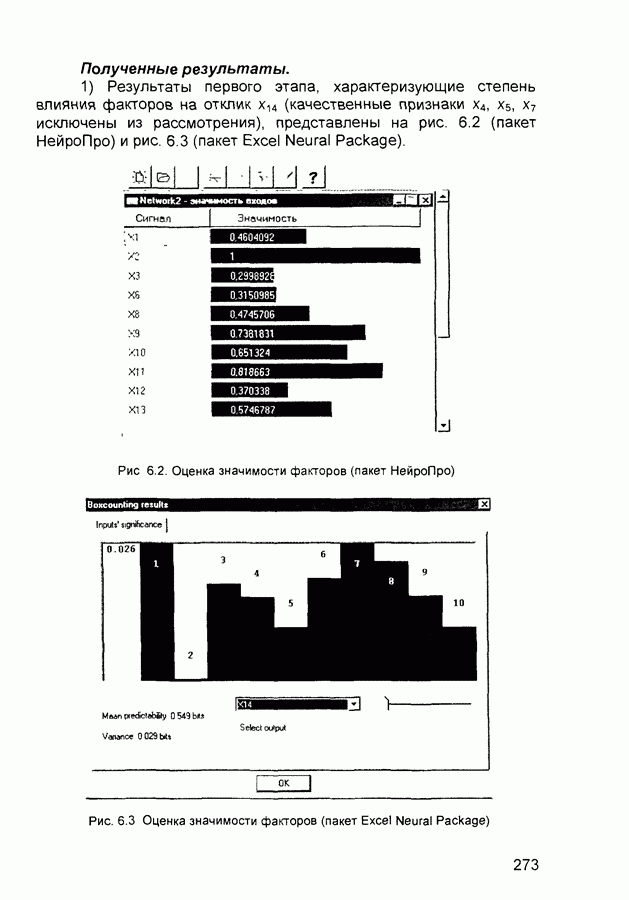
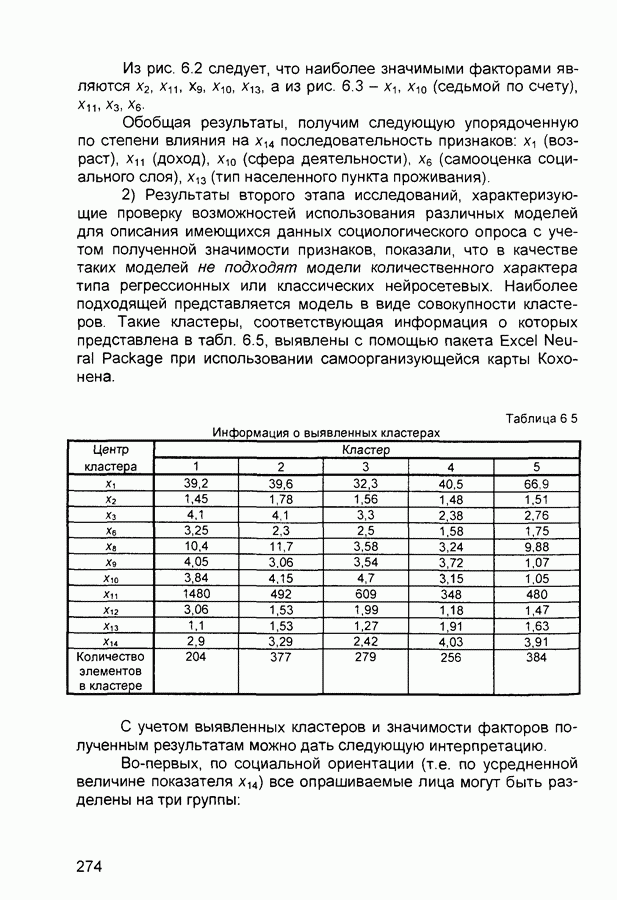
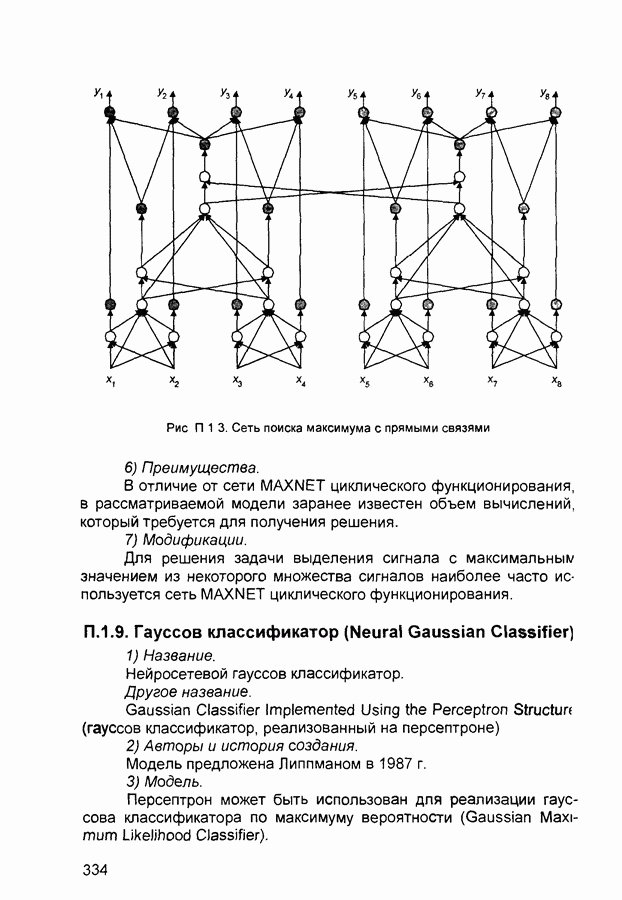
Рис. 2.7 Структура нейронной сети встречного распространения
Одними из определяющих характеристик сети встречного распространения являются ее хорошие способности к обобщению, позволяющие получать правильный выход даже при неполным или зашумленном входном векторе Это существенно для эффективного использования данной сети для распознавания и восстановления образов, а также для усиления сигналов
На рис 2 7 показана структура сети встречного распространения Нейроны входного слоя служат для передачи входных сигналов на все нейроны слоя Кохонена с соответствующими весовыми коэффициентами  Весовые коэффициенты входов нейронов
Весовые коэффициенты входов нейронов  слоя Кохонена образуют соответствующие весовые векторы
слоя Кохонена образуют соответствующие весовые векторы  для
для 
Каждый нейрон слоя Кохонена соединен с каждым нейроном из слоя Гроссберга весами  Веса входов нейронов к
Веса входов нейронов к  слоя Г россберга образуют соответствующие весовые векторы
слоя Г россберга образуют соответствующие весовые векторы  для/с
для/с 
Нейроны слоя Кохонена реализуют функцию порогового суммирования взвешенных входов Однако, в отличие от
остальных слоев, нейрон слоя Кохонена с максимальным значением взвешенной суммы (на заданный входной вектор) является «победителем» На его выходе формируется уровень логической «1», на выходах остальных нейронов слоя 
Нейроны же слоя Гроссберга на выходах выдают величины весов  которые связывают их с нейроном-«победителем» из слоя Кохонена
которые связывают их с нейроном-«победителем» из слоя Кохонена
Процесс обучения нейронной сети встречного распространения различен для слоев нейронов Кохонена и Гроссберга Рассмотрим вопросы, возникающие при обучении каждого из этих слоев
Перед обучением (самообучением) слоя Кохонена, протекающим без учителя, необходимо выполнить предварительную нормализацию входных  и весовых векторов
и весовых векторов 
Нормализация входных векторов осуществляется с целью их преобразования в единичные векторы с теми же направлениями перед предъявлением сети в соответствии со следующим выражением

Нормализация же начальных случайных значений весовых векторов приближает их к окончательным значениям, сокращая тем самым время обучения Эти окончательные значения весовых векторов совпадают с нормализованными значениями входных векторов
При обучении слоя Кохонена на вход подается нормализованный входной вектор На выходе нейрона с максимальным значением взвешенной суммы формируется уровень логической «1»
При этом процесс обучения после выбора нейрона-«победителя» с весовым вектором, наиболее близким к входному вектору, состоит в дальнейшей подстройке (приближении) компонентов весового вектора выбранного нейрона к предъявленному входному вектору в соответствии с выражением

где  - соответственно новое и предыдущее значения вектора весов выигравшего
- соответственно новое и предыдущее значения вектора весов выигравшего  -го нейрона-«победителя» для предъявленного входного вектора
-го нейрона-«победителя» для предъявленного входного вектора  коэффициент скорости обучения
коэффициент скорости обучения
Каждый коэффициент из весового вектора нейрона-«победителя» изменяется пропорционально разности между его
величиной и величиной входа, к которому он присоединен Знак изменения минимизирует разность между весовым коэффициентом и его входом По мере обучения коэффициент  постепенно уменьшается
постепенно уменьшается
В результате обучения нейрон-«победитель» будет активизироваться для совокупности ассоциированных с ним входных векторов, средняя величина которых совпадает с вектором весов этого нейрона
Однако существует ряд проблем обучения слоя Кохонена, от решения которых зависит эффективность использования нейронной сети встречного распространения в целом
Прежде всего, из-за того, что нормализованные входные векторы, как правило, неравномерно распределены по поверхности гиперсферы, большинство весовых векторов (изначально равномерно распределенных рандомизацией весов) будут значительно удалены от любого входного вектора Поэтому на выходах соответствующих им нейронов постоянно будет установлен уровень логического  и эти нейроны окажутся бесполезными С другой стороны, активных нейронов может оказаться недостаточно для эффективного разделения близкорасположенных входных векторов
и эти нейроны окажутся бесполезными С другой стороны, активных нейронов может оказаться недостаточно для эффективного разделения близкорасположенных входных векторов
Еще одна проблема заключается в сложности разделения на различные классы множеств сходных входных векторов в случае, если изначальная плотность весовых векторов в окрестности обучающих векторов будет недостаточной
Проблему может представлять также излишне высокая плотность весовых векторов вблизи несущественно различающихся входных векторов Что может привести к активизации нескольких нейронов слоя Кохонена,  формированию ложных классов входных векторов
формированию ложных классов входных векторов
Решением перечисленных проблем является распределение весовых векторов в соответствии со сложностью входных векторов Существует несколько путей приближенного достижения этой цели, из которых наиболее популярны следующие четыре
1) Метод выпуклой комбинации (convex combination method) Первоначально всем весовым коэффициентам присваиваются одинаковые значения  Каждый компонент входного вектора модифицируется в соответствии с правилом
Каждый компонент входного вектора модифицируется в соответствии с правилом  Сначала
Сначала  мало, и длина всех входных векторов близка к векторам
мало, и длина всех входных векторов близка к векторам
весов Затем в процессе обучения  постепенно увеличивается до единицы, что позволяет правильно разделить входные векторы
постепенно увеличивается до единицы, что позволяет правильно разделить входные векторы
Недостатком данного метода является увеличение времени обучения из-за необходимости подстройки весовых коэффициентов к постоянно изменяющимся значениям входных векторов
2) Зашумление входных векторов Входные векторы подвергаются случайным изменениям, благодаря чему захватывается ближайший весовой вектор Этот метод более медленный, чем метод выпуклой комбинации
3) Изменение числа корректируемых нейронов На начальной стадии процесса обучения подстраиваются веса всех нейронов слоя, а не только нейрона-«победителя» Далее подстройка весов производится лишь для ближайших к выигравшему нейронах Число этих нейронов по мере обучения сокращается И в конце остается лишь один нейрон
4) Наделение нейронов «чувством справедливости» Если нейрон становится «победителем», то порог его срабатывания временно увеличивается Это дает возможность обучаться и другим нейронам
Назначением нейронов слоя Гроссберга является формирование требуемых выходных векторов после того, как нейроны слоя Кохонена разделили входные векторы на классы Фактически каждый нейрон слоя Гроссберга лишь выдает значение веса, который связывает этот нейрон с нейроном-«победителем» слоя Кохонена В отличие от самообучающегося слоя Кохонена, слой Гроссберга обучается с учителем Различие же со стандартной обучающей процедурой заключается в том, что подстройке подвергаются только те веса нейронов слоя Гроссберга, которые соединены с ненулевым нейроном Кохонена Используется следующее правило

где  - выход
- выход  нейрона Кохонена,
нейрона Кохонена,  компонент требуемого выходного вектора Первоначально
компонент требуемого выходного вектора Первоначально  равен 0,1 и уменьшается в процессе обучения
равен 0,1 и уменьшается в процессе обучения
Отличие нейронной сети встречного распространения от других заключается также в особенностях функционирования В соответствии с приведенной на рис. 2.7 структурой на вход сети подаются нормализованные единичные векторы X и  а на выходе формируются их нормализованные аппроксимации
а на выходе формируются их нормализованные аппроксимации 
При обучении векторы X и Y подаются одновременно и как входные, и как требуемые выходные При этом вектор X является входным для вектора  а вектор У - для вектора У. В результате
а вектор У - для вектора У. В результате
такого обучения получается однозначное отображение векторов X и Y на их копии
После обучения в нейронной сети встречного распространения реализуется свойство ассоциативной памяти, заключающееся в том, что предъявление на вход только вектора X (или У) при отсутствии другого приводит к порождению на выходе как вектора X так и У
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
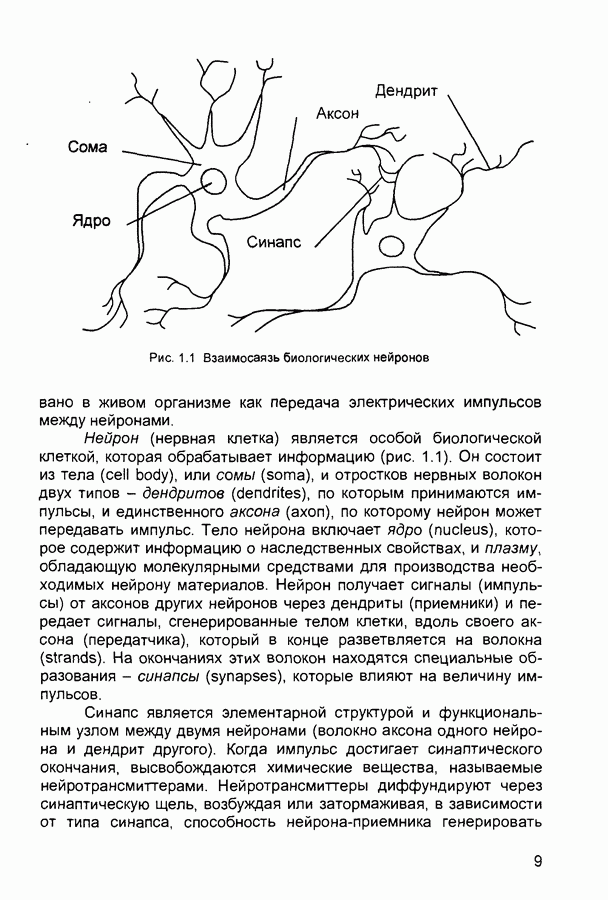
- 1.1. Биологический нейрон
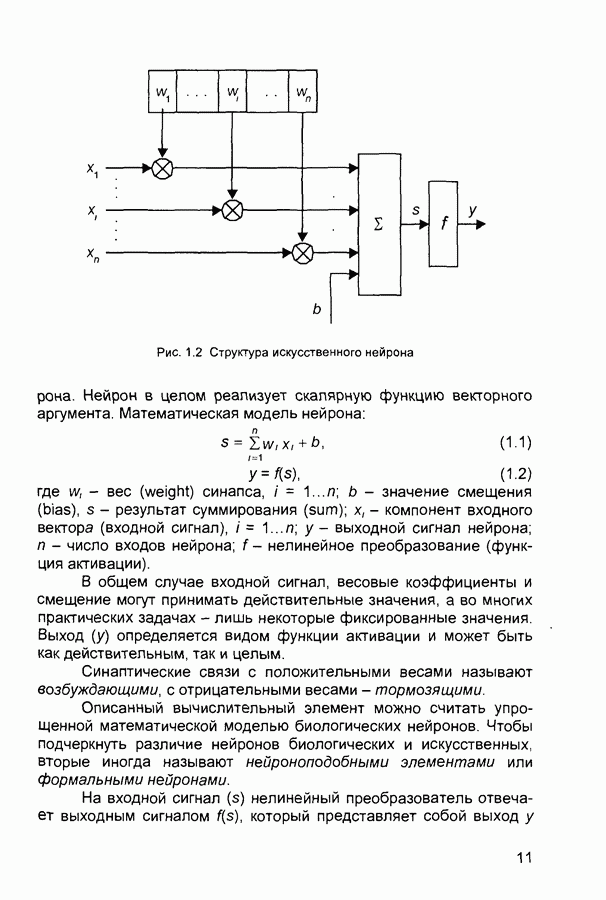
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
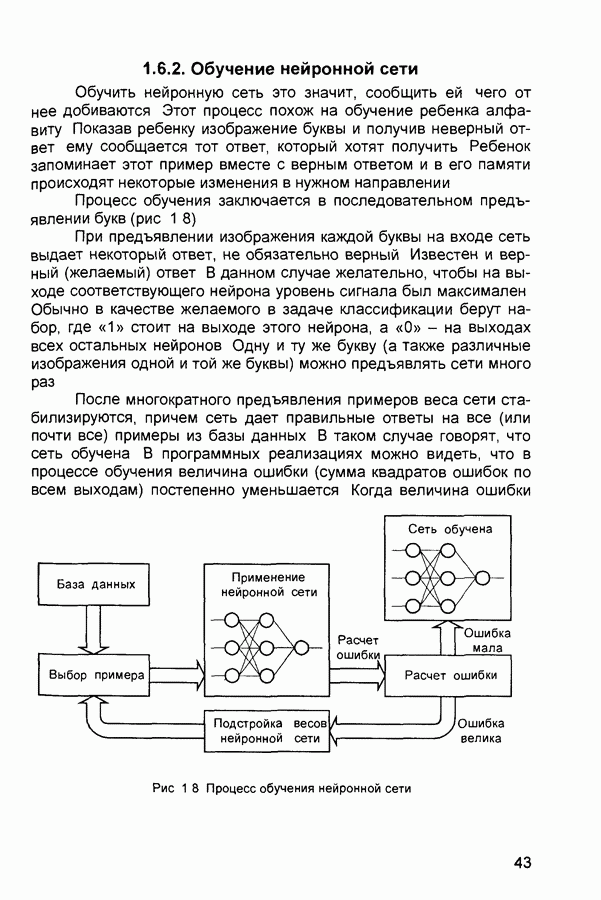
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
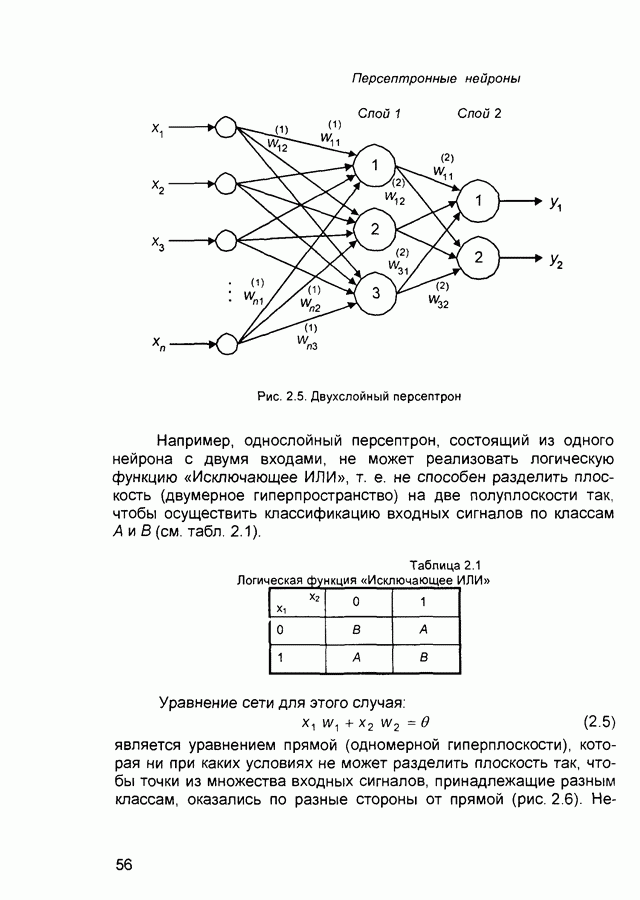
- 2.2. Персептроны
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
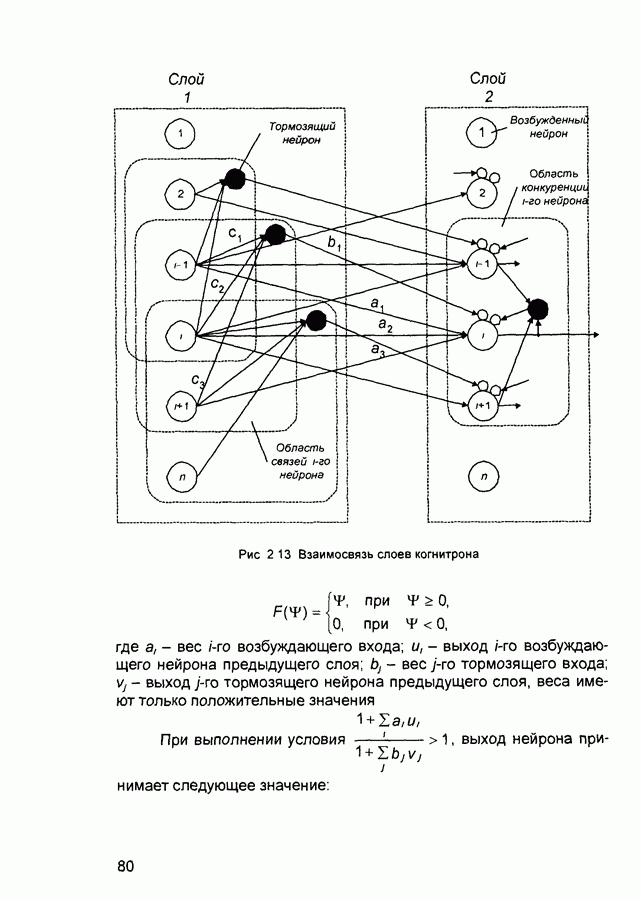
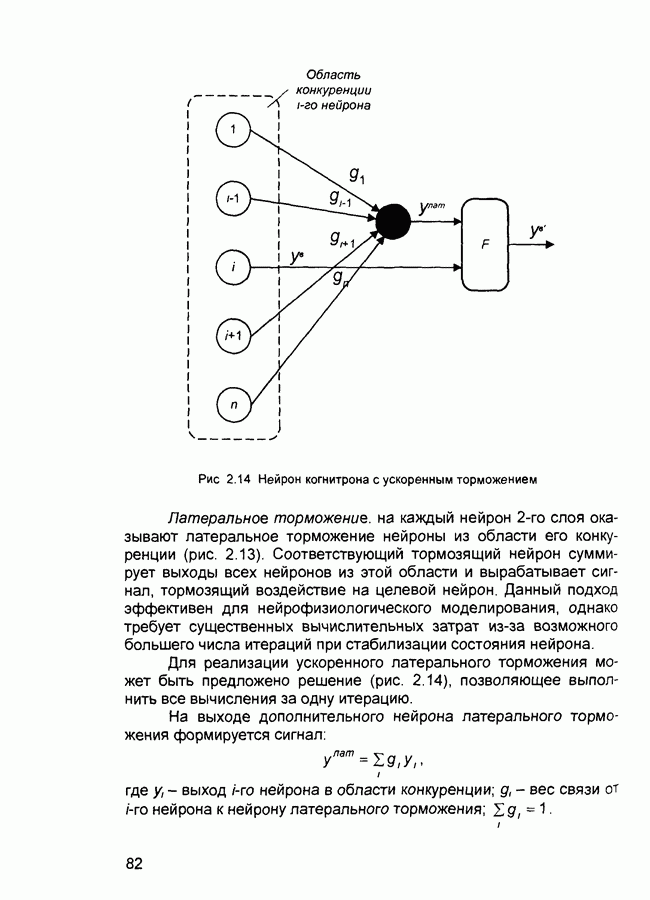
- 2.7. Когнитрон
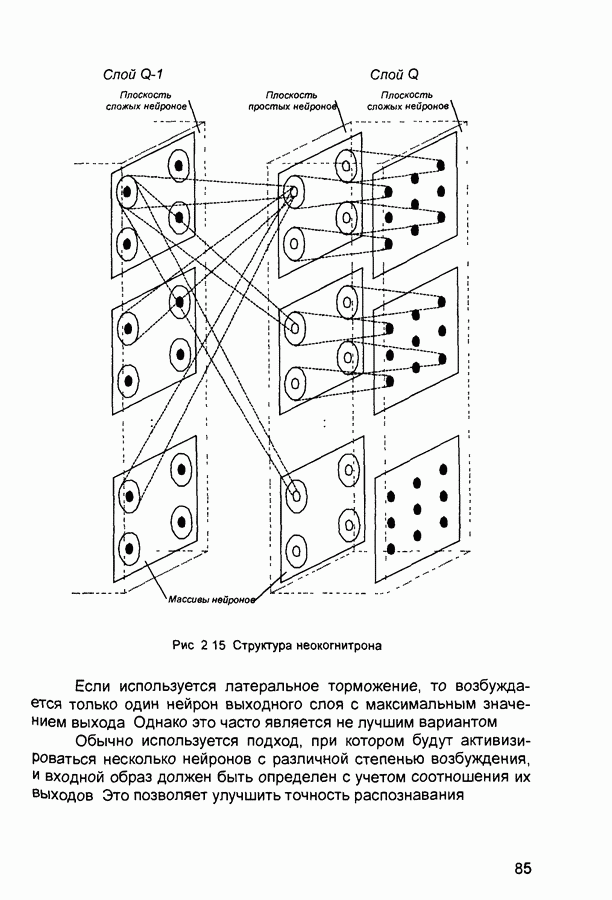
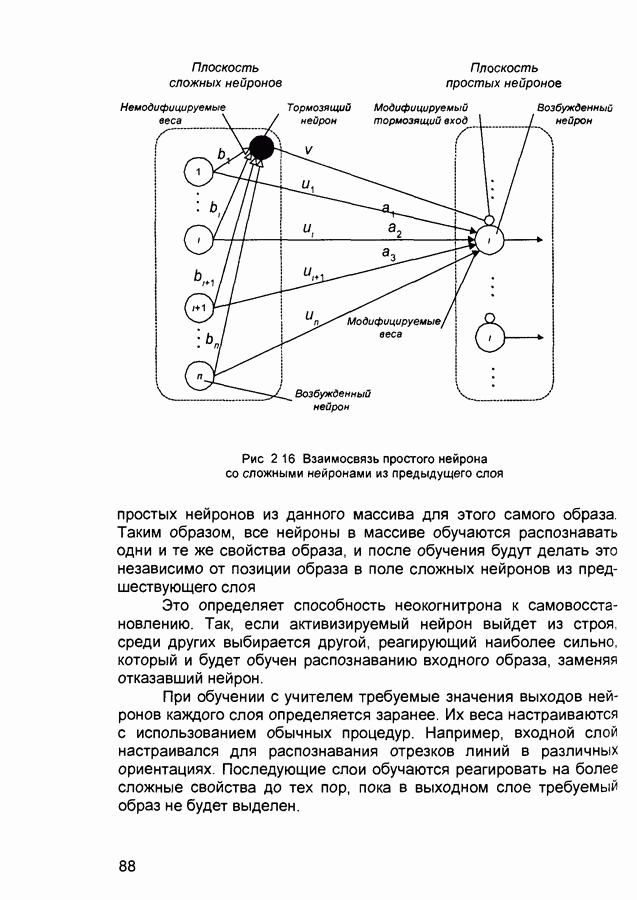
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
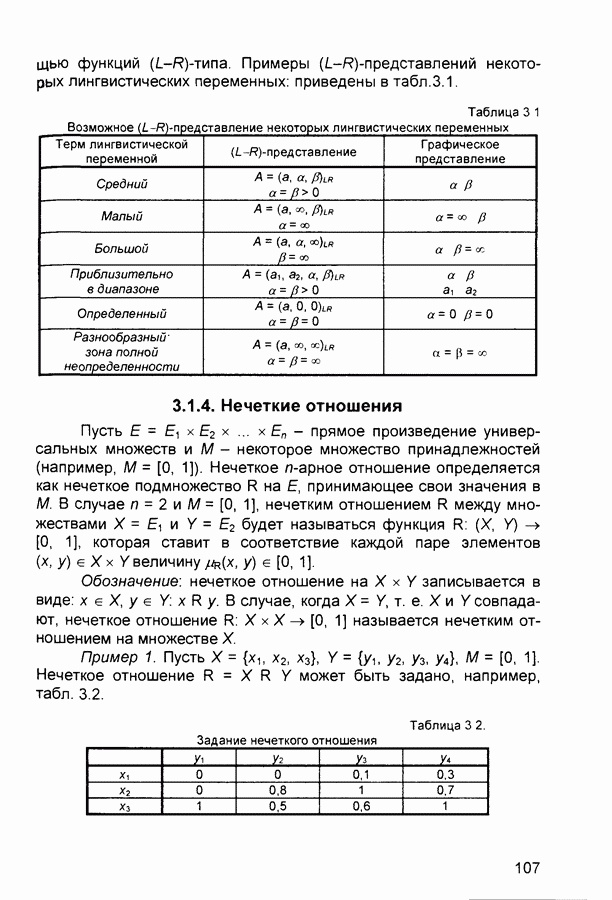
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
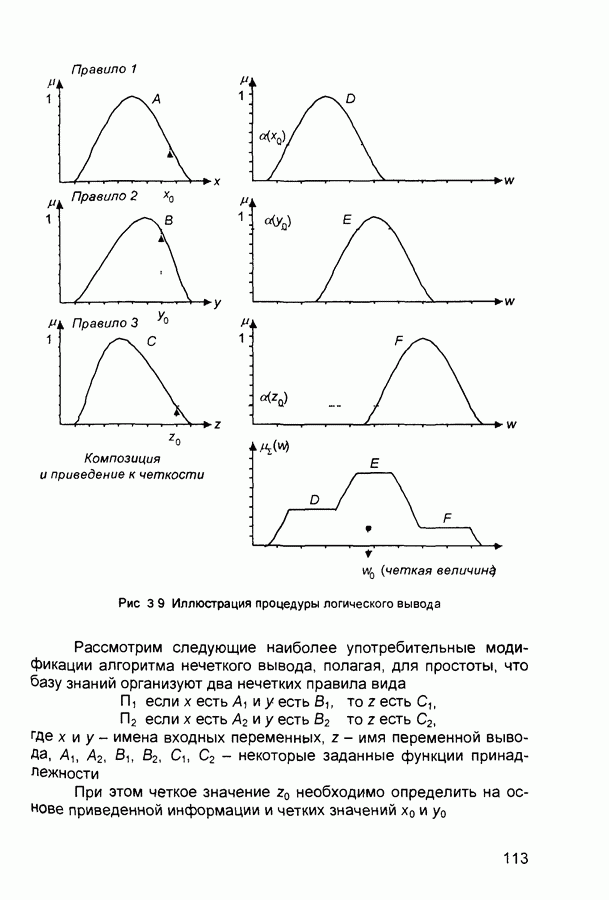
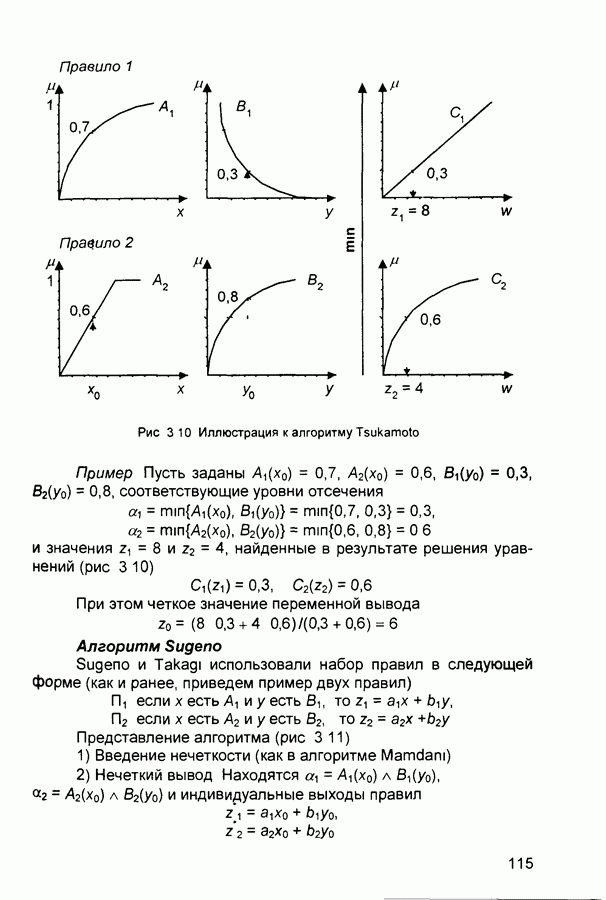
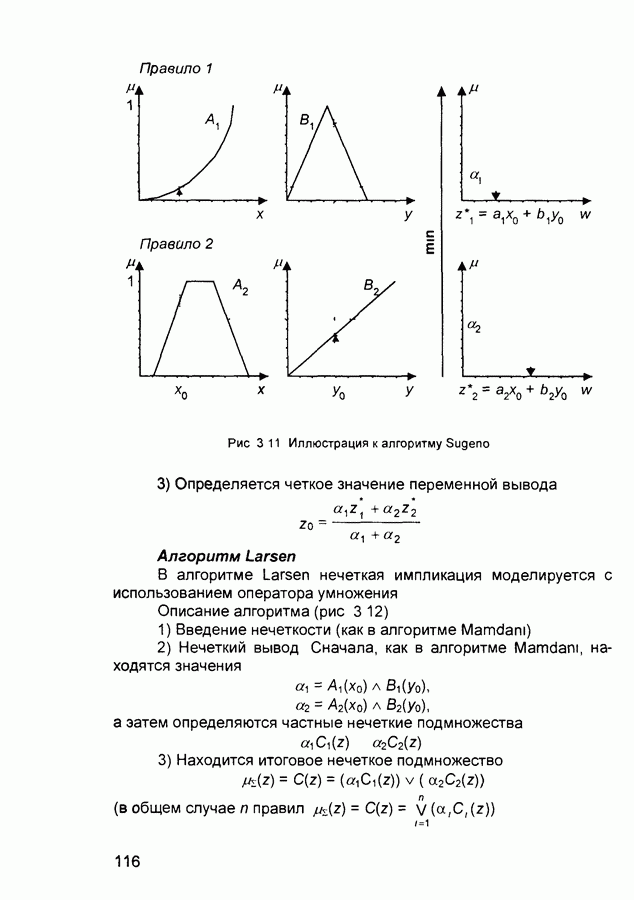
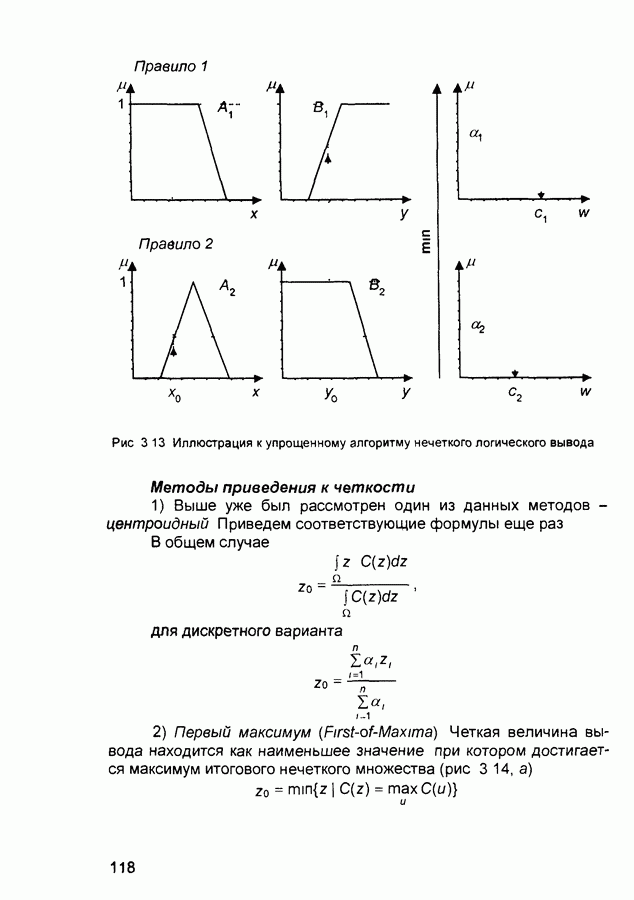
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
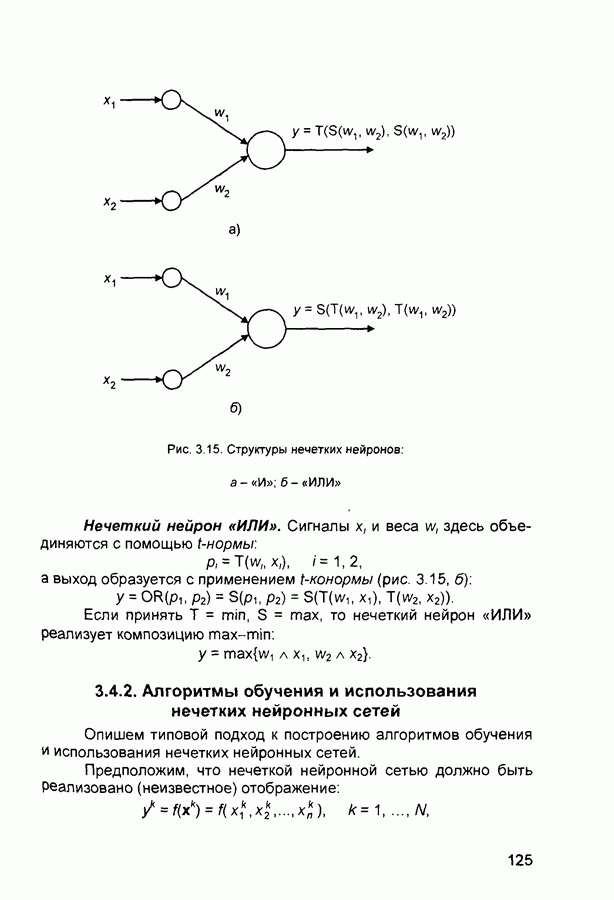
- 3.4. Синтез нечетких нейронных сетей
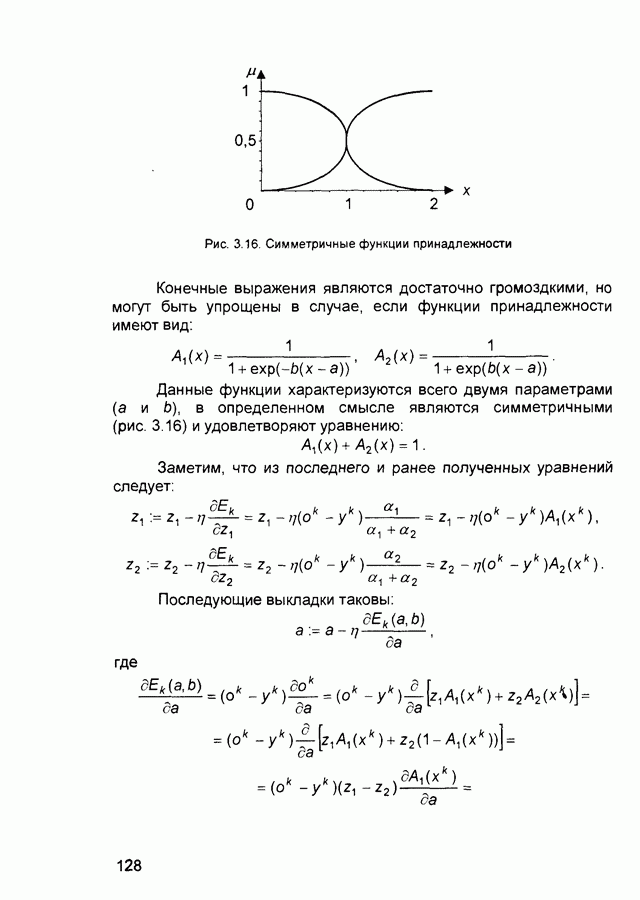
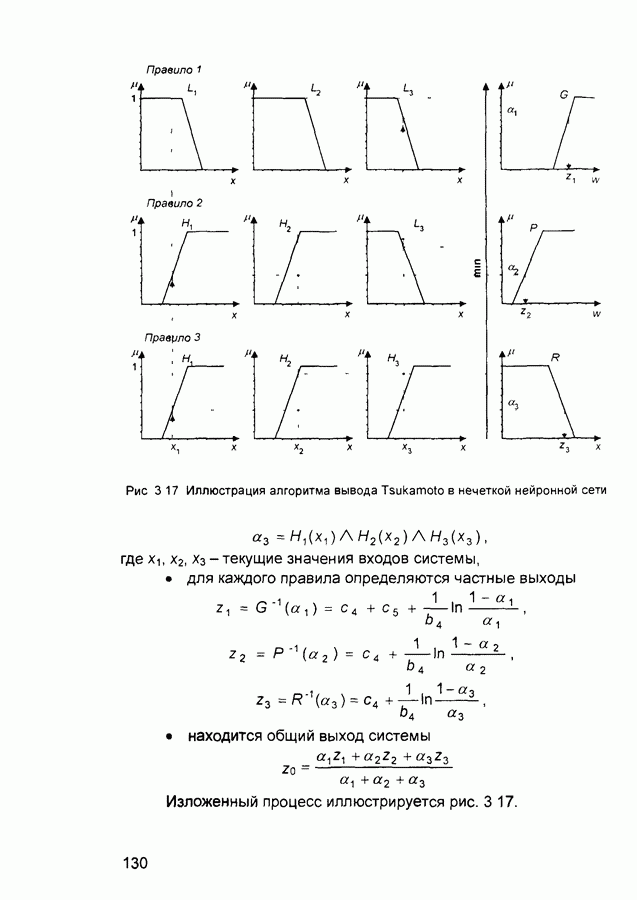
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
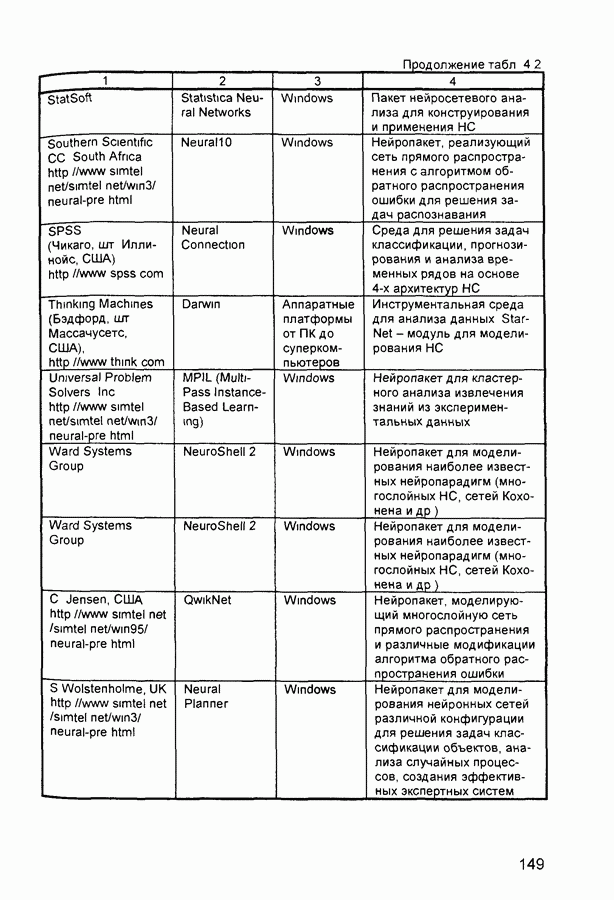
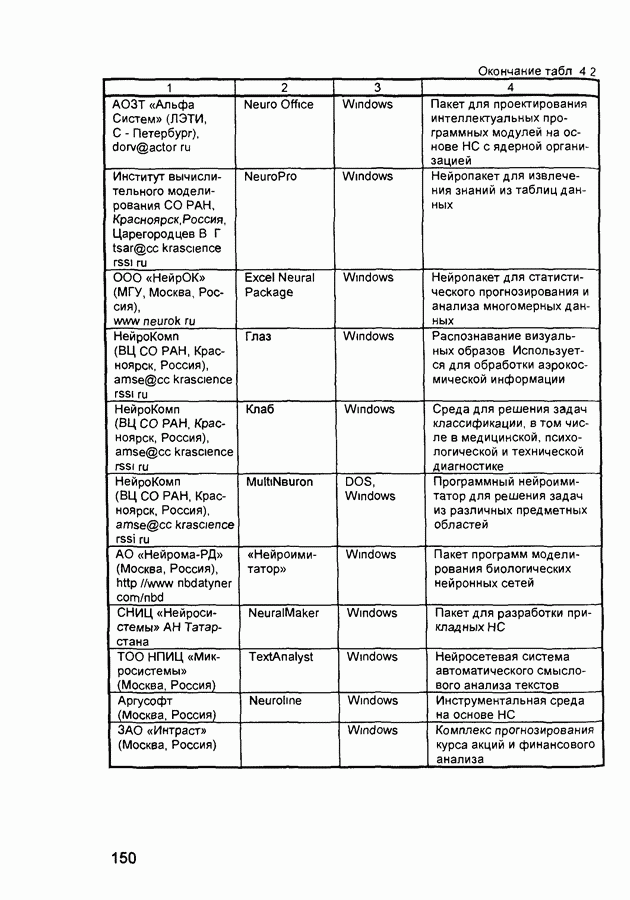
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
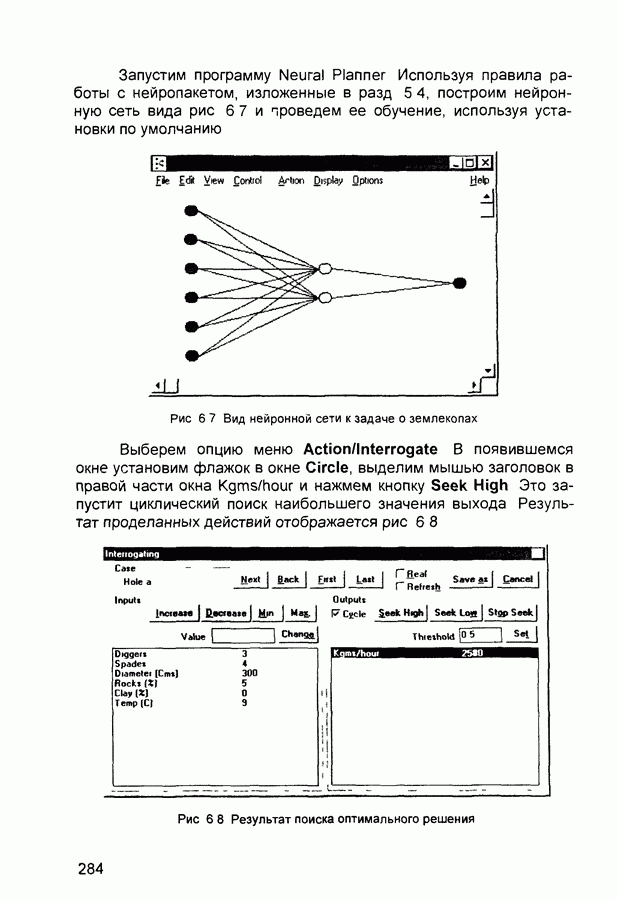
- 6.5. Задача о землекопах
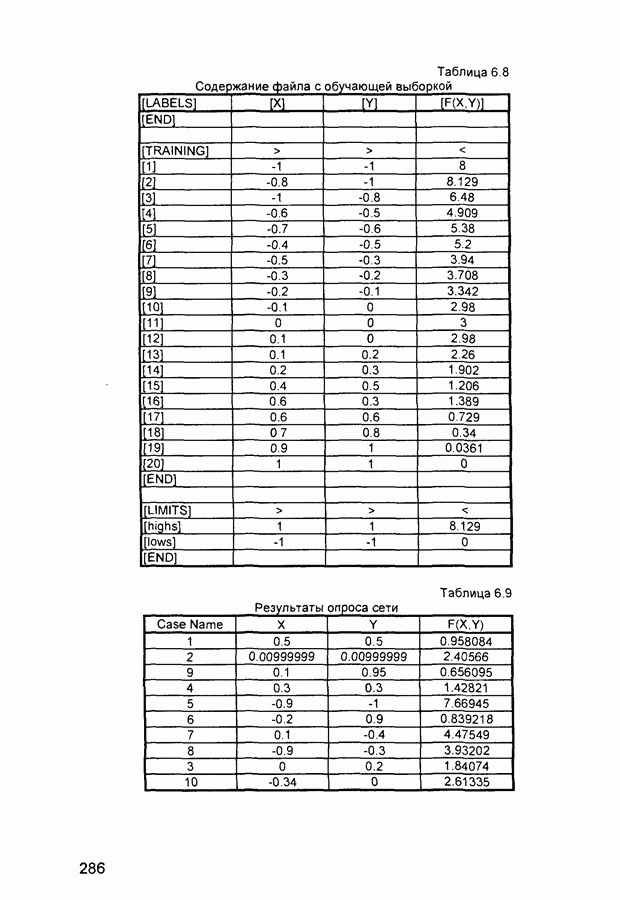
- 6.6. Аппроксимация функции
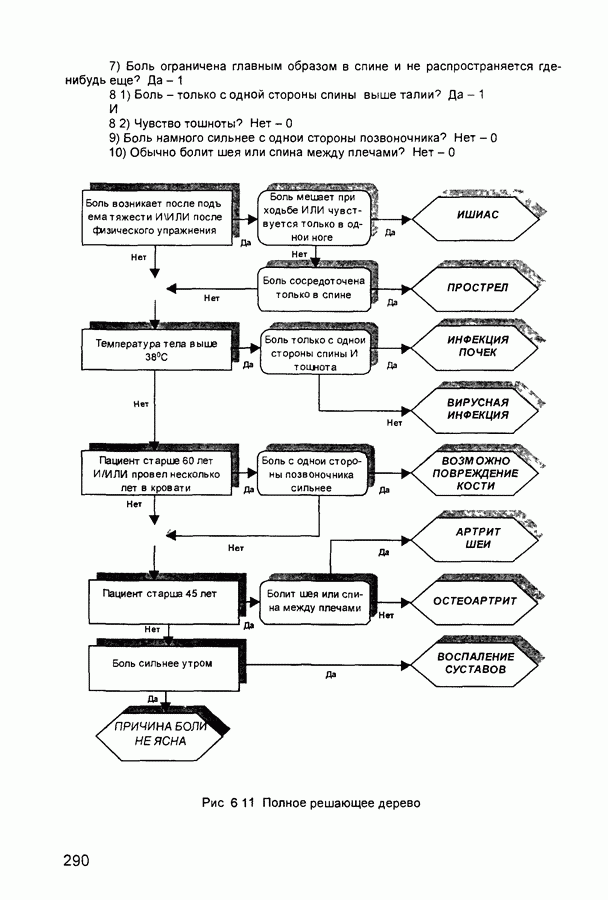
- 6.7. Нейросетевая экспертная система
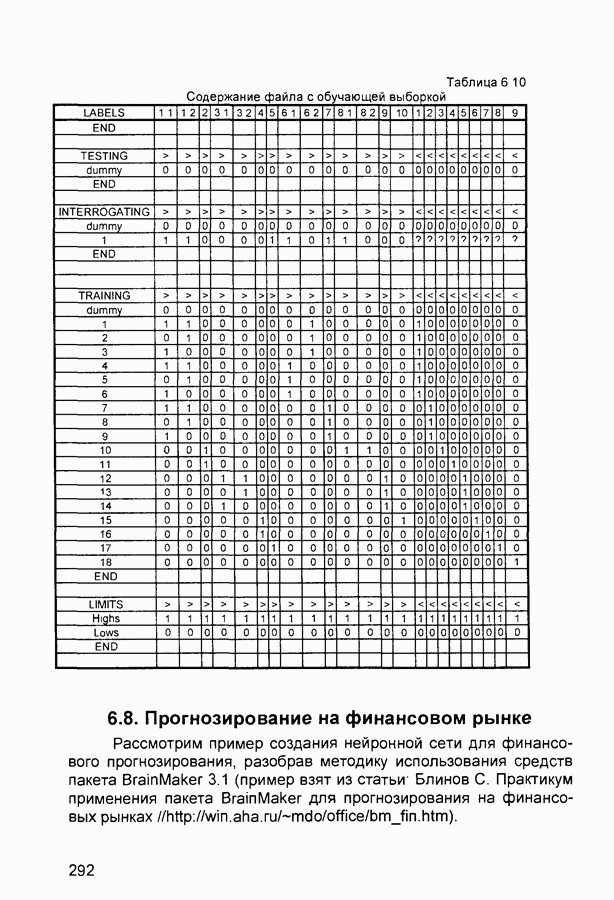
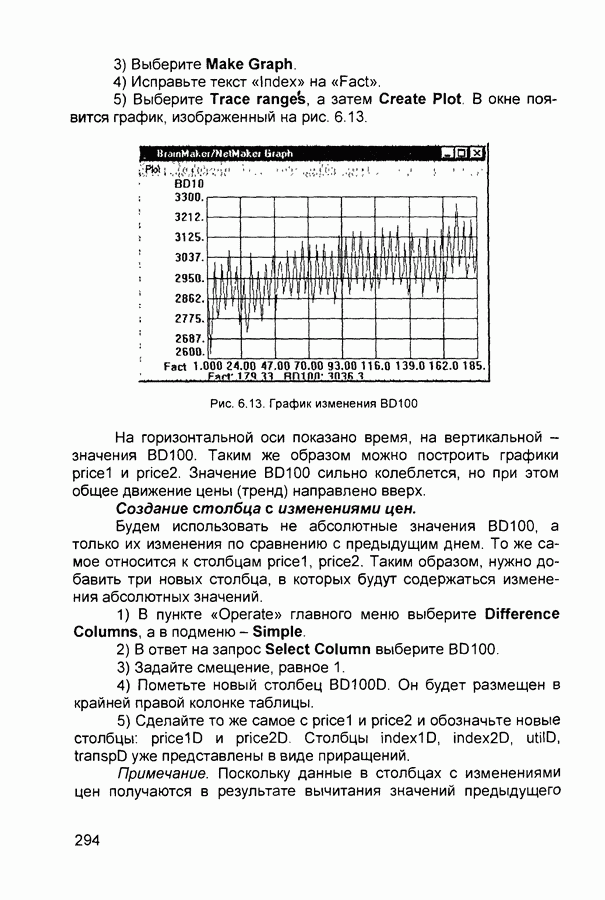
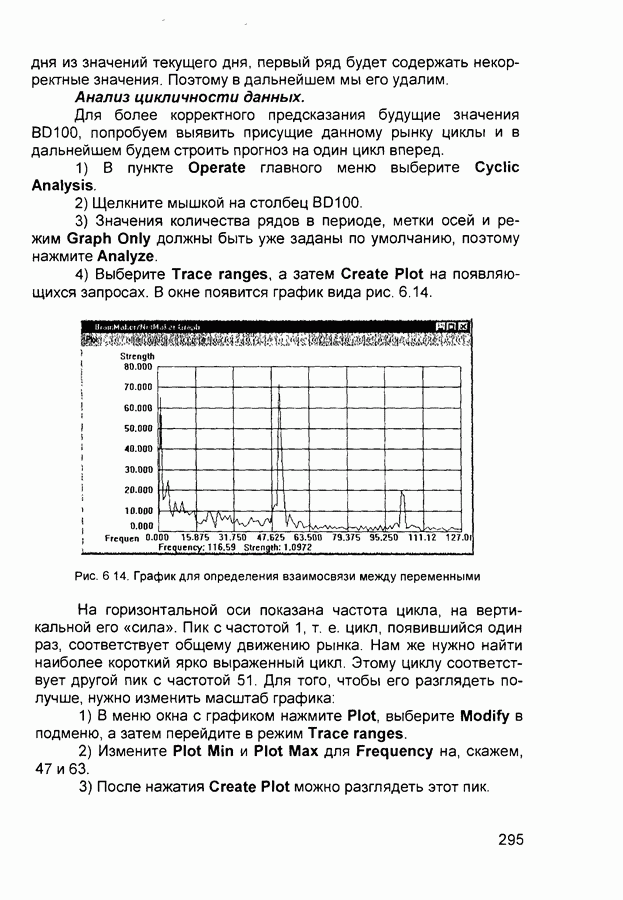
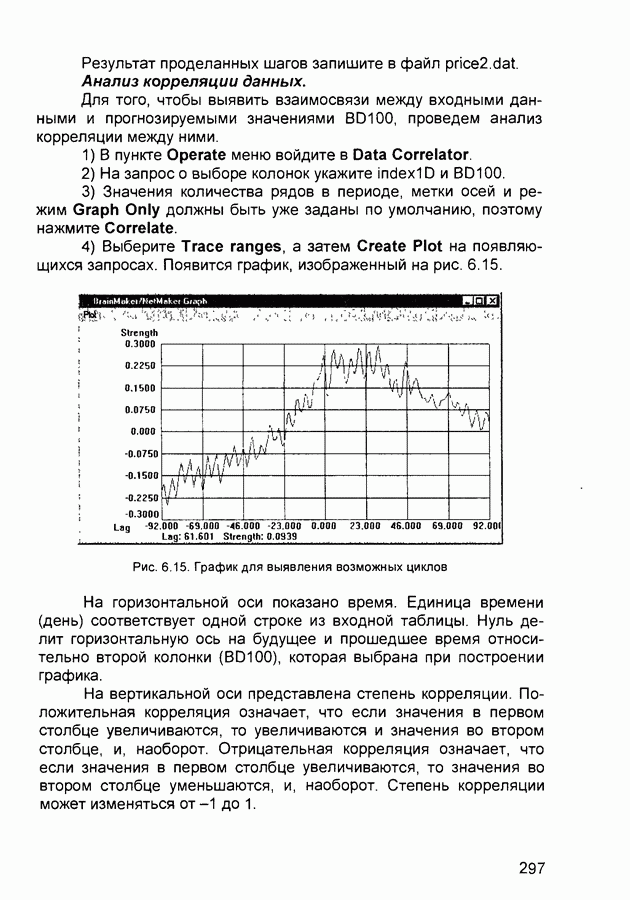
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы