| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.10. Компактное представление информации репликативными нейронными сетями
В процессе анализа или обработки удобно предположить, что анализируемые данные являются векторами многомерного, например, евклидова пространства, где они располагаются в соответствии с некоторой функцией распределения. В случае же, если многомерные данные не порождаются непосредственно пространственно-временной природой информации, то это также не мешает использовать такую модель для их представления. Примерами могут служить результаты измерений, полученные в ходе физических, биологических и других экспериментов, результаты медицинской диагностики, телеметрическая информация. При этом размерность пространства признаков (координат)  может достигать десятков тысяч.
может достигать десятков тысяч.
Естественные координаты. Опыт показывает, что объекты, как правило, не заполняют все  -мерное пространство, а располагаются на некоторой поверхности, имеющей невысокую размерность (десятки, сотни) Это означает, что существуют обобщенные (естественные) признаки, образованные из комбинаций исходных признаков и наиболее точно характеризующие исходные объекты.
-мерное пространство, а располагаются на некоторой поверхности, имеющей невысокую размерность (десятки, сотни) Это означает, что существуют обобщенные (естественные) признаки, образованные из комбинаций исходных признаков и наиболее точно характеризующие исходные объекты.
Доказана единственность системы естественных координат, а также известно, что эти координаты обладают рядом важных свойств, например, признаки объектов в естественных координатах являются попарно независимыми. Что делает естественные координаты весьма удобными для широкого класса вероятностных распределений.
Рассмотрим некий генератор данных в  -мерном пространстве. Предположим, что генерируемые им данные заполняют не все пространство, а лишь некоторое многообразие размерности
-мерном пространстве. Предположим, что генерируемые им данные заполняют не все пространство, а лишь некоторое многообразие размерности  где
где  Многообразие, на котором расположены данные, можно представлять как сложную поверхность, которая в окрестности каждой своей точки похожа на поверхность
Многообразие, на котором расположены данные, можно представлять как сложную поверхность, которая в окрестности каждой своей точки похожа на поверхность  -мерной сферы. Утверждается, что на многообразии существует такая функция распределения, которая сколь угодно близка к исходной функции распределения генератора в смысле средних значений. Это
-мерной сферы. Утверждается, что на многообразии существует такая функция распределения, которая сколь угодно близка к исходной функции распределения генератора в смысле средних значений. Это
позволяет вместо исходных данных, представляемых большим числом признаков, рассматривать генератор данных в пространстве существенного меньшего числа измерений.
Естественные координаты вводятся следующим образом. Рассмотрим взаимно-однозначное непрерывное отображение т-мерного многообразия в  -мерный единичный куб. Это означает, что каждый вектор X, лежащий на
-мерный единичный куб. Это означает, что каждый вектор X, лежащий на  -мерном многообразии, представляется вектором с
-мерном многообразии, представляется вектором с  координатами, причем каждая координата является числом, равномерно распределенным между нулем и единицей.
координатами, причем каждая координата является числом, равномерно распределенным между нулем и единицей.
Естественные координаты зависят только от внутренней, заранее определенной, вероятностной структуры многообразия данных: равные объемы внутри единичного куба соответствуют множествам с равной вероятностью на многообразии данных, хотя их геометрические размеры могут значительно различаться. Естественные координаты могут отражать сложную вероятностную структуру многообразия данных.
Естественные координаты - это единственная координатная система из независимых компонент, которая обеспечивает оптимальное кодирование информации, с учетом вероятностной структуры генератора данных.
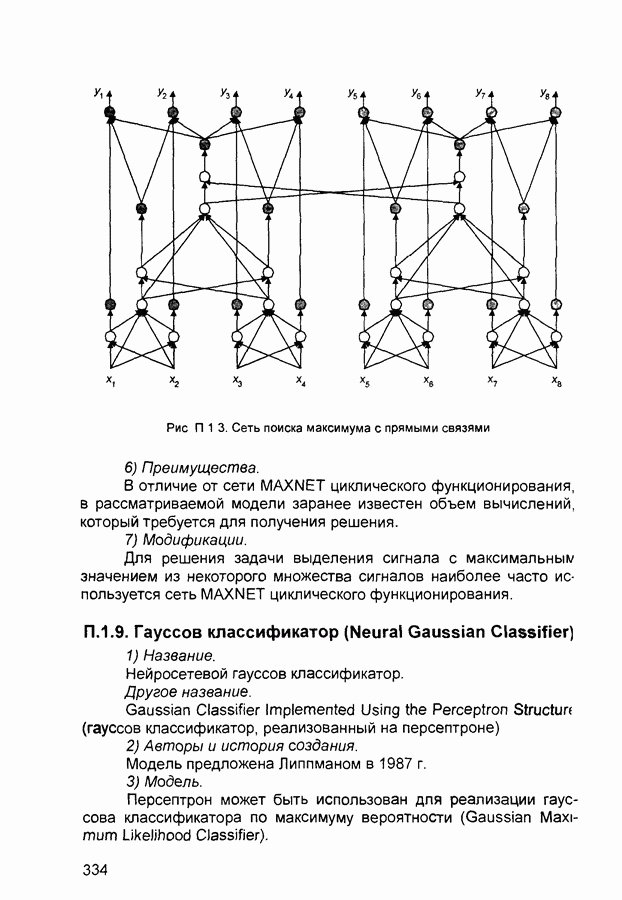
Репликативные нейронные сети. Для нахождения естественных координат можно использовать репликативные (копирующие) нейронные сети. Репликативная нейронная сеть представляет собой многослойный персептрон с тремя скрытыми слоями, число нейронов входного и выходного слоев которого одинаково. Первый и третий скрытые слои состоят из нейронов с сигмоидной активационной функцией. Размеры этих слоев подбираются в процессе обучения сети. Интересно отметить, что репликативные нейронные сети дают компактное и эффективное представление произвольных наборов векторов, имеющих сложное вероятностное распределение в пространстве, за счет того, что средний скрытый слой имеет меньше нейронов, чем входной и выходной слои.
Для вектора длины  подаваемого на входной слой, строится его отображение
подаваемого на входной слой, строится его отображение  в единичный куб. Для обученной сети это отображение реализует представление исходного вектора в системе естественных координат и, которое воспроизводится в среднем скрытом слое. Дальнейшее прохождение информации от среднего скрытого слоя до выходного слоя дает отображение
в единичный куб. Для обученной сети это отображение реализует представление исходного вектора в системе естественных координат и, которое воспроизводится в среднем скрытом слое. Дальнейшее прохождение информации от среднего скрытого слоя до выходного слоя дает отображение  (обратное
(обратное  из единичного куба в исходное
из единичного куба в исходное  -мерное пространство с заданной функцией распределения
-мерное пространство с заданной функцией распределения 
Средний скрытый слой состоит из  нейронов, где
нейронов, где  предполагаемое число естественных координат. Передаточная функция нейронов среднего скрытого слоя имеет вид наклонной или ступенчатой функции.
предполагаемое число естественных координат. Передаточная функция нейронов среднего скрытого слоя имеет вид наклонной или ступенчатой функции.
Цель обучения репликативной нейронной сети состоит в том, чтобы вектор, воспроизводимый выходным слоем сети, совпадал с вектором, поданным на входной слой. Передаточная функция нейронов выходного слоя выбирается линейной. Обучение проводится на обучающей выборке, полученной с помощью генератора данных с функцией распределения  Утверждается, что обученная репликативная нейронная сеть строит в среднем скрытом слое представление исходных векторов в естественных координатах. Таким образом, входной вектор длины
Утверждается, что обученная репликативная нейронная сеть строит в среднем скрытом слое представление исходных векторов в естественных координатах. Таким образом, входной вектор длины  передается на средний слой и там представляется естественными координатами в т-мерном единичном кубе
передается на средний слой и там представляется естественными координатами в т-мерном единичном кубе  Дальнейшая передача информации по сети от среднего скрытого слоя к выходному дает обратное отображение: вектор в естественных координатах переходит в n-мерный вектор, расположенный близко к входному.
Дальнейшая передача информации по сети от среднего скрытого слоя к выходному дает обратное отображение: вектор в естественных координатах переходит в n-мерный вектор, расположенный близко к входному.
Один из подходов к обучению репликативной нейронной сети основан на том, что известно, каким должен быть выходной сигнал у нейронов среднего скрытого слоя - это должны быть естественные координаты. Таким образом, можно использовать такой метод обучения, благодаря которому нейроны среднего скрытого слоя более активно производят выходные сигналы, равномерно и плотно заполняющие внутреннюю часть  -мерного единичного куба, а также обладают свойствами естественных координат.
-мерного единичного куба, а также обладают свойствами естественных координат.
Удаление шума. Репликативная сеть способна удалять аддитивный шум, присутствующий в исходных данных. Предположим, что вектор данных состоит из двух слагаемых: информационной части вектора и шумового случайного компонента, выбираемого в каждой точке многообразия данных в соответствии с условной плотностью распределения.
Утверждается, что репликативная нейронная сеть приводит шумовой компонент к среднему значению, и результат, получаемый на выходе сети, является суммой информативной части вектора (входного вектора) и среднего значения шума в данной точке многообразия. Если среднее значение равно нулю, то выходной слой воспроизводит входной вектор, удаляя случайный шум.
Определение размерности. До сих пор полагалось, что размерность  заранее известна. Однако такое бывает достаточно редко. Тем не менее эту размерность можно оценить. Рассмотрим большое количество данных, произведенных генератором, и упорядочим их по возрастанию евклидова расстояния до некоторой
заранее известна. Однако такое бывает достаточно редко. Тем не менее эту размерность можно оценить. Рассмотрим большое количество данных, произведенных генератором, и упорядочим их по возрастанию евклидова расстояния до некоторой
фиксированной точки из этого же набора. Такое упорядочение данных позволяет оценить размерность многообразия вблизи фиксированной точки.
Возьмем первые к векторов из упорядоченного набора, рассмотрим гауссовый ковариационный эллипсоид и определим количество не слишком коротких его осей. Эту величину назовем локальной размерностью и нарисуем график ее зависимости от числа к. Обычно этот график линейно возрастает при увеличении к, но при некотором его значении наклон графика резко уменьшается, образуя «колено». Соответствующую величину к будем рассматривать как аппроксимацию размерности в окрестности выбранной точки. Повторяя описанную процедуру определения локальной размерности для других точек, находим оценку размерности многообразия данных  как наибольшее из значений локальной размерности. Найденное значение
как наибольшее из значений локальной размерности. Найденное значение  используется в качестве размерности системы естественных координат. Если оно меньше, чем реальная размерность многообразия данных, то полученные естественные координаты будут образовывать решетку, заполняющую все пространство. С другой стороны, если значение
используется в качестве размерности системы естественных координат. Если оно меньше, чем реальная размерность многообразия данных, то полученные естественные координаты будут образовывать решетку, заполняющую все пространство. С другой стороны, если значение  больше, чем реальная размерность, то координатные объемы в естественной системе координат будут «сплюснуты» в такие множества, у которых, по крайней мере, один характерный размер много меньше других. Таким образом, чтобы определить правильное значение размерности, нужно найти компромисс между полнотой заполнения пространства (когда величина размерности выбирается слишком малой) и сильной деформацией координатной решетки в естественных координатах (когда величина размерности выбрана слишком большой).
больше, чем реальная размерность, то координатные объемы в естественной системе координат будут «сплюснуты» в такие множества, у которых, по крайней мере, один характерный размер много меньше других. Таким образом, чтобы определить правильное значение размерности, нужно найти компромисс между полнотой заполнения пространства (когда величина размерности выбирается слишком малой) и сильной деформацией координатной решетки в естественных координатах (когда величина размерности выбрана слишком большой).
Знание размерности многообразия данных и выбор правильного значения  может помочь избежать неэффективного использования системы естественных координат. Аналогичное замечание справедливо и для «испорченных» шумом векторов для выбора нужного число нейронов в среднем скрытом слое, после чего сеть может быть натренирована для очистки шума.
может помочь избежать неэффективного использования системы естественных координат. Аналогичное замечание справедливо и для «испорченных» шумом векторов для выбора нужного число нейронов в среднем скрытом слое, после чего сеть может быть натренирована для очистки шума.
Использование репликативных нейронных сетей. Решающим фактором в вопросе практического применения репликативных сетей является то, что большинство генераторов данных сильно структурированы и могут быть смоделированы посредством многообразия данных с относительно малой размерностью  . Такой подход заметно упрощает решение многих задач распознавания образов, управления, сжатия информации, поскольку вместо исходных векторов с большим числом признаков, могут использоваться естественные координаты с малым числом компонентов.
. Такой подход заметно упрощает решение многих задач распознавания образов, управления, сжатия информации, поскольку вместо исходных векторов с большим числом признаков, могут использоваться естественные координаты с малым числом компонентов.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
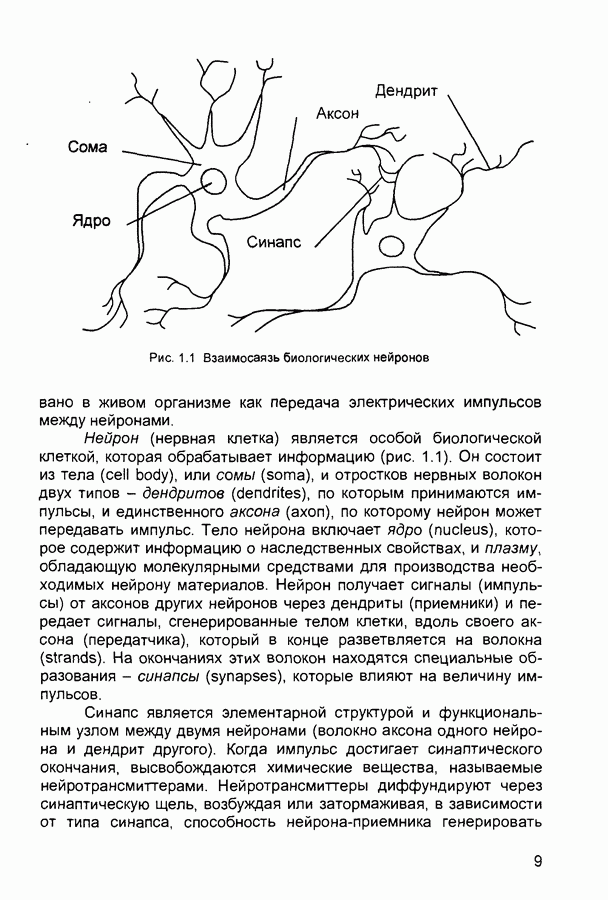
- 1.1. Биологический нейрон
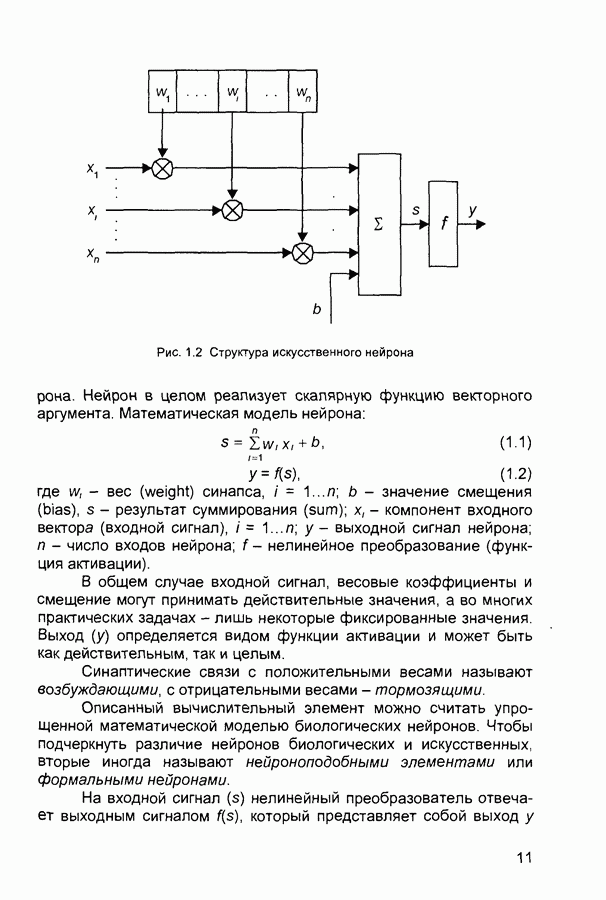
- 1.2. Структура и свойства искусственного нейрона
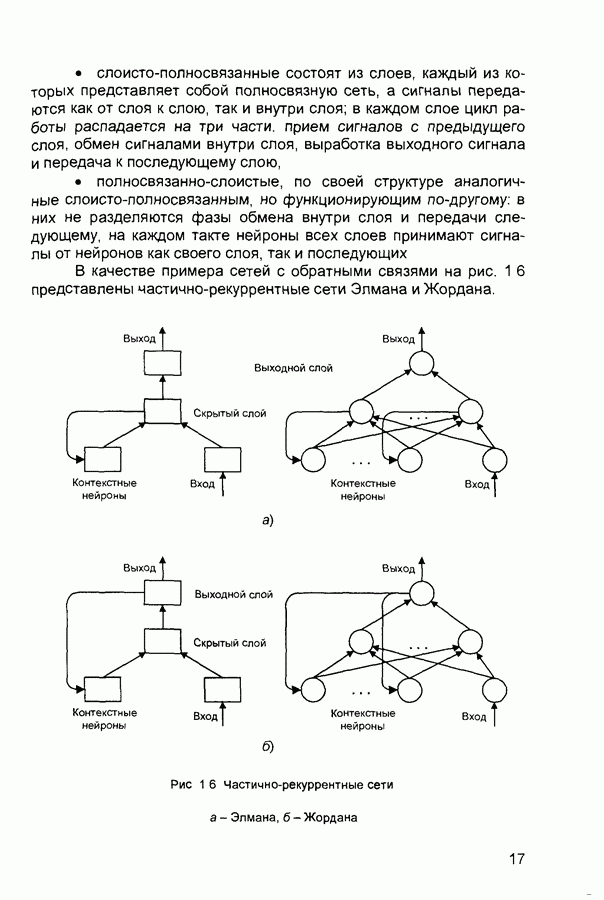
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
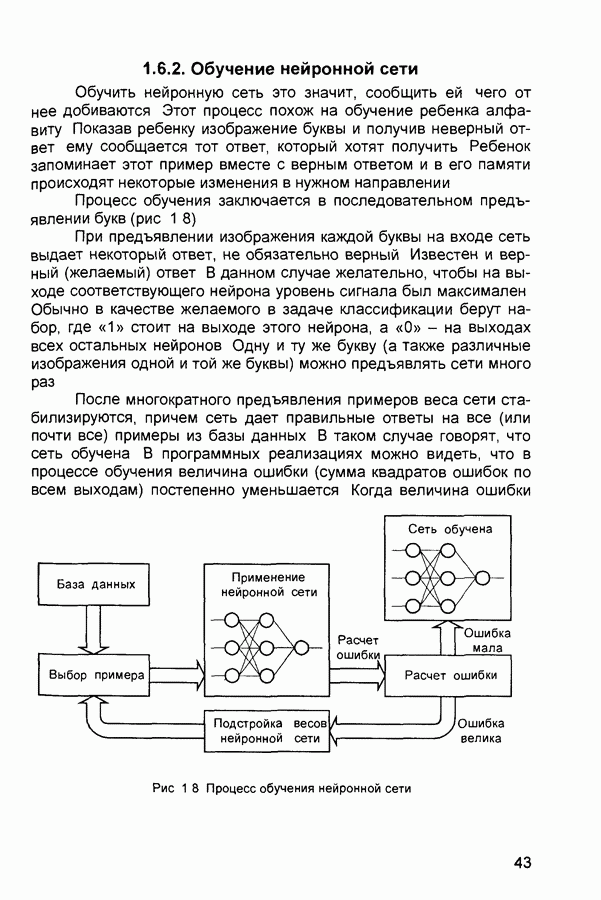
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
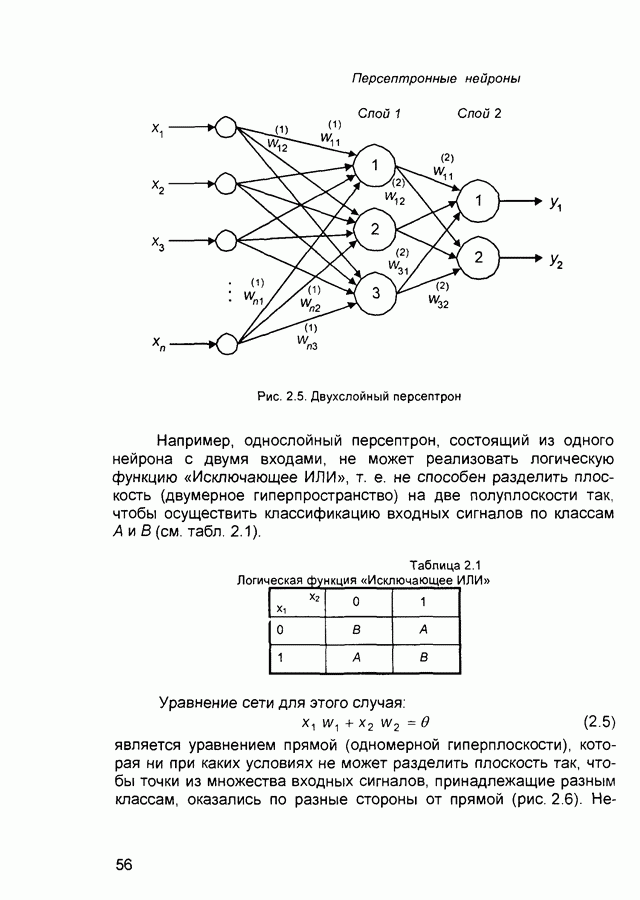
- 2.2. Персептроны
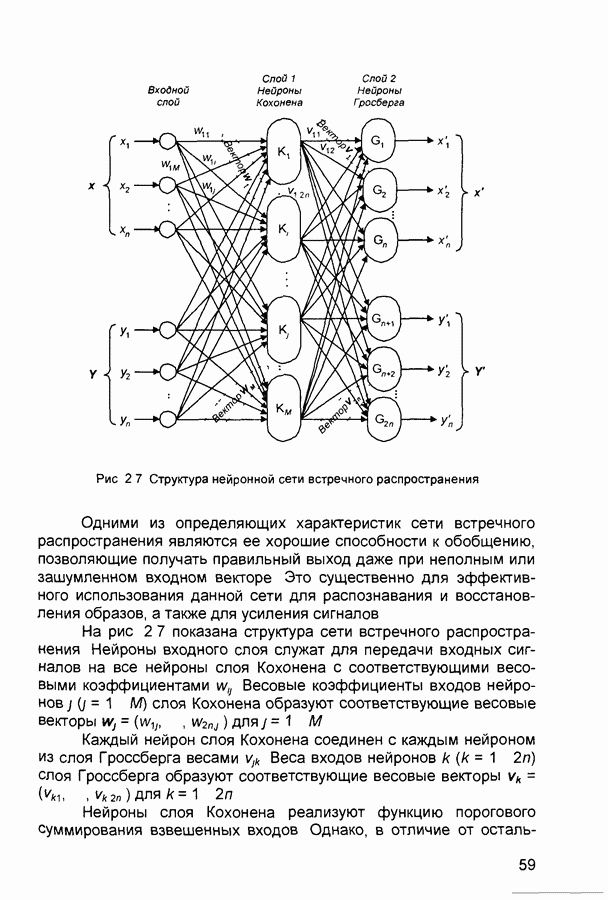
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
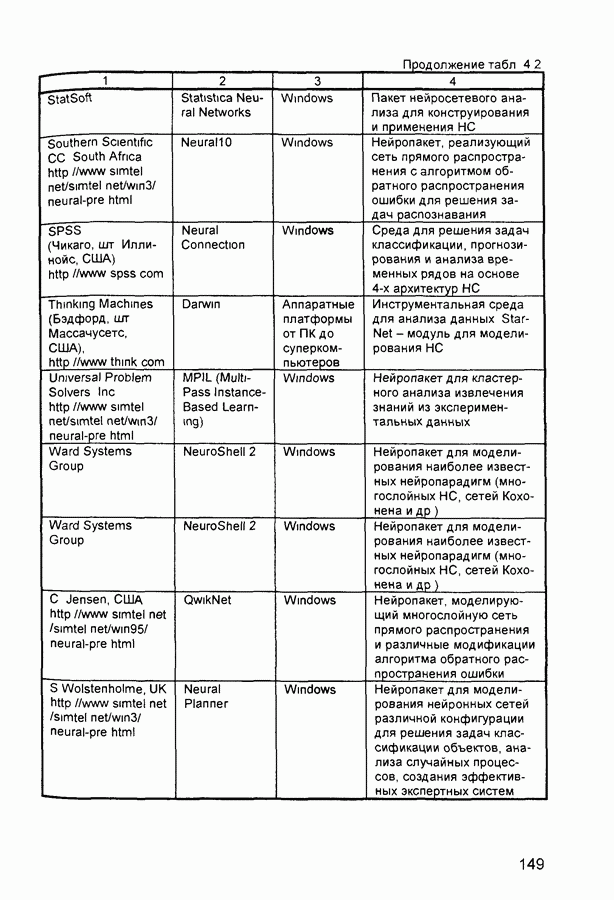
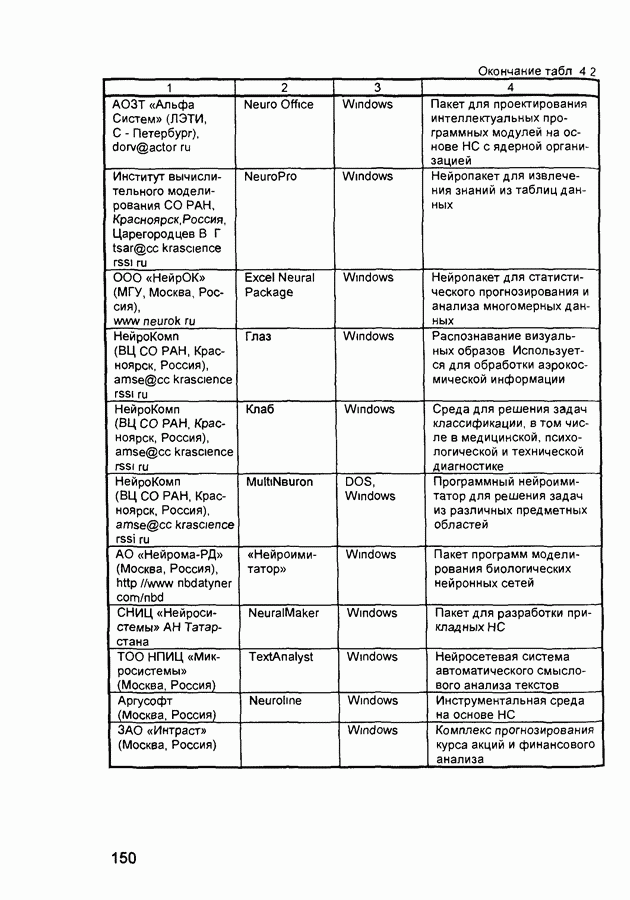
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
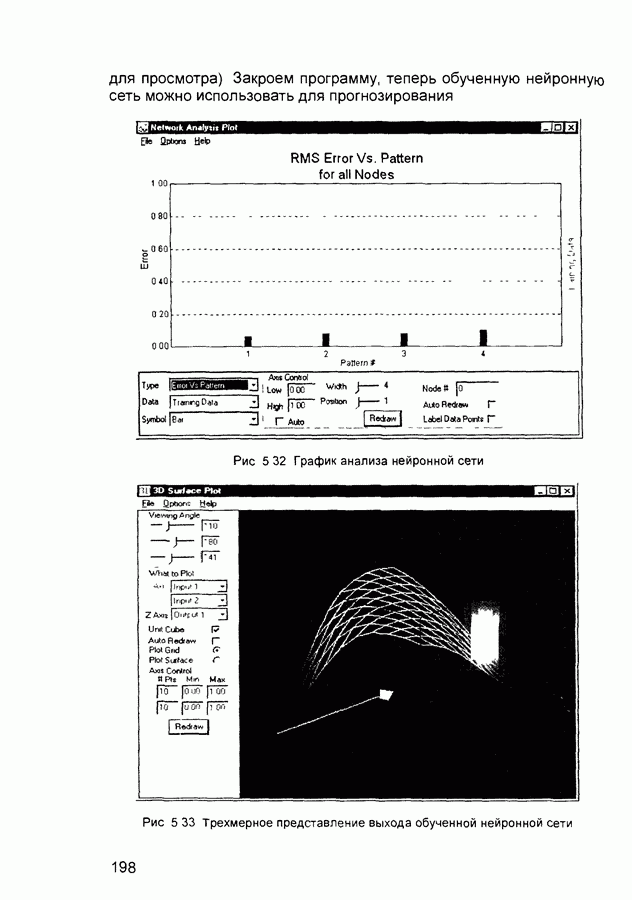
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
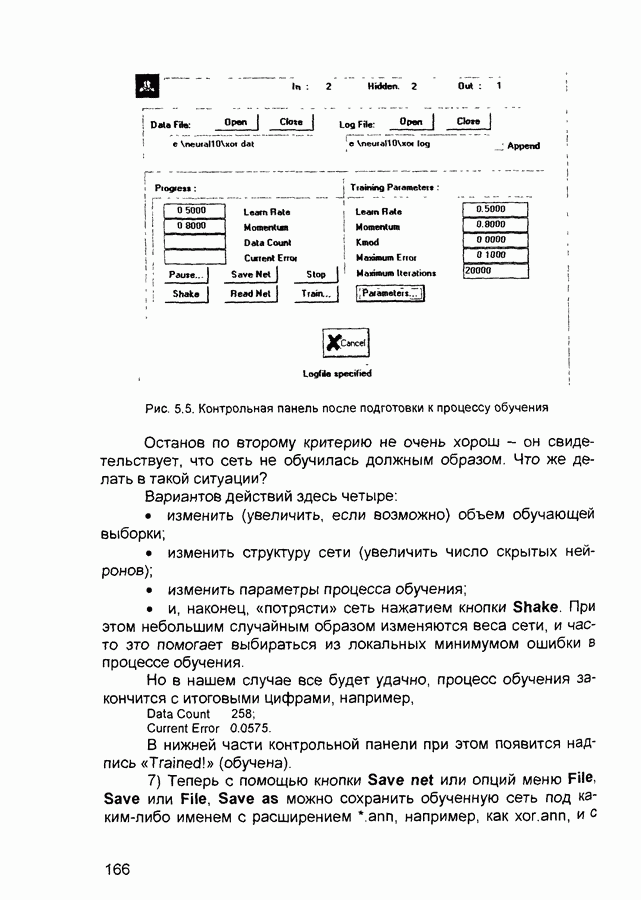
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
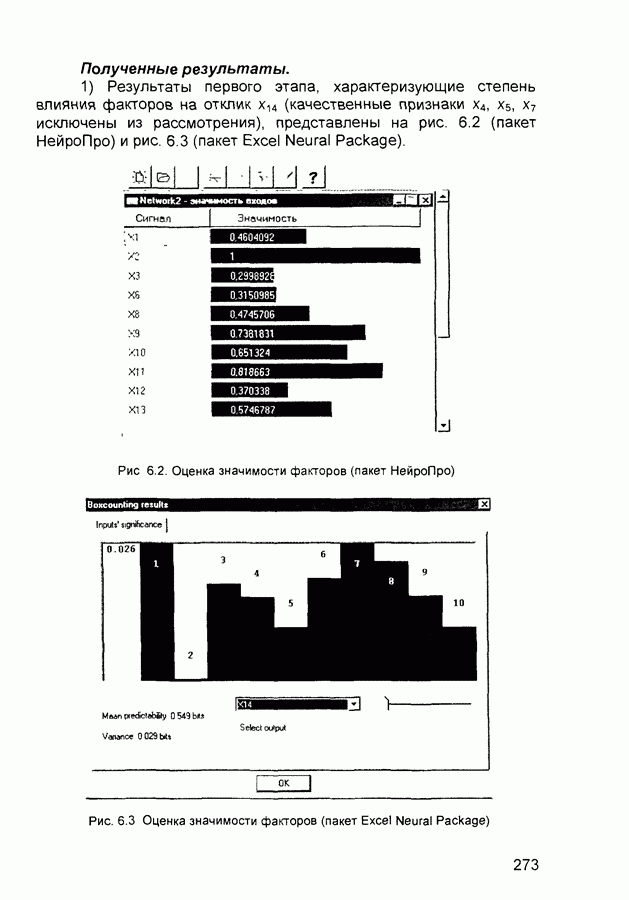
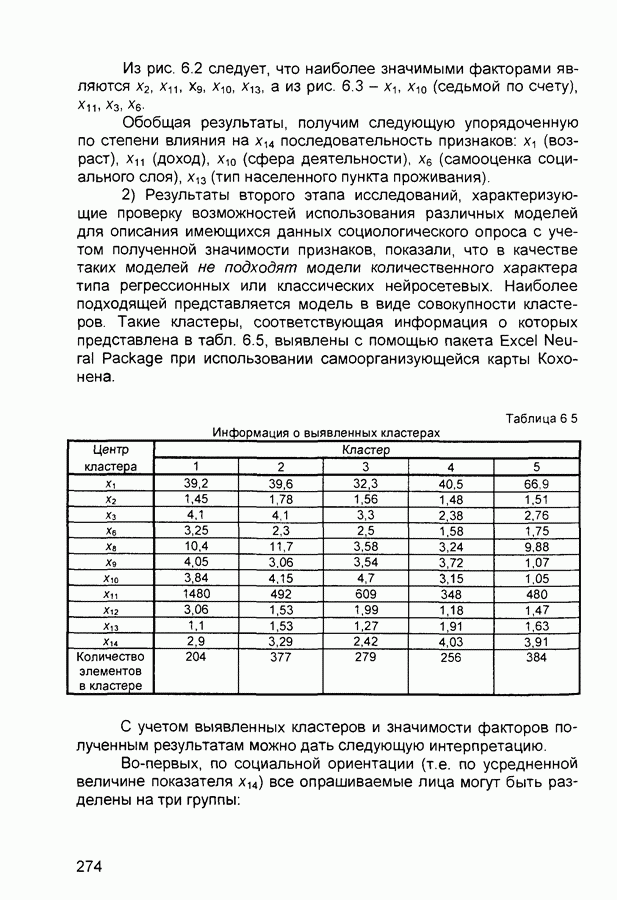
- 6.2. Анализ данных социологического опроса
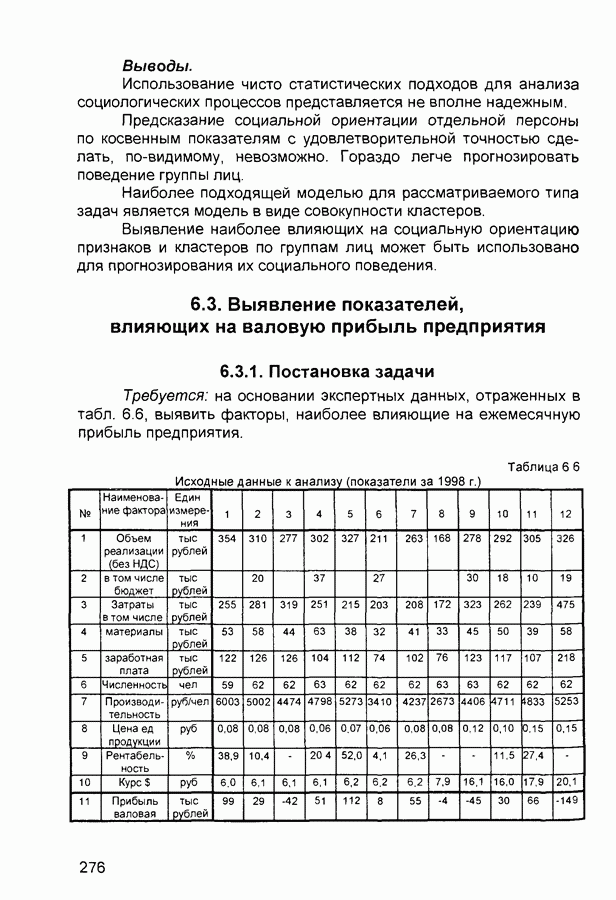
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
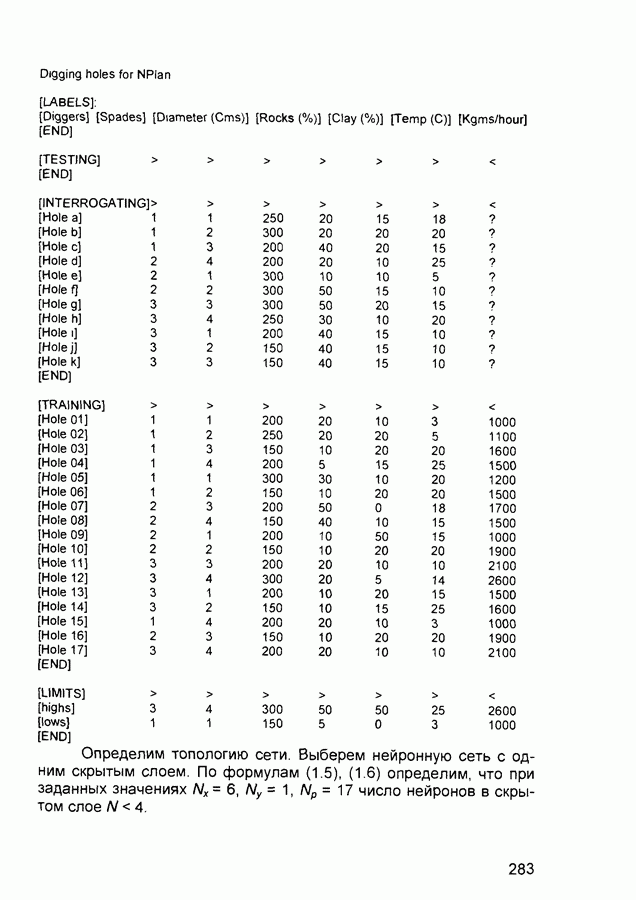
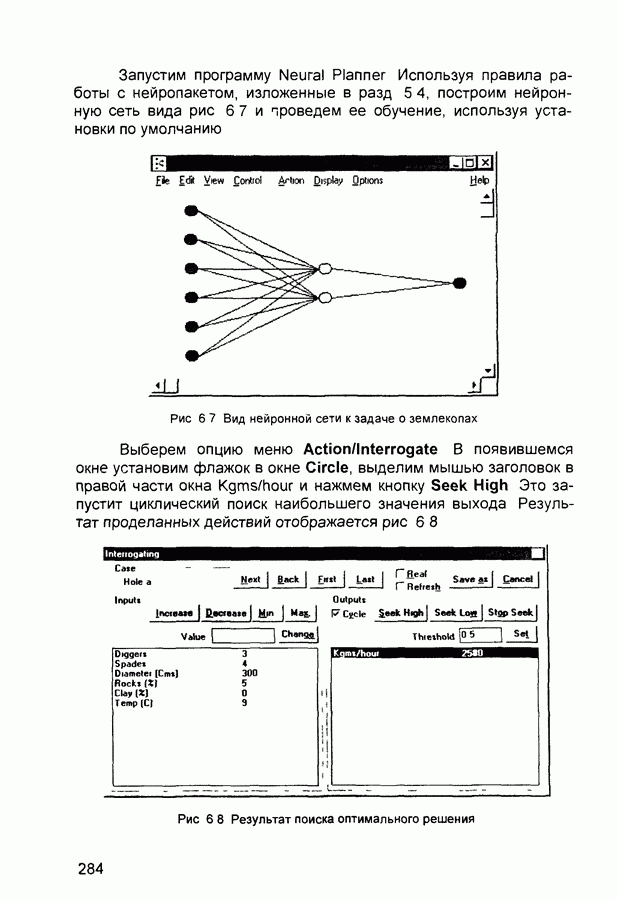
- 6.5. Задача о землекопах
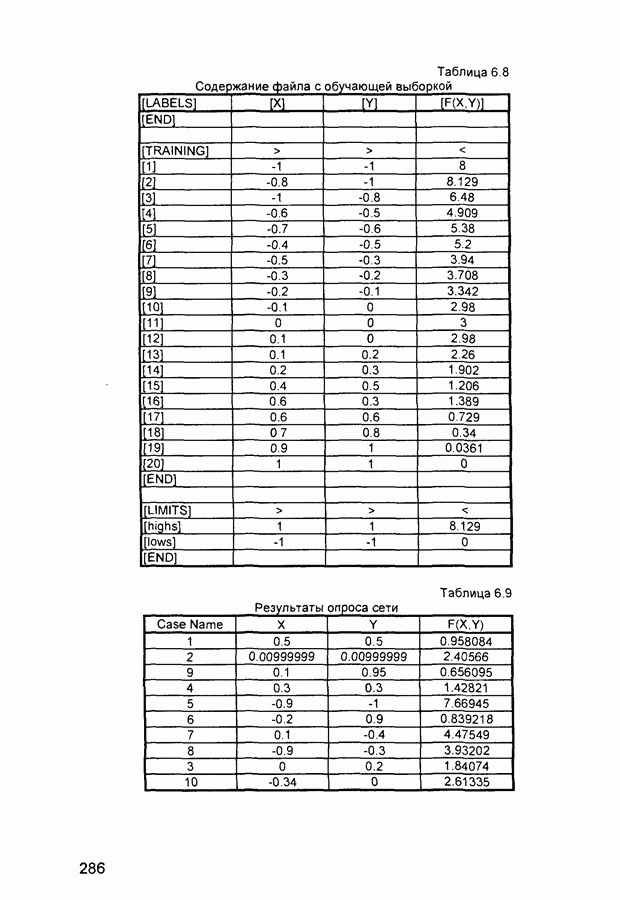
- 6.6. Аппроксимация функции
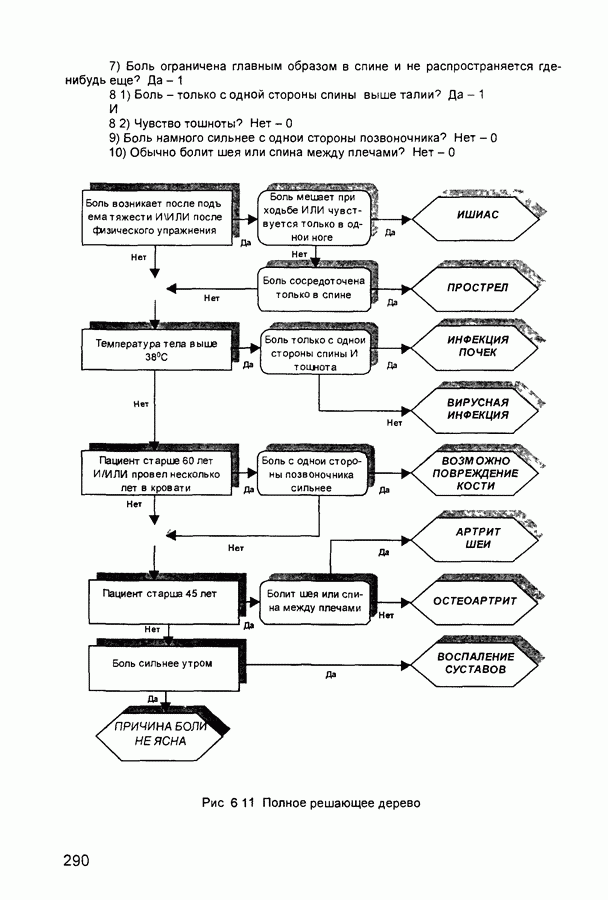
- 6.7. Нейросетевая экспертная система
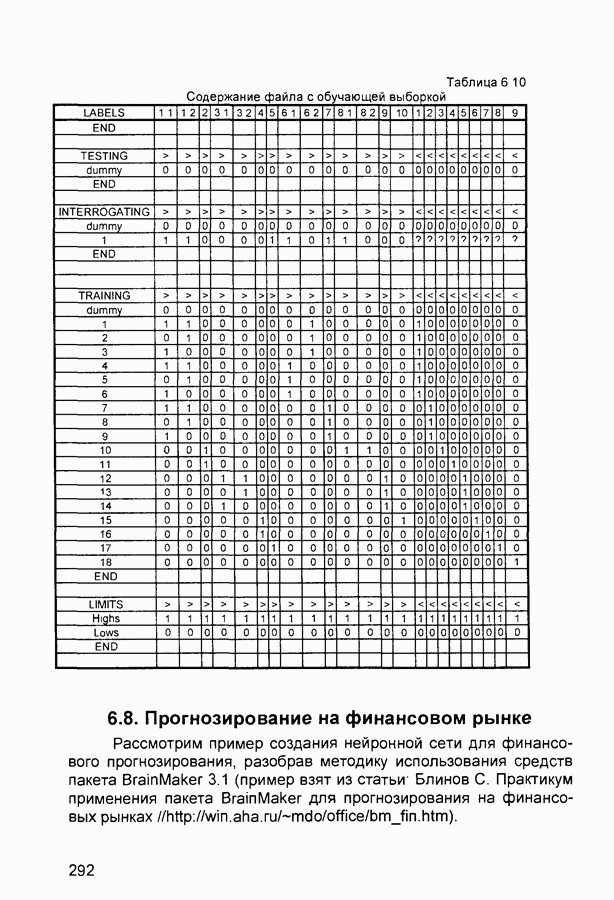
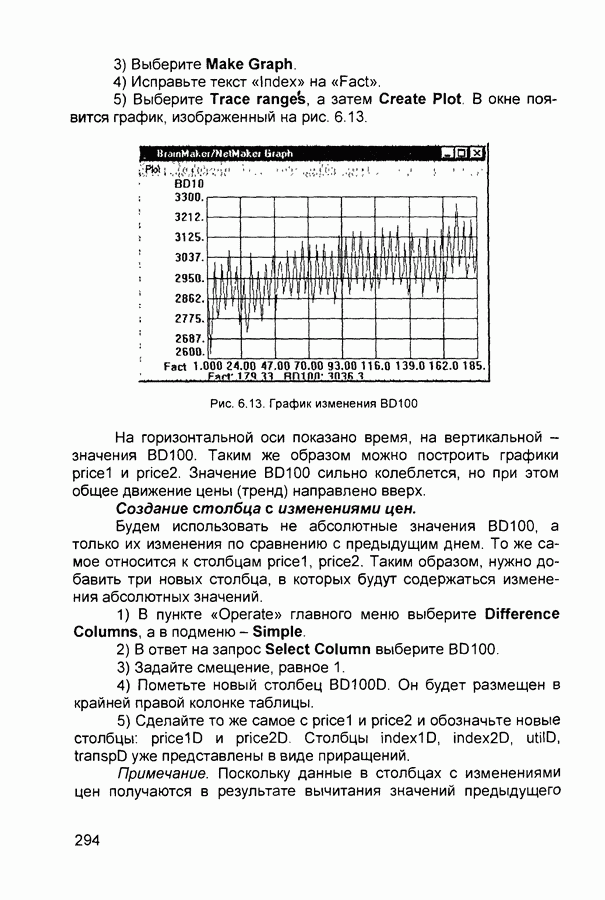
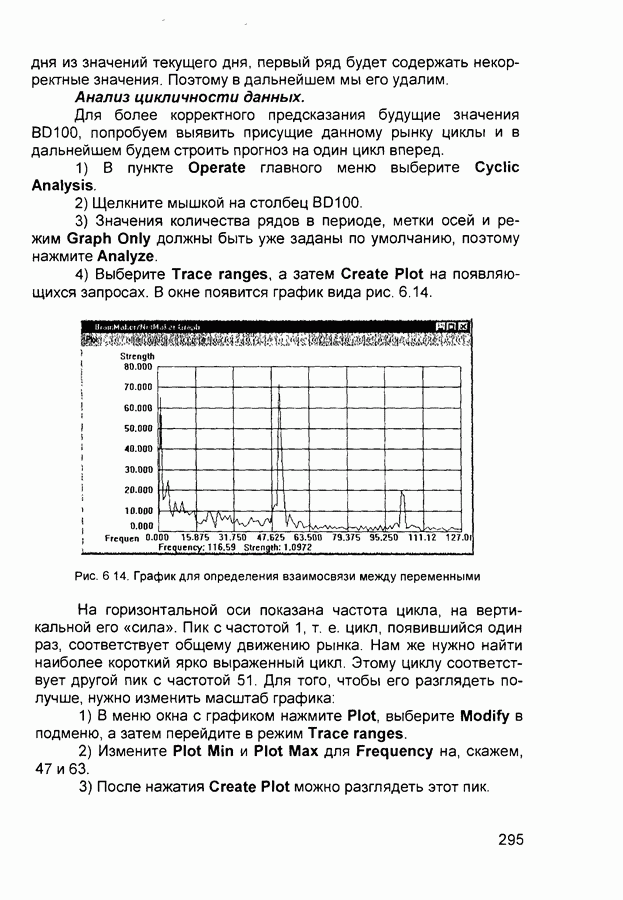
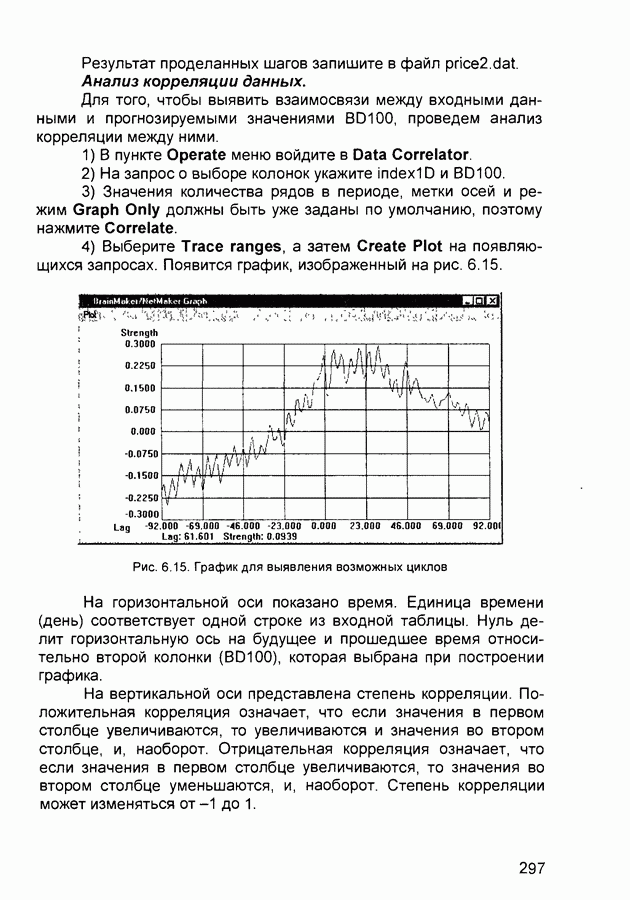
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы