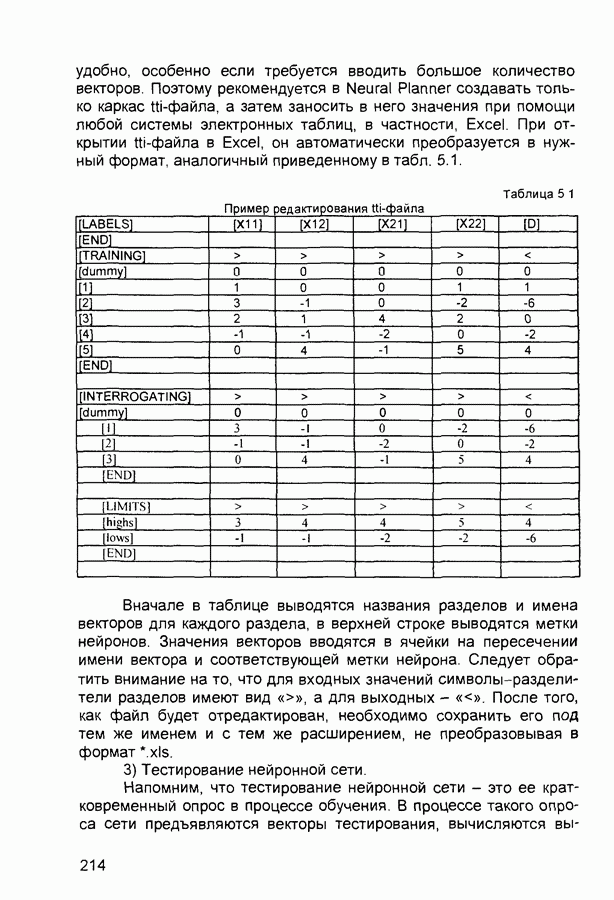
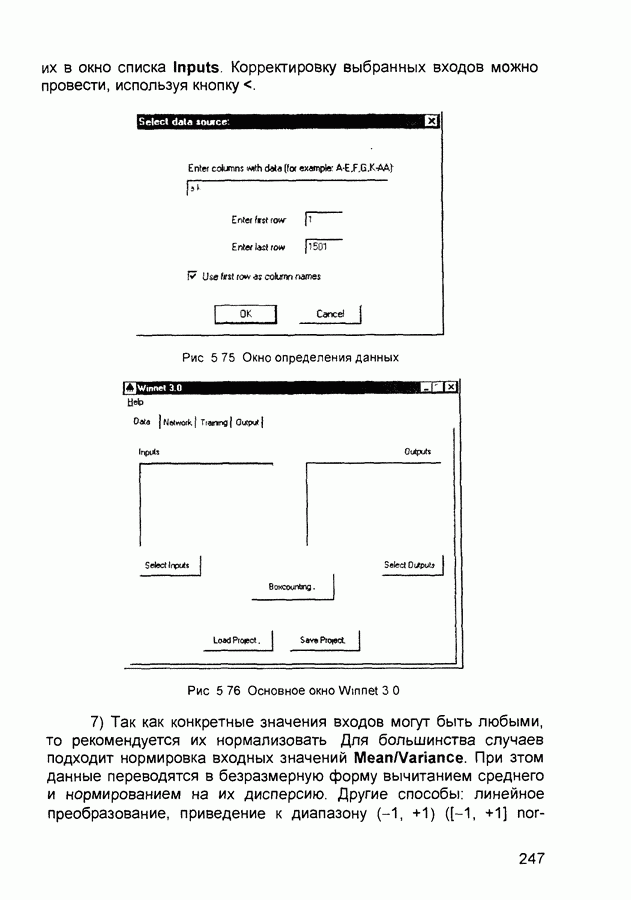
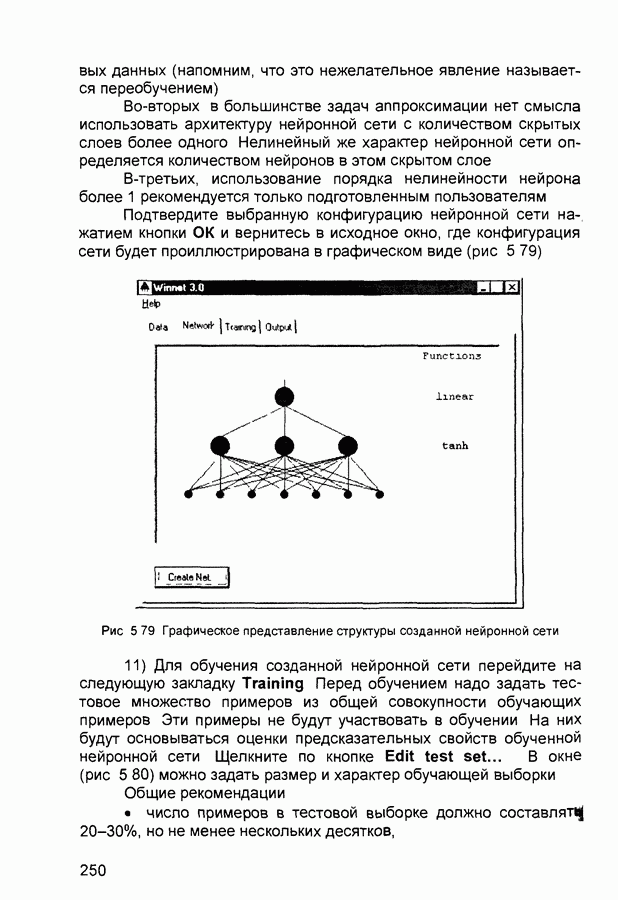
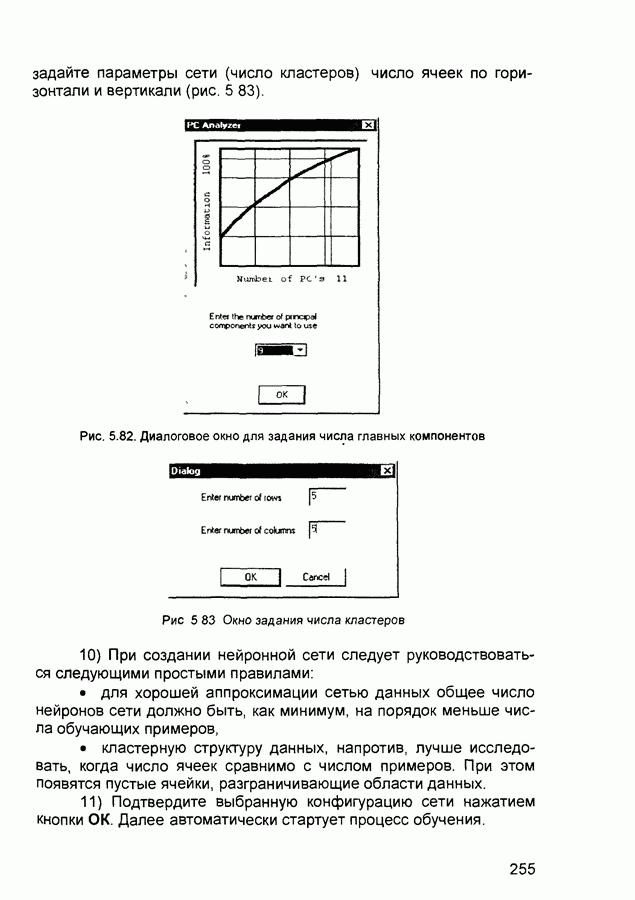
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
Очевидно, что процесс функционирования нейронной сети, сущность действий, которые она способна выполнять, зависит от величин синаптических связей. Поэтому, задавшись определенной структурой сети, соответствующей какой-либо задаче, необходимо найти оптимальные значения всех переменных весовых коэффициентов (некоторые синаптические связи могут быть постоянными).
Этот этап называется обучением нейронной сети, и от того, насколько качественно он будет выполнен, зависит способность сети решать поставленные перед ней проблемы во время функционирования.
В процессе функционирования нейронная сеть формирует выходной сигнал У в соответствии с входным сигналом X, реализуя некоторую функцию  Если архитектура сети задана,
Если архитектура сети задана,
то вид функции  определяется значениями синаптических весов и смещений сети. Обозначим через
определяется значениями синаптических весов и смещений сети. Обозначим через  множество всех возможных функций
множество всех возможных функций  соответствующих заданной архитектуре сети.
соответствующих заданной архитектуре сети.
Пусть решение некоторой задачи есть функция  заданная парами входных-выходных данных
заданная парами входных-выходных данных  , для которых
, для которых  - функция ошибки (функционал качества), показывающая для каждой из функций
- функция ошибки (функционал качества), показывающая для каждой из функций  степень близости к
степень близости к 
Решить поставленную задачу с помощью нейронной сети заданной архитектуры - это значит построить (синтезировать) функцию  подобрав параметры нейронов (синаптические веса и смещения) таким образом, чтобы функционал качества обращался в оптимум для всех пар (X, У.
подобрав параметры нейронов (синаптические веса и смещения) таким образом, чтобы функционал качества обращался в оптимум для всех пар (X, У.
Таким образом, задача обучения нейронной сети определяется совокупностью пяти компонентов:

Обучение состоит в поиске (синтезе) функции  , оптимальной по Е. Оно требует длительных вычислений и представляет собой итерационную процедуру. Число итераций может составлять от 103 до 108. На каждой итерации происходит уменьшение функции ошибки.
, оптимальной по Е. Оно требует длительных вычислений и представляет собой итерационную процедуру. Число итераций может составлять от 103 до 108. На каждой итерации происходит уменьшение функции ошибки.
Функция Е может иметь произвольный вид. Если выбраны множество обучающих примеров и способ вычисления функции ошибки, обучение нейронной сети превращается в задачу многомерной оптимизации, для решения которой могут быть использованы следующие методы:
• локальной оптимизации с вычислением частных производных первого порядка;
• локальной оптимизации с вычислением частных производных первого и второго порядка;
• стохастической оптимизации;
• глобальной оптимизации.
К первой группе относятся: градиентный метод (наискорейшего спуска); методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента; метод сопряженных градиентов; методы, учитывающие направление антиградиента на нескольких шагах алгоритма.
Ко второй группе относятся метод Ньютона, методы оптимизации с разреженными матрицами Гессе, квазиньютоновские методы, метод Гаусса-Ньютона, метод Левенберга-Маркардта.
Стохастическими методами являются: поиск в случайном направлении, имитация отжига, метод Монте-Карло (численный метод статистических испытаний).
Задачи глобальной оптимизации решаются с помощью перебора значений переменных, от которых зависит целевая функция.
Для сравнения методов обучения нейронных сетей необходимо использовать два критерия:
• количество шагов алгоритма для получения решения;
• количество дополнительных переменных для организации вычислительного процесса.
Для иллюстрации термина «дополнительные переменные» приведем следующий пример. Пусть  - некоторые параметры нейронной сети с заданными значениями. В процессе обучения сети на каждом шаге, по меньшей мере, два раза потребуется выполнить умножение
- некоторые параметры нейронной сети с заданными значениями. В процессе обучения сети на каждом шаге, по меньшей мере, два раза потребуется выполнить умножение  Дополнительная переменная требуется для сохранения значение произведения после первого умножения.
Дополнительная переменная требуется для сохранения значение произведения после первого умножения.
Предпочтение следует отдавать тем методам, которые позволяют обучить нейронную сеть за небольшое число шагов и требуют малого числа дополнительных переменных. Это связано с ограничением ресурсов вычислительных средств. Как правило, для обучения используются персональные компьютеры.
Пусть нейронная сеть содержит Р изменяемых параметров (синаптических весов и смещений). Существует лишь две группы алгоритмов обучения, которые требуют менее  дополнительных параметров и при этом дают возможность обучать нейронные сети за приемлемое число шагов. Это алгоритмы с вычислением частных производных первого порядка и, возможно, одномерной оптимизации. Именно эти алгоритмы и будут рассмотрены в следующих разделах.
дополнительных параметров и при этом дают возможность обучать нейронные сети за приемлемое число шагов. Это алгоритмы с вычислением частных производных первого порядка и, возможно, одномерной оптимизации. Именно эти алгоритмы и будут рассмотрены в следующих разделах.
Хотя указанные алгоритмы дают возможность находить только локальные экстремумы, они могут быть использованы на практике для обучения нейронных сетей с многоэкстремальными целевыми функциями (функциями ошибки), так как экстремумов у целевой функции, как правило, не очень много. Достаточно лишь раз или два вывести сеть из локального минимума с большим значением целевой функции для того, чтобы в результате итераций в соответствии с алгоритмом локальной оптимизации сеть оказалась в локальном минимуме со значением целевой функции, близким к нулю Если после нескольких попыток вывести сеть из локального минимума нужного эффекта добиться не удается, необходимо увеличить число нейронов во всех слоях с первого по
предпоследний и присвоить случайным образом их синаптическим весам и смещениям значения из заданного диапазона
Эксперименты по обучению нейронных сетей показали, что совместное использование алгоритма локальной оптимизации процедуры вывода сети из локального минимума и процедуры увеличения числа нейронов приводит к успешному обучению нейронных сетей
Кратко опишем недостатки других методов Стохастические алгоритмы требуют очень большого числа шагов обучения Это делает невозможным их практическое использование для обучения нейронных сетей больших размерностей Экспоненциальный рост сложности перебора с ростом размерности задачи в алгоритмах глобальной оптимизации при отсутствии априорной информации о характере целевой функции также делает невозможным их использование для обучения нейронных сетей больших размерностей Метод сопряженных градиентов очень чувствителен к точности вычислений, особенно при решении задач оптимизации большой размерности Для методов, учитывающих направление антиградиента на нескольких шагах алгоритма, и методов, включающих вычисление матрицы Гессе, необходимо более чем  дополнительных переменных В зависимости от способа разрежения, вычисление матрицы Гессе требует от
дополнительных переменных В зависимости от способа разрежения, вычисление матрицы Гессе требует от  до
до  дополнительных переменных
дополнительных переменных
Рассмотрим один из самых распространенных алгоритмов обучения - алгоритм обратного распространения ошибки
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
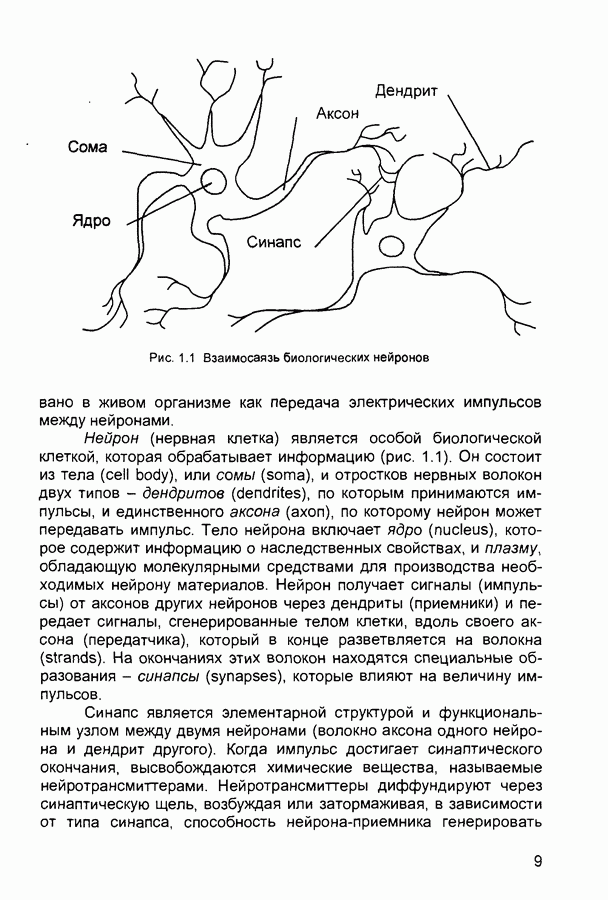
- 1.1. Биологический нейрон
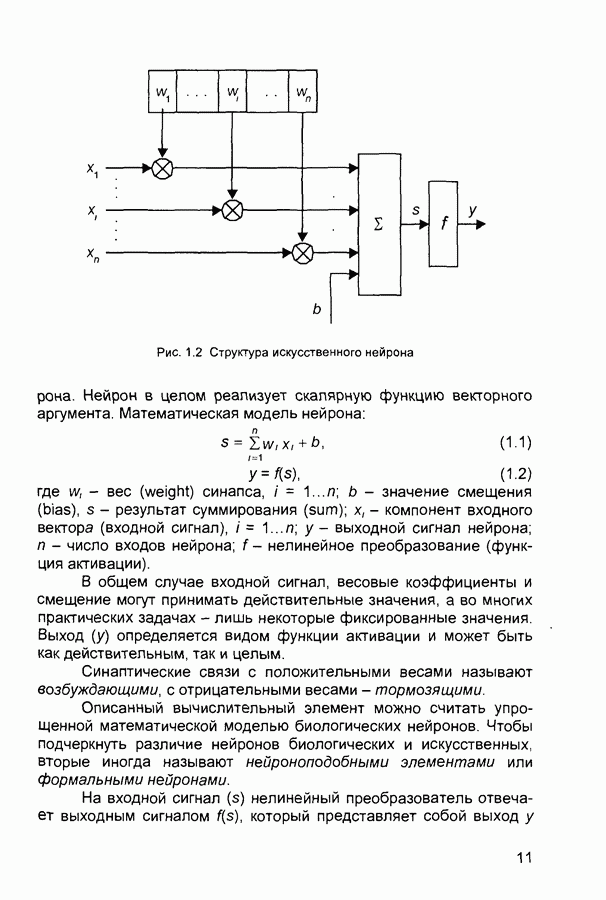
- 1.2. Структура и свойства искусственного нейрона
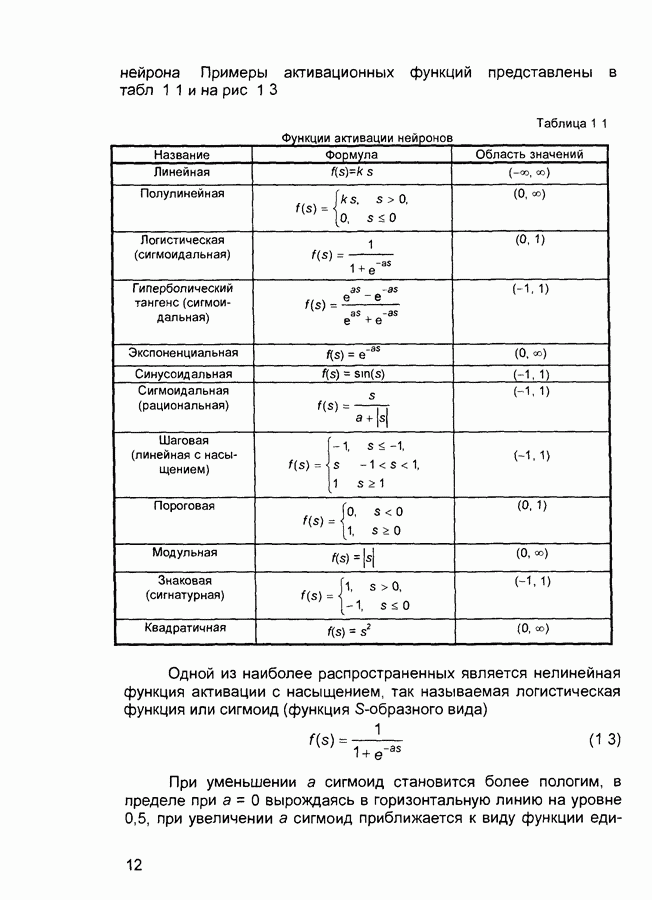
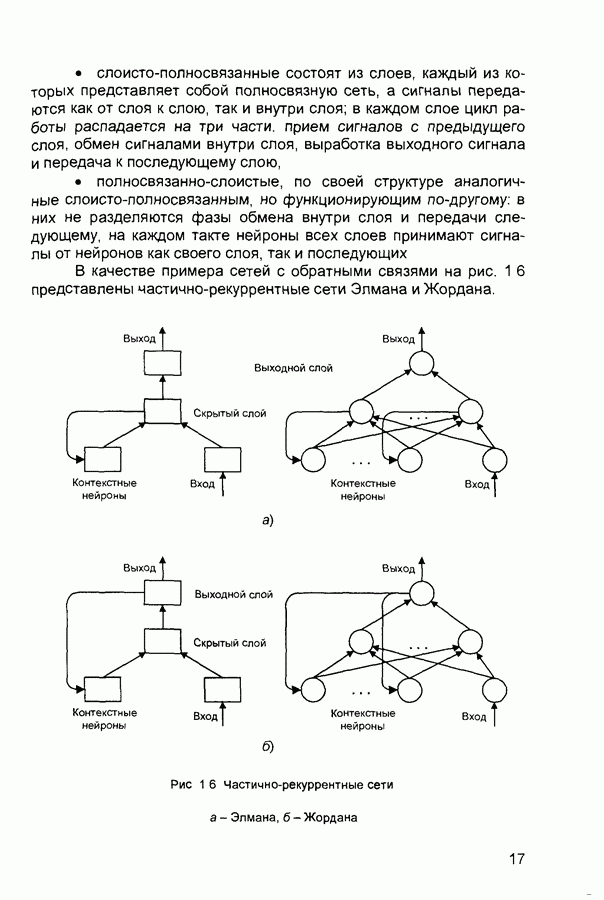
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
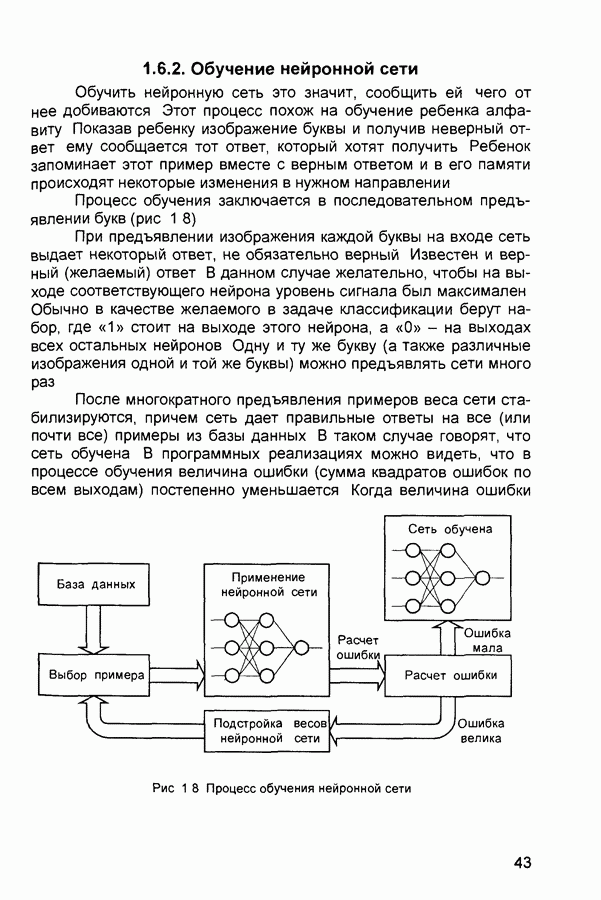
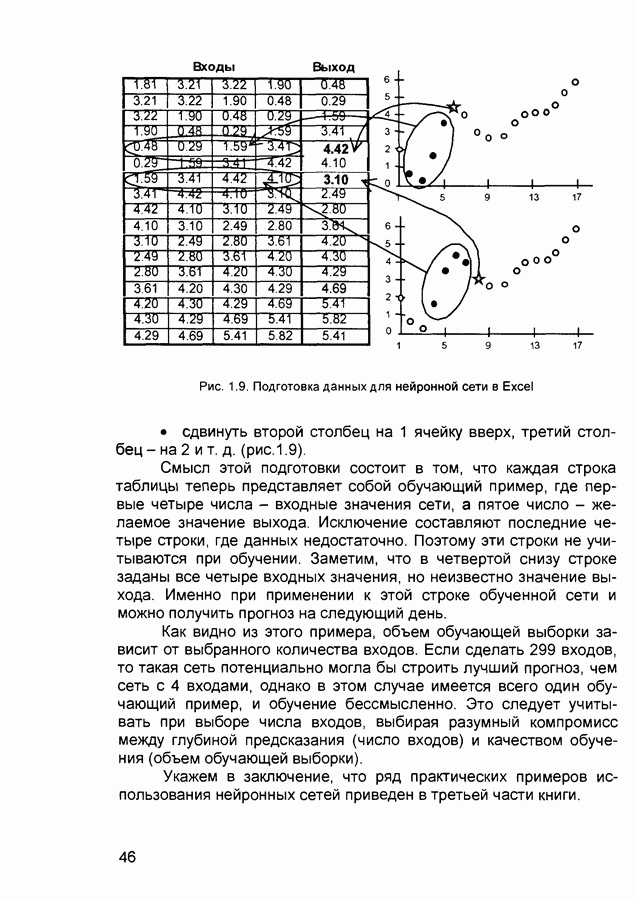
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
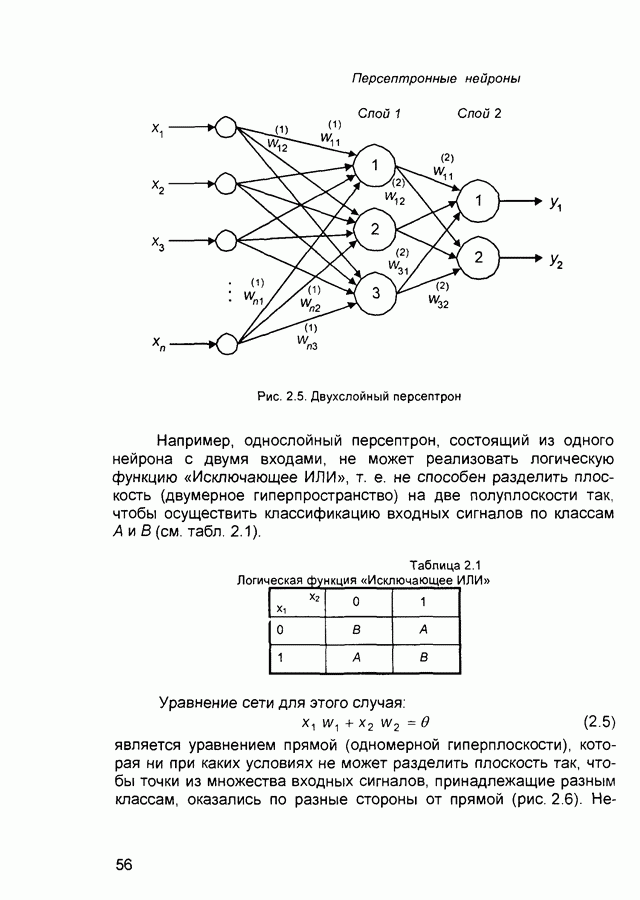
- 2.2. Персептроны
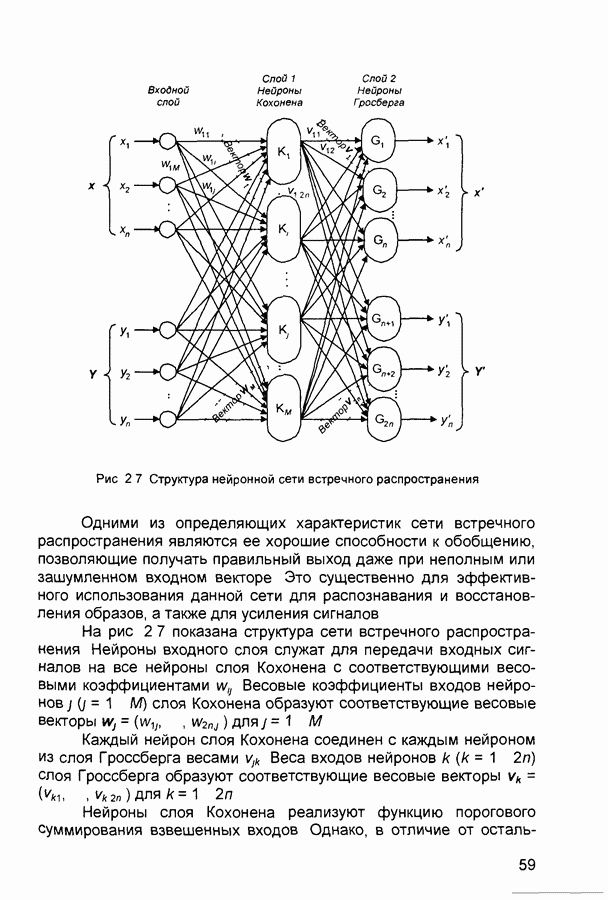
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
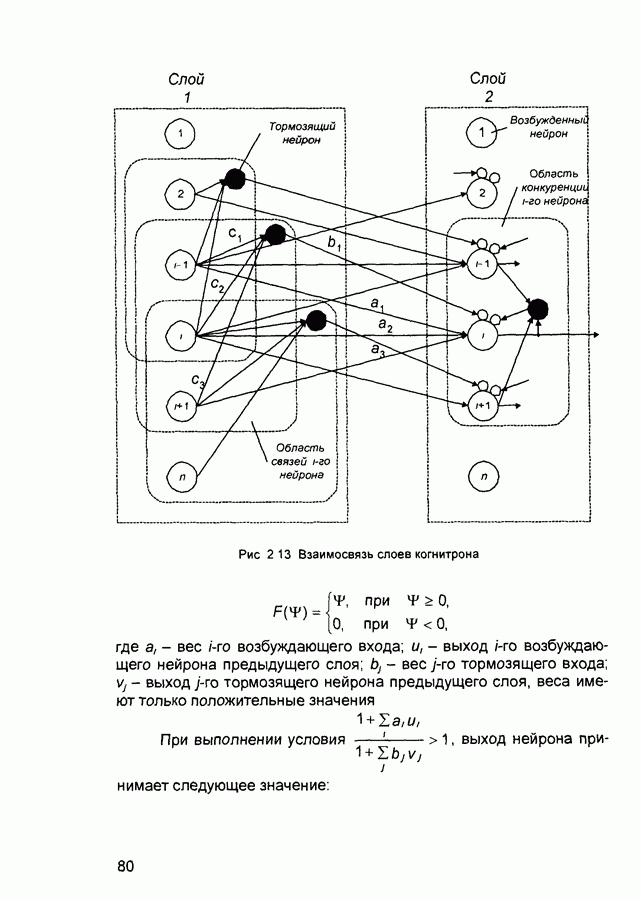
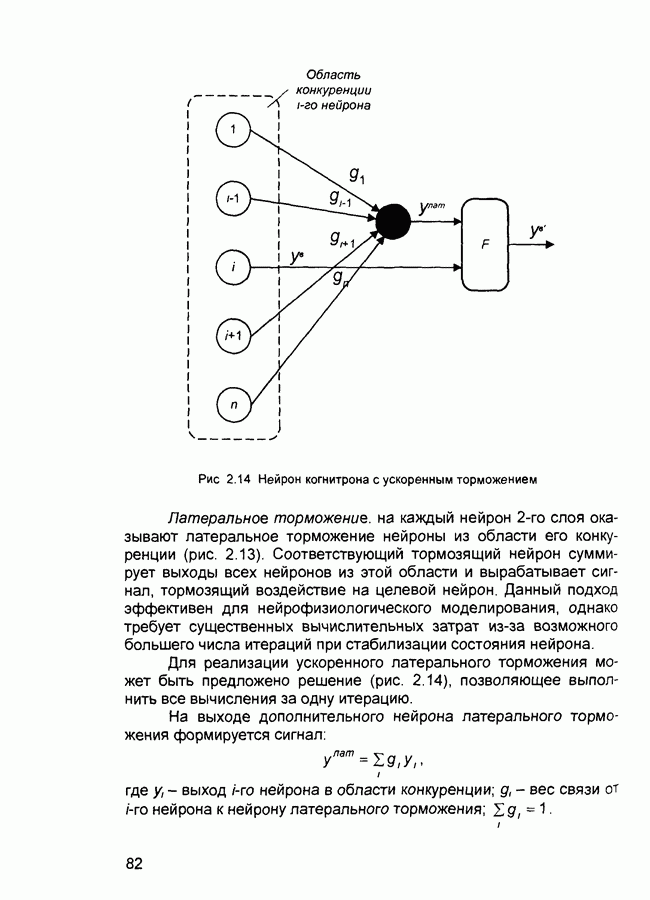
- 2.7. Когнитрон
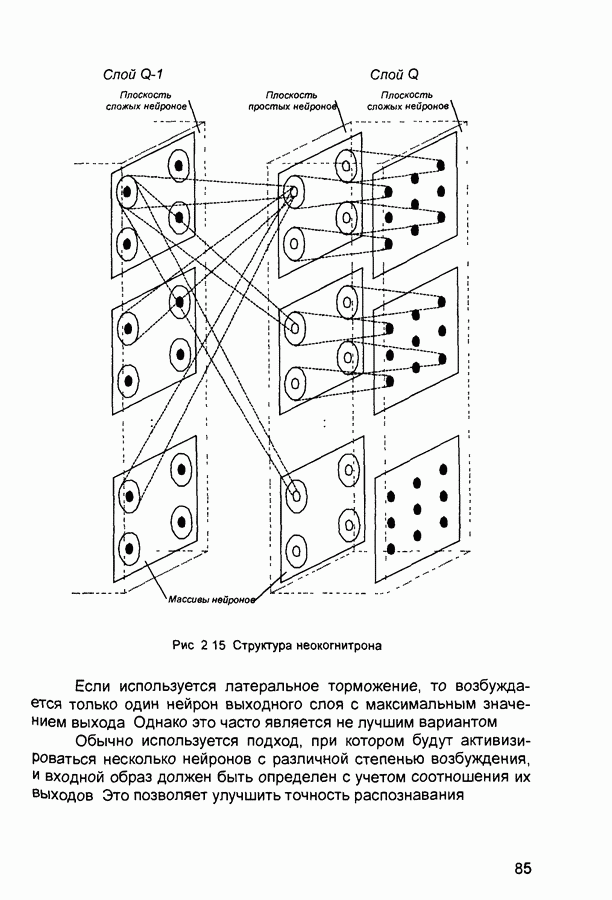
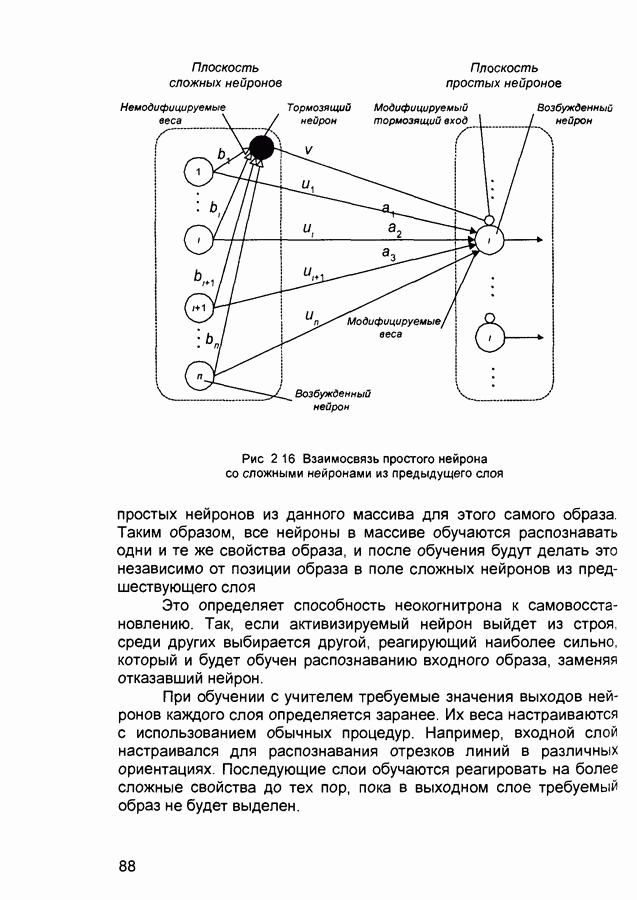
- 2.8. Неокогнитрон
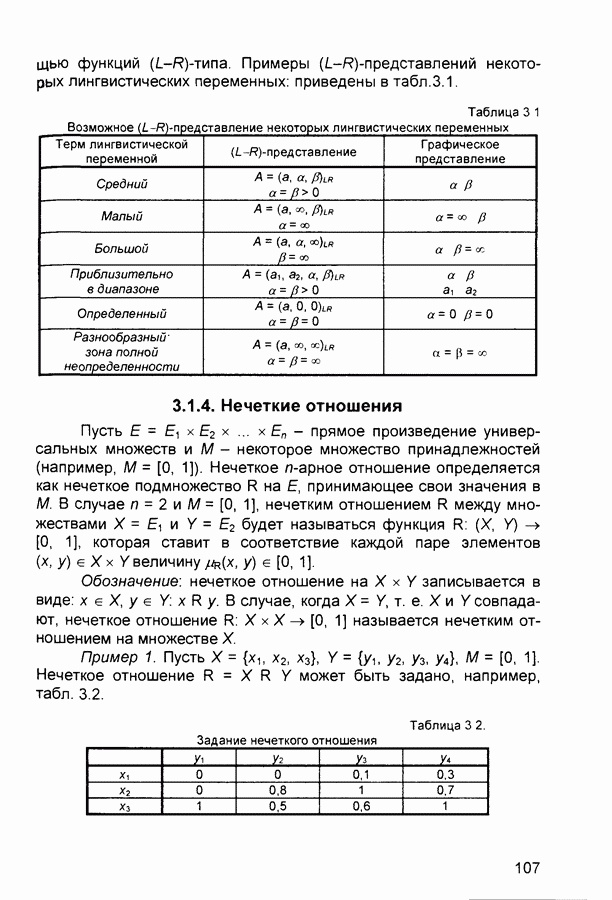
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
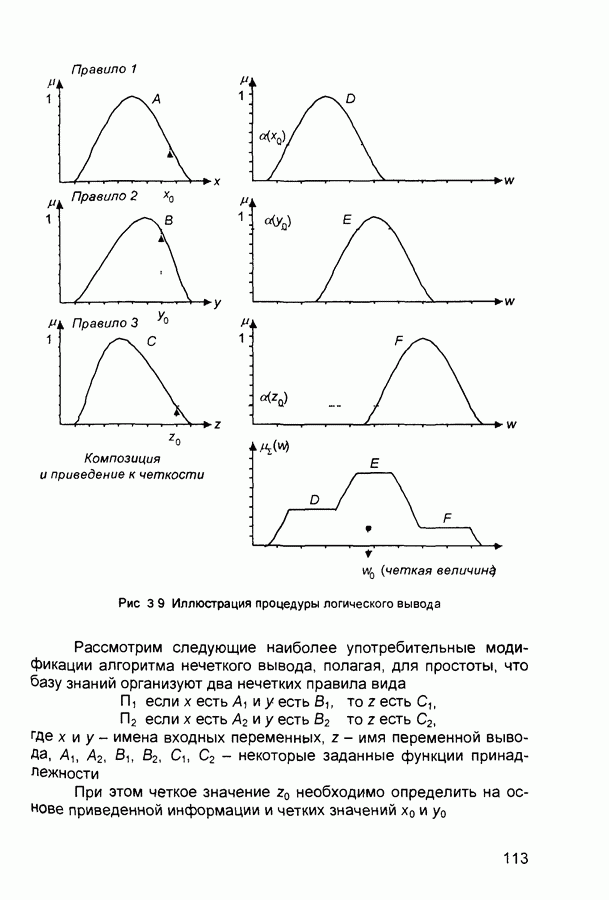
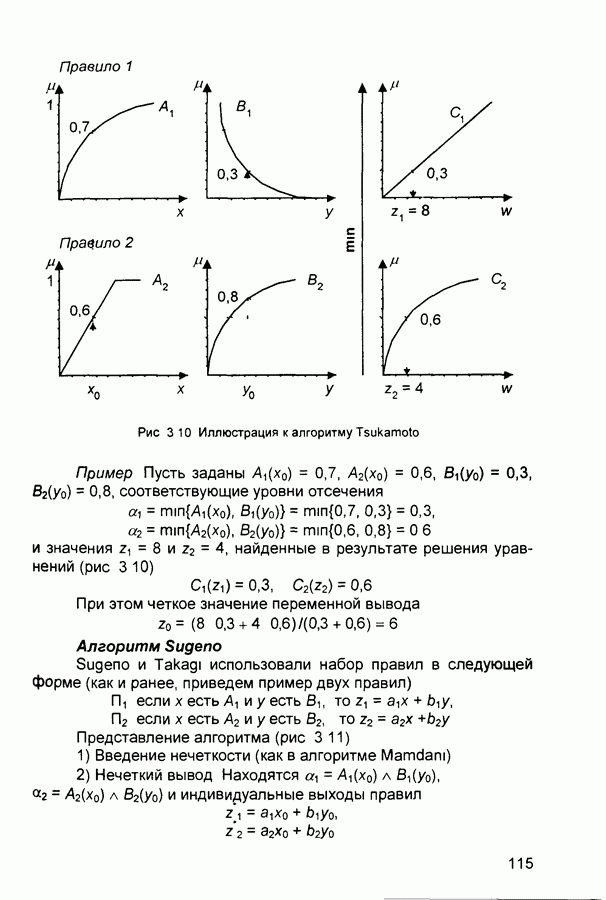
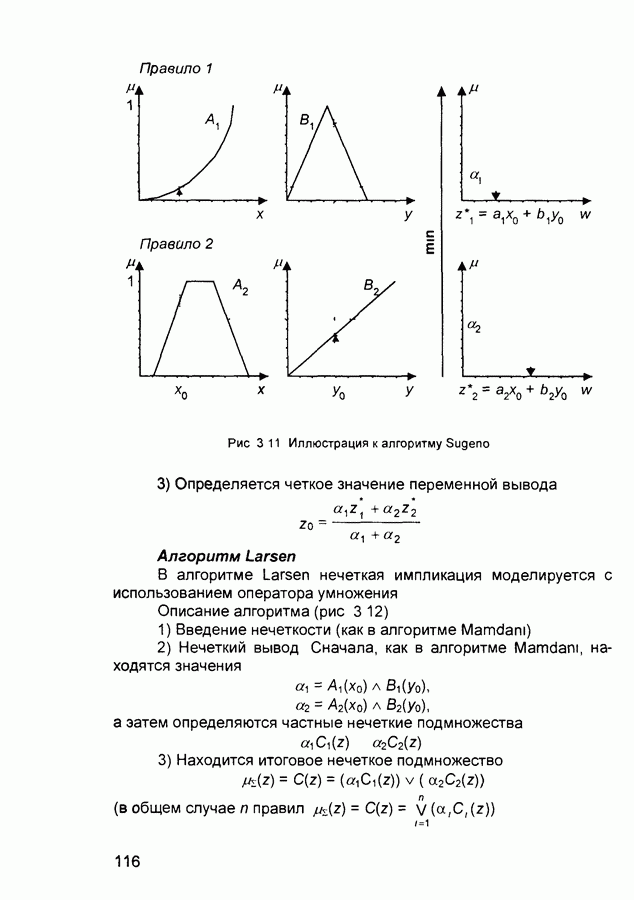
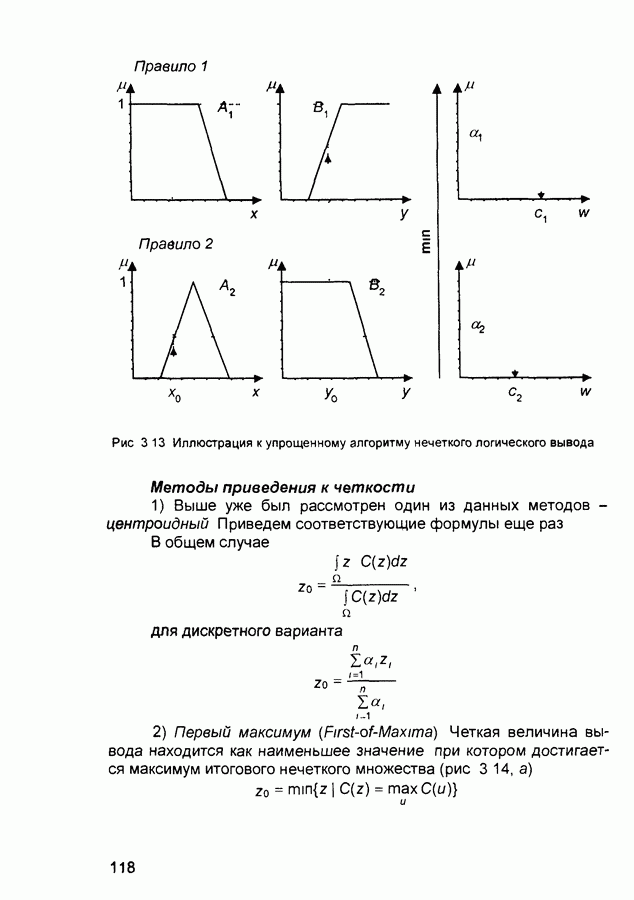
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
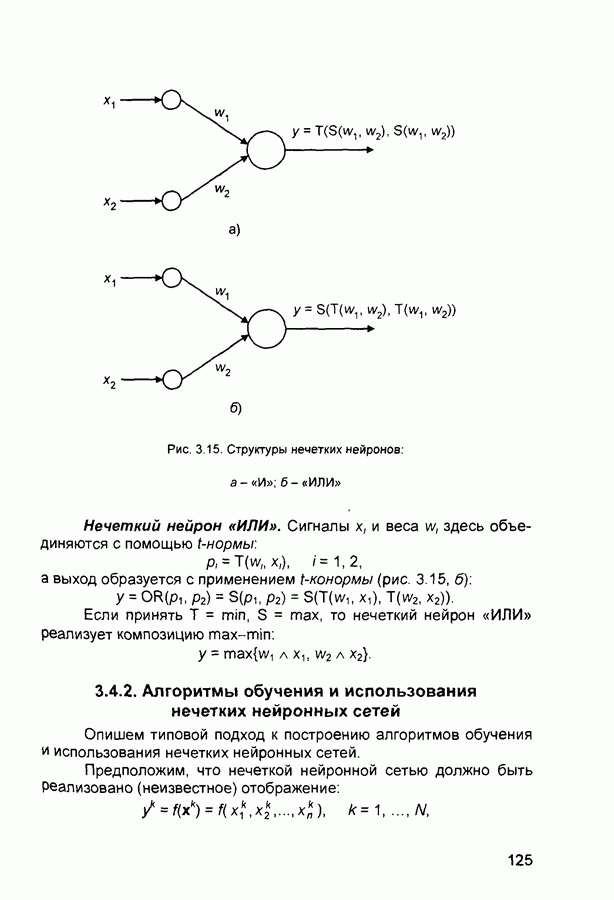
- 3.4. Синтез нечетких нейронных сетей
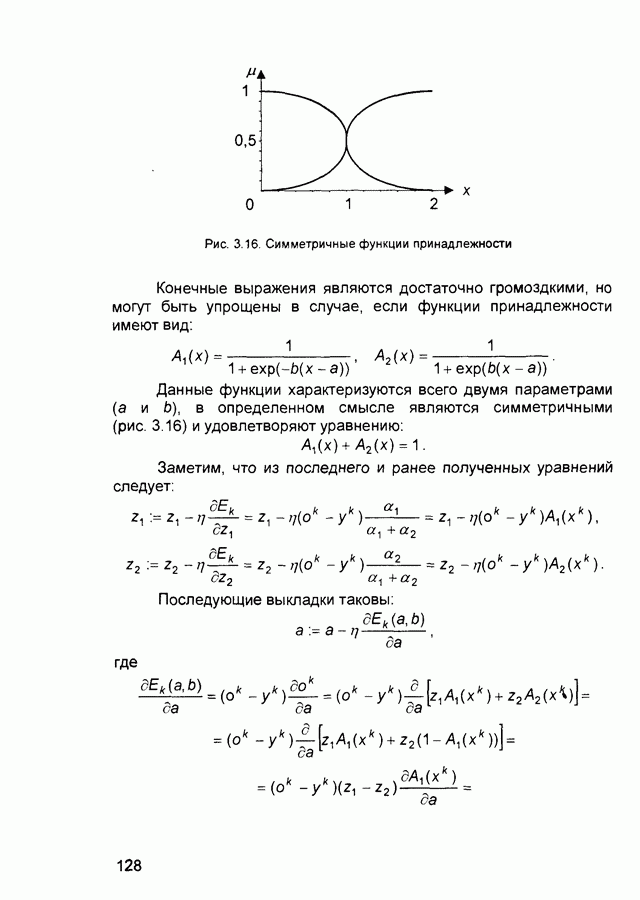
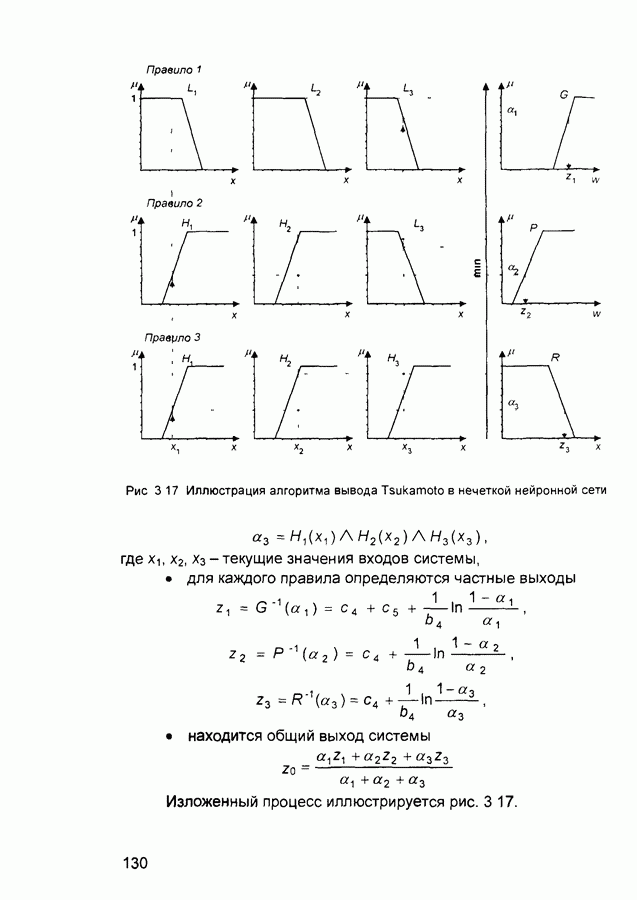
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
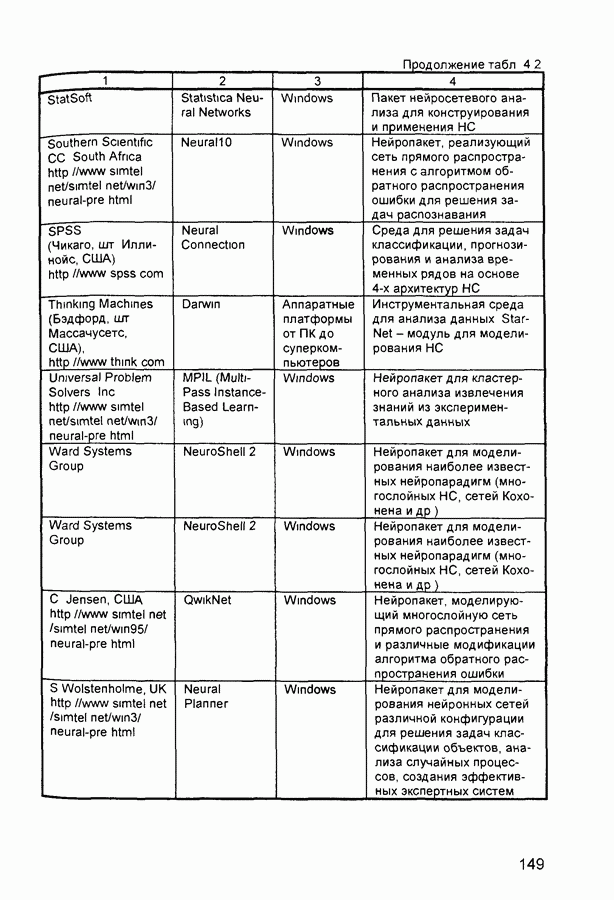
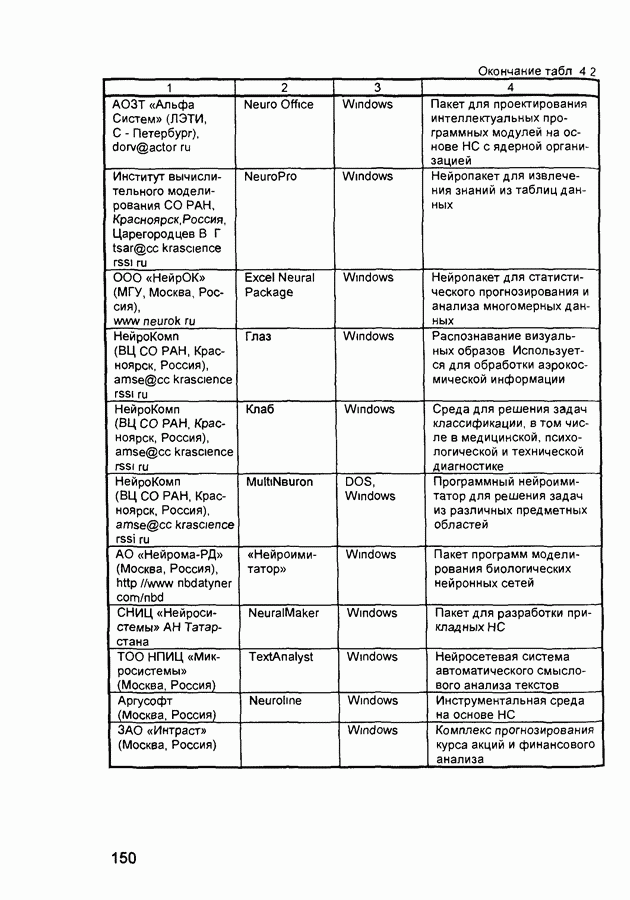
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
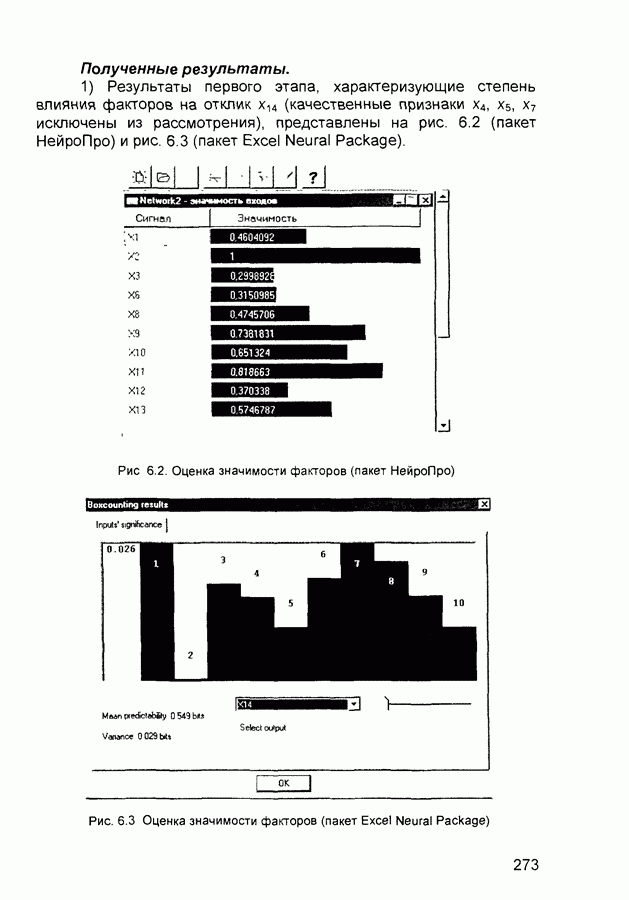
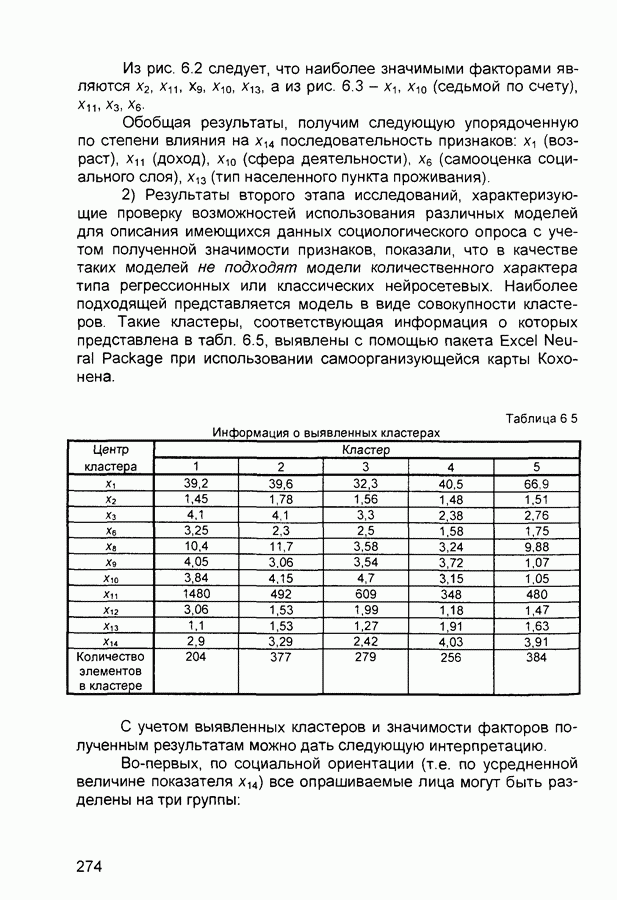
- 6.2. Анализ данных социологического опроса
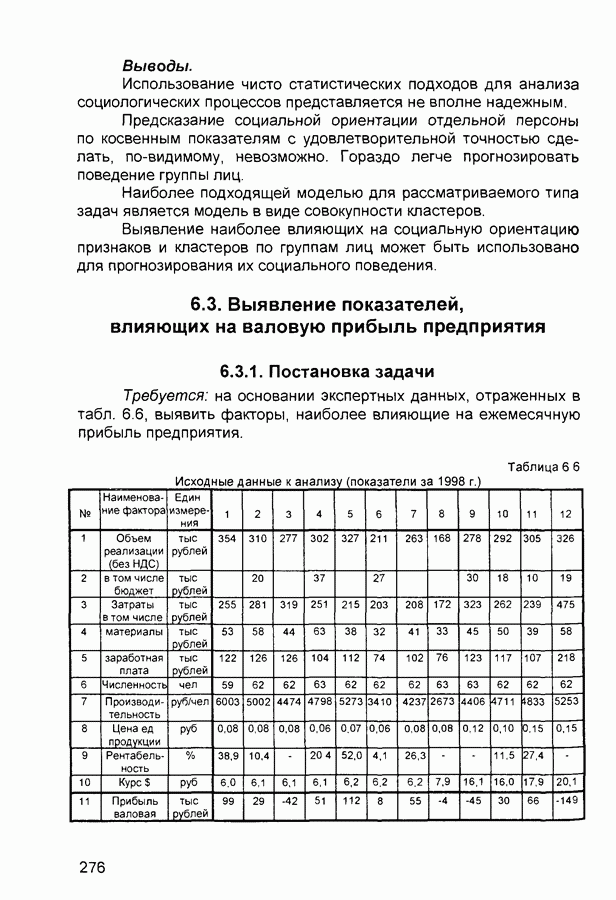
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
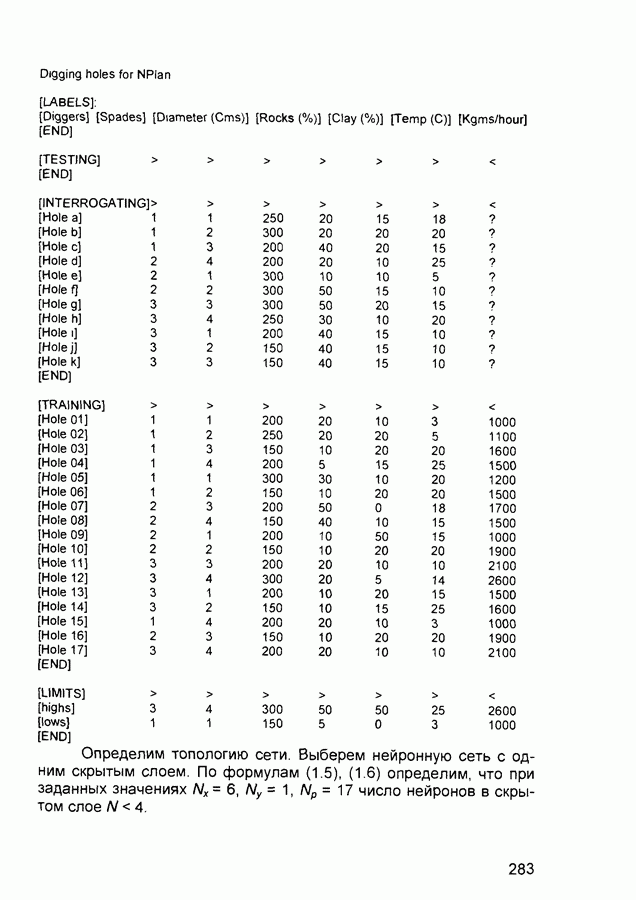
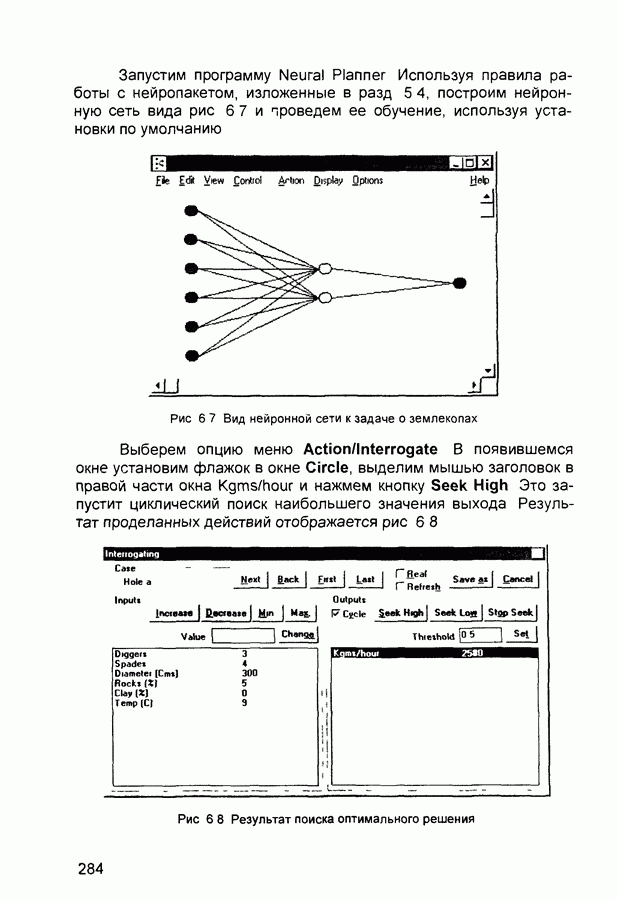
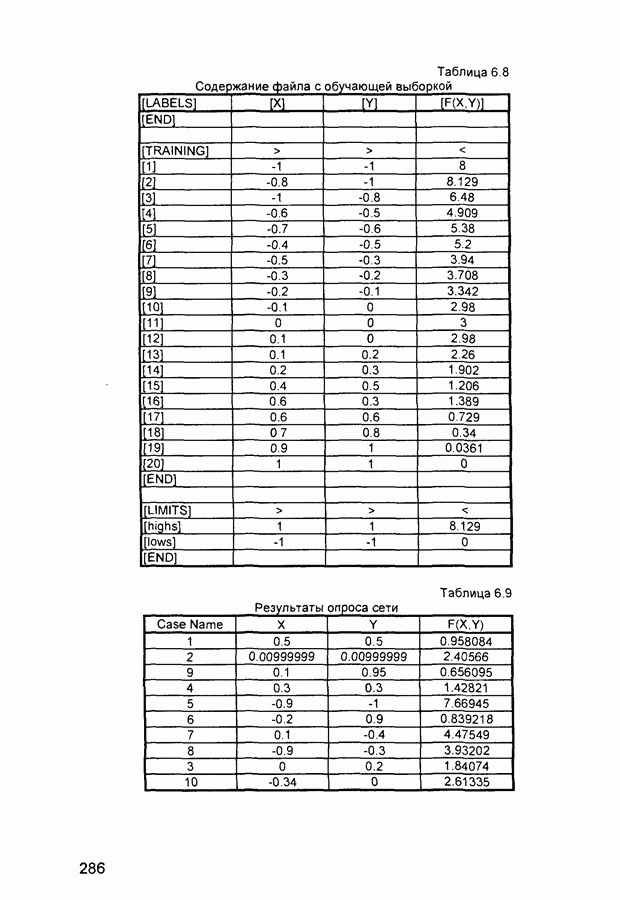
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
- 6.7. Нейросетевая экспертная система
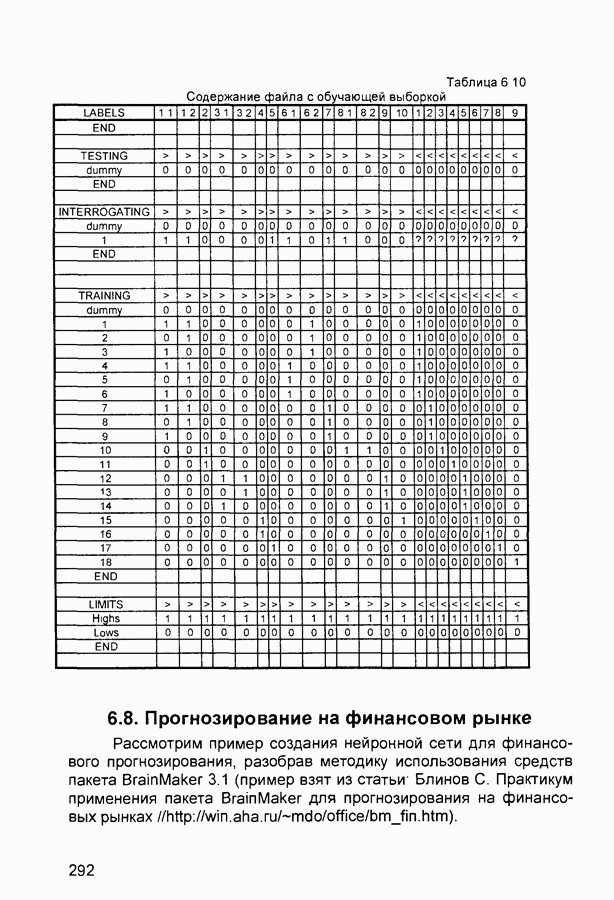
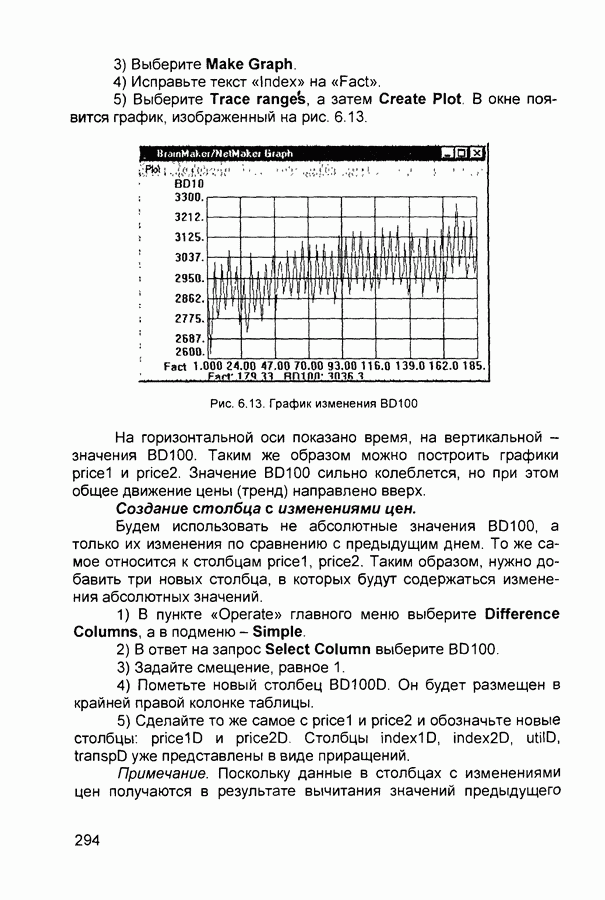
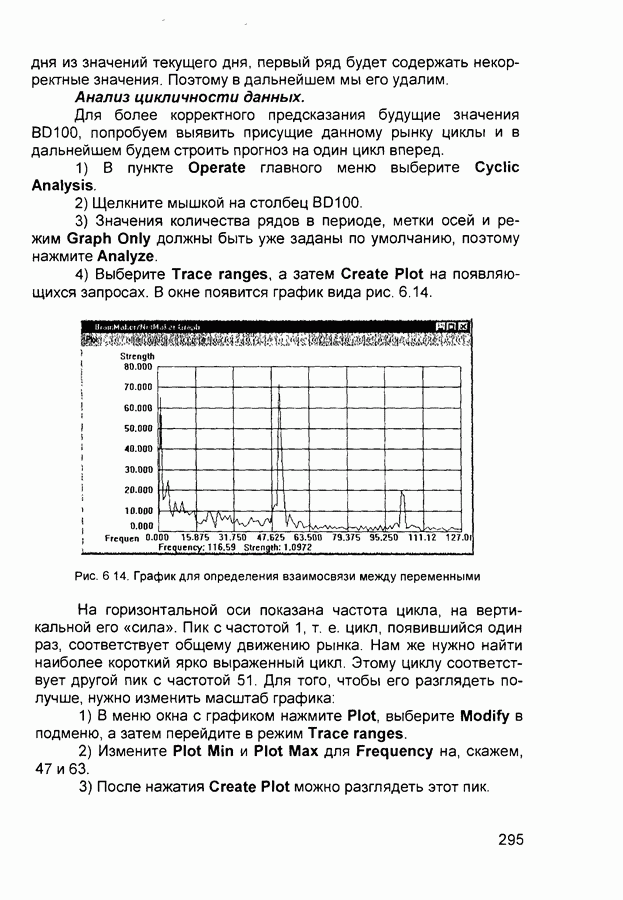
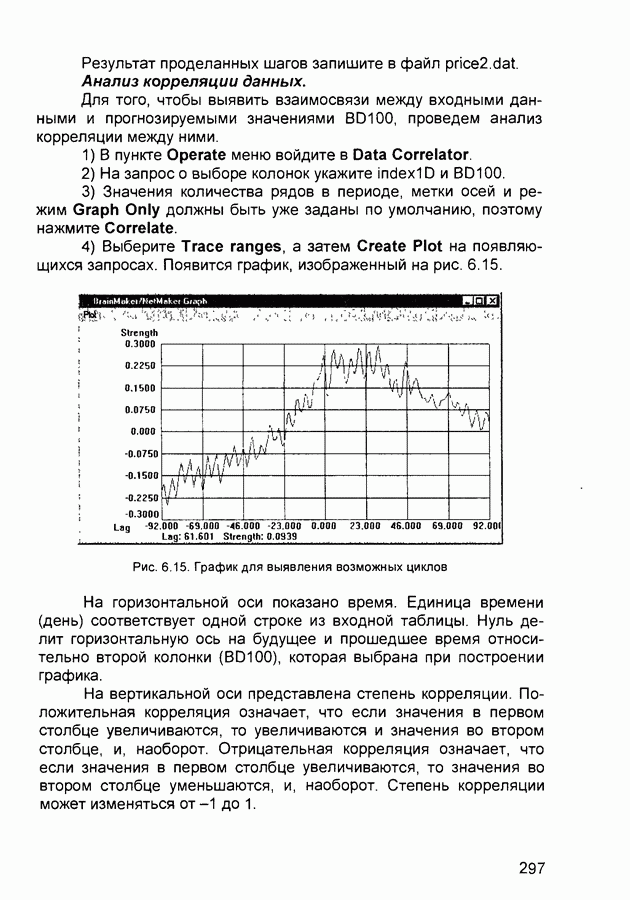
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
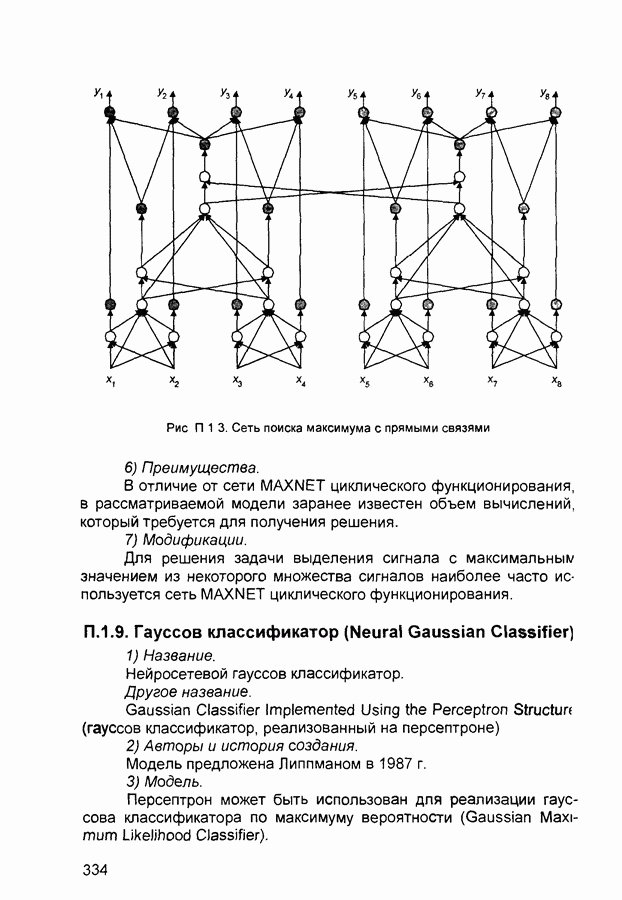
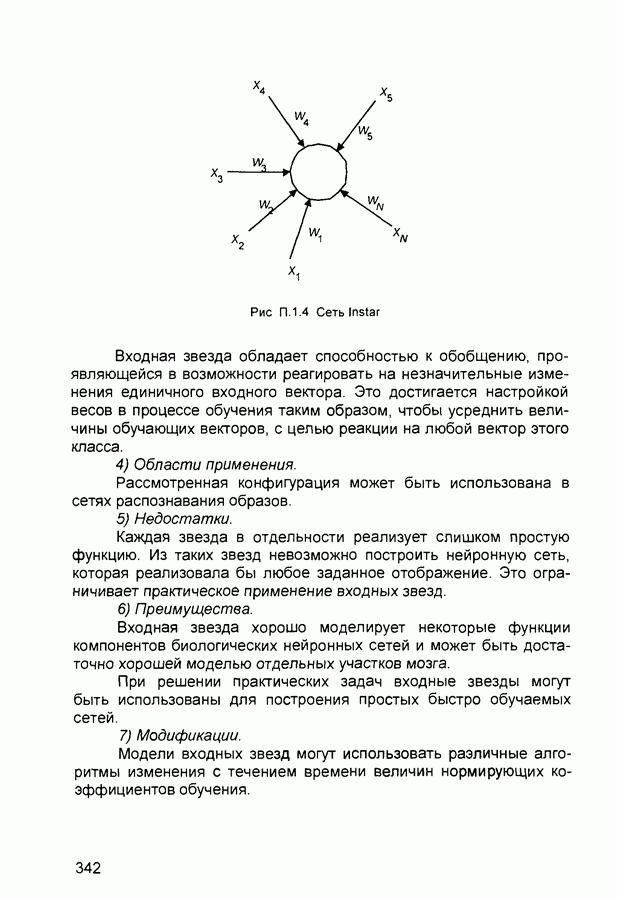
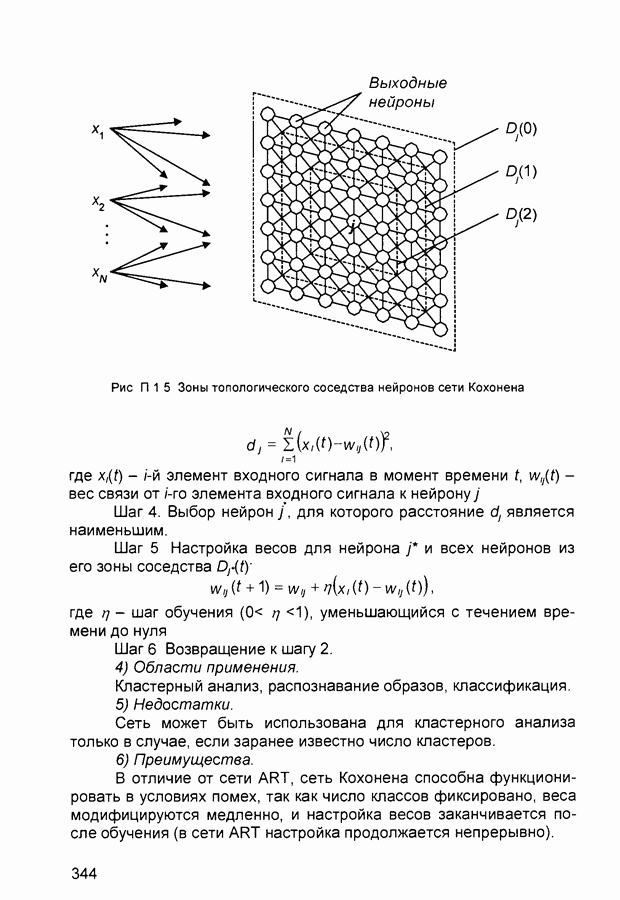
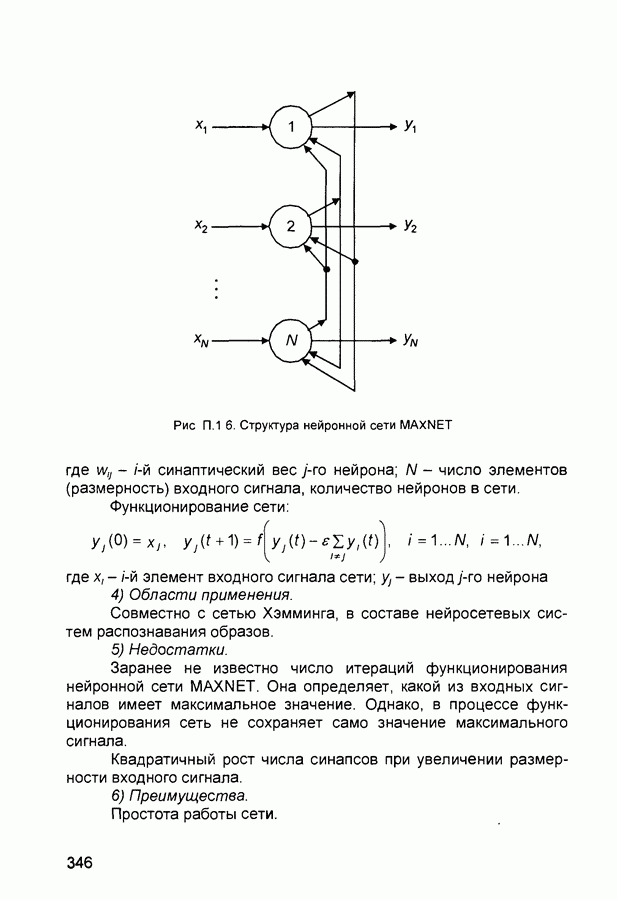
- П.1. Основные парадигмы нейронных сетей
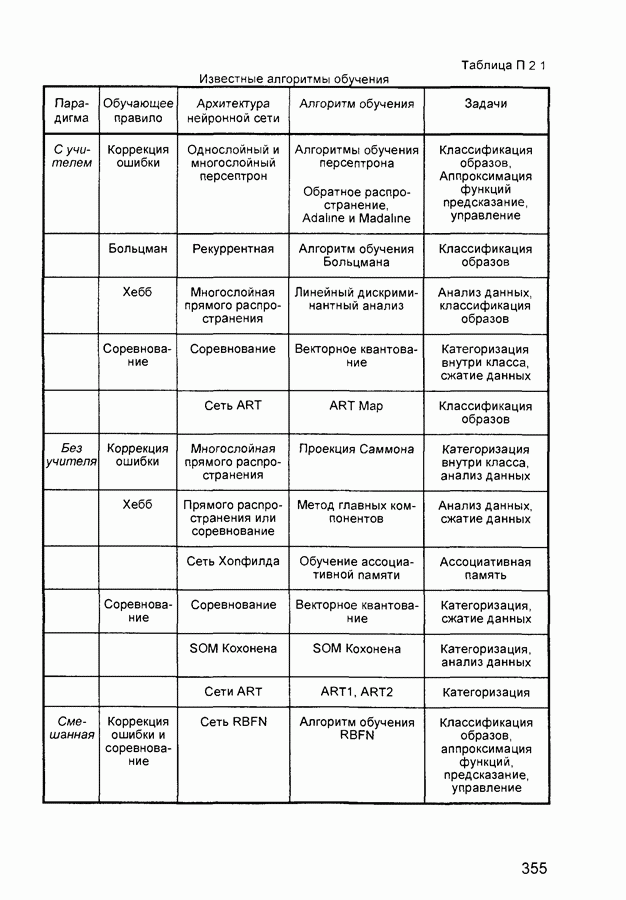
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы