| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
П.2. Алгоритмы обучения нейронных сетей
Процесс обучения нейронной сети может рассматриваться как настройка архитектуры и весов связей для эффективного выполнения поставленной задачи. Обычно итеративная настройка весов связей осуществляется в соответствии с обучающей выборкой. Свойство сети обучаться на примерах делает их более привлекательными по сравнению с системами, которые следуют системе правил функционирования, сформулированной экспертами.
Для организации процесса обучения, во-первых, надо иметь модель внешней среды, в которой функционирует нейронная сеть. Эта модель определяет парадигму обучения. Во-вторых, необходимо понять, как модифицировать весовые параметры сети.
Существуют три парадигмы обучения: с учителем, без учителя (самообучение) и смешанная. В первом случае на каждый входной пример существует требуемый ответ. Веса настраиваются таким образом, чтобы выходы сети как можно более близкие к требуемым ответам. Более «жесткий» вариант обучения с учителем предполагает, что известна только критическая оценка правильности выхода нейронной сети, а не сами требуемые значения выхода. Для обучения без учителя не нужно знания требуемых ответов на каждый пример обучающей выборки. В этом случае происходит распределение образцов по категориям (кластерам) в соответствии с внутренней структурой данных или степенью корреляции между образцами. При смешанном обучении весовые коэффициенты одной группы нейронов настраиваются посредством обучения с учителем, а другой группы - на основе самообучения.
В процессе обучения учитываются следующие свойства нейронных сетей: емкость сети, сложность образцов и вычислительная сложность. Под емкостью сети понимается число запоминаемых образцов, с учетом сформированных функций и границ принятия решений. Сложность образцов определяет число
обучающих примеров, необходимых для достижения способности сети к обобщению
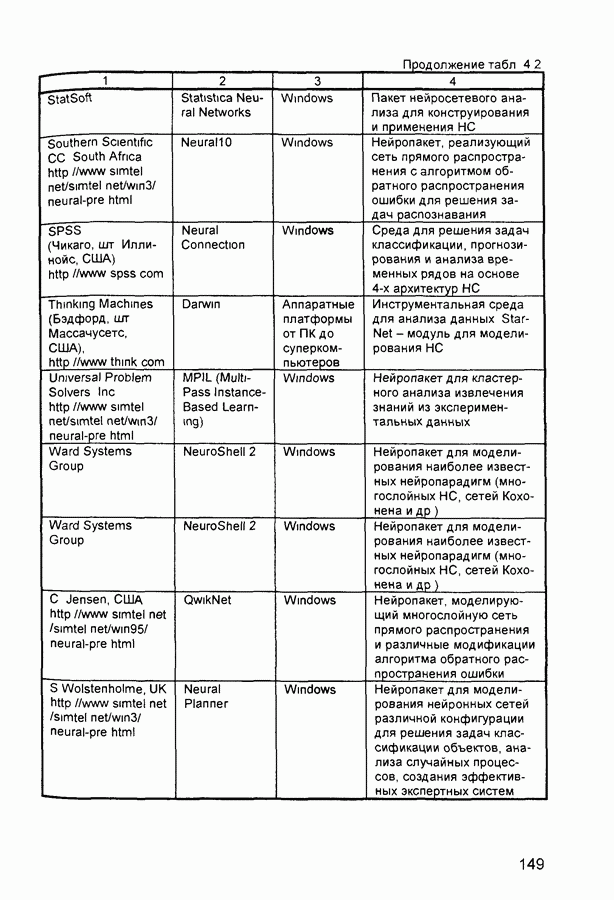
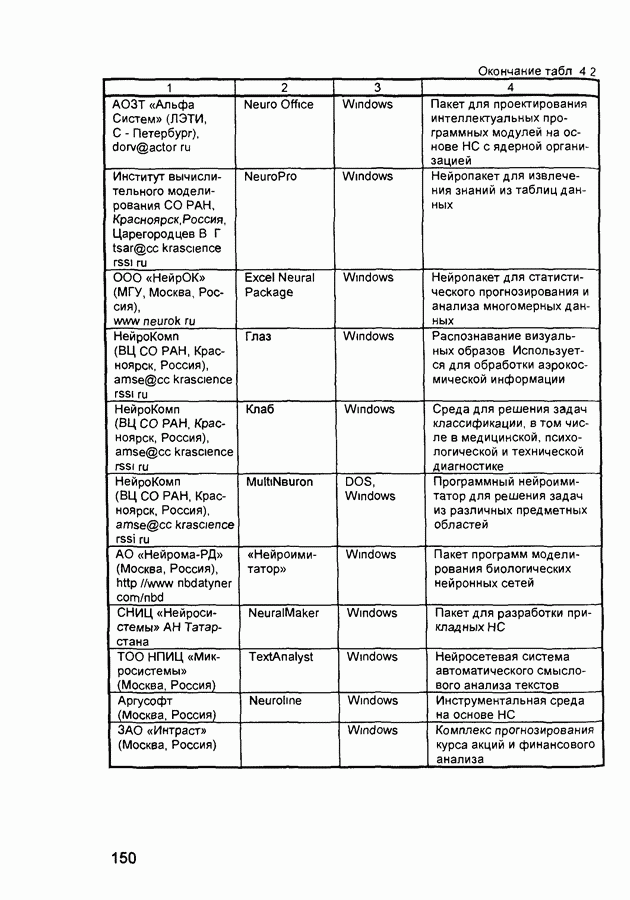
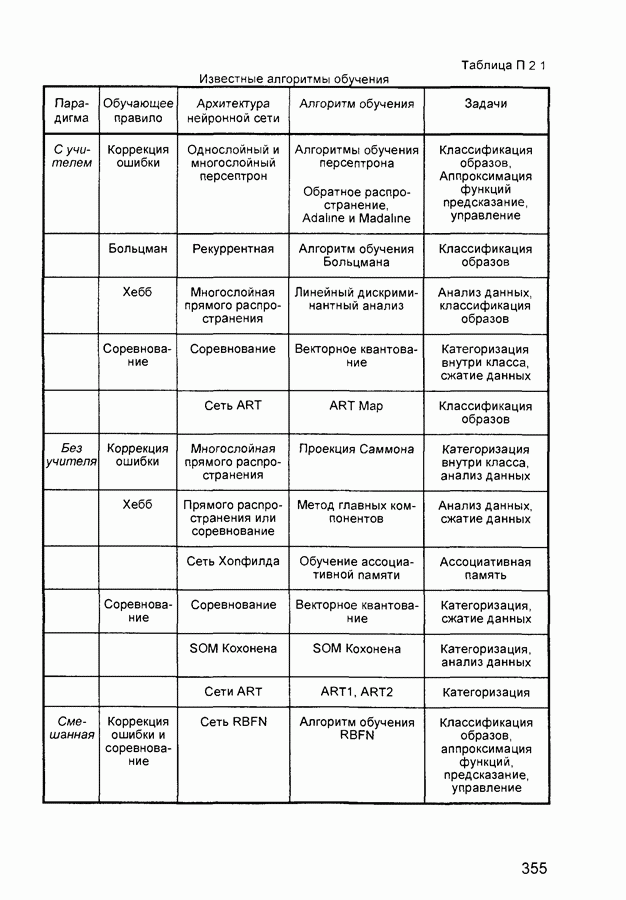
Известны четыре основных правила обучения, обусловленные связанными с ними архитектурами сетей (табл. П 2.1) коррекция ошибки, правило Больцмана, правило Хебба и метод соревнования
Коррекция ошибки
Для каждого входного примера задан требуемый выход  который может не совпадать с реальным у Правило обучения при коррекции по ошибке состоит в использовании разницы
который может не совпадать с реальным у Правило обучения при коррекции по ошибке состоит в использовании разницы  для изменения весов, с целью уменьшения ошибки рассогласования Обучение производится только в случае ошибочного результата Известны многочисленные модификации этого правила обучения
для изменения весов, с целью уменьшения ошибки рассогласования Обучение производится только в случае ошибочного результата Известны многочисленные модификации этого правила обучения
Правило Больцмана
Правило Больцмана является стохастическим правилом обучения, обусловленным аналогией с термодинамическими принципами. В результате его выполнения осуществляется настройка весовых коэффициентов нейронов в соответствии с требуемым распределением вероятностей Обучение правилу Больцмана может рассматриваться как отдельный случай коррекции по ошибке, в котором под ошибкой понимается расхождение корреляций состояний в двух режимах
Правило Хебба
Правило Хебба является самым известным алгоритмом обучения нейронных сетей, суть которого заключается в следующем если нейроны с обеих сторон синапса возбуждаются одновременно и регулярно, то сила синаптической связи возрастает Важной особенностью является то, что изменение синаптического веса зависит только от активности связанных этим синапсом нейронов Предложено большое количество разновидностей этого правила, различающихся особенностями модификации синаптических весов.
Метод соревнования
В отличие от правила Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, здесь выходные нейроны соревнуются между собой И выходной нейрон с максимальным значением взвешенной суммы является «победителем» («победитель забирает все»). Выходы же остальных выходных нейронов устанавливаются в неактивное состояние При обучении модифицируются только веса нейрона-«победителя» в сторону увеличения близости к данному входному примеру

(кликните для просмотра скана)
Это правило позволяет группировать входные данные на категории (кластеры) и представлять их отдельными выходными нейронами.
Нейронная сеть считается устойчивой, если после конечного числа итераций обучения ни один из примеров обучающей выборки не изменяет своей принадлежности в кластерах. Однако сеть не перестанет обучаться, если параметр скорости обучения не равен нулю. Но эта искусственная остановка обучения вызывает другую проблему, называемую пластичностью и связанную со способностью сети к адаптации к новым данным. Возникает дилемма стабильности-пластичности Г россберга.
Список представленных в табл. П.2.1 алгоритмов обучения нейронных сетей не является исчерпывающим. В последней колонке перечислены задачи, для которых может быть применены эти алгоритмы. Каждый алгоритм обучения ориентирован на сеть определенной архитектуры и предназначен для ограниченного класса задач. Кроме рассмотренных, следует упомянуть некоторые другие алгоритмы: Adaline и Madeline, линейный дискриминантный анализ, проекции Саммона, метод главных компонентов.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
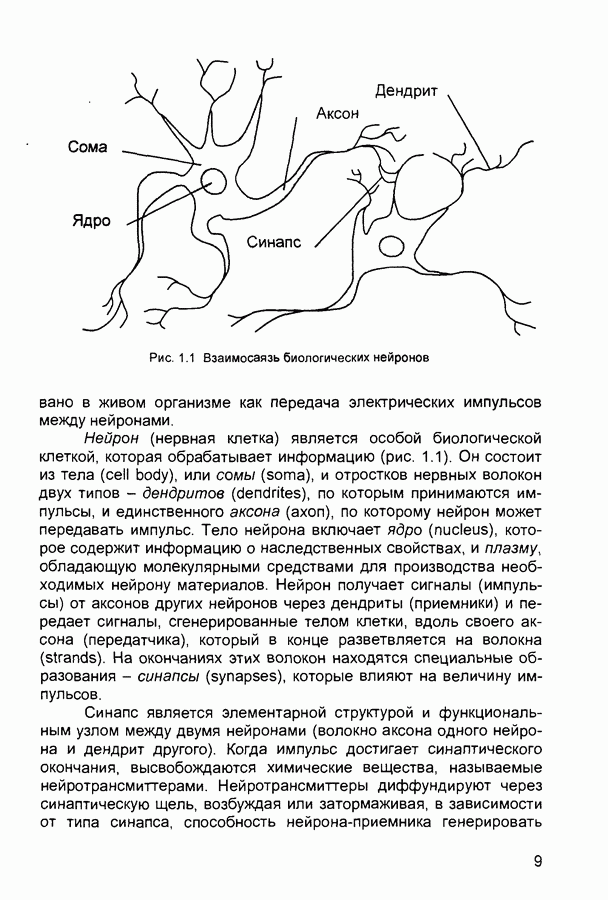
- 1.1. Биологический нейрон
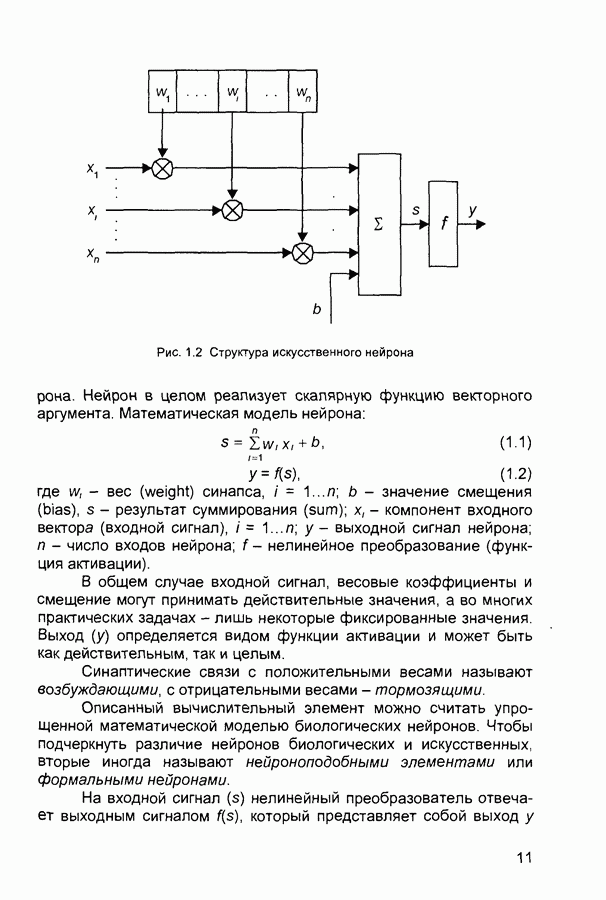
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
- 2.2. Персептроны
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
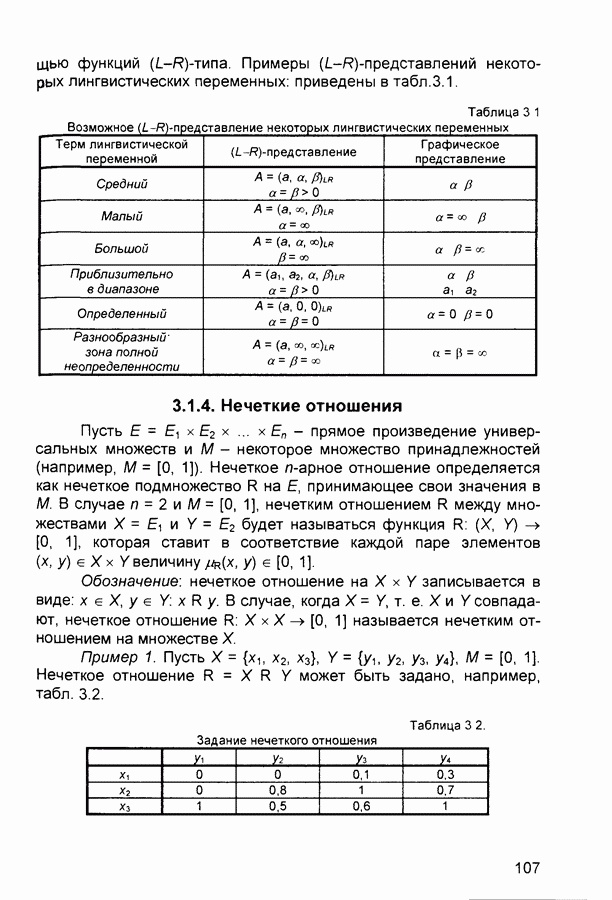
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
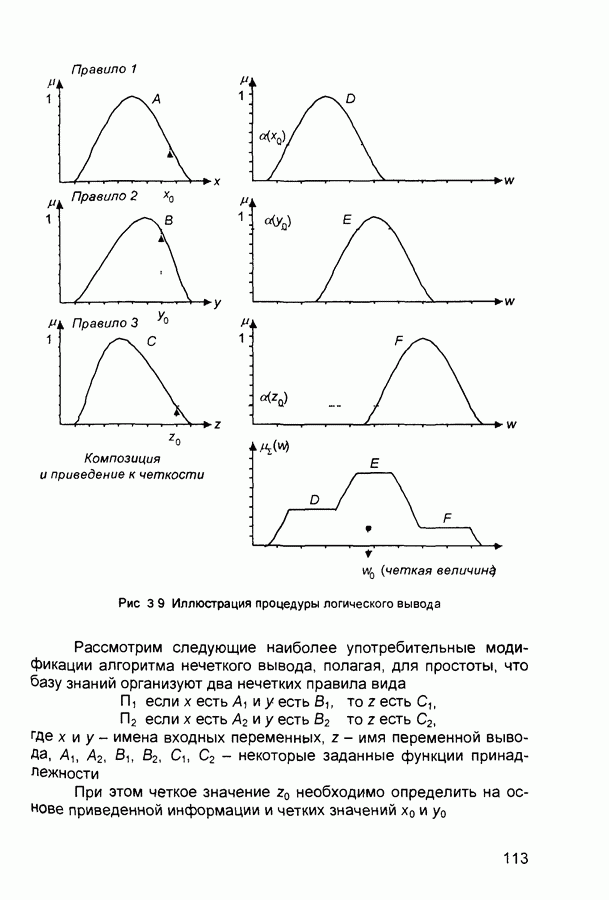
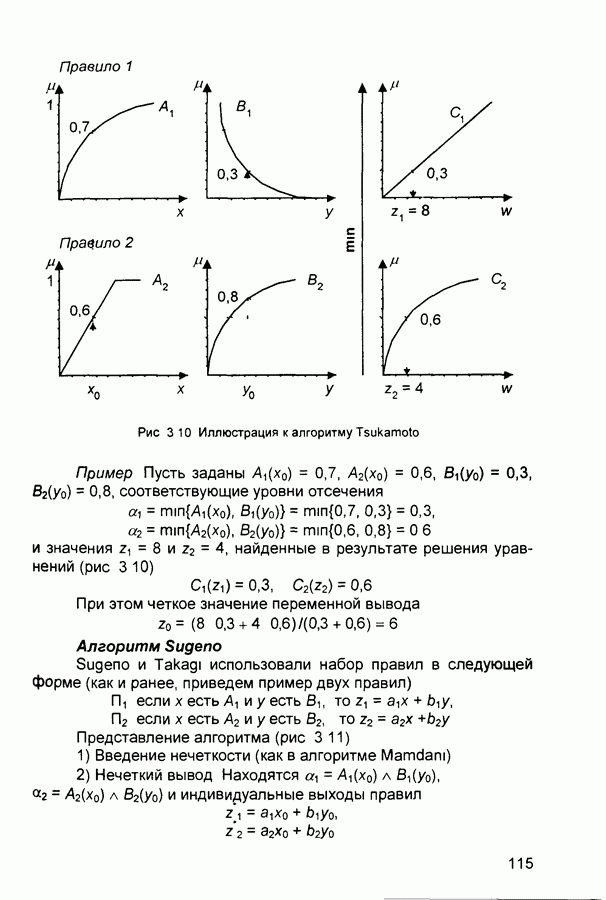
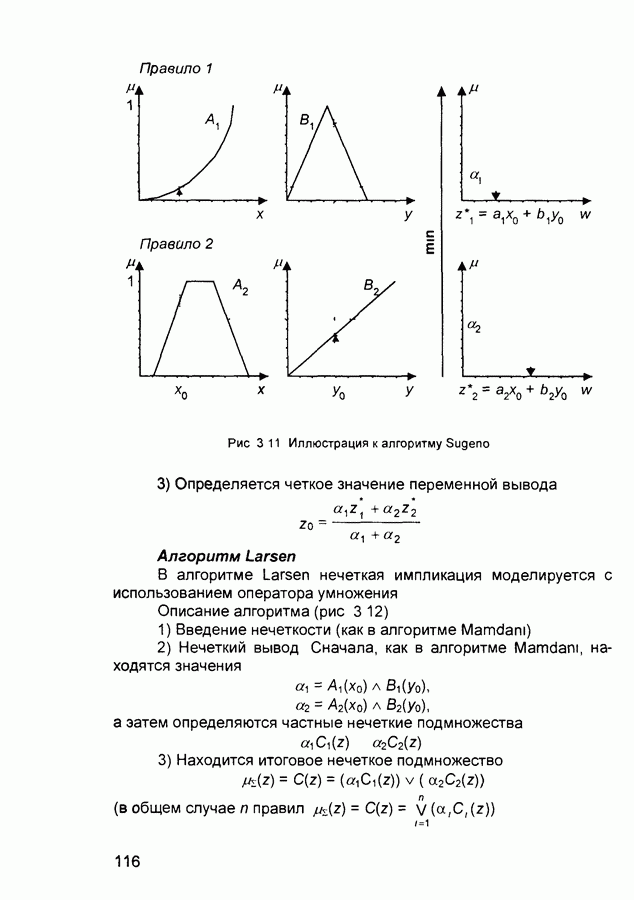
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
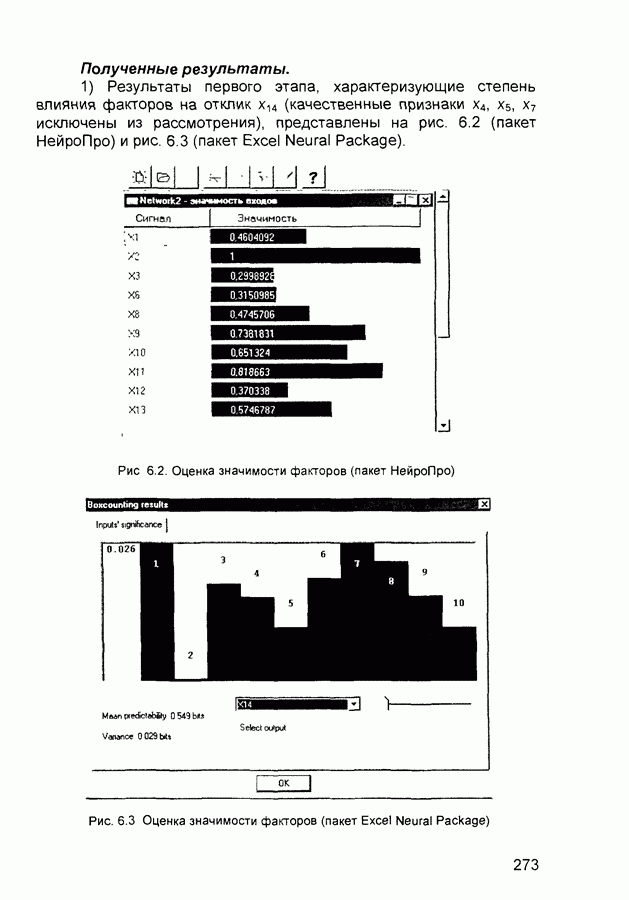
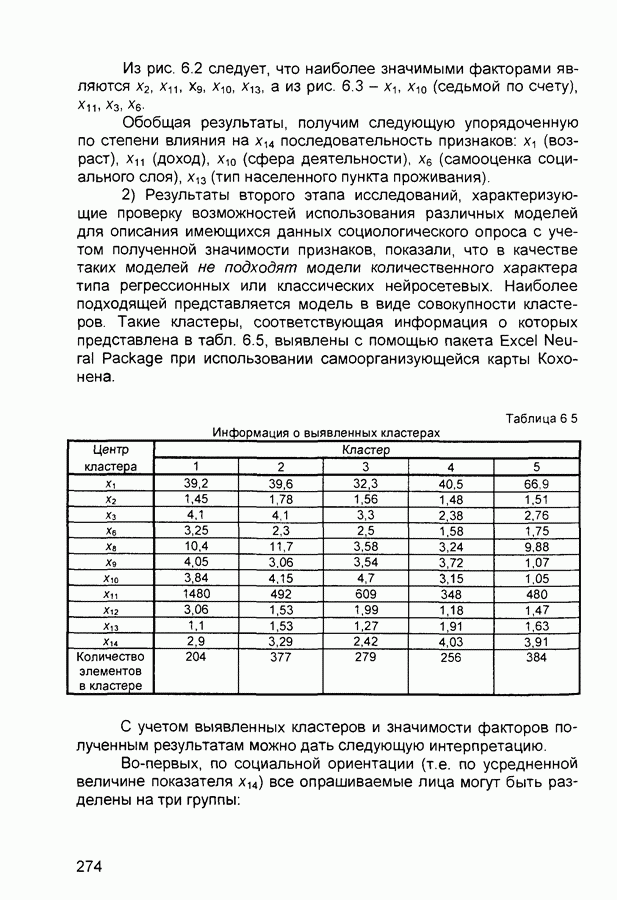
- 6.2. Анализ данных социологического опроса
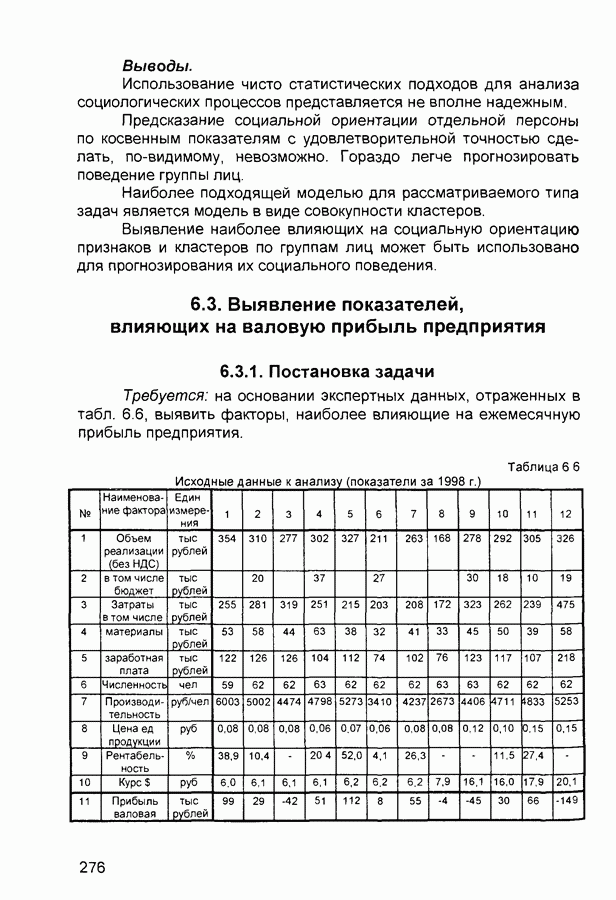
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
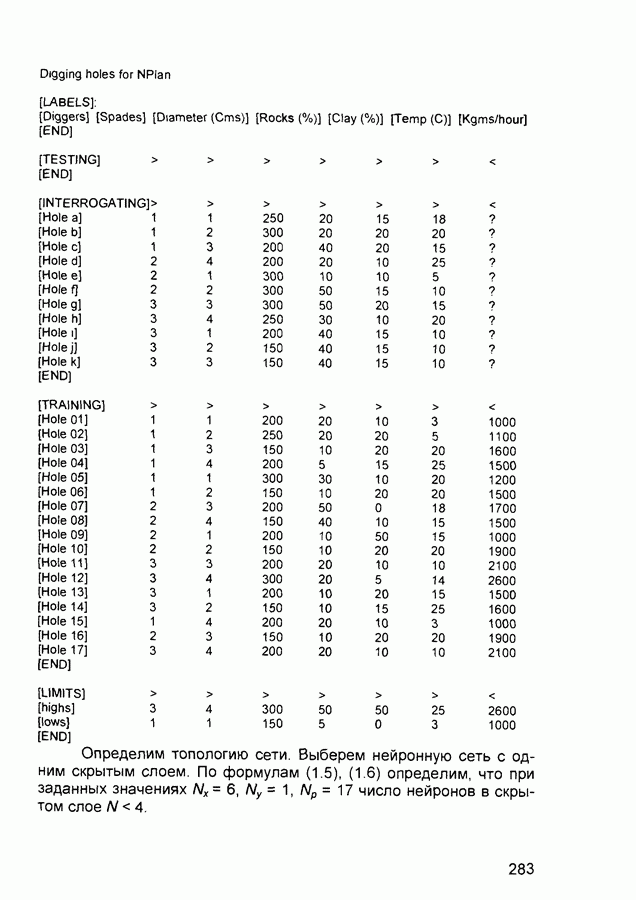
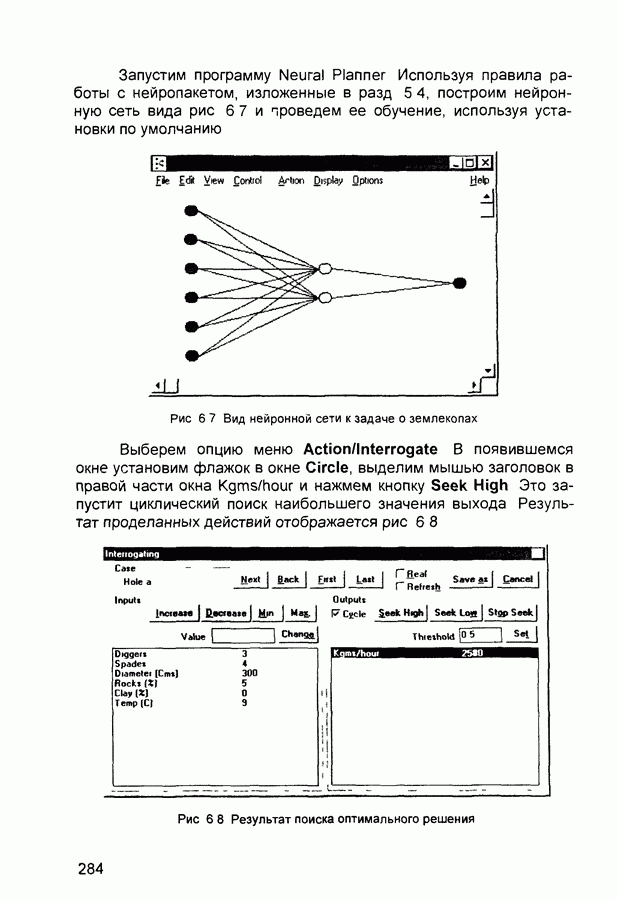
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
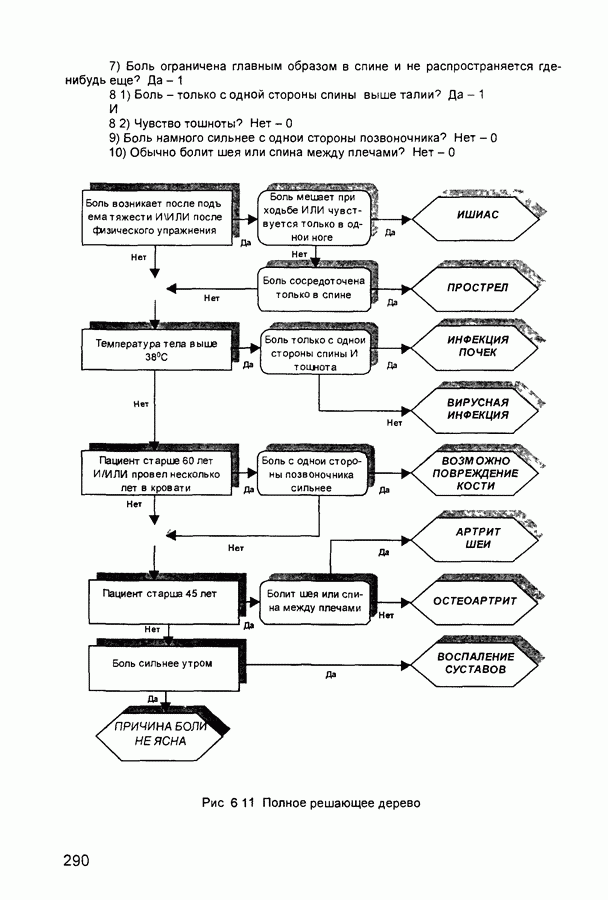
- 6.7. Нейросетевая экспертная система
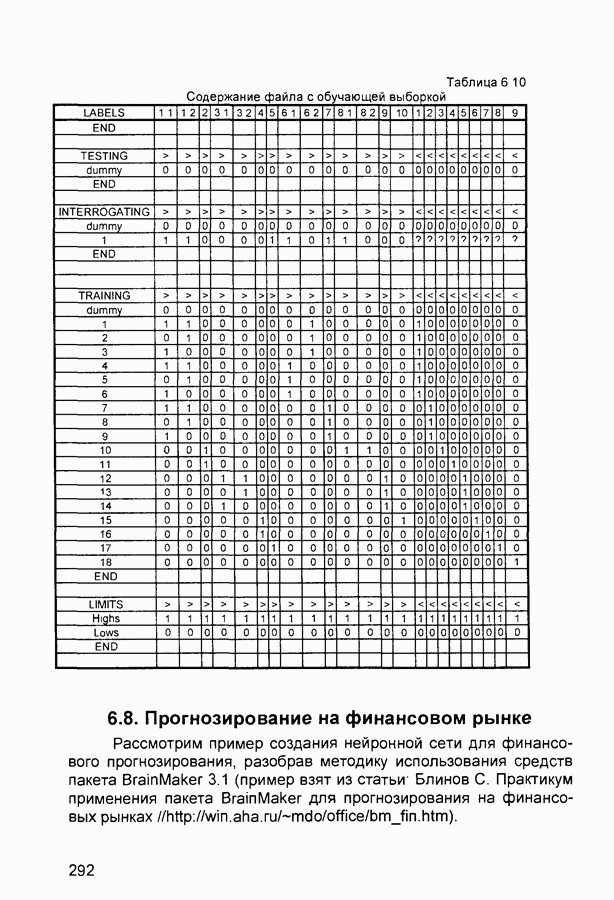
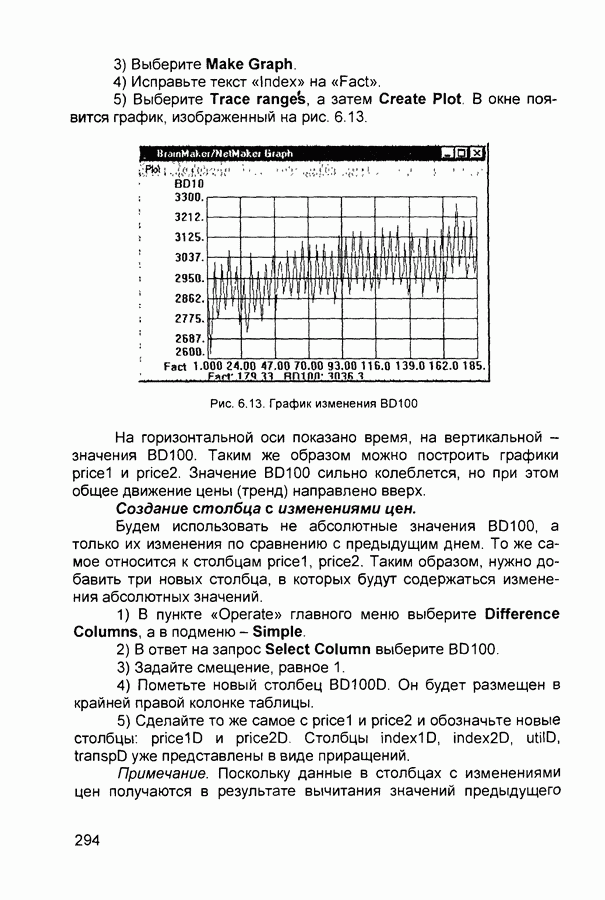
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы