| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
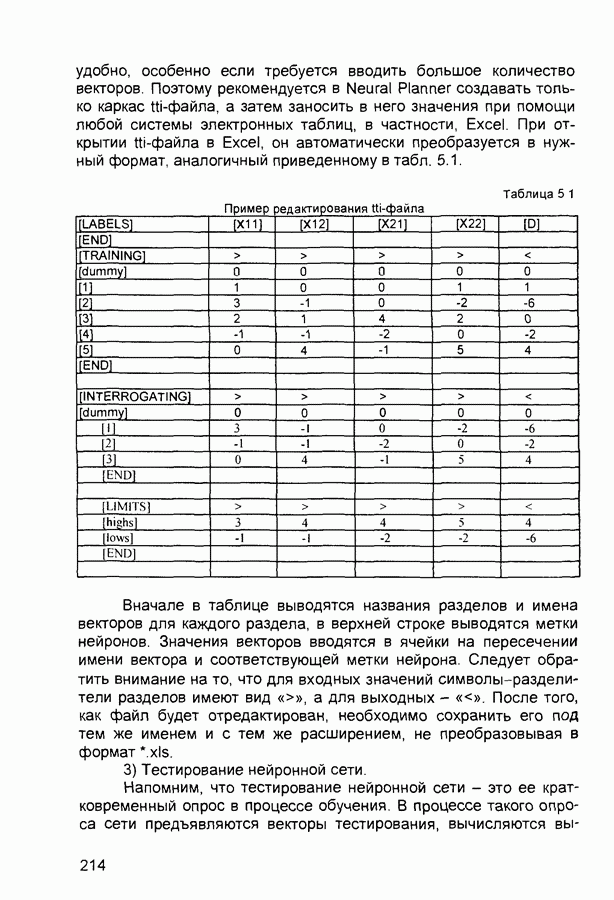
3.1. Нечеткая информация
Пожалуй, наиболее поразительным свойством человеческого интеллекта является способность принимать правильные решения в обстановке неполной и нечеткой информации. Построение моделей приближенных рассуждений человека и использование их в интеллектуальных компьютерных системах представляет сегодня одно из самых перспективных направлений развития современной вычислительной техники.
Значительный вклад в это направление внес Л. Заде (L. Zadeh). Его работа «Fuzzy Sets», опубликованная в 1965 г. в журнале «Information and Control», явилась толчком к развитию
новой математической теории. Заде расширил классическое понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале  , а не только значения 0 либо 1. Такие множества были названы им нечеткими
, а не только значения 0 либо 1. Такие множества были названы им нечеткими  Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modus ponens и modus tollens.
Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modus ponens и modus tollens.
Введя затем понятие лингвистической переменной и допустив, что в качестве ее значений (термов) выступают нечеткие множества, Заде предложил аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений. Это позволило создать фундамент теории нечетких множеств и нечеткой логики, а также предпосылки для внедрения методов нечеткого управления в инженерную практику.
Смещение центра исследований нечетких систем в сторону практических приложений привело к постановке целого ряда проблем таких, как новые архитектуры компьютеров для нечетких вычислений, элементная база нечетких компьютеров и контроллеров, инструментальные средства разработки, инженерные методы расчета и разработки нечетких систем управления и многое другое.
Математическая теория нечетких множеств позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы. Нечеткое управление оказывается особенно полезным, когда исследуемые процессы являются слишком сложными для анализа с помощью общепринятых методов, или когда доступные источники информации интерпретируются качественно, неточно или неопределенно. Нечеткая логика, предоставляющая эффективные средства отображения неопределенностей и неточностей реального мира, и на которой основано нечеткое управление, ближе к человеческому мышлению и естественным языкам, чем традиционные логические системы.
3.1.1. Нечеткие множества
Пусть Е - универсальное множество, х - элемент  - некоторое свойство. Обычное (четкое) подмножество А универсального множества Е, элементы которого удовлетворяют свойству
- некоторое свойство. Обычное (четкое) подмножество А универсального множества Е, элементы которого удовлетворяют свойству  определяется как множество упорядоченных пар:
определяется как множество упорядоченных пар:

где  - характеристическая функция, принимающая значение 1, если х удовлетворяет свойству
- характеристическая функция, принимающая значение 1, если х удовлетворяет свойству  и 0 - в противном случае.
и 0 - в противном случае.
Нечеткое подмножество отличается от обычного тем, что для элементов х из Е нет однозначного ответа «да-нет» относительно свойства  . В связи с этим нечеткое подмножество А универсального множества Е определяется как множество упорядоченных пар:
. В связи с этим нечеткое подмножество А универсального множества Е определяется как множество упорядоченных пар:

где  - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве М (например,
- характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве М (например,  ).
).
Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М называют множеством принадлежностей. Если  то нечеткое подмножество А может рассматриваться как обычное или четкое множество.
то нечеткое подмножество А может рассматриваться как обычное или четкое множество.
Примеры записи нечеткого множества
Пусть  - нечеткое множество, для которого
- нечеткое множество, для которого 
Тогда А можно представить в виде:  или
или 
Замечание. Здесь знак  не является обозначением операции сложения, а имеет смысл объединения.
не является обозначением операции сложения, а имеет смысл объединения.
Основные характеристики нечетких множеств
Пусть  и А - нечеткое множество с элементами из универсального множества Е и множеством принадлежностей М.
и А - нечеткое множество с элементами из универсального множества Е и множеством принадлежностей М.
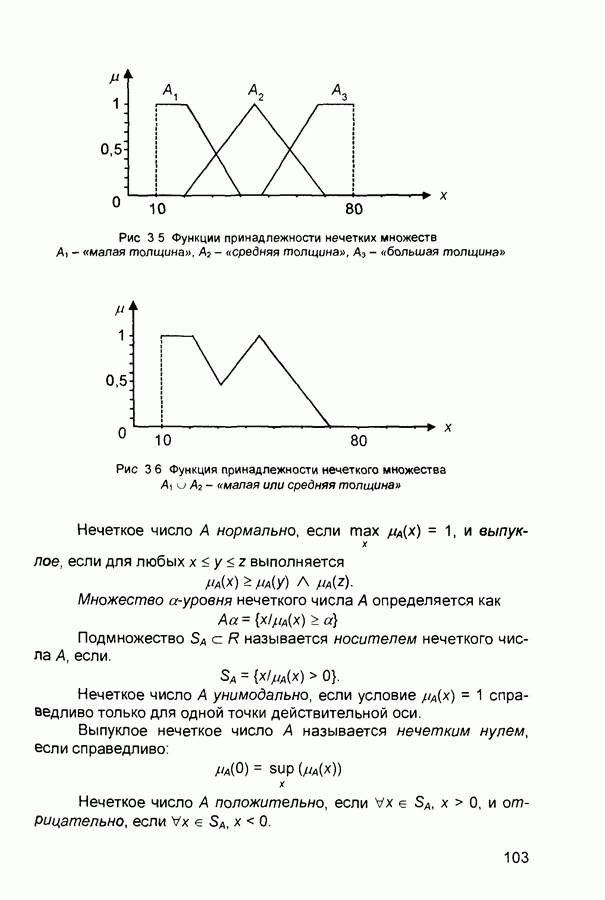
• Величина  называется высотой нечеткого множества А. Нечеткое множество А нормально, если его высота равна 1, т. е. верхняя граница его функции принадлежности равна
называется высотой нечеткого множества А. Нечеткое множество А нормально, если его высота равна 1, т. е. верхняя граница его функции принадлежности равна  При
При  нечеткое множество называется субнормальным.
нечеткое множество называется субнормальным.
• Нечеткое множество пусто, если  Непустое субнормальное множество можно нормализовать по формуле:
Непустое субнормальное множество можно нормализовать по формуле:

• Нечеткое множество унимодально,  только на одном х из Е.
только на одном х из Е.

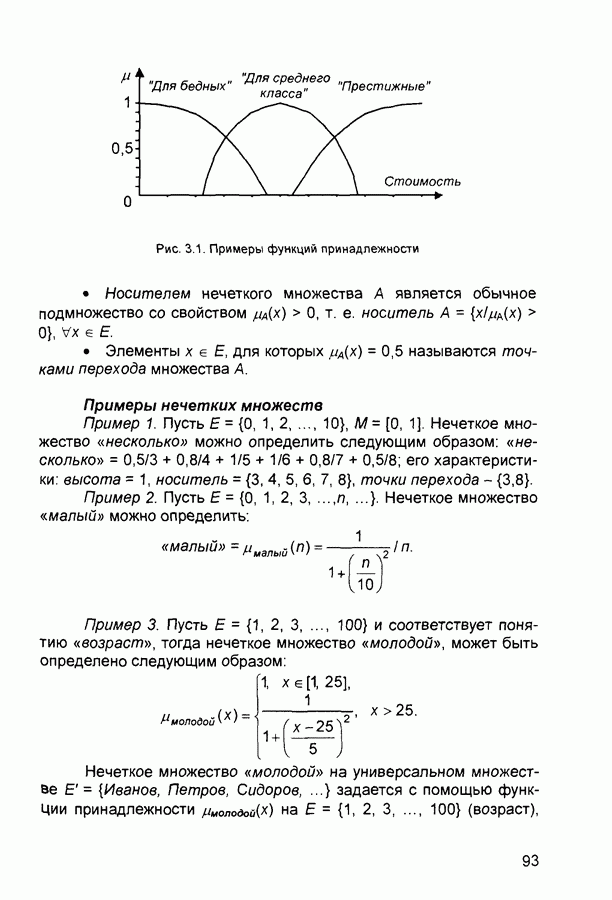
Рис. 3.1. Примеры функций принадлежности
• Носителем нечеткого множества А является обычное подмножество со свойством  т. е. носитель
т. е. носитель 
• Элементы  , для которых
, для которых  называются точками перехода множества А.
называются точками перехода множества А.
Примеры нечетких множеств
Пример 1. Пусть  . Нечеткое множество «несколько» можно определить следующим образом: «несколько»
. Нечеткое множество «несколько» можно определить следующим образом: «несколько»  его характеристики: высота
его характеристики: высота  носитель
носитель  точки перехода -
точки перехода - 
Пример 2. Пусть  Нечеткое множество «малый» можно определить:
Нечеткое множество «малый» можно определить:

Пример 3. Пусть  и соответствует понятию «возраст», тогда нечеткое множество «молодой», может быть определено следующим образом:
и соответствует понятию «возраст», тогда нечеткое множество «молодой», может быть определено следующим образом:

Нечеткое множество «молодой» на универсальном множестве  (Иванов, Петров, Сидоров,
(Иванов, Петров, Сидоров,  задается с помощью функции принадлежности
задается с помощью функции принадлежности  на
на  (возраст),
(возраст),

Рис. 3.2 Пример задания нечеткого множества
называемой по отношению к Е функцией совместимости, при этом
 где X - возраст Сидорова
где X - возраст Сидорова
Пример 4 Пусть  Жигули, Мерседес,
Жигули, Мерседес,  - множество марок автомобилей, а
- множество марок автомобилей, а  - универсальное множество «стоимость», тогда на Е можно определить нечеткие множества типа
- универсальное множество «стоимость», тогда на Е можно определить нечеткие множества типа  бедных», «для среднего класса», «престижные», с функциями принадлежности вида рис 3 1
бедных», «для среднего класса», «престижные», с функциями принадлежности вида рис 3 1
Имея эти функции и зная стоимости автомобилей из Е в данный момент времени, тем самым можно определить на Е нечеткие множества с этими же названиями
Так, например, нечеткое множество «для бедных», заданное на универсальном множестве  Жигули, Мерседес,
Жигули, Мерседес,  выглядит так, как показано на рис. 3.2
выглядит так, как показано на рис. 3.2
Аналогично можно определить Нечеткое множество «скоростные», «средние», «тихоходные» и 
Пример 5 Пусть Е - множество целых чисел

Тогда нечеткое подмножество чисел, по абсолютной величине близких к нулю можно определить, например, так

Методы построения функций принадлежности нечетких множеств
Существуют прямые и косвенные методы построения функций принадлежности
При использовании прямых методов эксперт просто задает для каждого  значение
значение  Как правило, прямые методы задания функции принадлежности используются для измеримых понятий, таких как скорость, время, расстояние, давление, температура и т. д., или когда выделяются полярные значения
Как правило, прямые методы задания функции принадлежности используются для измеримых понятий, таких как скорость, время, расстояние, давление, температура и т. д., или когда выделяются полярные значения
Во многих задачах при характеристике объекта можно выделить набор признаков и для каждого из них определить полярные значения, соответствующие значениям функции принадлежности, О или 1 Для конкретного объекта эксперт, исходя из приведенной шкалы, задает  , формируя векторную функцию принадлежности
, формируя векторную функцию принадлежности 
Разновидностью прямых методов построения функций принадлежности являются прямые групповые методы, когда, например, группе экспертов предъявляют конкретный объект, и каждый должен дать один из двух ответов принадлежит или нет этот объект к заданному множеству Тогда число утвердительных ответов, деленное на общее число экспертов, дает значение функции принадлежности объекта к данному нечеткому множеству
Косвенные методы определения значений функции принадлежности используются в случаях, когда нет измеримых элементарных свойств, через которые определяется нечеткое множество Как правило, это методы попарных сравнений Если бы значения функций принадлежности были известны, например,  то попарные сравнения можно представить матрицей отношений
то попарные сравнения можно представить матрицей отношений  где
где  (операция деления)
(операция деления)
На практике эксперт сам формирует матрицу А, при этом предполагается, что диагональные элементы равны 1, а для элементов, симметричных относительно главной диагонали,  если один элемент оценивается в а раз значимее чем другой, то этот последний должен быть в
если один элемент оценивается в а раз значимее чем другой, то этот последний должен быть в  раз значимее, чем первый В общем случае задача сводится к поиску вектора
раз значимее, чем первый В общем случае задача сводится к поиску вектора  удовлетворяющего уравнению вида
удовлетворяющего уравнению вида  где
где  - наибольшее собственное значение матрицы А Поскольку матрица А положительна по построению, решение данной задачи существует и является положительным
- наибольшее собственное значение матрицы А Поскольку матрица А положительна по построению, решение данной задачи существует и является положительным
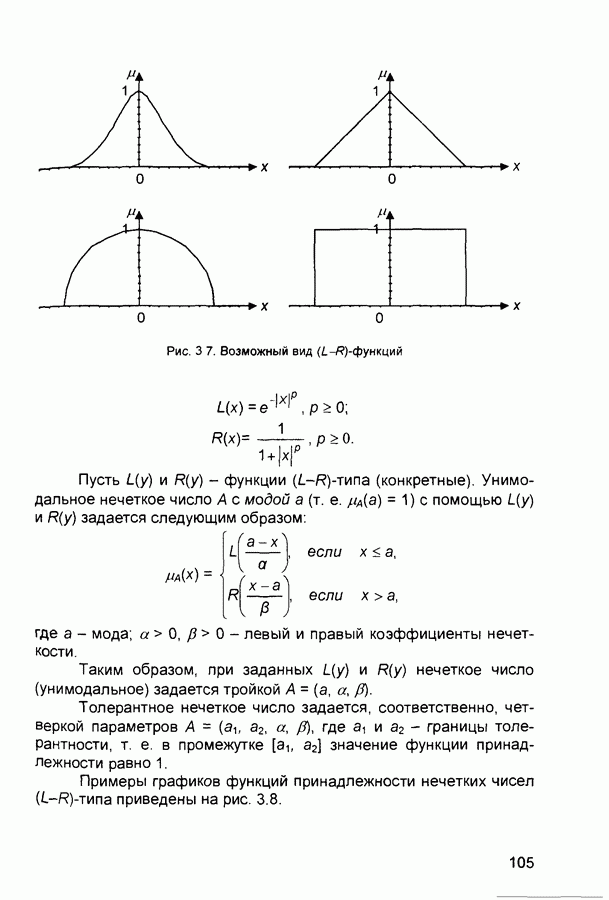
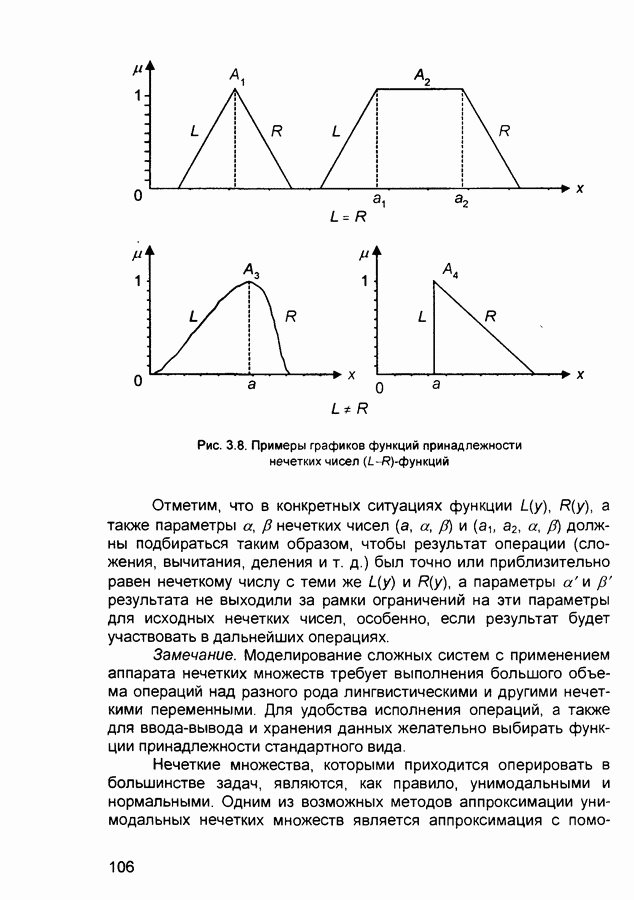
Использование типовых форм кривых для задания функций принадлежности (в форме  - см ниже) с уточнением их параметров в соответствии с данными эксперимента
- см ниже) с уточнением их параметров в соответствии с данными эксперимента
Использование относительных частот по данным эксперимента в качестве значений принадлежности
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
- 1.1. Биологический нейрон
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
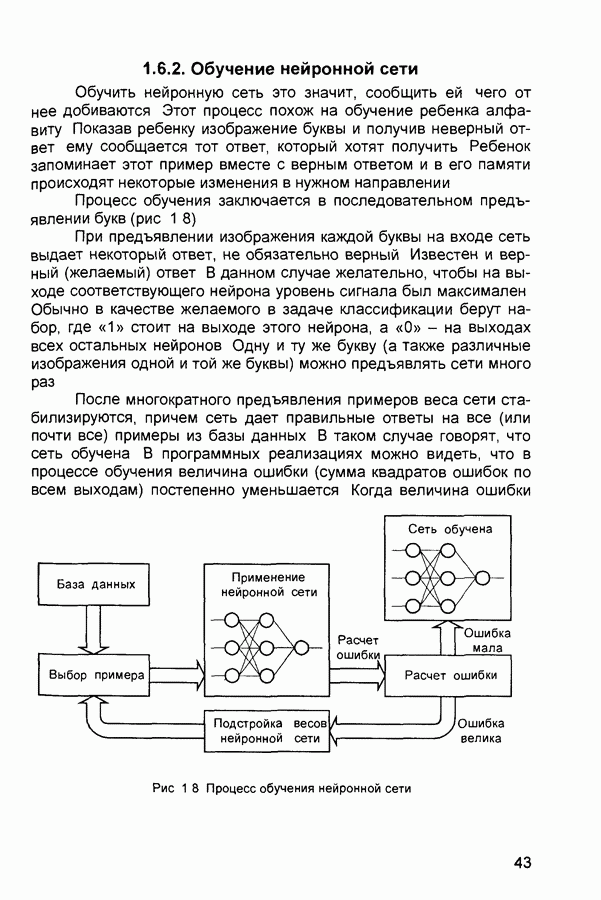
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
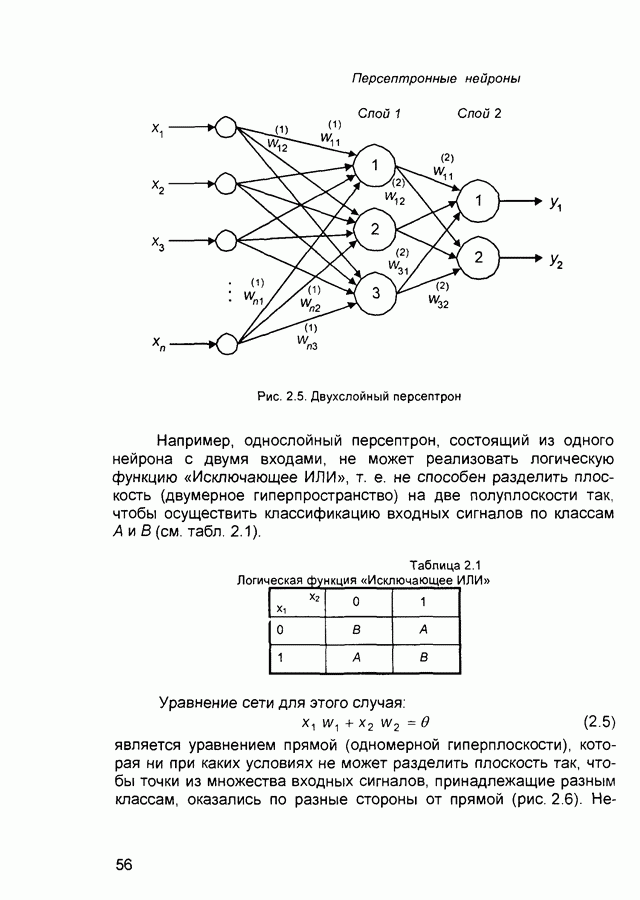
- 2.2. Персептроны
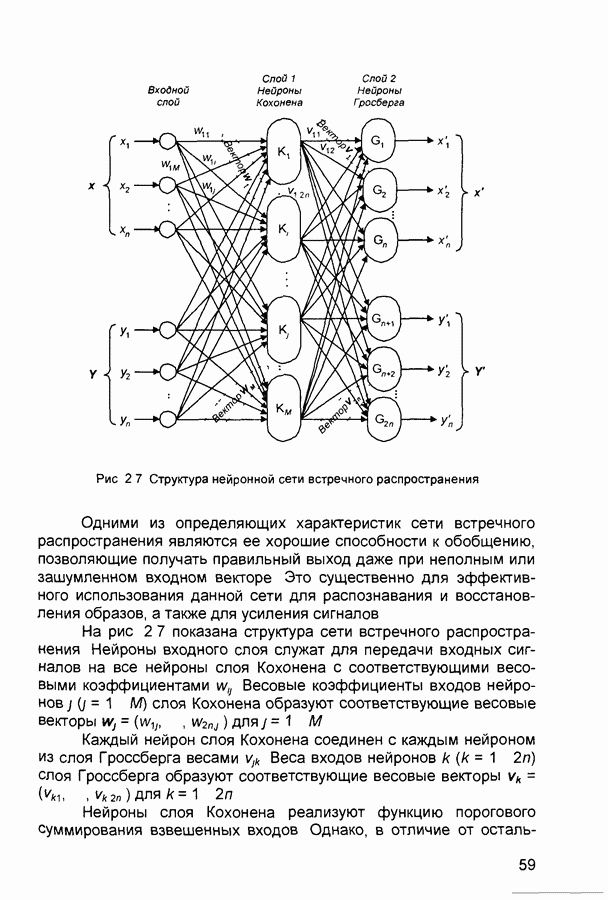
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
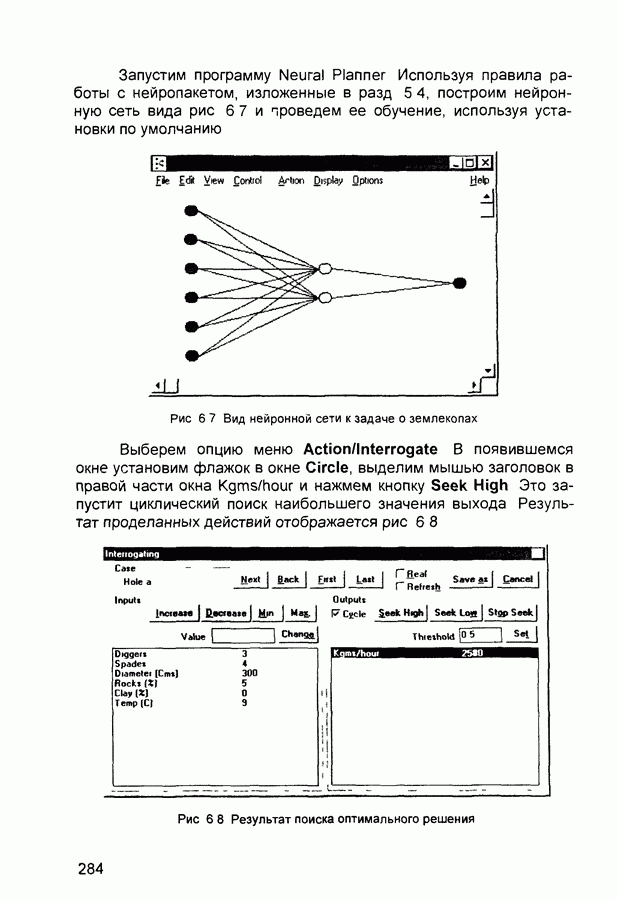
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
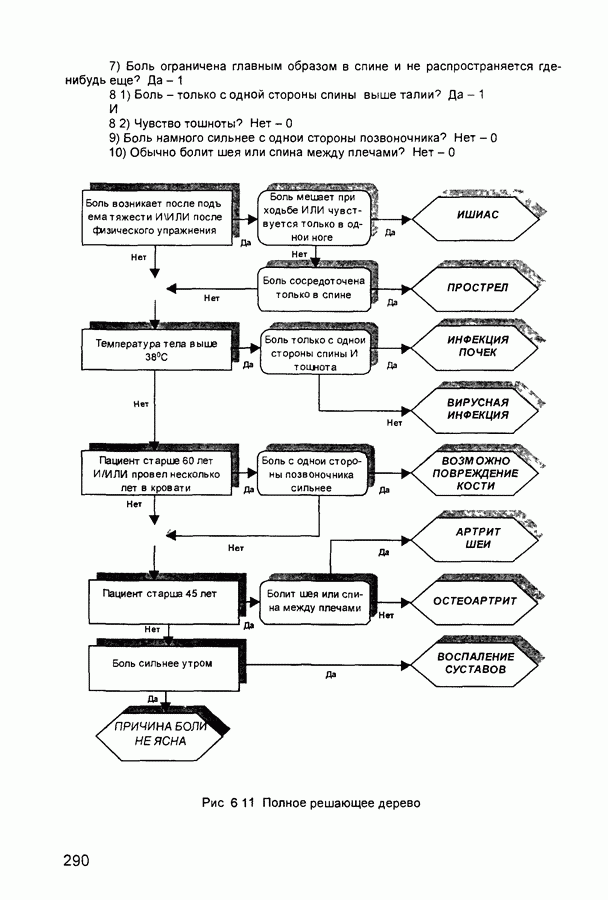
- 6.7. Нейросетевая экспертная система
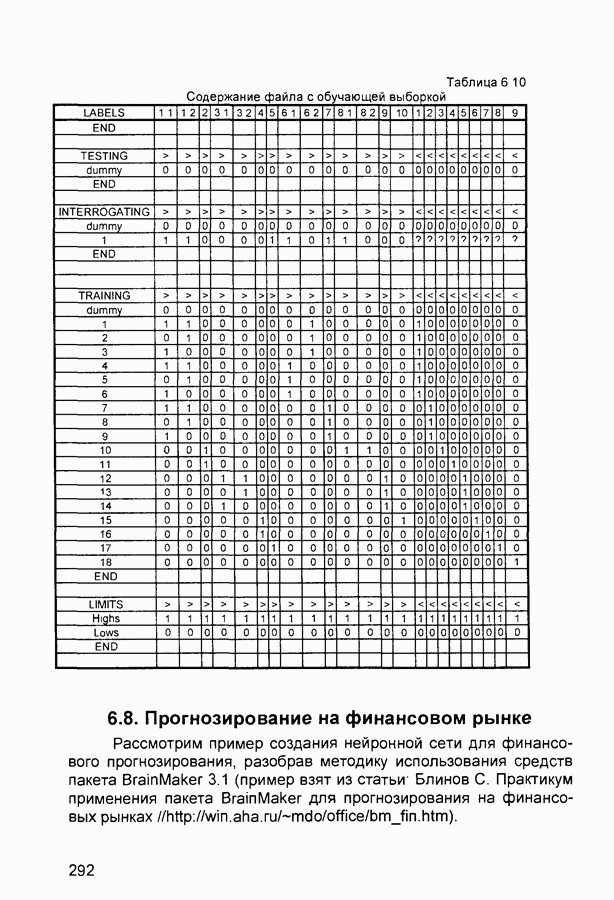
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы