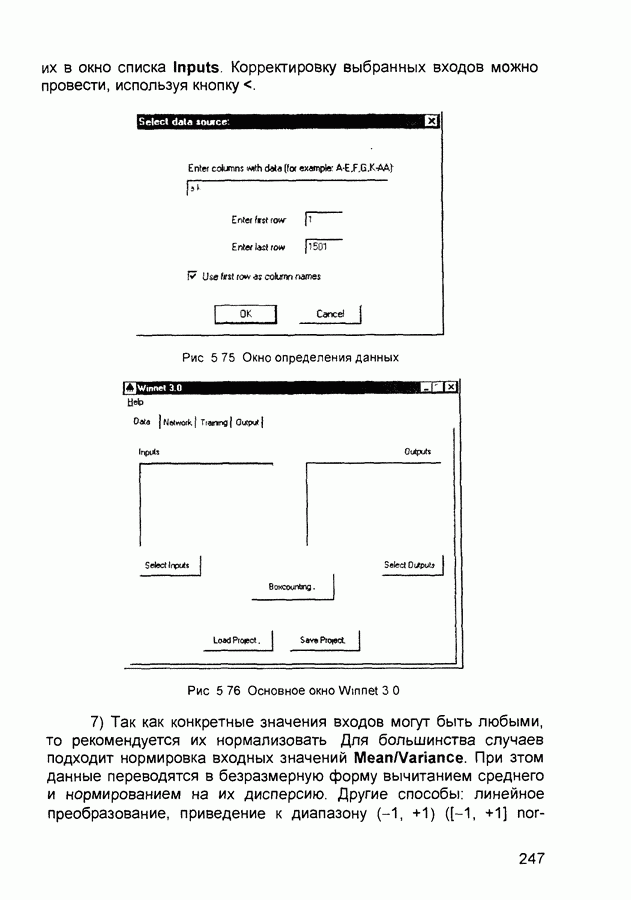
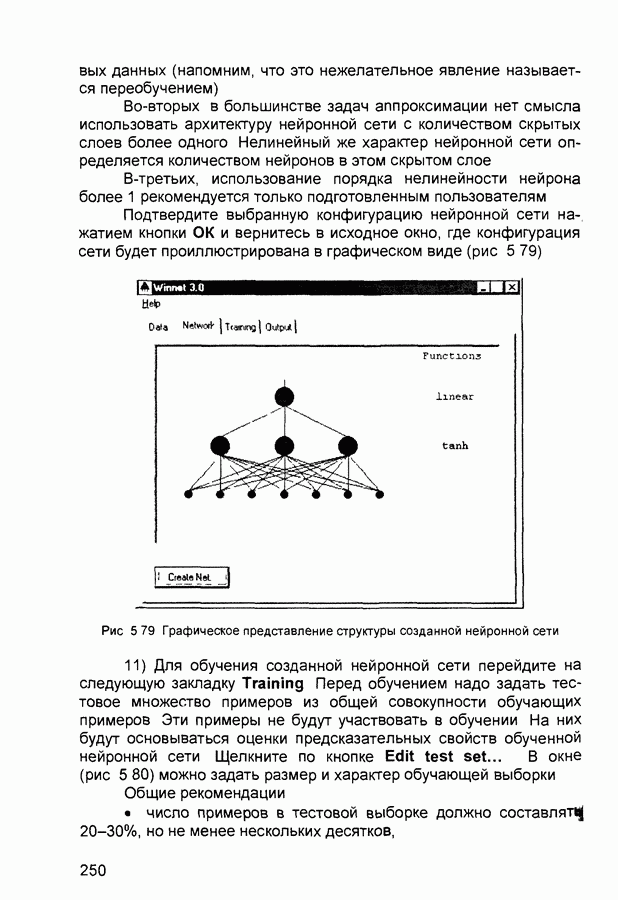
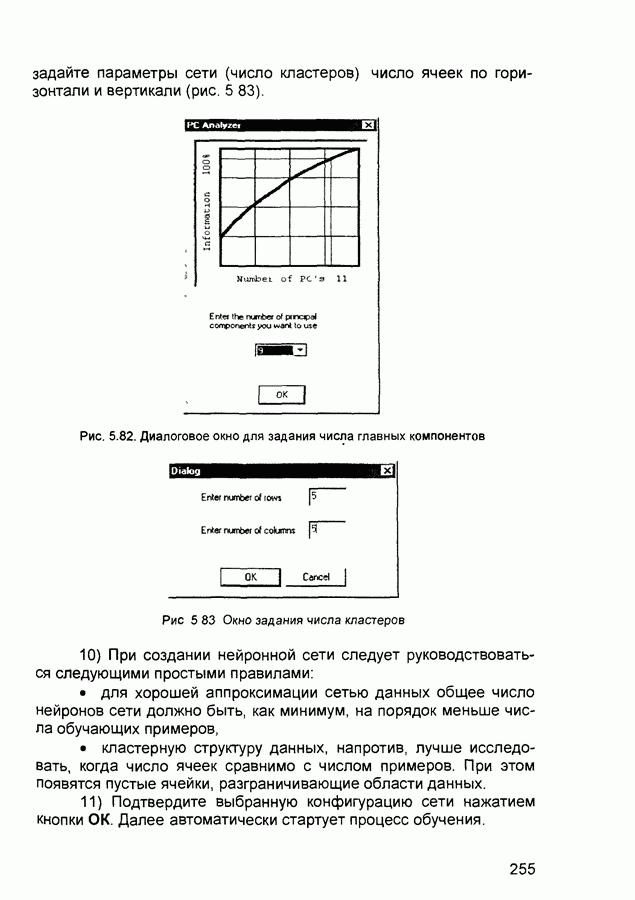
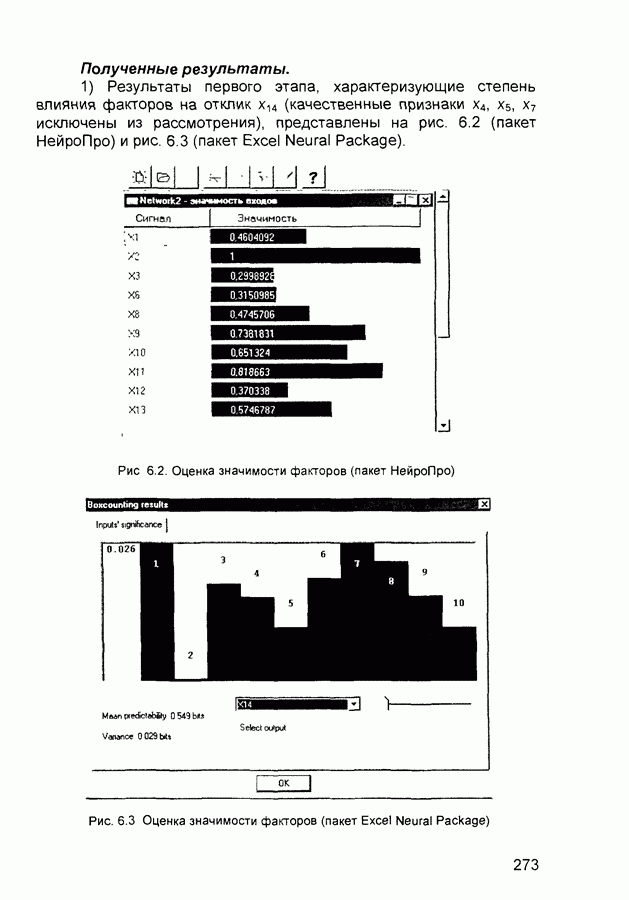
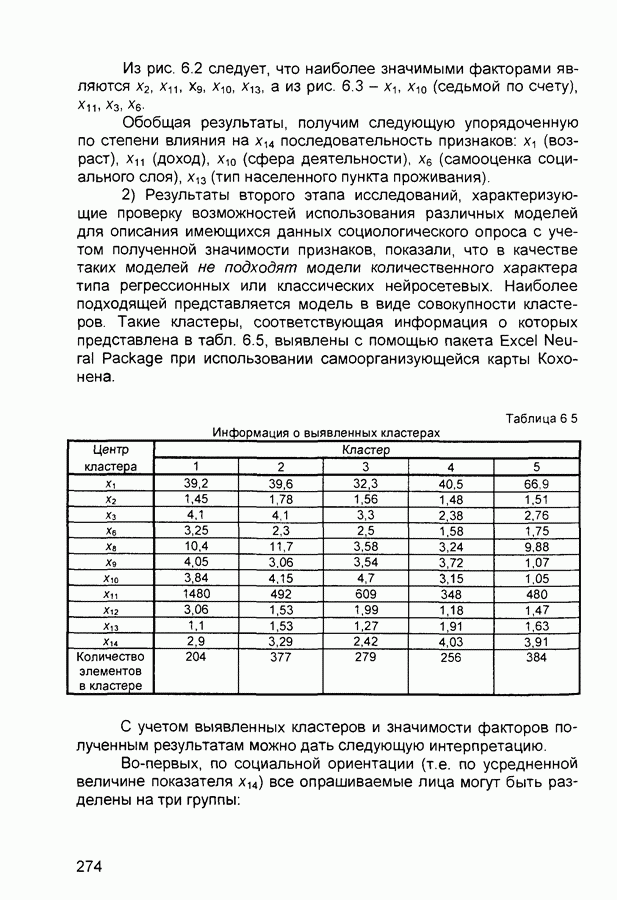
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. Нечеткий логический вывод
Используемый в различного рода экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида

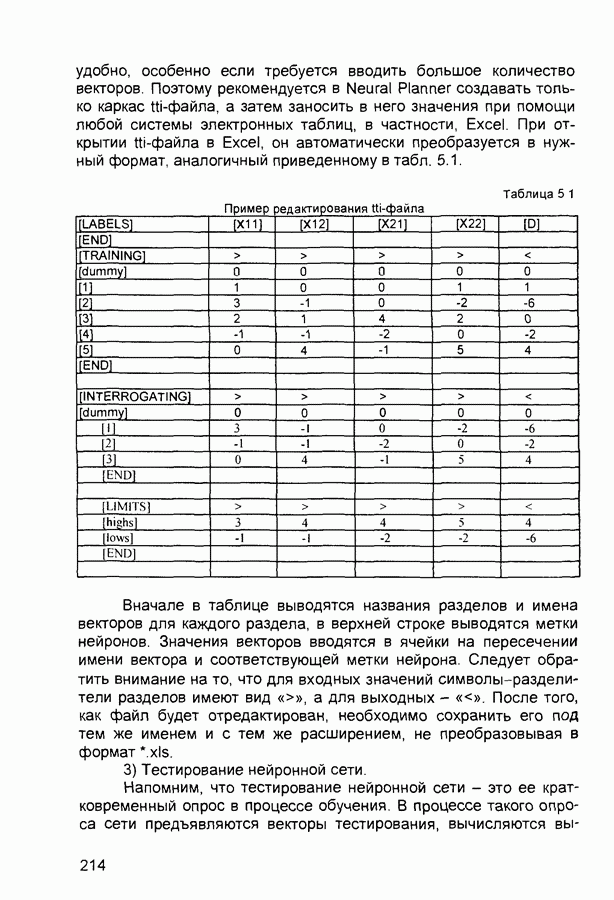
где х - входная переменная (имя для известных значений данных) у - переменная вывода (имя для значения данных, которое будет
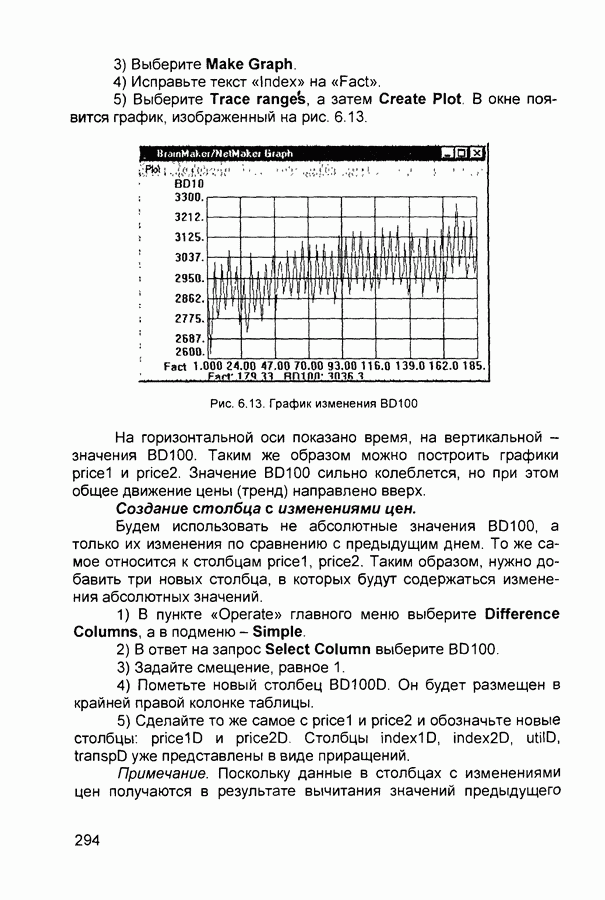
вычислено), А и В - функции принадлежности, определенные соответственно на х и у
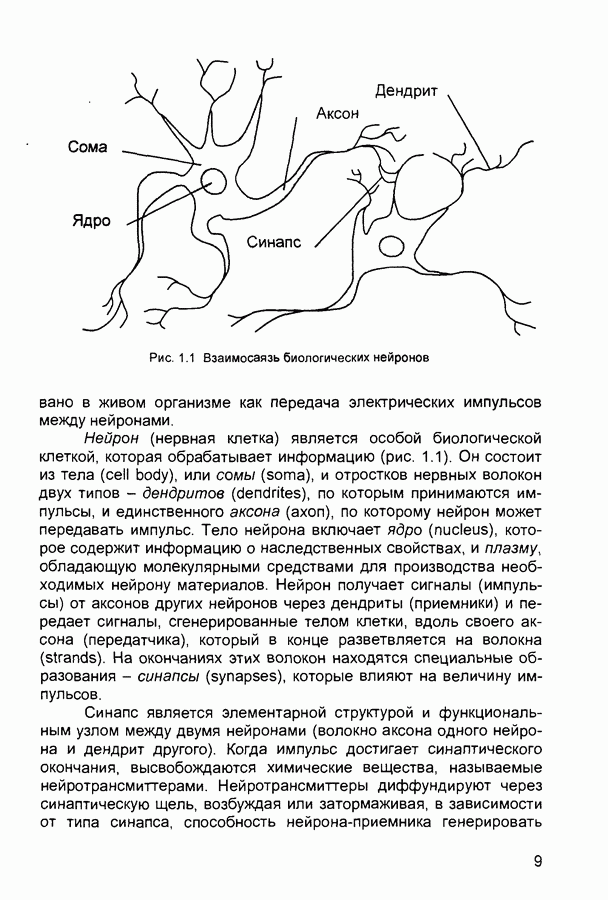
Приведем более детальное пояснение Знание эксперта  . В отражает нечеткое причинное отношение предпосылки и заключения, поэтому его можно назвать нечетким отношением и обозначить через
. В отражает нечеткое причинное отношение предпосылки и заключения, поэтому его можно назвать нечетким отношением и обозначить через 

где  называют нечеткой импликацией
называют нечеткой импликацией
Отношение  можно рассматривать как нечеткое подмножество прямого произведения
можно рассматривать как нечеткое подмножество прямого произведения  полного множества предпосылок X и заключений У Таким образом, процесс получения (нечеткого) результата вывода
полного множества предпосылок X и заключений У Таким образом, процесс получения (нечеткого) результата вывода  с использованием данного наблюдения А и знания
с использованием данного наблюдения А и знания  можно представить в виде композиционного правила нечеткий «modus ponens»
можно представить в виде композиционного правила нечеткий «modus ponens»

где «•» - введенная выше операция свертки
Как операцию композиции, так и операцию импликации в алгебре нечетких множеств можно реализовывать по-разному (при этом будет отличаться и получаемый результат), но в любом случае общий логический вывод осуществляется за следующие четыре этапа
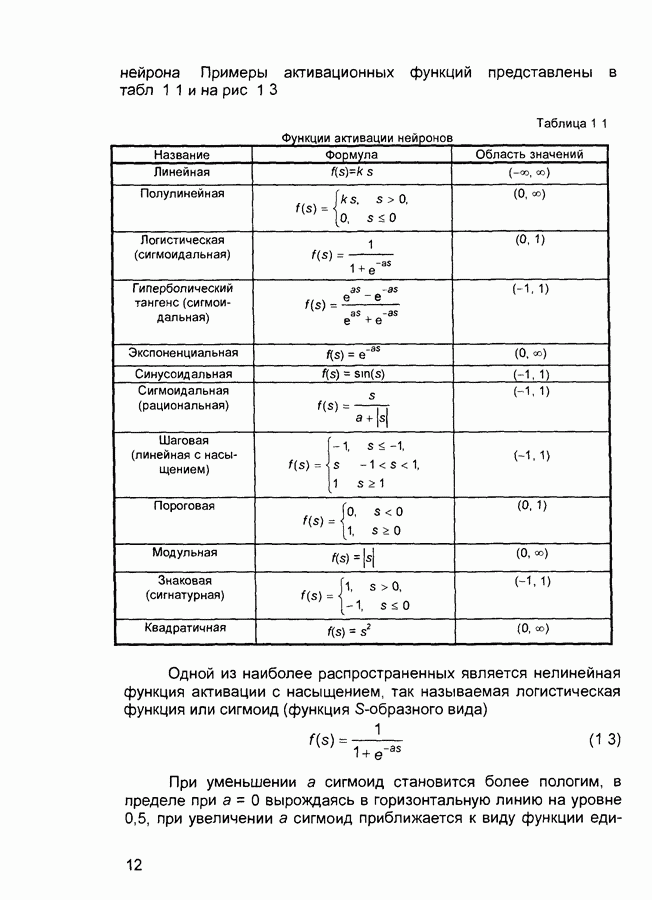
1) Введение нечеткости (фаззификация, fuzzification) Функции принадлежности, определенные на входных переменных, применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила
2) Логический вывод Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям каждого правила Это приводит к одному нечеткому подмножеству, которое будет назначено каждой переменной вывода для каждого правила В качестве правил логического вывода обычно используются только операции min (МИНИМУМ) или prod (УМНОЖЕНИЕ) В логическом выводе МИНИМУМА функция принадлежности вывода «отсекается» по высоте, соответствующей вычисленной степени истинности предпосылки правила (нечеткая логика «И») В логическом выводе УМНОЖЕНИЯ функция принадлежности вывода масштабируется при помощи вычисленной степени истинности предпосылки правила
3) Композиция Все нечеткие подмножества, назначенные к каждой переменной вывода (во всех правилах), объединяются вместе, чтобы сформировать одно нечеткое подмножество для всех переменных вывода При подобном объединении обычно используются операции max (МАКСИМУМ) или sum (СУММА) При
композиции МАКСИМУМА комбинированный вывод нечеткого подмножества конструируется как поточечный максимум по всем нечетким подмножествам (нечеткая логика «ИЛИ») При композиции СУММЫ комбинированный вывод нечеткого подмножества формируется как поточечная сумма по всем нечетким подмножествам, назначенным переменной вывода правилами логического вывода
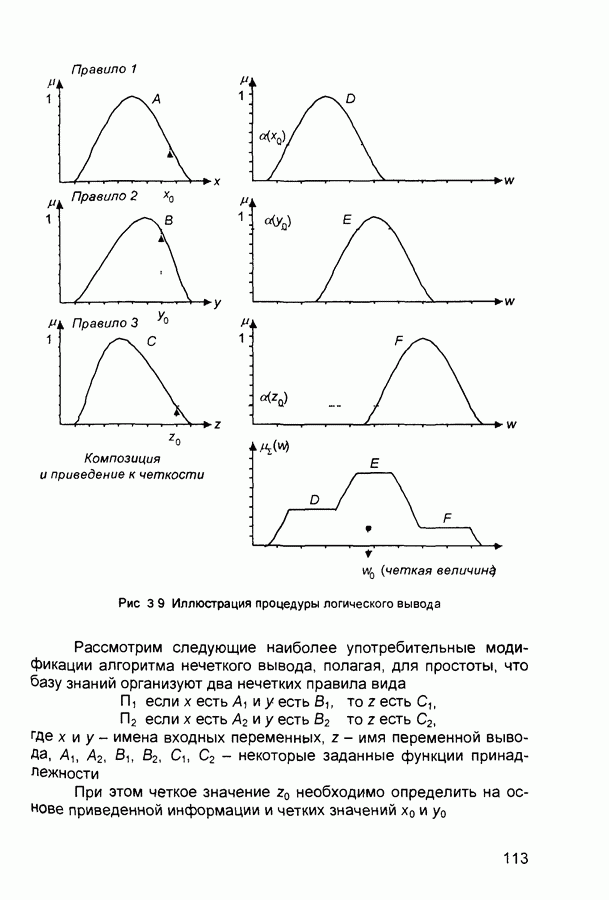
4) Приведение к четкости (дефаззификация, defuzzification) используется, если требуется преобразовать нечеткий набор выводов в четкое число Существует большее количество методов приведения к четкости, некоторые из которых рассмотрены ниже Пример Пусть некоторая система описывается следующими нечеткими правилами

где х, у и z - имена входных переменных,  - имя переменной вывода, а А, В, С, D, Е, F - заданные функции принадлежности (треугольной формы)
- имя переменной вывода, а А, В, С, D, Е, F - заданные функции принадлежности (треугольной формы)
Процедура получения логического вывода иллюстрируется рис 3 9 Предполагается, что заданы конкретные (четкие) значения входных переменных 
На первом этапе на основании данных значений и, исходя из функций принадлежности А, В, С, находятся степени истинности  для предпосылок каждого из трех приведенных правил
для предпосылок каждого из трех приведенных правил
На втором этапе происходит «отсекание» функций принадлежности заключений правил  на уровнях
на уровнях  На третьем этапе рассматриваются функции принадлежности, усеченные на предыдущем этапе, и производится их объединение с использованием операции
На третьем этапе рассматриваются функции принадлежности, усеченные на предыдущем этапе, и производится их объединение с использованием операции  в результате чего получается комбинированное нечеткое подмножество, описываемое функцией принадлежности
в результате чего получается комбинированное нечеткое подмножество, описываемое функцией принадлежности  соответствующее логическому выводу для выходной переменной
соответствующее логическому выводу для выходной переменной 
Наконец, на четвертом этапе находится, при необходимости четкое значение выходной переменной, например, с применением центроидного метода четкое значение выходной переменной определяется как центр тяжести для кривой 


Рис. 3.9 Иллюстрация процедуры логического вывода
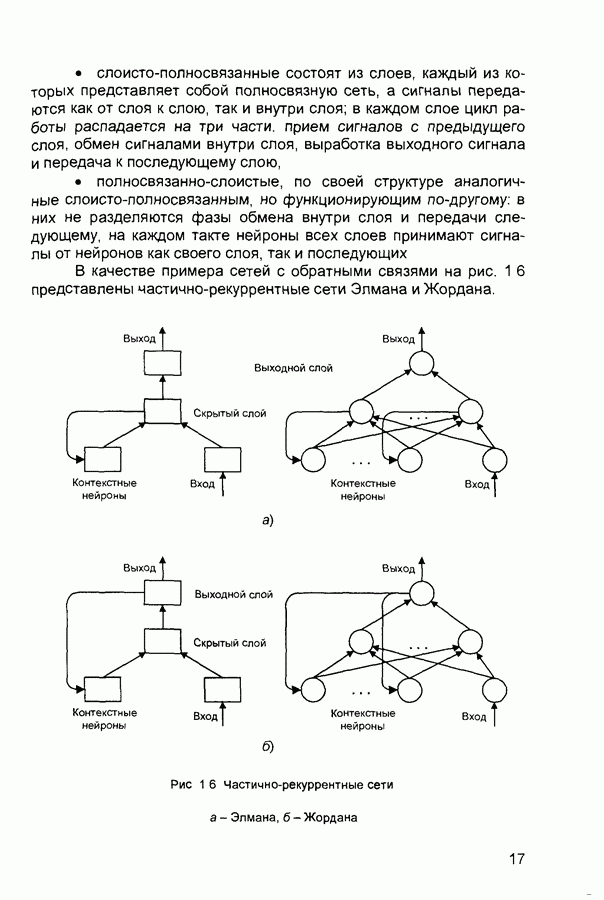
Рассмотрим следующие наиболее употребительные модификации алгоритма нечеткого вывода, полагая, для простоты, что базу знаний организуют два нечетких правила вида

где х и у - имена входных переменных, z - имя переменной вывода, А,, А2, Вь В2, С,, С2 - некоторые заданные функции принадлежности
При этом четкое значение z0 необходимо определить на основе приведенной информации и четких значений 
Алгоритм Mamdani
Данный алгоритм соответствует рассмотренному примеру и рис. 3.9 В рассматриваемой ситуации он математически может быть описан следующим образом
1) Введение нечеткости Находятся степени истинности для предпосылок каждого правила 
2) Логический вывод Находятся уровни «отсечения» для предпосылок каждого из правил (с использованием операции МИНИМУМ)

 где через
где через  обозначена операция логического минимума
обозначена операция логического минимума 
Затем находятся «усеченные» функции принадлежности 

3) Композиция Производится объединение найденных усеченных функций с использованием операции МАКСИМУМ (max далее обозначаемой как  что приводит к получению итогового нечеткого подмножества для переменной выхода с функцией принадлежности
что приводит к получению итогового нечеткого подмножества для переменной выхода с функцией принадлежности

4) Приведение к четкости Проводится для нахождения  например, центроидным методом
например, центроидным методом
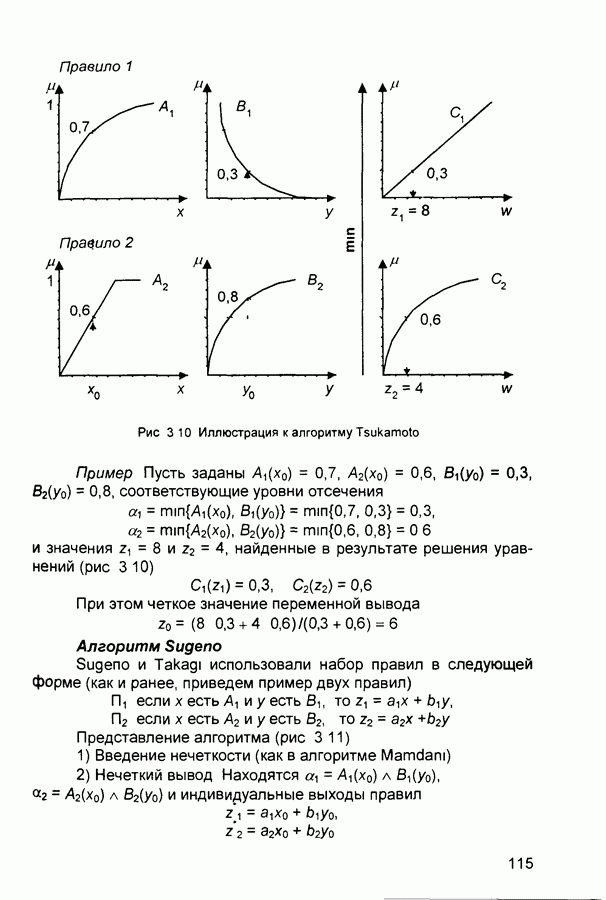
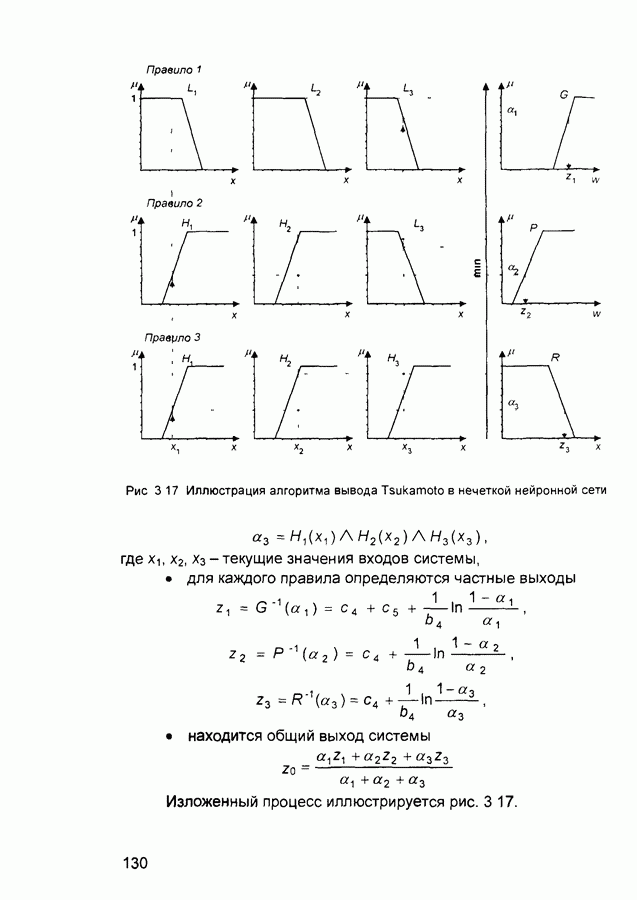
Алгоритм Tsukamoto
Исходные посылки - как у предыдущего алгоритма, но здесь предполагается, что функции  являются монотонными
являются монотонными
1) Введение нечеткости (как в алгоритме 
2) Нечеткий вывод Сначала находятся уровни «отсечения»  (как в алгоритме
(как в алгоритме  а затем решением уравнений
а затем решением уравнений

определяются четкие значения  для каждого исходного правила
для каждого исходного правила
3) Определяется четкое значение переменной вывода (как взвешенное среднее  и
и 

в общем случае (дискретный вариант центроидного метода)


Рис. 3.10 Иллюстрация к алгоритму Tsukamoto
Пример Пусть заданы  соответствующие уровни отсечения
соответствующие уровни отсечения

и значения  найденные в результате решения уравнений (рис 3 10)
найденные в результате решения уравнений (рис 3 10)

При этом четкое значение переменной вывода

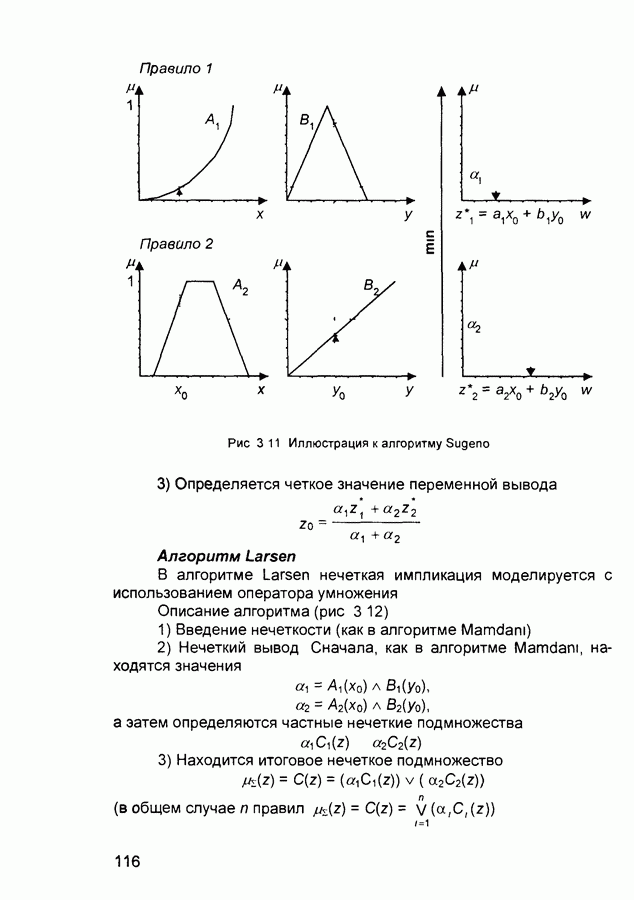
Алгоритм Sugeno
Sugeno и Takagi использовали набор правил в следующей форме (как и ранее, приведем пример двух правил)

Представление алгоритма (рис 3 11)
1) Введение нечеткости (как в алгоритме Mamdam)
2) Нечеткий вывод Находятся  и индивидуальные выходы правил
и индивидуальные выходы правил


Рис. 3.11 Иллюстрация к алгоритму Sugeno
3) Определяется четкое значение переменной вывода

Алгоритм Larsen
В алгоритме Larsen нечеткая импликация моделируется с использованием оператора умножения Описание алгоритма (рис 3 12)
1) Введение нечеткости (как в алгоритме Mamdam)
2) Нечеткий вывод Сначала, как в алгоритме Mamdam, находятся значения

а затем определяются частные нечеткие подмножества

3) Находится итоговое нечеткое подмножество

(в общем случае  правил
правил 

Рис. 3.12 Иллюстрация к алгоритму Larsen
4) При необходимости производится приведение к четкости (как в ранее рассмотренных алгоритмах)
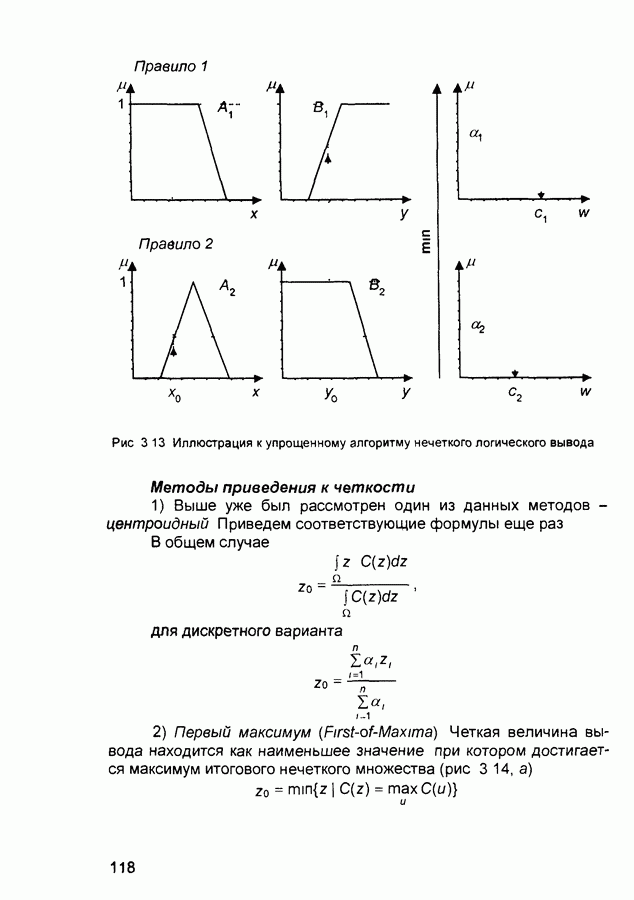
Упрощенный алгоритм нечеткого вывода Исходные правила в данном случае задаются в виде

где  — некоторые четкие числа Описание алгоритма (рис 3 13)
— некоторые четкие числа Описание алгоритма (рис 3 13)
1) Введение нечеткости (как в алгоритме Mamdam)
2) Нечеткий вывод Находятся числа 
3) Определяется четкое значение выходной переменной

(в общем случае  правил
правил 

Рис. 3.13 Иллюстрация к упрощенному алгоритму нечеткого логического вывода
Методы приведения к четкости
1) Выше уже был рассмотрен один из данных методов - центроидный Приведем соответствующие формулы еще раз
В общем случае

для дискретного варианта

2) Первый максимум (First-of-Maxima) Четкая величина вывода находится как наименьшее значение при котором достигается максимум итогового нечеткого множества (рис 3 14, а)


Рис. 3.14 Иллюстрация к методам приведения к четкости а - первый максимум б - средний максимум
3) Средний максимум  Четкое значение находится по формуле
Четкое значение находится по формуле

где  - подмножество элементов, максимизирующих С (рис. 3.14 б)
- подмножество элементов, максимизирующих С (рис. 3.14 б)
Для дискретного варианта (С дискретно)

4) Критерий максимума  Четкое значение выбирается произвольно среди множества элементов, для которых С достигает максимума
Четкое значение выбирается произвольно среди множества элементов, для которых С достигает максимума

5) Высотная дефаззификация  Элементы области определения
Элементы области определения  для которых значения функции принадлежности меньше, чем некоторый уровень а в расчет не принимаются и четкое значение рассчитывается в соответствии с выражением
для которых значения функции принадлежности меньше, чем некоторый уровень а в расчет не принимаются и четкое значение рассчитывается в соответствии с выражением

где  - нечеткое множество
- нечеткое множество  -уровня (см выше)
-уровня (см выше)
Нисходящие нечеткие логические выводы
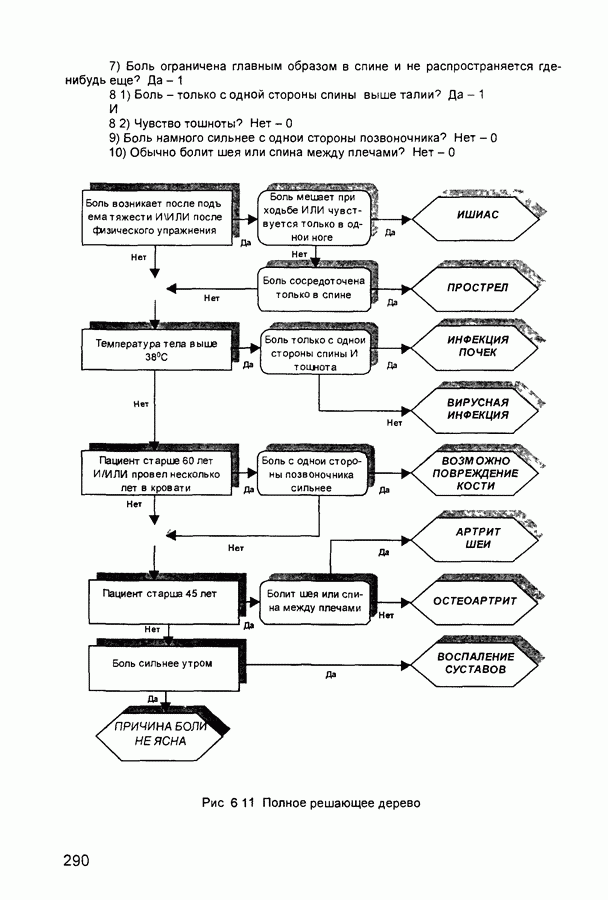
Ранее рассмотренные нечеткие логические выводы являются восходящими выводами от предпосылок к заключениям. В диагностических нечетких системах часто применяются нисходящие выводы. Рассмотрим механизм подобного вывода.
Пусть задано полное пространство предпосылок  и полное пространство заключений
и полное пространство заключений 
Между х, и у, существуют нечеткие причинные отношения  которые можно представить в виде некоторой матрицы
которые можно представить в виде некоторой матрицы  с элементами
с элементами  Предпосылки и заключения можно рассматривать как нечеткие множества А и В на пространствах X и Y, отношения которых можно представить в виде:
Предпосылки и заключения можно рассматривать как нечеткие множества А и В на пространствах X и Y, отношения которых можно представить в виде:

где «•», как и раньше, обозначает правило композиции нечетких выводов, например max-min-композицию.
В данном случае направление выводов является обратным для правил, т. е. задана матрица  (знания эксперта), наблюдаются выходы В (заключения) и определяются входы А (предпосылки).
(знания эксперта), наблюдаются выходы В (заключения) и определяются входы А (предпосылки).
Пусть задана модель диагностики системы, состоящая из двух предпосылок и трех заключений:  а матрица нечетких отношений имеет вид:
а матрица нечетких отношений имеет вид:

Допустим в результате диагностики системы были получены следующие заключения:

Необходимо найти приведшие к этому предпосылки:

С учетом конкретных данных отношения между предпосылками и заключениями будут представлены следующим образом:

либо в транспонированном виде.

При использовании max-min-композиции последнее соотношение преобразуется к виду:


При решении данной системы заметим, что в первом уравнении второй член правой части не влияет на левую часть, поэтому:

Из второго уравнения получим:

Полученное решение удовлетворяет третьему уравнению. Таким образом:

При решении практических задач могут одновременно использоваться различные правила композиции нечетких выводов, сама схема выводов может быть многокаскадной. В настоящее время общих методов решения подобных задач, по-видимому, не существует.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
- 1.1. Биологический нейрон
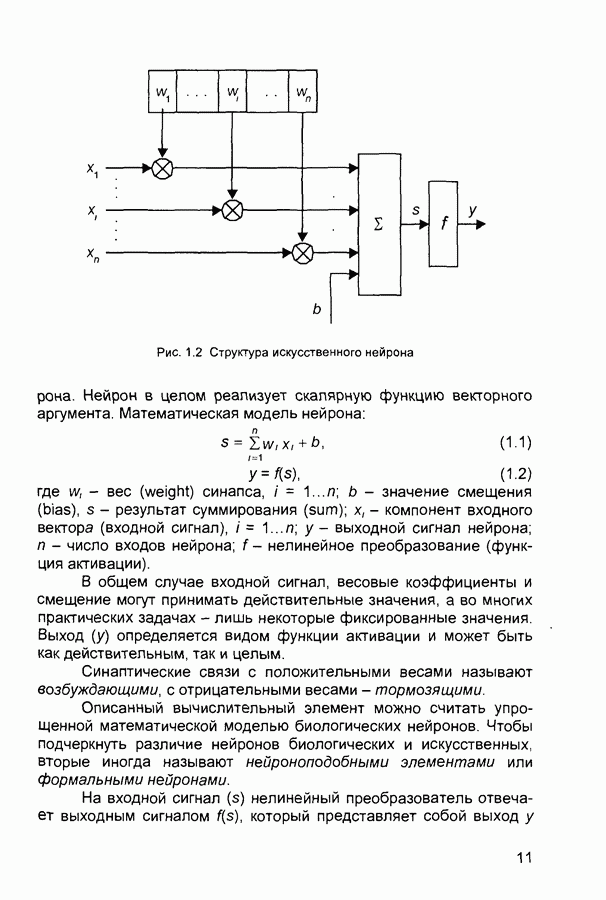
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
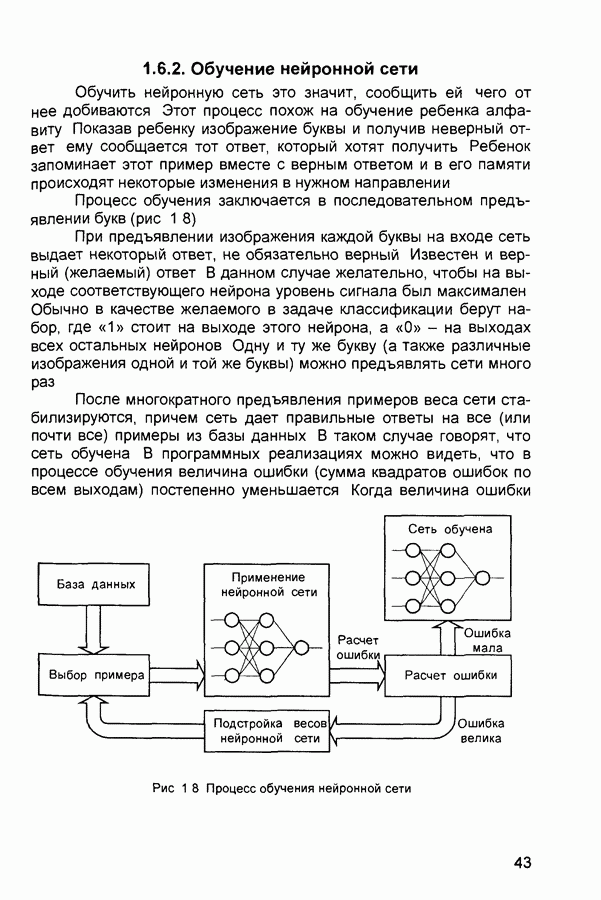
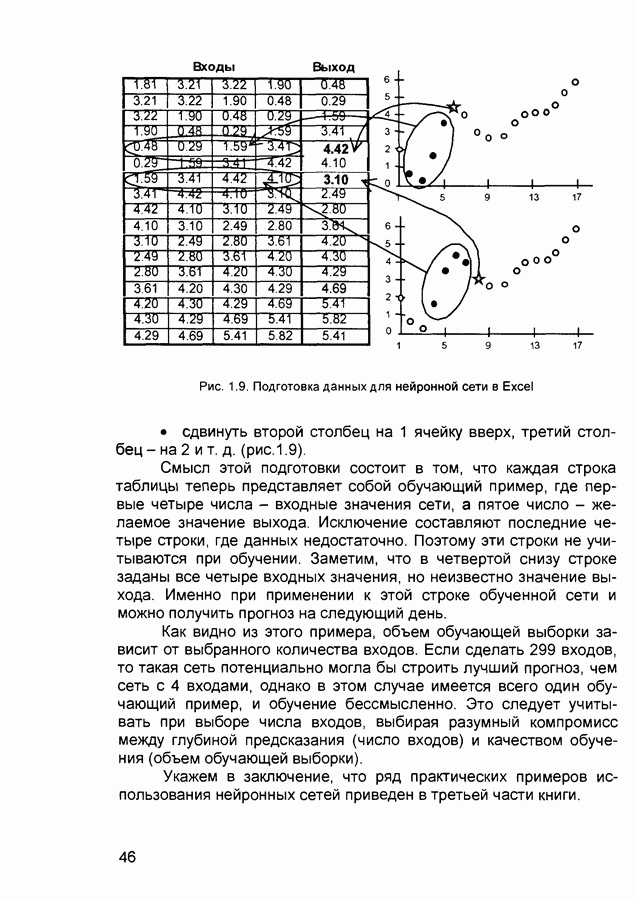
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
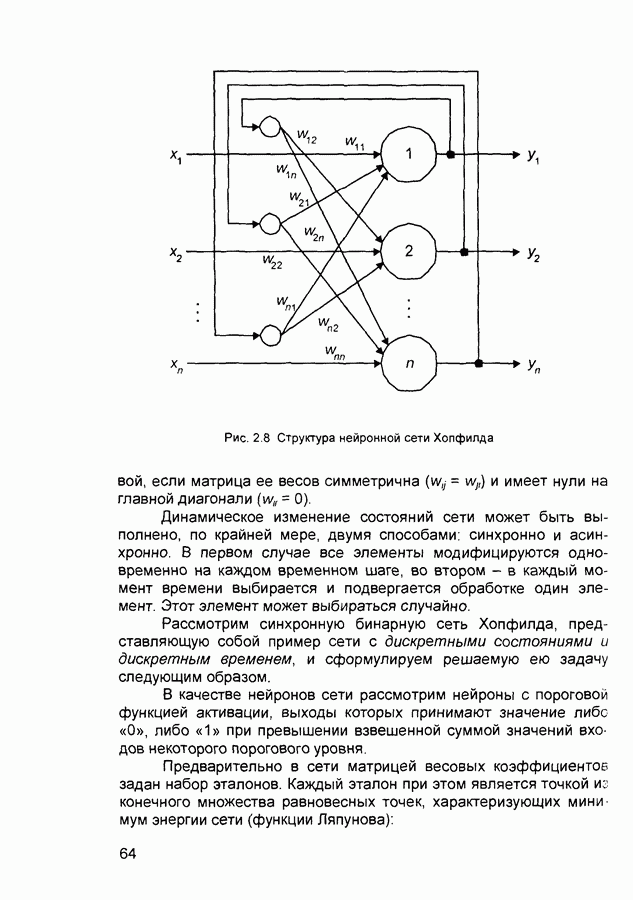
- 2.1. Ассоциативная память нейронных сетей
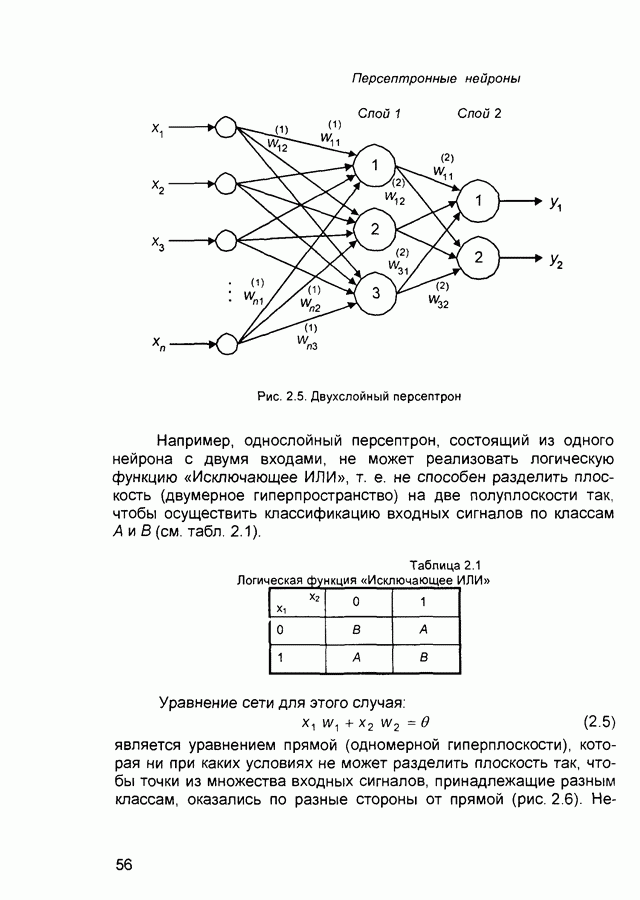
- 2.2. Персептроны
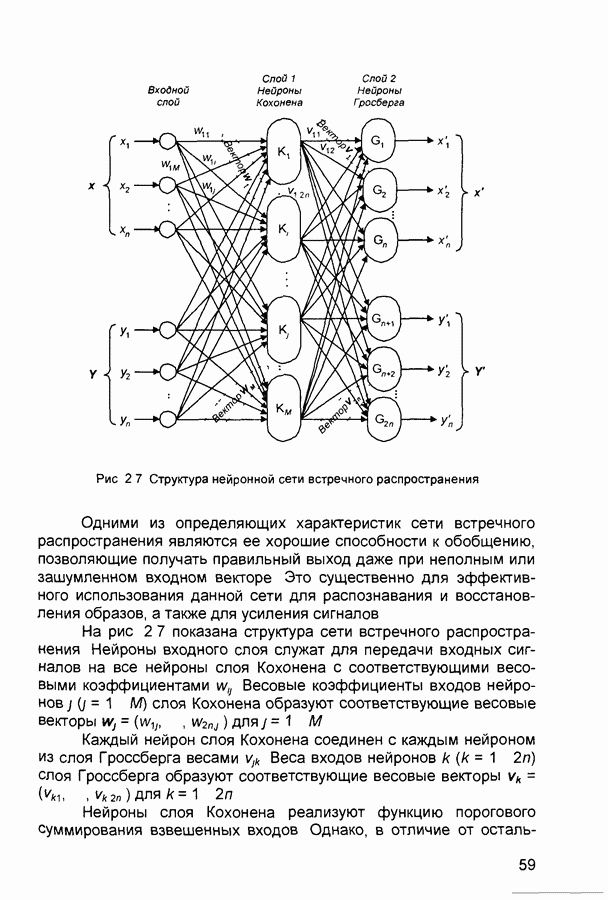
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
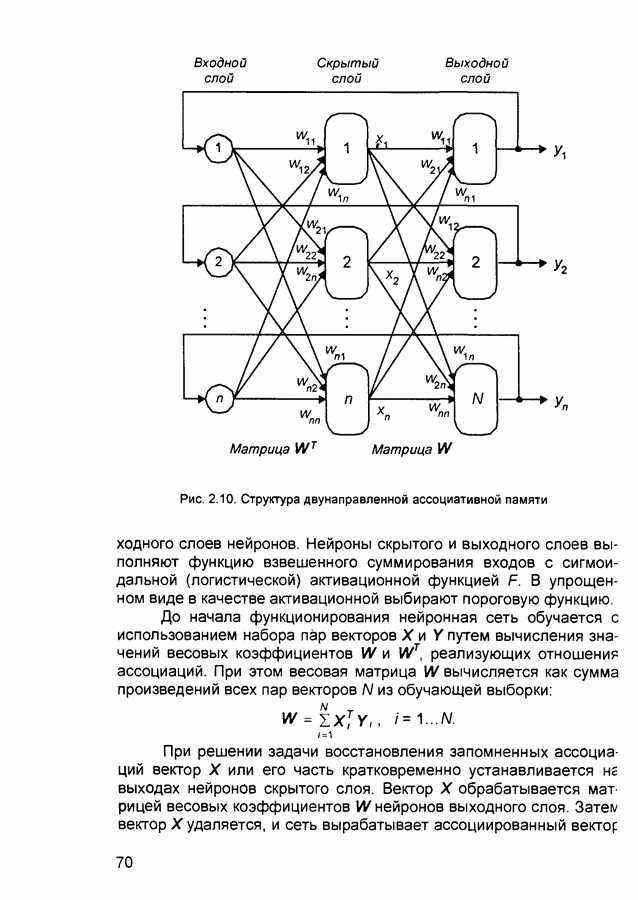
- 2.5. Двунаправленная ассоциативная память
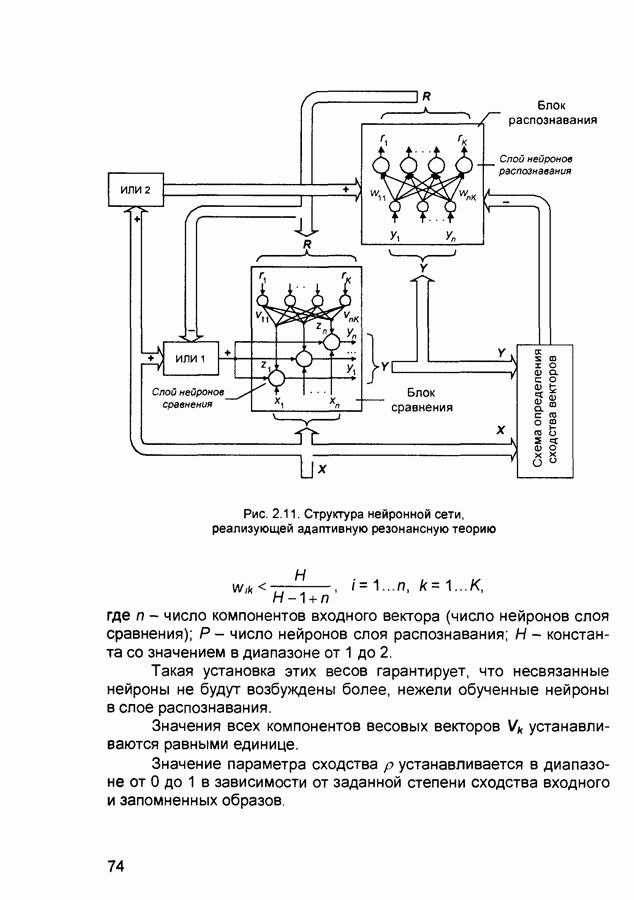
- 2.6. Сети адаптивной резонансной теории
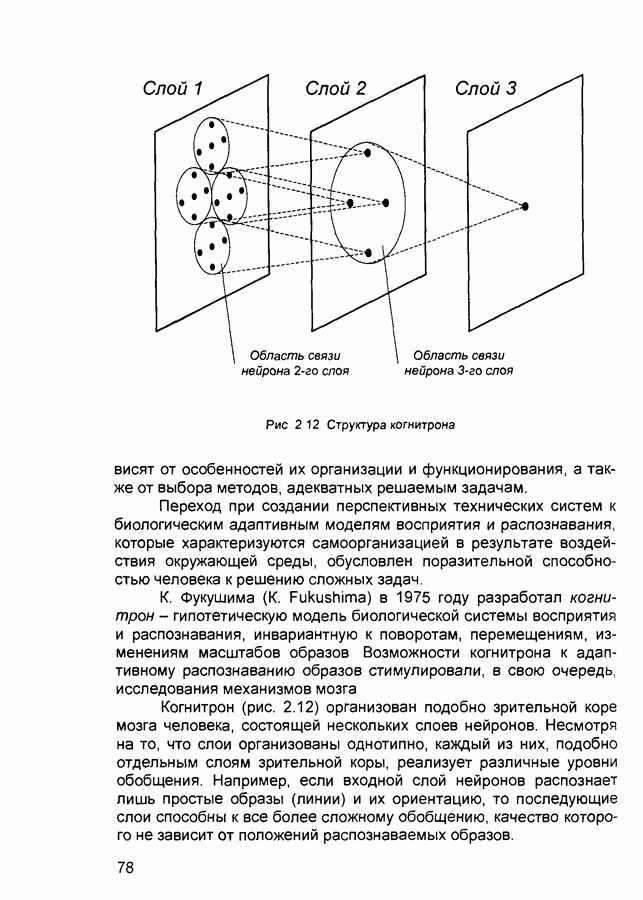
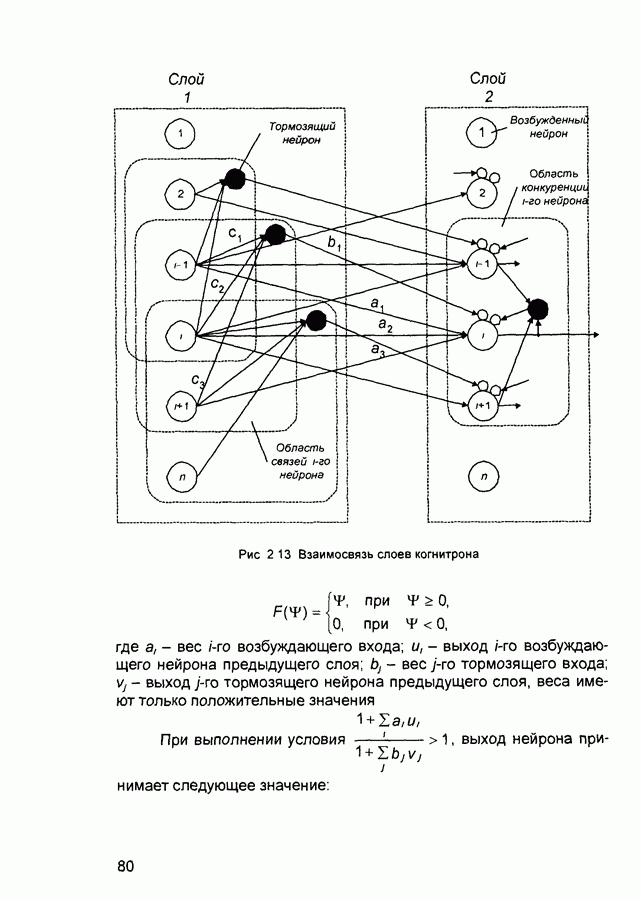
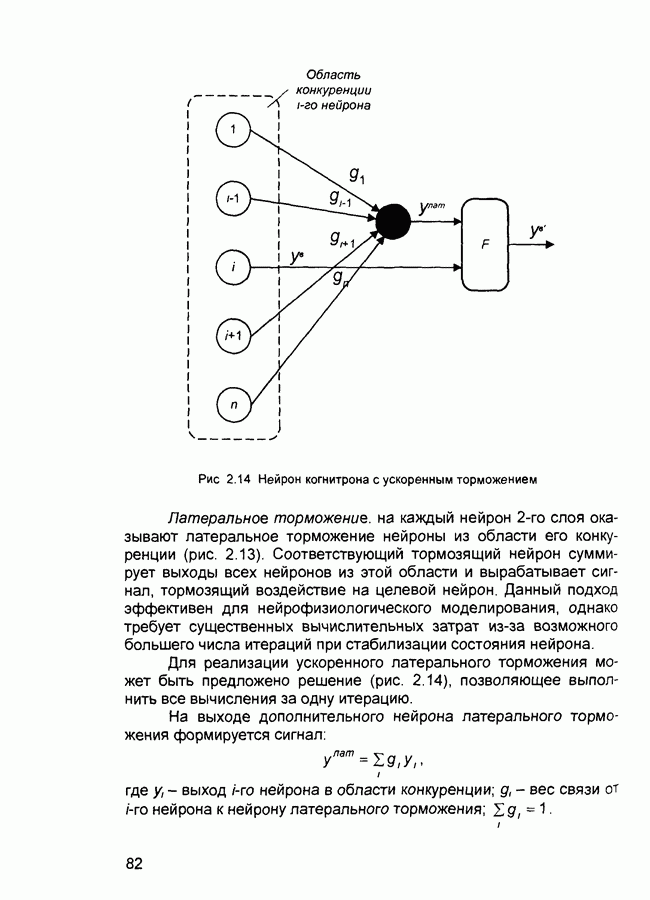
- 2.7. Когнитрон
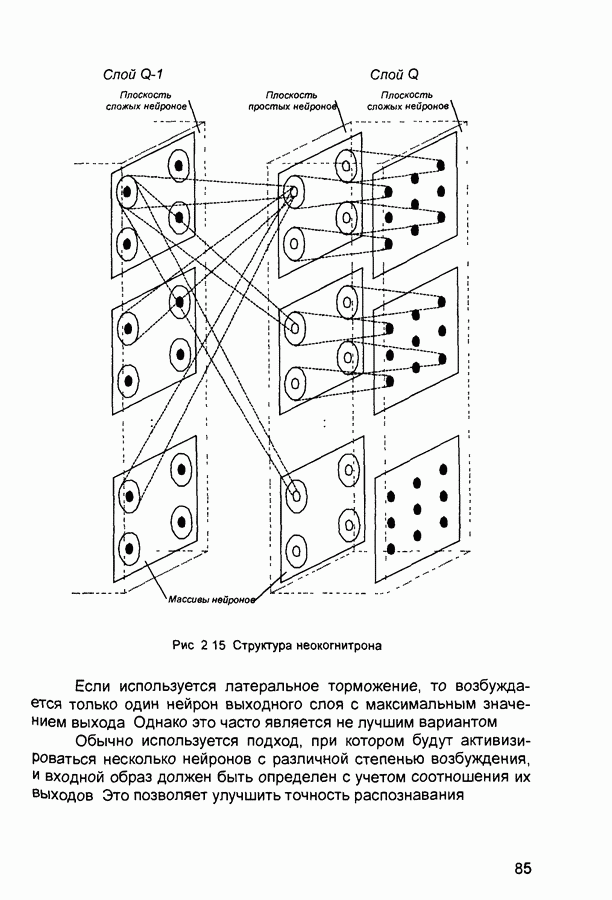
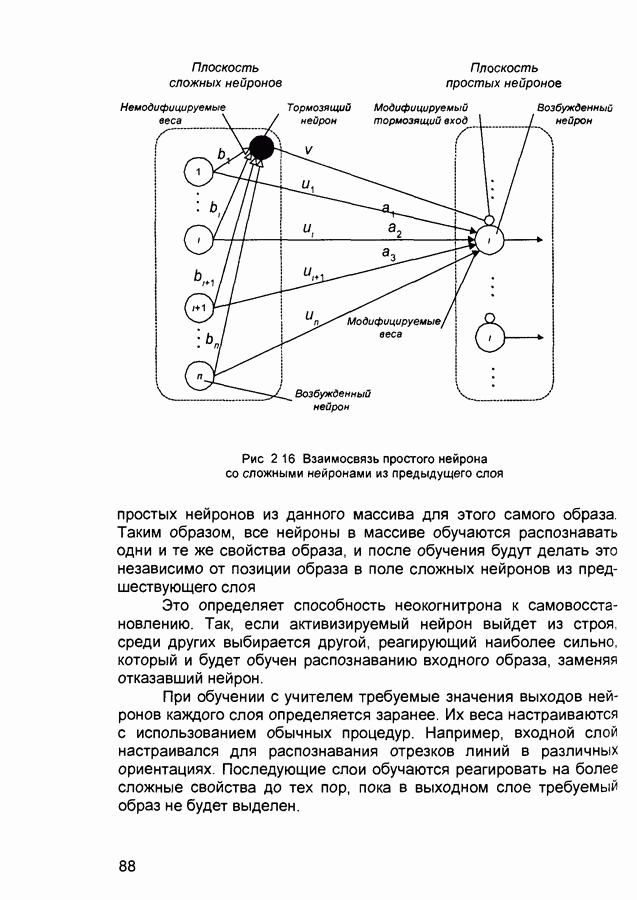
- 2.8. Неокогнитрон
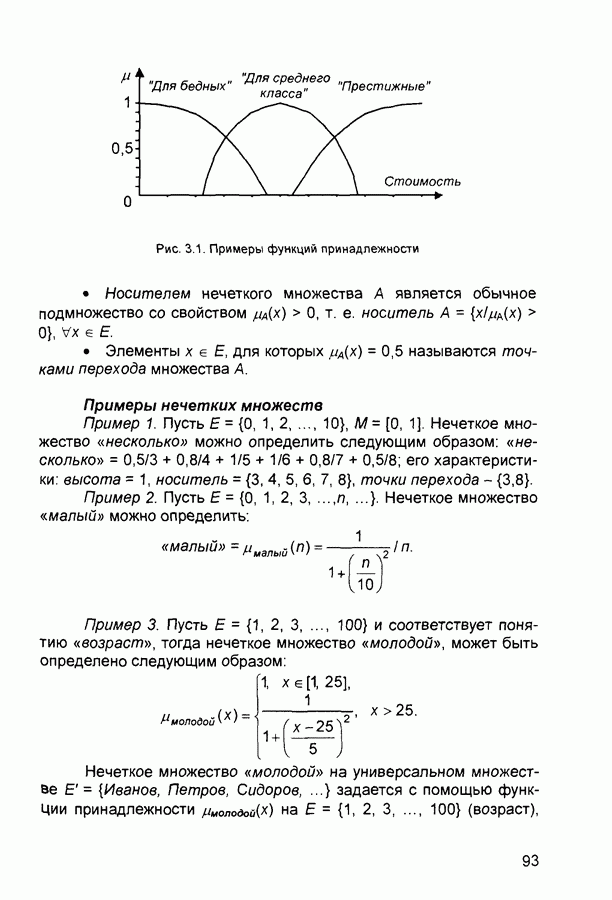
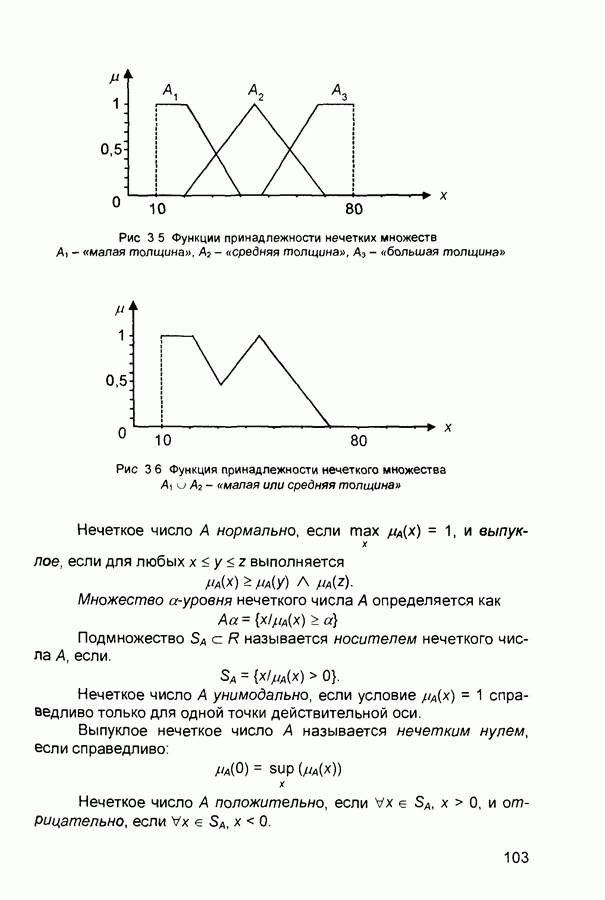
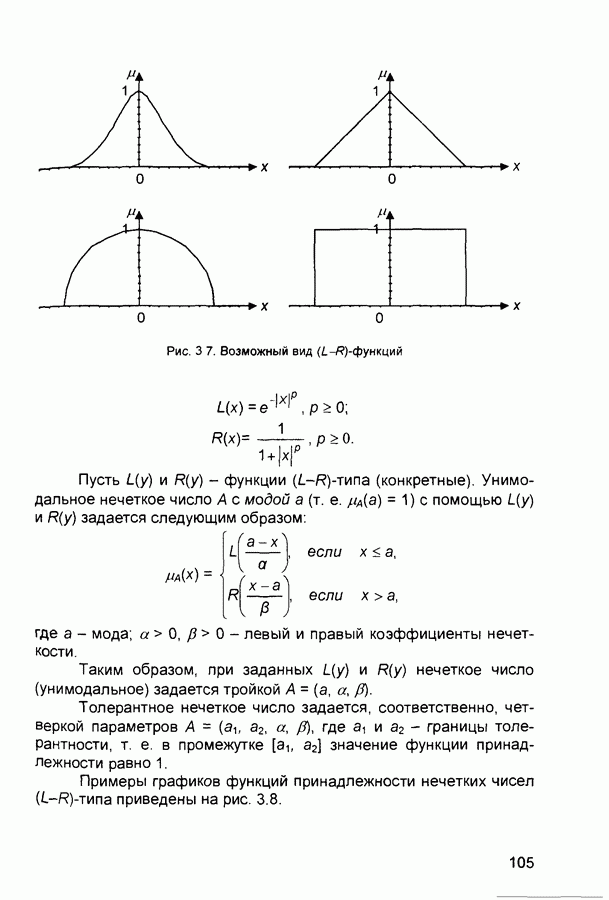
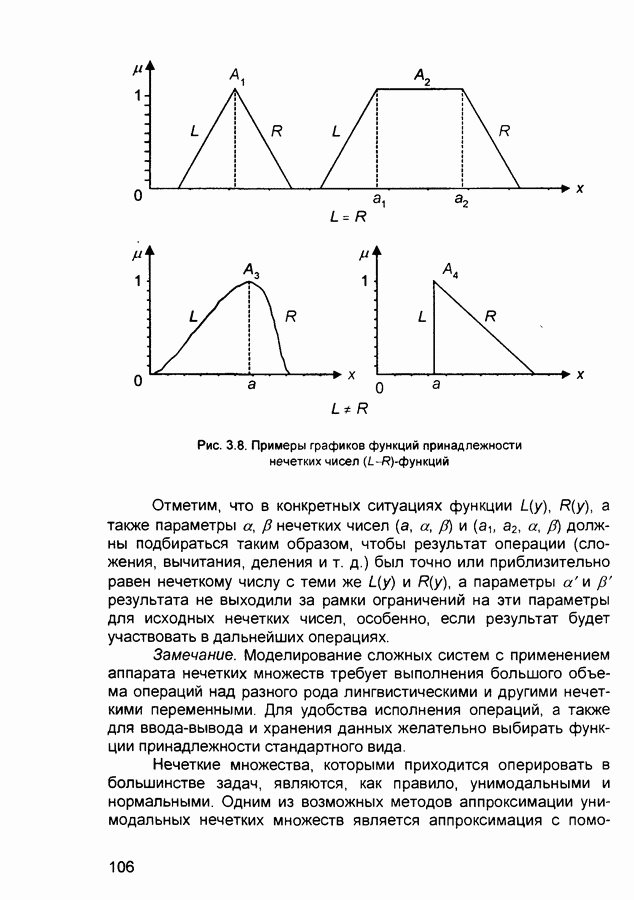
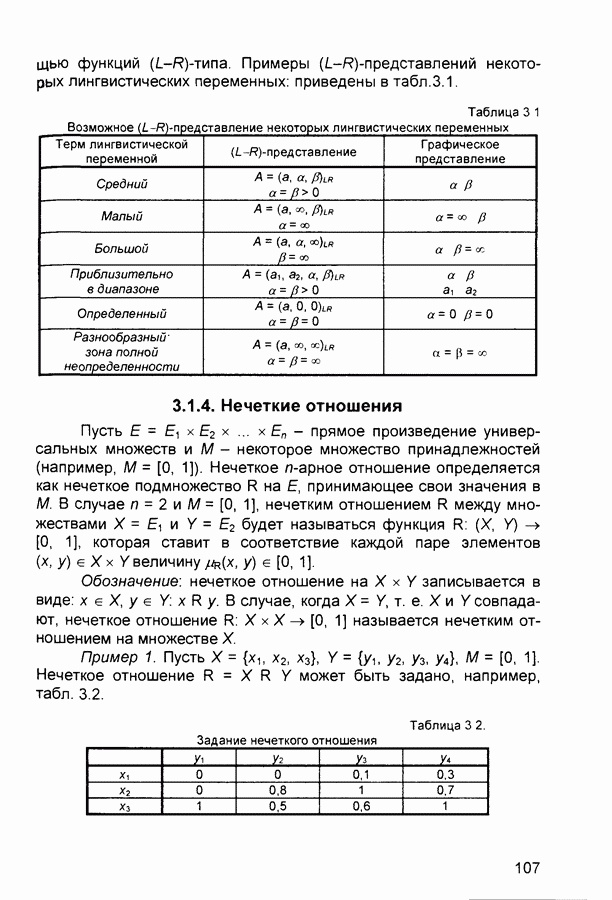
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
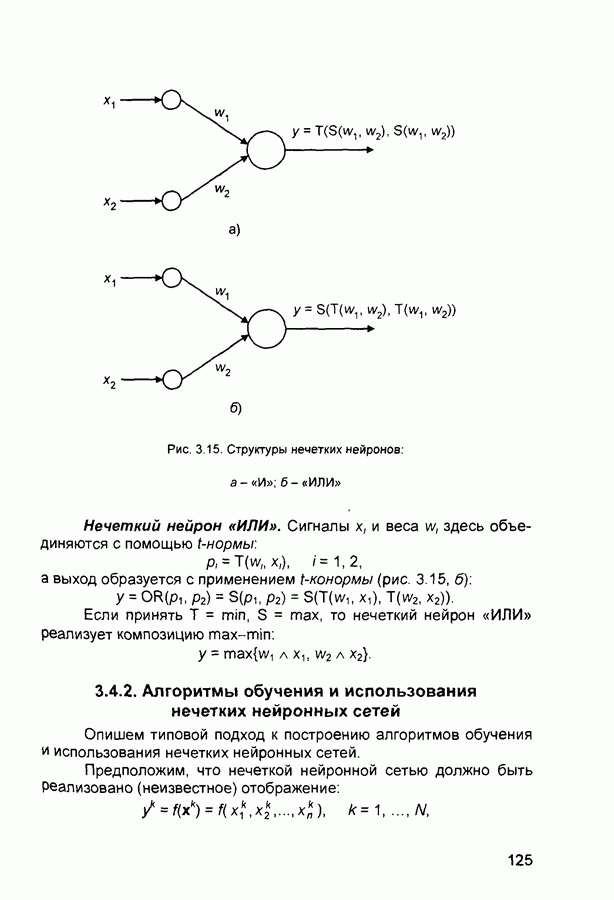
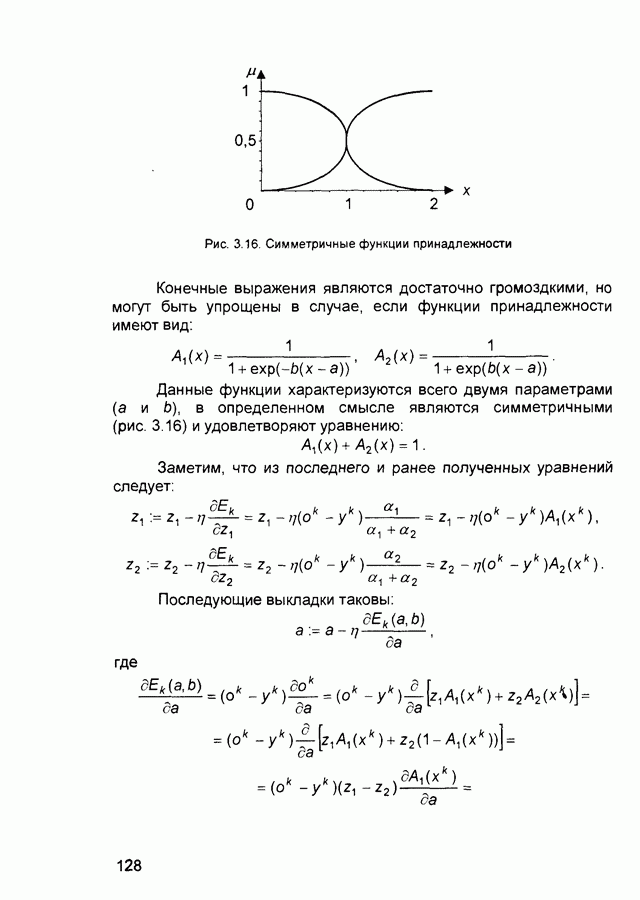
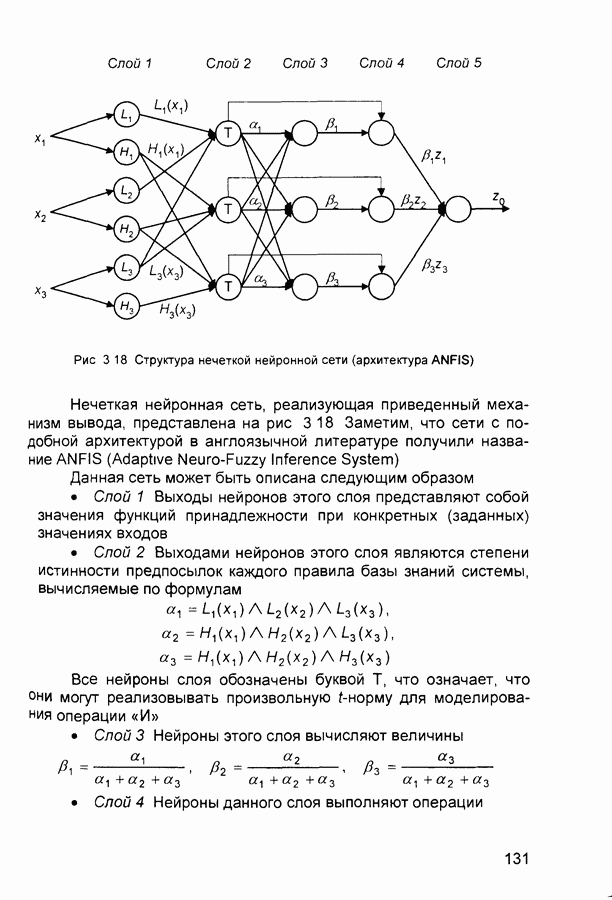
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
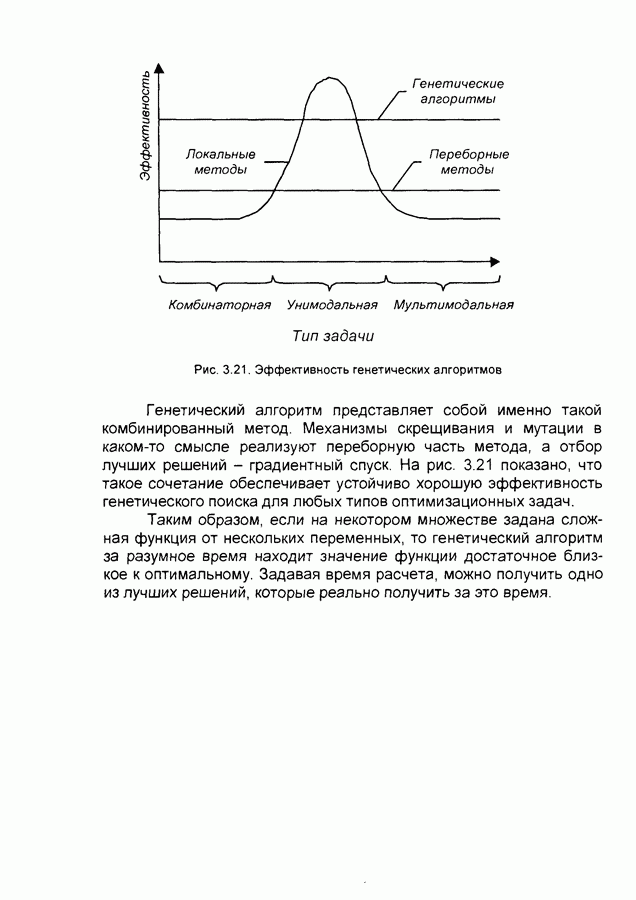
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
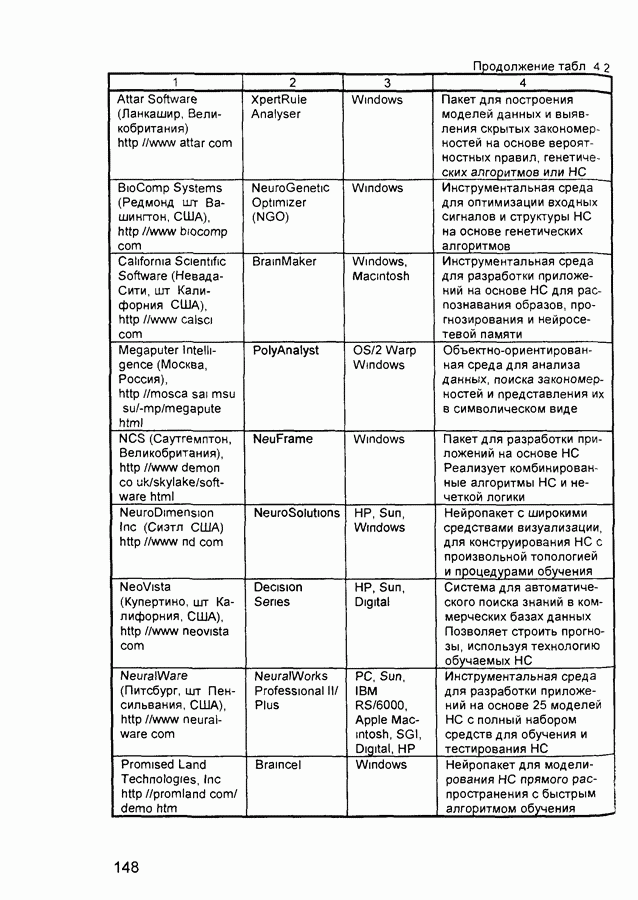
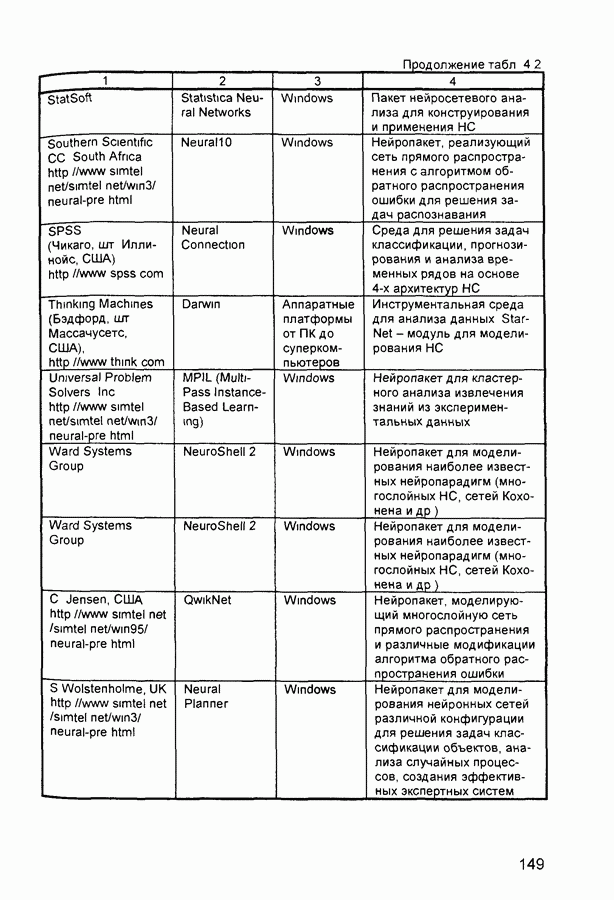
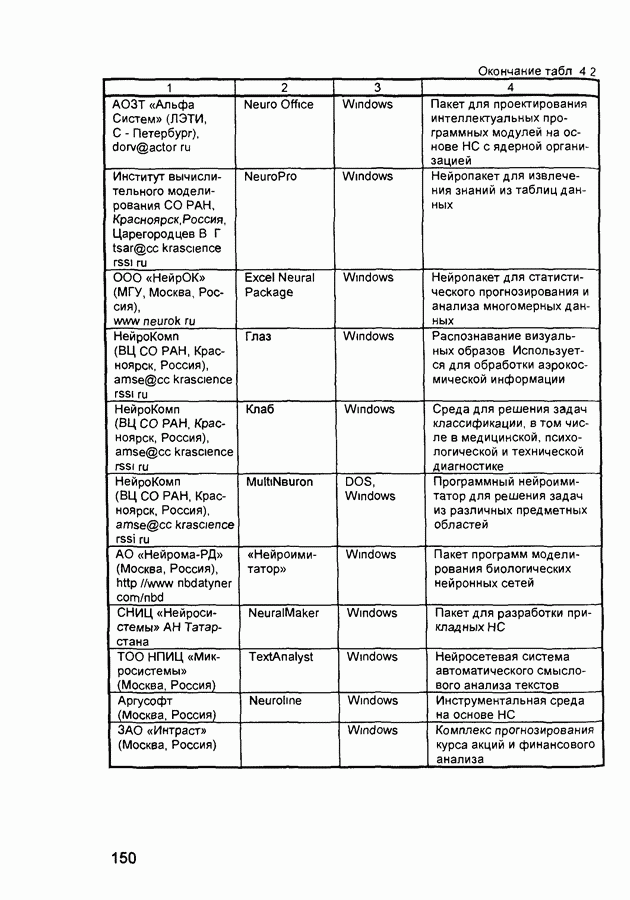
- 4.2. Характеристики современных нейропакетов
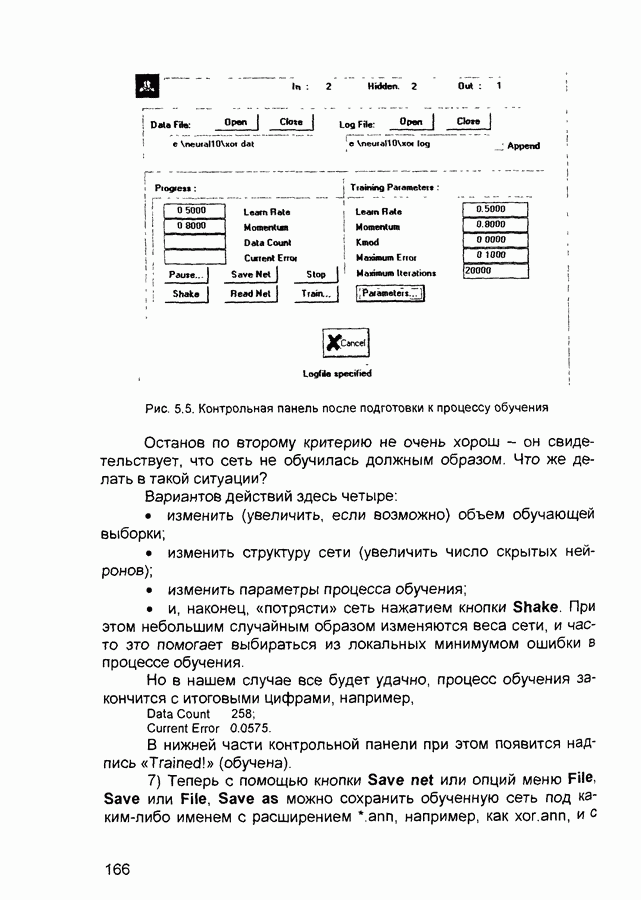
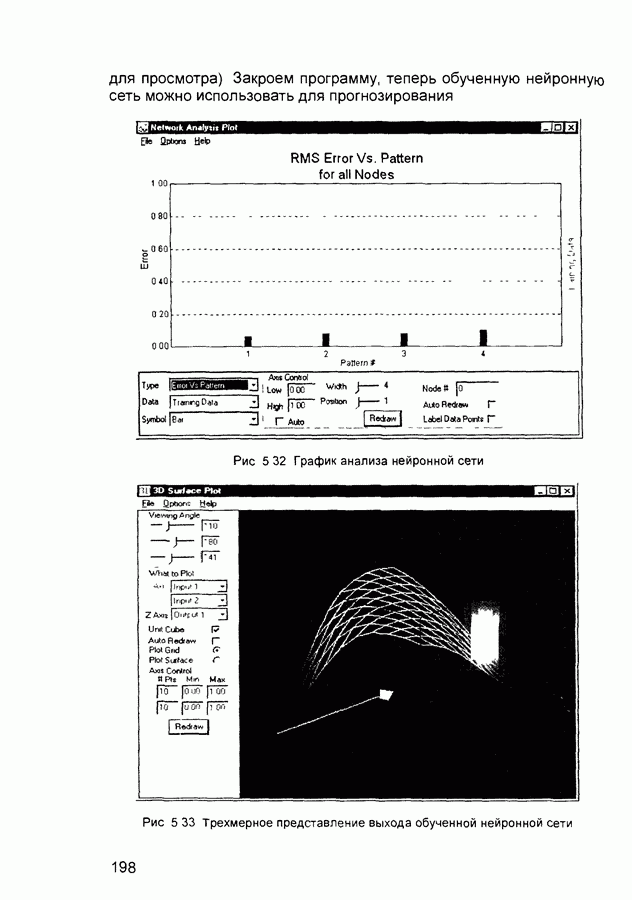
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
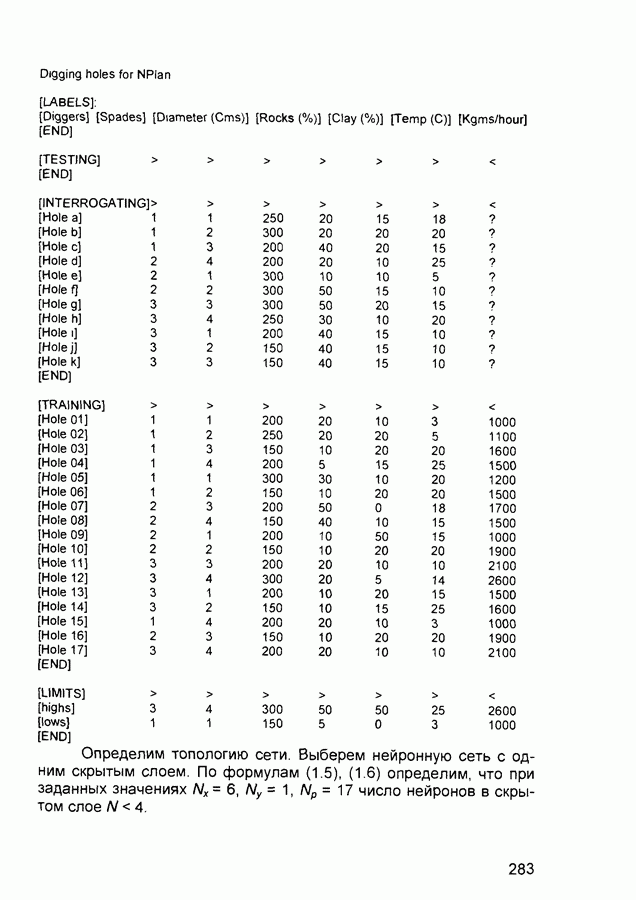
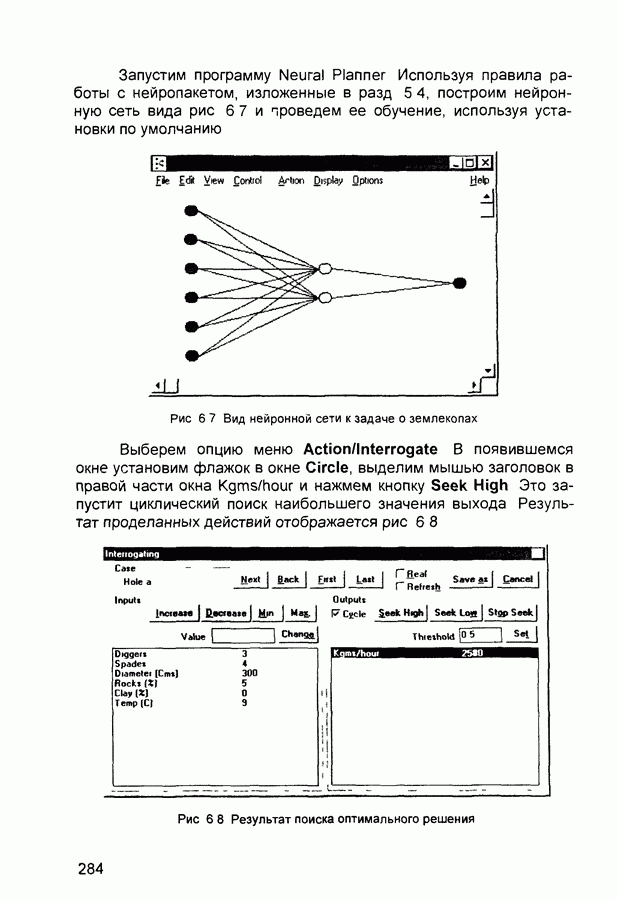
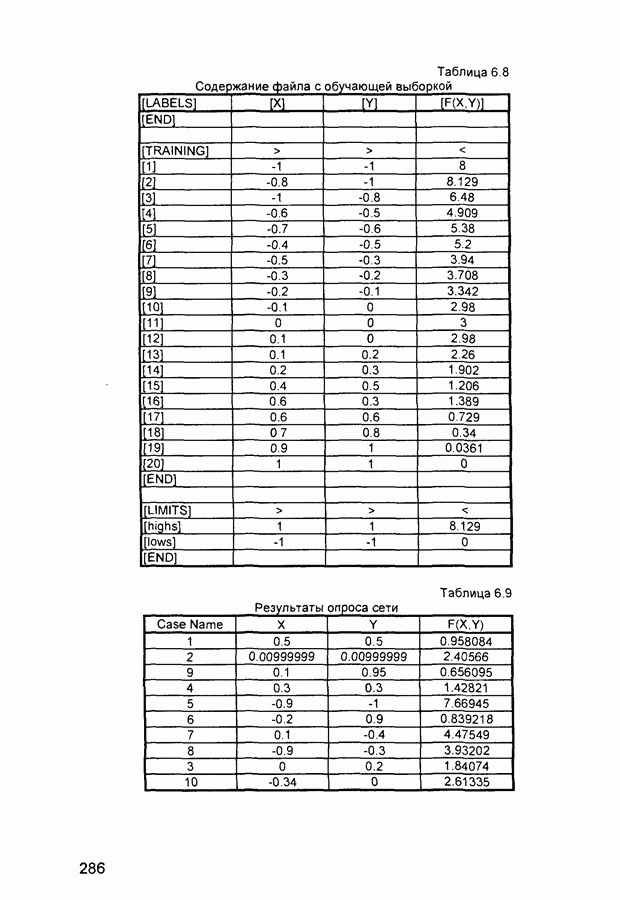
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
- 6.7. Нейросетевая экспертная система
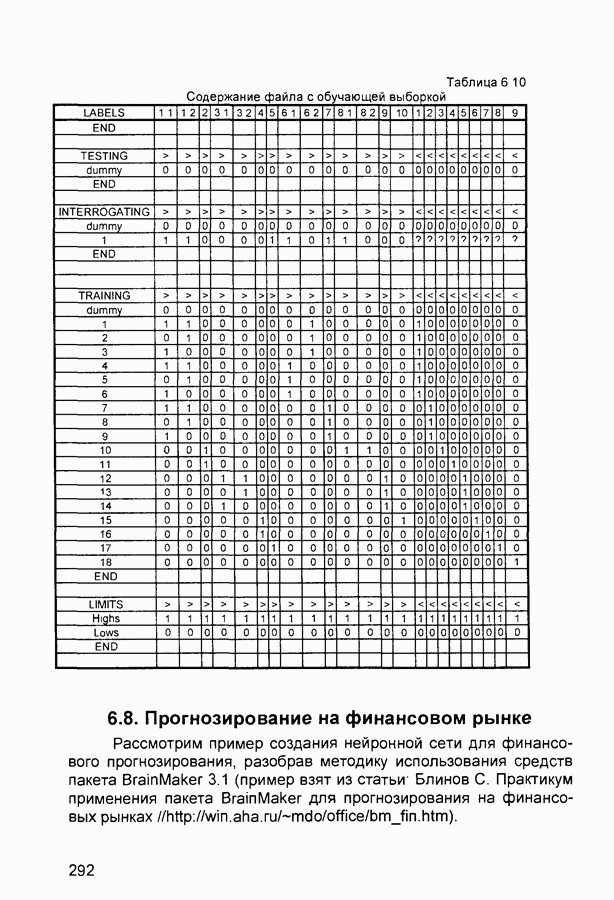
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
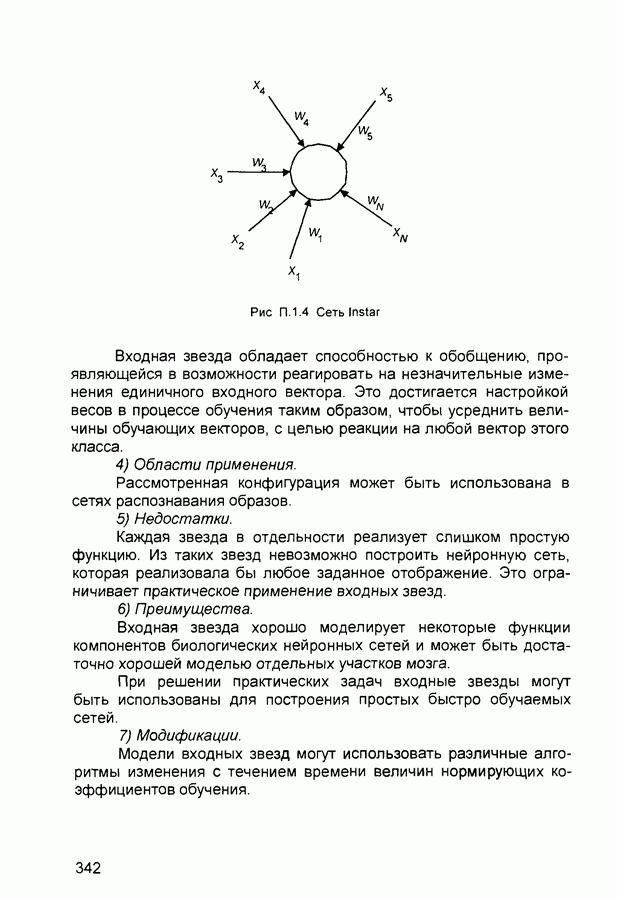
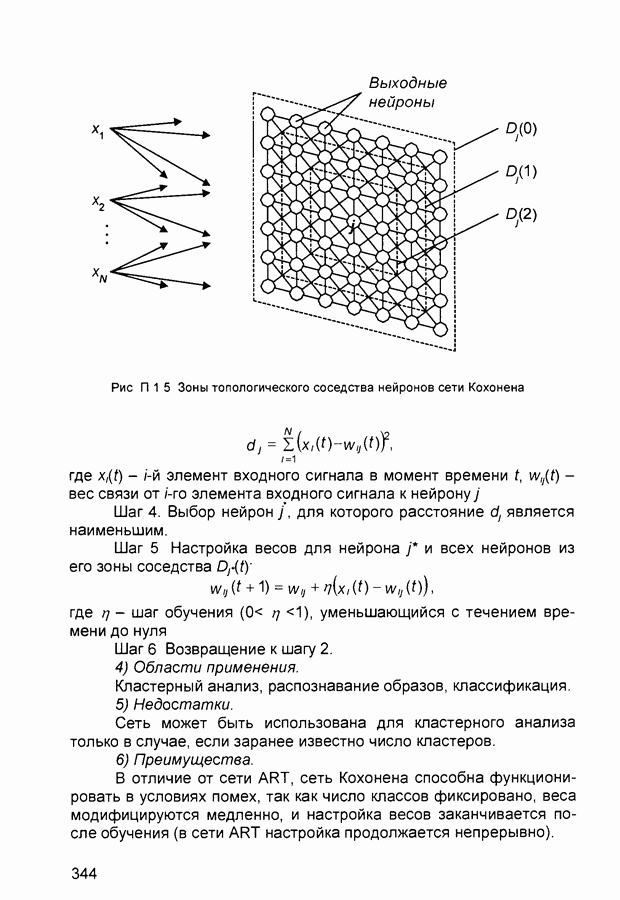
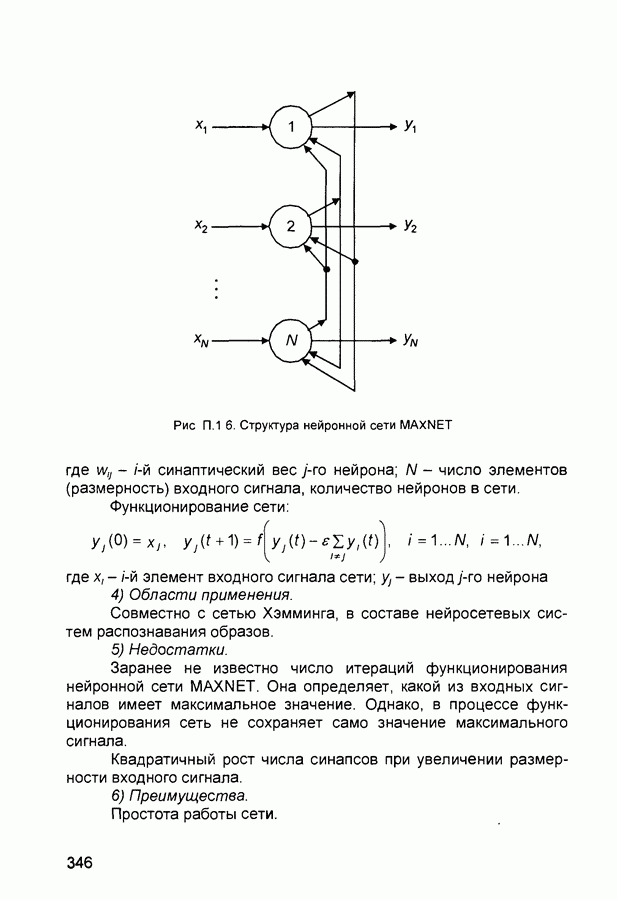
- П.1. Основные парадигмы нейронных сетей
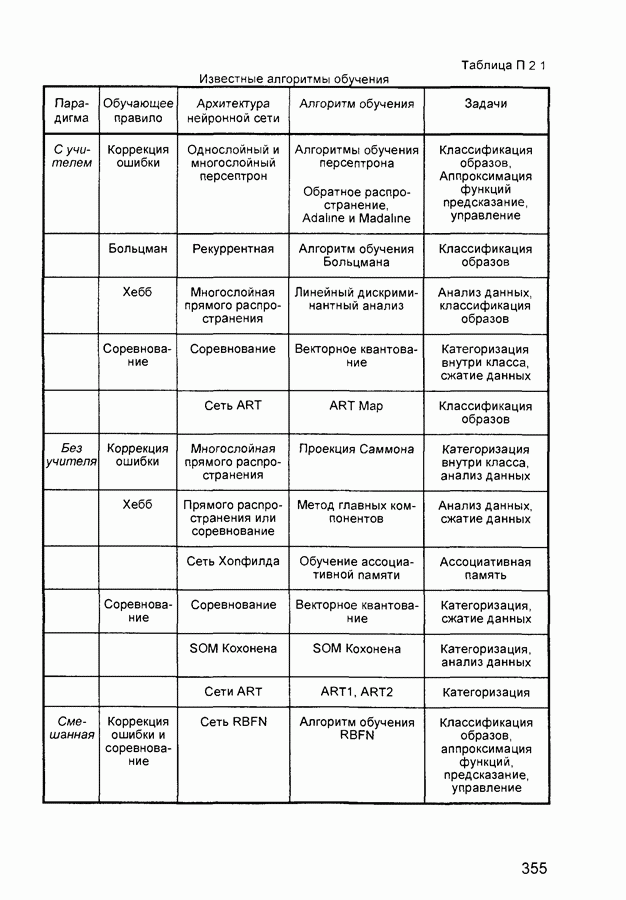
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы