| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.1.4. Нечеткие отношения
Пусть  - прямое произведение универсальных множеств и М - некоторое множество принадлежностей (например,
- прямое произведение универсальных множеств и М - некоторое множество принадлежностей (например,  Нечеткое п-арное отношение определяется как нечеткое подмножество
Нечеткое п-арное отношение определяется как нечеткое подмножество  на Е, принимающее свои значения в М. В случае
на Е, принимающее свои значения в М. В случае  нечетким отношением
нечетким отношением  между множествами
между множествами  будет называться функция
будет называться функция  , которая ставит в соответствие каждой паре элементов
, которая ставит в соответствие каждой паре элементов  величину
величину 
Обозначение: нечеткое отношение на  записывается в виде:
записывается в виде:  . В случае, когда
. В случае, когда  т. е. X и Y совпадают, нечеткое отношение
т. е. X и Y совпадают, нечеткое отношение  называется нечетким отношением на множестве X.
называется нечетким отношением на множестве X.
Пример 1. Пусть  Нечеткое отношение
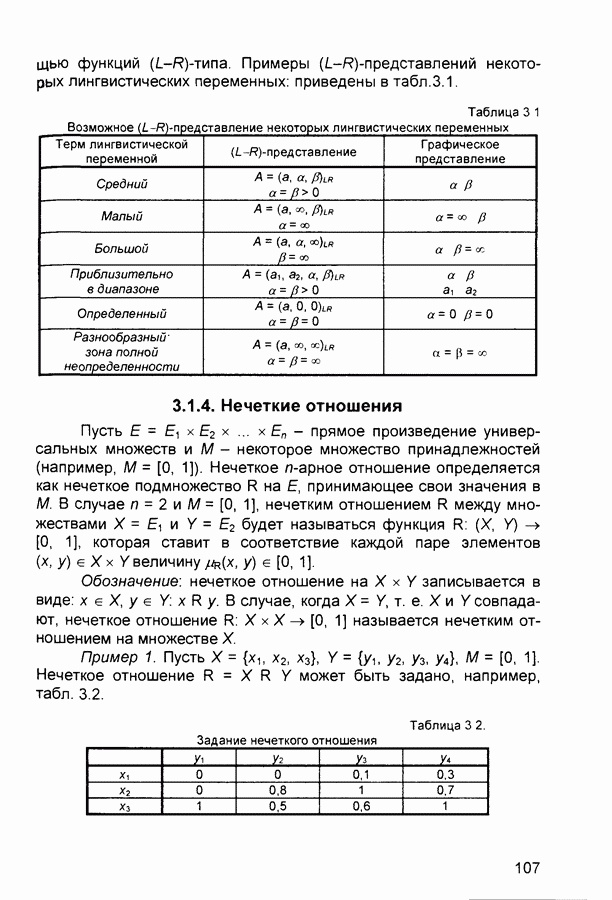
Нечеткое отношение  может быть задано, например, табл. 3.2.
может быть задано, например, табл. 3.2.
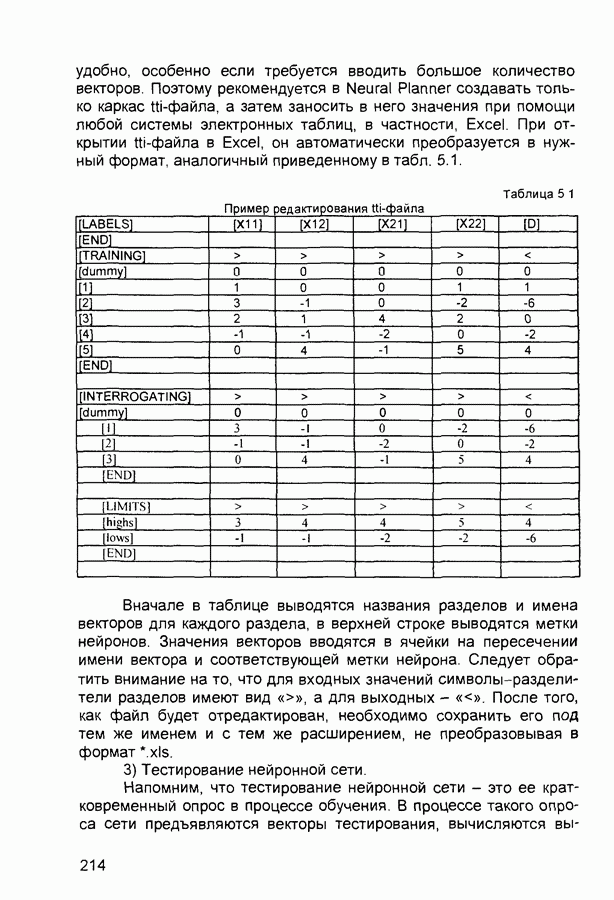
Таблица 3 2. Задание нечеткого отношения

Пример 2. Пусть  т. е. множество всех действительных чисел. Отношение
т. е. множество всех действительных чисел. Отношение  можно задать функцией принадлежности
можно задать функцией принадлежности

Пример 3. Отношение  для которого
для которого  при достаточно больших к можно интерпретировать так:
при достаточно больших к можно интерпретировать так:  и у близкие друг к другу числа».
и у близкие друг к другу числа».
Операции над нечеткими отношениями
Объединение
Объединение двух отношений обозначается  и определяется выражением:
и определяется выражением:

Пересечение
Пересечение двух отношений  обозначается
обозначается  и определяется выражением:
и определяется выражением:

Алгебраическое произведение
Алгебраическое произведение двух отношений  и
и  обозначается
обозначается  и определяется выражением:
и определяется выражением:

Алгебраическая сумма
Алгебраическая сумма двух отношений  и
и  обозначается
обозначается  и определяется выражением:
и определяется выражением:

Для введенных операций справедливы следующие свойства дистрибутивности:

Дополнение отношения
Дополнение отношения  обозначается
обозначается  и определяется функцией принадлежности:
и определяется функцией принадлежности:

Дизъюнктивная сумма
Дизъюнктивная сумма двух отношений  и
и  обозначается и определяется выражением:
обозначается и определяется выражением:

Обычное отношение, ближайшее к нечеткому
Пусть  - нечеткое отношение с функцией принадлежности
- нечеткое отношение с функцией принадлежности  Обычное отношение, ближайшее к нечеткому, обозначается
Обычное отношение, ближайшее к нечеткому, обозначается  и определяется выражением:
и определяется выражением:

По договоренности принимают  при
при  Композиция (свертка)
Композиция (свертка)
Пусть  - нечеткое отношение
- нечеткое отношение  между X и Y, и
между X и Y, и  - нечеткое отношение
- нечеткое отношение  между
между  Нечеткое отношение между X и
Нечеткое отношение между X и  обозначаемое
обозначаемое  определенное через
определенное через  выражением:
выражением:

называется  отношений
отношений  и
и 
Пример. Пусть

Тогда

При этом 

Замечание В этом примере сначала использован «аналитический» способ композиции отношений  и
и  строка
строка  «умножается» на
«умножается» на  столбец
столбец  с использованием операции
с использованием операции  затем полученный результат «свертывается» с использованием операции
затем полученный результат «свертывается» с использованием операции  в
в 
Свойства max-min композиции Операция  -композиции ассоциативна, т. е.
-композиции ассоциативна, т. е.

дистрибутивна относительно объединения, но недистрибутивна относительно пересечения

Кроме того, для  -композиции выполняется следующее важное свойство если
-композиции выполняется следующее важное свойство если  то
то 
 -композиция
-композиция
В выражении  для
для  -композиции отношений
-композиции отношений  операцию
операцию  можно заменить любой другой, для которой выполняются те же ограничения что и для
можно заменить любой другой, для которой выполняются те же ограничения что и для  ассоциативность и монотонность (в смысле неубывания) по каждому аргументу
ассоциативность и монотонность (в смысле неубывания) по каждому аргументу  . Тогда
. Тогда

В частности, операция  может быть заменена алгебраическим умножением, тогда говорят о
может быть заменена алгебраическим умножением, тогда говорят о  -композиции
-композиции
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
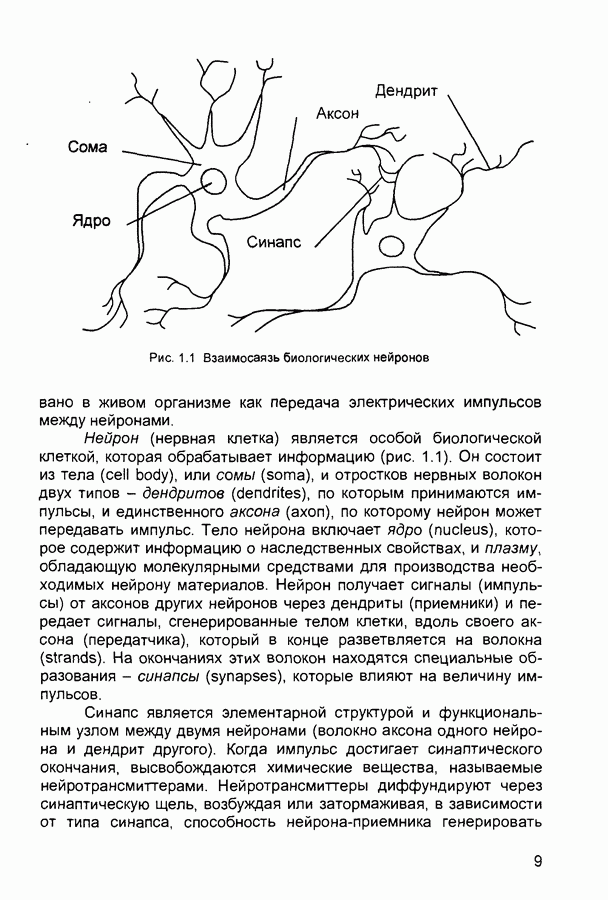
- 1.1. Биологический нейрон
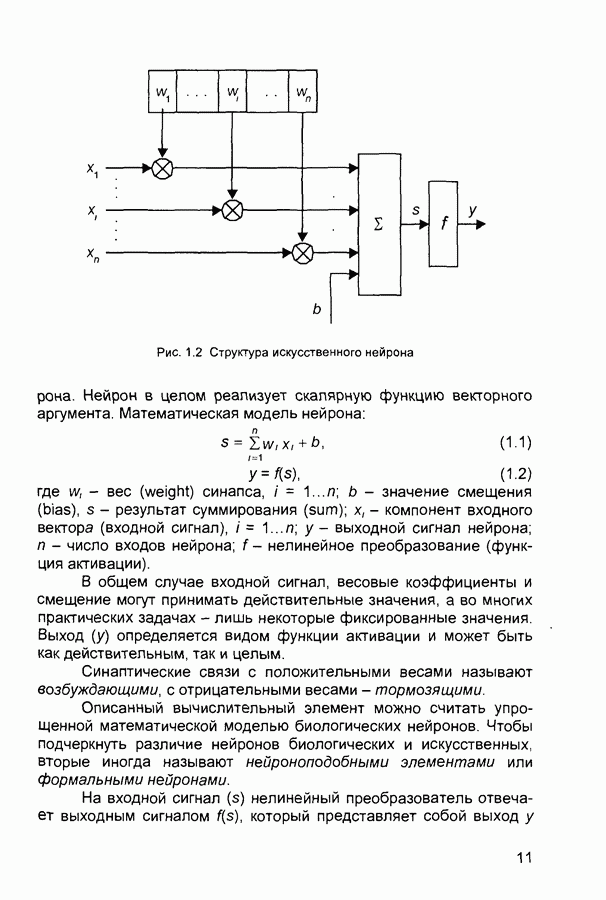
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
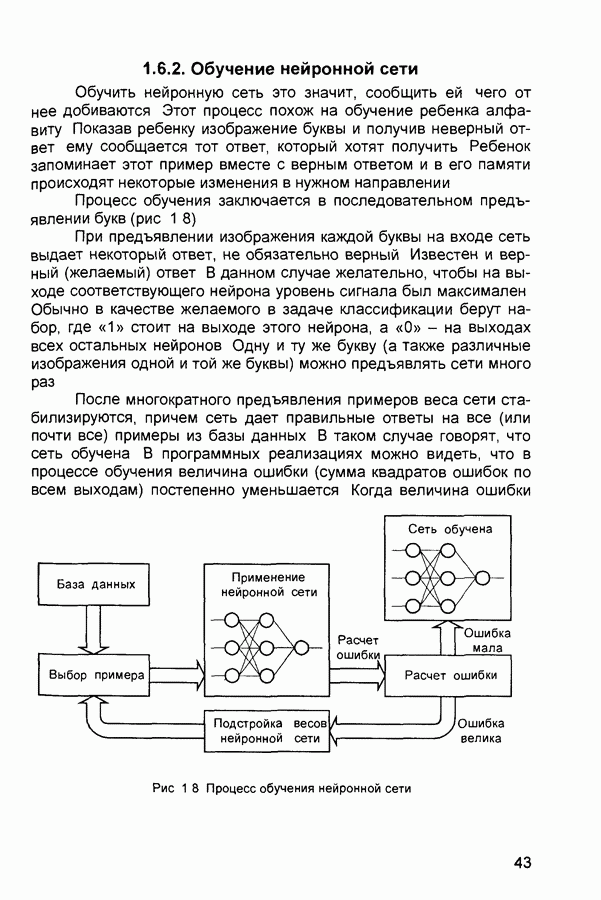
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
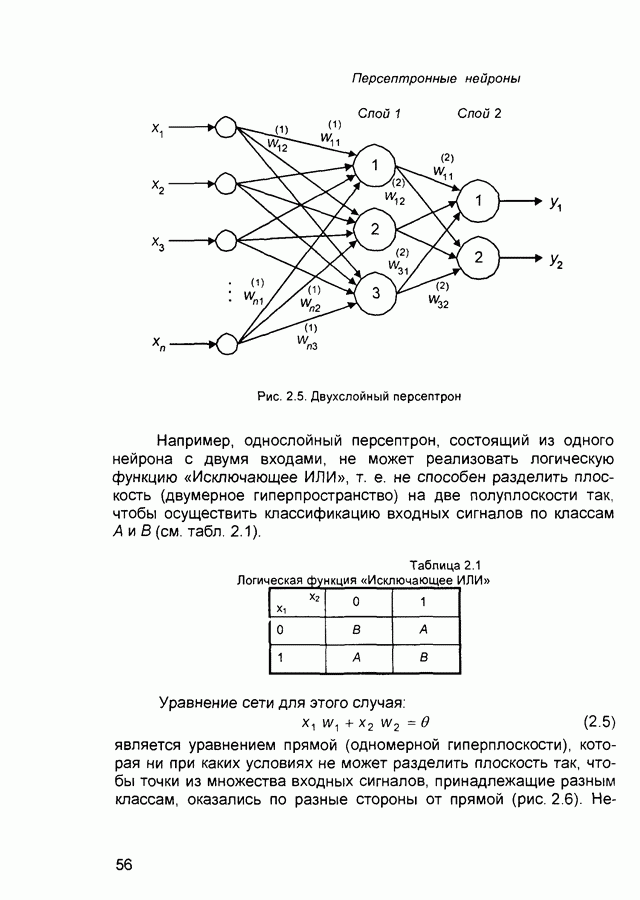
- 2.2. Персептроны
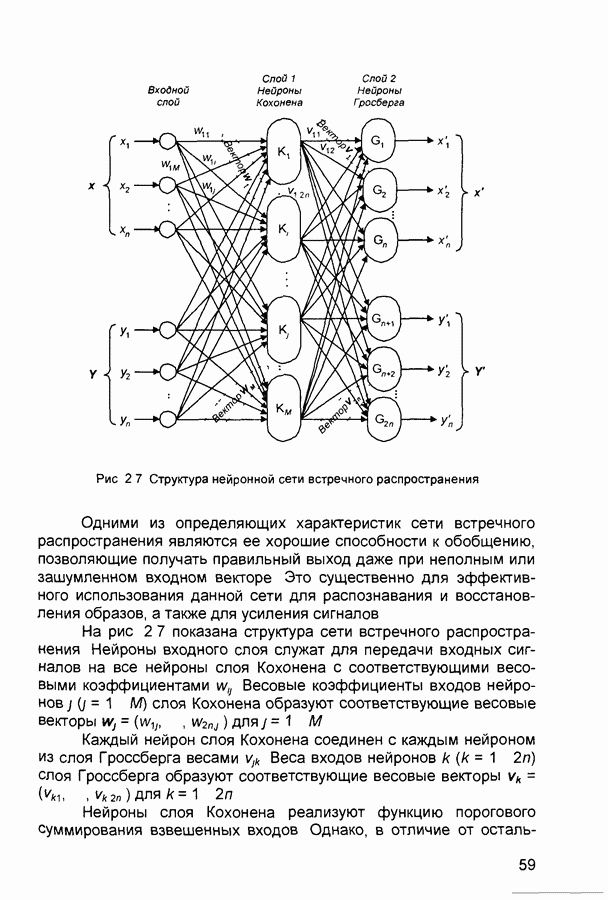
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
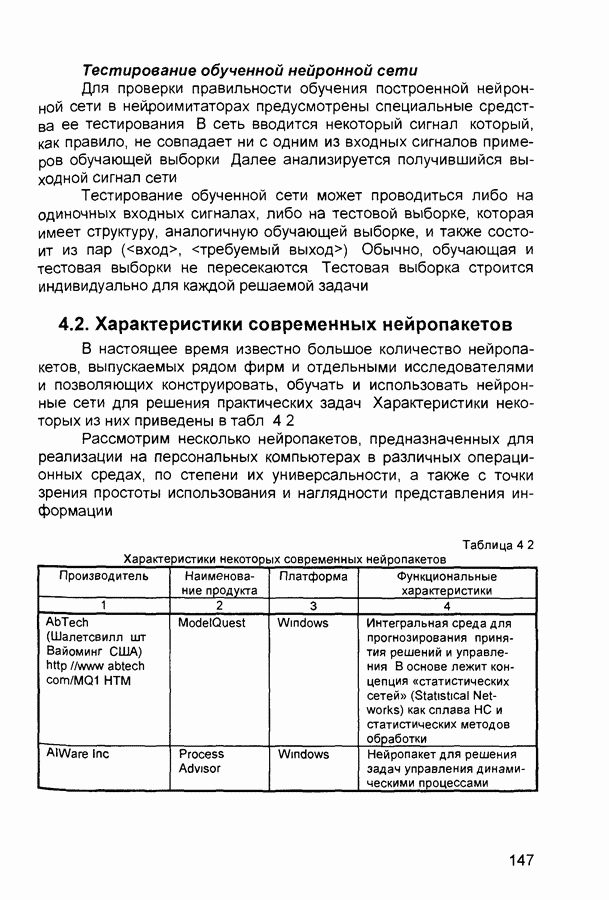
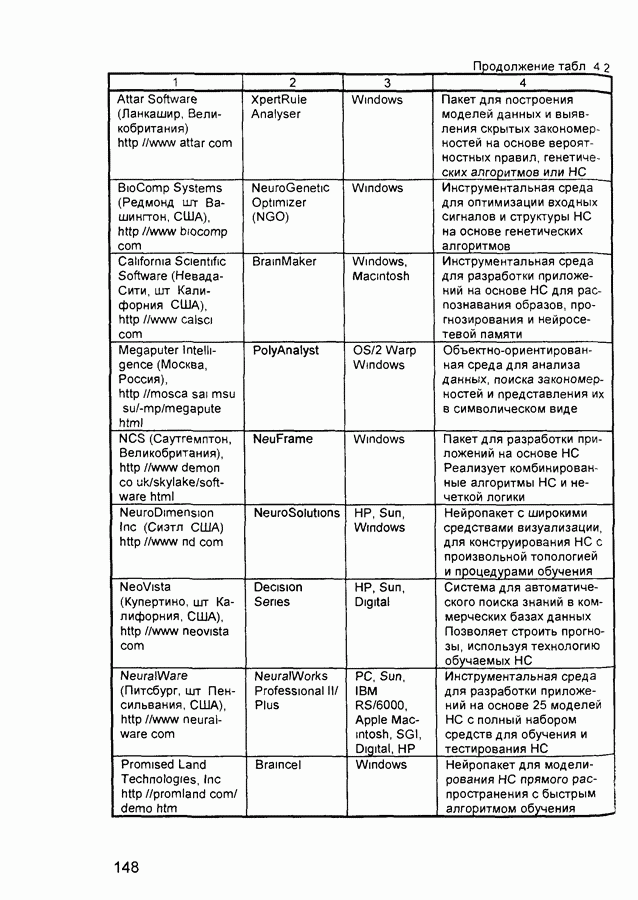
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
- 6.7. Нейросетевая экспертная система
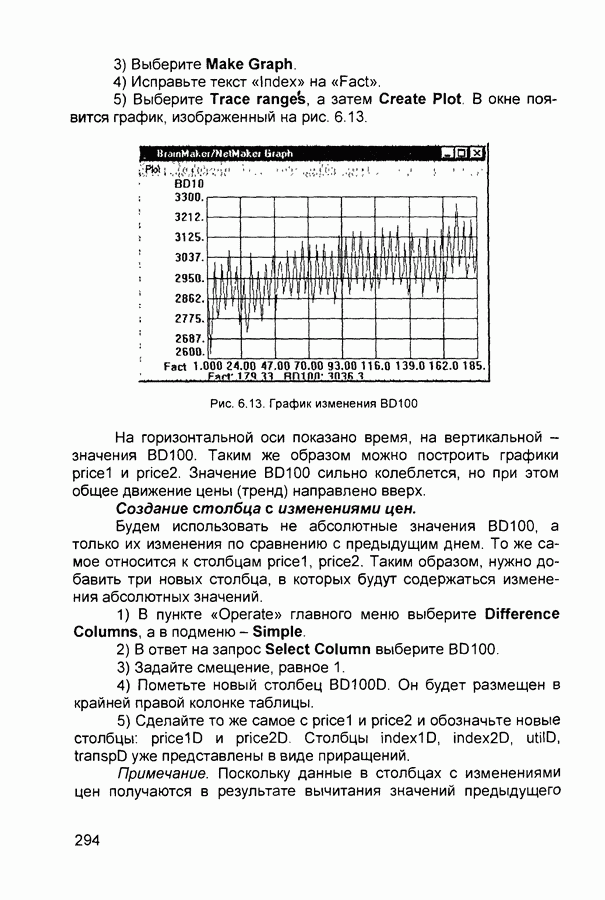
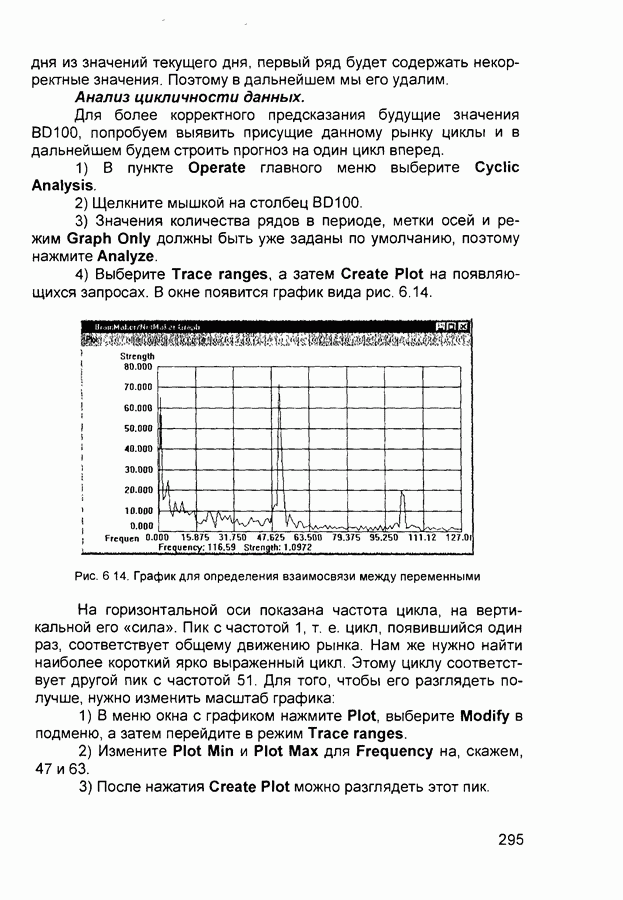
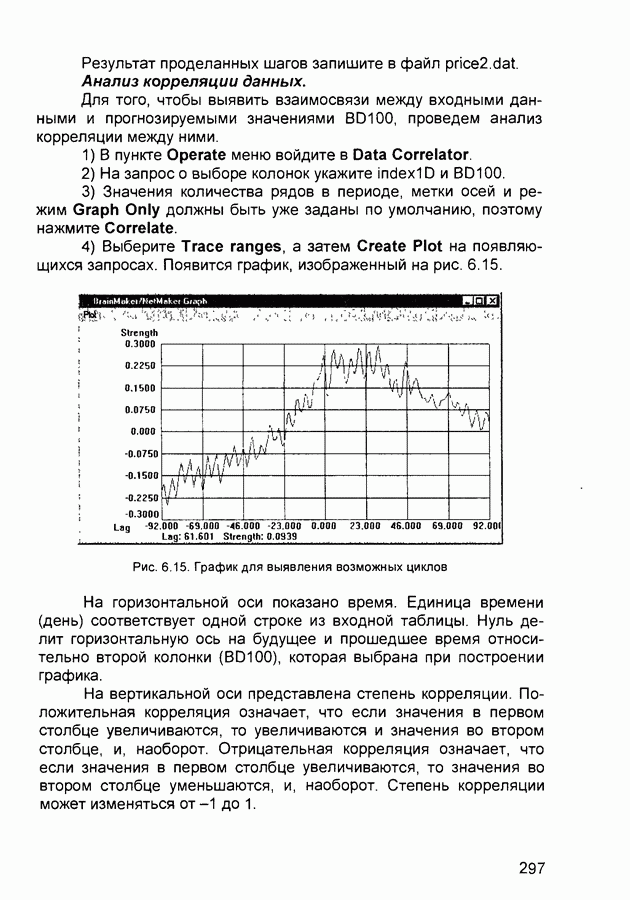
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
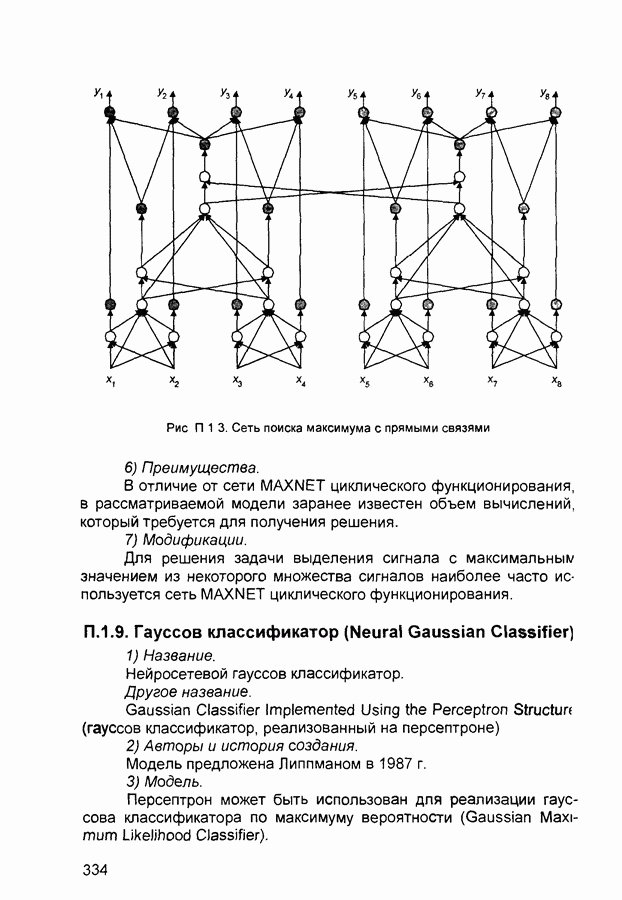
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы