| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
П.1. Основные парадигмы нейронных сетей
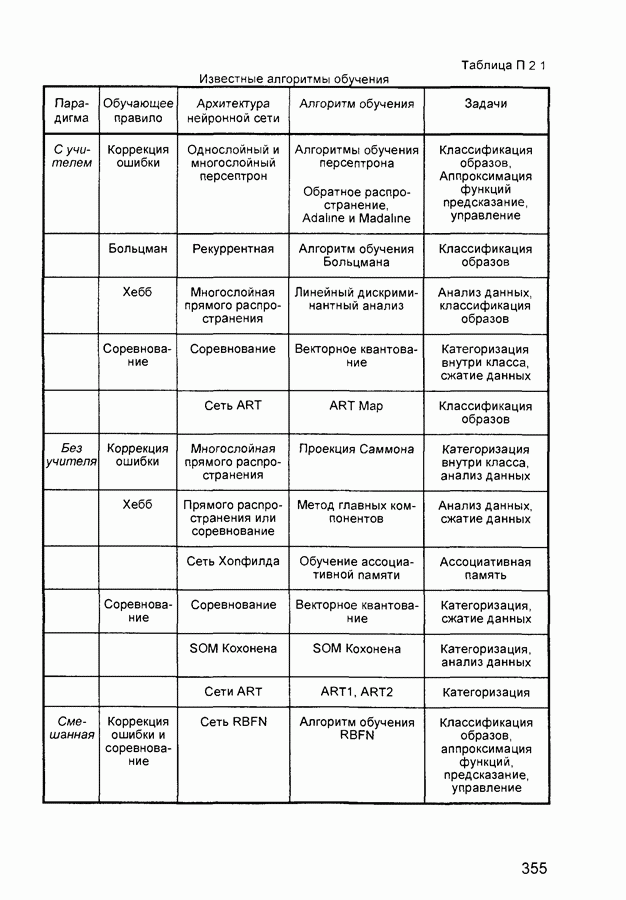
Таблица П.1.1 (см. скан) Наименования парадигм
П.1.1. Искусственный резонанс - 1.
ART-1 Network (Adaptive Resonance Theory Network - 1).
1) Название.
Adaptive Resonance Theory Network (сеть теории адаптивного резонанса).
Другие названия.
Сеть адаптивной резонансной теории - 1 (АРТ-1).
Carpenter-Grossberg Classifier (классификатор Карпентера-Гроссберга).
2) Авторы и история создания.
Разработана Карпентером и Гроссбергом в 1986 г.
3) Модель.
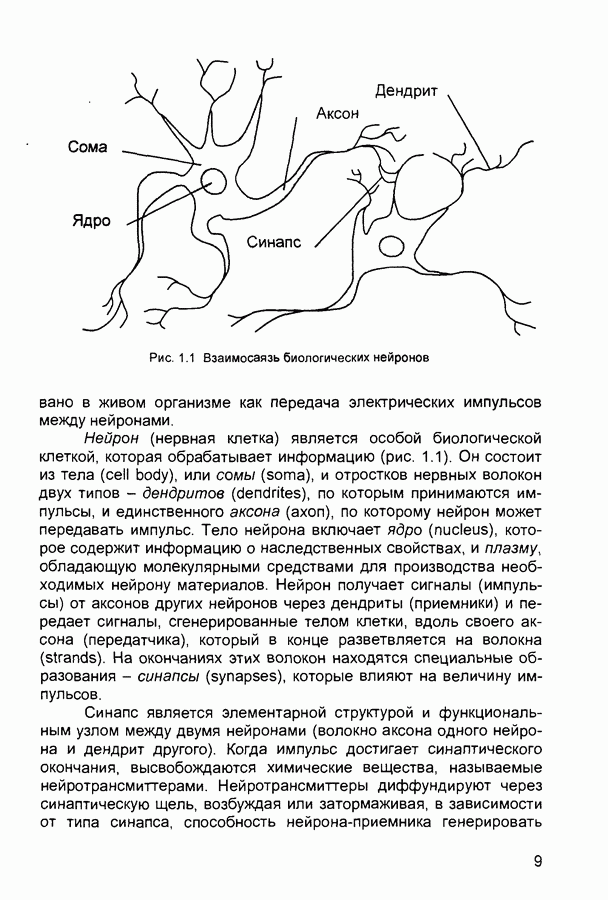
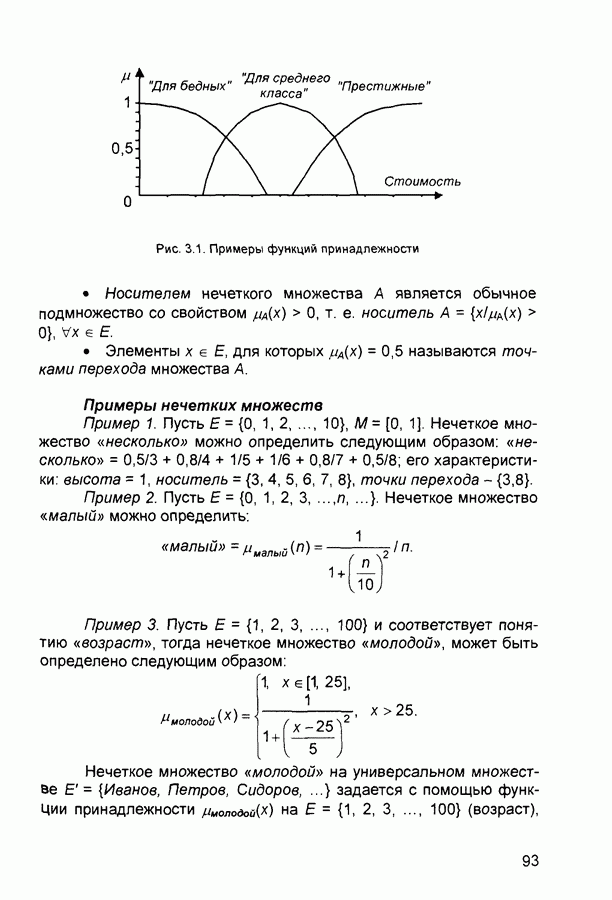
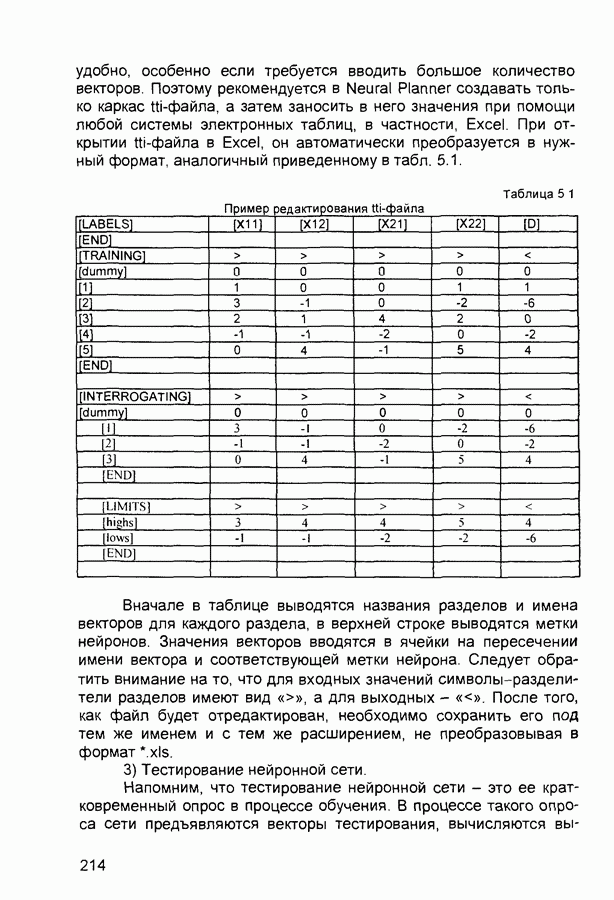
Сеть ART-1 (рис. П. 1.1) обучается без учителя. Она реализует алгоритм кластеризации, подобный алгоритму «последовательного лидера» (Sequential Leader Clustering Algorithm). В соответствии с алгоритмом первый входной сигнал считается эталоном первого кластера. Следующий входной сигнал сравнивается с эталоном первого кластера. Говорят, что входной сигнал «следует за лидером» и принадлежит первому кластеру, если расстояние до эталона первого кластера меньше порога. В противном случае второй входной сигнал становится эталоном второго кластера. Процесс повторяется для всех следующих входных сигналов. Таким образом, число кластеров растет с течением времени и зависит как от значения порога, так и от меры сходства, использующейся для сравнения входных сигналов и эталонов классов.
Основная часть сети ART-1 схожа с сетью Хэмминга, которая дополнена полносвязной сетью MAXNET. С помощью после-

Рис. П. 1.1. Основные компоненты классификатора Карпентера-Гроссберга
довательных связей высчитывается соответствие входных сигналов и образцов кластеров. Максимальное значение соответствия усиливается с помощью взаимного латерального торможения выходных нейронов. Сеть ART-1 отличается от сети Хэмминга обратными связями от выходных нейронов к входным Кроме того, имеется возможность отключать выходной нейрон с максимальным значением соответствия и проводить пороговое тестирование соответствия входного сигнала и образцов кластеров, как того требует алгоритм «последовательного лидера».
Алгоритм функционирования сети
ШАГ 1. Инициализация сети:

где  - синаптический вес связи от
- синаптический вес связи от  нейрона первого слоя к
нейрона первого слоя к  нейрону второго слоя в момент времени
нейрону второго слоя в момент времени  - синаптический вес связи от
- синаптический вес связи от  нейрона второго слоя к
нейрона второго слоя к  нейрону первого слоя в момент времени
нейрону первого слоя в момент времени  - значение порога,
- значение порога,  - константа со значением в диапазоне от 1 до 2.
- константа со значением в диапазоне от 1 до 2.
Веса  определяют эталон, соответствующий нейрону
определяют эталон, соответствующий нейрону  Порог
Порог  показывает, насколько должен входной сигнал совпадать с одним их запомненных эталонов, чтобы они считались похожими. Близкое к единице значение порога требует почти полного совпадения. При малых значениях порога даже сильно различающиеся входной сигнал и эталон считаются принадлежащими одному кластеру.
показывает, насколько должен входной сигнал совпадать с одним их запомненных эталонов, чтобы они считались похожими. Близкое к единице значение порога требует почти полного совпадения. При малых значениях порога даже сильно различающиеся входной сигнал и эталон считаются принадлежащими одному кластеру.
ШАГ 2. Предъявление сети нового бинарного входного сигнала первому слою нейронов аналогично тому, как это делается в сети Хэмминга.
ШАГ 3. Вычисление значений соответствия.

Значения соответствия вычисляются параллельно для всех эталонов, запомненных в сети, аналогично сети Хэмминга.
ШАГ 4. Выбор образца с наибольшим соответствием:

Эта операция выполняется с помощью латерального торможения аналогично сети MAXNET.
ШАГ 5. Вычисление отношения скалярного произведения входного сигнала и эталона с наибольшим значением соответствия к числу единичных бит входного сигнала. Значение отношения сравнивается с порогом, введенном на шаге 1.

Если значение отношения больше порога, то входной сигнал считается похожим на эталон с наибольшим значением соответствия. В этом случае эталон модифицируется путем выполнения операции «Логического И» на входной сигнал
Если значение отношения меньше порога, то считается, что входной сигнал отличается от всех эталонов и рассматривается как новый эталон. В сеть вводится нейрон, соответствующий новому эталону, и рассчитываются значения синаптических весов.
ШАГ 6 Исключение нейрона с наибольшим значением соответствия:
Выход нейрона с наибольшим значением соответствия временно устанавливается равным нулю и более не принимает участие в шаге 4
ШАГ 7. Адаптация нейрона с наибольшим значением соответствия:

ШАГ 8 Включение всех исключенных на шаге 6 эталонов. Возвращение к шагу 2.
Характеристики сети.
Тип входных сигналов - бинарные Размерность входных и выходных сигналов ограничена при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации - технологическими возможностями. Емкость сети совпадает с числом нейронов второго слоя и может увеличиваться в процессе функционирования сети.
4) Области применения
Распознавание образов, кластерный анализ.
5) Недостатки.
Неограниченное увеличение числа нейронов в процессе функционирования сети.
При наличии шума возникают значительные проблемы, связанные с неконтролируемым ростом числа эталонов
6) Преимущества.
Обучение без учителя.
7) Модификации.
Модель ART-2 с непрерывными значениями входных сигналов.
П.1.2. Двунаправленная ассоциативная память. Bi-Directional Associative Memory (ВАМ).
1) Название.
Bi-Directional Associative Memory ВАМ (двунаправленная ассоциативная память ДАП).
2) Авторы и история создания.
Совокупность моделей двунаправленной ассоциативной памяти разработана под руководством Б. Коско (Университет Южной Калифорнии). Большая часть публикаций, посвященных этим моделям, датирована второй половиной 1980-х годов.
3) Модель.
Двунаправленная ассоциативная память является гетероас-социативной. Входной вектор поступает на один набор нейронов, а соответствующий выходной вектор вырабатывается на другом наборе нейронов. Входные образы ассоциируются с выходными.
Для сравнения: сеть Хопфилда является автоассоциатив-ной. Входной образ может быть восстановлен или исправлен сетью, но не может быть ассоциирован с другим образом. В сети Хопфилда используется одноуровневая структура ассоциативной памяти, в которой выходной вектор появляется на выходе тех же нейронов, на которые поступает входной вектор.
Двунаправленная ассоциативная память, как и сеть Хопфилда, способна к обобщению, вырабатывая правильные выходные сигналы, несмотря на искаженные входы.
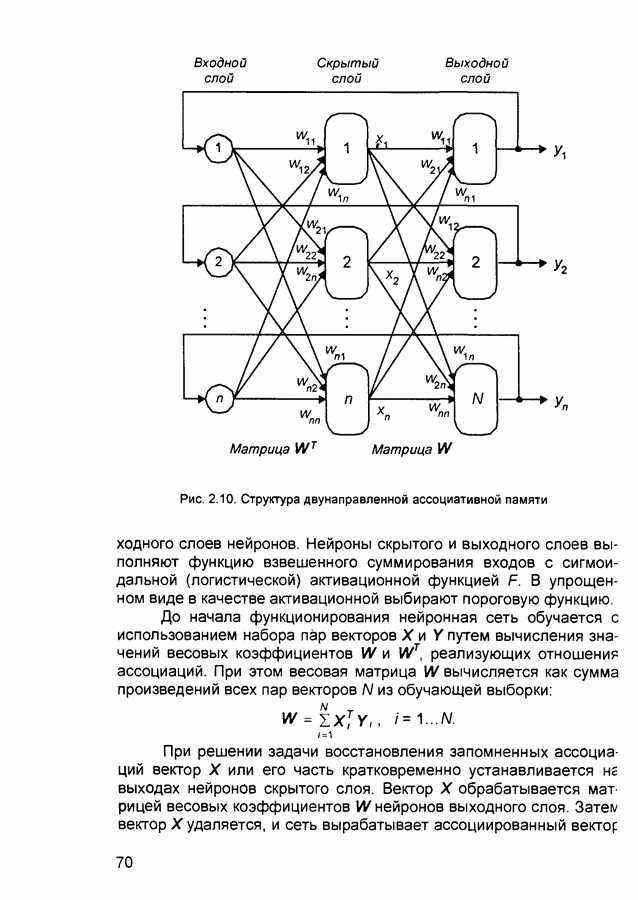
На рис. 2.10 приведена схема двунаправленной ассоциативной памяти. В результате обработки входного вектора X матрицей  весов (нейронами первого слоя) вырабатывается выходной вектор
весов (нейронами первого слоя) вырабатывается выходной вектор  который затем обрабатывается транспонированной матрицей
который затем обрабатывается транспонированной матрицей  весов (нейронами второго слоя) и преобразуется в новый входной вектор
весов (нейронами второго слоя) и преобразуется в новый входной вектор  Этот процесс повторяется до достижения сетью стабильного состояния. В качестве функции активации используется экспоненциальная сигмоида.
Этот процесс повторяется до достижения сетью стабильного состояния. В качестве функции активации используется экспоненциальная сигмоида.
Формула для вычисления значений синаптических весов:

где  и
и  - входные и выходные сигналы обучающей выборки. Весовая матрица вычисляется как сумма произведений всех векторных пар обучающей выборки.
- входные и выходные сигналы обучающей выборки. Весовая матрица вычисляется как сумма произведений всех векторных пар обучающей выборки.
Системы с обратной связью имеют тенденцию к колебаниям. Они могут переходить от состояния к состоянию, никогда не достигая стабильности. Доказано, что ДАП безусловно стабильна при любых значениях весов сети.
4) Области применения.
Ассоциативная память, распознавание образов.
5) Недостатки.
Емкость ДАП жестко ограничена. Если  - количество нейронов в меньшем слое, то число векторов, которые могут быть запомнены в сети, не превышает:
- количество нейронов в меньшем слое, то число векторов, которые могут быть запомнены в сети, не превышает:

Так, если  то сеть способна запомнить не более 25 образов. Кроме того, ДАП обладает некоторой непредсказуемостью в процессе функционирования. Возможны ложные ответы.
то сеть способна запомнить не более 25 образов. Кроме того, ДАП обладает некоторой непредсказуемостью в процессе функционирования. Возможны ложные ответы.
6) Преимущества.
По сравнению с автоассоциативной памятью (например, с сетью Хопфилда), двунаправленная ассоциативная память дает возможность строить ассоциации между векторами X и  которые в общем случае имеют разные размерности. За счет таких возможностей гетероассоциативная память используется для более широкого класса приложений, чем автоассоциативная память.
которые в общем случае имеют разные размерности. За счет таких возможностей гетероассоциативная память используется для более широкого класса приложений, чем автоассоциативная память.
Процесс формирования синаптических весов является простым и достаточно быстрым. Сеть быстро сходится в процессе функционирования.
Двунаправленная ассоциативная память - простая сеть, которая может быть реализована в виде отдельной СБИС или оптоэлектронным способом.
7) Модификации.
Предложена негомогенная двунаправленная ассоциативная память, в которой пороговые значения подбираются индивидуально для каждого нейрона (в исходной модели ДАП все нейроны имеют нулевые пороговые значения). Емкость негомогенной сети выше, чем исходной модели.
Сигналы в сети могут быть как дискретными, так и непрерывными. Для обоих случаев доказана стабильность сети.
Предложены модели двунаправленной ассоциативной памяти с обучением без учителя (адаптивная ДАП).
Введение латеральных связей внутри слоя дает возможность реализовать конкурирующую тип ДАП. Веса связей формируют матрицу с положительными значениями элементов главной диагонали и отрицательными значениями остальных элементов. Теорема Кохонена-Гроссберга доказывает, что такая сеть является стабильной.
П.1.3. Машина Больцмана (Boltzmann Machine)
1) Название.
Boltzmann Machine (машина Больцмана).
Другое название.
Больцмановское обучение.
2) Авторы и история создания.
Машина Больцмана была предложена и исследовалась во второй половине 1980-х годов.
3) Модель.
Алгоритм больцмановского обучения:
ШАГ 1. Определить переменную Г, представляющую искусственную температуру.
ШАГ 2. Предъявить сети множество входов и вычислить выходы и целевую функцию.
ШАГ 3. Дать случайное изменение весу и пересчитать выход сети и изменение целевой функции в соответствии со сделанным изменением веса.
ШАГ 4. Если целевая функция улучшилась (уменьшилась), то сохранить изменение веса.
Если изменение веса приводит к увеличению целевой функции, то вероятность сохранения этого изменения вычисляется с помощью распределения Больцмана:

где  - вероятность изменения параметра с в целевой функции; к - константа, аналогичная константе Больцмана, выбираемая в зависимости от задачи.
- вероятность изменения параметра с в целевой функции; к - константа, аналогичная константе Больцмана, выбираемая в зависимости от задачи.
Выбирается случайное число  из равномерного распределения от нуля до единицы. Если
из равномерного распределения от нуля до единицы. Если  больше, чем
больше, чем  то изменение сохраняется, в противном случае величина веса возвращается к предыдущему значению.
то изменение сохраняется, в противном случае величина веса возвращается к предыдущему значению.
Эта процедура дает возможность системе делать случайный шаг в направлении, «портящем» целевую функцию, позволяя ей тем самым выходить из локальных минимумов.
Шаги 3 и 4 повторяются для каждого из весов сети, постепенно уменьшая температуру Г, пока не будет достигнуто допустимо низкое значение целевой функции. В этот момент предъявляется другой входной вектор и процесс обучения повторяется. Сеть обучается на всех векторах обучающего множества, пока целевая функция не станет допустимой для всех из них.
Скорость уменьшения температуры должна быть обратно пропорциональна логарифму времени. При этом сеть сходится к глобальному минимуму.
4) Области применения.
Распознавание образов, классификация.
5) Недостатки.
Медленный алгоритм обучения
6) Преимущества.
Алгоритм дает возможность сети выбираться из локальных минимумов адаптивного рельефа.
7) Модификации.
Случайные изменения могут проводиться не только для отдельных весов, но и для всех нейронов слоя в многослойных сетях или даже для всех нейронов сети одновременно. Эти модификации алгоритма дают возможность сократить общее число итераций обучения.
П.1.4. Обратное распространение (Neural Network with Back Propagation Training Algorithm)
1) Название.
Нейронная сеть с обучением по методу обратного распространения ошибки.
Другие названия.
Backprop.
Back Propagation (Neural) Network.
Сеть обратного распространения (ошибки).
Multi-Layer Perceptron with Back Propagation Training Algorithm (многослойный персептрон с обучением по методу обратного распространения ошибки).
2) Авторы и история создания.
Многослойные персептроны были предложены и исследованы в 1960-х годах Розенблаттом, Минским, Пейпертом и др. Лишь в середине 1980-х годов был предложен эффективный алгоритм обучения многослойных персептронов, основанный на вычислении градиента функции ошибки и названный обратным распространением ошибки.
3) Модель.
Алгоритм обратного распространения - это итеративный градиентный алгоритм, который используется с целью минимизации среднеквадратического отклонения текущего выхода многослойного персептрона и требуемого выхода.
Он используется для обучения многослойных нейронных сетей с последовательными связями. Нейроны в таких сетях делятся на группы с общим входным сигналом - слои. На каждый нейрон первого слоя подаются все элементы внешнего входного сигнала. Все выходы нейронов  слоя подаются на каждый нейрон слоя
слоя подаются на каждый нейрон слоя  Нейроны выполняют взвешенное суммирование входных сигналов. К сумме элементов входных сигналов, помноженных на соответствующие синаптические веса, прибавляется смещение нейрона. Над результатом суммирования выполняется нелинейное преобразование - функция активации (передаточная функция). Значение функции активации есть выход нейрона.
Нейроны выполняют взвешенное суммирование входных сигналов. К сумме элементов входных сигналов, помноженных на соответствующие синаптические веса, прибавляется смещение нейрона. Над результатом суммирования выполняется нелинейное преобразование - функция активации (передаточная функция). Значение функции активации есть выход нейрона.
Характеристики сети.
Тип входных сигналов - целые или действительные. Тип выходных сигналов - действительные из интервала, заданного передаточной функцией нейронов. Тип передаточной функции - сигмоидальная. В нейронных сетях применяются несколько вариантов сигмоидальных передаточных функций.
Функция Ферми (экспоненциальная сигмоида):

где  — выход сумматора нейрона, а - некоторый параметр.
— выход сумматора нейрона, а - некоторый параметр.
Рациональная сигмоида:

Гиперболический тангенс:

Перечисленные функции относятся к однопараметрическим. Значение функции зависит от аргумента и одного параметра. Используются также и многопараметрические передаточные функции, например:

Сигмоидальные функции являются монотонно возрастающими и имеют отличные от нуля производные на всей области определения. Эти характеристики обеспечивают правильное функционирование и обучение сети.
Наиболее эффективной передаточной функцией является рациональная сигмоида. Для вычисления гиперболического тангенса требуются большие вычислительные затраты.
Функционирование многослойной нейронной сети осуществляется в соответствии с формулами:

где  - выход сумматора,
- выход сумматора,  - вес связи, у - выход нейрона,
- вес связи, у - выход нейрона,  - смещение,
- смещение,  - номер нейрона,
- номер нейрона,  - число нейронов в слое,
- число нейронов в слое,  - номер слоя,
- номер слоя,  - число слоев,
- число слоев,  -функция активации.
-функция активации.
Обучение сети разбивается на следующие этапы:
ШАГ 1. Инициализация сети.
Весовым коэффициентам и смещениям сети присваиваются малые случайные значения из установленных диапазонов.
ШАГ 2. Определение элемента обучающей выборки:
 <требуемый
<требуемый  Текущие входы
Текущие входы  должны различаться для всех элементов обучающей выборки. При использовании многослойного персептрона в качестве классификатора требуемый выходной сигнал
должны различаться для всех элементов обучающей выборки. При использовании многослойного персептрона в качестве классификатора требуемый выходной сигнал  состоит из нулей за исключением одного единичного элемента, соответствующего классу, к которому принадлежит текущий входной сигнал.
состоит из нулей за исключением одного единичного элемента, соответствующего классу, к которому принадлежит текущий входной сигнал.
ШАГ 3. Вычисление текущего выходного сигнала.
Текущий выходной сигнал определяется в соответствии с традиционной схемой функционирования многослойной нейронной сети.
ШАГ 4. Настройка синаптических весов.
Для настройки весовых коэффициентов используется рекурсивный алгоритм, который сначала применяется к выходным нейронам сети, а затем проходит сеть в обратном направлении до первого слоя. Синаптические веса настраиваются в соответствии с формулой:

где  - вес от нейрона
- вес от нейрона  или от элемента входного сигнала
или от элемента входного сигнала  к нейрону
к нейрону  в момент времени
в момент времени  - выход нейрона
- выход нейрона  или
или  элемент входного сигнала,
элемент входного сигнала,  - коэффициент скорости обучения;
- коэффициент скорости обучения;  - значение ошибки для нейрона
- значение ошибки для нейрона 
Если нейрон с номером  принадлежит последнему слою, то
принадлежит последнему слою, то

где  - соответственно требуемый и текущий выход
- соответственно требуемый и текущий выход  нейрона.
нейрона.
Если  нейрон принадлежит одному из слоев с первого по предпоследний, то:
нейрон принадлежит одному из слоев с первого по предпоследний, то:

где  нейрон принадлежит предыдущему слою, а индекс к пробегает все нейроны последующего слоя.
нейрон принадлежит предыдущему слою, а индекс к пробегает все нейроны последующего слоя.
Смещения нейронов  настраиваются аналогичным образом.
настраиваются аналогичным образом.
4) Области применения.
Распознавание образов, классификация, прогнозирование, синтез речи, контроль, адаптивное управление, построение экспертных систем
5) Недостатки.
Многокритериальная задача оптимизации в методе обратного распространения рассматривается как набор однокритериальных - на каждой итерации происходят изменения значений параметров сети, улучшающие работу лишь с одним примером обучающей выборки. Такой подход существенно уменьшает скорость обучения.
Классический метод обратного распространения относится к алгоритмам с линейной сходимостью. Для увеличения скорости сходимости необходимо использовать матрицы вторых производных функции ошибки.
6) Преимущества.
Обратное распространение - первый эффективный алгоритм обучения многослойных нейронных сетей. Один из самых популярных алгоритмов обучения, с его помощью решены и решаются многочисленные практические задачи.
7) Модификации.
Модификации алгоритма обратного распространения связаны с использованием различных функций ошибки, различных процедур определения направления и величины шага:
функции ошибки:
• интегральные функции ошибки по всей совокупности обучающих примеров;
• функции ошибки целых и дробных степеней;
процедуры определения величины шага на каждой итерации.
• дихотомия;
• инерционные соотношения, например,

где а — некоторое положительное число, меньше единицы;
• отжиг;
процедуры определения направления шага
• с использованием матрицы производных второго порядка (метод Ньютона и др );
• с использованием направлений на нескольких шагах (партан метод и др.).
П.1.5. Сеть встречного распространения (Counter Propagation Network)
1) Название.
Counter Propagation Network (сеть встречного распространения).
Другое название.
Hecht-Nielsen Neurocomputer.
2) Авторы и история создания.
Разработаны Р. Хехт-Нильсенем (University of California, San Diego) в 1986 г.
3) Модель.
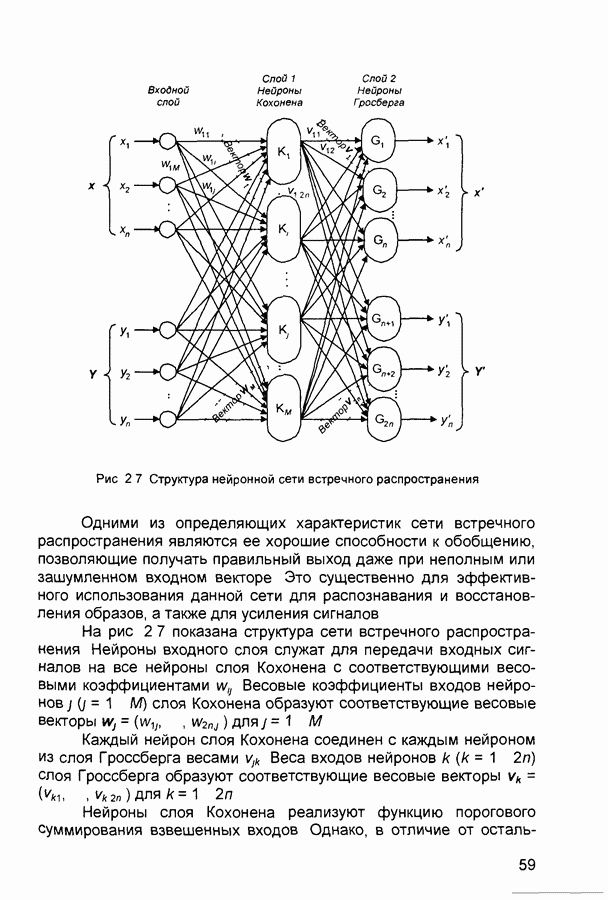
В сети встречного распространения объединены две нейропарадигмы: самоорганизующаяся карта Кохонена и звезда Гроссберга. Считается, что в мозге именно соединения модулей различной специализации позволяют выполнять требуемые вычисления.
В процессе обучения сети встречного распространения входные векторы ассоциируются с соответствующими выходными векторами. Эти векторы могут быть двоичными или непрерывными. После обучения сеть формирует выходные сигналы, соответствующие входным сигналам. Обобщающая способность сети дает возможность получать правильный выход, когда входной вектор неполон или искажен.
В режиме обучения на вход сети подается входной сигнал и веса корректируются, чтобы сеть выдавала требуемый выходной сигнал.
Слой Кохонена функционирует по правилу «победитель получает все». Для данного входного вектора только один нейрон этого слоя выдает логическую единицу, все остальные - нули Выход каждого нейрона Кохонена является просто суммой взвешенных элементов входных сигналов
Выходы нейронов слоя Гроссберга также являются взвешенными суммами выходов нейронов слоя Кохонена. Однако каждый нейрон слоя Гроссберга выдает величину веса, который связывает этот нейрон с единственным нейроном Кохонена, чей выход отличен от нуля.
На этапе предварительной обработки входных сигналов осуществляется нормализация входных векторов.
На этапе обучения слой Кохонена классифицирует входные векторы в группы схожих. Это достигается с помощью такой подстройки весов слоя Кохонена, что близкие входные векторы активируют один и тот же нейрон данного слоя. Какой именно нейрон будет активироваться при предъявлении конкретного входного сигнала, заранее трудно предсказать, так как слой Кохонена обучается без учителя.
Затем задачей слоя Гроссберга является получение требуемых выходов. Обучение слоя Гроссберга - это обучение с учителем. Выходы нейронов вычисляются как при обычном функционировании. Далее каждый вес корректируется лишь в случае, если он соединен с нейроном Кохонена, имеющим ненулевой выход. Величина коррекции веса пропорциональна разности между весом и требуемым выходом нейрона Гроссберга.
В режиме функционирования сети предъявляется входной сигнал и формируется выходной сигнал.
В полной модели сети встречного распространения имеется возможность получать выходные сигналы по входным и наоборот. Этим двум действиям соответствуют прямое и обратное распространение сигналов.
4) Области применения.
Распознавание и восстановление образов (ассоциативная память), сжатие данных (с потерями), статистический анализ.
5) Недостатки.
Сеть не дает возможности строить точные аппроксимации. В этом она значительно уступает сетям с обратным распространением ошибки.
Слабая теоретическая проработка модификаций этой сети.
6) Преимущества.
Сеть встречного распространения проста. Она дает возможность извлекать статистические характеристики из множеств входных сигналов. Кохоненом показано, что для полностью обученной сети вероятность того, что случайно выбранный входной вектор (в соответствии с функцией плотности вероятности входного множества) будет ближайшим к любому заданному весовому вектору, равна  - число нейронов Кохонена.
- число нейронов Кохонена.
Сеть быстро обучается Время ее обучения по сравнению с обратным распространением может быть в 100 раз меньше.
По своим возможностям строить отображения сеть встречного распространения значительно превосходит однослойные персептроны.
Сеть полезна для приложений, в которых требуется быстрая начальная аппроксимация.
Сеть дает возможность строить функцию и обратную к ней, что находит применение при решении практических задач.
7) Модификации.
Сети встречного распространения могут различаться способами определения начальных значений синаптических весов. Так, кроме случайных значений из заданного диапазона, могут быть использованы значения в соответствии с известным методом выпуклой комбинации.
Для повышения эффективности обучения применяется добавление шума к входным векторам.
Еще один метод повышения эффективности обучения - наделение каждого нейрона «чувством справедливости». Если нейрон становится победителем чаще, чем  то ему временно увеличивают порог, предоставляя, тем самым, возможность обучаться и другим нейронам.
то ему временно увеличивают порог, предоставляя, тем самым, возможность обучаться и другим нейронам.
Кроме метода аккредитации, при котором для каждого входного вектора активируется лишь один нейрон Кохонена, может быть использован метод интерполяции, при использовании которого группа нейронов Кохонена, имеющих наибольшие выходы, может передавать свои выходные сигналы в слой Гроссберга. Этот метод повышает точность отображений, реализуемых сетью.
П.1.6. Delta Bar Delta сеть
1) Название.
Delta Bar Delta Network (DBD).
2) История создания.
Алгоритм  создан Якобсом с целью ускорения обучения сети за счет использования эвристического подхода. Алгоритм использует предыдущие значения градиента функции, на основе которых осуществляются изменения в пространстве весов с помощью ряда эвристических правил.
создан Якобсом с целью ускорения обучения сети за счет использования эвристического подхода. Алгоритм использует предыдущие значения градиента функции, на основе которых осуществляются изменения в пространстве весов с помощью ряда эвристических правил.
Опыт показывает, что размерности пространства весов могут значительно различаться с точки зрения общей поверхности ошибки. Якобс предложил ряд эвристик, суть которых в том, что каждый вес должен изменяться в соответствии с индивидуальной
скоростью обучения, так как размер шага обучения для одного веса не всегда подходит в качестве шага обучения для всех весов. Более того, этот размер может со временем изменяться.
Первые эвристики по изменению индивидуальных шагов обучения нейронов были введены Кестеном Он предложил, что если последовательные изменения веса имеют противоположные знаки, то значит данный вес осциллирует, и, следовательно, скорость обучения должна быть уменьшена. Позднее Садирис ввел следующее правило: если серия последовательных изменений веса имеет одинаковые знаки, то скорость обучения должна быть увеличена.
3) Модель.
Изменение веса на последующем шаге:

Расчет среднего изменения градиента на шаге t

Расчет изменения скорости обучения на шаге 

где  - ошибка обучения на шаге
- ошибка обучения на шаге  - значение веса;
- значение веса;  - изменение веса;
- изменение веса;  - коэффициент скорости обучения;
- коэффициент скорости обучения;  - изменение скорости обучения;
- изменение скорости обучения;  - градиент изменения веса;
- градиент изменения веса;  - взвешенное среднее изменение градиента; convex - фактор выпуклости весов;
- взвешенное среднее изменение градиента; convex - фактор выпуклости весов;  - константа увеличения скорости обучения;
- константа увеличения скорости обучения;  - константа уменьшения скорости обучения.
- константа уменьшения скорости обучения.
Линейное увеличение изменения скорости позволяет избежать быстрого роста скорости. Геометрическое уменьшение позволяет проследить, что скорость обучения всегда положительная. Более того, скорость может уменьшаться более быстро на сильно нелинейных участках.
4) Области применения.
Распознавание образов, классификация.
5) Недостатки.
Стандартный алгоритм DBD не использует эвристики, основанные на моменте.
Даже небольшое линейное увеличение коэффициента может привести к значительному росту скорости обучения, что вызовет скачки в пространстве весов.
Геометрическое уменьшение коэффициента иногда оказывается недостаточно быстрым.
6) Преимущества.
Парадигма Delta Bar Delta является попыткой ускорить процесс конвергенции алгоритма обратного распространения за счет использования дополнительной информации об изменении параметров и весов во время обучения.
П.1.7. Расширенная DBD сеть (Extended Delta Bar Delta Network)
1) Название.
Extended Delta Bar Delta Network (EDBD).
2) История создания.
Сеть Extended Delta Bar Delta разработана Minai и Williams. Ими был использован параметр момента связи (momentum), представляющий собой некоторое число, пропорциональное предыдущему изменению веса. Они использовали значения момента для ускорения обучения с помощью ряда эвристических правил.
3) Модель.
Изменение веса на последующем шаге:

Расчет среднего изменения градиента на шаге 

Расчет изменения скорости обучения на шаге 

Расчет изменения момента на шаге 

где  - ошибка обучения на шаге
- ошибка обучения на шаге  - значение веса;
- значение веса;  - изменение веса;
- изменение веса;  - коэффициент скорости обучения;
- коэффициент скорости обучения;  - изменение скорости обучения;
- изменение скорости обучения;  - градиент изменения веса;
- градиент изменения веса;  взвешенное среднее изменение градиента; convex - фактор выпуклости весов;
взвешенное среднее изменение градиента; convex - фактор выпуклости весов;  - значение момента;
- значение момента;  - изменение значения момента;
- изменение значения момента;  - фактор масштабирования скорости обучения;
- фактор масштабирования скорости обучения;  - фактор масштабирования момента;
- фактор масштабирования момента;  - экспоненциальный фактор скорости обучения;
- экспоненциальный фактор скорости обучения;  - экспоненциальный фактор
- экспоненциальный фактор
момента;  фактор масштабирования скорости обучения;
фактор масштабирования скорости обучения;  фактор масштабирования момента; атах - верхняя граница скорости обучения; ттах - верхняя граница момента.
фактор масштабирования момента; атах - верхняя граница скорости обучения; ттах - верхняя граница момента.
Коэффициенты скорости обучения и скорости изменения момента имеют различные константы, контролирующие их увеличение и уменьшение.
Для всех связей принимаются следующие ограничения:

Если текущая ошибка превышает минимальную предыдущую ошибку с учетом максимального отклонения, то все связи восстанавливаются для наилучшего варианта и коэффициенты обучения и момента уменьшаются.
4) Области применения.
Распознавание образов, классификация.
П.1.8. Сеть поиска максимума с прямыми связями (Feed-Forward MAXNET)
1) Название.
Feed-Forward MAXNET (сеть поиска максимума с прямыми связями).
Другое название.
Сеть поиска максимума, основанная на двоичном дереве и нейросетевых компараторах.
2) Авторы и история создания.
Сеть предложена в качестве дополнения к сети Хэмминга.
3) Модель.
Многослойная сеть с прямыми связями. Входные сигналы попарно сравниваются друг с другом. Наибольший сигнал в каждой паре передается на следующий слой для дальнейших сравнений. На выходе сети лишь один сигнал имеет ненулевое значение. Он соответствует максимальному сигналу на входе сети.
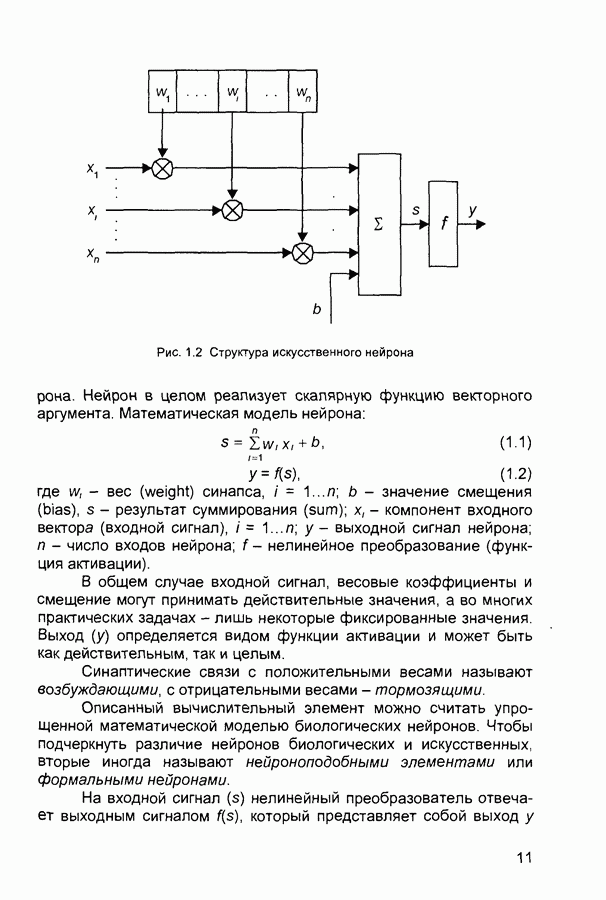
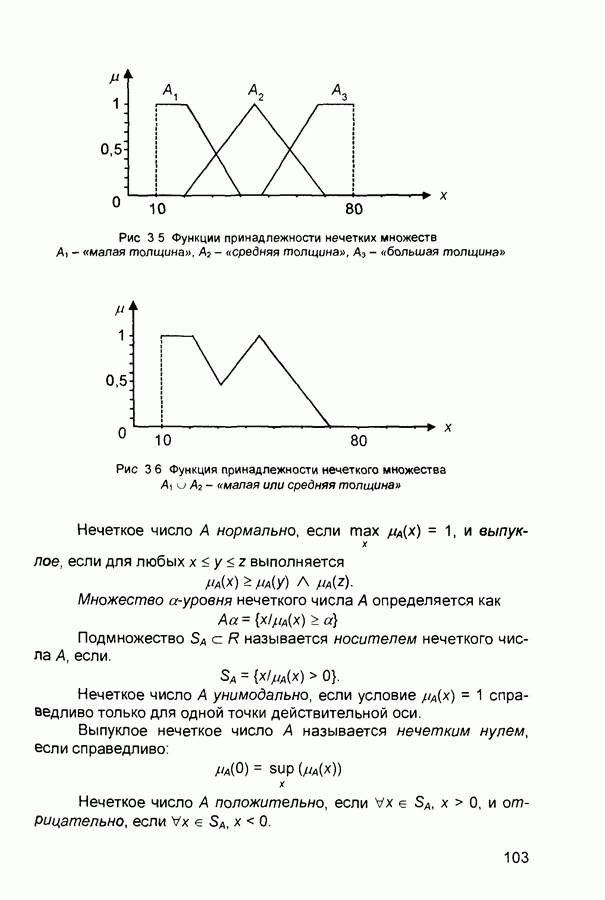
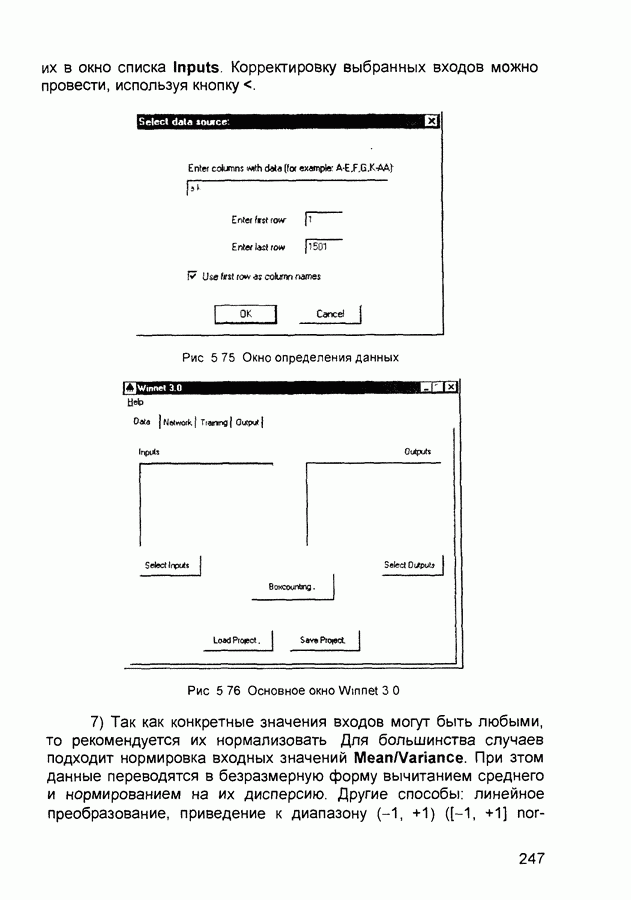
Основу сети составляет показанный на рис. П. 1.2 нейросетевой компаратор, который выполняет сравнение двух аналоговых сигналов  На выходе z - значение максимального сигнала
На выходе z - значение максимального сигнала  или
или  Выходы
Выходы  показывают, какой именно входной сигнал имеет максимальное значение. На рисунке проставлены значения синаптических весов. Смещения всех нейронов сети - нулевые. Нейроны, помеченные темным цветом, имеют жесткие пороговые передаточные функции, передаточные функции у остальных нейронов - линейные с насыщением.
показывают, какой именно входной сигнал имеет максимальное значение. На рисунке проставлены значения синаптических весов. Смещения всех нейронов сети - нулевые. Нейроны, помеченные темным цветом, имеют жесткие пороговые передаточные функции, передаточные функции у остальных нейронов - линейные с насыщением.

Рис. П.1.2. Нейросетевой компаратор
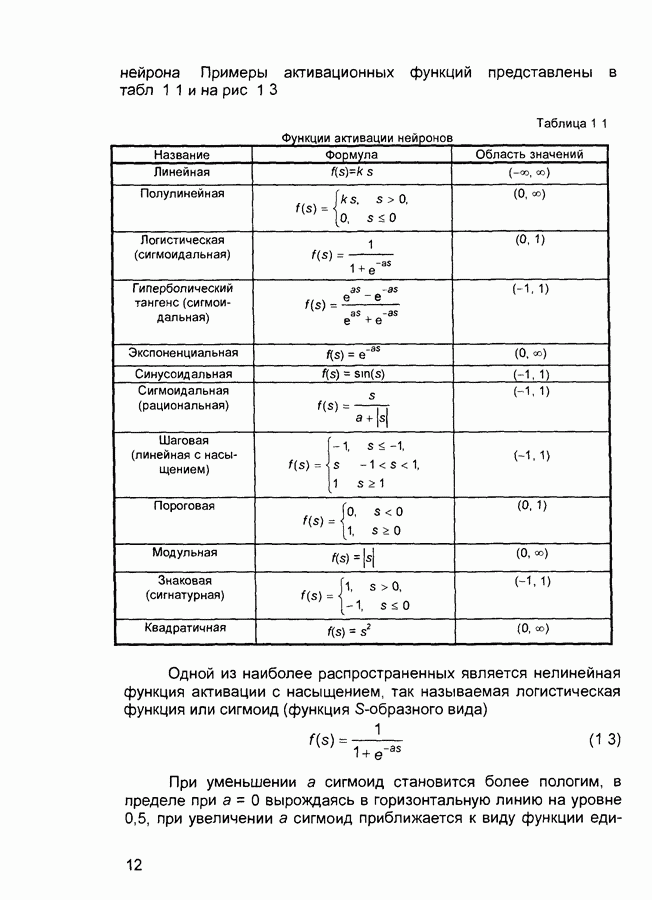
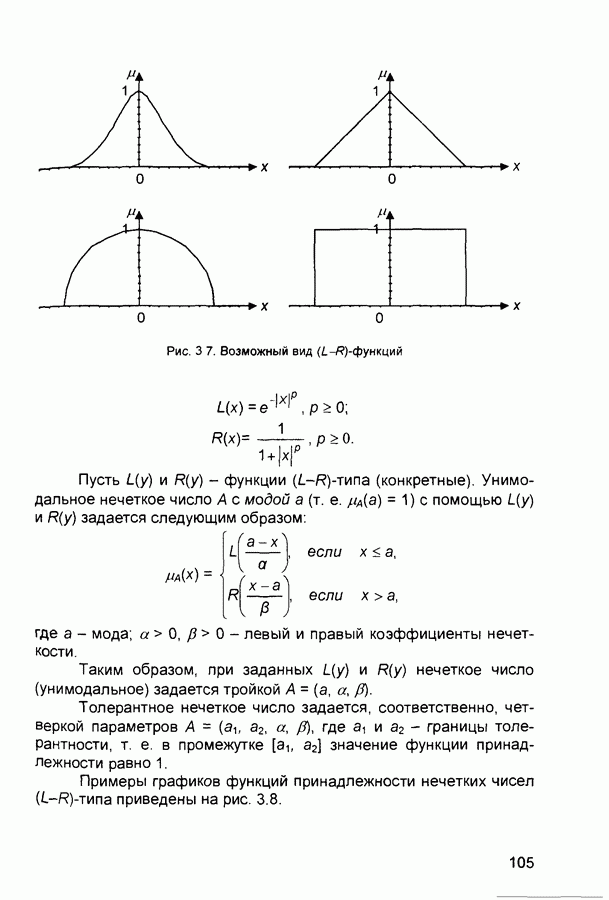
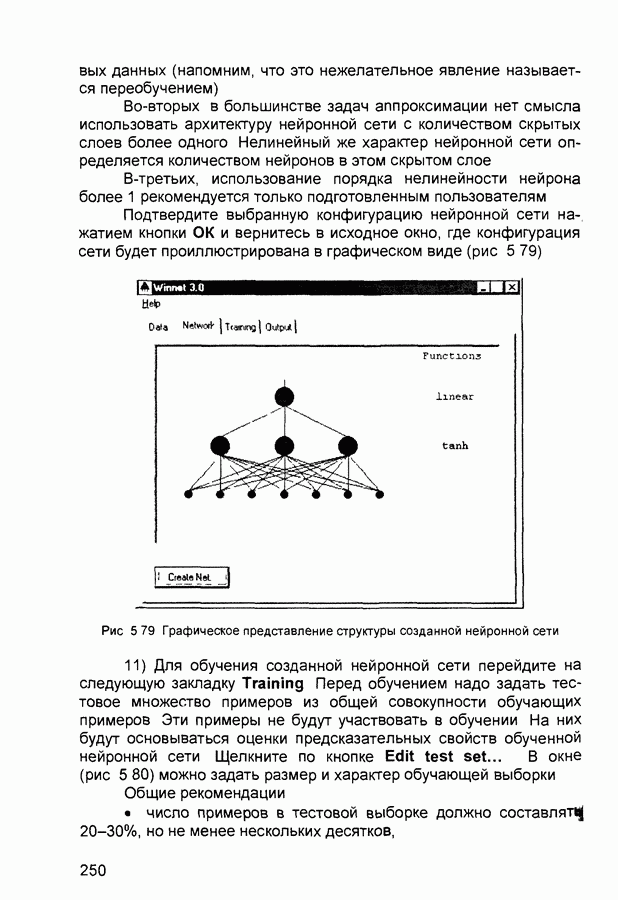
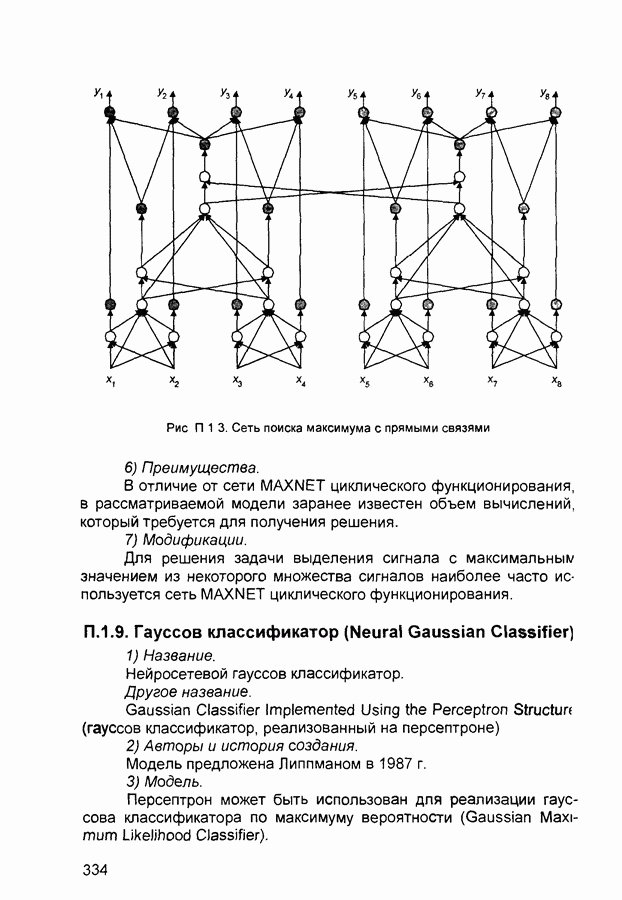
На рис. П. 1.3 показан пример построения нейронной сети для поиска максимума с прямыми связями, которая дает возможность определять максимальный сигнал из восьми входных сигналов. Сеть состоит из нескольких компараторов и дополнительных нейронов и синаптических связей. Синаптические веса компараторов такие же, как и на рис. П. 1.2. Веса других связей - единичные. Зачерненные нейроны имеют жесткие пороговые функции с нулевым смещением, активационные (передаточные) функции белых нейронов - линейные с насыщением. Активационные функции нейронов последнего слоя представляют собой пороговые функции со смещением 2,5.
Характеристики сети.
Типы входных сигналов - аналоговые (целые или действительные числа), тип выходных сигналов - целые, размерности входных и выходных сигналов совпадают и ограничены только возможностями реализуемой вычислительной системы. Число слоев в сети приблизительно равно  где
где  - размерность входного сигнала.
- размерность входного сигнала.
4) Области применения.
Совместно с сетью Хэмминга, в составе нейросетевых систем распознавания образов.
5) Недостатки.
Число слоев сети растет с увеличением размерности входного сигнала.

Рис. П.1.3. Сеть поиска максимума с прямыми связями
6) Преимущества.
В отличие от сети MAXNET циклического функционирования, в рассматриваемой модели заранее известен объем вычислений, который требуется для получения решения.
7) Модификации.
Для решения задачи выделения сигнала с максимальным значением из некоторого множества сигналов наиболее часто используется сеть MAXNET циклического функционирования.
П.1.9. Гауссов классификатор (Neural Gaussian Classifier)
1) Название.
Нейросетевой гауссов классификатор.
Другое название.
Gaussian Classifier Implemented Using the Perceptron Structure (гауссов классификатор, реализованный на персептроне)
2) Авторы и история создания.
Модель предложена Липпманом в 1987 г.
3) Модель.
Персептрон может быть использован для реализации гауссова классификатора по максимуму вероятности (Gaussian Maximum Likelihood Classifier).
В классическом алгоритме обучения персептрона не используются предположения относительно распределений примеров обучающих выборок, а рассматривается функция ошибки. Этот алгоритм работает более устойчиво, если входные сигналы формируются в результате нелинейных процессов и распределены несимметрично и не по гауссову закону
В основе построения гауссова классификатора лежат предположения о распределениях входных сигналов Считается, что эти распределения известны и соответствует закону Гаусса
Формулы для расчета параметров нейросетевого гауссова классификатора определяются следующим образом. Пусть  - среднее значение и отклонение (математическое ожидание и дисперсия) входного сигнала
- среднее значение и отклонение (математическое ожидание и дисперсия) входного сигнала  когда входной сигнал принадлежит классу
когда входной сигнал принадлежит классу  - среднее значение и отклонение входного сигнала
- среднее значение и отклонение входного сигнала  когда входной сигнал принадлежит классу
когда входной сигнал принадлежит классу  Тогда значения вероятности, используемые классификатором по максимуму вероятности пропорциональны следующим величинам:
Тогда значения вероятности, используемые классификатором по максимуму вероятности пропорциональны следующим величинам:

Классификатор по максимуму вероятности должен вычислять  и выбирать класс с наибольшей вероятностью. Первые слагаемые в формулах идентичны. Поэтому их можно опустить. Вторые слагаемые могут быть вычислены путем умножения входных сигналов на синаптические веса. Третьи слагаемые являются константами, значения которых можно присвоить смещению нейрона.
и выбирать класс с наибольшей вероятностью. Первые слагаемые в формулах идентичны. Поэтому их можно опустить. Вторые слагаемые могут быть вычислены путем умножения входных сигналов на синаптические веса. Третьи слагаемые являются константами, значения которых можно присвоить смещению нейрона.
Значения синаптических весов и смещения:

Характеристики сети.
Тип входных сигналов - бинарные или аналоговые (действительные). Размерности входа и выхода ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации - технологическими возможностями.
4) Области применения
Распознавание образов, классификация.
5) Недостатки.
Примитивные разделяющие поверхности (гиперплоскости) дают возможность решать лишь самые простые задачи распознавания. Считаются априорно известными распределения входных сигналов, соответствующие разным классам.
6) Преимущества.
Программные или аппаратные реализации модели очень просты. Простой и быстрый алгоритм формирования синаптических весов и смещений.
7) Модификации.
Адаптивный гауссов классификатор.
П.1.10. Генетический алгоритм (Genetic Algorithm)
1) Название.
Neural Network with Genetic Training Algorithm (нейронная сеть с генетическим алгоритмом обучения).
2) Авторы и история создания.
Впервые идея использования генетических алгоритмов для обучения (machine learning) была предложена Дж. Голландом (J. Holland) в 1970-е годы. Во второй половине 1980-х годов к этой идее вернулись в связи с обучением нейронных сетей.
3) Модель.
Использование механизмов генетической эволюции для обучения нейронных сетей кажется естественным, поскольку модели нейронных сетей разрабатываются по аналогии с мозгом и реализуют некоторые его особенности, появившиеся в результате биологической эволюции.
Основные компоненты генетических алгоритмов: стратегии репродукций, мутаций и отбор «индивидуальных» нейронных сетей (по аналогии с отбором индивидуальных особей).
Первая проблема построения алгоритмов генетической эволюции - это кодировка информации, содержащейся в модели нейронной сети. Коды называют хромосомами. Для фиксированной топологии (архитектуры) нейронной сети эта информация полностью содержится в значениях синаптических весов (W) и смещений (В). Набор W, В) рассматривается как хромосома. Возможны более сложные способы кодирования информации.
Для реализации концепции отбора необходимо ввести способ сопоставления различных хромосом в соответствии с их возможностями решения поставленных задач. Для сетей с последовательными связями это может быть евклидово расстояние.
В отличие от большинства других алгоритмов обучения, для генетических алгоритмов формируется не один, а несколько наборов начальных значений параметров, которые называются популяцией хромосом. Популяция обрабатывается с помощью алгоритмов репродукции, изменчивости (мутаций), генетической композиции. Эти алгоритмы напоминают биологические процессы. Наиболее важные среди них: случайные мутации данных в индивидуальных хромосомах, переходы (кроссовер), рекомбинация генетического материала, содержащегося в индивидуальных родительских хромосомах (аналогично гетеросексуальной репродукции), миграция генов.
Генетический алгоритм работает следующим образом. Инициализируется популяция и все хромосомы сравниваются в соответствии с выбранной функцией оценки. Далее (возможно многократно) выполняется процедура репродукции популяции хромосом. Родители выбираются случайным образом в соответствии со значениями оценки (вероятность того, что данная хромосома станет родителем, пропорциональна полученной оценке). Репродукция происходит индивидуально для одного родителя путем мутации хромосомы либо для двух родителей путем кроссовера генов. Получившиеся потомки оцениваются в соответствии с заданной функцией и помещаются в популяцию.
В результате использования описанных операций на каждой стадии эволюции получаются популяции со все более совершенными вариантами.
4) Области применения.
Распознавание образов, классификация, прогнозирование.
5) Недостатки.
Сложны для понимания и программной реализации.
6) Преимущества.
Генетические алгоритмы особенно эффективны в поиске глобальных минимумов адаптивных рельефов, так как ими исследуются большие области допустимых значений параметров нейронных сетей.
Достаточно высокая скорость обучения, хотя и меньшая, чем скорость сходимости градиентных алгоритмов.
Генетические алгоритмы дают возможность оперировать дискретными значениями параметров нейронных сетей, что упрощает аппаратную реализацию нейронных сетей и приводит к сокращению общего времени обучения.
7) Модификации.
В рамках генетического подхода в последнее время разработаны многочисленные алгоритмы обучения нейронных сетей,
различающиеся способами представления данных нейронной сети в хромосомах, стратегиями репродукции, мутаций, отбора.
П.1.11. Сеть Хэмминга (Hamming Net)
1) Название.
Hamming Net сеть Хэмминга).
Другие названия.
Нейросетевая модель ассоциативной памяти, основанная на вычислении расстояния Хэмминга
Классификатор по минимуму расстояния Хэмминга.
2) Авторы и история создания.
Нейросетевые модели, основанные на вычислениях расстояния Хэмминга в задачах передачи двоичных сигналов фиксированной длины, введены Липпманом в 1987 г.
3) Модель
Расстояние Хэмминга между двумя бинарными векторами одинаковой длины - это число несовпадающих бит в этих векторах. Нейронная сеть, которая реализует параллельное вычисление расстояний Хэмминга от входного вектора до нескольких векторов-образцов, носит название сети Хэмминга.
Характеристики сети.
Тип входных сигналов - бинарные векторы; тип выходных сигналов - целые числа. Размерности входа и выхода ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации - технологическими возможностями. Размерности входных и выходных сигналов могут не совпадать. Тип передаточной функции - линейная с насыщением. Число синапсов в сети равно произведению числа нейронов в сети на размерность входного сигнала.
Формирование синаптических весов и смещений сети.

Функционирование сети:

где  синаптический вес
синаптический вес  нейрона;
нейрона;  элемент входного сигнала сети;
элемент входного сигнала сети;  - выход
- выход  нейрона,
нейрона,  - смещение
- смещение  нейрона,
нейрона,  - размерность входного сигнала; М - количество нейронов в сети;
- размерность входного сигнала; М - количество нейронов в сети;  элемент
элемент  вектора-образца.
вектора-образца.
Наиболее часто рассматривается модель, синаптические веса и смещения в которой вычисляются по формулам:

4) Области применения.
Распознавание образов, классификация, ассоциативная память, надежная передача сигналов в условиях помех.
5) Недостатки.
Сеть способна правильно распознавать (классифицировать) только слабо зашумленные входные сигналы Возможность использования только бинарных входных сигналов существенно ограничивает область применения.
6) Преимущества.
Сеть работает предельно просто и быстро Выходной сигнал (решение задачи) формируется в результате прохода сигналов всего лишь через один слой нейронов. Для сравнения: в многослойных сетях сигнал проходит через несколько слоев, в сетях циклического функционирования сигнал многократно проходит через нейроны сети, причем число итераций, необходимое для получения решения, бывает заранее не известно
В модели использован один из самых простых алгоритмов формирования синаптических весов и смещений сети
В отличие от сети Хопфилда, емкость сети Хэмминга не зависит от размерности входного сигнала, она в точности равна количеству нейронов. Сеть Хопфилда с входным сигналом размерностью 100 может запомнить 10 образцов, при этом у нее будет 10000 синапсов. У сети Хэмминга с такой же емкостью будет всего лишь 1000 синапсов.
7) Модификации.
Сеть Хэмминга может быть дополнена сетью MAXNET, которая определяет, какой из нейронов сети Хэмминга имеет выход с максимальным значением.
П.1.12. Сеть Хопфилда (Hopfield Network)
1) Название
Hopfield Network (сеть Хопфилда).
Другие названия.
Ассоциативная память, адресуемая по содержанию.
Модель Хопфилда.
2) Авторы и история создания.
Сеть разработана Хопфилдом в 1982 г. С нее началось возрождение интереса к нейронным сетям. С тех пор были предложены ее многочисленные модификации, направленные на увеличение емкости, улучшение сходимости.
3) Модель
Одна из первых предложенных сетей Хопфилда используется как автоассоциативная память Исходными данными для расчета значений синаптических весов сети являются векторы-образцы классов Выход каждого из нейронов подается на входы всех остальных нейронов.
Формирование синаптических весов сети

Функционирование сети:

где  синаптический вес
синаптический вес  нейрона;
нейрона;  элемент входного сигнала сети;
элемент входного сигнала сети;  элемент
элемент  вектора-образца,
вектора-образца,  - выход
- выход  нейрона;
нейрона;  - размерность входного сигнала; М - количество векторов-образцов
- размерность входного сигнала; М - количество векторов-образцов
Сеть функционирует циклически В процессе функционирования уменьшается энергетическая функция:

Критерием останова - неизменность выходов сети.
Характеристики сети.
Тип входных и выходных сигналов - биполярный (+1 и -1).
Размерности входа и выхода ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации - технологическими возможностями. Размерности входных и выходных сигналов совпадают.
Тип передаточной функции - жесткая пороговая; число синапсов в сети равно  Сеть, содержащая
Сеть, содержащая  нейронов, может запомнить не более
нейронов, может запомнить не более  образов. При этом запоминаемые образы не должны быть сильно коррелированы.
образов. При этом запоминаемые образы не должны быть сильно коррелированы.
4) Области применения.
Ассоциативная память, адресуемая по содержанию; распознавание образов; задачи оптимизации (в том числе, комбинаторной оптимизации).
5) Недостатки.
Сеть обладает небольшой емкостью. Кроме того, наряду с запомненными образами в сети хранятся и их «негативы».
Размерность и тип входных сигналов совпадают с размерностью и типом выходных сигналов Это существенно ограничивает применение сети в задачах распознавания образов.
При использовании сильно коррелированных векторов-образцов возможно зацикливание сети в процессе функционирования
Квадратичный рост числа синапсов при увеличении размерности входного сигнала
6) Преимущества.
Позволяет восстановить искаженные сигналы
7) Модификации.
Существует различные модификации сети Хопфилда как с дискретными, так и с непрерывными состояниями и временем.
Для увеличения емкости сети и повышения качества распознавания образов используют мультипликативные нейроны Сети, состоящие из таких нейронов называются сетями высших порядков.
Были предложены многослойные сети Хопфилда, которые обладают определенными преимуществами по сравнению с первоначальной моделью.
П.1.13. Входная звезда (Instar)
1) Название.
Instar (входная звезда).
2) Авторы и история создания.
Конфигурация Instar - фрагмент нейронных сетей, являющаяся моделью отдельных участков биологического мозга, была предложена и использована Гроссбергом во многих нейросетевых архитектурах.
3) Модель.
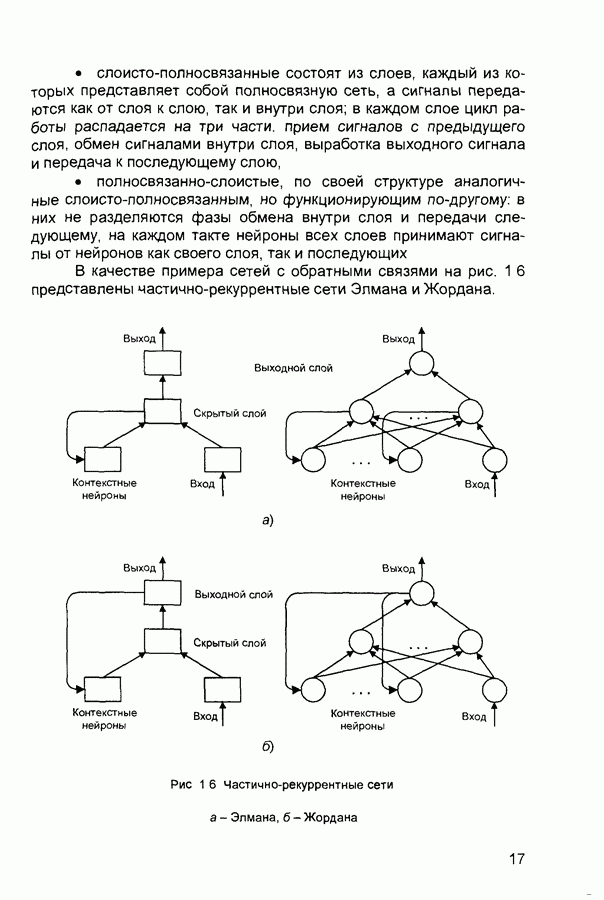
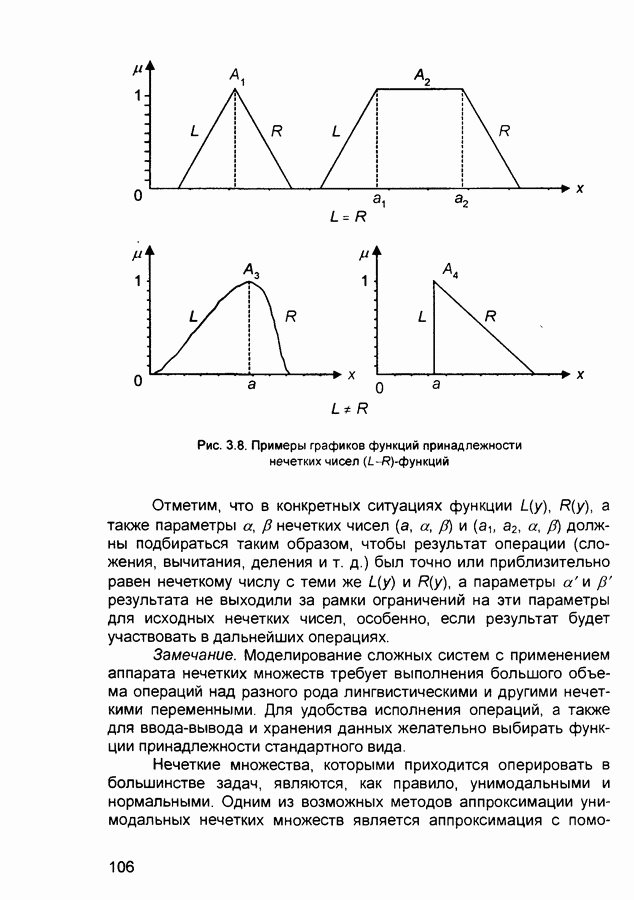
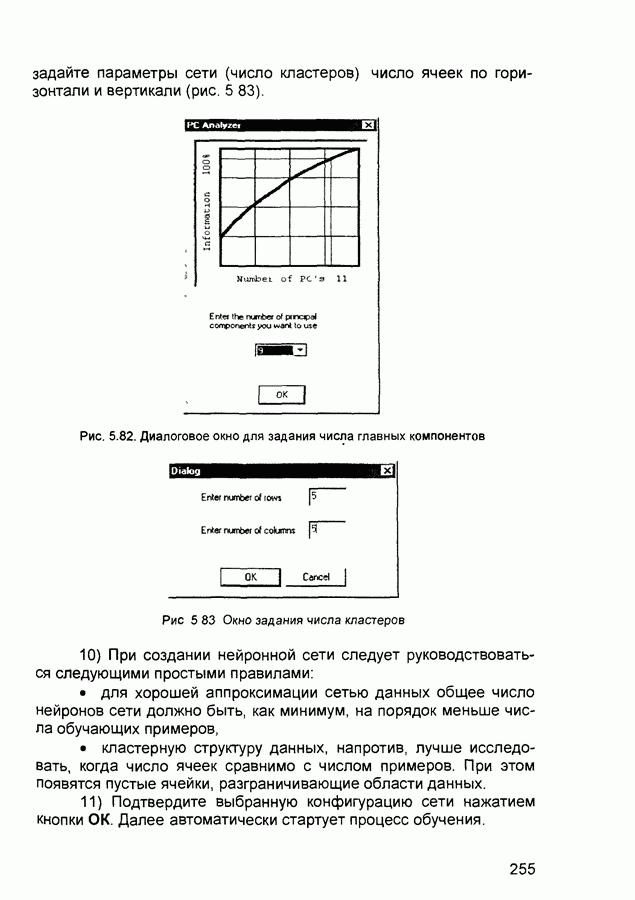
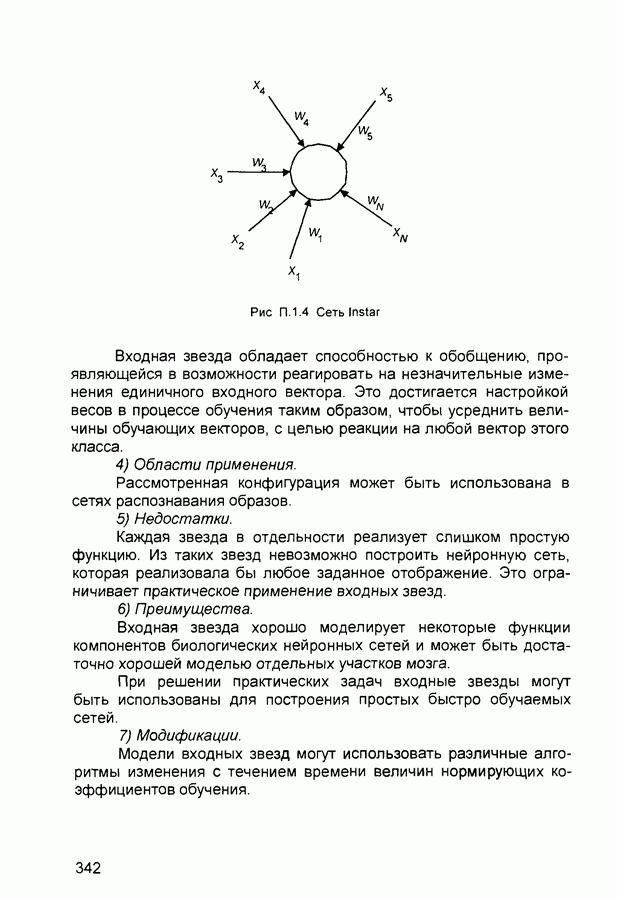
Входная звезда (на рис. П.1 4) представляет собой нейрон, на который подаются входные сигналы через синаптические веса.
Входная звезда реагирует на определенный входной вектор, которому она обучена Это обеспечивается настройкой весов на соответствующий входной вектор. На выходе звезды формируется взвешенная сумма ее входов, представляющая свертку входного вектора с весовым вектором.
В процессе обучения осуществляется модификация весовых коэффициентов:

где  - коэффициент скорости обучения, равный в начальный момент 0,1 и уменьшающийся в процессе обучения до нуля.
- коэффициент скорости обучения, равный в начальный момент 0,1 и уменьшающийся в процессе обучения до нуля.

Рис. П.1.4 Сеть Instar
Входная звезда обладает способностью к обобщению, проявляющейся в возможности реагировать на незначительные изменения единичного входного вектора. Это достигается настройкой весов в процессе обучения таким образом, чтобы усреднить величины обучающих векторов, с целью реакции на любой вектор этого класса.
4) Области применения.
Рассмотренная конфигурация может быть использована в сетях распознавания образов.
5) Недостатки.
Каждая звезда в отдельности реализует слишком простую функцию. Из таких звезд невозможно построить нейронную сеть, которая реализовала бы любое заданное отображение. Это ограничивает практическое применение входных звезд.
6) Преимущества.
Входная звезда хорошо моделирует некоторые функции компонентов биологических нейронных сетей и может быть достаточно хорошей моделью отдельных участков мозга.
При решении практических задач входные звезды могут быть использованы для построения простых быстро обучаемых сетей.
7) Модификации.
Модели входных звезд могут использовать различные алгоритмы изменения с течением времени величин нормирующих коэффициентов обучения.
П.1.14. Сеть Кохонена (Kohonens Neural Network)
1) Название.
Kohonens Neural Network (сеть Кохонена)
Другое название.
Kohonens Self Organizing Feature Map (SOFM) (самоорганизующаяся карта признаков Кохонена).
2) Авторы и история создания.
Предложена Кохоненом в 1984 г. К настоящему времени существует множество модификаций исходной модели с развитой математической теорией построения и функционирования.
3) Модель.
Хотя строение мозга в значительной степени предопределяется генетически, отдельные структуры мозга формируются в результате самоорганизации. Алгоритм Кохонена в некоторой степени подобен процессам, происходящим в мозге на основе самообучения.
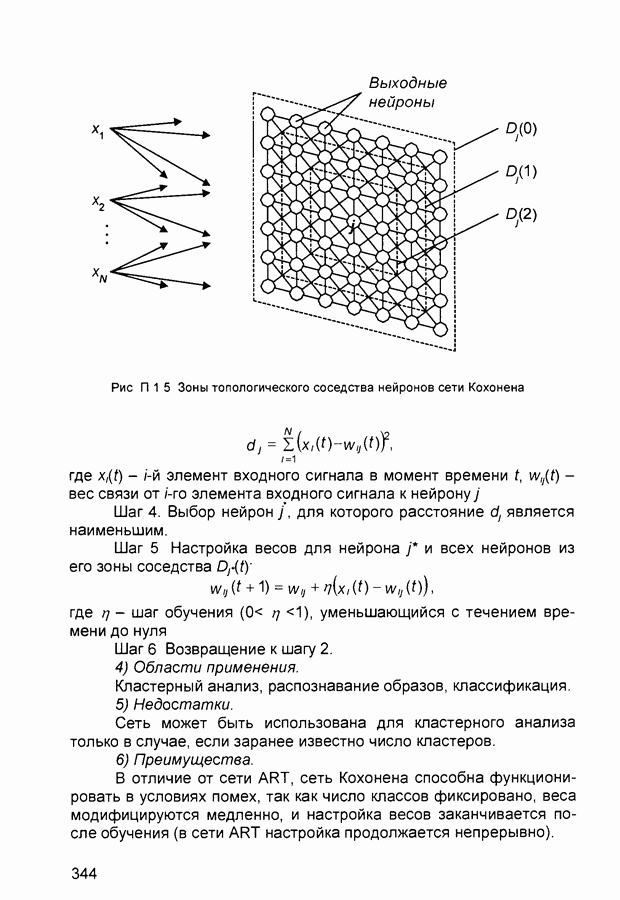
Сеть Кохонена предназначена для разделения векторов входных сигналов на подгруппы. Сеть состоит из М нейронов, образующих прямоугольную решетку на плоскости (рис. П.1.5). Элементы входных сигналов подаются на входы всех нейронов сети. В процессе работы алгоритма настраиваются синаптические веса нейронов.
Входные сигналы (вектора действительных чисел) последовательно предъявляются сети, при этом требуемые выходные сигналы не определяются. После предъявления достаточного числа входных векторов, синаптические веса сети определяют кластеры. Кроме того, веса организуются так, что топологически близкие нейроны чувствительны к похожим входным сигналам.
Для реализации алгоритма необходимо определить меру соседства нейронов (меру близости) На рис. П.1.5 показаны зоны топологического соседства нейронов в различные моменты времени.  - множество нейронов, которые считаются соседями нейрона
- множество нейронов, которые считаются соседями нейрона  в момент времени
в момент времени  Размеры зоны соседства уменьшаются с течением времени.
Размеры зоны соседства уменьшаются с течением времени.
Алгоритм Кохонена:
ШАГ 1. Инициализация сети: весовым коэффициентам сети, общее число которых равно  присваиваются малые случайные значения.
присваиваются малые случайные значения.  - начальная зона соседства.
- начальная зона соседства.
ШАГ 2. Предъявление сети нового входного сигнала.
ШАГ 3. Вычисление расстояния  от входного сигнала до каждого нейрона
от входного сигнала до каждого нейрона  по формуле:
по формуле:

Рис. П.1.5. Зоны топологического соседства нейронов сети Кохонена

где  элемент входного сигнала в момент времени
элемент входного сигнала в момент времени  - вес связи от
- вес связи от  элемента входного сигнала к нейрону
элемента входного сигнала к нейрону 
Шаг 4. Выбор нейрон  для которого расстояние
для которого расстояние  является наименьшим.
является наименьшим.
Шаг 5 Настройка весов для нейрона  и всех нейронов из его зоны соседства
и всех нейронов из его зоны соседства 

где  - шаг обучения
- шаг обучения  уменьшающийся с течением времени до нуля
уменьшающийся с течением времени до нуля
Шаг 6 Возвращение к шагу 2.
4) Области применения.
Кластерный анализ, распознавание образов, классификация.
5) Недостатки.
Сеть может быть использована для кластерного анализа только в случае, если заранее известно число кластеров.
6) Преимущества.
В отличие от сети ART, сеть Кохонена способна функционировать в условиях помех, так как число классов фиксировано, веса модифицируются медленно, и настройка весов заканчивается после обучения (в сети ART настройка продолжается непрерывно).
7) Модификации.
Одна из модификаций состоит в добавлении к сети Кохонена сети MAXNET, которая определяет нейрон с наименьшим расстоянием до входного сигнала
П.1.15. Сеть поиска максимума (MAXNET)
1) Название.
MAXNET (сеть поиска максимума).
Другие названия.
MAXNET with Competition through Lateral Inhibition (сеть поиска максимума с конкуренцией посредством латерального торможения).
Одна из сетей группы «winner takes all» («победитель получает все»).
Максимизатор.
2) Авторы и история создания
Простая сеть, имеющая давнюю историю использования.
3) Модель.
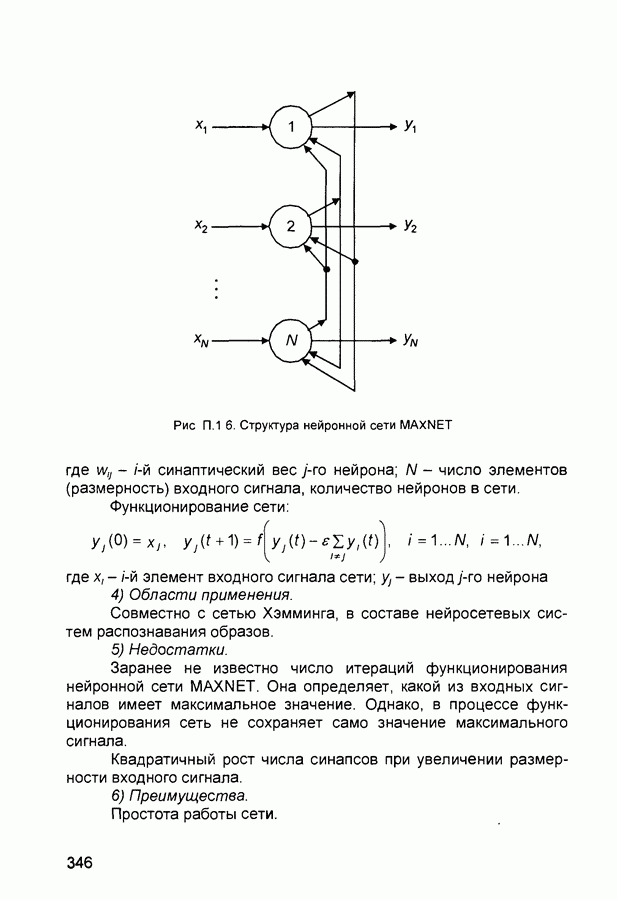
MAXNET (рис П.1 6) является сетью циклического функционирования. На каждой итерации большие сигналы на выходах нейронов подавляют слабые сигналы на выходах других нейронов. Это достигается за счет использования латеральных связей. Если в начале функционирования сети сигнал на выходе одного из нейронов имеет максимальное значение, то в конце функционирования на выходах всех нейронов, кроме максимального, формируются значения, близкие к нулю. Итерации сети завершаются после того, как выходные сигналы нейронов перестают меняться. Таким образом нейрон с наибольшим выходным сигналом «побеждает».
Характеристики сети.
Типы входных сигналов - целые или действительные; тип выходных сигналов - действительные. Размерности входа и выхода ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации - технологическими возможностями. Размерности входных и выходных сигналов совпадают. Тип передаточной функции - линейная с насыщением (используется линейный участок). Число синапсов в сети равно 
Формирование синаптических весов сети:


Рис. П.1.6. Структура нейронной сети MAXNET
где  синаптический вес
синаптический вес  нейрона;
нейрона;  - число элементов (размерность) входного сигнала, количество нейронов в сети.
- число элементов (размерность) входного сигнала, количество нейронов в сети.
Функционирование сети:

где  элемент входного сигнала сети; у, - выход
элемент входного сигнала сети; у, - выход  нейрона
нейрона
4) Области применения.
Совместно с сетью Хэмминга, в составе нейросетевых систем распознавания образов.
5) Недостатки.
Заранее не известно число итераций функционирования нейронной сети MAXNET. Она определяет, какой из входных сигналов имеет максимальное значение. Однако, в процессе функционирования сеть не сохраняет само значение максимального сигнала.
Квадратичный рост числа синапсов при увеличении размерности входного сигнала.
6) Преимущества.
Простота работы сети.
7) Модификации.
Для выделения сигнала с максимальным значением из некоторого множества сигналов может быть использована многослойная нейронная сеть с последовательными связями.
П.1.16. Выходная звезда (Outstar)
1) Название.
Outstar ( выходная звезда).
2) Авторы и история создания.
Конфигурация Outstar - фрагмент нейронных сетей, предложенный и использованный Гроссбергом во многих нейросетевых архитектурах, и также, как и входная звезда, является моделью отдельных участков биологического мозга.
3) Модель.
Выходная звезда представляет собой нейрон, управляющий весовыми коэффициентами (рис. П.1.7). При возбуждении она вырабатывает требуемый сигнал для других нейронов.
При обучении веса выходной звезды настраиваются на множество векторов, близких к эталонному вектору в соответствии с выражением:

где  - коэффициент, изменяющийся в процессе обучения от единицы до нуля.
- коэффициент, изменяющийся в процессе обучения от единицы до нуля.
Выходной сигнал выходной звезды представляет собой статистическую характеристику обучающего набора.
Входные и выходные звезды могут быть взаимно соединены в сети любой сложности.

Рис. П.1.7. Сеть Outstar
4) Области применения.
Рассмотренная конфигурация может быть использована как компонент нейронных сетей для распознавания образов.
5) Недостатки.
Каждая звезда в отдельности реализует слишком простую функцию. Вычислительные возможности нейронных сетей, составленных из таких звезд, ограничены.
6) Преимущества.
При решении практических задач выходные звезды могут быть использованы для построения простых быстро обучаемых сетей.
7) Модификации.
В моделях выходных звезд могут быть использованы различные алгоритмы изменения с течением времени величин нормирующих коэффициентов обучения.
П.1.17. Сеть радиального основания (Radial Basis Function Network)
1) Название.
Radial Basis Function Network (RBFN).
Другое название.
Сеть радиальных базисных функций.
2) Авторы и история создания.
Под парадигмой RBFN понимается архитектура, предложенная Moody и Darken в 1989 г. К классу RBFN относят также вероятностные и регрессионные нейронные сети.
3) Модель.
В общем случае под термином Radial Basis Function Network понимается нейронная сеть, которая содержит слой скрытых нейронов с радиально симметричной активационной функцией, каждый из которых предназначен для хранения отдельного эталонного вектора (в виде вектора весов). Для построения RBFN необходимо выполнение следующих условий.
Во-первых, наличие эталонов, представленных в виде весовых векторов нейронов скрытого слоя. Во-вторых, наличие способа измерения расстояния входного вектора от эталона. Обычно это стандартное евклидово расстояние. В-третьих, специальная функция активации нейронов скрытого слоя, задающая выбранный способ измерения расстояния. Обычно используется функция Гаусса, существенно усиливающая малую разницу между входным и эталонным векторами.
Другими словами, выходной сигнал эталонного нейрона скрытого слоя у, - это функция (гауссиан) только от расстояния  между входным и эталонным векторами:
между входным и эталонным векторами:

где  - входной вектор;
- входной вектор;  - весовой вектор
- весовой вектор  эталонного нейрона скрытого слоя;
эталонного нейрона скрытого слоя;  - параметры активационной функции;
- параметры активационной функции;  - число эталонов.
- число эталонов.
Обучение слоя образцов-нейронов сети подразумевает предварительное проведение кластеризации для нахождения эталонных векторов и определенных эвристик для определения значений 
Нейроны скрытого слоя соединены по полносвязной схеме с нейронами выходного слоя, которые осуществляют взвешенное суммирование. Для нахождения значения весов от нейронов скрытого к выходному слою используется линейная регрессия.
В общем случае активационные функции нейронов скрытого слоя могут отражать законы распределения случайных величин (вероятностные нейронные сети) либо характеризовать различные аналитические зависимости между переменными (регрессионные нейронные сети).
4) Области применения.
Распознавание образов, классификация.
5) Недостатки.
Заранее должно быть известно число эталонов, а также эвристики для построения активационных функций нейронов скрытого слоя.
6) Преимущества.
Отсутствие этапа обучения в принятом смысле этого слова.
7) Модификации.
В моделях RBFN могут быть использованы различные способы измерения расстояния между векторами, а также функции активации нейронов скрытого слоя.
П.1.18. Нейронные сети, имитирующие отжиг (Neural Networks with Simulated Annealing Training Algorithm)
1) Название.
Neural Networks with Simulated Annealing Training Algorithm (нейронные сети, обучаемые по методу имитации отжига).
2) Авторы и история создания.
В 50-е годы была разработана математическая модель отжига металла, согласно которой металл в процессе кристаллизации из жидкой фазы проходит через ряд состояний, характеризующихся различным значением энергии. Атомы металла стремятся к состоянию минимума энергии. При высоких температурах атомы могут совершать движения, приводящие к переходу в состояния с большими значениями энергии. В процессе постепенного охлаждения металла достигается глобальный минимум энергии.
Алгоритм имитации отжига - вариант итеративного решения оптимизационных задач, в соответствии с которым, как и в реальных условиях отжига, разрешаются шаги, повышающие значения функции ошибки (энергии).
На основе этой математической модели в 80-е годы был создан алгоритм оптимизации, обладающий высокой эффективностью при обучении нейронных сетей.
3) Модель.
Алгоритм имитации отжига может быть использован для обучения как многослойных, так и полносвязных сетей. При этом функции активации сети не обязательно должны быть непрерывно дифференцируемыми. В качестве функции ошибки можно использовать среднеквадратическое отклонение.
Используются градиентный и стохастический алгоритмы имитации отжига.
В градиентном алгоритме на каждой итерации вычисляется направление антиградиента адаптивного рельефа и делается шаг заданной величины. В процессе обучения величина шага уменьшается. Большие значения шага на начальных итерациях обучения могут приводить к возможному возрастанию значения функции ошибки. В конце обучения величина шагов мала и значение функции ошибки уменьшается на каждой итерации.
При обучении нейронной сети на основе стохастического алгоритма имитации отжига совершаются шаги по адаптивному рельефу в случайных направлениях. Пусть на итерации к система находится в точке  адаптивного рельефа, характеризующейся значением энергии Е. При этом шаг из точки
адаптивного рельефа, характеризующейся значением энергии Е. При этом шаг из точки  в точку
в точку  со значением энергии
со значением энергии  приводящий к увеличению значения функции ошибки (энергии) на величину
приводящий к увеличению значения функции ошибки (энергии) на величину  допускается с заданной вероятностью.
допускается с заданной вероятностью.
Критерии останова функционирования сети:
• функционирование многослойных сетей без обратных связей заканчивается после получения выходных сигналов нейронов последнего слоя;
• для сетей циклического функционирования (попносвяз-ных, многослойных с обратными связями и др.): останов после К итераций; останов после прекращения изменения выходных сигналов;
• достижение некоторого заданного значения функции ошибки.
Характеристики сети.
Типы входных и выходных сигналов - любые. Размерности входа и выхода - любые, ограничения связаны с заданной скоростью обучения (медленная сходимость для сетей большой размерности). Емкость сети в общем случае не определена. Тип передаточной функции - любая, ограниченная по области значений. Количество синапсов и смещений сети ограничено скоростью обучения. Для сетей с числом синапсов порядка нескольких сотен алгоритм имитации отжига очень эффективен. Для программно реализованных на персональном компьютере сетей с десятками тысяч настраиваемых параметров процесс обучения по методу отжига длится катастрофически долго
4) Области применения.
С помощью алгоритма имитации отжига можно строить отображения векторов различной размерности. К построению таких отображений сводятся многие задачи распознавания образов, адаптивного управления, многопараметрической идентификации, прогнозирования и диагностики.
5) Недостатки.
Низкая скорость сходимости при обучении нейронных сетей большой размерности.
6) Преимущества.
«Тепловые флуктуации», заложенные в алгоритм, дают возможность избегать локальных минимумов. Показано, что алгоритм имитации отжига может быть использован для поиска глобального оптимума адаптивного рельефа нейронной сети.
7) Модификации.
Алгоритмы имитации отжига различаются структурами нейронных сетей, для обучения которых они используются, а также правилами, в соответствии с которыми допускаются шаги, увеличивающие энергию системы.
Модифицированные алгоритмы имитации отжига используются также для решения задач комбинаторной оптимизации.
П.1.19. Однослойный персептрон (Single Layer Perceptron)
1) Название.
Single Layer Perceptron (однослойный персептрон).
2) Авторы и история создания.
Разработан Ф. Розенблаттом в 1959 г.
3) Модель.
Однослойный персептрон способен распознавать простейшие образы. Отдельный персептронный нейрон вычисляет взвешенную сумму элементов входного сигнала, вычитает значение смещения и пропускает результат через жесткую пороговую функцию, выход которой равен  или -1 в зависимости от принадлежности входного сигнала к одному из двух классов.
или -1 в зависимости от принадлежности входного сигнала к одному из двух классов.
Персептрон, состоящий из одного нейрона, формирует две решающие области, разделенные гиперплоскостью. Уравнение, задающее разделяющую гиперплоскостью (прямую - в случае двухвходового персептронного нейрона), зависит от значений синаптических весов и смещения.
Классический алгоритм настройки персептрона, предложенный Розенблаттом, заключается в следующем.
ШАГ 1. Инициализация синаптических весов  и смещения
и смещения  некоторыми малыми случайным числами.
некоторыми малыми случайным числами.
ШАГ 2. Предъявление персептрону нового входного вектора  требуемого выходного сигнала
требуемого выходного сигнала 
3. Вычисление выходного сигнала персептрона:

ШАГ 4. Настройка значений весов персептрона:

где  коэффициент скорости обучения
коэффициент скорости обучения 
Если решение правильное, веса не модифицируются.
ШАГ 5. Переход к шагу 2.
Характеристики сети.
Тип входных сигналов - бинарные или аналоговые (действительные). Размерности входа и выхода ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации - технологическими возможностями. Емкость сети совпадает с числом нейронов.
4) Области применения:
Распознавание образов, классификация.
5) Недостатки.
Простые разделяющие поверхности (гиперплоскости) дают возможность решать лишь несложные задачи распознавания.
6) Преимущества.
Программные или аппаратные реализации модели очень просты. Простой и быстрый алгоритм обучения.
7) Модификации.
Многослойные персептроны дают возможность строить более сложные разделяющие поверхности и поэтому находят более широкое применение при решении задач распознавания.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
- 1.1. Биологический нейрон
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
- 2.2. Персептроны
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
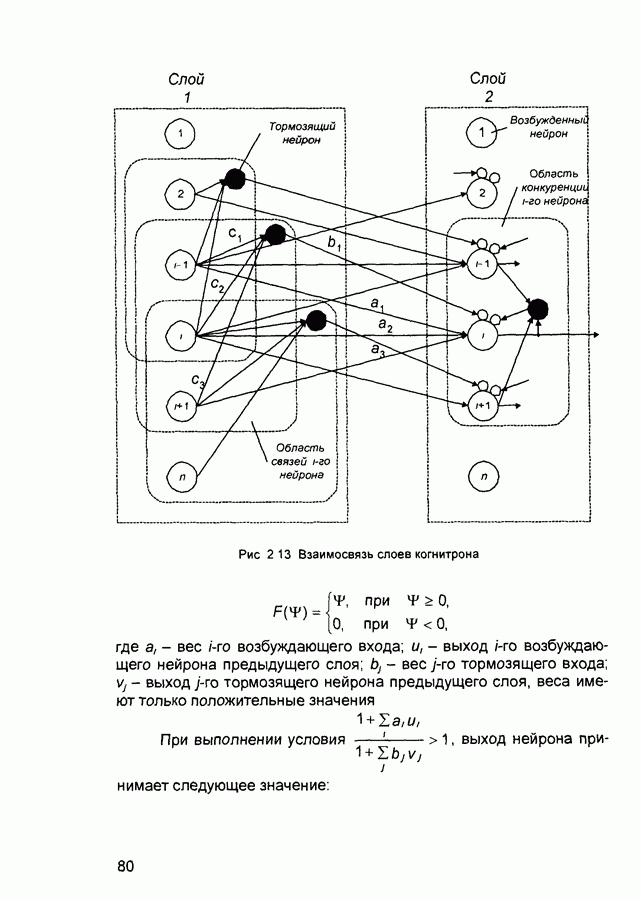
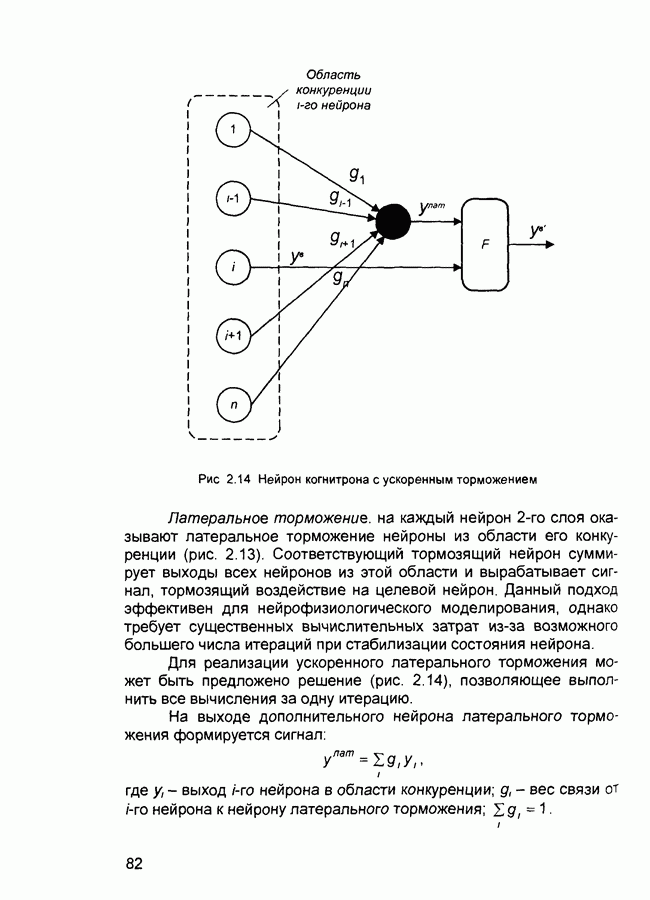
- 2.7. Когнитрон
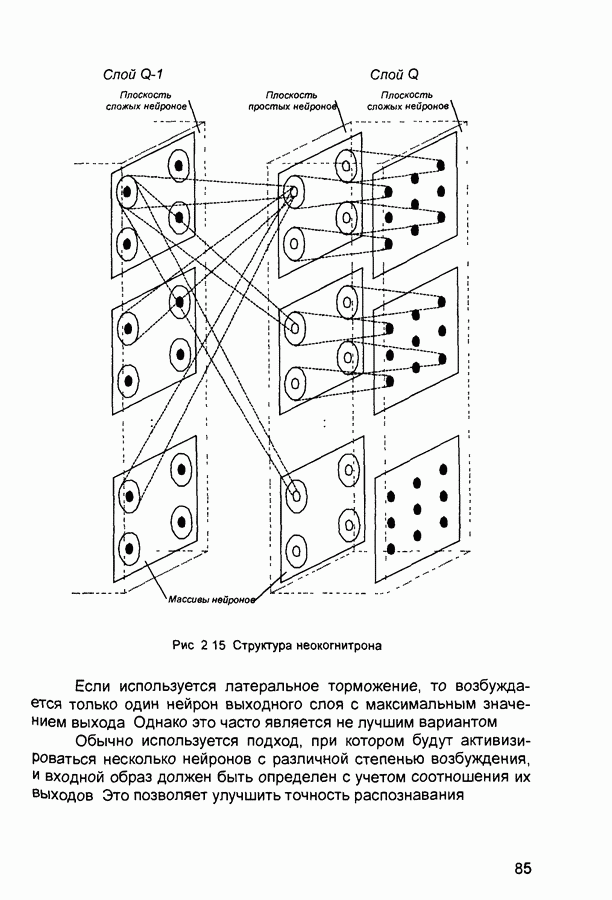
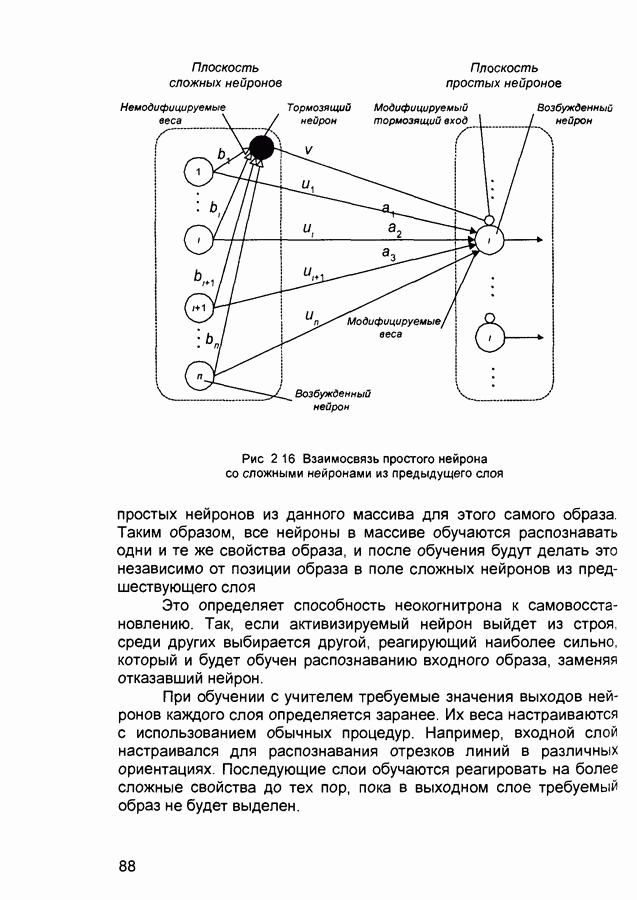
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
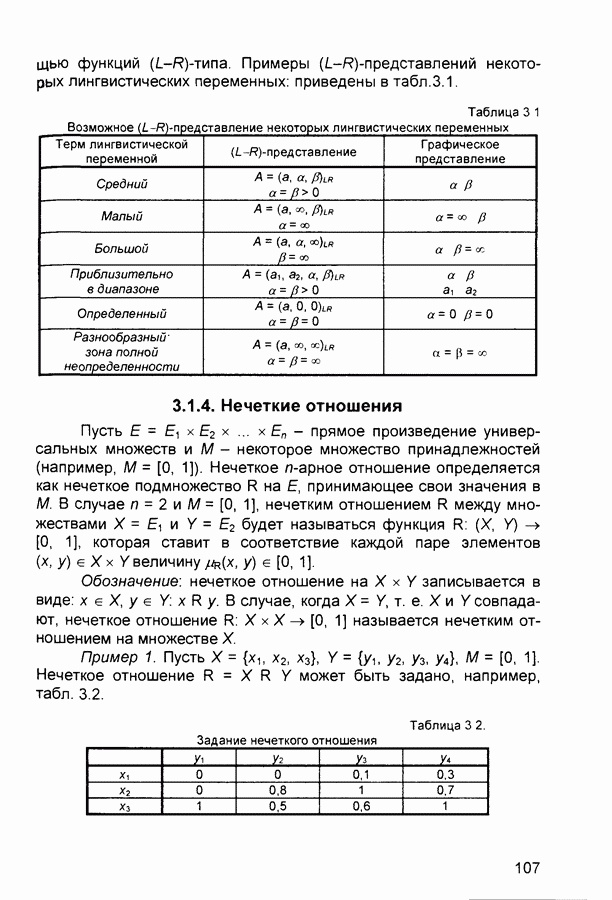
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
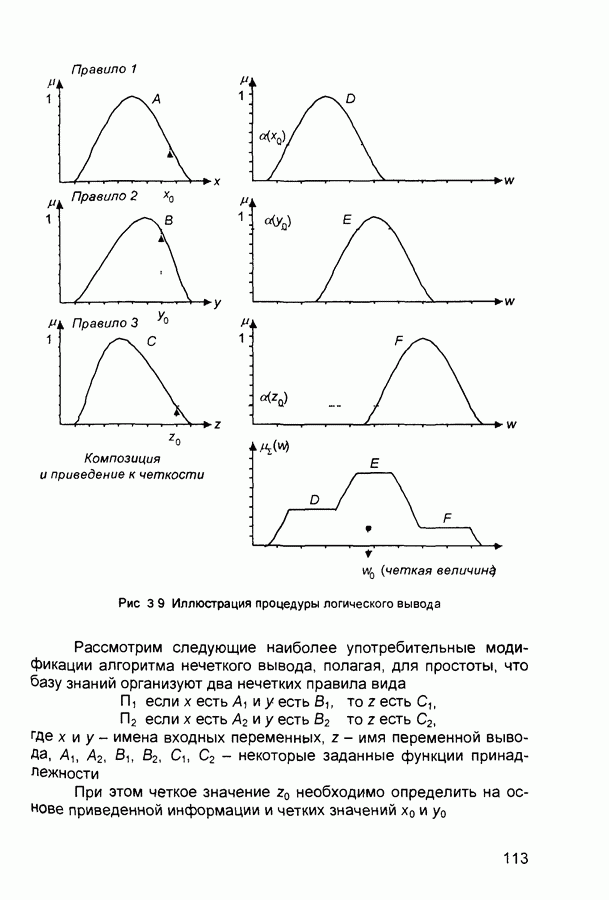
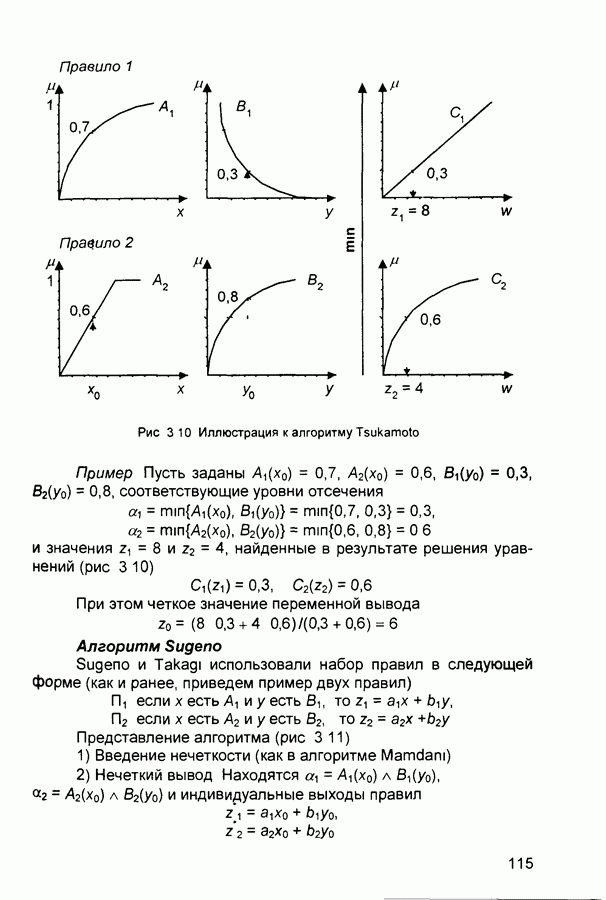
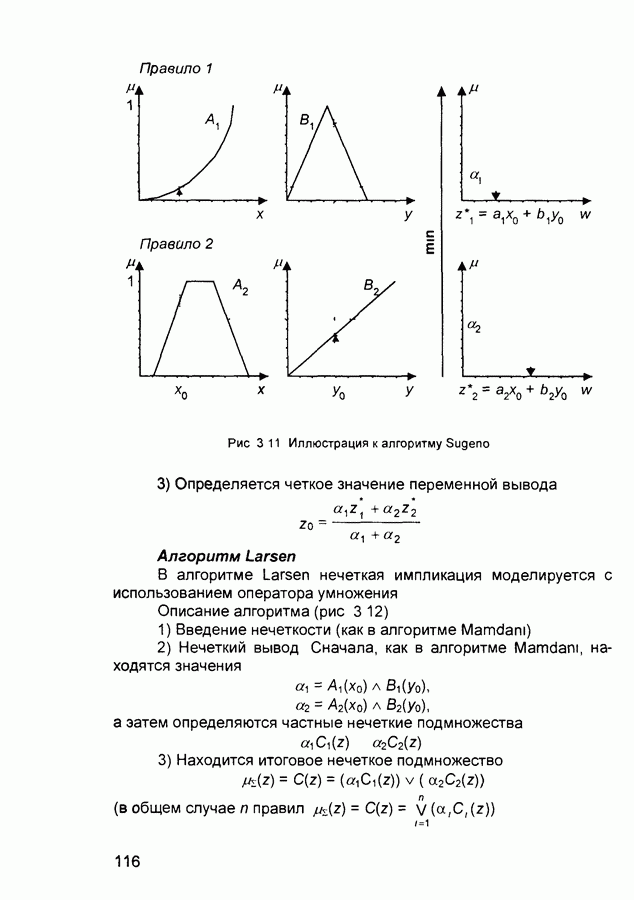
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
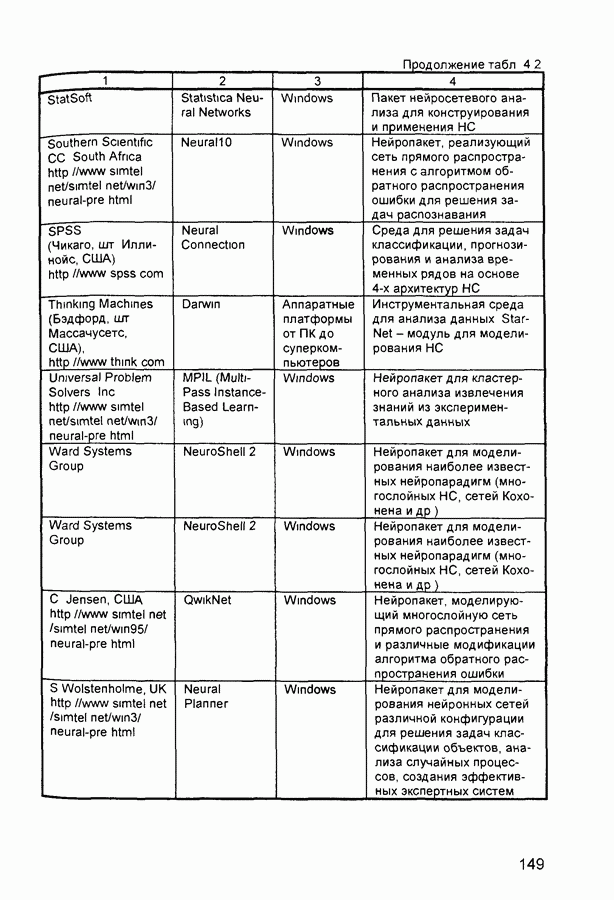
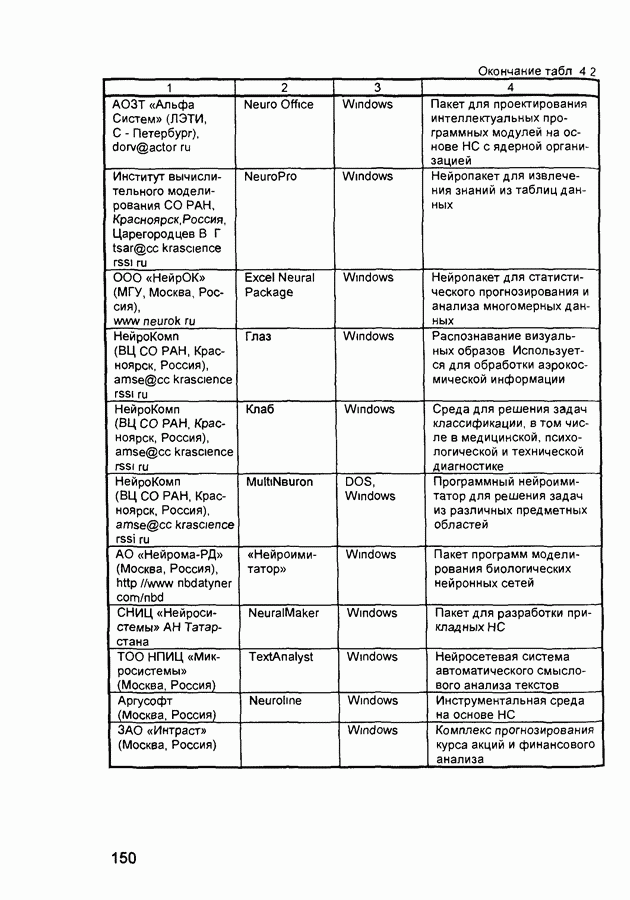
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
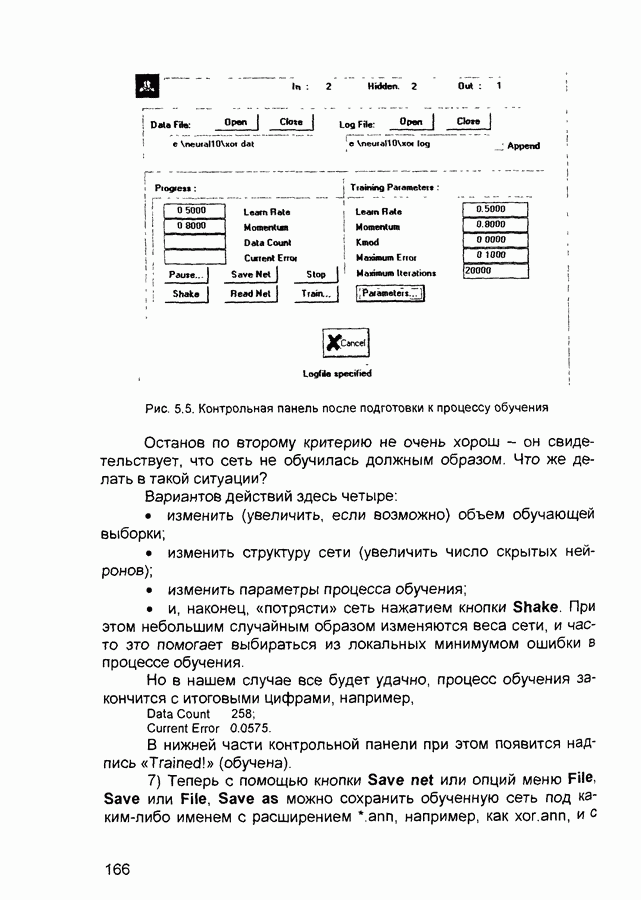
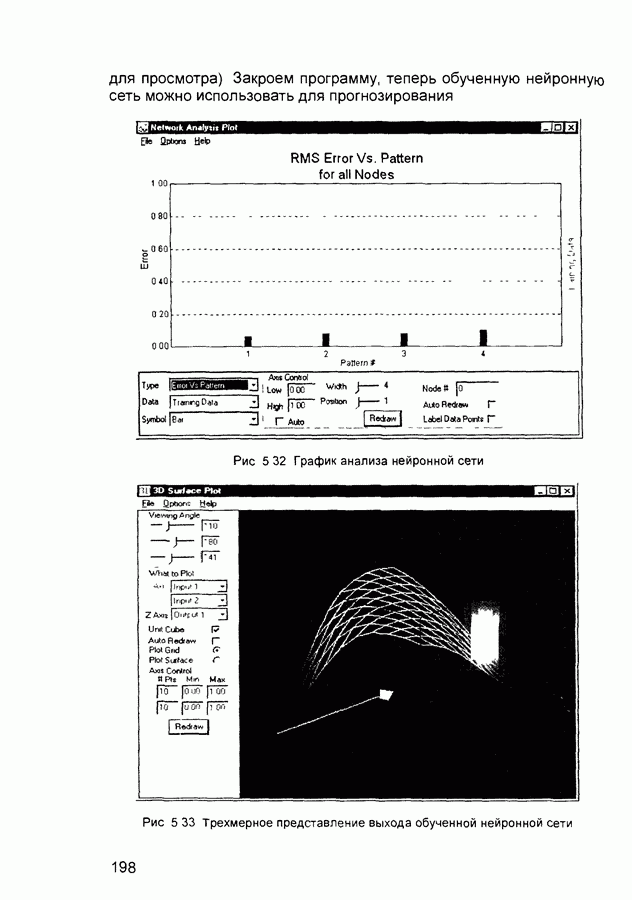
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
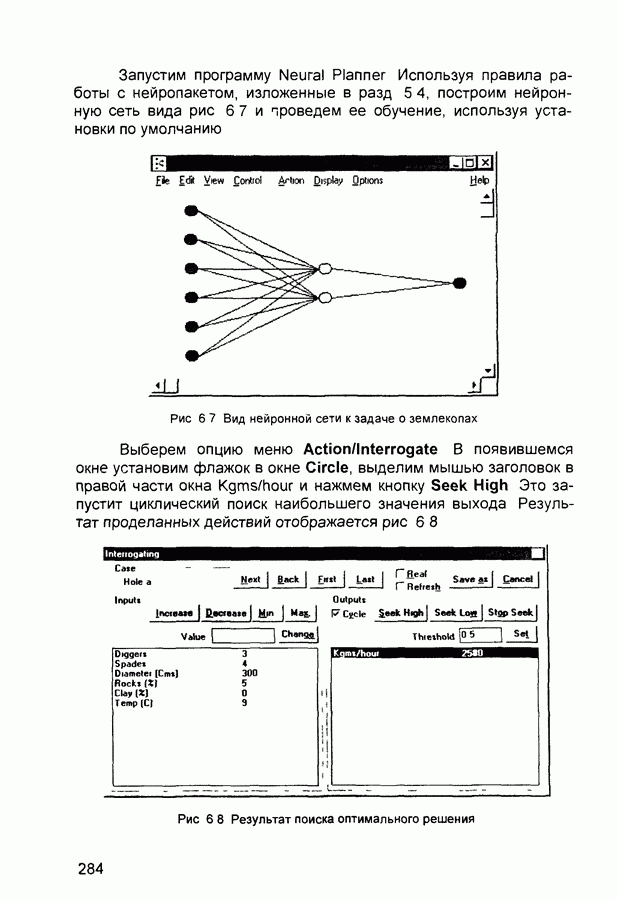
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
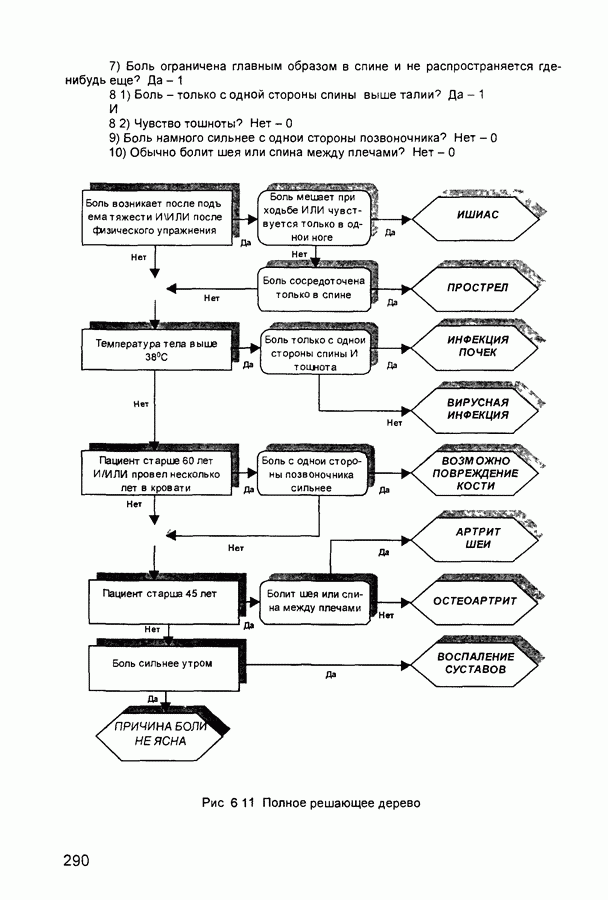
- 6.7. Нейросетевая экспертная система
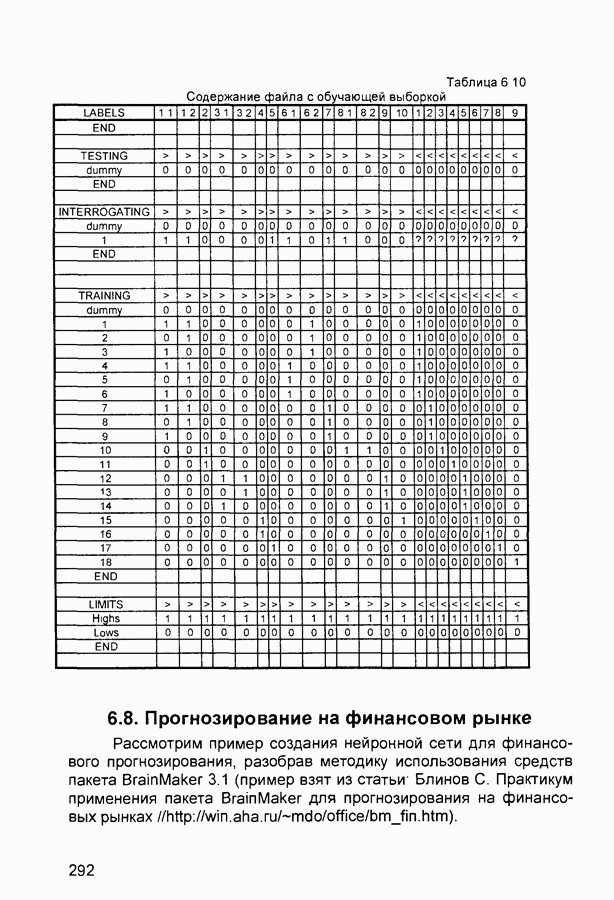
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы