| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.3.3. Следствия из теоремы Колмогорова-Арнольда - Хехт-Нильсена
Следствие 1. Из теоремы Хехт-Нильсена следует представимость любой многомерной функции нескольких переменных с помощью нейронной сети фиксированной размерности Неизвестными остаются следующие характеристики функций активации нейронов
• ограничения области значений (координаты асимптот) сигмоидальных функций активации нейронов скрытого слоя,
• наклон сигмоидальных функций активации,
• вид функций активации нейронов выходного слоя
Про функции активации нейронов выходного слоя из теоремы Хехт-Нильсена известно только то, что они представляют собой нелинейные функции общего вида В одной из работ, продолжающих развитие теории, связанной с рассматриваемой теоремой, доказывается, что функции активации нейронов выходного слоя должны быть монотонно возрастающими Это утверждение в некоторой степени сужает класс функций, которые могут использоваться при реализации отображения с помощью двухслойной нейронной сети
На практике требования теоремы Хехт-Нильсена к функциям активации удовлетворяются следующим образом В нейронных сетях как для первого (скрытого), так и для второго (выходного) слоя используют сигмоидальные передаточные функции с настраиваемыми параметрами То есть в процессе обучения индивидуально для каждого нейрона задается максимальное и минимальное значение, а также наклон сигмоидальной функции
Следствие 2. Для любого множества пар  (где У - скаляр) существует двухслойная однородная (с одинаковыми функциями активации) нейронная сеть первого порядка с последовательными связями и с конечным числом нейронов, которая выполняет отображение
(где У - скаляр) существует двухслойная однородная (с одинаковыми функциями активации) нейронная сеть первого порядка с последовательными связями и с конечным числом нейронов, которая выполняет отображение  , выдавая на каждый входной сигнал X правильный выходной сигнал
, выдавая на каждый входной сигнал X правильный выходной сигнал  Нейроны в такой двухслойной нейронной сети должны иметь сигмоидальные передаточные функции
Нейроны в такой двухслойной нейронной сети должны иметь сигмоидальные передаточные функции
К сожалению, эта теорема не конструктивна В ней не заложена методика определения числа нейронов в сети для некоторой конкретной обучающей выборки
Для многих задач единичной размерности выходного сигнала недостаточно Необходимо иметь возможность строить с помощью нейронных сетей функции  , где У имеет произвольную размерность Следующее утверждение является теоретической
, где У имеет произвольную размерность Следующее утверждение является теоретической
основой для построения таких функций на базе однородных нейронных сетей.
Утверждение. Для любого множества пар входных-выходных векторов произвольной размерности  существует однородная двухслойная нейронная сеть с последовательными связями, с сигмоидальными передаточными функциями и с конечным числом нейронов, которая для каждого входного вектора X формирует соответствующий ему выходной вектор У.
существует однородная двухслойная нейронная сеть с последовательными связями, с сигмоидальными передаточными функциями и с конечным числом нейронов, которая для каждого входного вектора X формирует соответствующий ему выходной вектор У.
Таким образом, для представления многомерных функций многих переменных может быть использована однородная двухслойная нейронная сеть с сигмоидальными передаточными функциями.
Для оценки числа нейронов с скрытых слоях однородных нейронных сетей можно воспользоваться формулой для оценки необходимого числа синаптических весов  в многослойной сети с сигмоидальными передаточными функциями:
в многослойной сети с сигмоидальными передаточными функциями:

где  - размерность входного сигнала,
- размерность входного сигнала,  - размерность выходного сигнала,
- размерность выходного сигнала,  - число элементов обучающей выборки.
- число элементов обучающей выборки.
Оценив необходимое число весов, можно рассчитать число нейронов в скрытых слоях. Например, для двухслойной сети это число составит:

Известны и другие формулы для оценки, например:

Точно так же можно рассчитать число нейронов в сетях с большим числом слоев.
Иногда целесообразно использовать сети с большим числом слоев. Такие многослойные нейронные сети могут иметь меньшие размерности матриц синаптических весов нейронов одного слоя, чем двухслойные сети, реализующие то же самое отображение. Однако строгой методики построения таких сетей пока нет.
Аналогичная ситуация складывается и с многослойными нейронными сетями, в которых помимо последовательных связей используются и прямые (связи от слоя с номером  к слою с номером
к слою с номером  где
где  Нет строгой теории, которая показывала бы возможность и целесообразность построения таких сетей.
Нет строгой теории, которая показывала бы возможность и целесообразность построения таких сетей.
Наибольшие проблемы возникают при использовании сетей циклического функционирования. К этой группе относятся многослойные сети с обратными связями (от слоя с номером  к слою с номером
к слою с номером  где
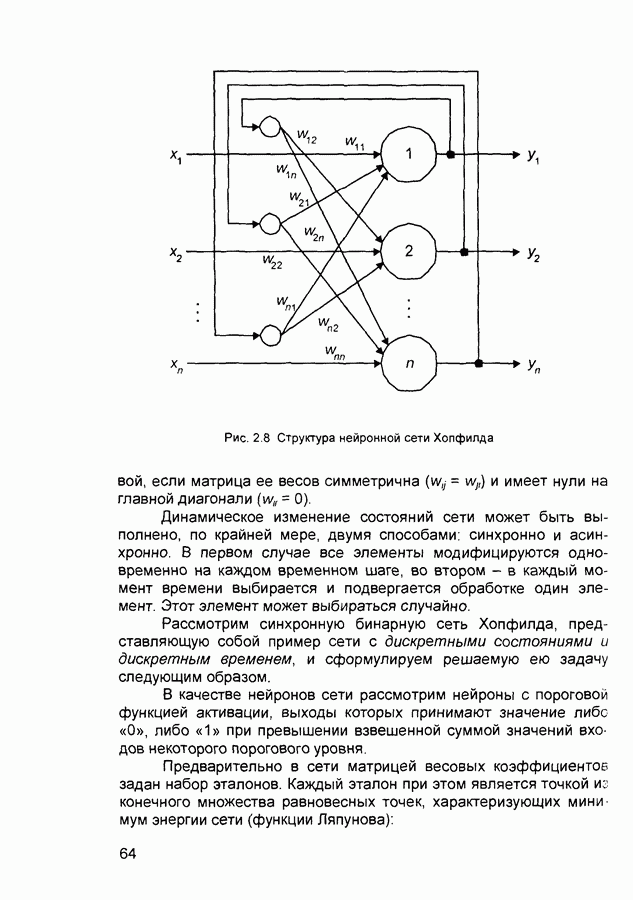
где  а также полносвязные сети. Для успешного функционирования таких сетей необходимо соблюдение условий динамической устойчивости, иначе сеть может не сойтись к правильному решению, либо, достигнув на некоторой итерации правильного значения выходного сигнала, после нескольких итераций уйти от этого значения. Проблема динамической устойчивости подробно исследована, пожалуй, лишь для одной модели из рассматриваемой группы - нейронной сети Хопфилда.
а также полносвязные сети. Для успешного функционирования таких сетей необходимо соблюдение условий динамической устойчивости, иначе сеть может не сойтись к правильному решению, либо, достигнув на некоторой итерации правильного значения выходного сигнала, после нескольких итераций уйти от этого значения. Проблема динамической устойчивости подробно исследована, пожалуй, лишь для одной модели из рассматриваемой группы - нейронной сети Хопфилда.
Отсутствие строгой теории для перечисленных моделей нейронных сетей не препятствует исследованию возможностей их применения.
Отметим, что отечественному читателю приведенные результаты известны в более фрагментарной форме - в виде так называемой теоремы о полноте.
Теорема о полноте.
Любая непрерывная функция на замкнутом ограниченном множестве может быть равномерно приближена функциями, вычисляемыми нейронными сетями, если функция активации нейрона дважды непрерывно дифференцируема и непрерывна.
Таким образом, нейронные сети являются универсальными структурами, позволяющими реализовать любой вычислительный алгоритм.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
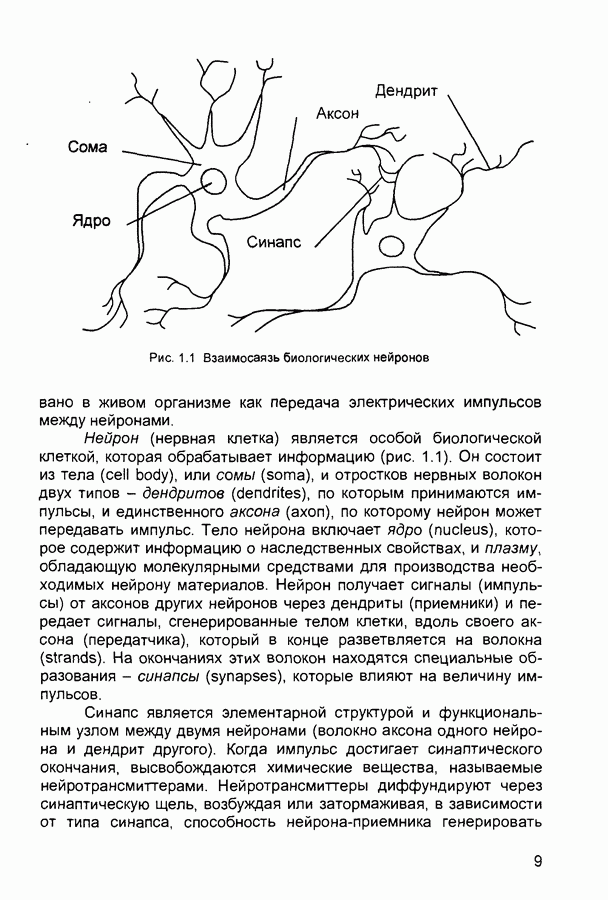
- 1.1. Биологический нейрон
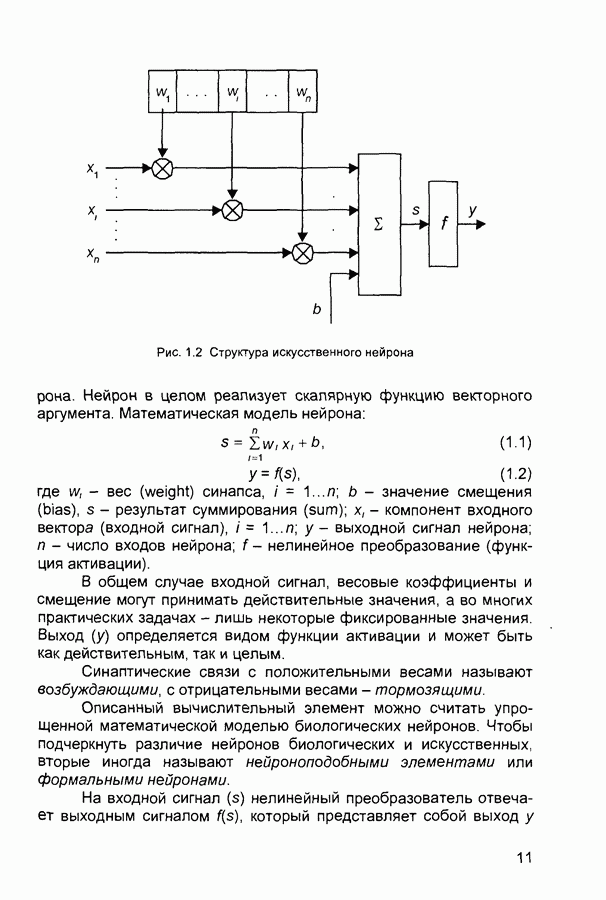
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
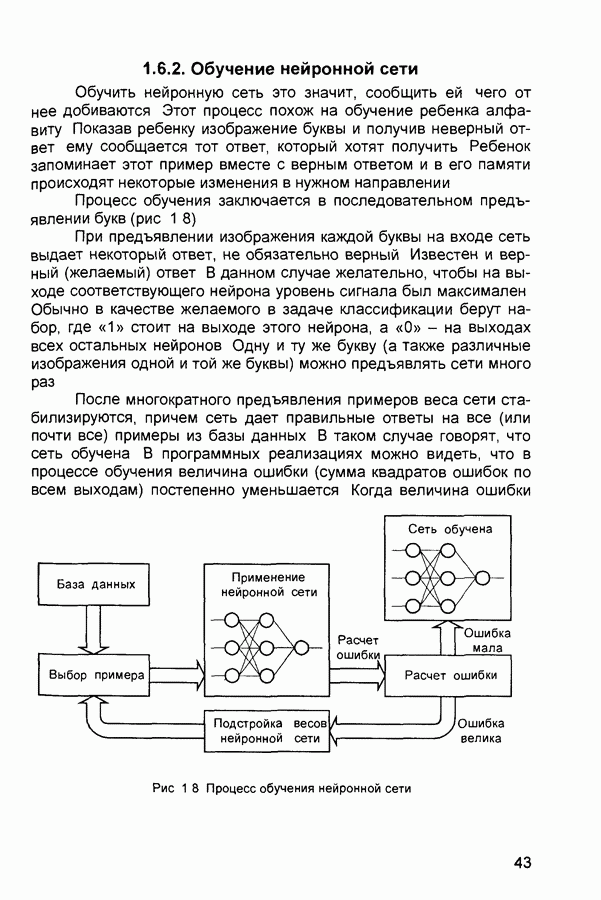
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
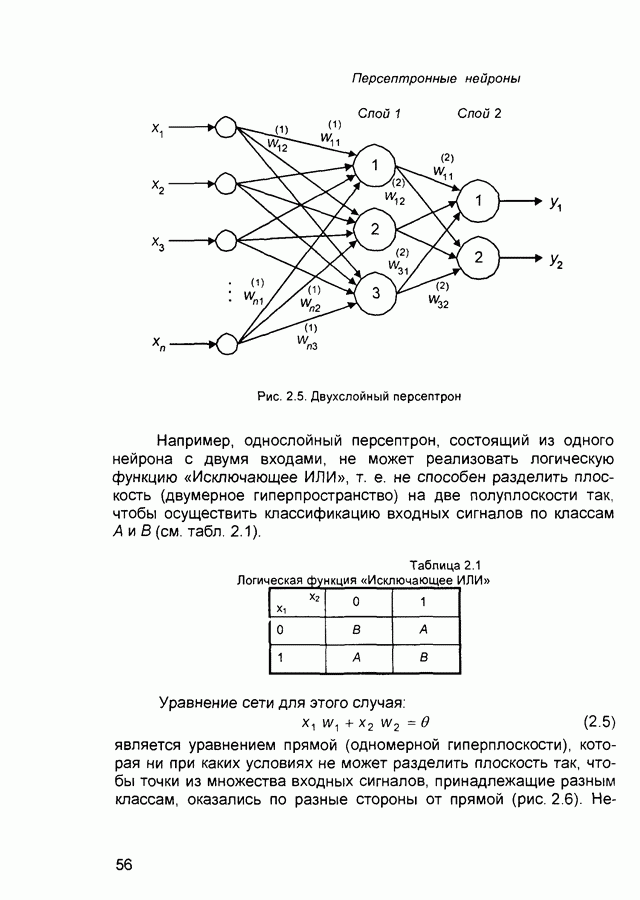
- 2.2. Персептроны
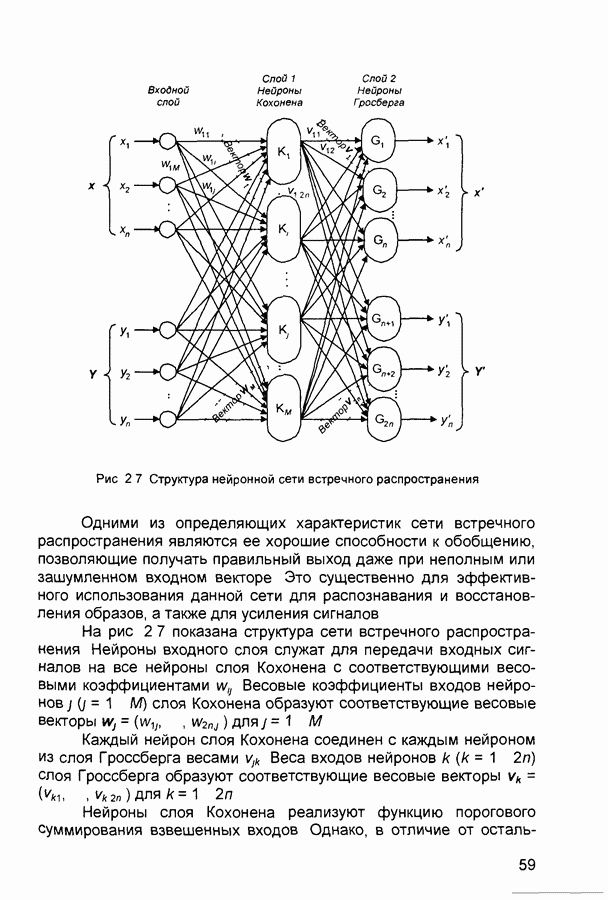
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
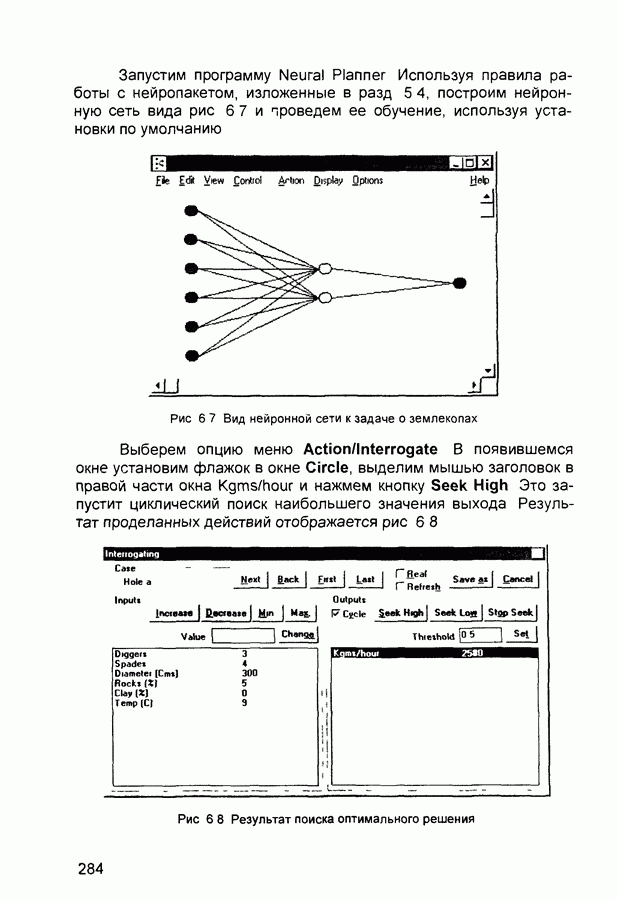
- 6.5. Задача о землекопах
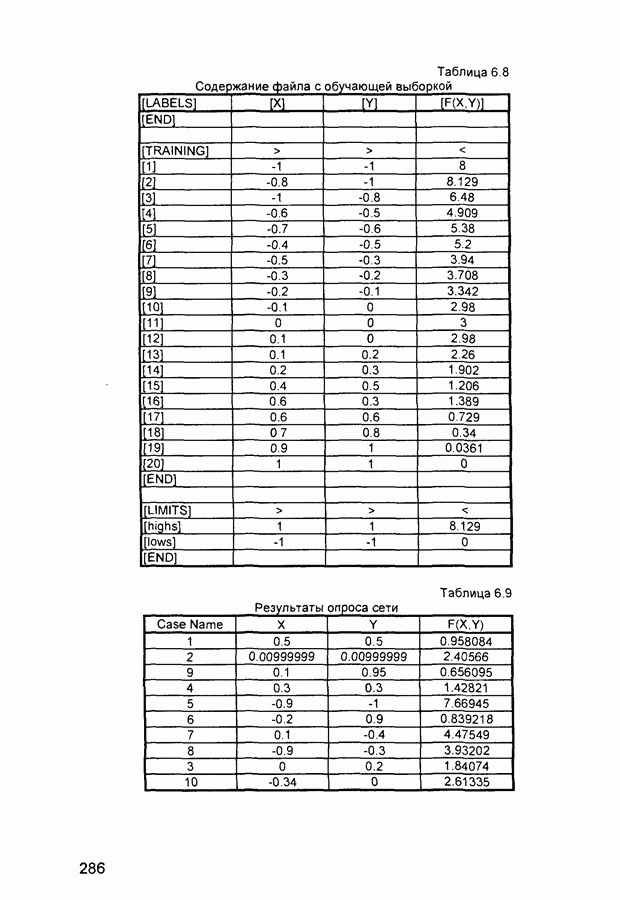
- 6.6. Аппроксимация функции
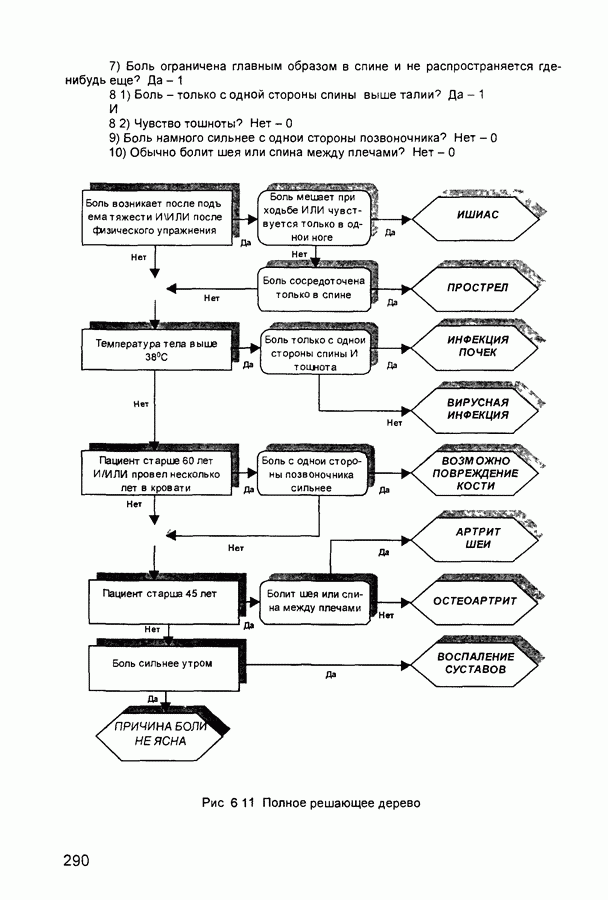
- 6.7. Нейросетевая экспертная система
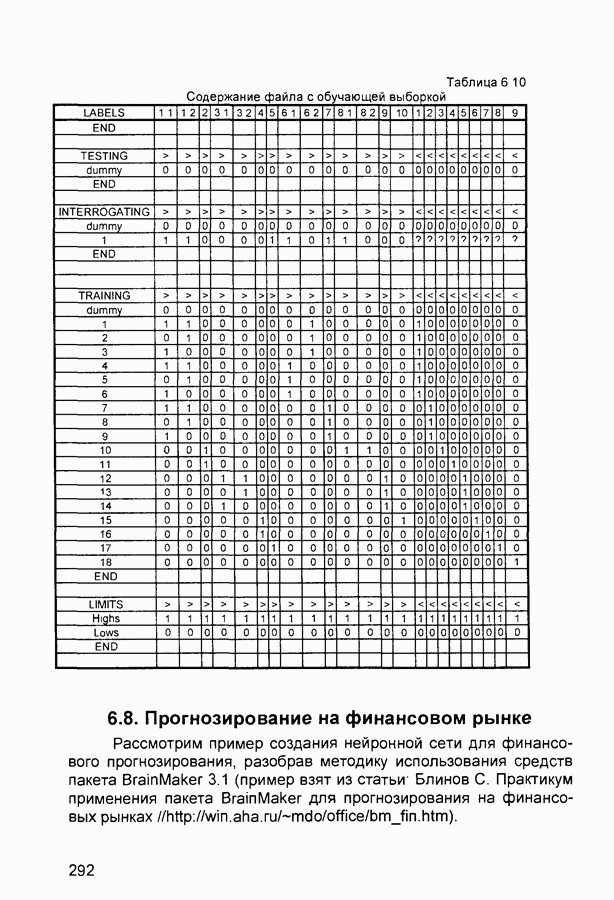
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы