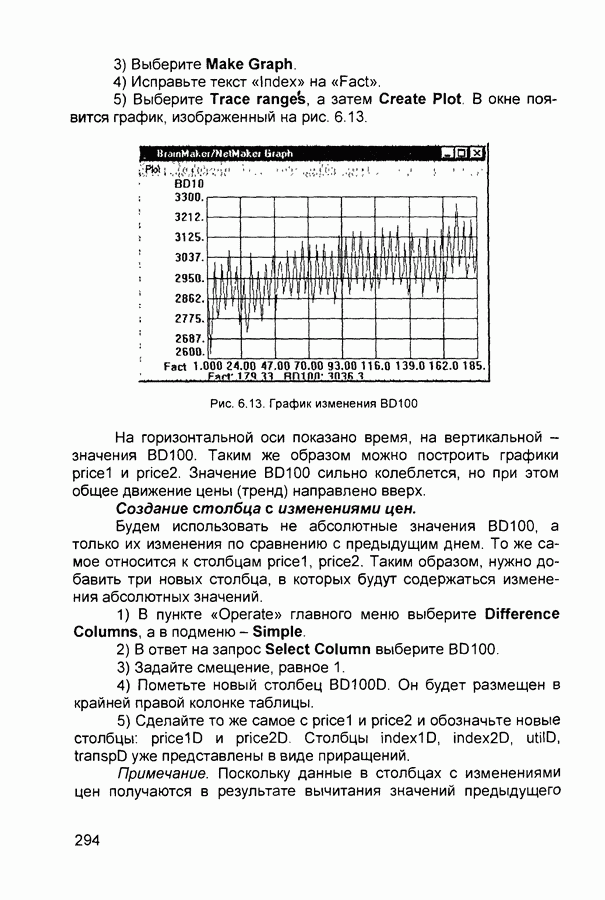
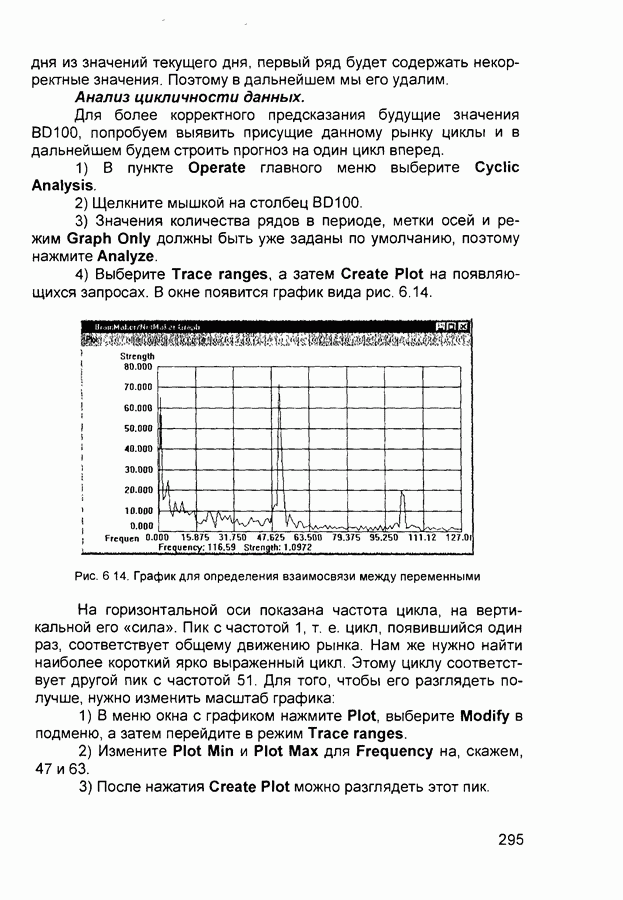
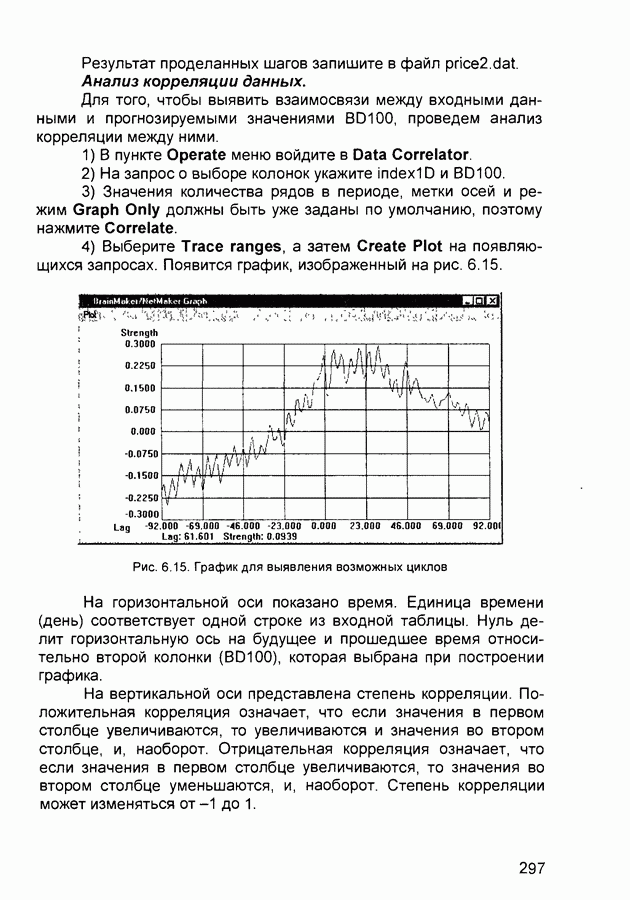
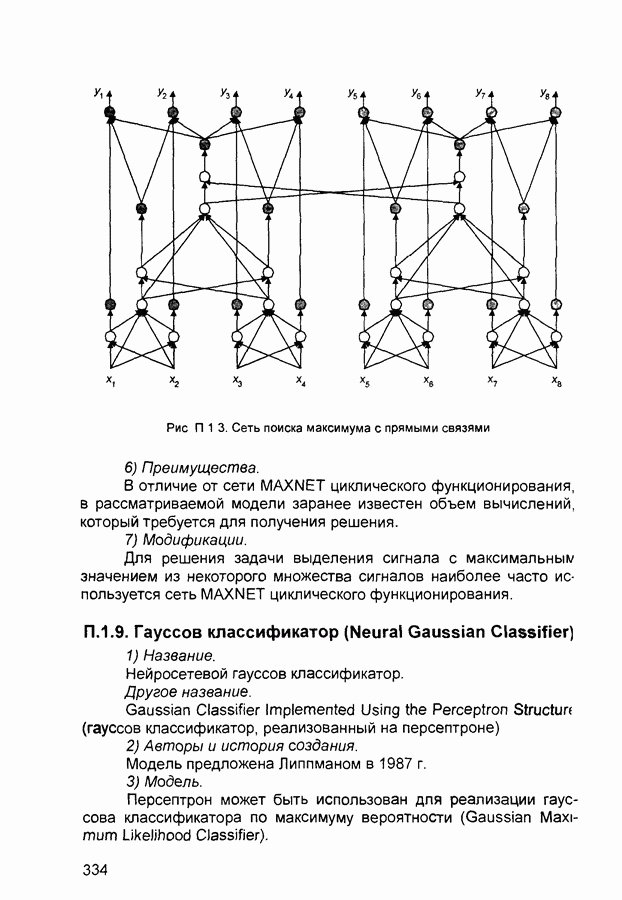
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3. Эффективность нечетких систем принятия решений
Возможность использования аппарата нечеткой логики базируется на следующих результатах.
1) В 1992 г. Wang показал, что нечеткая система является универсальным аппроксиматором, т. е. может аппроксимировать любую непрерывную функцию на компакте  с произвольной точностью, если использует набор
с произвольной точностью, если использует набор  правил:
правил:
П: если х, есть А, и у, есть  тогда
тогда  есть
есть  при следующих условиях:
при следующих условиях:
• гауссовых функциях принадлежности:

• композиции в виде произведения:

• импликации в форме (Larsen):

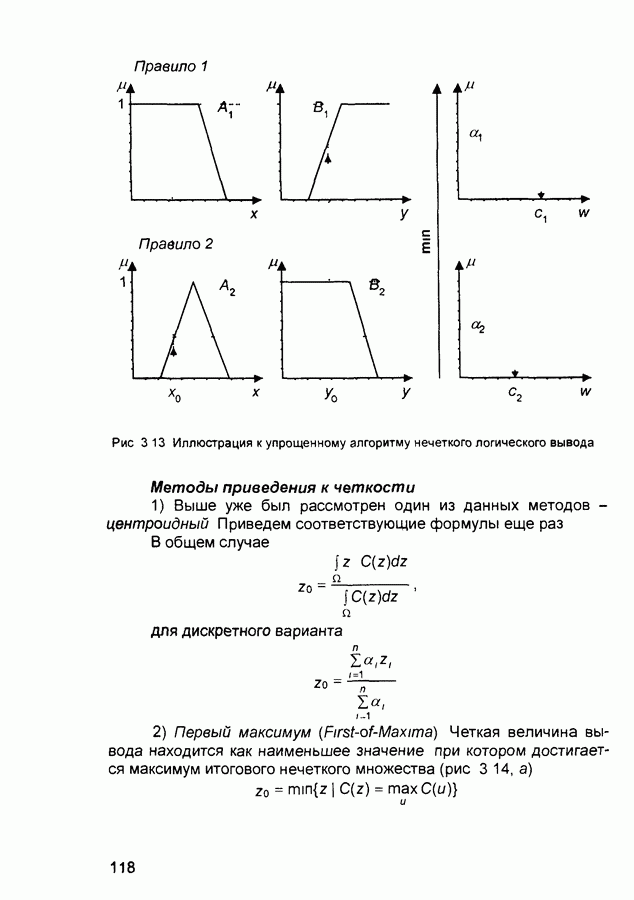
• центроидном методе приведения к четкости:

где  - центры
- центры 
Иначе говоря, Wang доказал теорему: для каждой вещественной непрерывной функции  заданной на компакте
заданной на компакте  и для произвольного
и для произвольного  существует нечеткая система, формирующая выходную функцию
существует нечеткая система, формирующая выходную функцию  такую, что
такую, что

где  - символ принятого расстояния между функциями
- символ принятого расстояния между функциями
2) В 1995 г. Castro показал, что логический контроллер Mamdani также является универсальным аппроксиматором при:
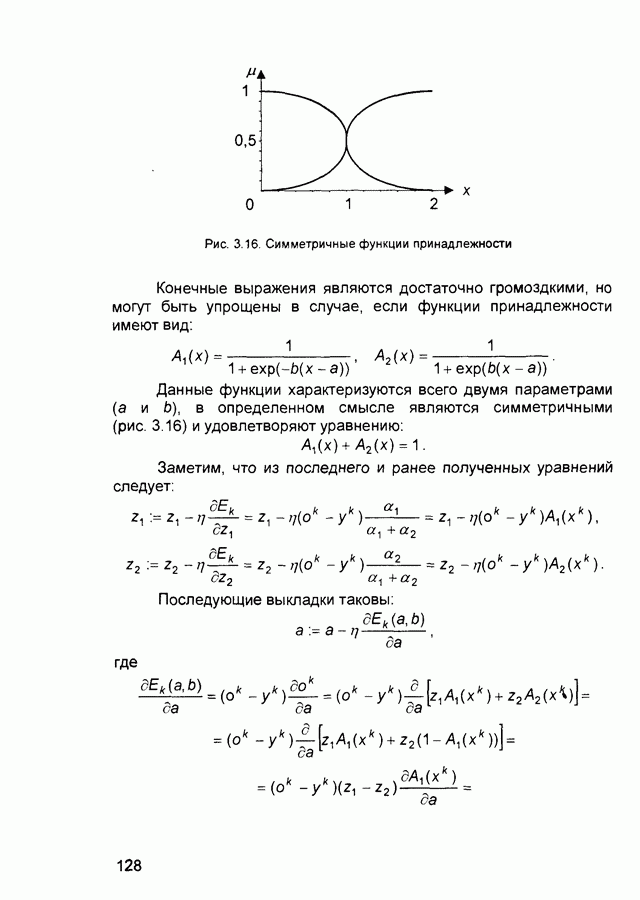
• симметричных треугольных функциях принадлежности:

• композиции с использованием операции 

• импликации в форме Mamdani и центроидного метода приведения к четкости:

где с, - центры 
Вообще говоря, системы с нечеткой логикой целесообразно применять в следующих случаях:
• для сложных процессов, когда нет простой математической модели;
• если экспертные знания об объекте или о процессе можно сформулировать только в лингвистической форме.
Системы, базирующиеся на нечеткой логике, применять нецелесообразно:
• если требуемый результат может быть получен каким-либо другим (стандартным) путем;
• когда для объекта или процесса уже найдена адекватная и легко исследуемая математическая модель
Отметим, что основными недостатками систем с нечеткой логикой являются то, что:
• исходный набор постулируемых нечетких правил формулируется экспертом-человеком и может оказаться неполным или противоречивым,
• вид и параметры функций принадлежности, описывающих входные и выходные переменные системы, выбираются субъективно и могут оказаться не вполне отражающими реальную действительность.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
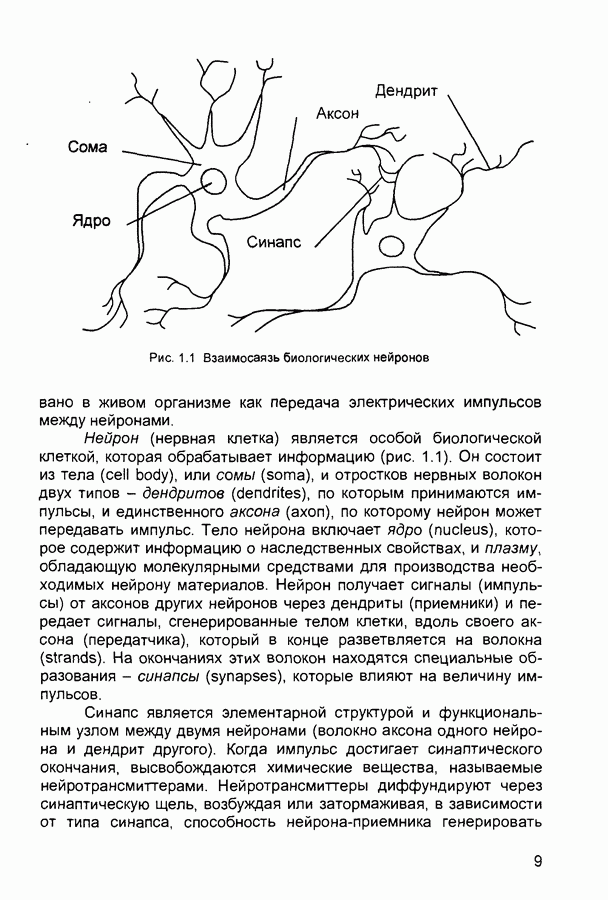
- 1.1. Биологический нейрон
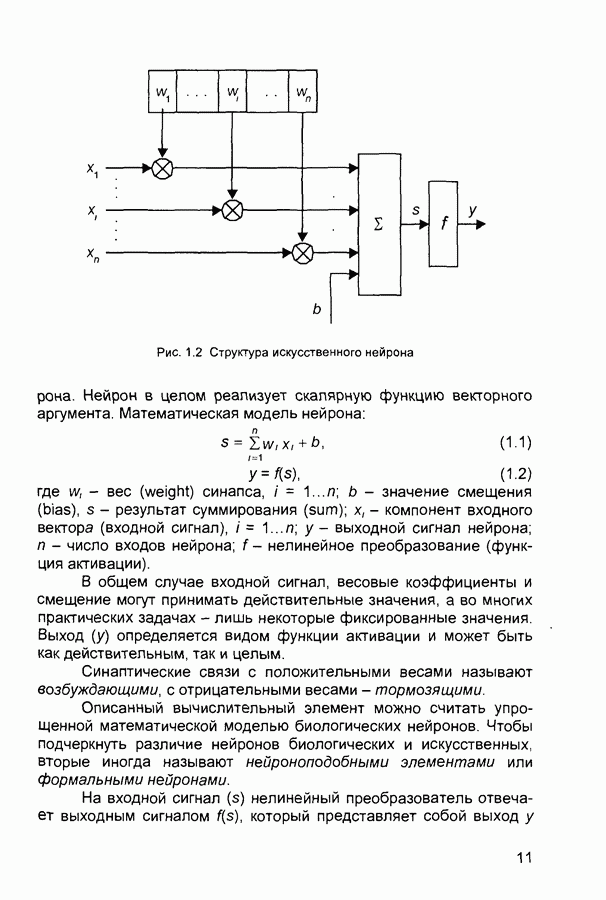
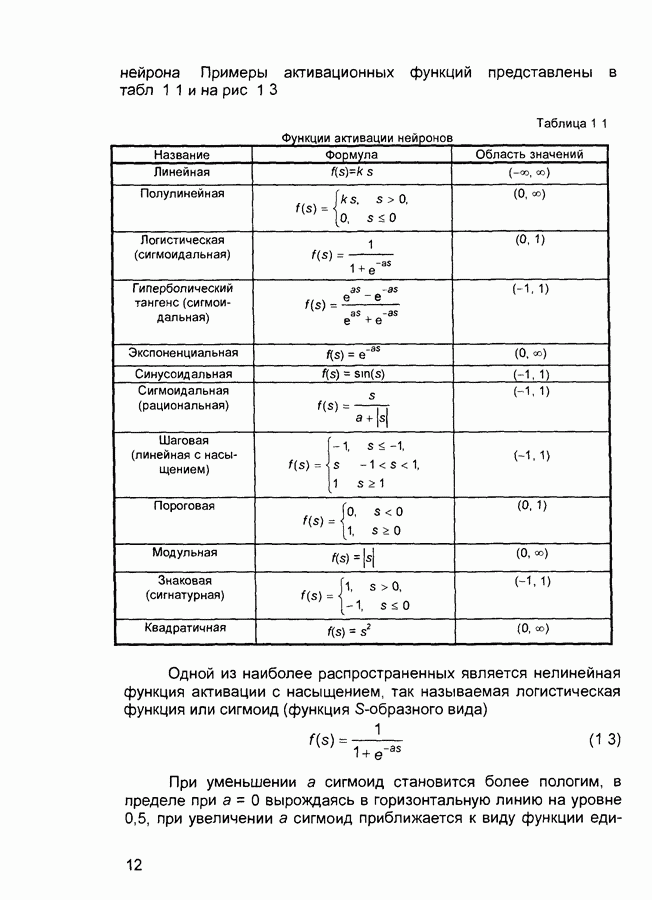
- 1.2. Структура и свойства искусственного нейрона
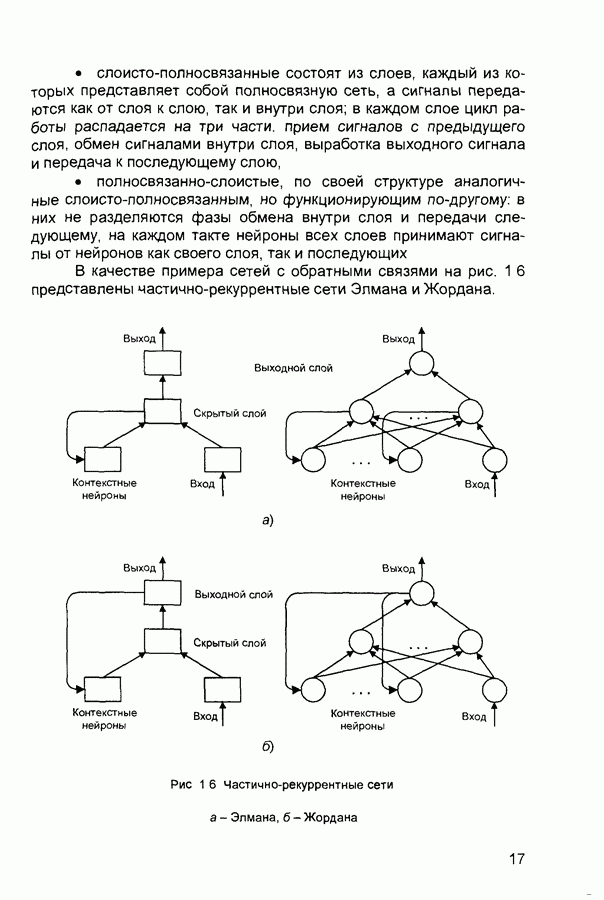
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
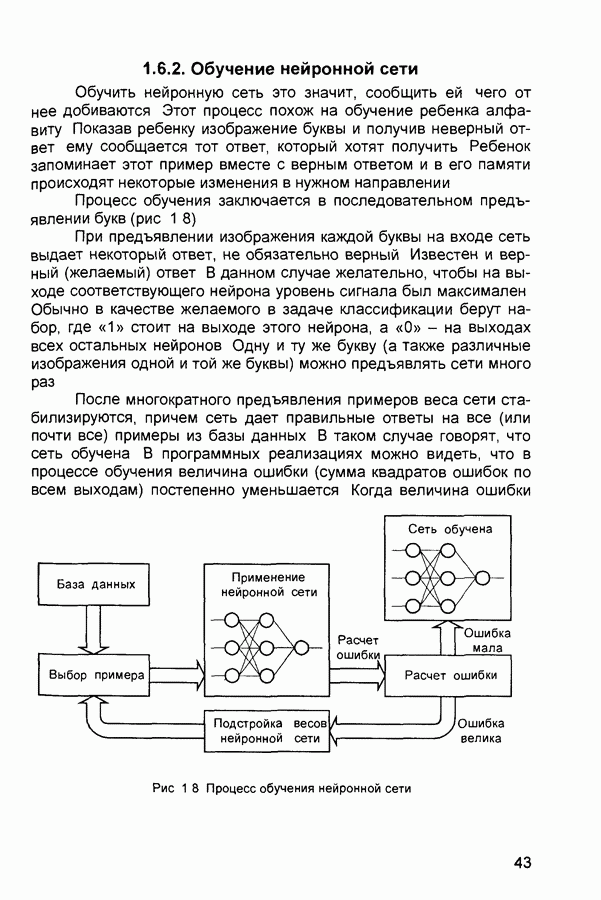
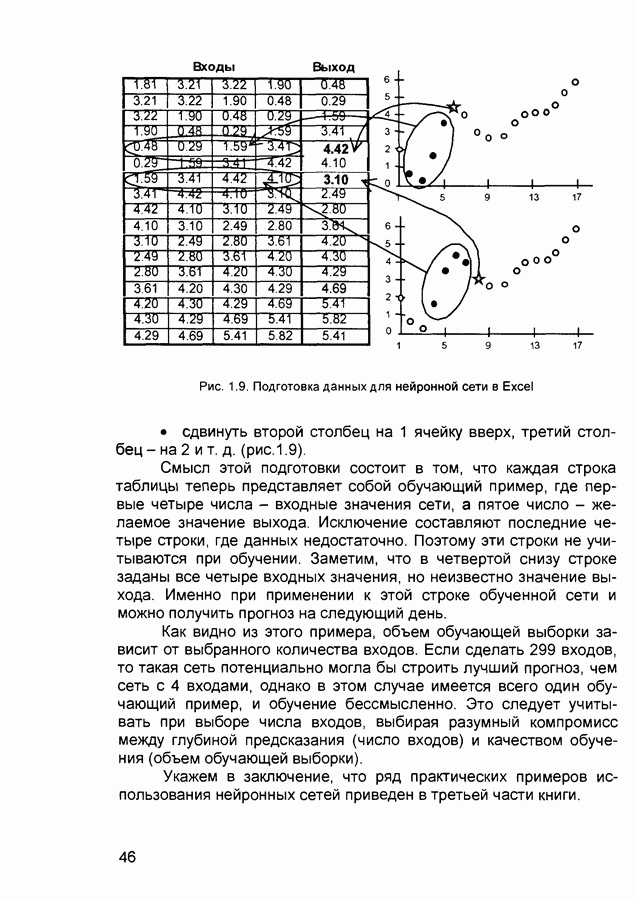
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
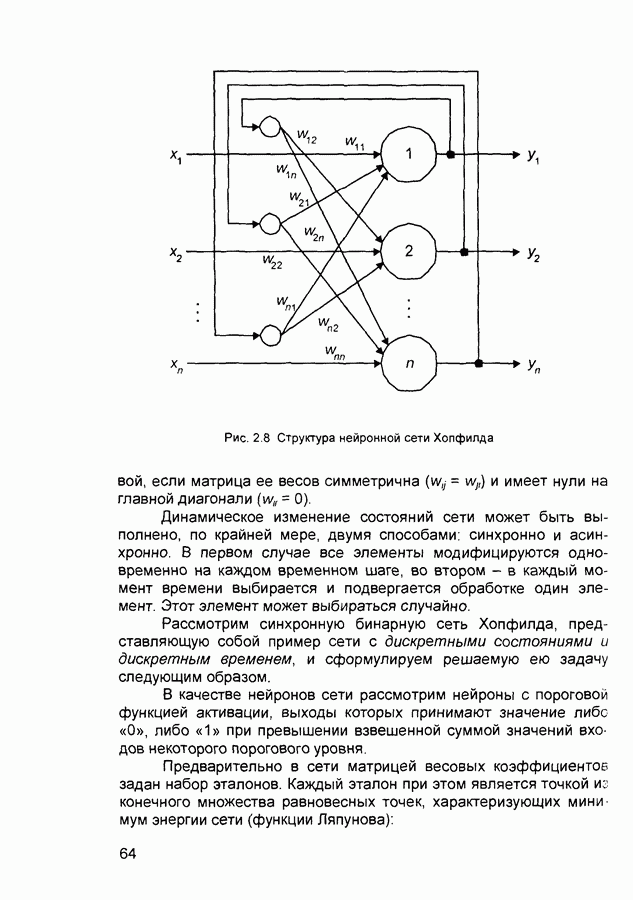
- 2.1. Ассоциативная память нейронных сетей
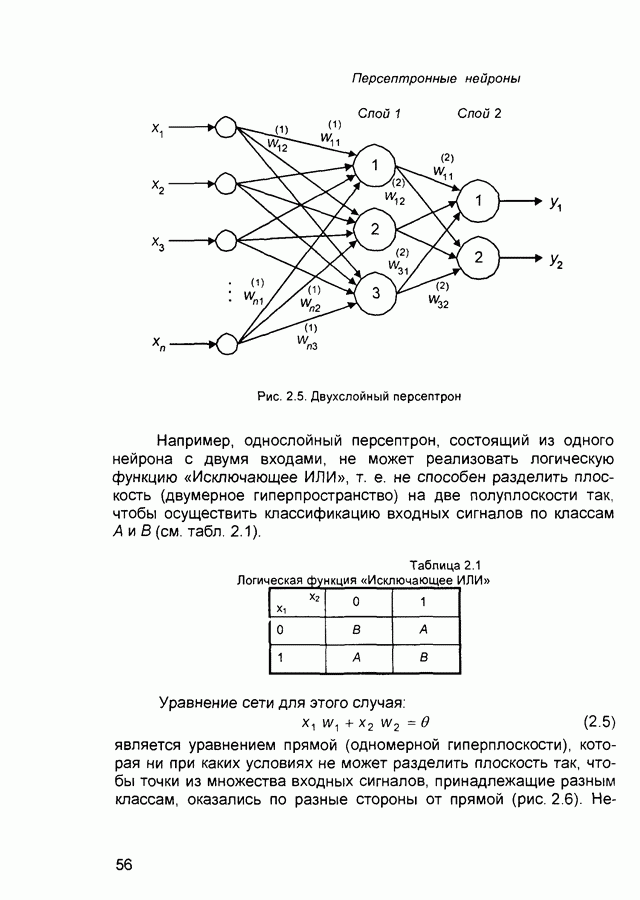
- 2.2. Персептроны
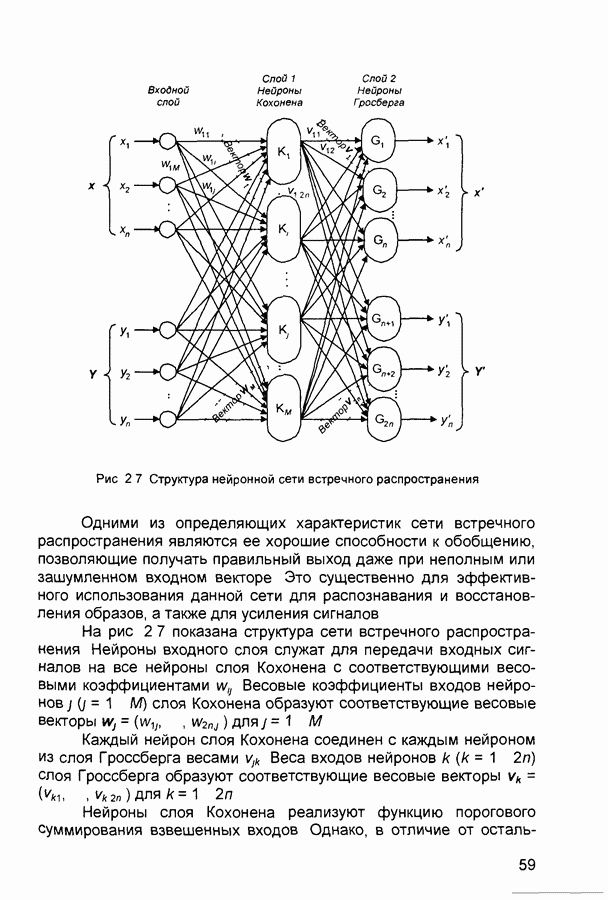
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
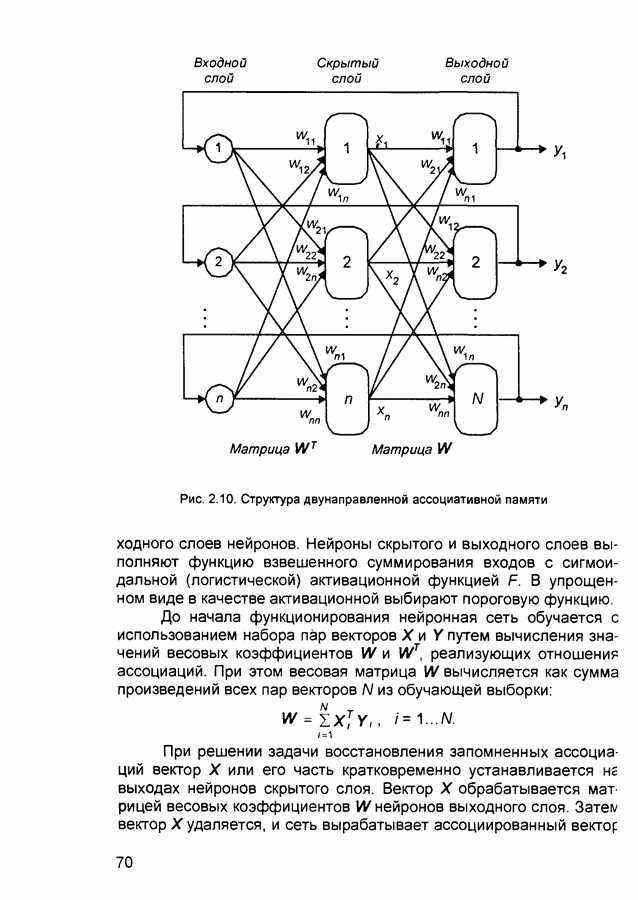
- 2.5. Двунаправленная ассоциативная память
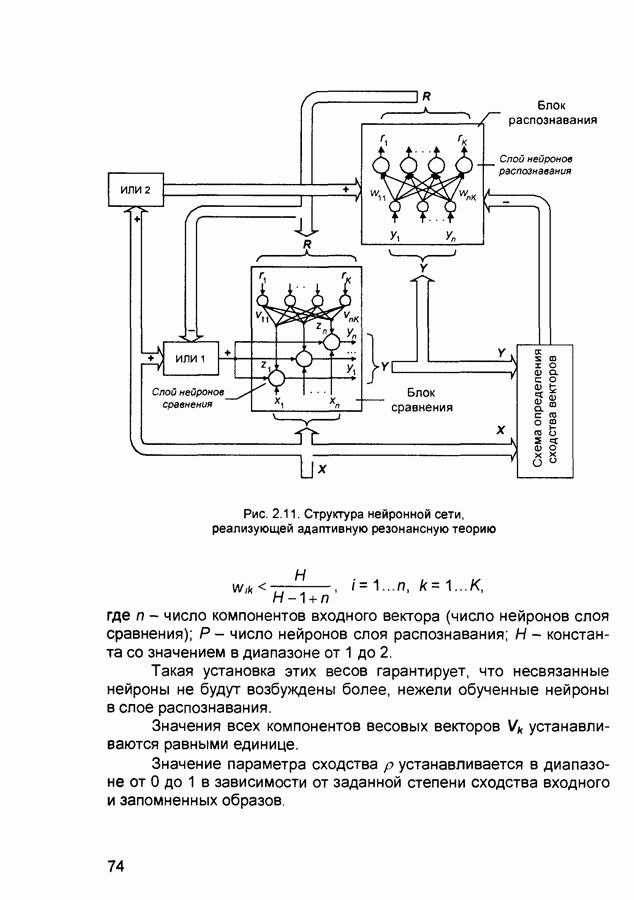
- 2.6. Сети адаптивной резонансной теории
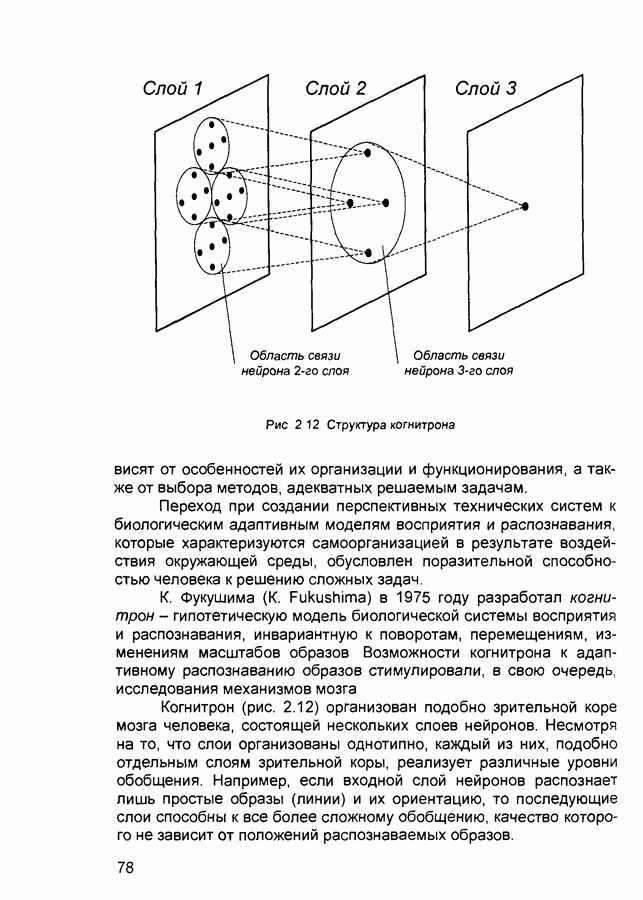
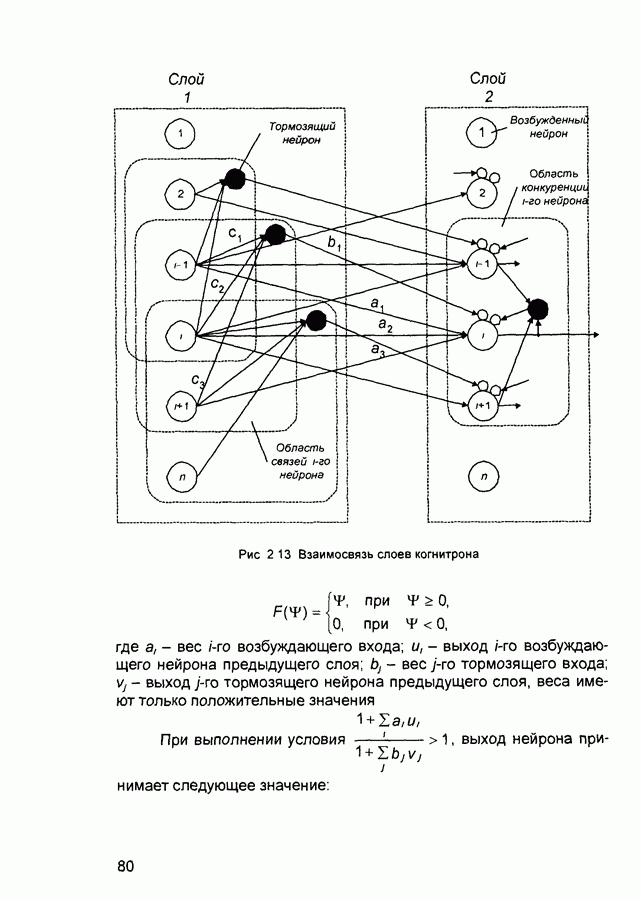
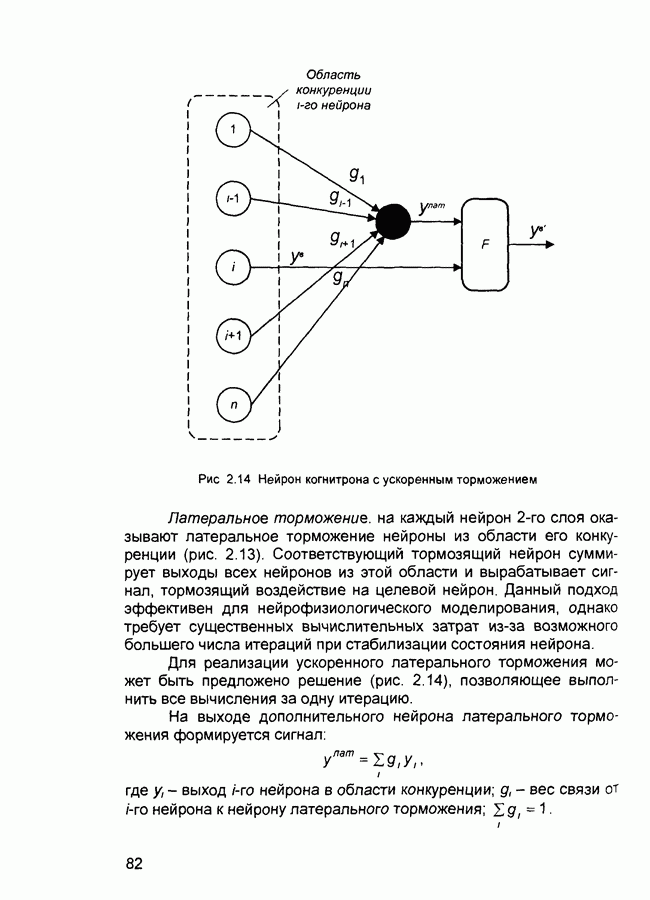
- 2.7. Когнитрон
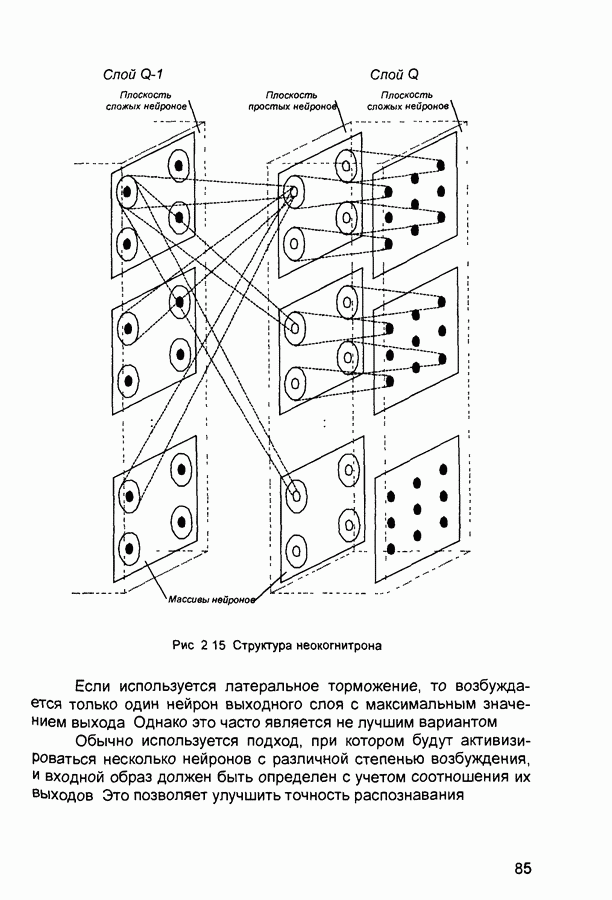
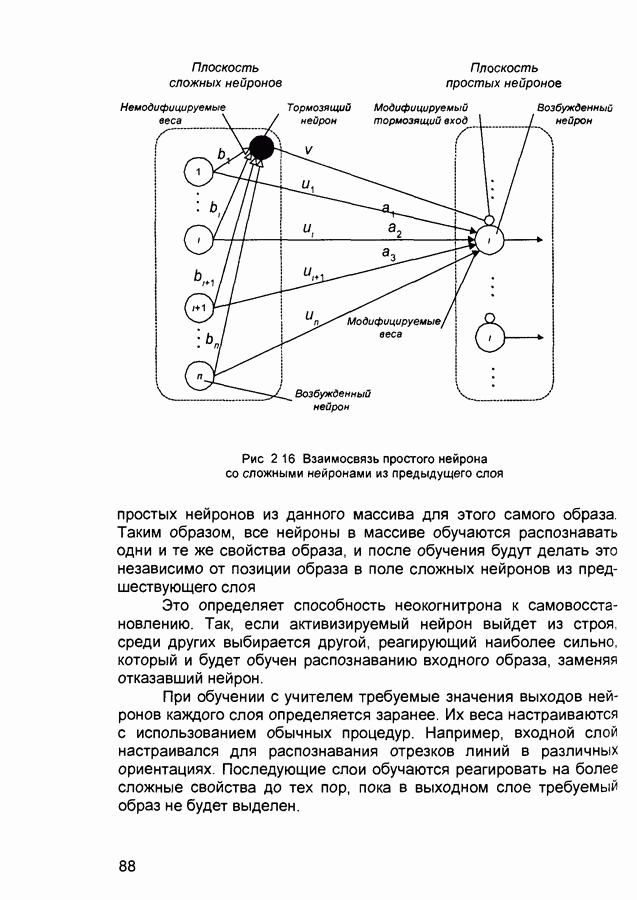
- 2.8. Неокогнитрон
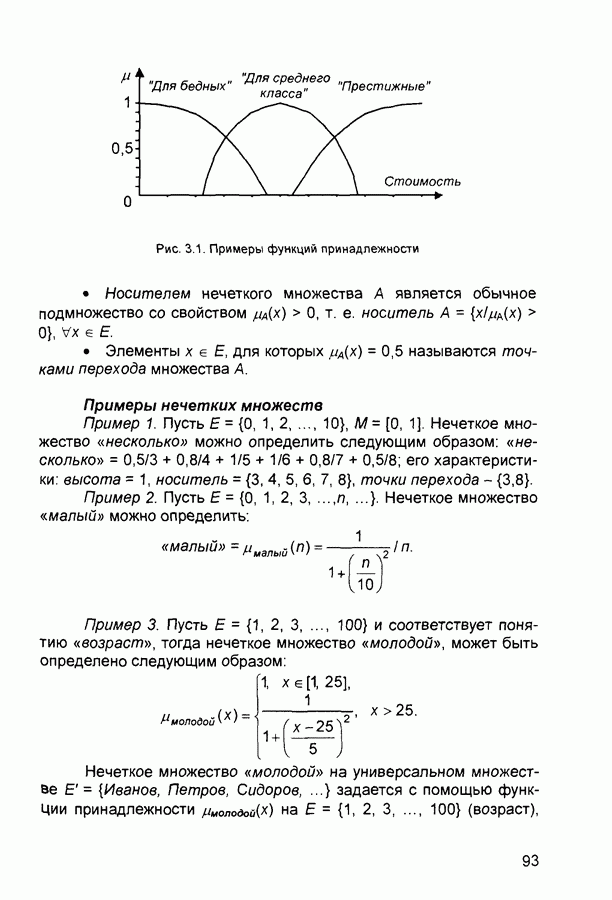
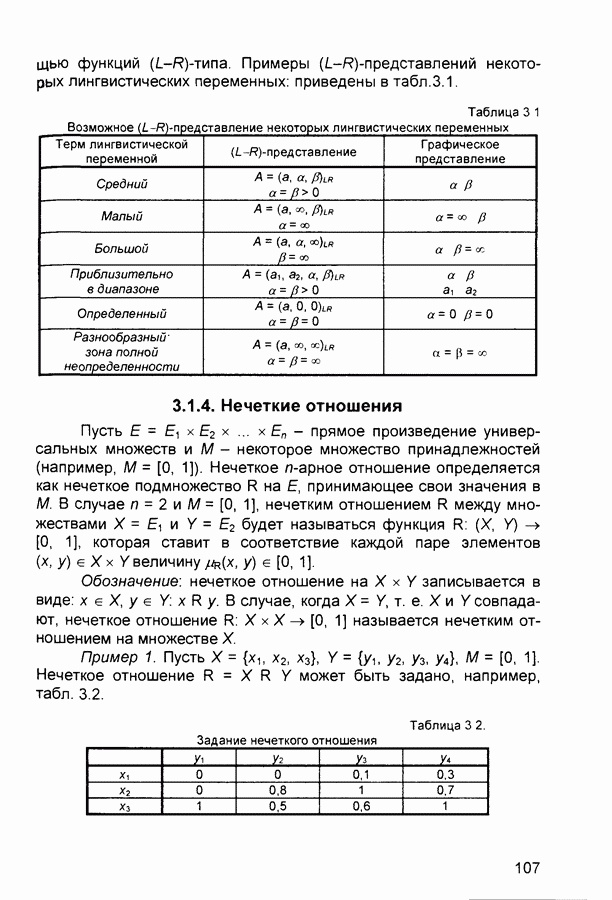
- 3.1. Нечеткая информация
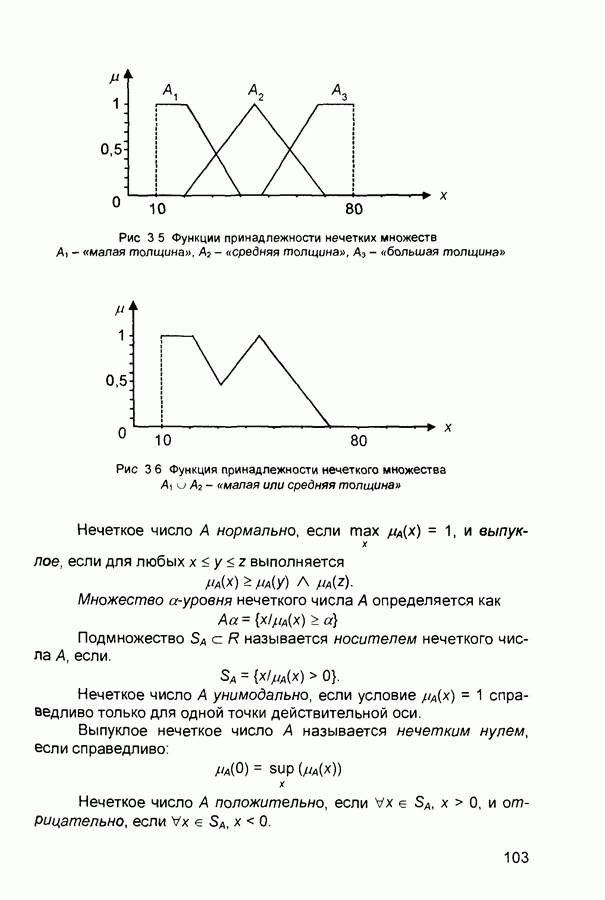
- 3.1.2. Операции над нечеткими множествами
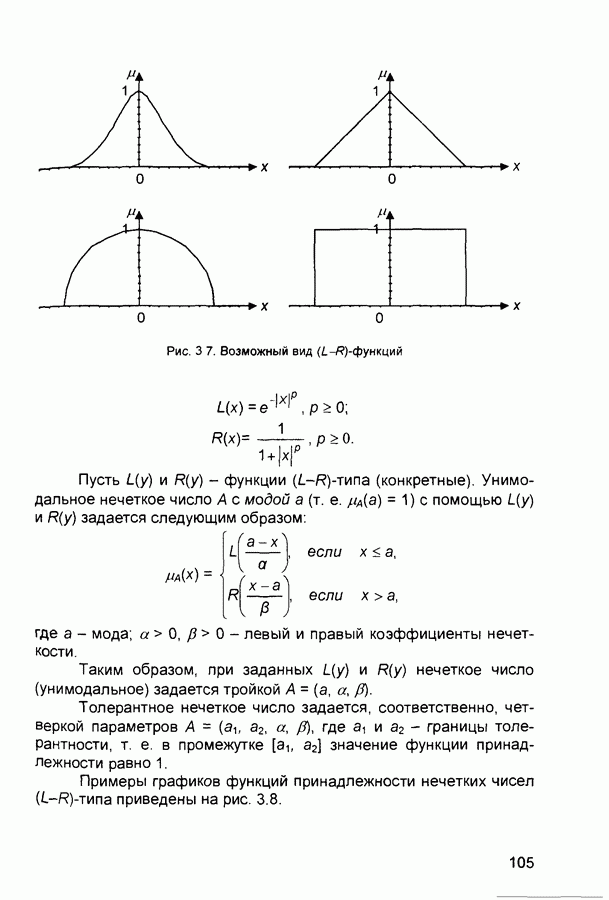
- 3.1.3. Нечеткие и лингвистические переменные
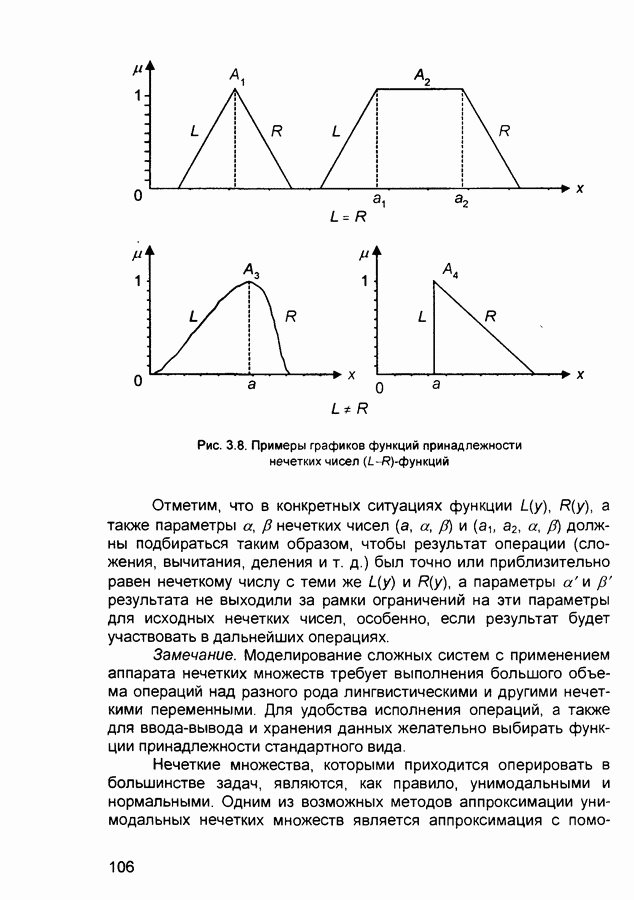
- 3.1.4. Нечеткие отношения
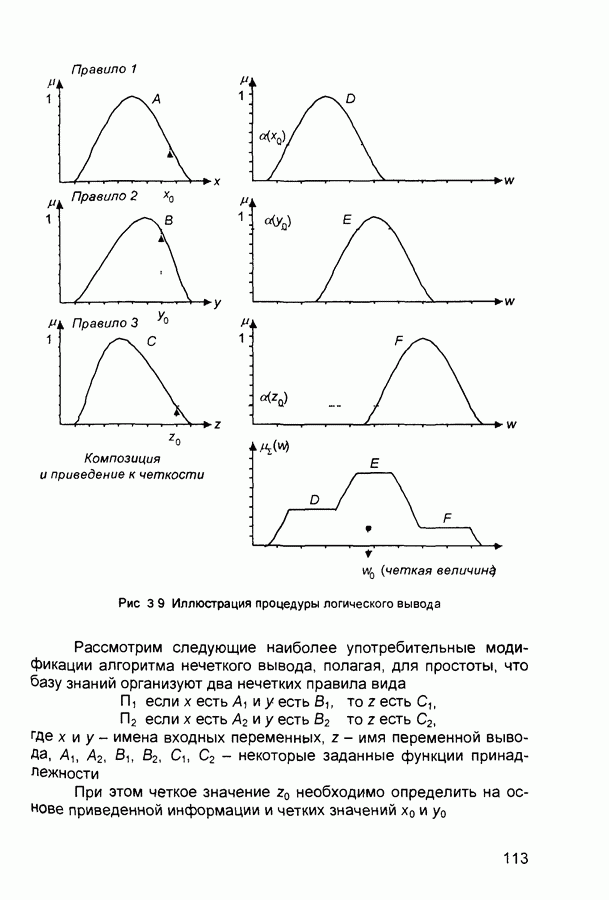
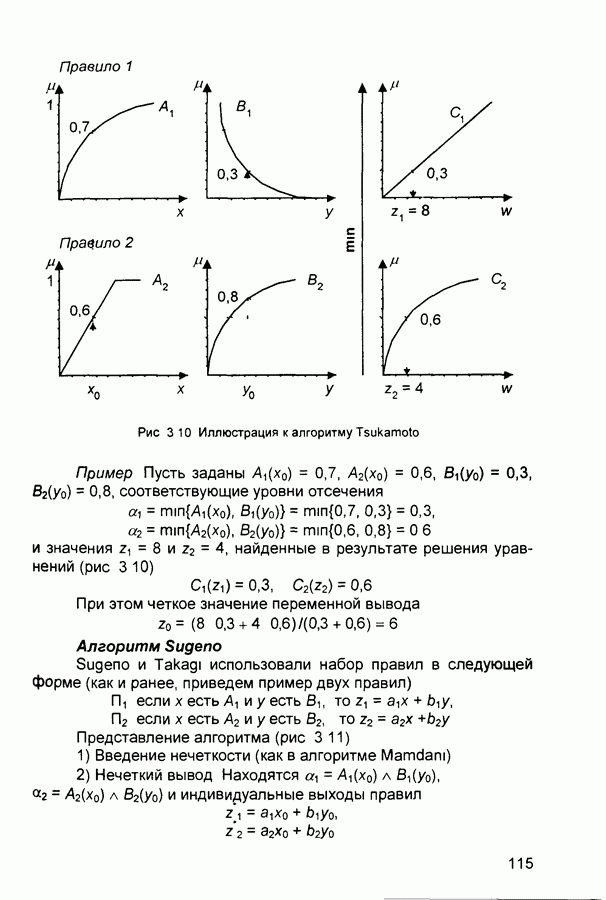
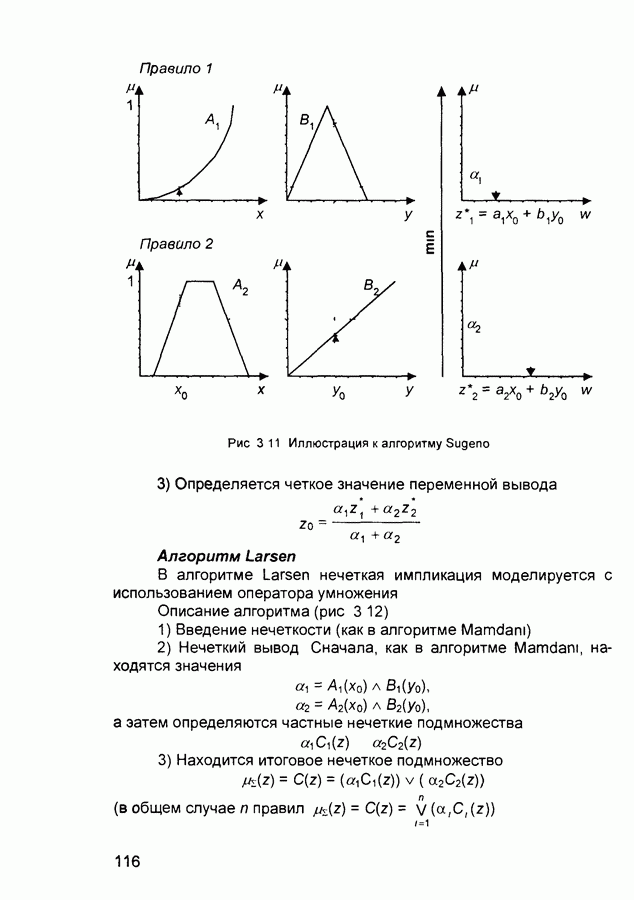
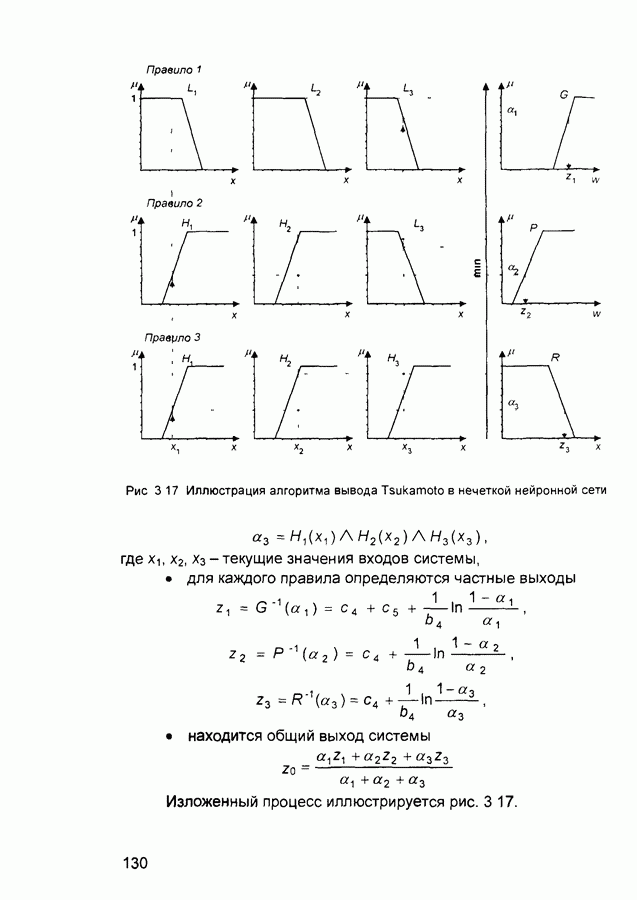
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
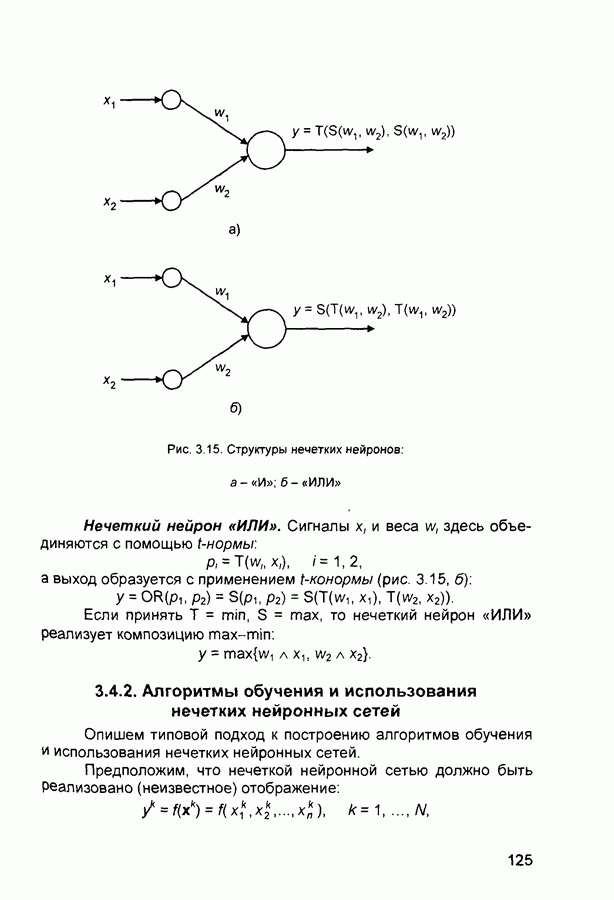
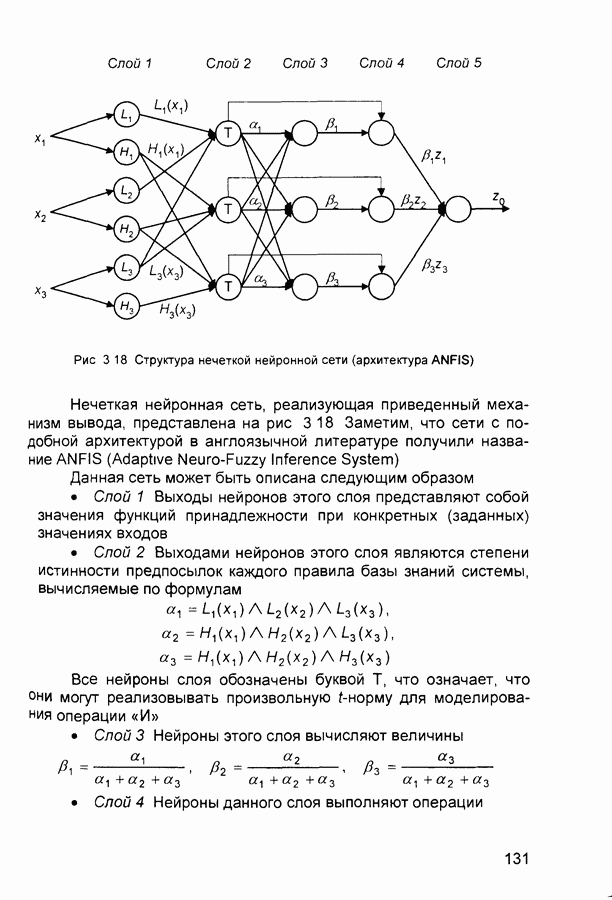
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
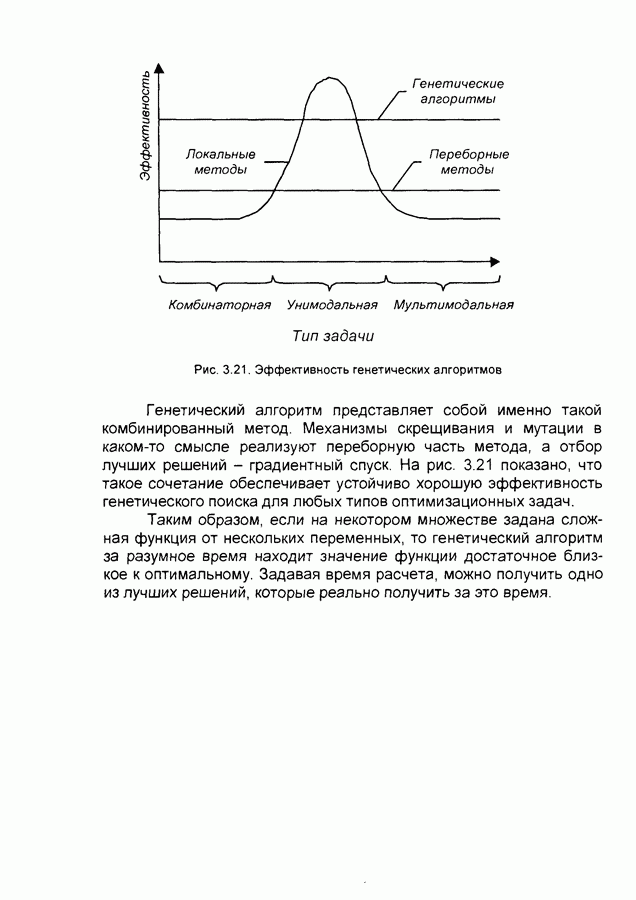
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
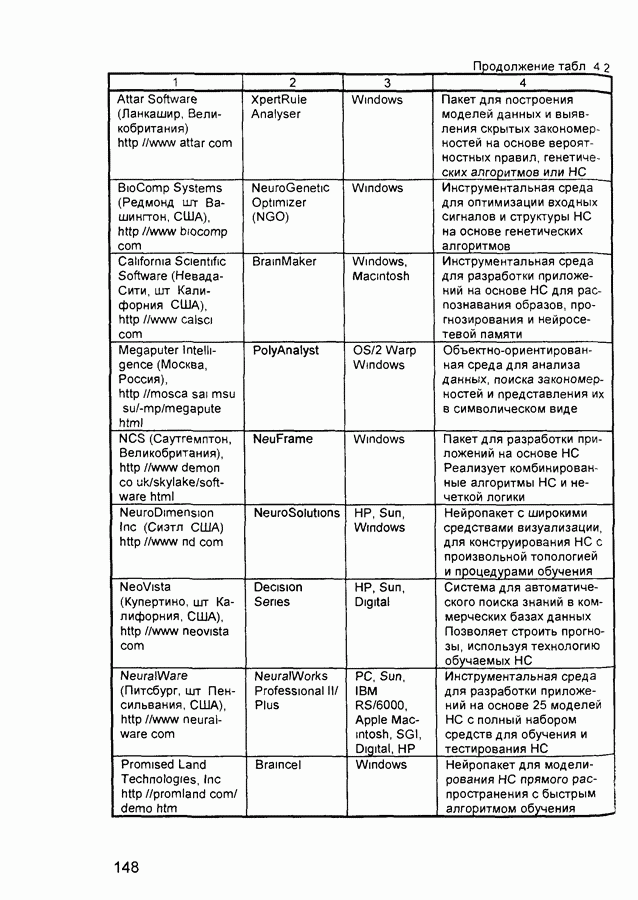
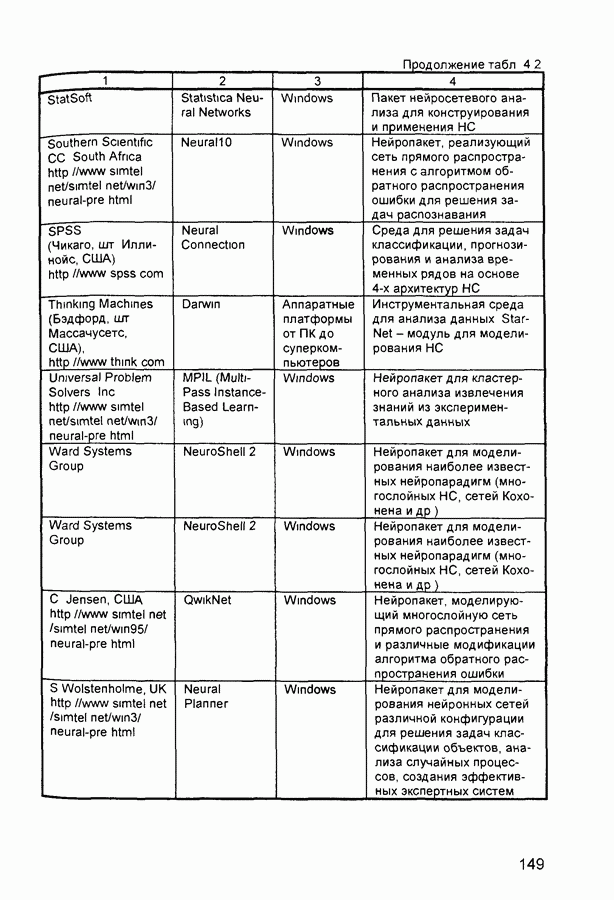
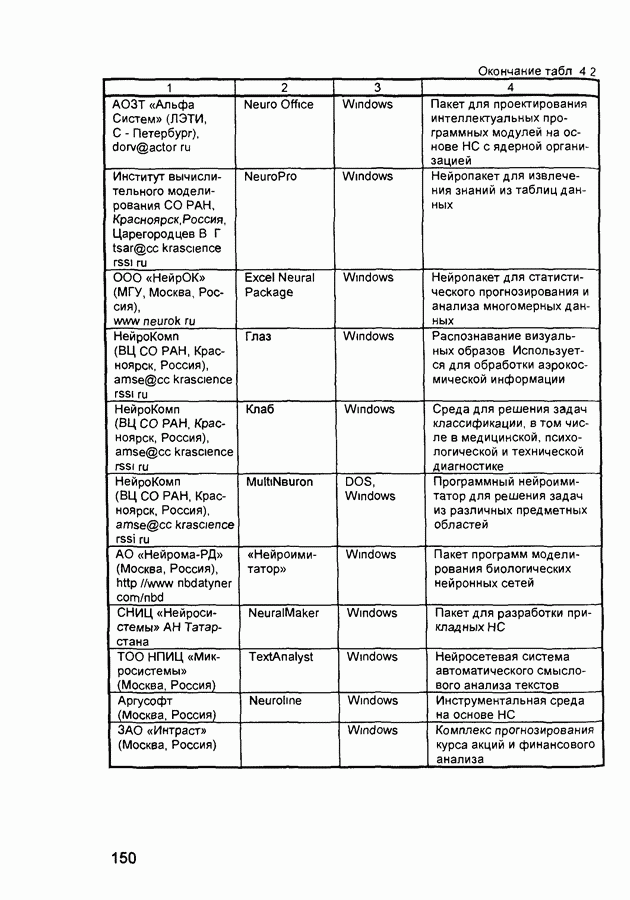
- 4.2. Характеристики современных нейропакетов
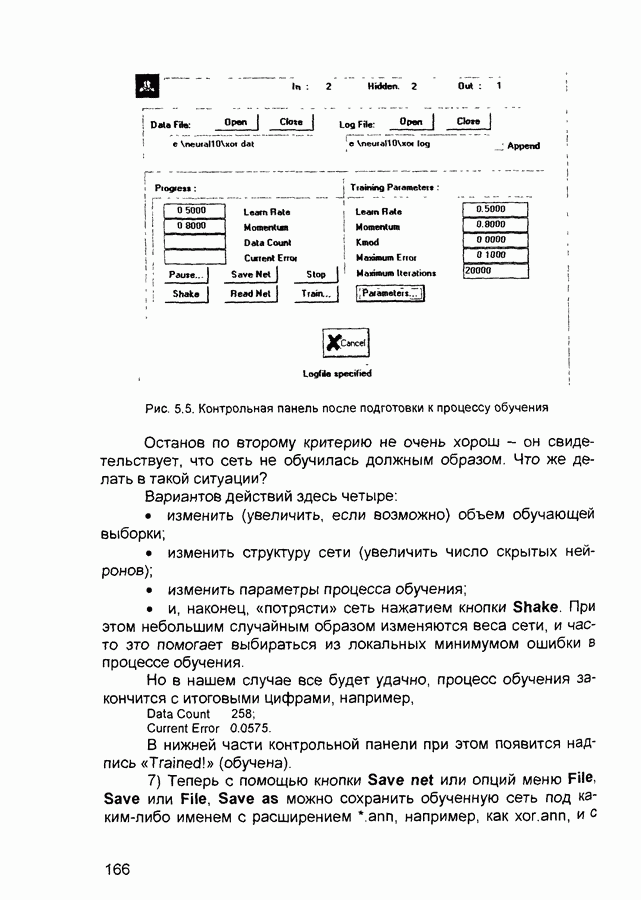
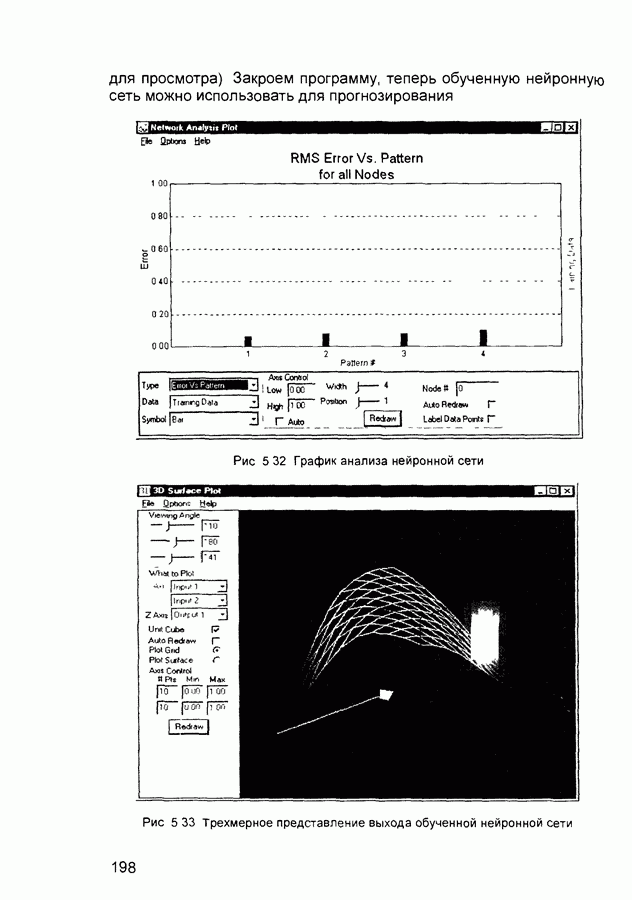
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
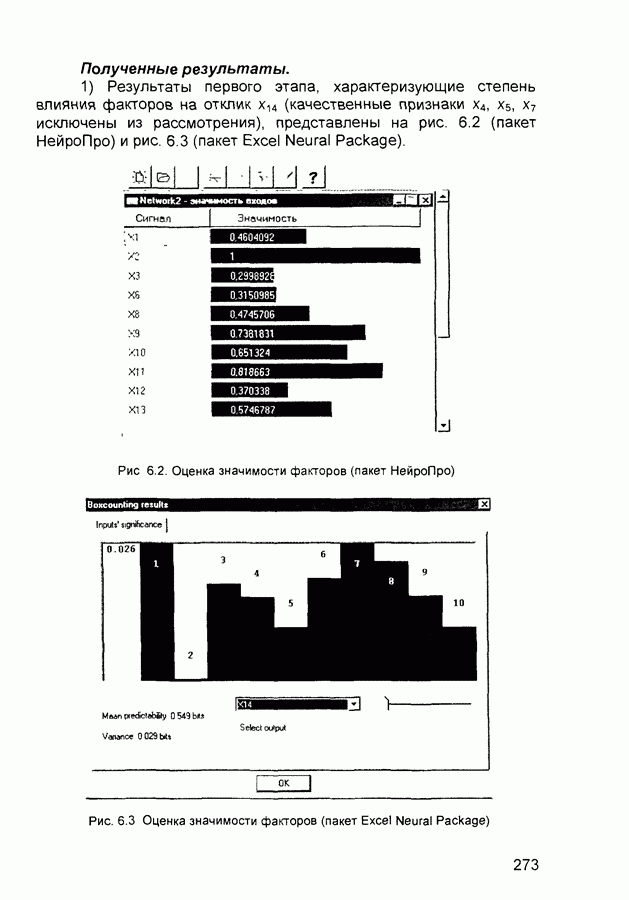
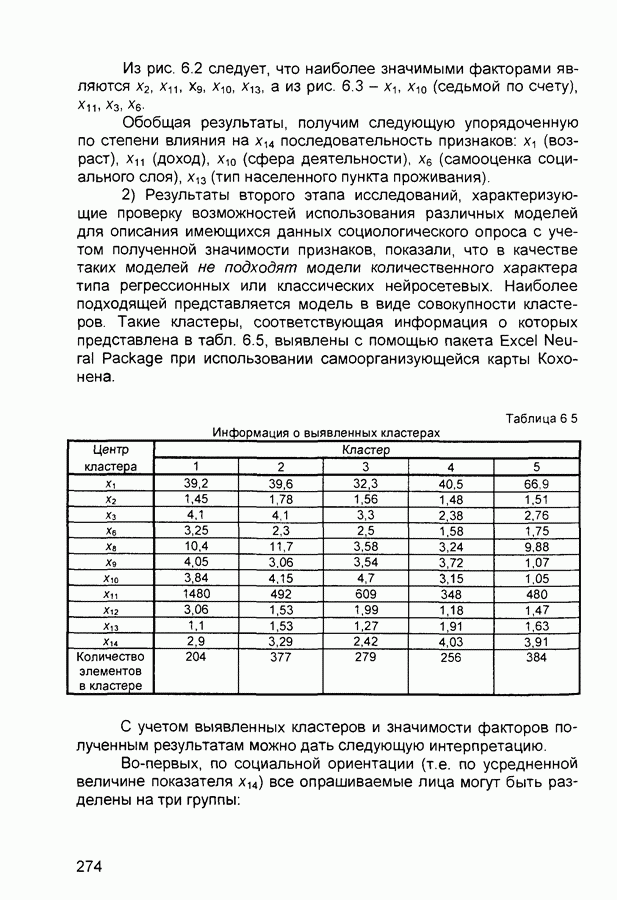
- 6.2. Анализ данных социологического опроса
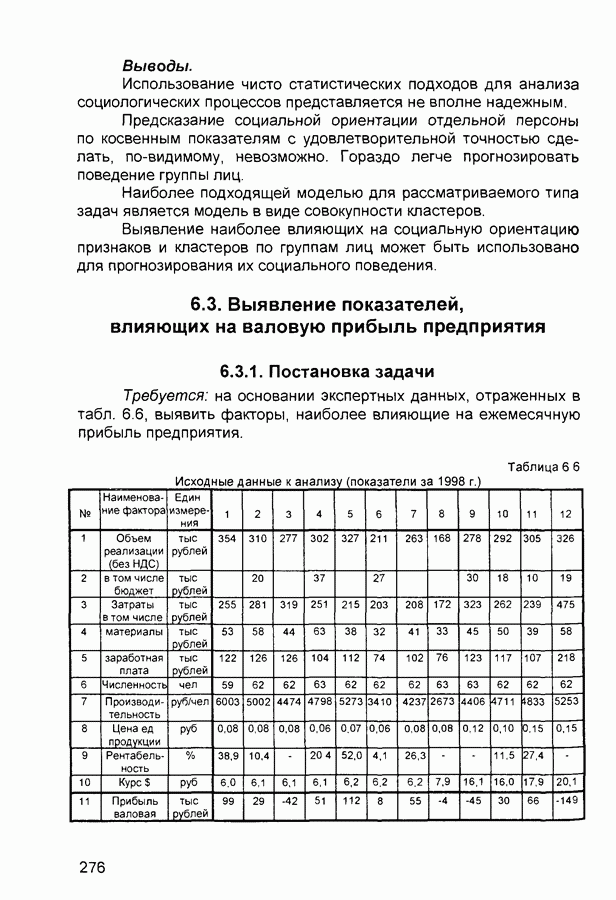
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
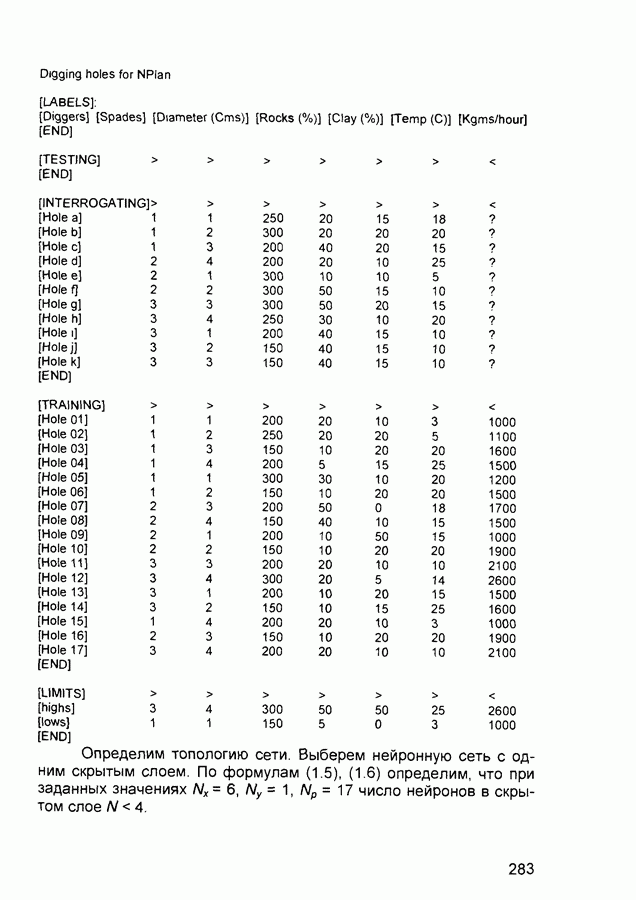
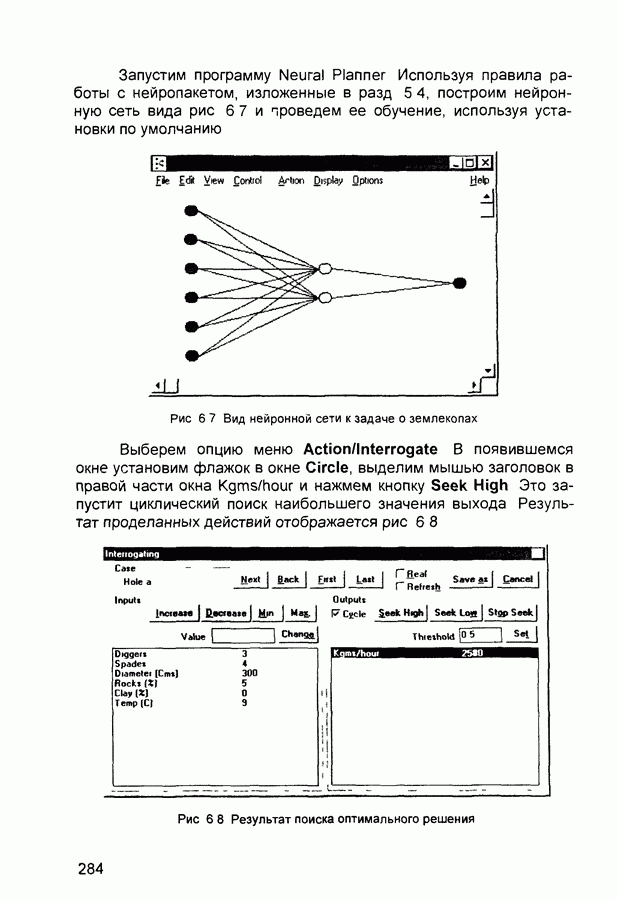
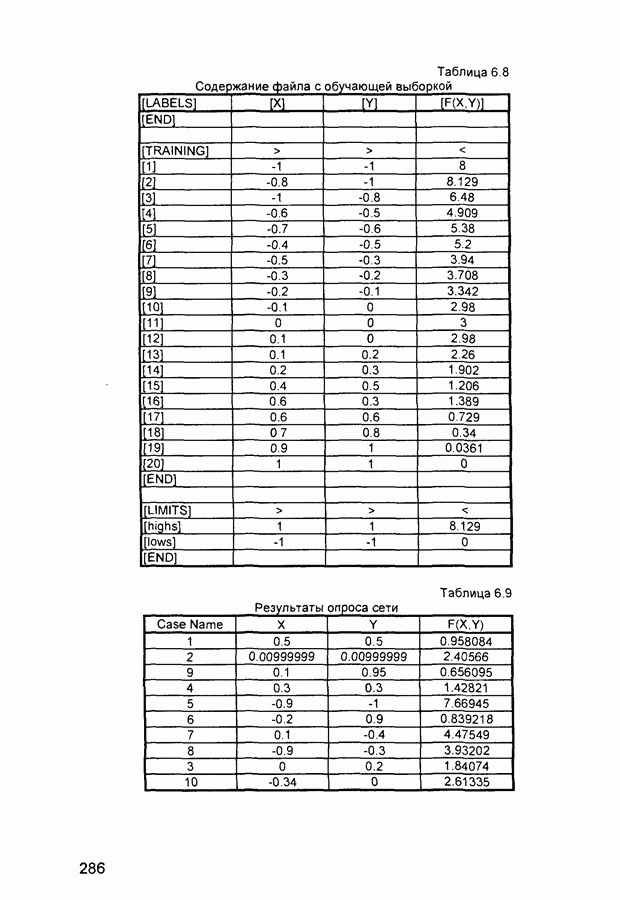
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
- 6.7. Нейросетевая экспертная система
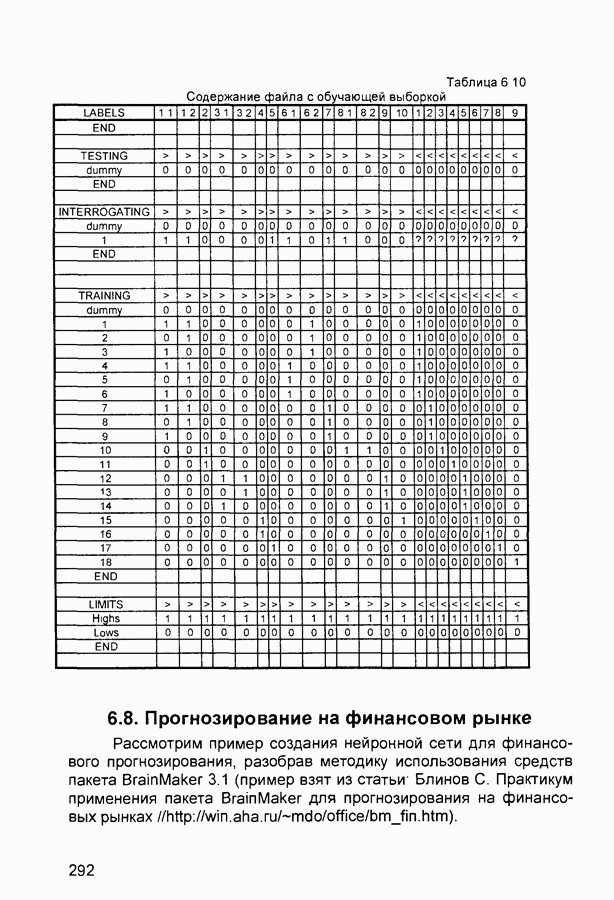
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
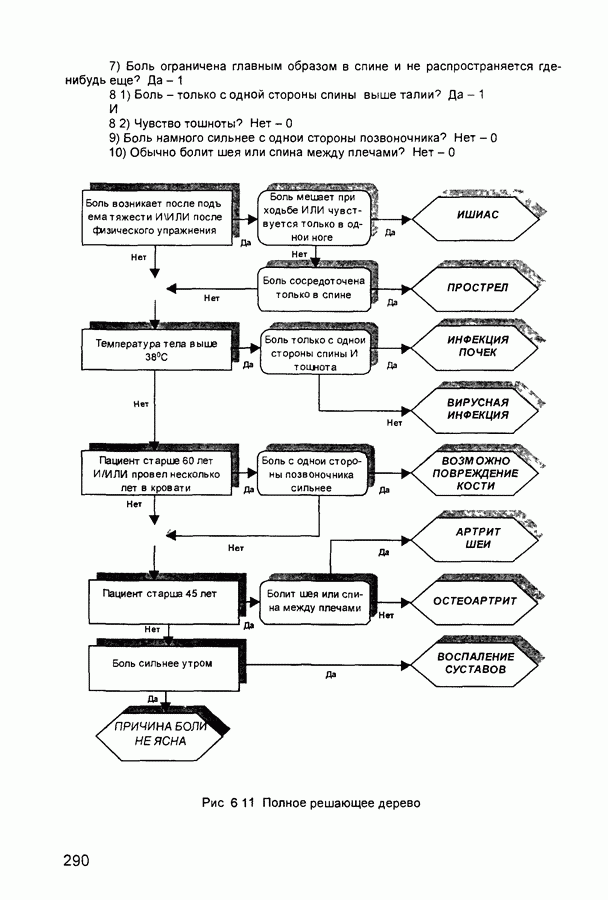
- 6.11. Кратко о других задачах
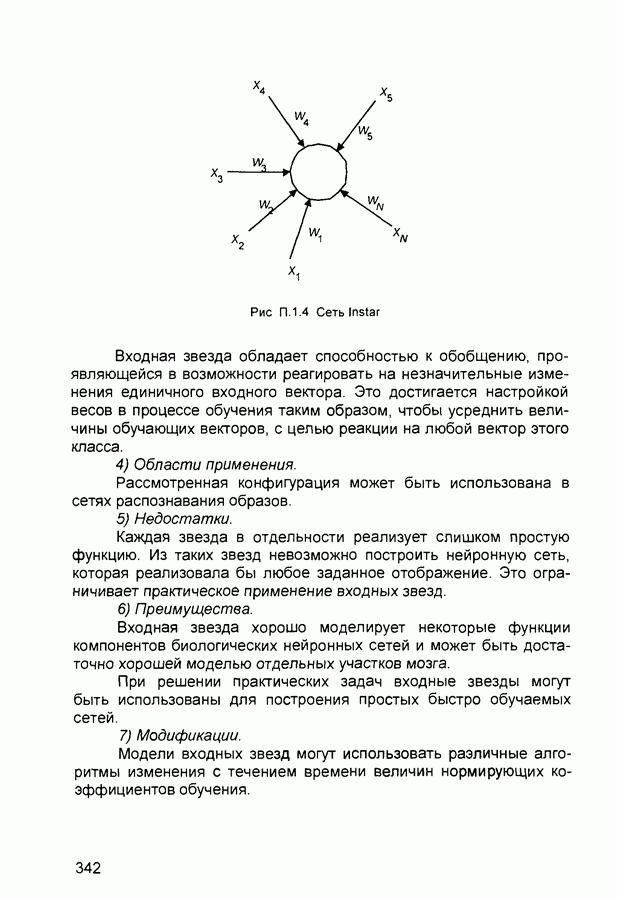
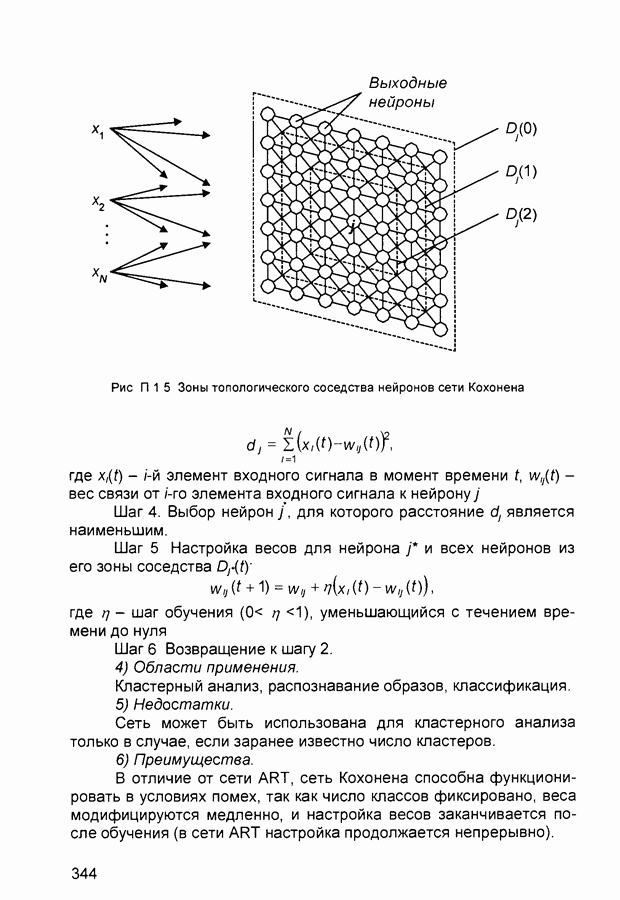
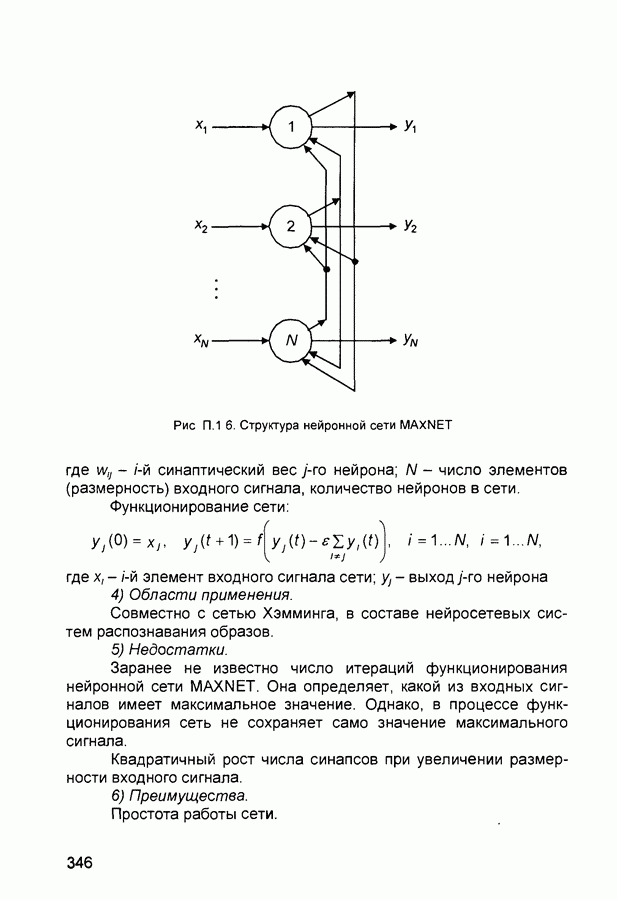
- П.1. Основные парадигмы нейронных сетей
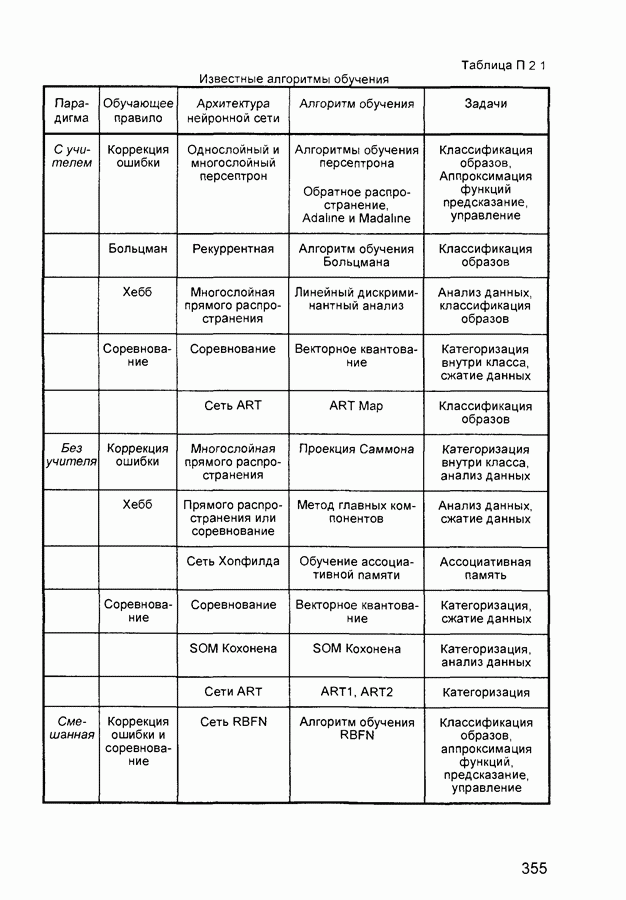
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы