| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
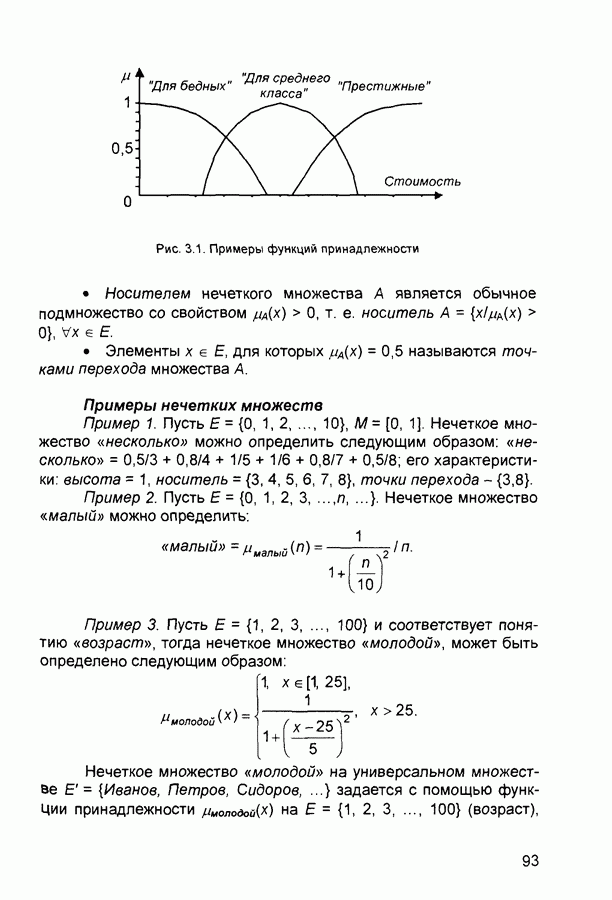
2.2. Персептроны
Систематическое изучение искусственных нейронных сетей было начато Маккалохом и Питтсом в 1943 году. Позднее они исследовали нейросетевые парадигмы для распознавания изображений, подвергаемых сдвигам и поворотам, используя при этом нейронную модель, показанную на рис. 2.3. Элемент X умножает каждый вход х, на вес  и суммирует взвешенные входы. Если эта сумма больше заданного порогового значения, выход равен единице, в противном случае - нулю. Эти системы (и множество им подобных) получили название персептронов. Они состоят из одного слоя искусственных нейронов, соединенных с помощью весовых коэффициентов с множеством входов (рис. 2.4), хотя в
и суммирует взвешенные входы. Если эта сумма больше заданного порогового значения, выход равен единице, в противном случае - нулю. Эти системы (и множество им подобных) получили название персептронов. Они состоят из одного слоя искусственных нейронов, соединенных с помощью весовых коэффициентов с множеством входов (рис. 2.4), хотя в

Рис. 2.3. Персептронный нейрон
принципе описываются и более сложные системы
В 60-е годы персептроны вызвали большой интерес Розенблатт доказал теорему об обучении персептронов Уидроу продемонстрировал возможности систем персептронного типа Однако дальнейшие исследования показали, что персептроны не способны обучиться решению ряда простых задач Минский строго проанализировал эту проблему и показал, что существуют жесткие ограничения на то, что могут выполнять однослойные персептроны, и, следовательно, на то, чему они могут обучаться Так как в то время методы обучения многослойных сетей не были известны, исследования в области нейронных сетей пришли в упадок Возрождение интереса к нейронным сетям связано в большей степени со сравнительно недавним открытием с таких методов
Работа Минского возможно и охладила пыл первых исследователей нейронных сетей, однако обеспечила необходимое время для развития лежащей в их основе теории Важно отметить, что анализ Минского не был опровергнут и до сих пор остается весьма существенным
Несмотря на ограничения, персептроны широко изучались Теория персептронов является основой для изучения многих других типов искусственных нейронных сетей
Рассмотрим в качестве примера трехнейронный персептрон (рис. 2.4), нейроны которого имеют активационную функцию в виде единичного скачка

Рис. 2.4 Персептрон со многими выходами
На  входов подаются входные сигналы, поступающие далее по синапсам на три нейрона, которые образуют единственный слой этой сети На выходах сети формируются сигналы
входов подаются входные сигналы, поступающие далее по синапсам на три нейрона, которые образуют единственный слой этой сети На выходах сети формируются сигналы

Весовые коэффициенты синапсов одного слоя нейронов можно свести в матрицу  в которой каждый элемент
в которой каждый элемент  задает величину
задает величину  синаптической связи
синаптической связи  нейрона Таким образом, процесс, происходящий в нейронной сети, может быть записан в матричной форме
нейрона Таким образом, процесс, происходящий в нейронной сети, может быть записан в матричной форме

где X и Y - соответственно входной и выходной векторы (под вектором понимается вектор-строка),  - активационная функция, применяемая поэлементно к компонентам вектора
- активационная функция, применяемая поэлементно к компонентам вектора 
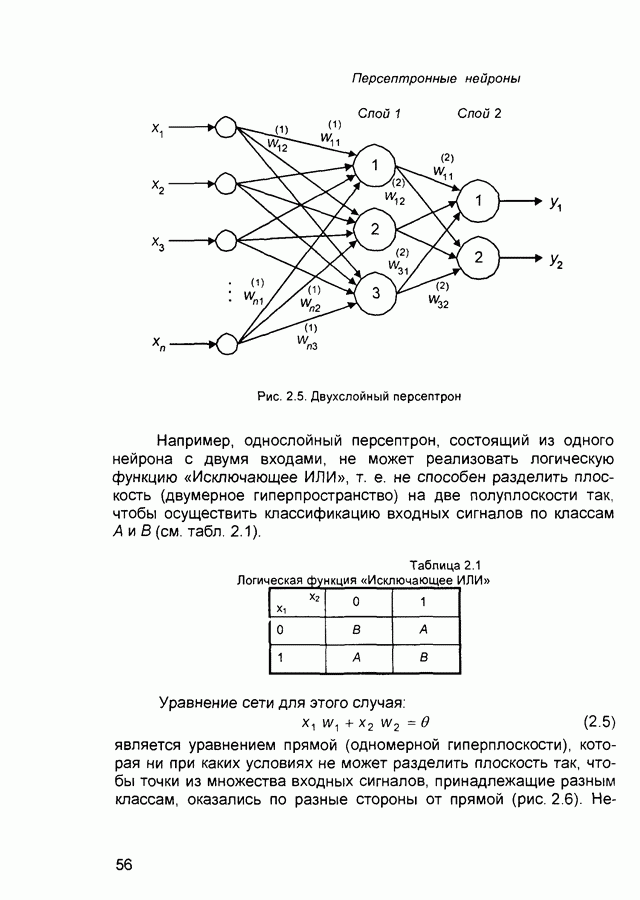
На рис 2 5 представлен двухслойный персептрон, образованный из однослойного добавлением второго слоя, состоящего из двух нейронов
Отметим важную роль нелинейности активационной функции, так как, если бы она не обладала данным свойством, результат функционирования любой  -слойной нейронной сети с весовыми матрицами
-слойной нейронной сети с весовыми матрицами  для каждого слоя
для каждого слоя  свелся бы к перемножению входного вектора сигналов X на матрицу
свелся бы к перемножению входного вектора сигналов X на матрицу

Фактически такая  -слойная нейронная сеть эквивалентна сети с одним скрытым слоем и с весовой матрицей единственного слоя
-слойная нейронная сеть эквивалентна сети с одним скрытым слоем и с весовой матрицей единственного слоя

Работа персептрона сводится к классификации (обобщению) входных сигналов, принадлежащих  -мерному гиперпространству, по некоторому числу классов С математической точки зрения это происходит путем разбиения гиперпространства гиперплоскостями Для однослойного персептрона
-мерному гиперпространству, по некоторому числу классов С математической точки зрения это происходит путем разбиения гиперпространства гиперплоскостями Для однослойного персептрона

Каждая полученная область является областью определения отдельного класса Число таких классов для персептрона не превышает  где
где  - число его выходов Однако не все из классов могут быть разделимы данной нейронной сетью
- число его выходов Однако не все из классов могут быть разделимы данной нейронной сетью

Рис. 2.5. Двухслойный персептрон
Например, однослойный персептрон, состоящий из одного нейрона с двумя входами, не может реализовать логическую функцию «Исключающее ИЛИ», т. е. не способен разделить плоскость (двумерное гиперпространство) на две полуплоскости так, чтобы осуществить классификацию входных сигналов по классам А и В (см. табл. 2.1).
Таблица 2.1 (см. скан) Логическая функция «Исключающее ИЛИ»
Уравнение сети для этого случая:

является уравнением прямой (одномерной гиперплоскости), которая ни при каких условиях не может разделить плоскость так, чтобы точки из множества входных сигналов, принадлежащие разным классам, оказались по разные стороны от прямой (рис. 2.6).

Рис. 2 6. Линейная нераздепимость функции Исключающее ИЛИ
Невозможность реализации однослойным персептроном этой функции получила название проблемы «Исключающего ИЛИ».
Отметим, что функции, которые не реализуются однослойным персептроном, называются линейно неразделимыми. Решение задач, подпадающих под это ограничение, заключается в применении 2-х и более слойных сетей или сетей с нелинейными синапсами, однако и тогда существует вероятность, что корректное разделение некоторых входных сигналов на классы невозможно.
Рассмотрим более подробно алгоритм обучения с учителем персептрона на примере, представленном на рис. 2.4.
ШАГ 1. Проинициализировать элементы весовой матрицы небольшими случайными значениями.
ШАГ 2. Подать на входы один из входных векторов, которые сеть должна научиться различать, и вычислить ее выход.
ШАГ 3. Если выход правильный, перейти на шаг 4. Иначе - вычислить разницу между требуемым и полученным значениями выхода:

Модифицировать веса в соответствии с формулой:

где  и
и  - номера текущей и следующей итераций;
- номера текущей и следующей итераций;  - коэффициент скорости обучения,
- коэффициент скорости обучения,  номер входа;
номер входа;  - номер нейрона в слое.
- номер нейрона в слое.
Очевидно, что если  то весовые коэффициенты будут увеличены и, тем самым, уменьшат ошибку. В противном случае они будут уменьшены, и У тоже уменьшится, приближаясь к
то весовые коэффициенты будут увеличены и, тем самым, уменьшат ошибку. В противном случае они будут уменьшены, и У тоже уменьшится, приближаясь к 
Шаг 4. Цикл с шага 2, пока сеть не перестанет ошибаться.
На шаге 2 на разных итерациях поочередно в случайном порядке предъявляются все возможные входные вектора. К
сожалению, нельзя заранее определить число итераций, которые потребуется выполнить, а в некоторых случаях и гарантировать полный успех Этот вопрос будет затронут в дальнейшем
Сходимость рассмотренной процедуры устанавливается следующими теоремами Теорема 2 1
Класс элементарных персептронов, для которых существует решение для любой задуманной классификации, не является пустым
Эта теорема утверждает, что для любой классификации обучающей выборки можно подобрать такой набор (из бесконечного набора) элементарных нейронов, в котором будет осуществлено разделение обучающей последовательности при помощи линейного решающего правила Теорема 2 2
Если для некоторой классификации решение существует, то в процессе обучения персептрона с коррекцией ошибок, начинающегося с произвольного исходного состояния, это решение будет достигнуто в течение конечного промежутка времени
Смысл теоремы состоит в том, что если относительно задуманной классификации можно найти набор элементов, в котором существует решение, то в рамках этого набора оно будет достиг нуто за конечный промежуток времени
Интересную область исследований представляют много слойные персептроны и персептроны с перекрестными связями однако теория этих систем практически не разработана
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
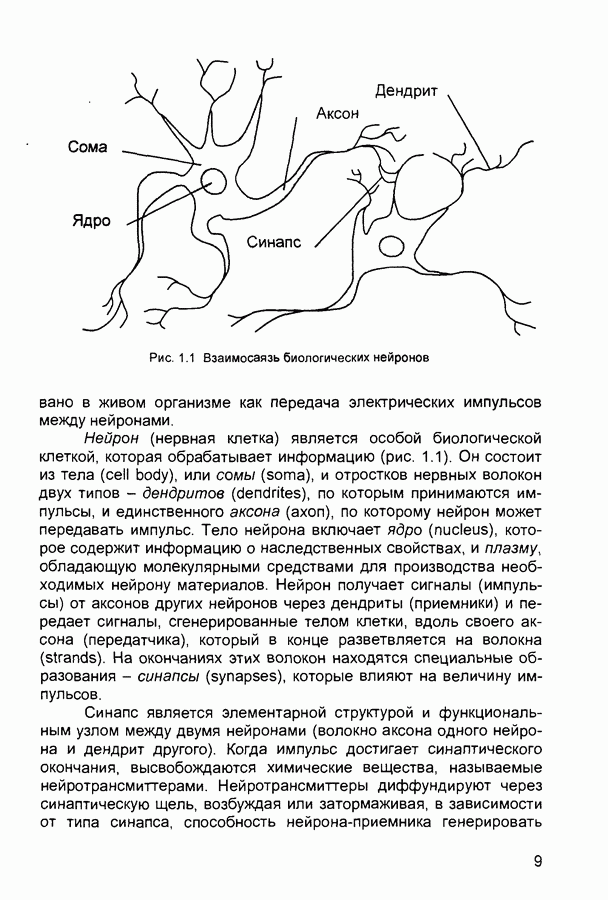
- 1.1. Биологический нейрон
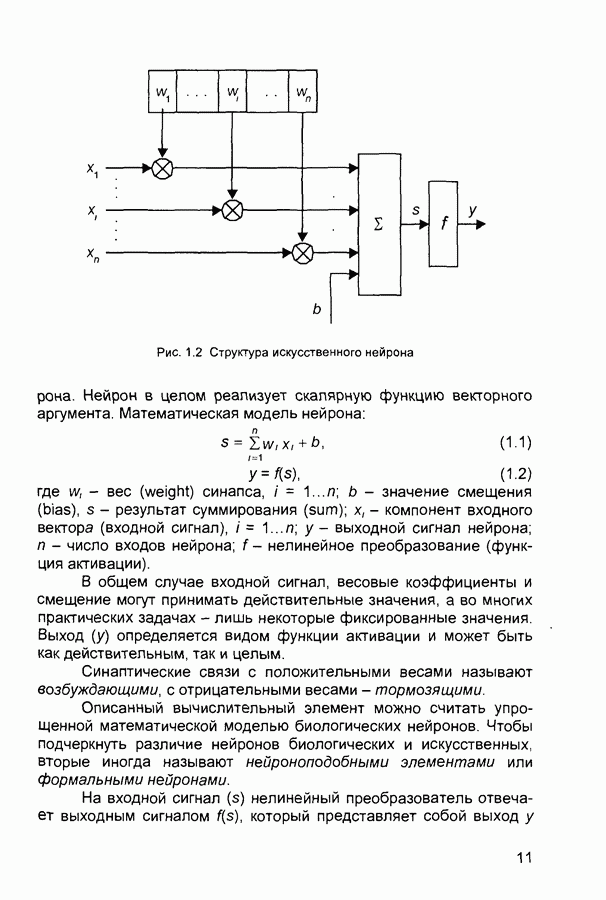
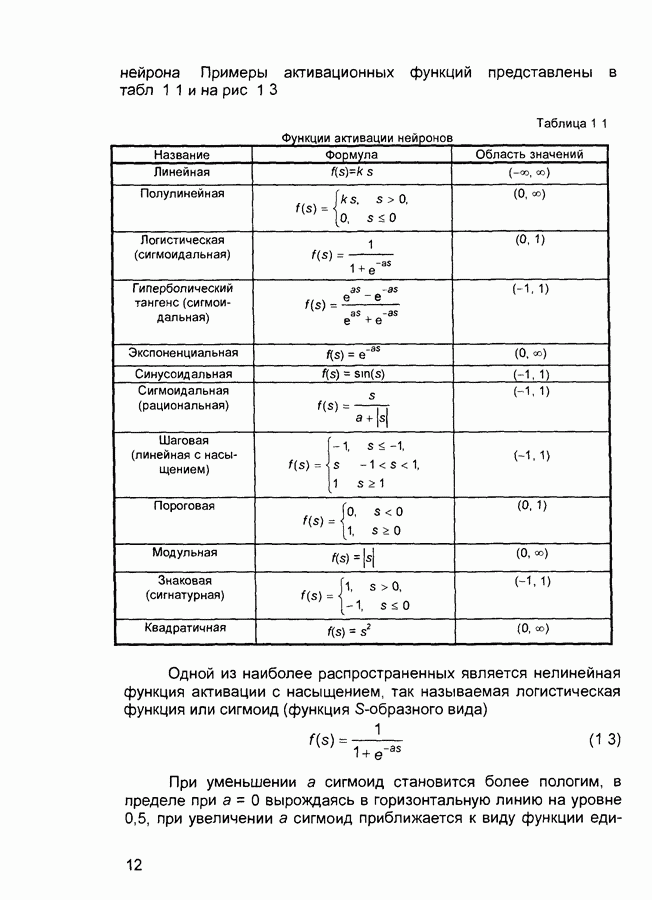
- 1.2. Структура и свойства искусственного нейрона
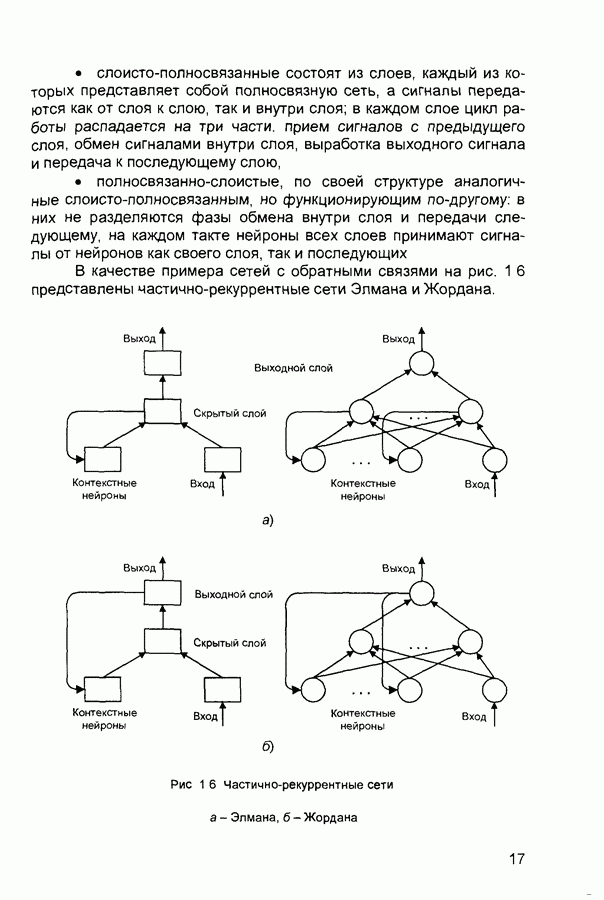
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
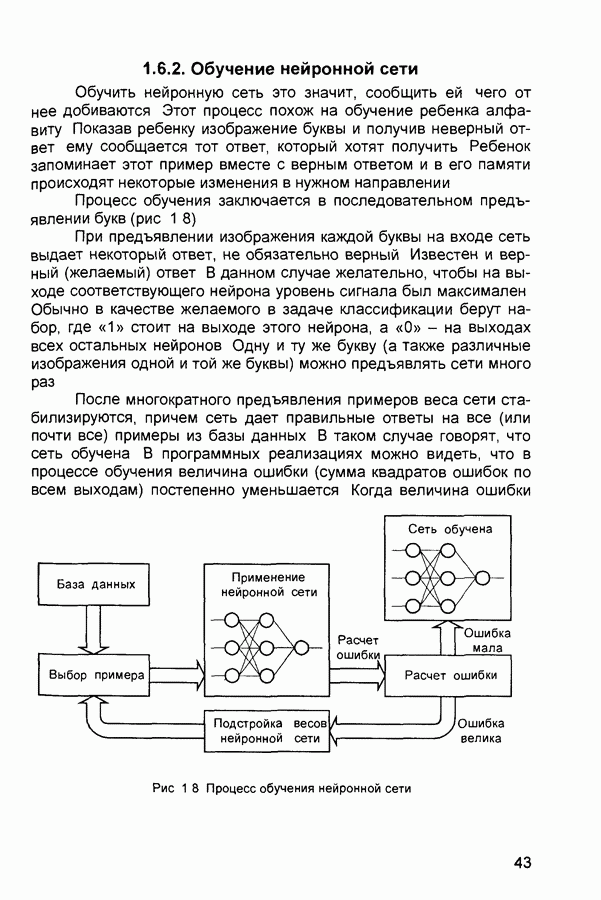
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
- 2.2. Персептроны
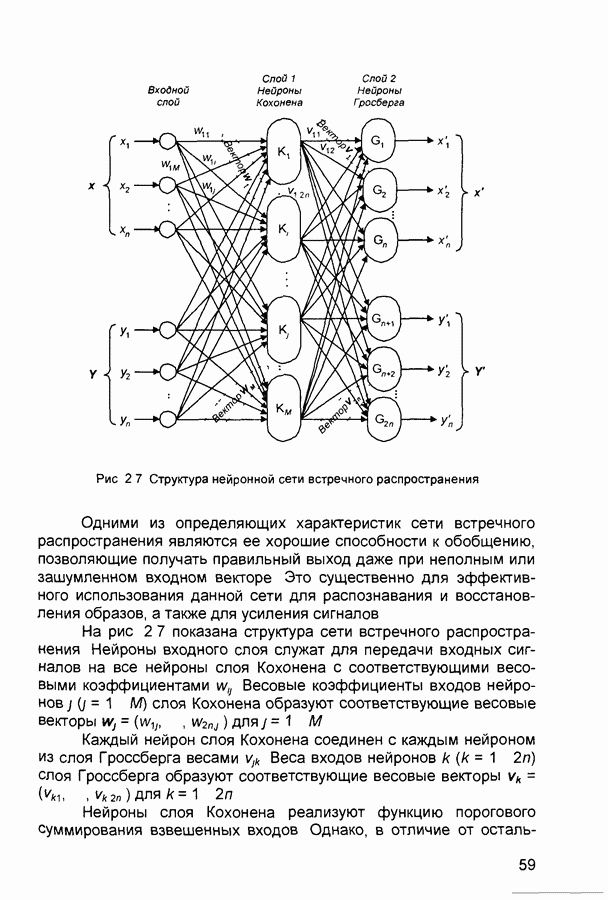
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
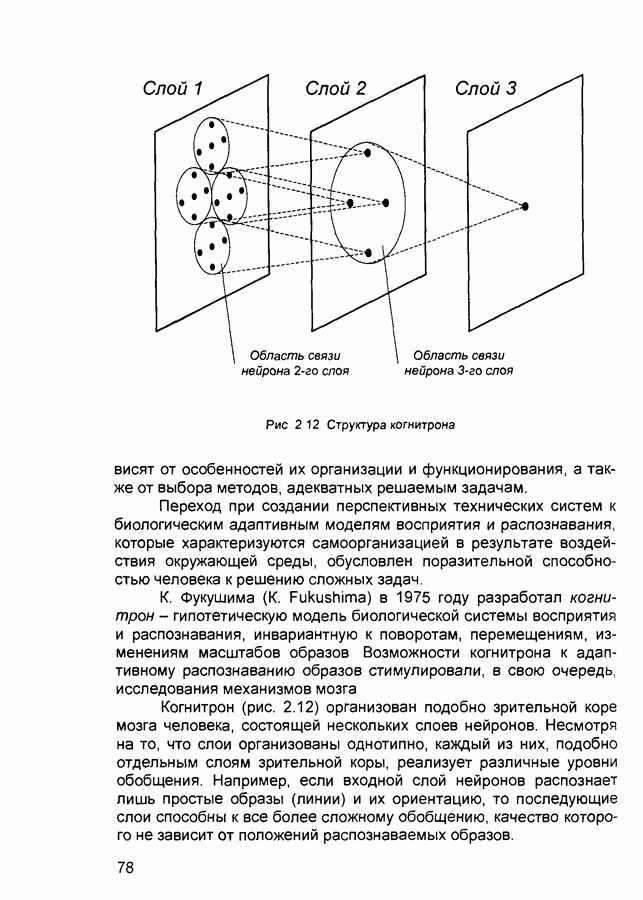
- 2.7. Когнитрон
- 2.8. Неокогнитрон
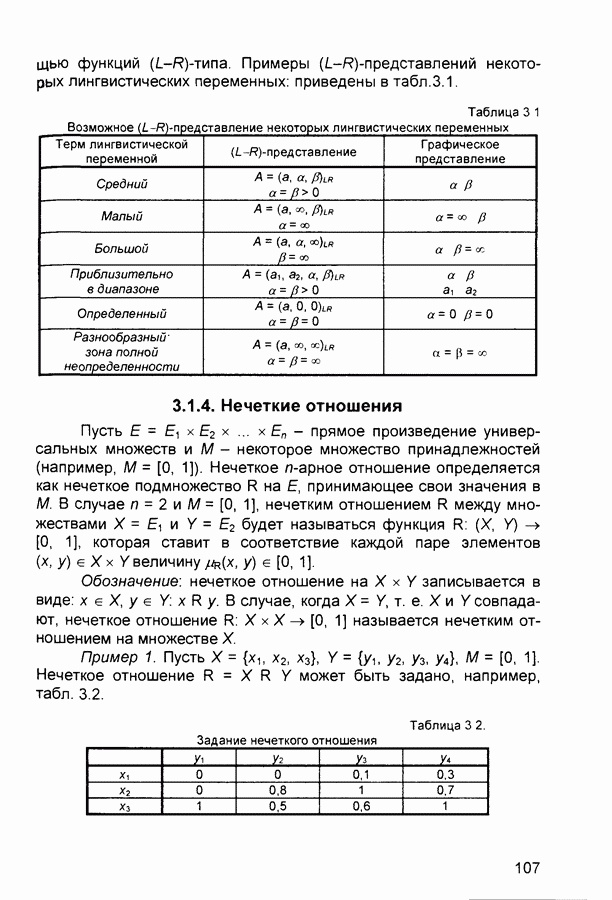
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
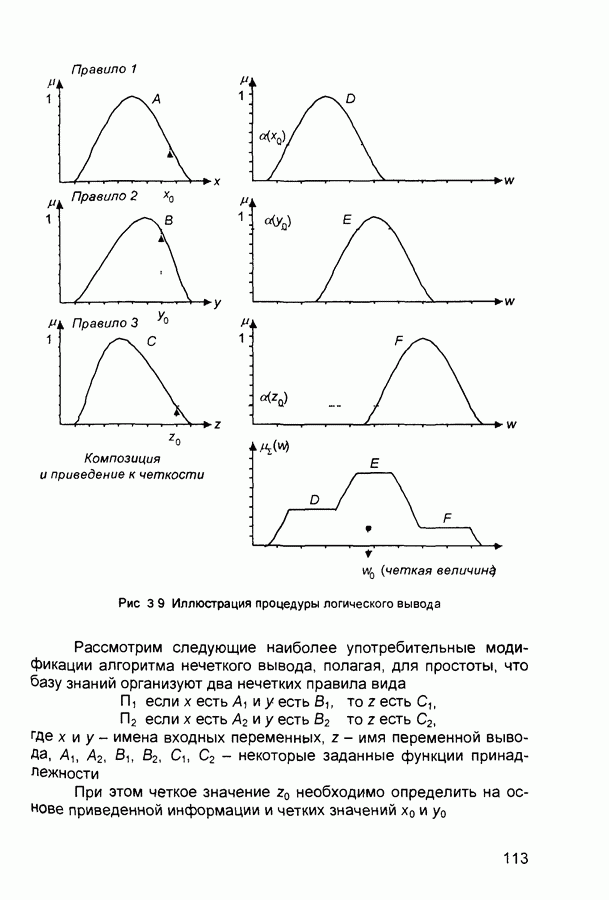
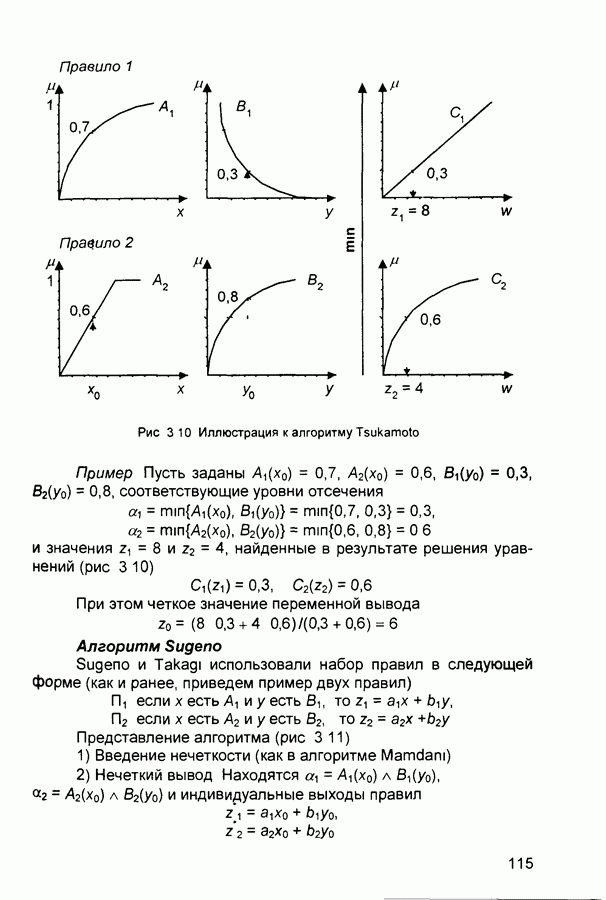
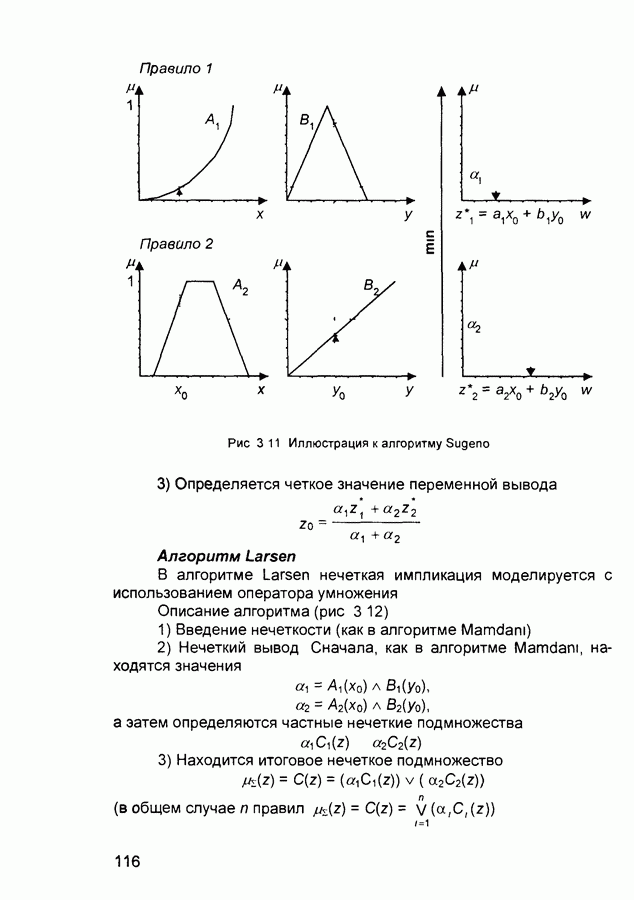
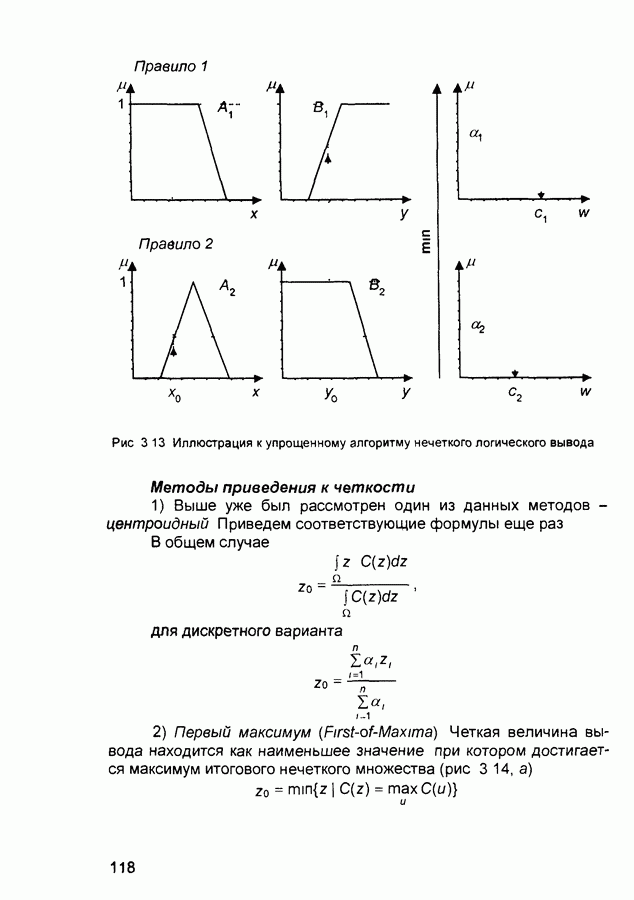
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
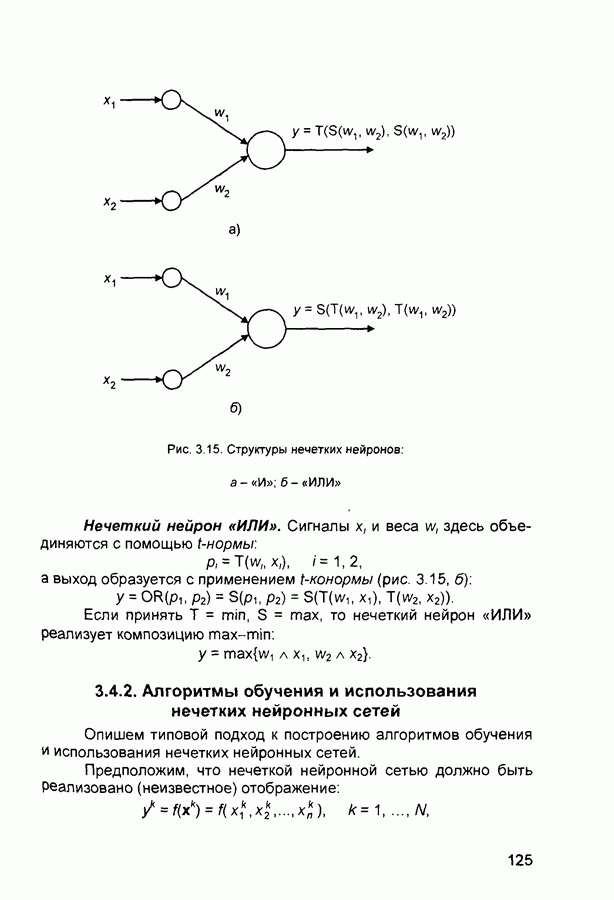
- 3.4. Синтез нечетких нейронных сетей
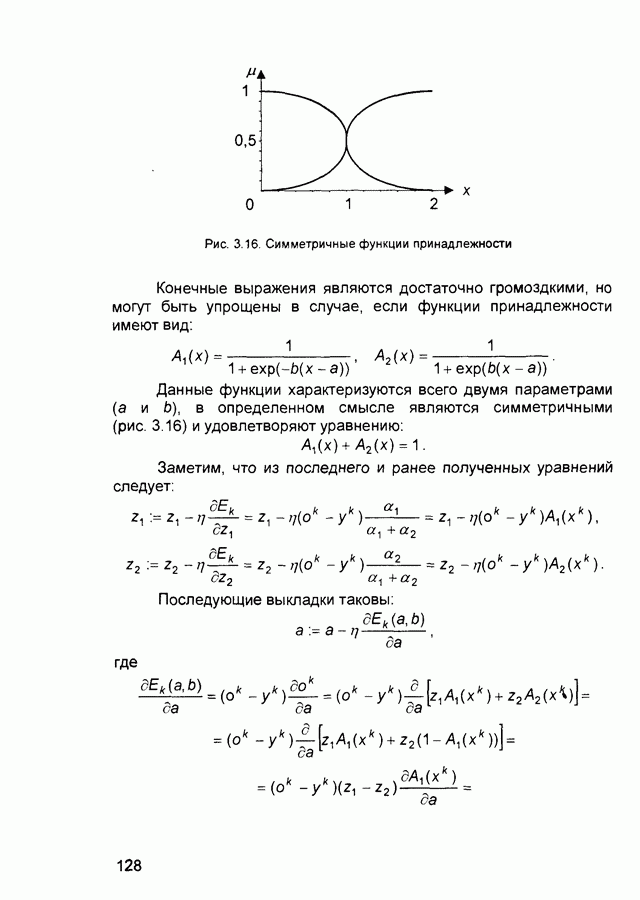
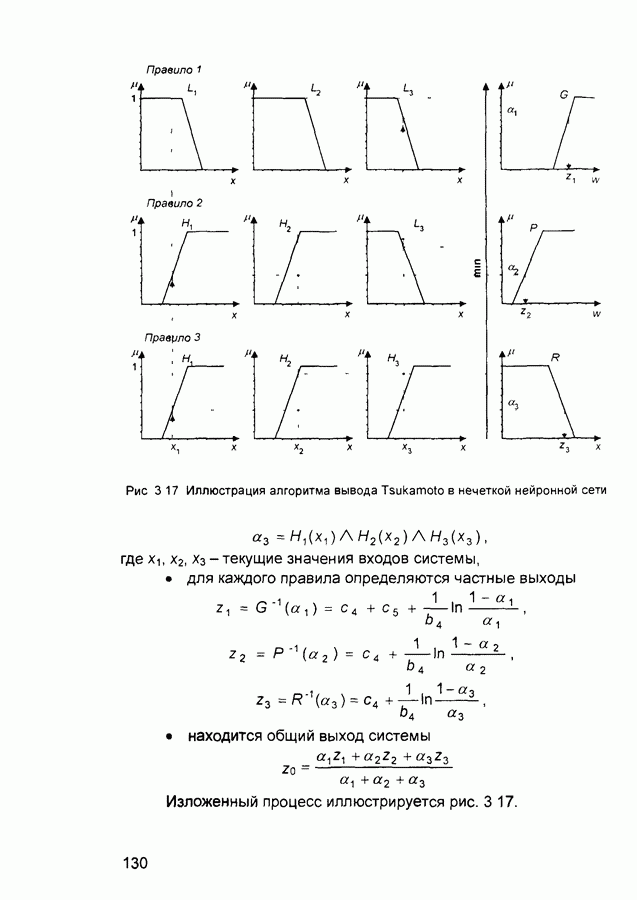
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
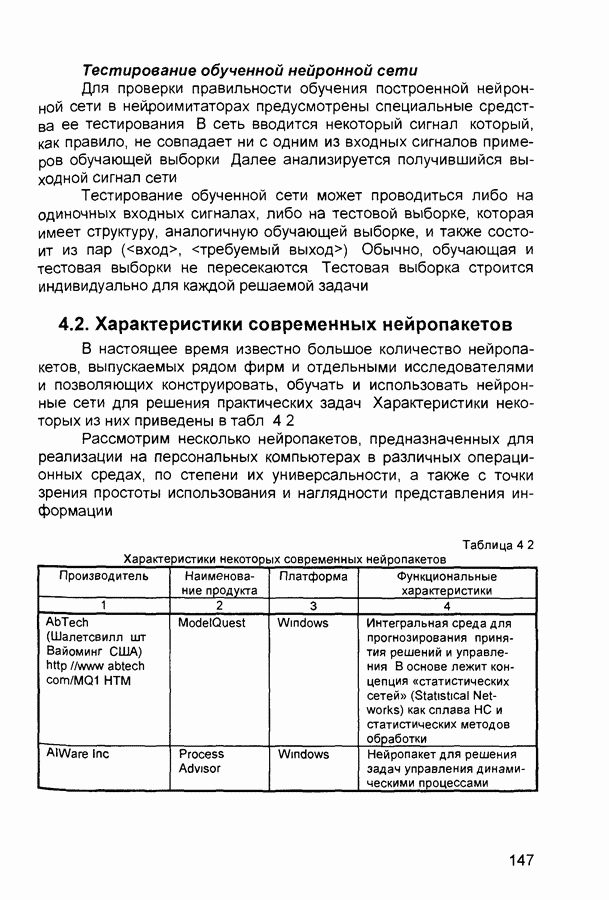
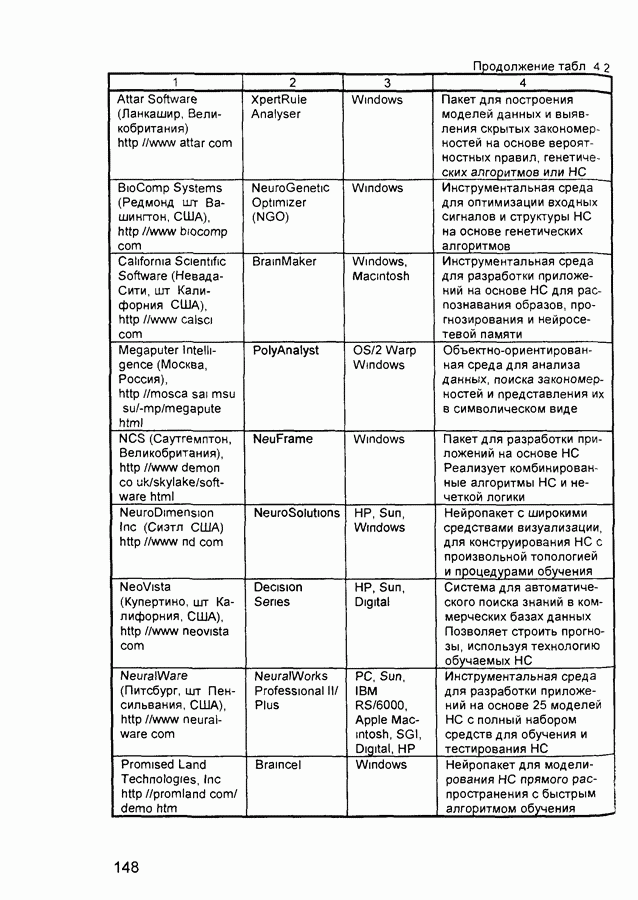
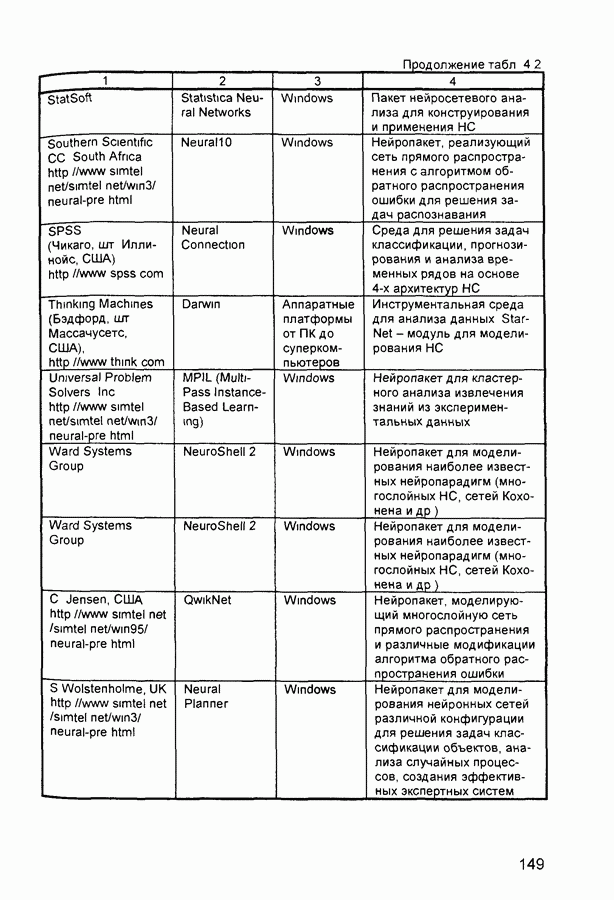
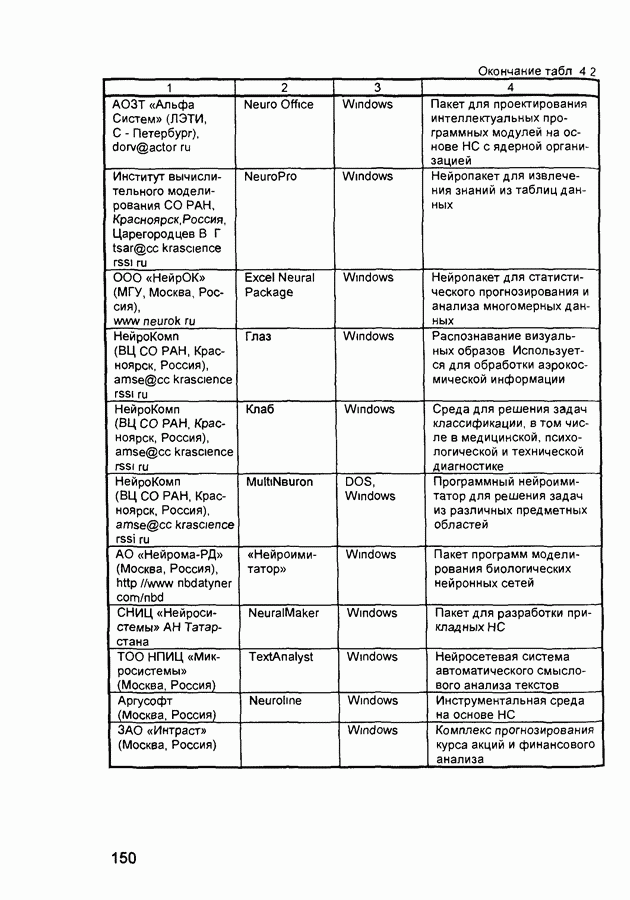
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
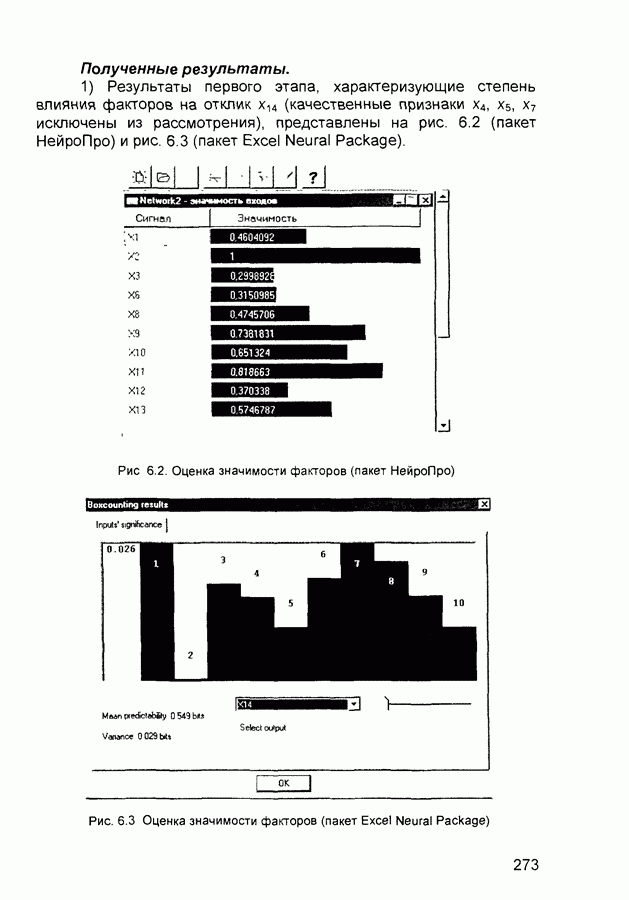
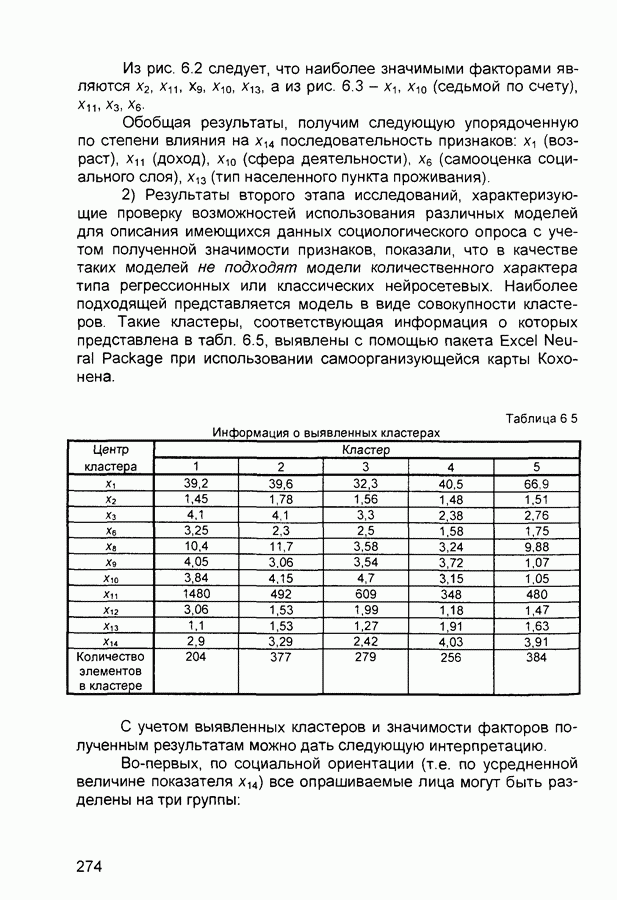
- 6.2. Анализ данных социологического опроса
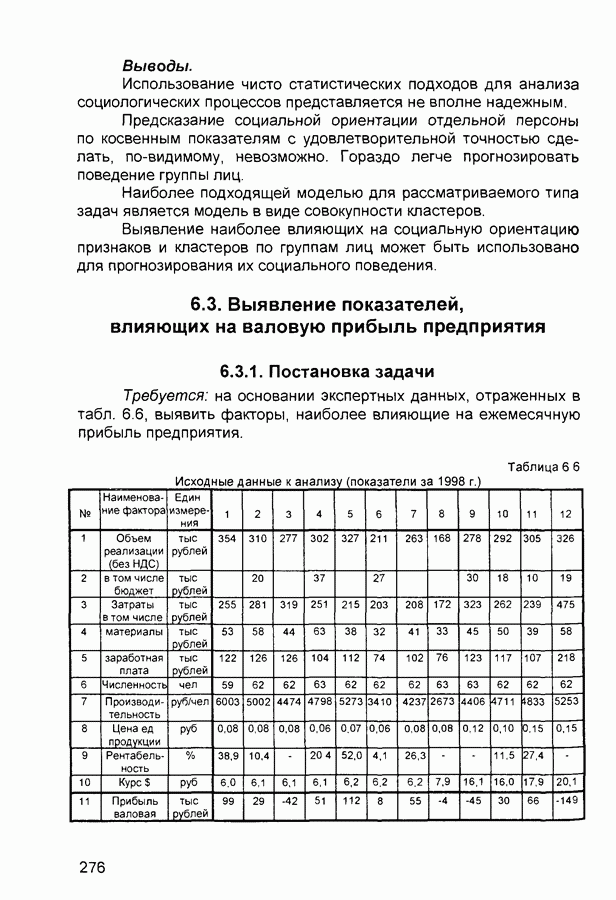
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
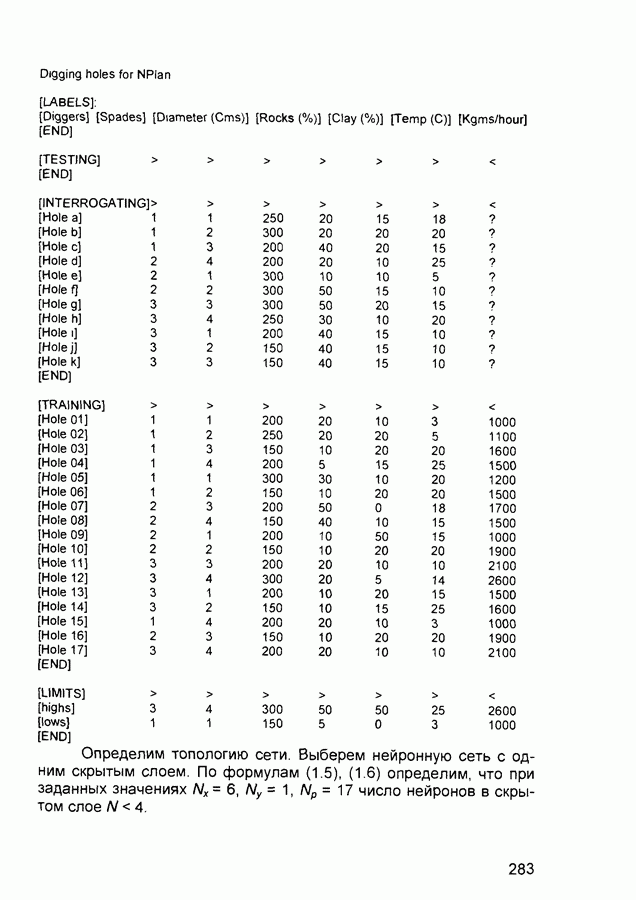
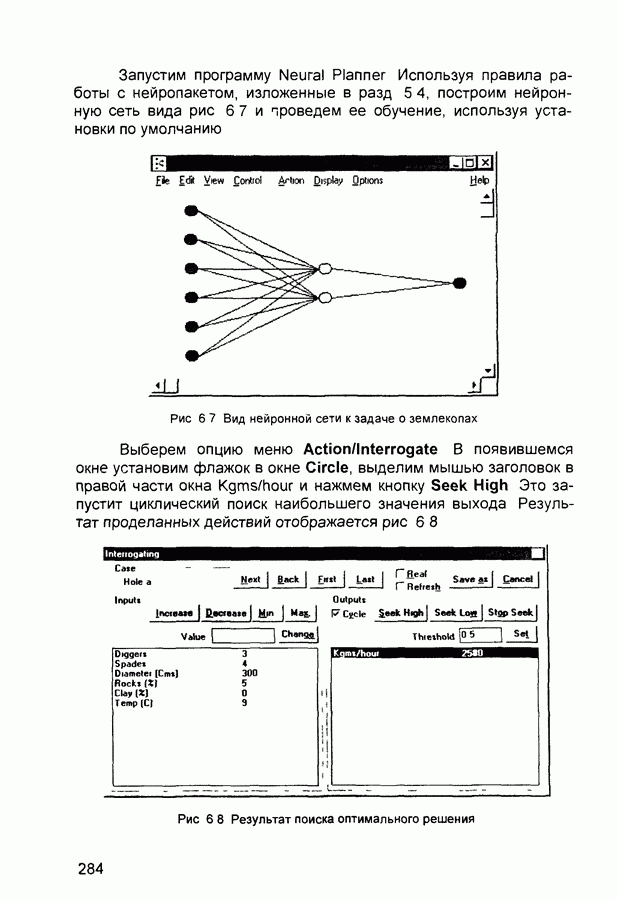
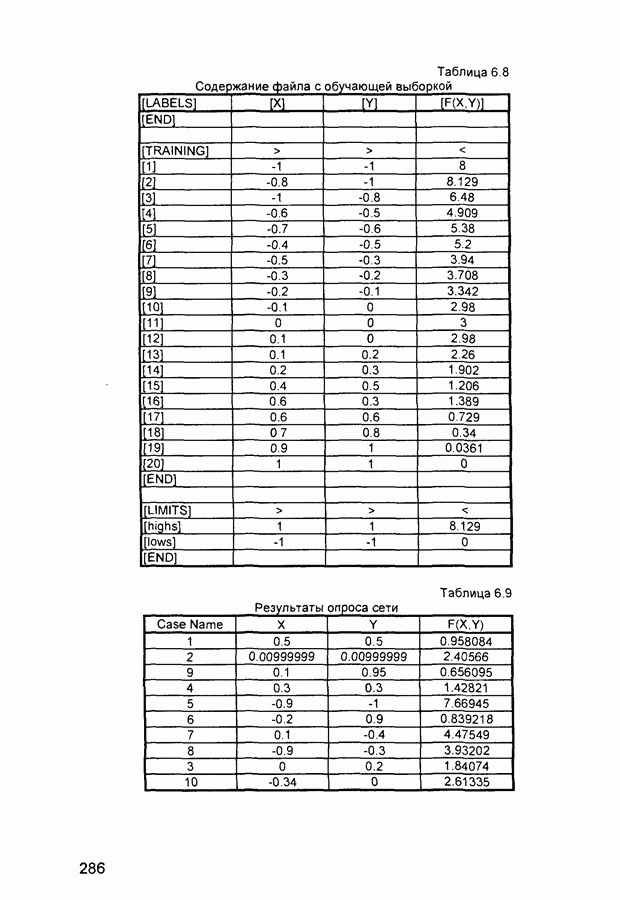
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
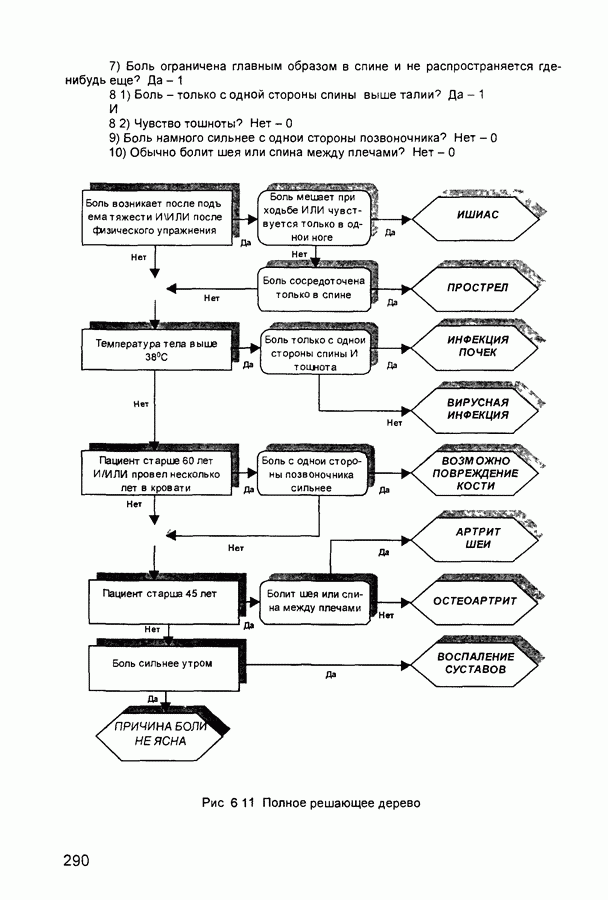
- 6.7. Нейросетевая экспертная система
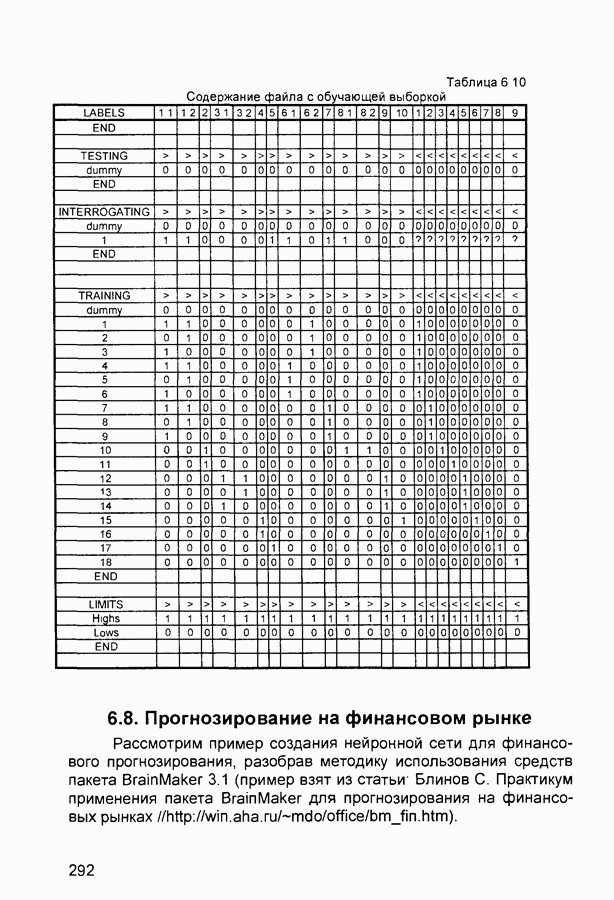
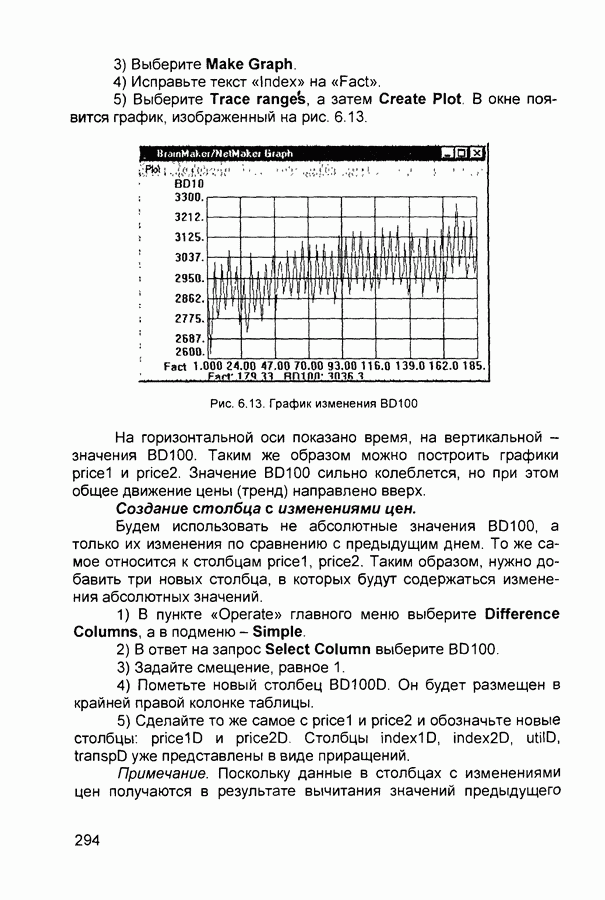
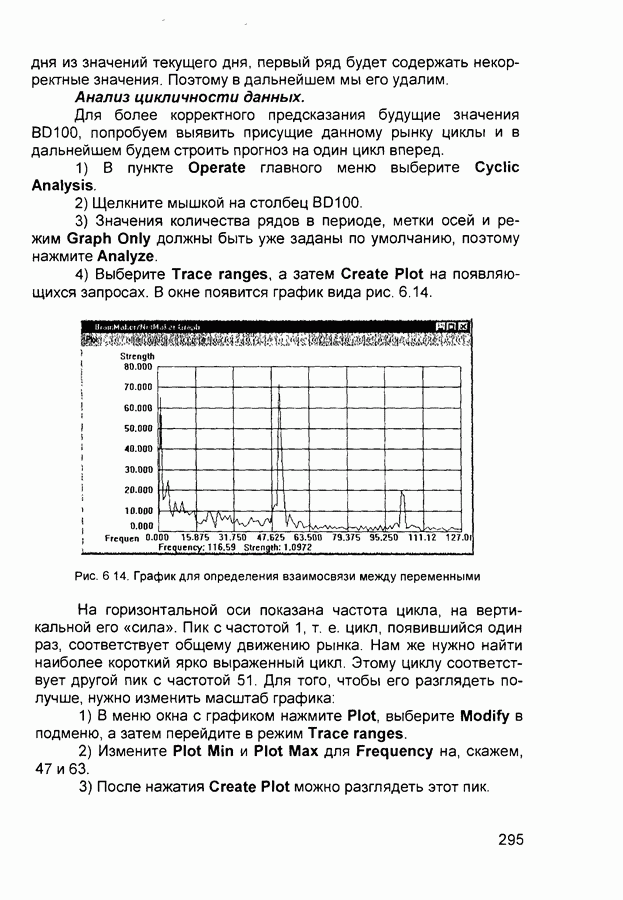
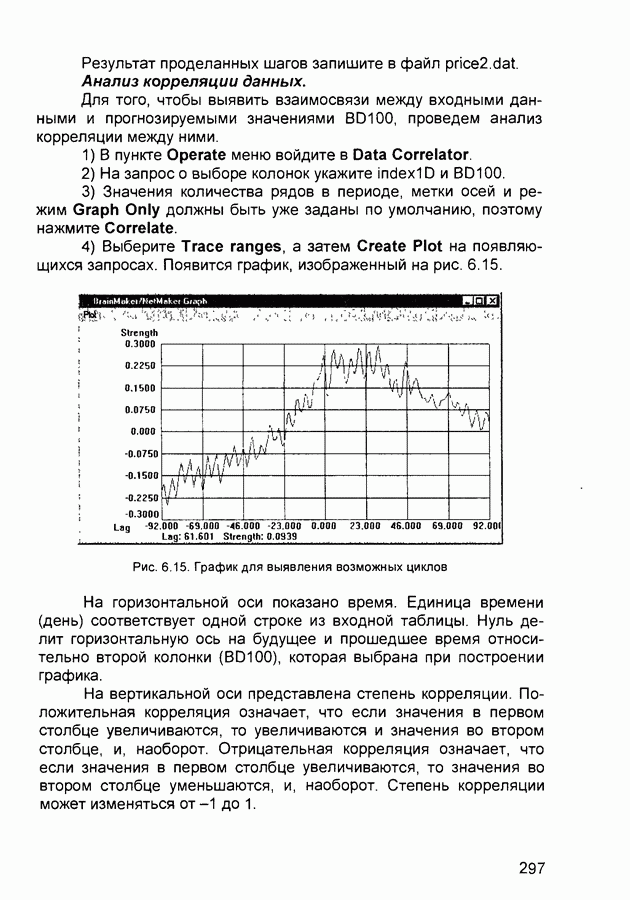
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
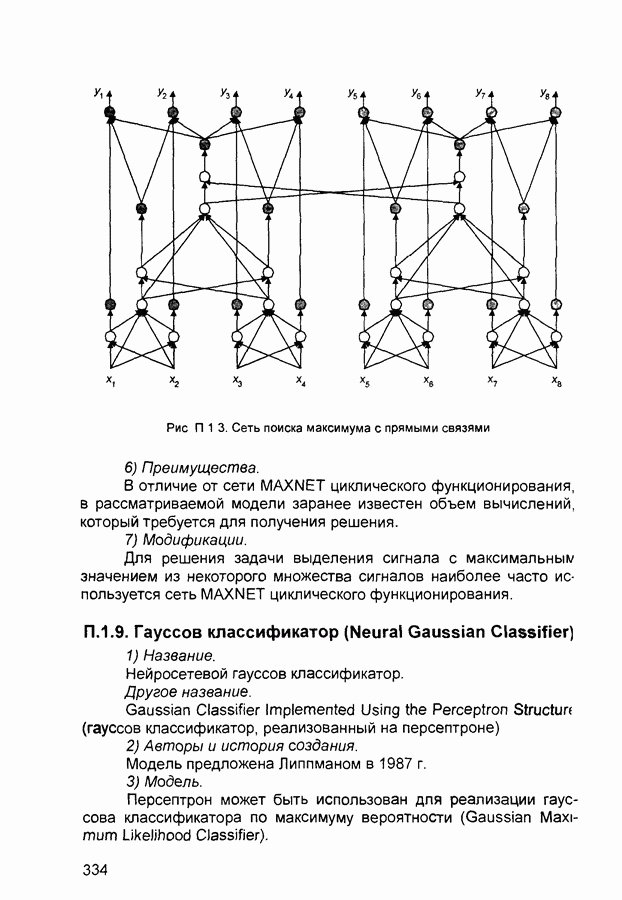
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы