| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
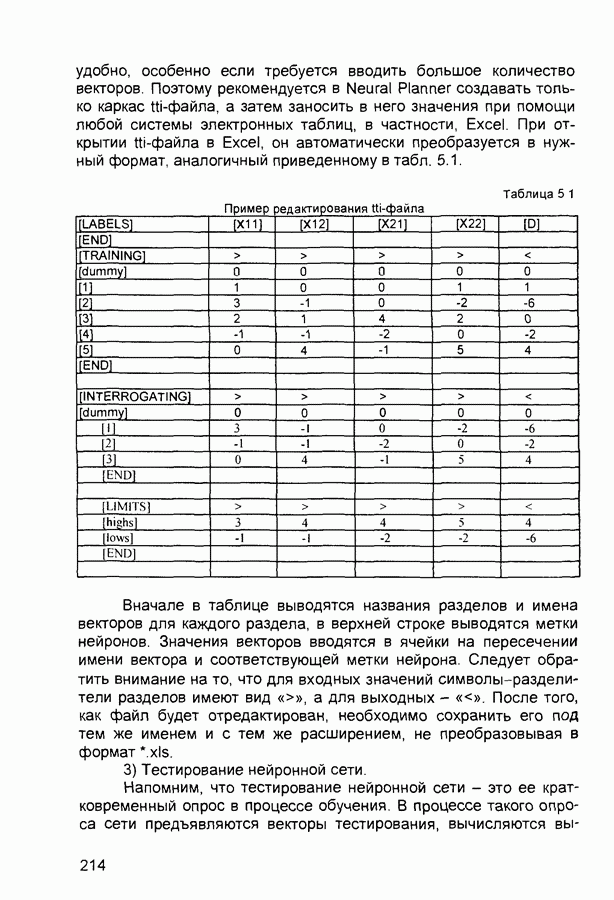
1.2. Структура и свойства искусственного нейрона
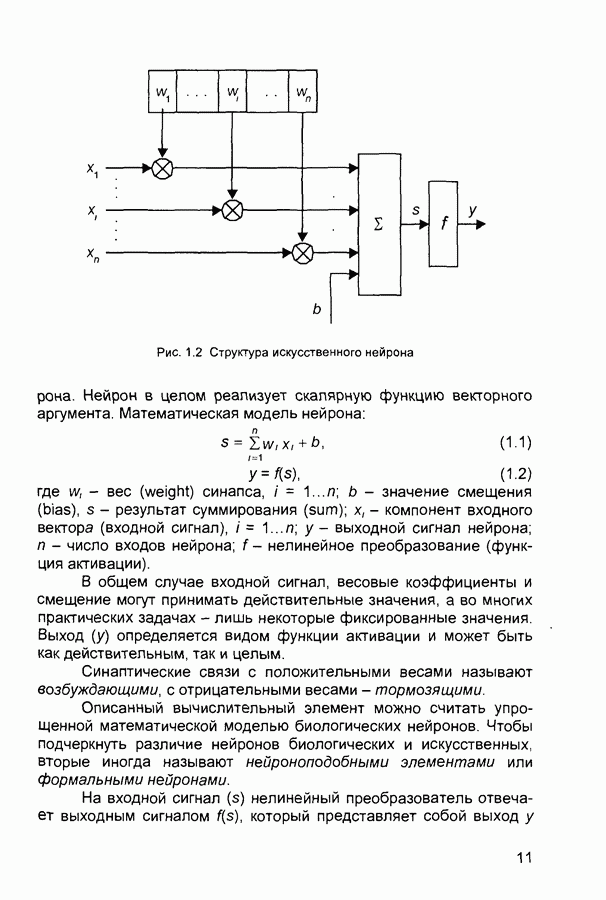
Нейрон является составной частью нейронной сети. На рис. 1 2 показана его структура Он состоит из элементов трех типов: умножителей (синапсов), сумматора и нелинейного преобразователя. Синапсы осуществляют связь между нейронами, умножают входной сигнал на число, характеризующее силу связи, (вес синапса). Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента - выхода сумматора. Эта функция называется функцией активации или передаточной функцией

Рис. 1.2 Структура искусственного нейрона
нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента. Математическая модель нейрона:

где  - вес (weight) синапса,
- вес (weight) синапса,  — значение смещения (bias), s - результат суммирования (sum); х - компонент входного вектора (входной сигнал),
— значение смещения (bias), s - результат суммирования (sum); х - компонент входного вектора (входной сигнал),  выходной сигнал нейрона;
выходной сигнал нейрона;  - число входов нейрона;
- число входов нейрона;  - нелинейное преобразование (функция активации).
- нелинейное преобразование (функция активации).
В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения, а во многих практических задачах - лишь некоторые фиксированные значения. Выход  определяется видом функции активации и может быть как действительным, так и целым.
определяется видом функции активации и может быть как действительным, так и целым.
Синаптические связи с положительными весами называют возбуждающими, с отрицательными весами - тормозящими.
Описанный вычислительный элемент можно считать упрощенной математической моделью биологических нейронов. Чтобы подчеркнуть различие нейронов биологических и искусственных, вторые иногда называют нейроноподобными элементами или формальными нейронами.
На входной сигнал  нелинейный преобразователь отвечает выходным сигналом
нелинейный преобразователь отвечает выходным сигналом  который представляет собой выход у
который представляет собой выход у
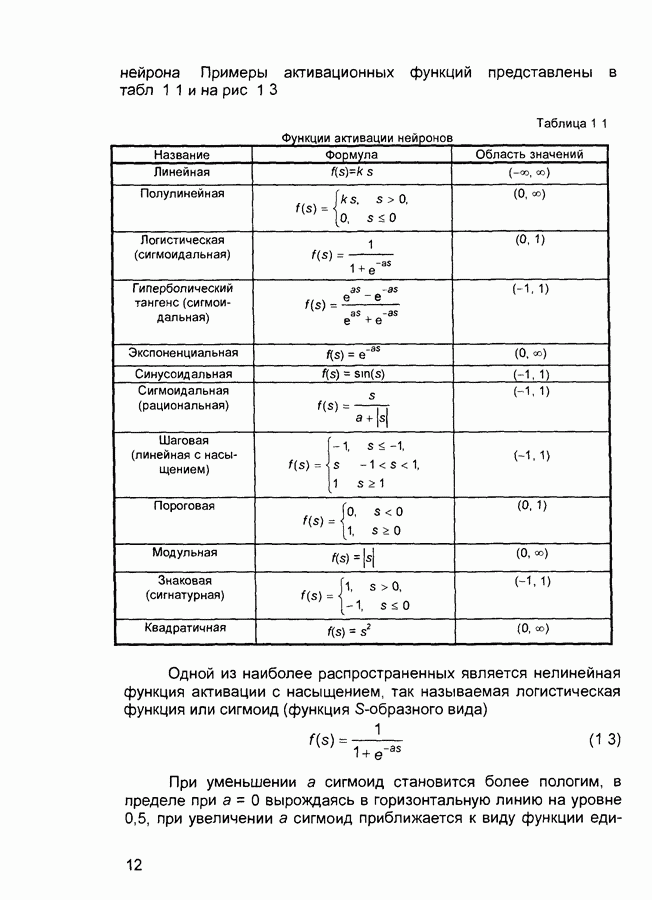
нейрона Примеры активационных функций представлены в табл. 1.1 и на рис. 1.3
Таблица 1.1 (см. скан) Функции активации нейронов
Одной из наиболее распространенных является нелинейная функция активации с насыщением, так называемая логистическая функция или сигмоид (функция S-образного вида)

При уменьшении а сигмоид становится более пологим, в пределе при  вырождаясь в горизонтальную линию на уровне 0,5, при увеличении а сигмоид приближается к виду функции
вырождаясь в горизонтальную линию на уровне 0,5, при увеличении а сигмоид приближается к виду функции

Рис. 1.3 Примеры активационных функций а - функция единичного скачка, б - линейный порог (гистерезис), в - сигмоид (логистическая функция), г - сигмоид (гиперболический тангенс)
единичного скачка с порогом  Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне
Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне  Одно из ценных свойств сигмоидальной функции - простое выражение для ее производной, применение которой будет рассмотрено в дальнейшем
Одно из ценных свойств сигмоидальной функции - простое выражение для ее производной, применение которой будет рассмотрено в дальнейшем

Следует отметить, что сигмоидальная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения Кроме того, она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
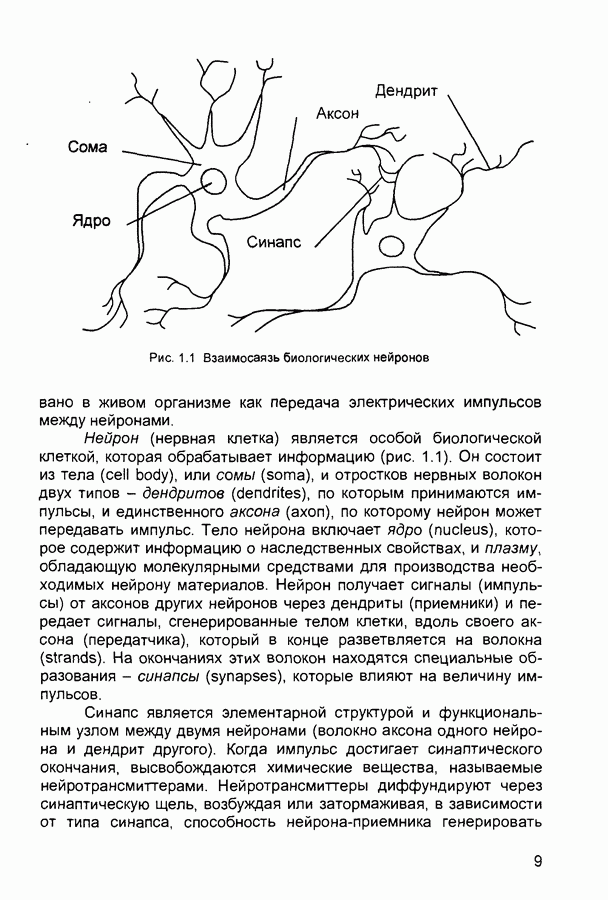
- 1.1. Биологический нейрон
- 1.2. Структура и свойства искусственного нейрона
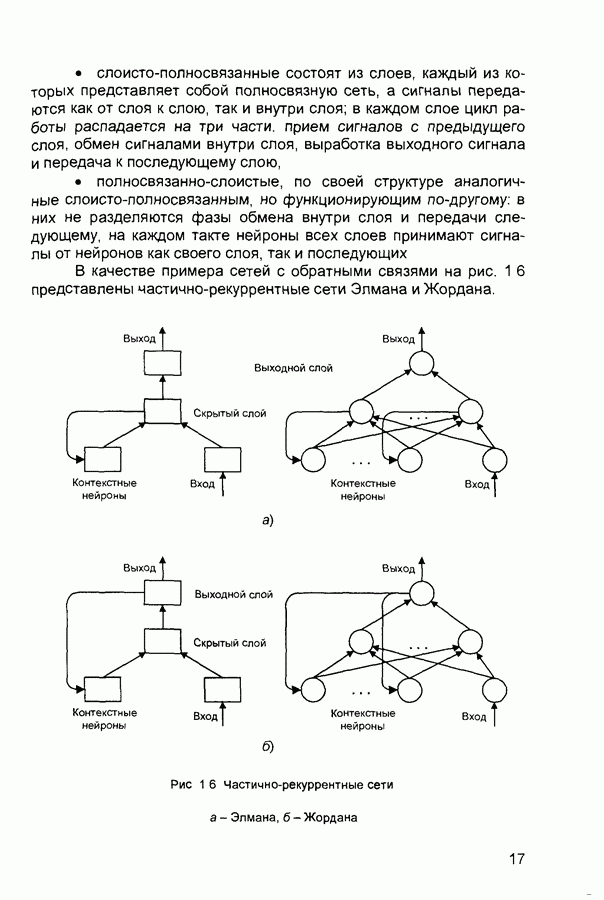
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
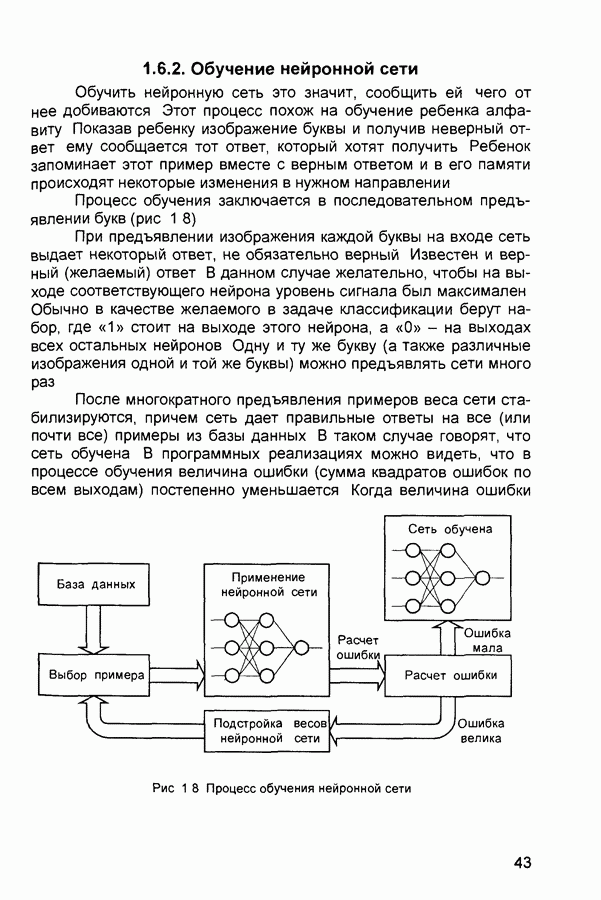
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
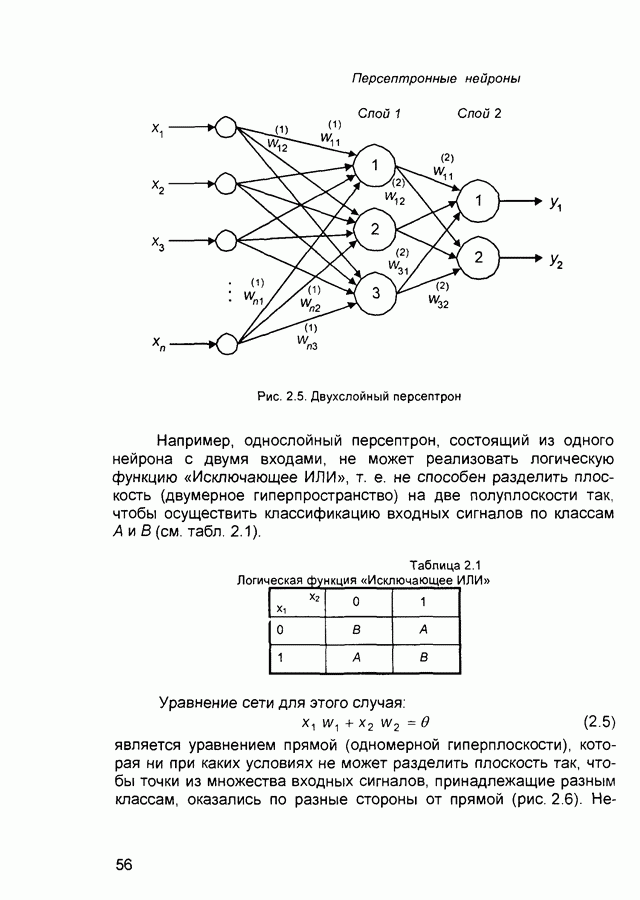
- 2.2. Персептроны
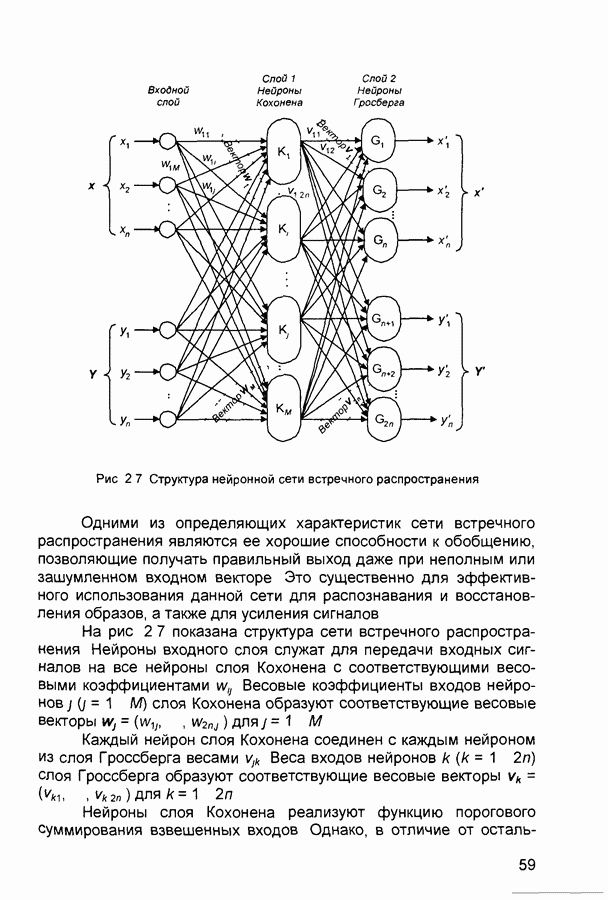
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
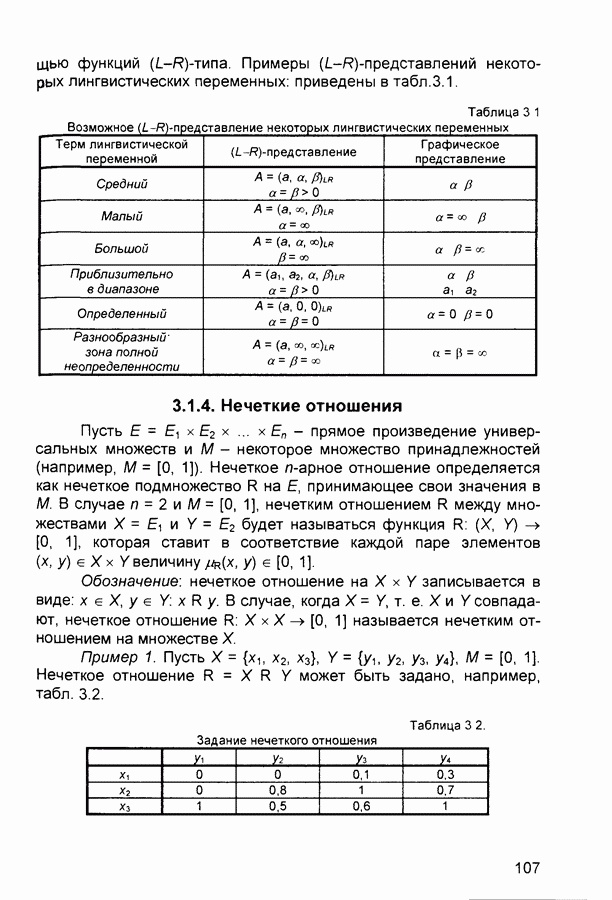
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
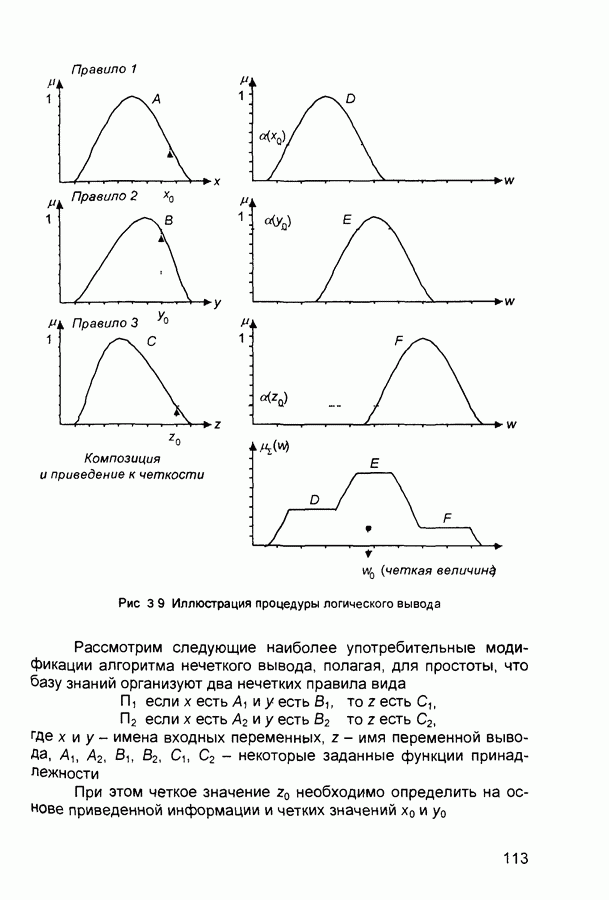
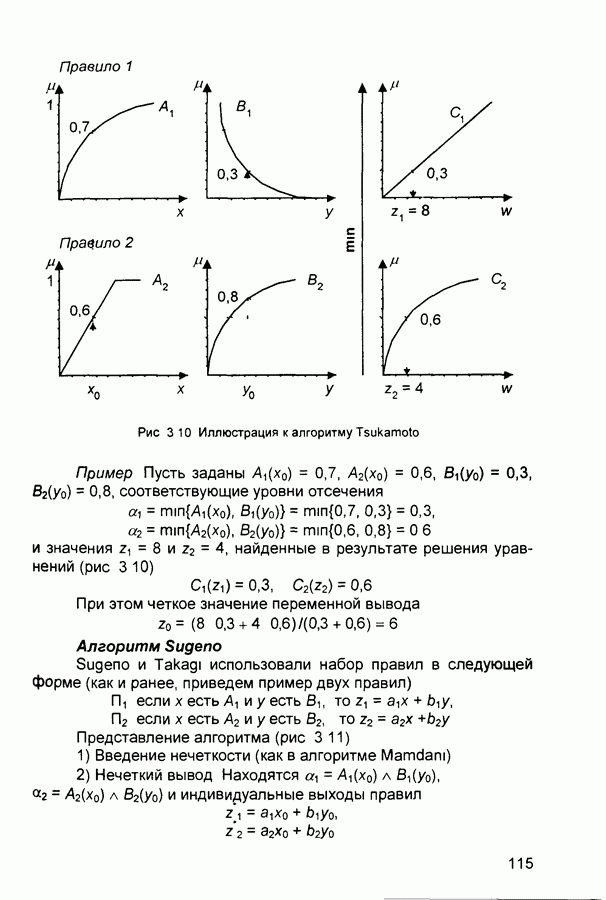
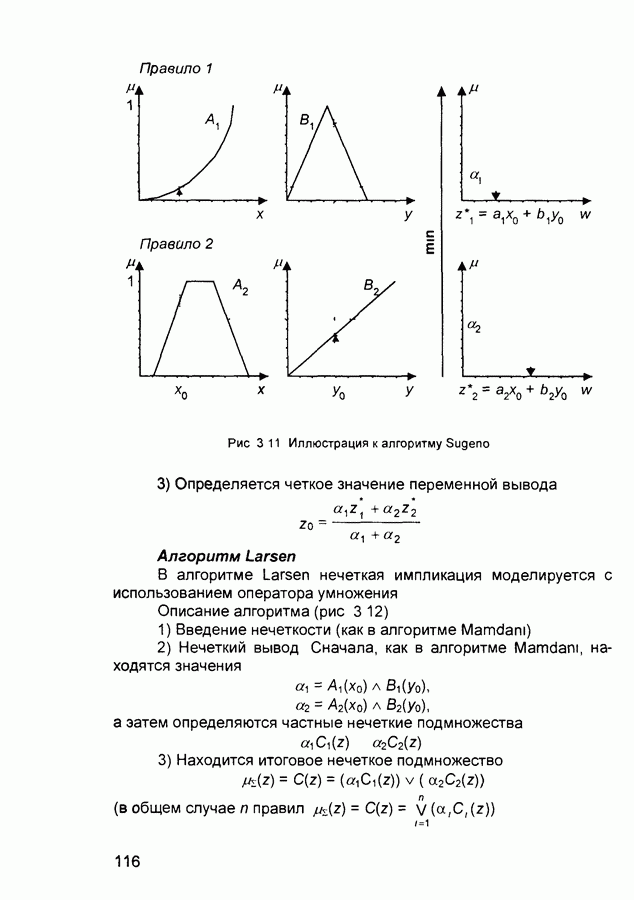
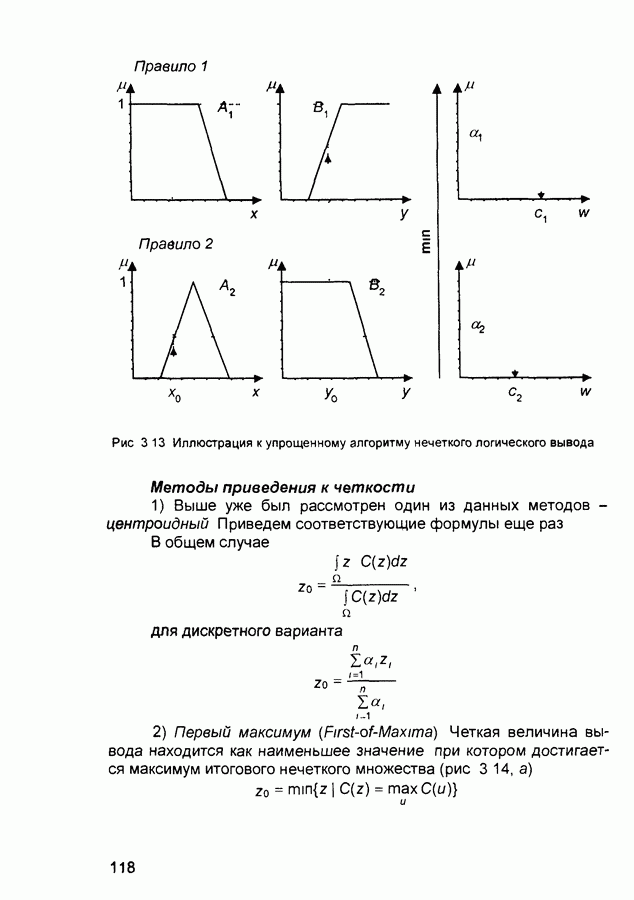
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
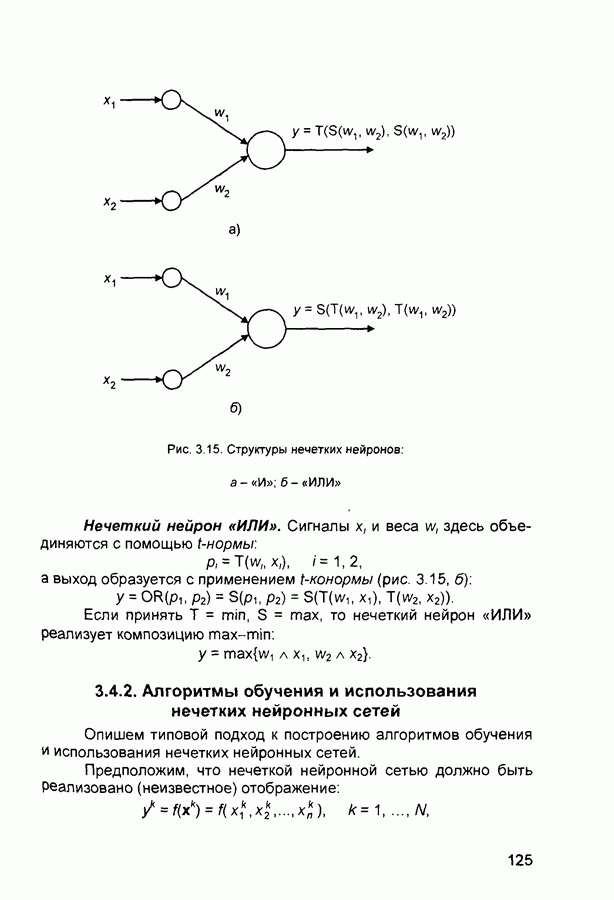
- 3.4. Синтез нечетких нейронных сетей
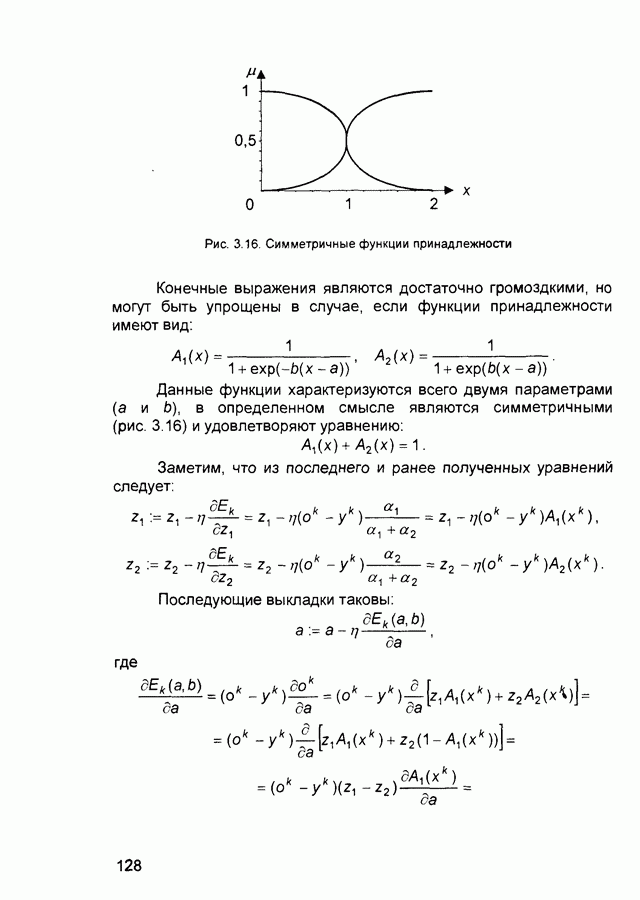
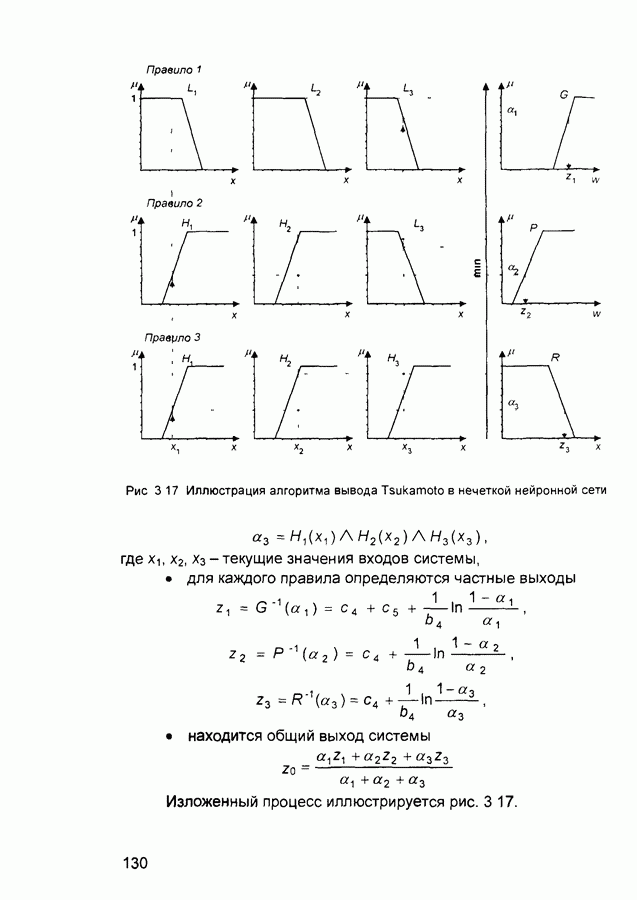
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
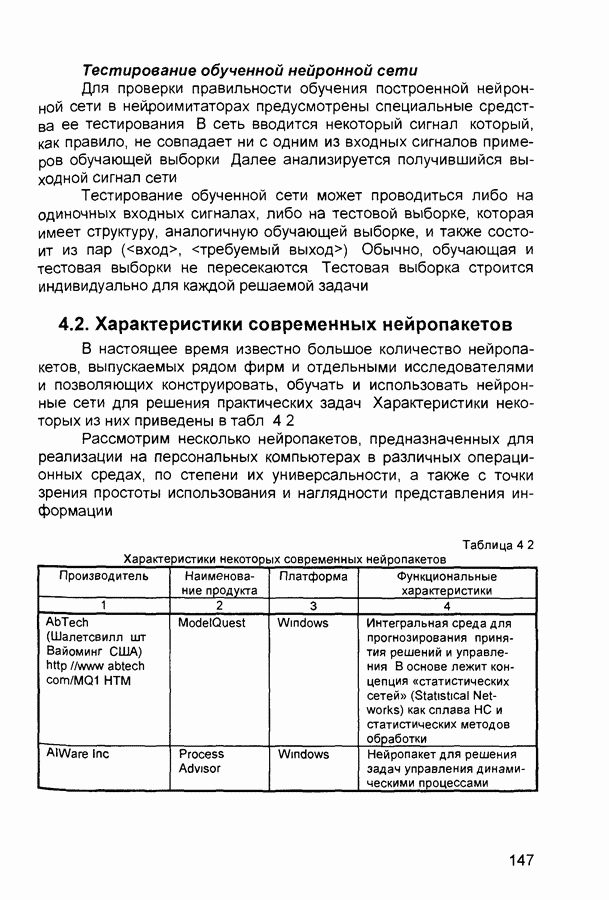
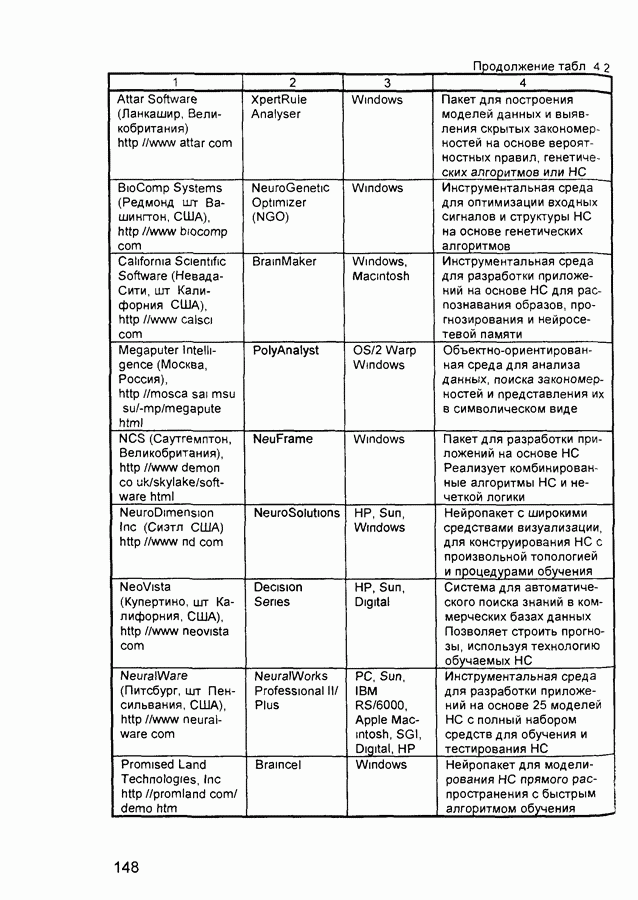
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
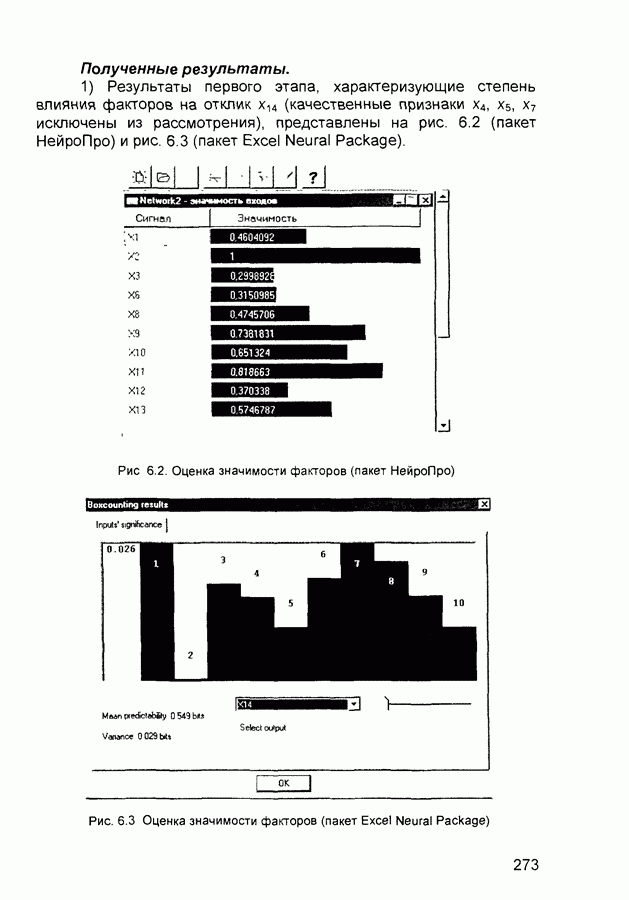
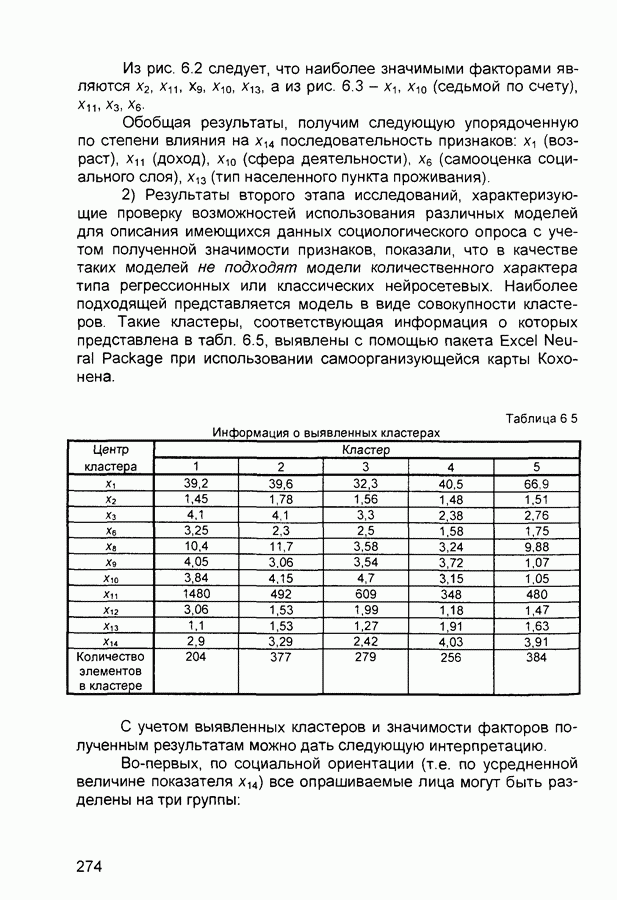
- 6.2. Анализ данных социологического опроса
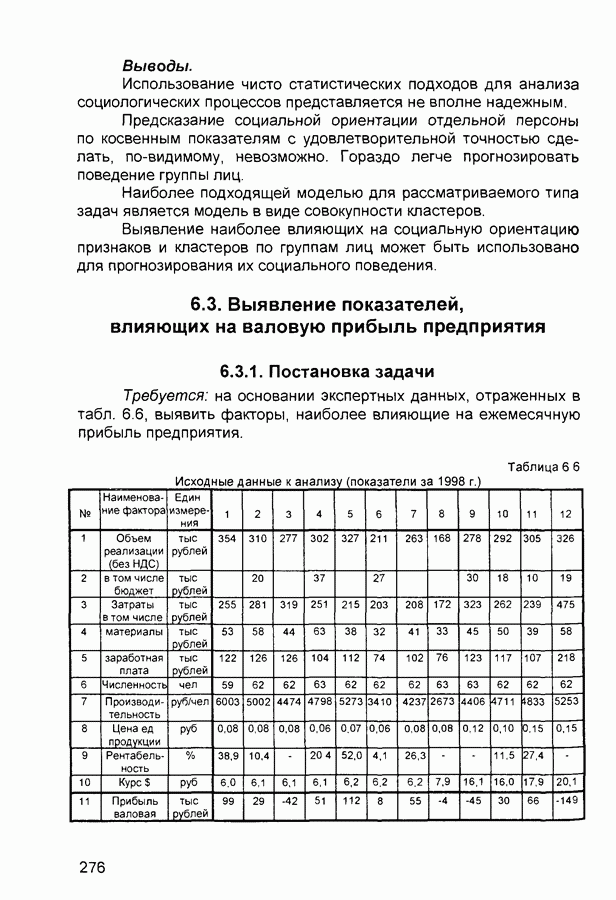
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
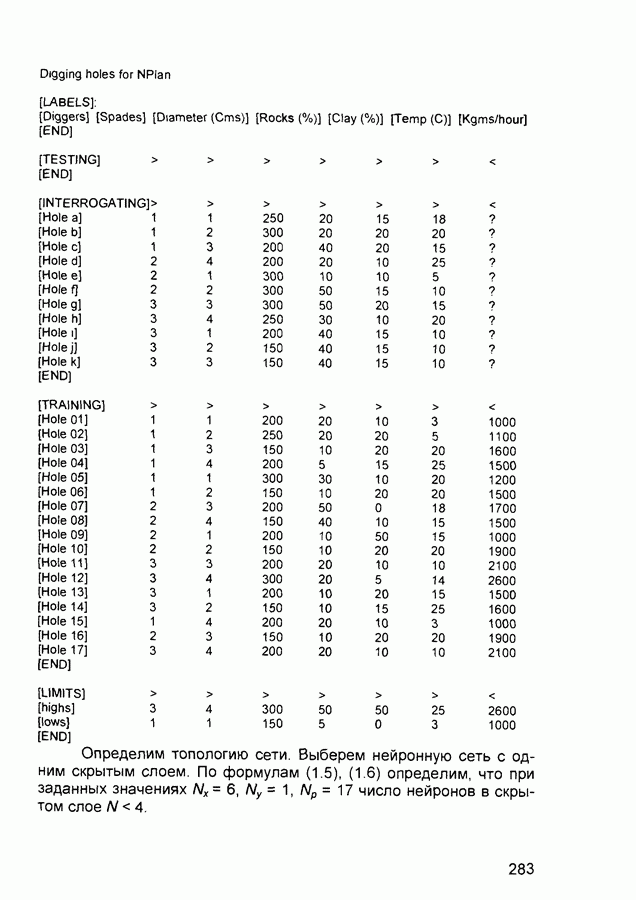
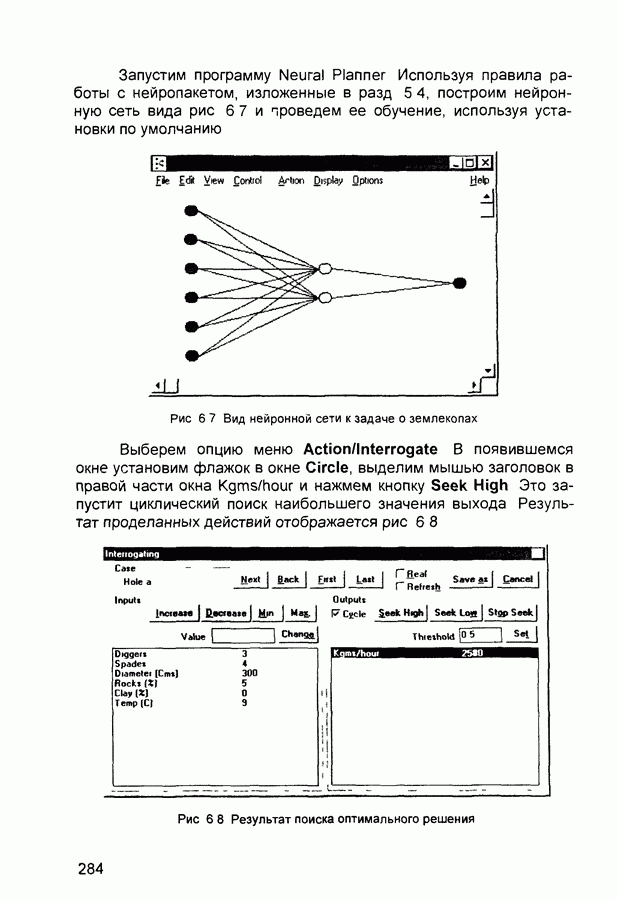
- 6.5. Задача о землекопах
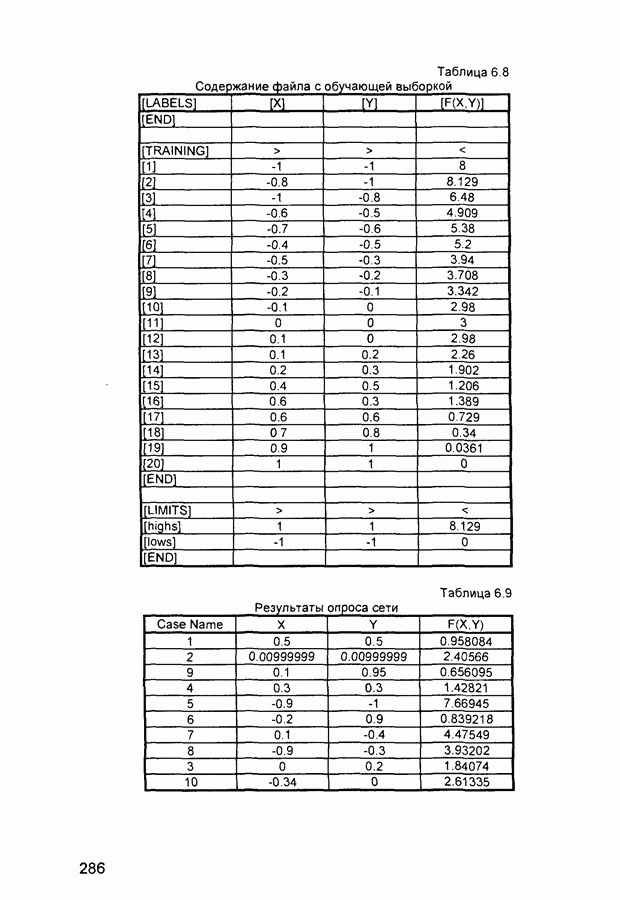
- 6.6. Аппроксимация функции
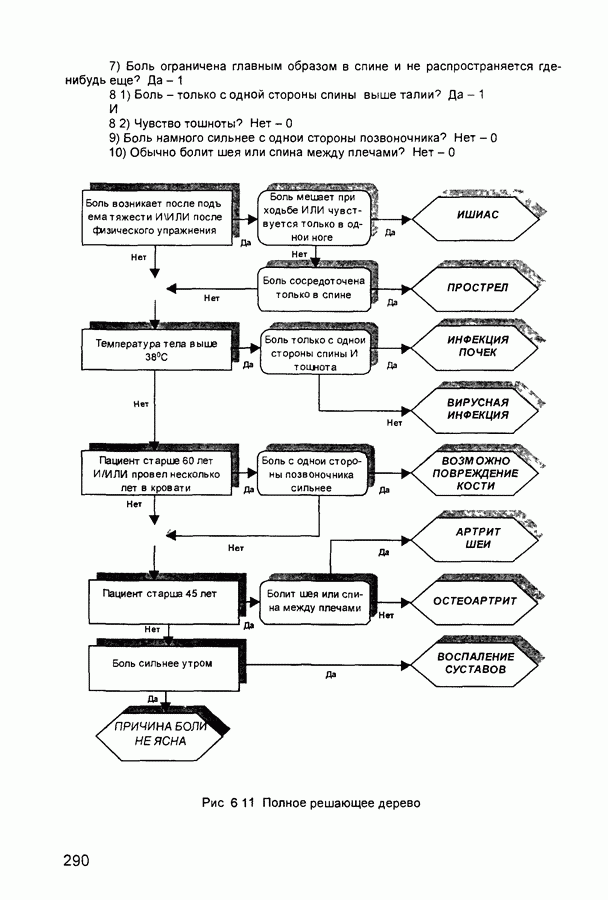
- 6.7. Нейросетевая экспертная система
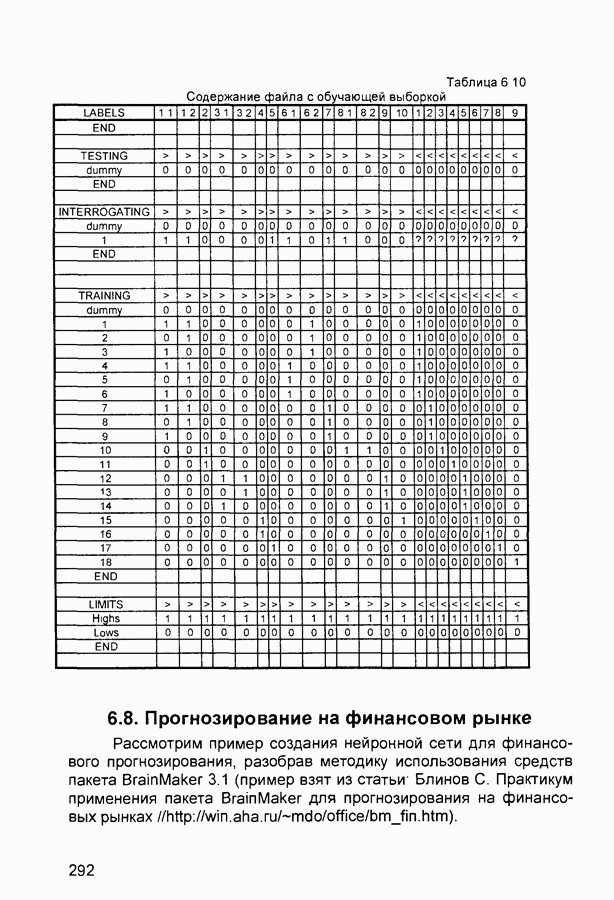
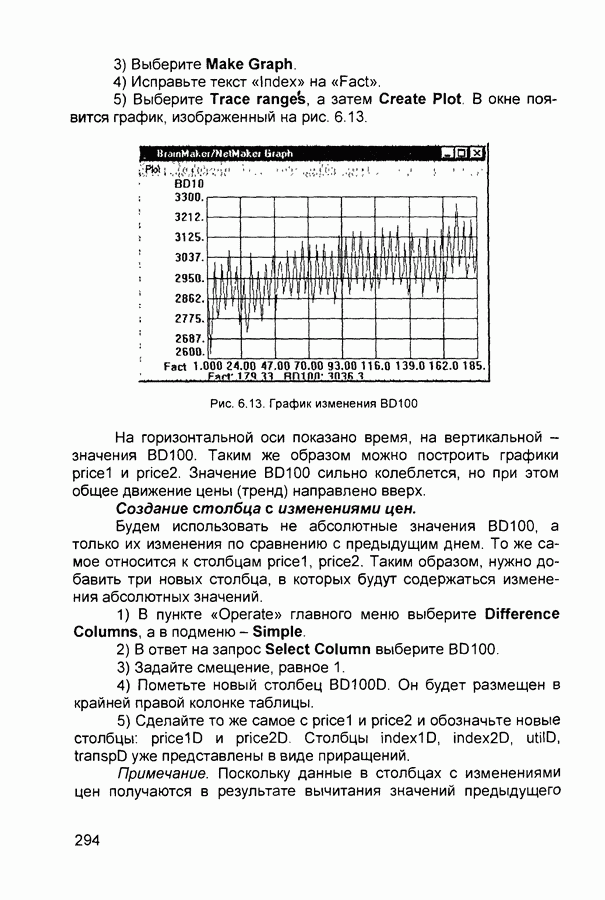
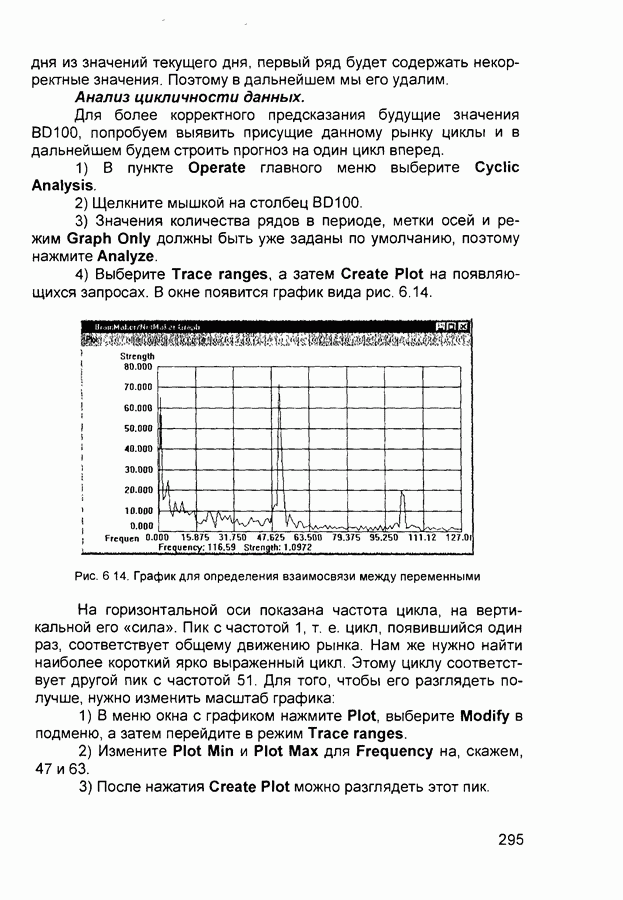
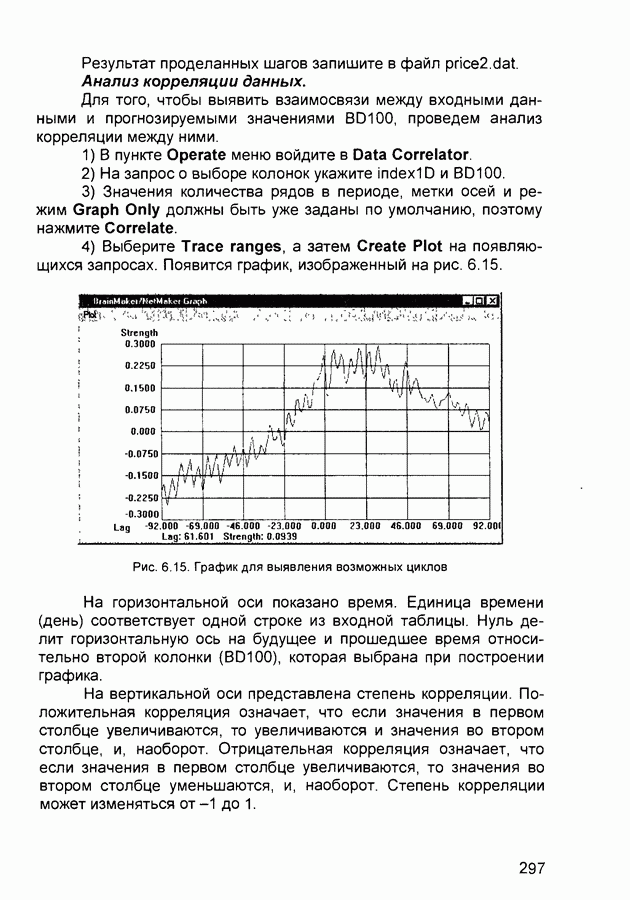
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
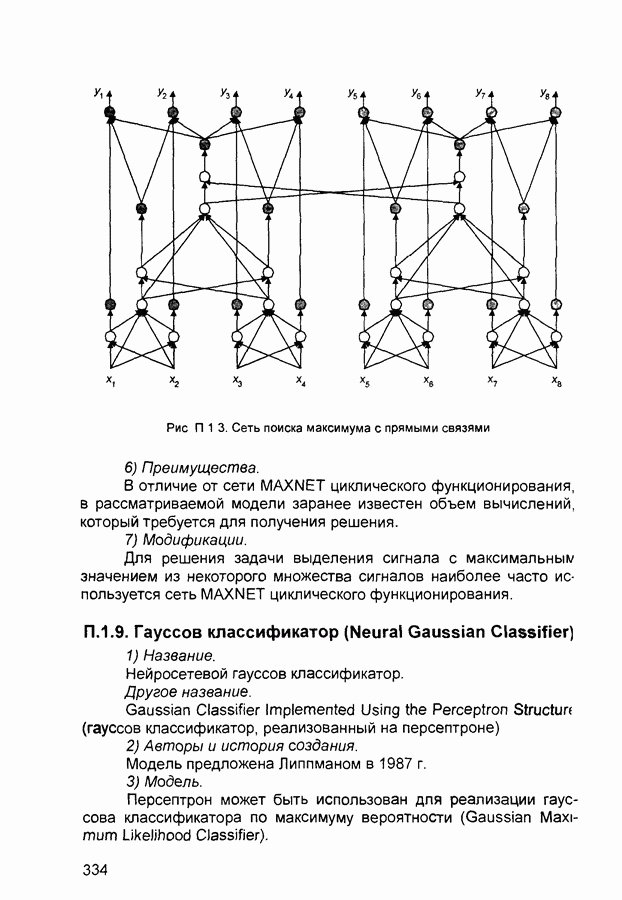
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы