| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. Оптимизирующие нейронные сети
2.4.1. Нейронные сети Хопфилда
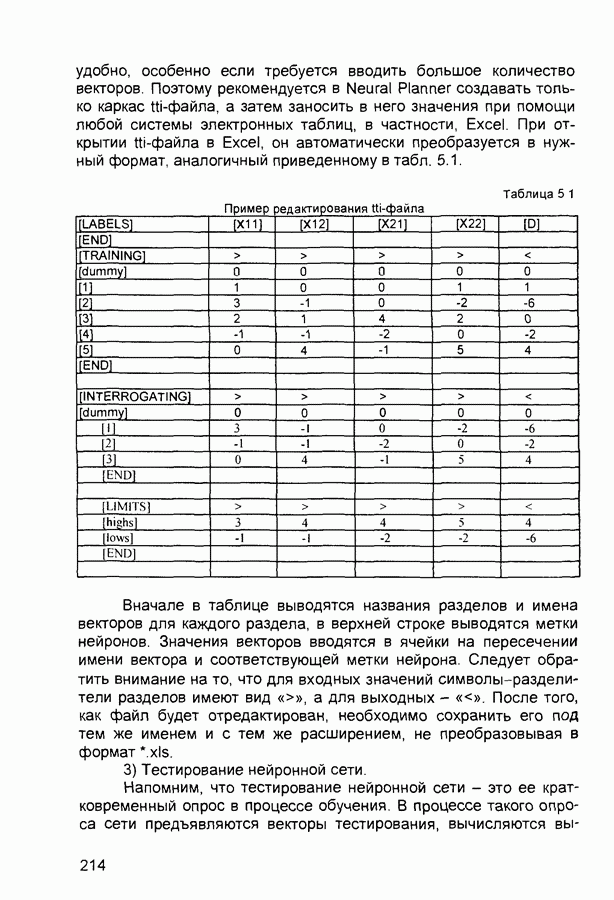
Нейронная сеть Хопфилда реализует существенное свойство автоассоциативной памяти - восстановление по искаженному (зашумленному) образу ближайшего к нему эталонного В этом случае входной вектор используется как начальное состояние сети, и далее сеть эволюционирует согласно своей динамике Причем любой пример, находящийся в области притяжения хранимого образца, может быть использован как указатель для его восстановления Выходной (восстановленный) образец устанавливается, когда сеть достигает равновесия
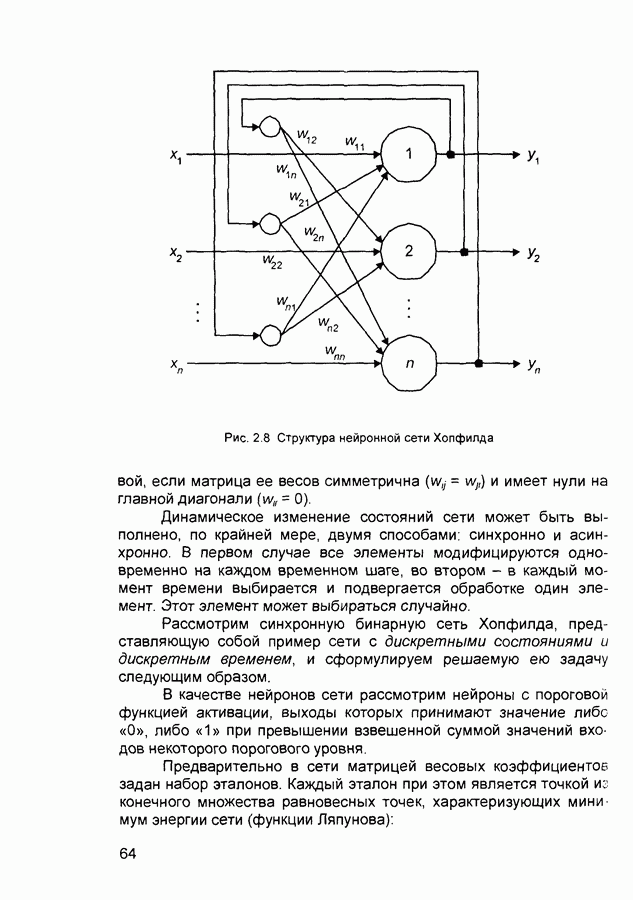
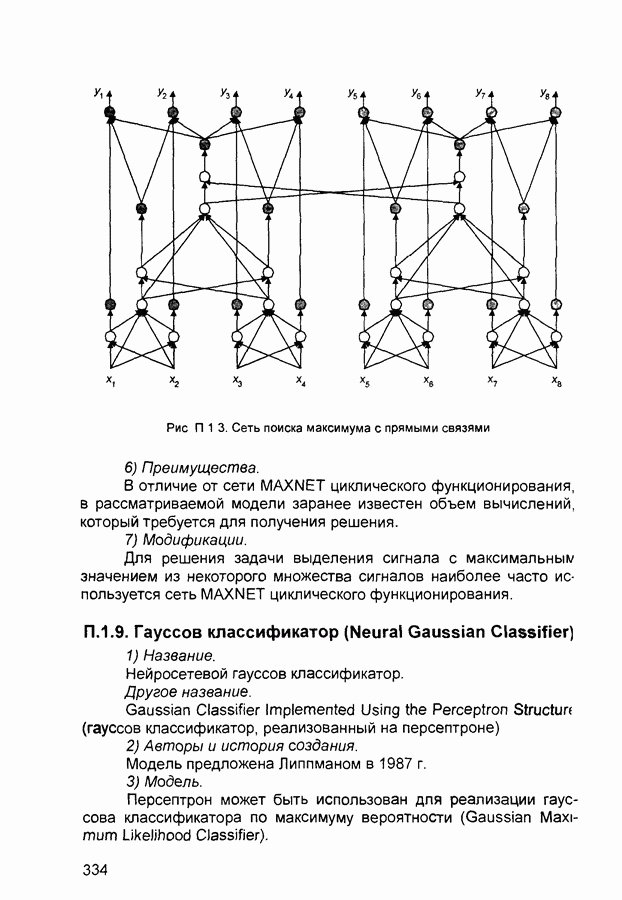
Структура сети Хопфилда приведена на рис 2 8 Она состоит из одного слоя нейронов, число которых определяет число входов и выходов сети Выход каждого нейрона соединен с входами всех остальных нейронов Подача входных векторов осуществляется через отдельные входы нейронов
Сети Хопфилда отличаются от ранее рассмотренных типов нейронных сетей следующими существенными признаками
• наличие обратных связей, идущих с выходов сетей на их входы по принципу «со всех на все»,
• расчет весовых коэффициентов нейронов проводится на основе исходной информации лишь перед началом функционирования сети, и все обучение сети сводится именно к этому расчету без обучающих итераций,
• при предъявлении входного вектора, сеть «сходится» к одному из запомненных в сети эталонов, представляющих множество равновесных точек, которые являются локальными минимумами функции энергии, содержащей в себе всю структуру взаимосвязей в сети
Проблема устойчивости сети Хопфилда была решена после того, как Кохеном и Гроссбергом была доказана теорема, определяющая достаточное условие устойчивости сетей с обратными связями, а именно, сеть с обратными связями является

Рис. 2.8 Структура нейронной сети Хопфилда
устойчивой, если матрица ее весов симметрична  и имеет нули на главной диагонали
и имеет нули на главной диагонали 
Динамическое изменение состояний сети может быть выполнено, по крайней мере, двумя способами: синхронно и асинхронно. В первом случае все элементы модифицируются одновременно на каждом временном шаге, во втором - в каждый момент времени выбирается и подвергается обработке один элемент. Этот элемент может выбираться случайно.
Рассмотрим синхронную бинарную сеть Хопфилда, представляющую собой пример сети с дискретными состояниями и дискретным временем, и сформулируем решаемую ею задачу следующим образом.
В качестве нейронов сети рассмотрим нейроны с пороговой функцией активации, выходы которых принимают значение либс «0», либо «1» при превышении взвешенной суммой значений входов некоторого порогового уровня.
Предварительно в сети матрицей весовых коэффициентов задан набор эталонов. Каждый эталон при этом является точкой из конечного множества равновесных точек, характеризующих минимум энергии сети (функции Ляпунова):

где Е - искусственная энергия сети;  - вес от выхода
- вес от выхода  ко входу
ко входу  нейрона;
нейрона;  - вход и выход
- вход и выход  нейрона;
нейрона;  - порог
- порог  нейрона.
нейрона.
Главное свойство энергетической функции состоит в том, что в процессе эволюции состояний нейронной сети согласно уравнению она уменьшается и достигает локального минимума (аттрактора), в котором сохраняет постоянную энергию. Это позволяет решать задачи комбинаторной оптимизации, если они могут быть сформулированы как задачи минимизации энергии.
Обозначим вектор, описывающий  эталон, через
эталон, через  , К - число эталонов.
, К - число эталонов.
На вход сети подается произвольный вектор 
В результате серии итераций сеть должна выделить эталон, соответствующий входному вектору, или дать заключение о том, что входные данные не соответствуют ни одному из эталонов.
После отдельной итерации общее изменение энергии сети, вызванное изменением состояний всех нейронов, составит:

где  - изменение выхода
- изменение выхода  нейрона после итерации.
нейрона после итерации.
Анализ этого выражения показывает, что любое изменение состояния нейронов либо уменьшит значение Е, либо оставит его без изменения. Второй случай указывает на достижение сетью устойчивого состояния и выделение ею эталона, наилучшим образом сочетающимся с входным вектором.
При распознании входного вектора (частично представленного или искаженного) выходы сети будут содержать соответствующий эталон, т. е.  где
где  - выходной вектор. В противном случае, выходной вектор не совпадет ни с одним эталоном.
- выходной вектор. В противном случае, выходной вектор не совпадет ни с одним эталоном.
Для безошибочной работы сети Хопфилда число запоминаемых эталонов  не должно превышать
не должно превышать 
Кроме того, в случае высокой степени корреляции нескольких эталонов возможно возникновение перекрестных ассоциаций при их предъявлении на входах сети. Требование достаточного (но не необходимого) условия слабой коррелируемости образов можно представить как выполнение следующего неравенства:

или в виде более сильного условия:

Нейронные сети Хопфилда с непрерывными состояниями отличается от вышерассмотренной сети непрерывной активационной функцией нейронов, в качестве которой наиболее часто выбирают сигмоидальную или логистическую функцию. Концептуально вопросы организации и функционирования этих сетей схожи
Недостатком классического варианта сетей Хопфилда является их тенденция к стабилизации в локальных, а не глобальных минимумах сети. Предложены статистические сети Хопфилда в которых этот недостаток преодолевается за счет задания статистических, а не детерминистских правил изменения состояний нейронов.
Для этого для каждого  нейрона вводится вероятность изменения его состояния
нейрона вводится вероятность изменения его состояния  как функция от величины, на которую выход нейрона
как функция от величины, на которую выход нейрона  превышает его порог
превышает его порог  (для бинарной сети Хопфилда):
(для бинарной сети Хопфилда):

где  - параметр, изменяемый в процессе стабилизации сети.
- параметр, изменяемый в процессе стабилизации сети.
Тогда после начального задания весовых коэффициентов нейронов процедура поиска минимума энергии сети для установленного входного вектора выглядит следующим образом.
ШАГ 1. Задать большое значение параметра  .
.
ШАГ 2. Установить на выходе  нейрона значение «1» с вероятностью
нейрона значение «1» с вероятностью  и значение
и значение  с вероятностью
с вероятностью 
ШАГ 3. Постепенно уменьшать значение параметра  пока не будет достигнуто равновесие.
пока не будет достигнуто равновесие.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Часть I. ТЕОРИЯ
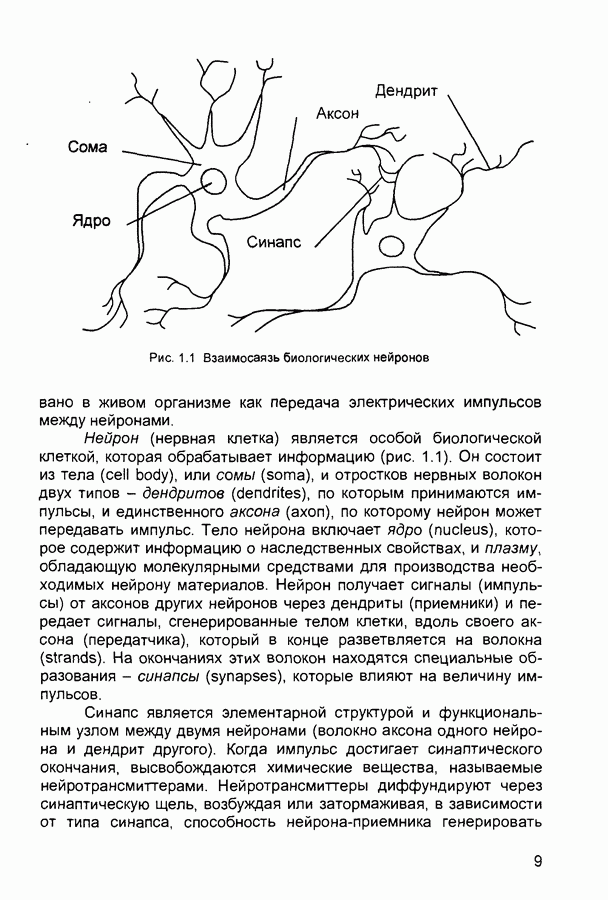
- 1.1. Биологический нейрон
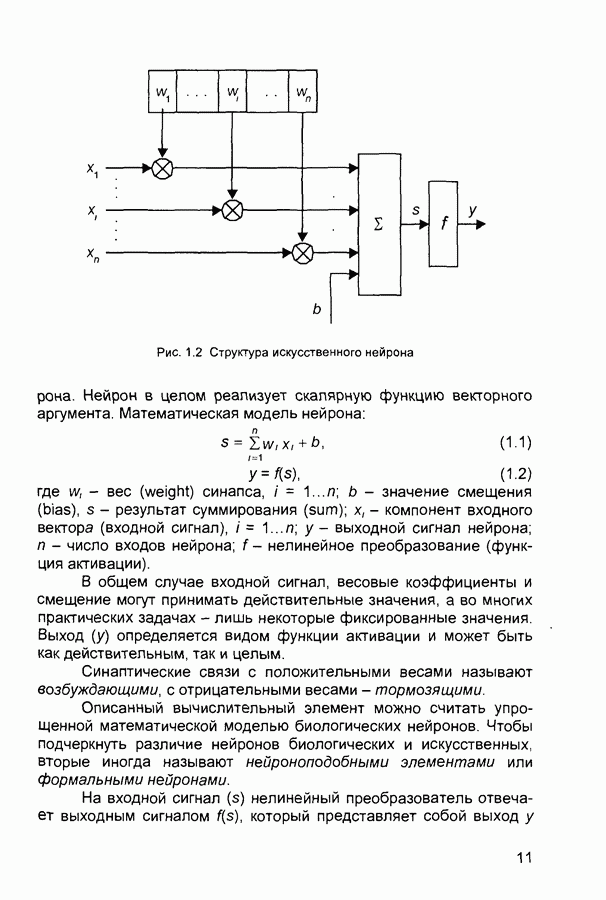
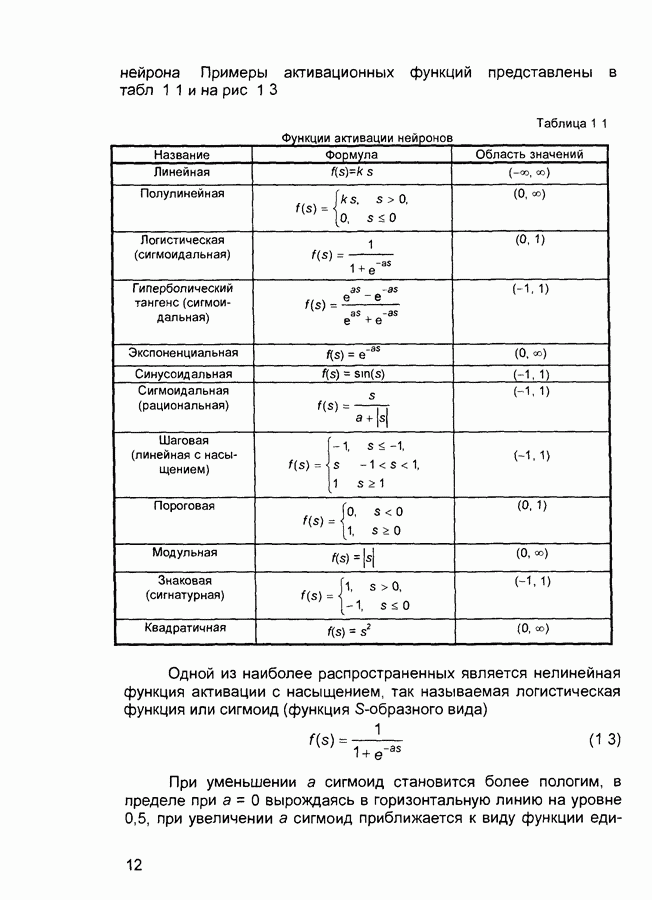
- 1.2. Структура и свойства искусственного нейрона
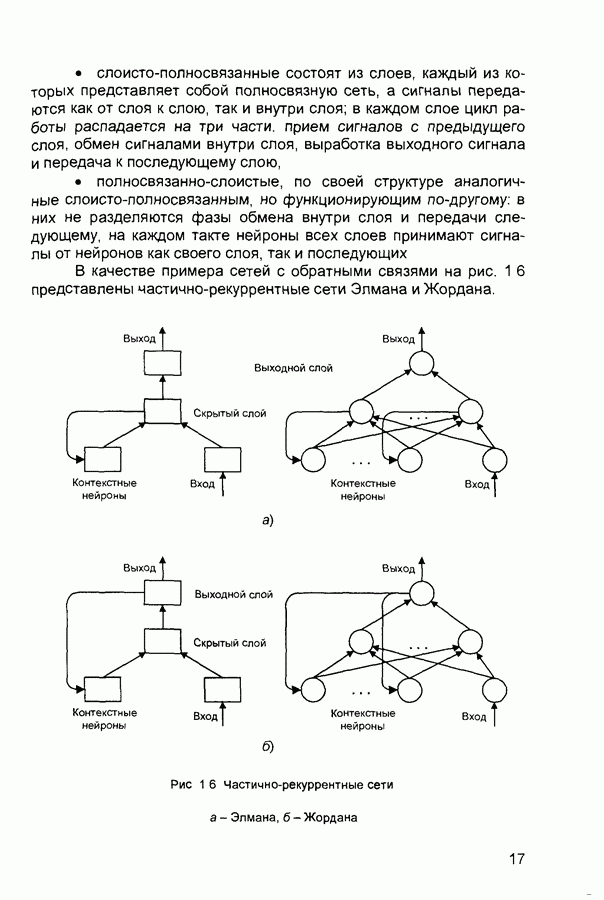
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда — Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
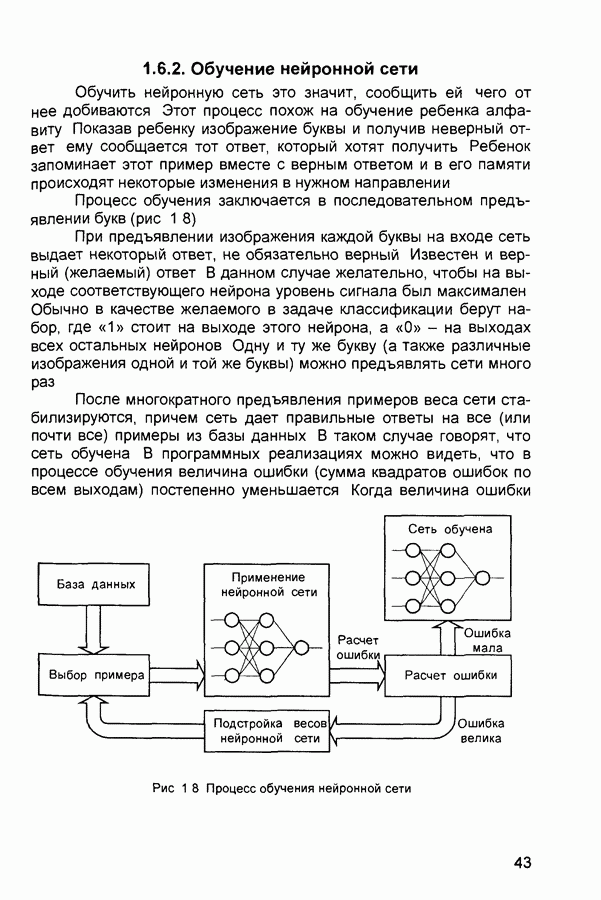
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
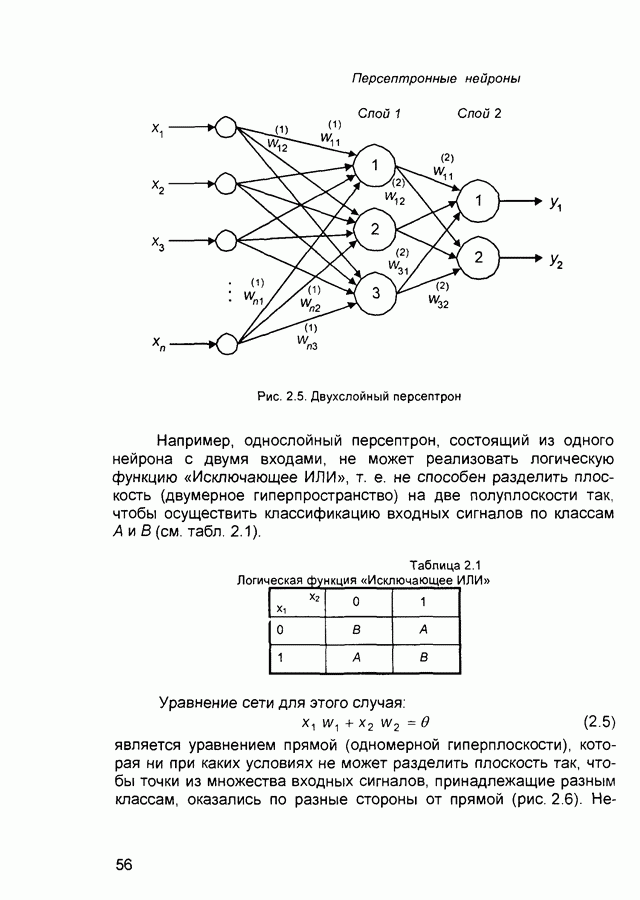
- 2.2. Персептроны
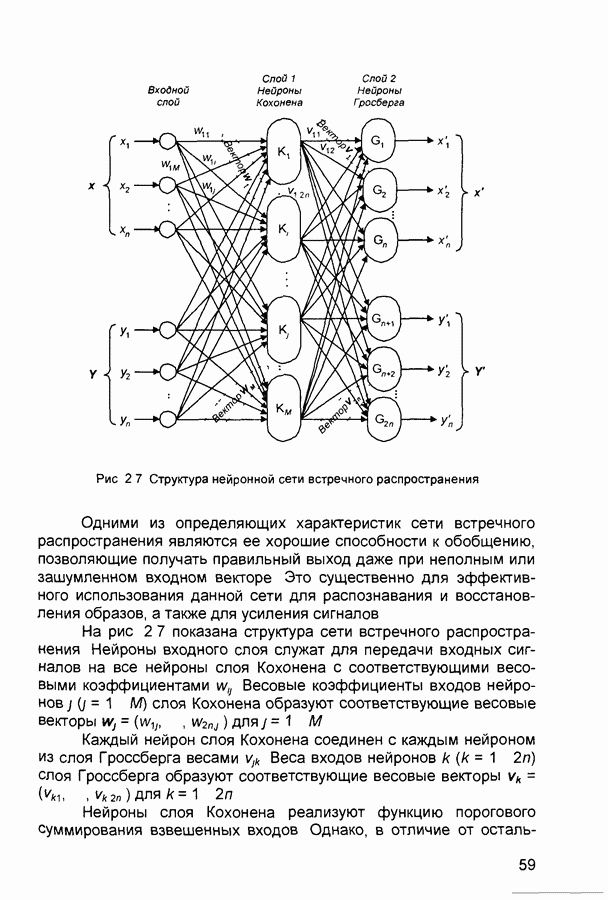
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
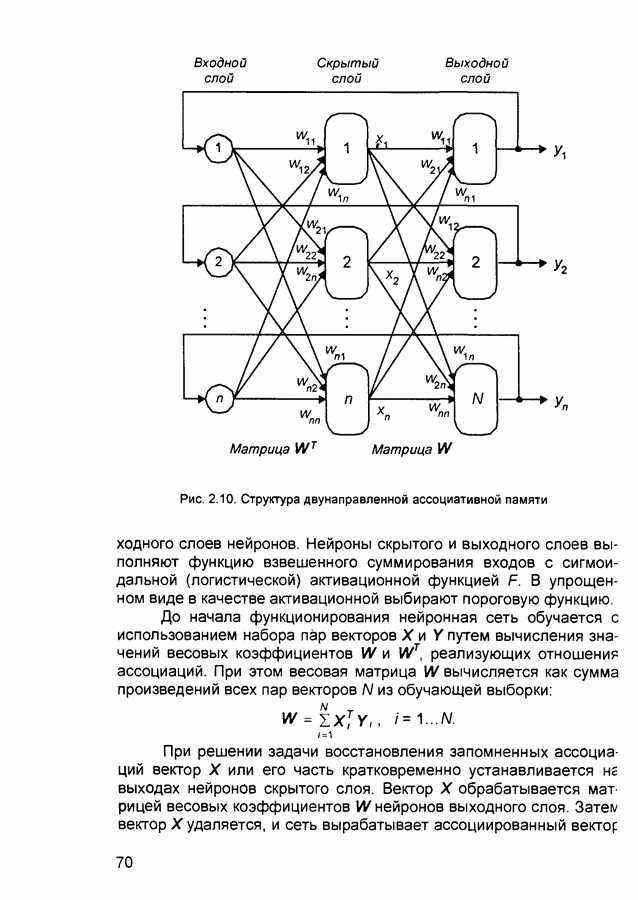
- 2.5. Двунаправленная ассоциативная память
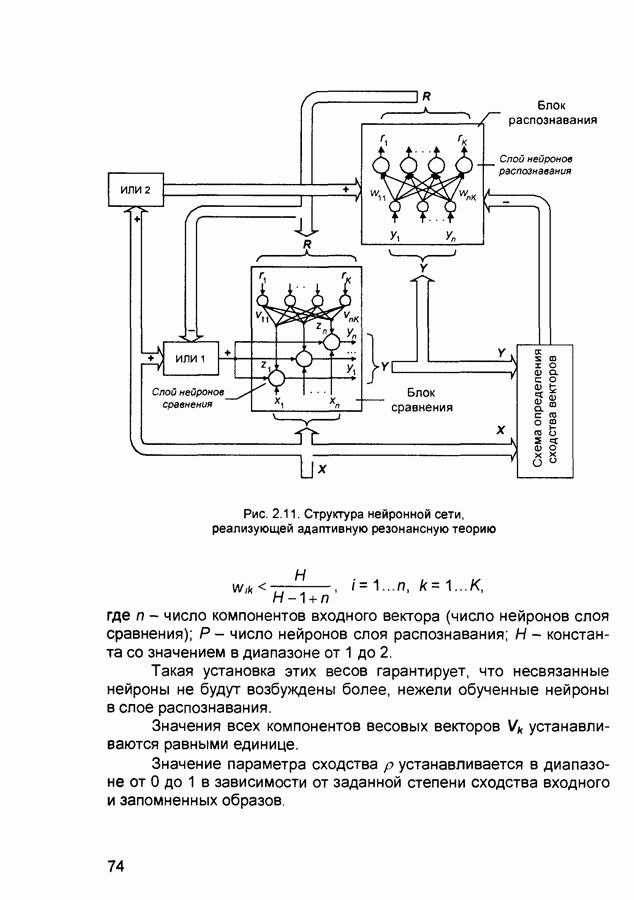
- 2.6. Сети адаптивной резонансной теории
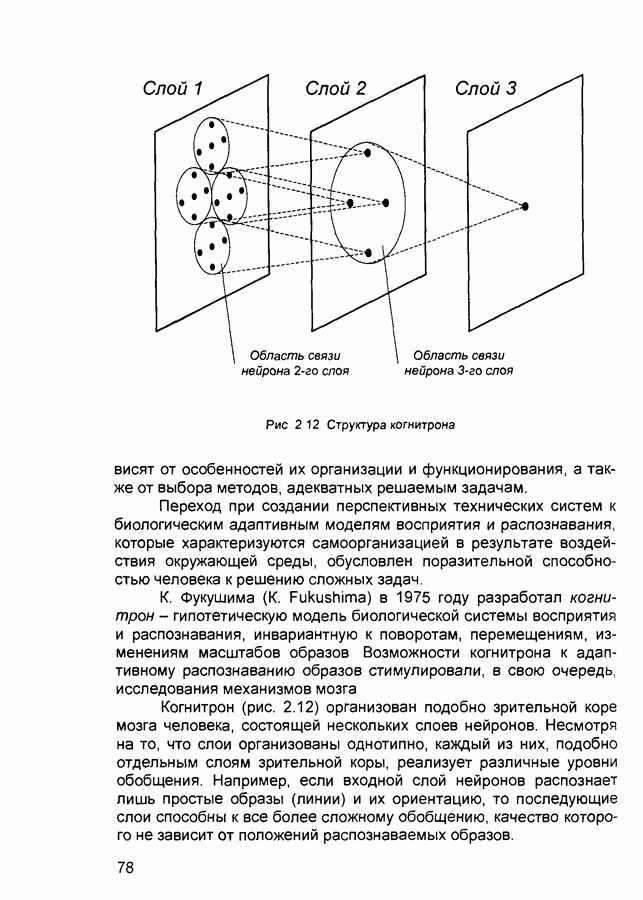
- 2.7. Когнитрон
- 2.8. Неокогнитрон
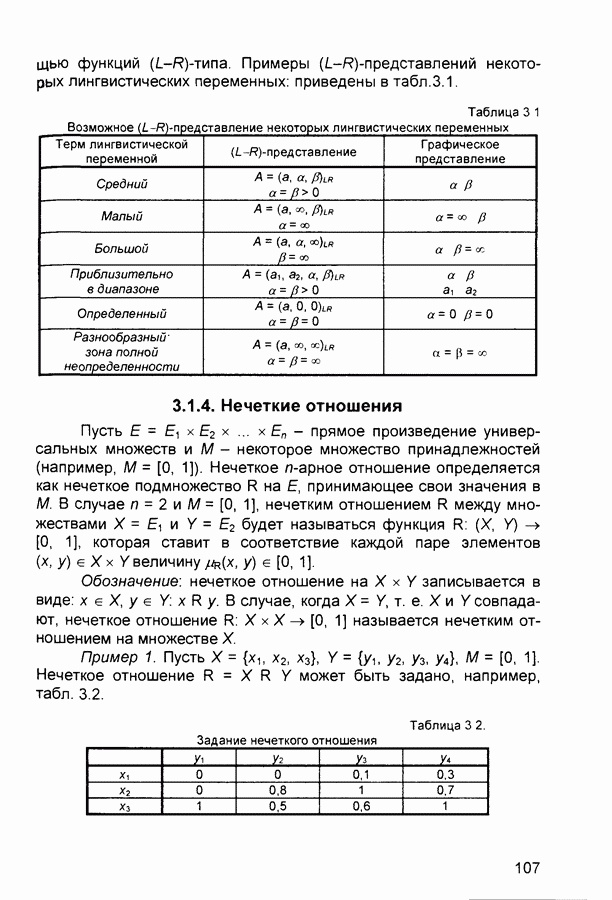
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
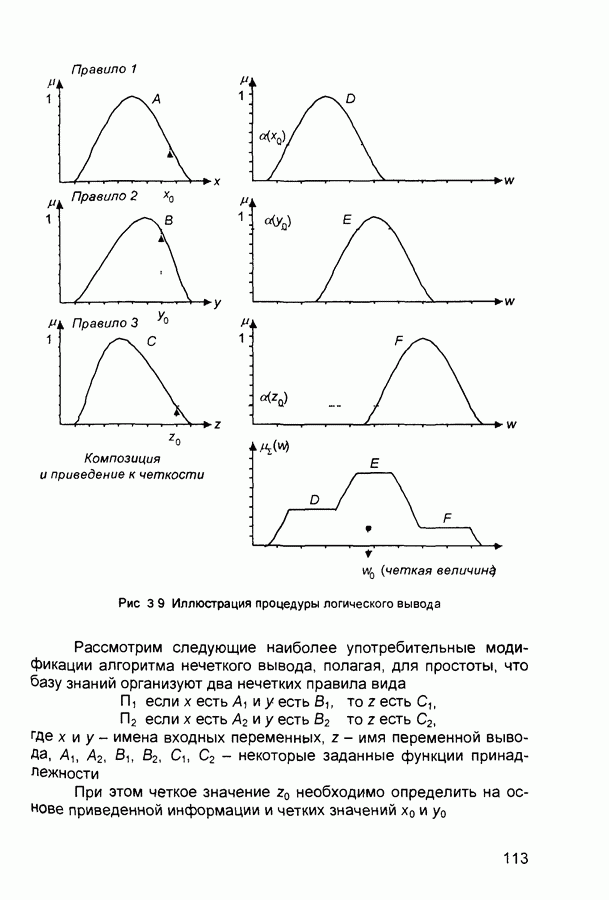
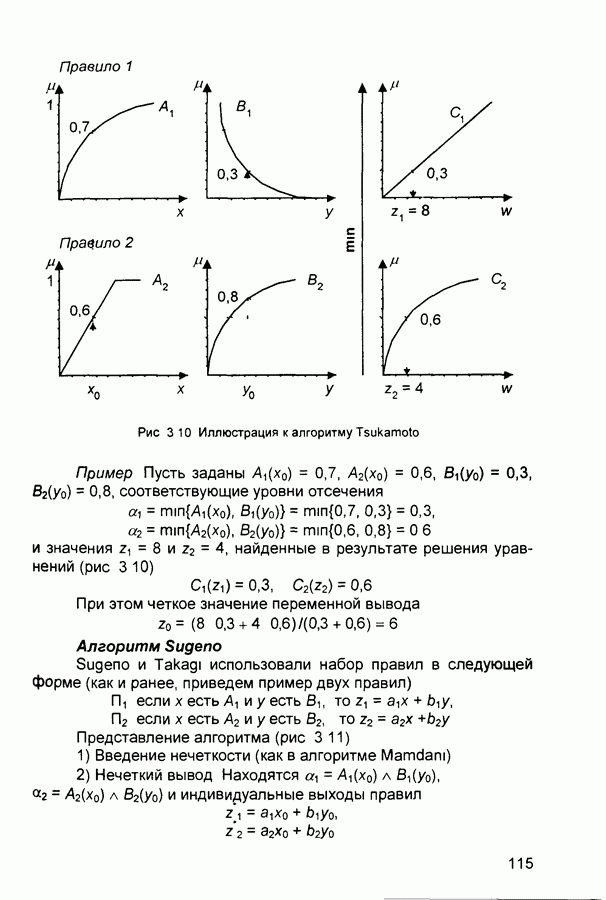
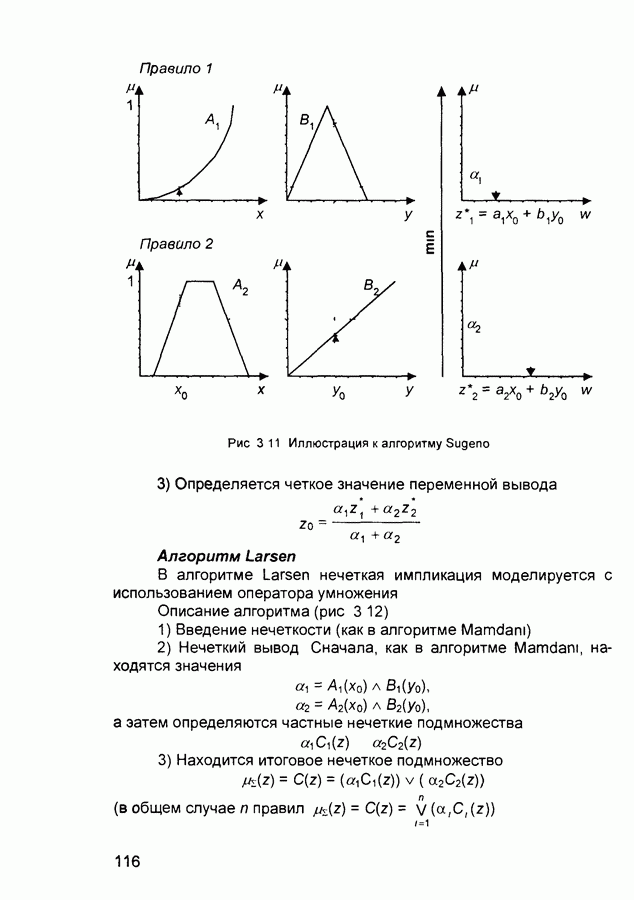
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
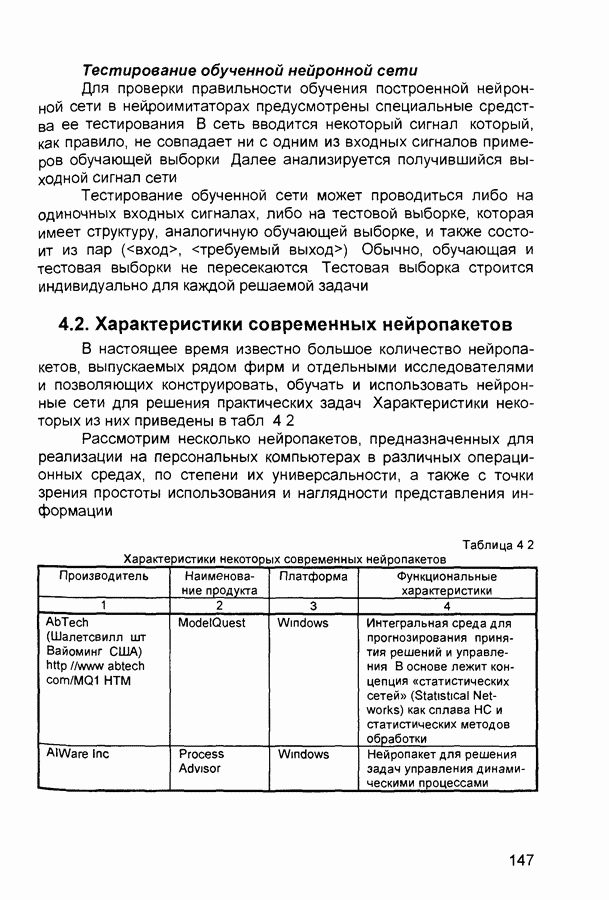
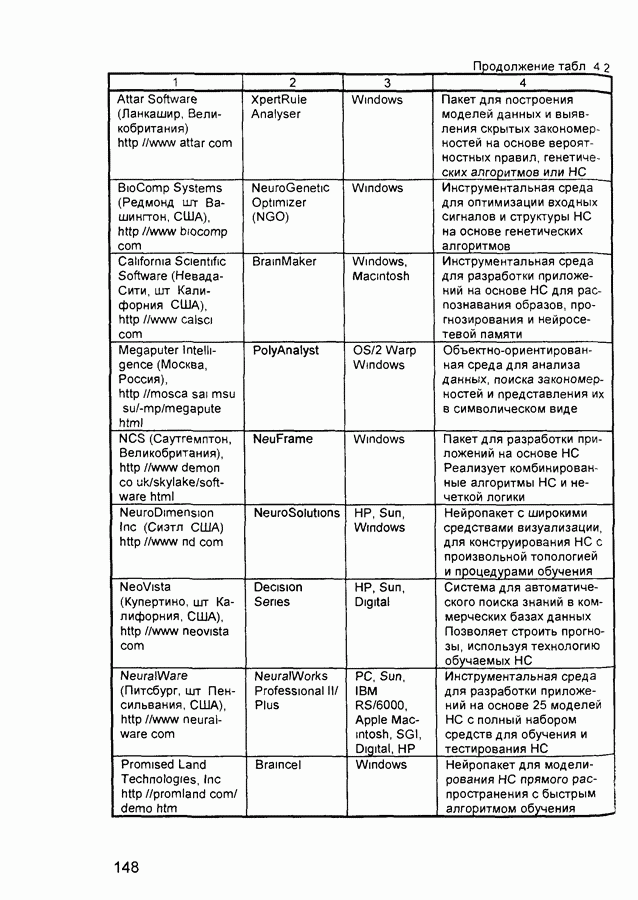
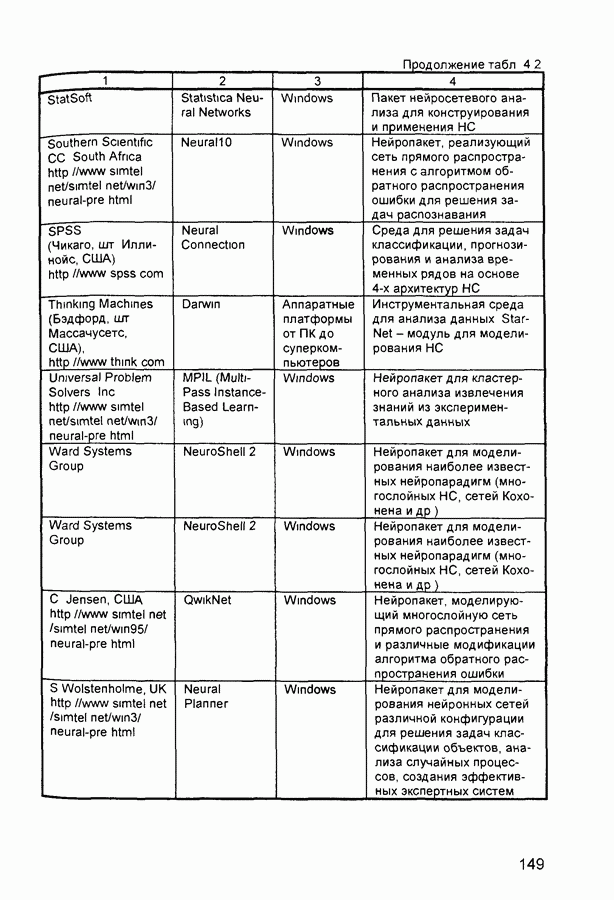
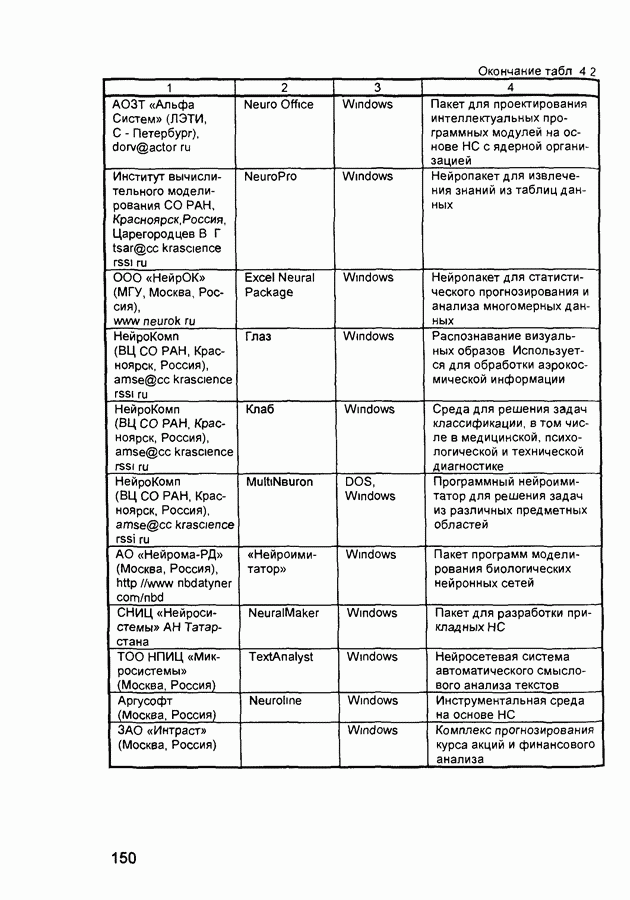
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
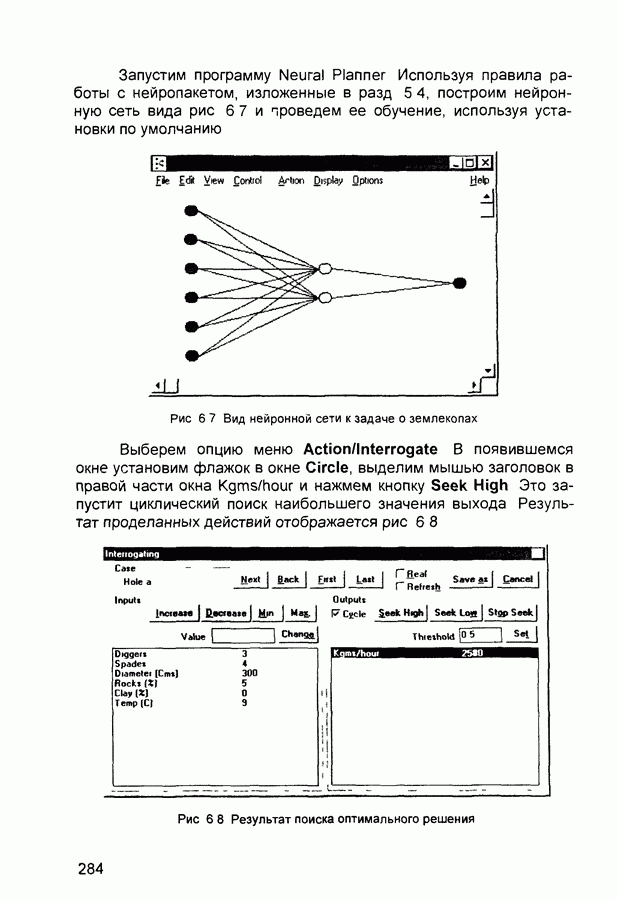
- 6.5. Задача о землекопах
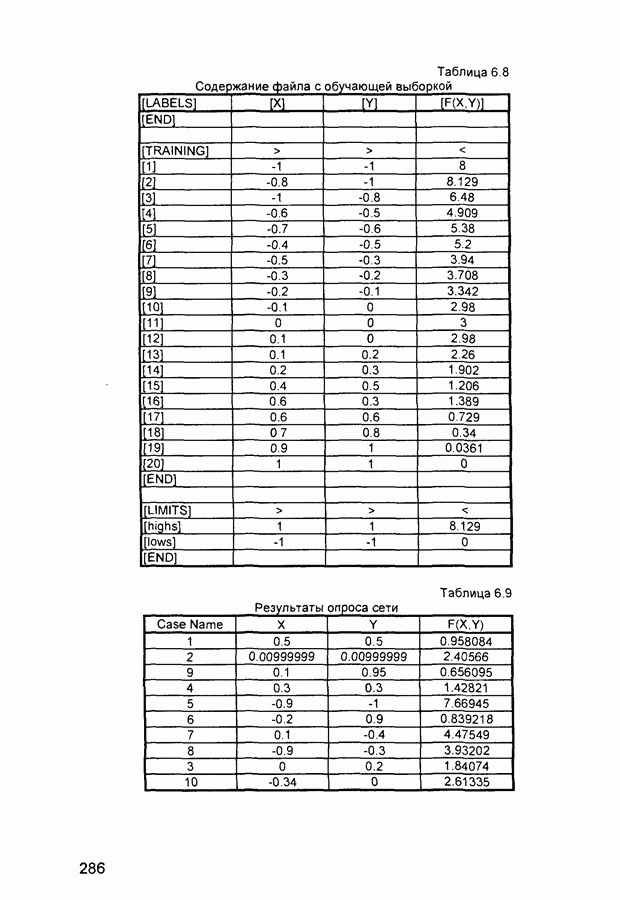
- 6.6. Аппроксимация функции
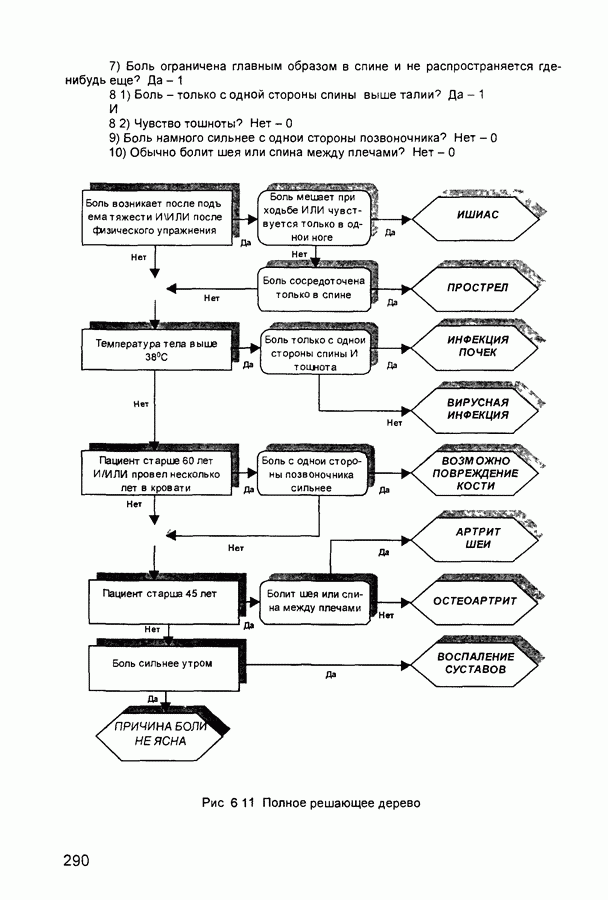
- 6.7. Нейросетевая экспертная система
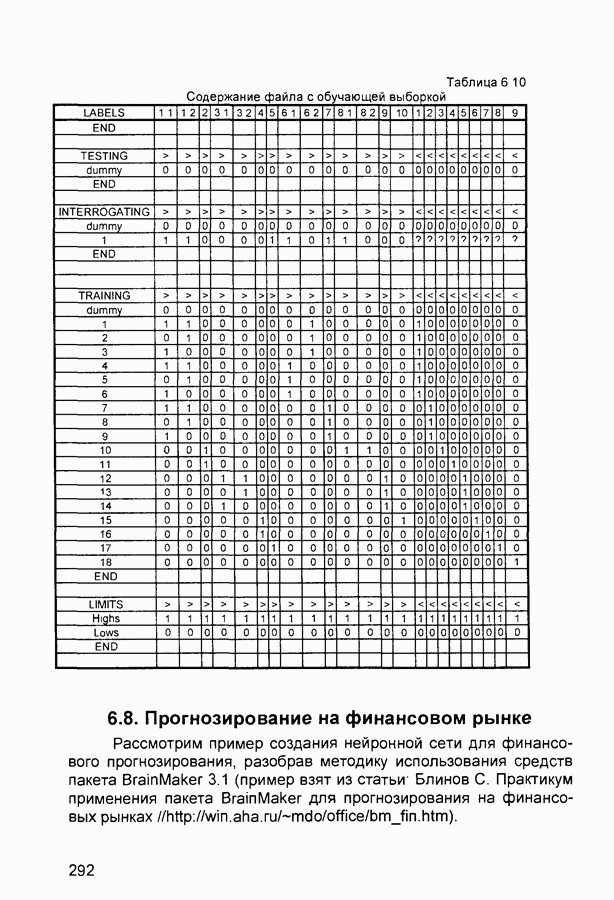
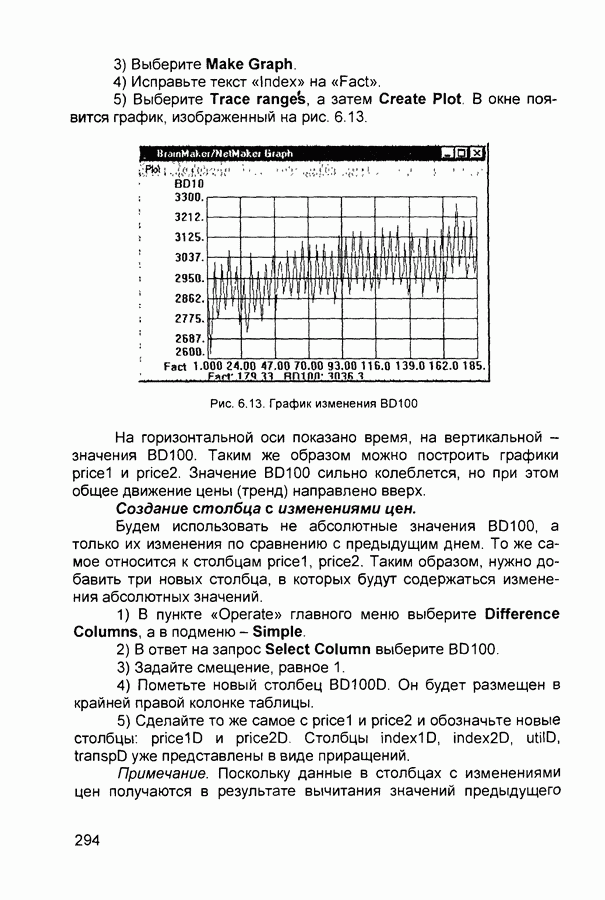
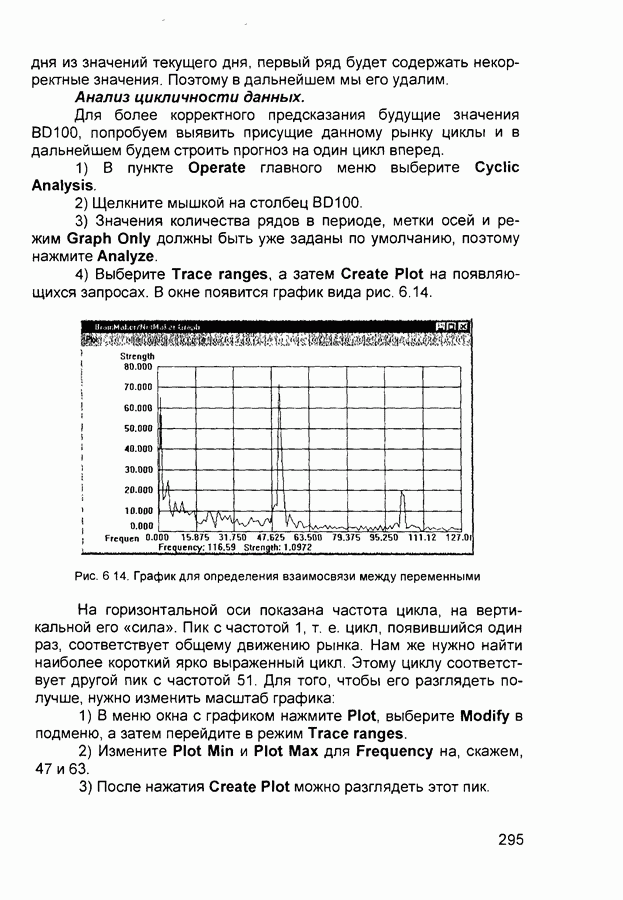
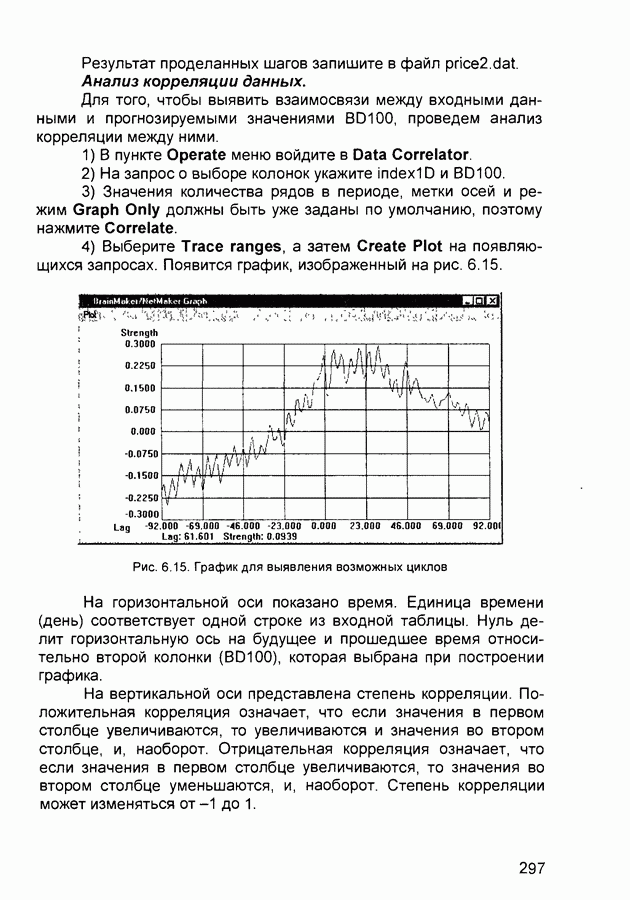
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы