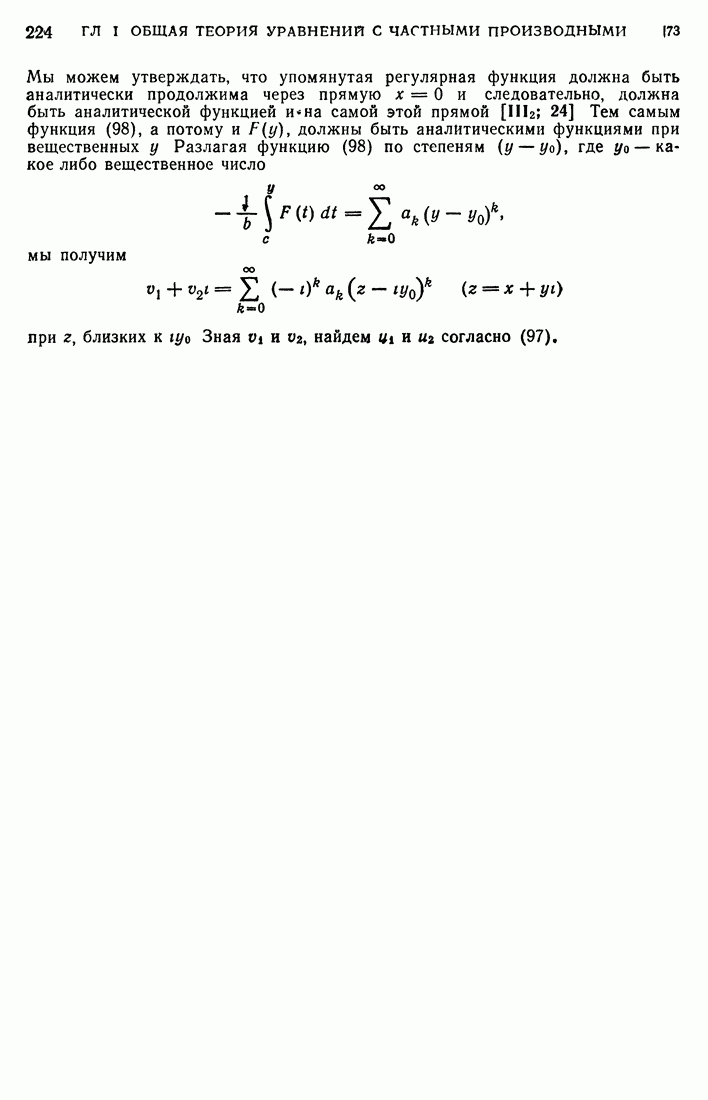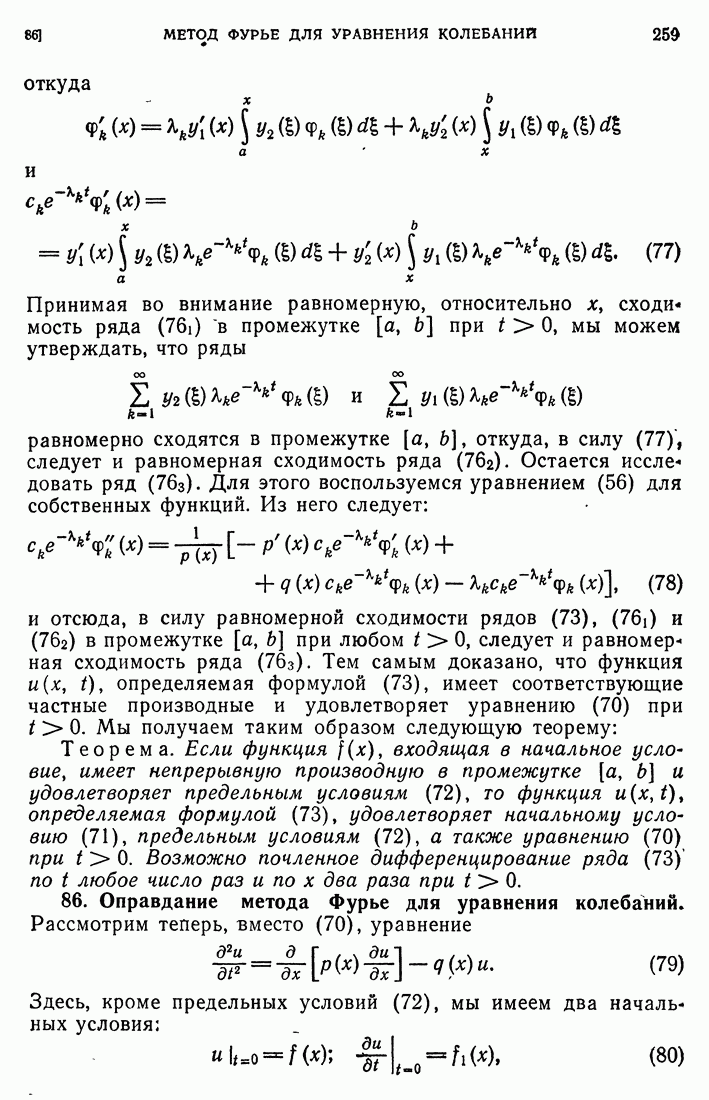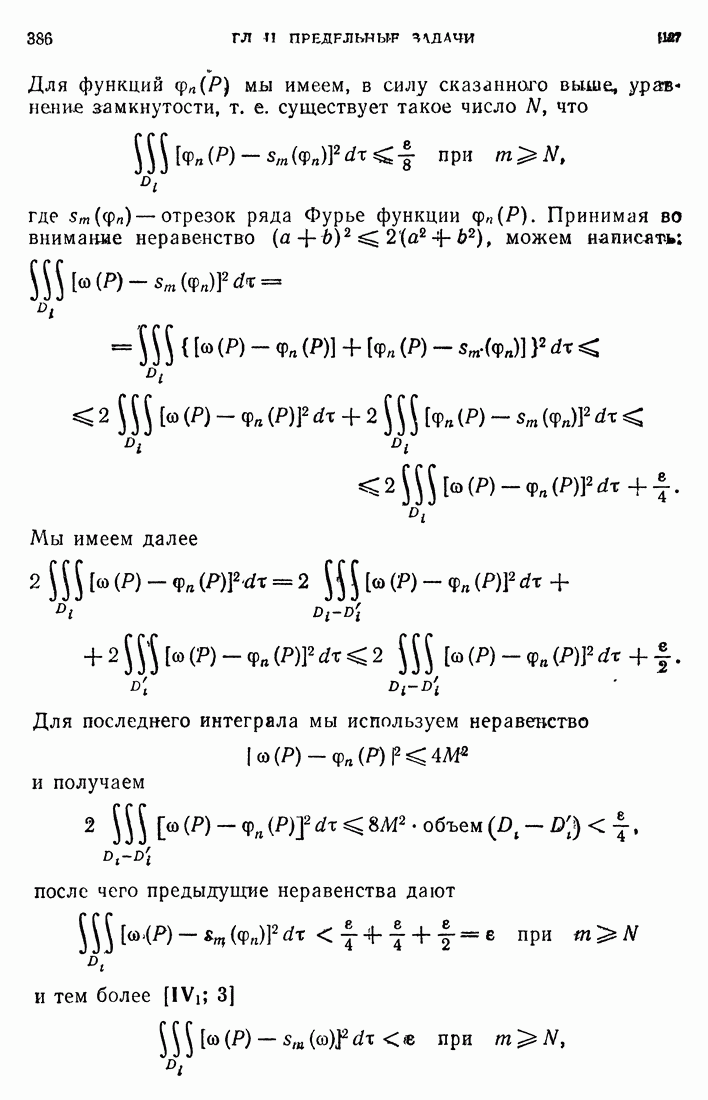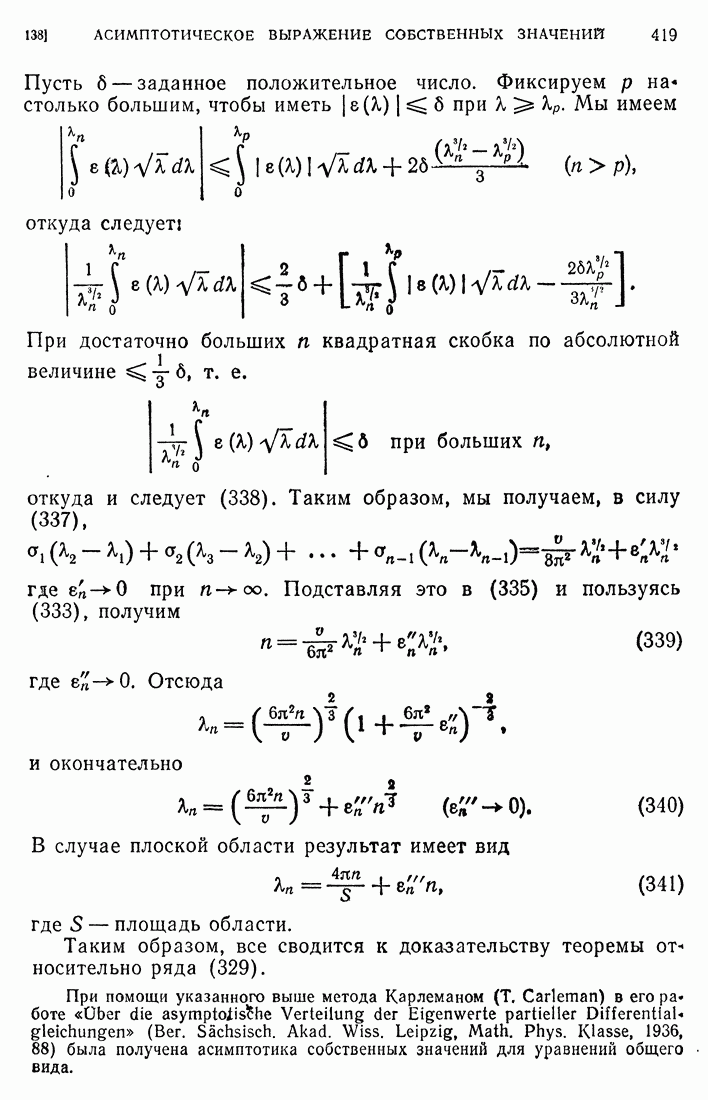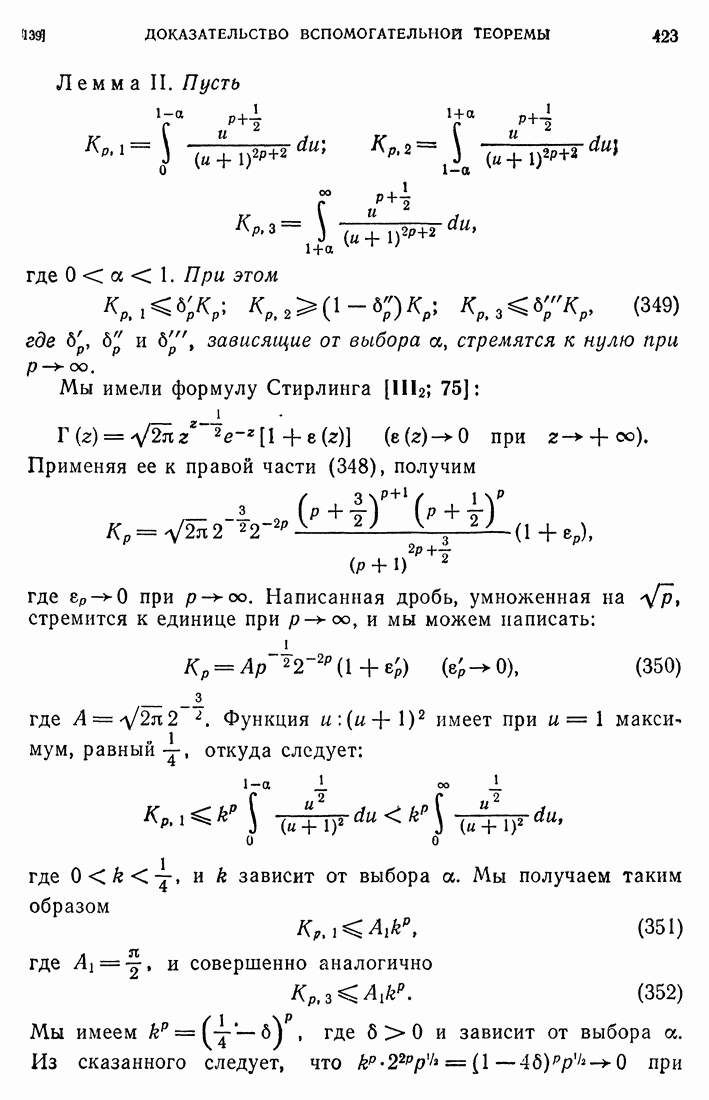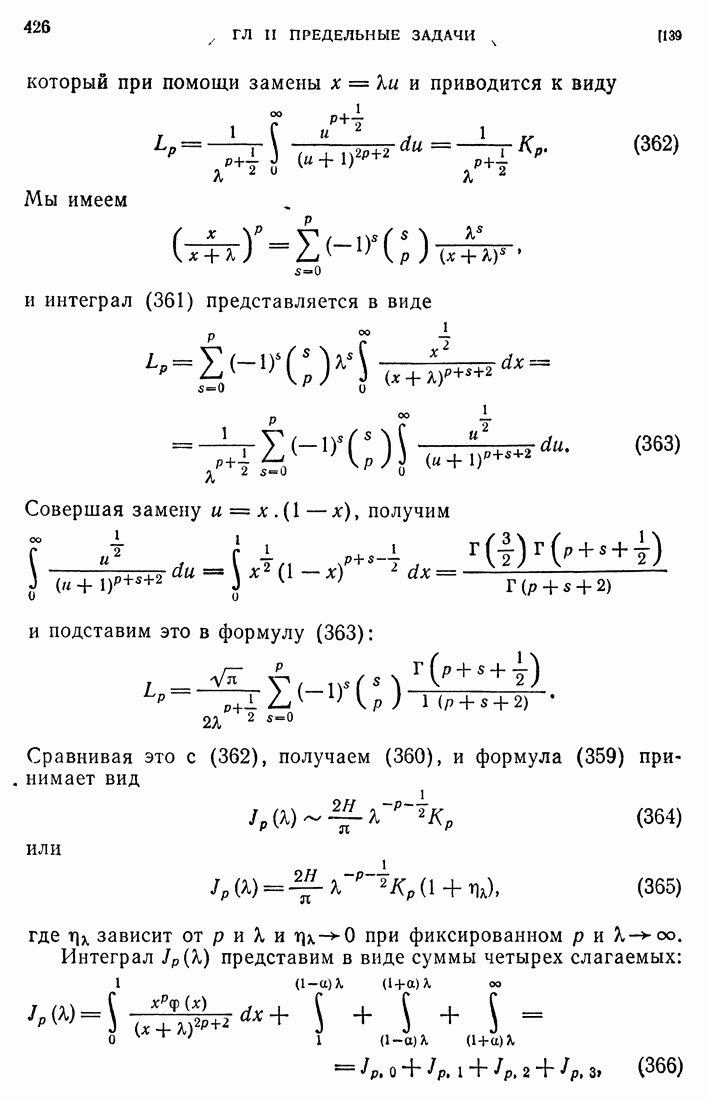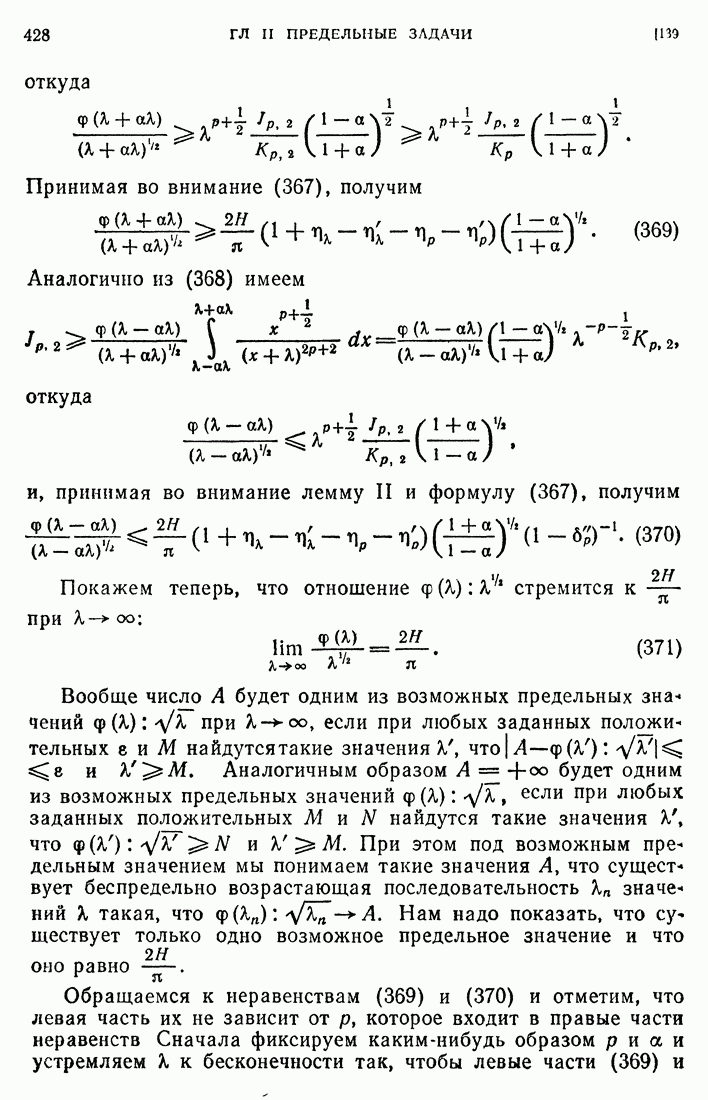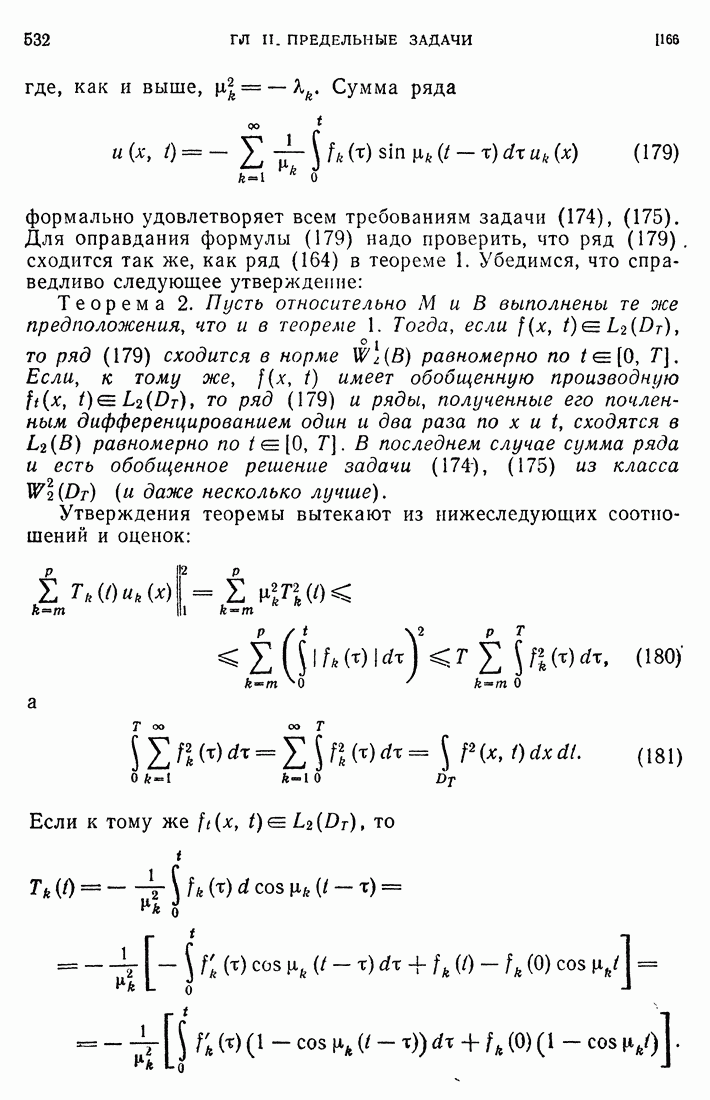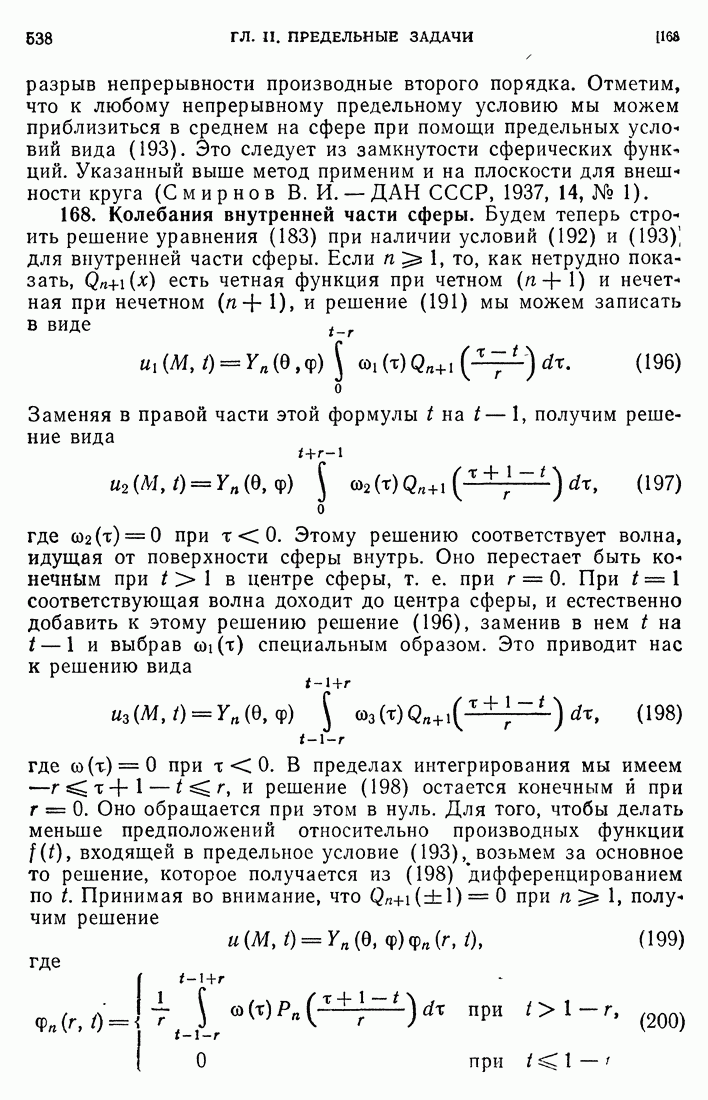| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
163. Метод Фурье для параболических уравнений.
Установим однозначную разрешимость первой начально-краевой задачи для параболических уравнений вида

Граничное условие будем считать однородным:

а начальное условие

определяемым функцией  Пусть относительно коэф. фидиентов оператора М и области В выполнены условия
Пусть относительно коэф. фидиентов оператора М и области В выполнены условия
теоремы 2 [148]. В силу теоремы 1 из [150] спектральная задача

где  — граница области В, имеет вещественный спектр
— граница области В, имеет вещественный спектр  который можно считать занумерованным в порядке убывания значений
который можно считать занумерованным в порядке убывания значений  , причем
, причем  при
при  . Предположим, ради несущественных упрощений в записи, что
. Предположим, ради несущественных упрощений в записи, что  Тогда все Я отрицательны. Будем считать также, что система всех собственных функций
Тогда все Я отрицательны. Будем считать также, что система всех собственных функций  ортонормирована в
ортонормирована в  т. е.
т. е.

причем  соответствует значению
соответствует значению  . В [150] доказано, что все
. В [150] доказано, что все  принадлежат пространству
принадлежат пространству  и образуют базис в пространствах
и образуют базис в пространствах  Кроме того, там же доказано, что в пространствах
Кроме того, там же доказано, что в пространствах  можно ввести новые скалярные произведения
можно ввести новые скалярные произведения

и

соответственно, которым отвечают нормы  эквивалентные исходным нормам пространств
эквивалентные исходным нормам пространств  . В этих новых скалярных произведениях система собственных функций
. В этих новых скалярных произведениях система собственных функций  ортогональна, причем
ортогональна, причем

а

Функции  при любых числах
при любых числах  являются решениями уравнения (126), удовлетворяющими краевому условию (127). Они и все их производные по t принадлежат при всех
являются решениями уравнения (126), удовлетворяющими краевому условию (127). Они и все их производные по t принадлежат при всех  пространству
пространству  . Уравнению (126) они удовлетворяют при всех
. Уравнению (126) они удовлетворяют при всех  для почти всех
для почти всех  из В. Будем решение и задачи (126) — (128) искать в виде ряда
из В. Будем решение и задачи (126) — (128) искать в виде ряда

Формально, подставляя этот ряд в (128) и используя соотношения (130), мы найдем выражения для  :
:

Наша дальнейшая цель состоит в том, чтобы исследовать характер сходимости ряда

и убедиться, что он дает обобщенное решение задачи (126) — (128) из такого класса, в котором есть теорема единственности. Во-первых, легко видеть, что ряд (133) сходится в  равномерно относительно
равномерно относительно  . Действительно, при любых тира
. Действительно, при любых тира 

причем числовой ряд  сходится и его сумма равна
сходится и его сумма равна  Следовательно, сумма и ряда (133) при любом
Следовательно, сумма и ряда (133) при любом  есть элемент
есть элемент  непрерывно зависящий от
непрерывно зависящий от  в норме
в норме  Последнее означает, что
Последнее означает, что  При
При  ряд (133) сходится к
ряд (133) сходится к  в норме
в норме  и потому
и потому  при
при  Покажем, что при
Покажем, что при  ряд (133) сходится в норме пространства
ряд (133) сходится в норме пространства  равномерно относительно
равномерно относительно  где
где  — любое положительное число. Действительно, в силу (132)
— любое положительное число. Действительно, в силу (132)

Но при  функции при всех к
функции при всех к  не превосходят некоторого числа
не превосходят некоторого числа  зависящего лишь от
зависящего лишь от  . Поэтому при
. Поэтому при 

Но это и доказывает желаемую сходимость ряда (133) Из нее следует, что сумма и ряда (133) есть элемент  непрерывно зависящий от t в норме этого пространства при
непрерывно зависящий от t в норме этого пространства при  .
.
Почленное дифференцирование ряда (133) по t дает ряд

который сходится в норме  и даже в норме
и даже в норме  равномерно по t при
равномерно по t при  где
где  — произвольное положительное число. Доказывается это так же, как и выше, с учетом того, что функции
— произвольное положительное число. Доказывается это так же, как и выше, с учетом того, что функции  полупрямой
полупрямой  не превосходят некоторого числа
не превосходят некоторого числа  , зависящего лишь от
, зависящего лишь от  . Такая сходимость ряда (134) гарантирует принадлежность его суммы к
. Такая сходимость ряда (134) гарантирует принадлежность его суммы к  при всех
при всех  и то, что эта сумма есть обобщенная производная по t суммы
и то, что эта сумма есть обобщенная производная по t суммы  ряда (133) в областях
ряда (133) в областях  Из всего сказанного следует, что сумма
Из всего сказанного следует, что сумма  ряда (133) есть обобщенное решение задачи (126) — (128) в области
ряда (133) есть обобщенное решение задачи (126) — (128) в области  из класса
из класса  элементы которого
элементы которого  обладают следующими свойствами: они суть элементы
обладают следующими свойствами: они суть элементы  непрерывно зависящие от
непрерывно зависящие от  в норме
в норме  они имеют обобщенную производную
они имеют обобщенную производную  причем
причем  являются элементами
являются элементами  непрерывно зависящими от
непрерывно зависящими от  . Сумма
. Сумма  ряда (133) при любом
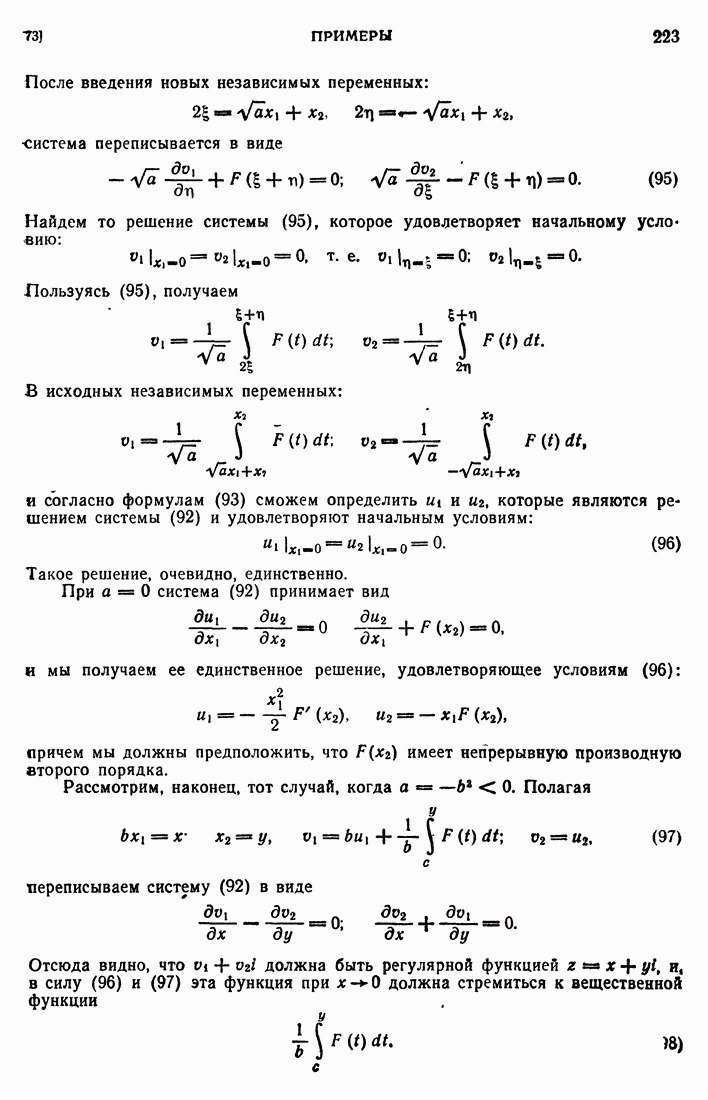
ряда (133) при любом  и почти всех
и почти всех  из В удовлетворяет уравнению (126). Граничному условию (127) она удовлетворяет в том смысле, что при
из В удовлетворяет уравнению (126). Граничному условию (127) она удовлетворяет в том смысле, что при  является элементом
является элементом  . Начальное же условие выполняется «в среднем»:
. Начальное же условие выполняется «в среднем»:

Покажем, что в таком классе задача (126) — (128) не может иметь двух разных решений. Одно из них, определенное формулой (133), мы уже нашли. Пусть  есть другое обобщенное решение задачи (126) — (128) из класса
есть другое обобщенное решение задачи (126) — (128) из класса  . Тогда их разность
. Тогда их разность  есть обобщенное решение из того же класса
есть обобщенное решение из того же класса  однородной задачи
однородной задачи  т. е. задачи
т. е. задачи

В области  это решение обладает той гладкостью, которая требовалась при выводе энергетического неравенства (124), следовательно, для него справедливы оценки
это решение обладает той гладкостью, которая требовалась при выводе энергетического неравенства (124), следовательно, для него справедливы оценки

при любом  . Устремляя в этом неравенстве
. Устремляя в этом неравенстве  к нулю и используя то, что
к нулю и используя то, что  при
при  убедимся, что
убедимся, что  . Теорема единственности доказана.
. Теорема единственности доказана.
Если на  наложить дополнительные условия, то ряд (133) будет сходиться лучше, и его сумма будет обладать лучшими дифференциальными свойствами. Например, если
наложить дополнительные условия, то ряд (133) будет сходиться лучше, и его сумма будет обладать лучшими дифференциальными свойствами. Например, если
 , то ряд (133) сходится в норме
, то ряд (133) сходится в норме  равномерно относительно
равномерно относительно  и его сумма, тем самым, будет элементом
и его сумма, тем самым, будет элементом  непрерывно зависящим от t в норме
непрерывно зависящим от t в норме  при всех
при всех  .
.
Действительно, благодаря (131) и (129)

и

т. е. ряд (133) сходится в норме  равномерно относительно
равномерно относительно  Покажем, что при
Покажем, что при  ряды, полученные двукратным почленным дифференцированием ряда (133) по
ряды, полученные двукратным почленным дифференцированием ряда (133) по  , сходятся в норме
, сходятся в норме  где
где  любое конечное число. Это так, ибо
любое конечное число. Это так, ибо

при  . Это же неравенство гарантирует и сходимость ряда (134) в
. Это же неравенство гарантирует и сходимость ряда (134) в  Наконец, из того факта, что система
Наконец, из того факта, что система  образует базис в пространстве
образует базис в пространстве  следует, что при
следует, что при  ряд (133) сходится в норме
ряд (133) сходится в норме  равномерно от носительно
равномерно от носительно  и его сумма есть элемент
и его сумма есть элемент  непрерывно зависящий от
непрерывно зависящий от  в норме
в норме  . Ряд (134) при этом будет сходиться в норме
. Ряд (134) при этом будет сходиться в норме  равномерно относительно
равномерно относительно  и его сумма
и его сумма  будет элементом
будет элементом  непрерывно зависящим от
непрерывно зависящим от  в норме
в норме 
Итак, мы доказали следующую теорему:
Теорема 1. Пусть коэффициенты уравнения (126) и область В удовлетворяют условиям теоремы  . Тогда решение задачи (126) — (128) дается рядом
. Тогда решение задачи (126) — (128) дается рядом
(133), который сходится в  равномерно относительно
равномерно относительно  при
при  он сходится в норме
он сходится в норме  равномерно относительно
равномерно относительно  , где
, где  — произвольное положительное число. Ряд, полученный почленным дифференцированием ряда (133) по t, сходится в
— произвольное положительное число. Ряд, полученный почленным дифференцированием ряда (133) по t, сходится в  при
при  равномерно относительно
равномерно относительно  . Сумма ряда (133) есть обобщенное решение задачи из класса
. Сумма ряда (133) есть обобщенное решение задачи из класса  любым
любым  , причем в этом классе имеет место теорема единственности. Если
, причем в этом классе имеет место теорема единственности. Если  то ряд (133) сходится
то ряд (133) сходится  равномерно по
равномерно по  , а ряды, полученные его почленным дифференцированием один раз по t или два раза по
, а ряды, полученные его почленным дифференцированием один раз по t или два раза по  сходятся в норме
сходятся в норме  . Наконец, при
. Наконец, при  сходится в норме
сходится в норме  а ряд (134) в норме
а ряд (134) в норме  равномерно относительно
равномерно относительно  .
.
Рассмотрим еще задачу

где L — то же, что и в  . Ей формально удовлетворяет сумма ряда
. Ей формально удовлетворяет сумма ряда

где  Покажем, что ряд (138) и ряды, в полученные его почленным дифференцированием по
Покажем, что ряд (138) и ряды, в полученные его почленным дифференцированием по  один и два раза сходятся в норме
один и два раза сходятся в норме  так что сумма ряда
так что сумма ряда  и ее производные
и ее производные  будут элементами
будут элементами  . Для этого достаточно убедиться, что
. Для этого достаточно убедиться, что

стремится к нулю при  . Это верно, ибо благодаря (132)
. Это верно, ибо благодаря (132)

а для функций  из
из  верны равенства
верны равенства

Из этой оценки  следует также, что ряд, полученный почленным дифференцированием ряда (133) по t, сходится в
следует также, что ряд, полученный почленным дифференцированием ряда (133) по t, сходится в  Так как конечные суммы
Так как конечные суммы

удовлетворяют (при почти всех  из
из  ) уравнению
) уравнению  сходится к
сходится к  в норме
в норме  то сумма ряда (138) будет при почти всех
то сумма ряда (138) будет при почти всех  из
из  удовлетворять уравнению (137). Чтобы проверить выполнение начального и граничного условия из (137), убедимся, что ряд (138) сходится в норме
удовлетворять уравнению (137). Чтобы проверить выполнение начального и граничного условия из (137), убедимся, что ряд (138) сходится в норме  при любом
при любом  Действительно, используя те же соображения, что и при оценке
Действительно, используя те же соображения, что и при оценке  , получим
, получим

Отсюда ясно, что при любом  сумма
сумма  есть элемент
есть элемент 
Тем самым мы доказали теорему:
Теорема 2. Если относительно L и В выполнены предположения теоремы  , то решение задачи (137) в
, то решение задачи (137) в  дается рядом (138). Этот ряд и ряды, полученные его почленным дифференцированием один раз по t и
дается рядом (138). Этот ряд и ряды, полученные его почленным дифференцированием один раз по t и  и два раза по
и два раза по  сходятся в норме
сходятся в норме  . Сумма ряда (138) при почти всех
. Сумма ряда (138) при почти всех  удовлетворяет уравнению (137), при любом
удовлетворяет уравнению (137), при любом  она есть элемент
она есть элемент  и при
и при 
Заметим, что решения второй и третьей начально-краевых задач для уравнения  определяются рядами вида (133) и (138), только в качестве
определяются рядами вида (133) и (138), только в качестве  в них надо брать собственные функции L, отвечающие соответствующему краевому условию.
в них надо брать собственные функции L, отвечающие соответствующему краевому условию.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 1. Линейные уравнения с двумя независимыми переменными.
- 2. Задача Коши и характеристики.
- 3. Случай любого числа переменных.
- 4. Примеры.
- 5. Вспомогательная теорема.
- 6. Нелинейные уравнения первого порядка.
- 7. Характеристические многообразия.
- 8. Метод Коши.
- 9. Задача Коши.
- 10. Единственность решения.
- 11. Особый случай.
- 12. Любое число независимых переменных.
- 13. Полный, общий и особый интегралы.
- 14. Полный интеграл и задача Коши.
- 15. Примеры.
- 16. Случай любого числа переменных.
- 17. Теорема Якоби.
- 18. Системы двух уравнений первого порядка.
- 19. Метод Лагранжа—Шарпи.
- 20. Системы линейных уравнений.
- 21. Полные и якобиевы системы.
- 22. Интегрирование полных систем.
- 23. Скобки Пуассона.
- 24. Метод Якоби.
- 25. Канонические системы.
- 26. Примеры.
- 27. Метод мажорантных рядов.
- 28. Теорема Ковалевской.
- 29. Уравнения, высших порядков.
- § 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 30. Типы уравнений второго порядка.
- 31. Уравнения с постоянными коэффициентами.
- 32. Нормальные формы при двух независимых переменных.
- 33. Задача Коши.
- 34. Характеристические полосы.
- 35. Производные высших порядков.
- 36. Вещественные и мнимые характеристики.
- 37. Основные теоремы.
- 38. Промежуточные интегралы.
- 39. Уравнения Монжа — Ампера.
- 40. Характеристики при любом числе независимых переменных.
- 41. Бихарактеристики.
- 42. Связь с вариационной задачей.
- 43. Распространение поверхности разрыва.
- 44. Сильные разрывы.
- 45 Метод Римана.
- 46. Характеристические начальные данные.
- 47. Теоремы существования.
- 48. Формула интегрирования по частям и формула Грина.
- 49. Метод Вольтерра.
- 50. Формула Соболева.
- 51. Формула Соболева (продолжение).
- 52. Построение функции «сигма».
- 53. Общий случай начальных данных.
- 54. Обобщенное волновое уравнение.
- 55. Случай любого числа независимых переменных.
- 56. Энергетическое неравенство.
- 57. Теоремы единственности и непрерывной зависимости решений.
- 58. Случай волнового уравнения.
- 59. Теорема вложения в пространство непрерывных функций и некоторые ее следствия.
- 60. Обобщенные решения уравнений второго порядка.
- 61. О существовании и единственности обобщенных решений задачи Коши для волнового уравнения.
- 62. Уравнения эллиптического типа.
- § 3. СИСТЕМЫ УРАВНЕНИЙ
- 63. Характеристики систем уравнений.
- 64. Кинематические условия совместности.
- 65. Динамические условия совместности.
- 66. Уравнения гидродинамики.
- 67. Уравнения теории упругости.
- 68. Анизотропное упругое тело.
- 69. Электромагнитные волны.
- 70. Сильные разрывы в теории упругости.
- 71. Характеристики и большие частоты.
- 72. Случай двух независимых переменных.
- 73. Примеры.
- ГЛАВА II. ПРЕДЕЛЬНЫЕ ЗАДАЧИ
- 74. Функция Грина линейного уравнения второго порядка.
- 75. Приведение к интегральному уравнению.
- 76. Симметрия функции Грина.
- 77. Собственные значения и собственные функции предельной задачи.
- 78. Знак собственных значений.
- 79. Примеры.
- 80. Обобщенная функция Грина.
- 81. Полиномы Лежандра.
- 82. Функции Эрмита и Лагерра.
- 83. Уравнения четвертого порядка.
- 84. Уточненные теоремы разложения Стеклова.
- 85. Оправдание метода Фурье для уравнения теплопроводности.
- 86. Оправдание метода Фурье для уравнения колебаний.
- 87. Теоремы единственности.
- 88. Экстремальные свойства собственных значений и функций.
- 89. Теорема Куранта.
- 90. Асимптотическое выражение собственных значений.
- 91. Асимптотическое выражение для собственных функций.
- 92. Метод Ритца.
- 93. Пример Ритца.
- § 2. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- 94. Ньютонов потенциал.
- 95. Потенциал двойного слоя.
- 96. Свойства потенциала простого слоя.
- 97. Нормальная производная потенциала простого слоя.
- 98. Нормальная производная потенциала простого слоя (продолжение).
- 99. Прямое значение нормальной производной.
- 100. Производная потенциала простого слоя по любому направлению.
- 101. Логарифмический потенциал.
- 102. Интегральные формулы и параллельные поверхности.
- 103. Последовательности гармонических функций.
- 104. Постановка внутренних предельных задач для уравнения Лапласа.
- 105. Внешние задачи в случае плоскости.
- 106. Преобразование Кельвина.
- 107. Единственность решения задачи Неймана.
- 108. Решение предельных задач в трехмерном случае.
- 109. Исследование интегральных уравнений.
- 110. Сводка результатов, касающихся решений предельных задач.
- 111. Предельные задачи на плоскости.
- 112. Интегральное уравнение сферических функций.
- 113. Тепловое равновесие излучающего тела.
- 114. Метод Шварца.
- 115. Доказательство леммы.
- 116. Метод Шварца (продолжение).
- 117. Суб- и супергармонические функции.
- 118. Вспомогательные предложения.
- 119. Метод нижних и верхних функций.
- 120. Исследование граничных значений.
- 121. Уравнение Лапласа в n-мерном пространстве.
- 122. Функция Грина оператора Лапласа.
- 123. Свойства функции Грина.
- 124. Функция Грина в случае плоскости.
- 125. Примеры.
- 126. Функция Грина и неоднородное уравнение.
- 127. Собственные значения и собственные функции.
- 128. Нормальная производная собственных функций.
- 129. Экстремальные свойства собственных значений и функций.
- 130. Уравнение Гельмгольца и принцип излучения.
- 131. Теорема единственности.
- 132. Принцип предельной амплитуды и принцип предельного поглощения.
- 133. Предельные задачи для уравнения Гельмгольца.
- 134. Дифракция электромагнитной волны.
- 135. Вектор магнитной напряженности.
- 136. Единственность решения задачи Дирихле для эллиптических уравнений.
- 137. Уравнение …
- 138. Асимптотическое выражение собственных значений.
- 139. Доказательство вспомогательной теоремы.
- 140. Линейные уравнения более общего вида.
- 141. Тензор Грина.
- 142. Плоская статическая задача теории упругости.
- 143. О результатах Шаудера.
- 144. Обобщенные решения класса …
- 145. Первое основное (энергетическое) неравенство.
- 146. Пространство … и второе основное неравенство.
- 147. Некоторые сведения о гильбертовых пространствах и операторах, действующих в них.
- 148. О разрешимости задачи Дирихле в пространстве …
- 149. О фредгольмовой разрешимости задачи Дирихле.
- 150. О спектре симметричного оператора.
- § 3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПОВ
- 151. Зависимость решений уравнения теплопроводности от начального и предельного условий и свободного члена.
- 152. Потенциалы для уравнения теплопроводности в одномерном случае.
- 153. Тепловые источники в многомерном случае.
- 154. Функция Грина уравнения теплопроводности.
- 155. Применение преобразования Лапласа.
- 156. Применение конечных разностей.
- 157. Метод Фурье для уравнения теплопроводности.
- 158. Неоднородное уравнение.
- 159. Свойства решений уравнения теплопроводности.
- 160. Обобщенные потенциалы простого и двойного слоя в одномерном случае.
- 161. Суб- и суперпараболические функции.
- 162. Параболические уравнения общего вида. Энергетическое неравенство.
- 163. Метод Фурье для параболических уравнений.
- 164. Второе основное неравенство и разрешимость первой начально-краевой задачи.
- 165. Гиперболические уравнения общего вида. Энергетическое неравенство для первой начально-краевой задачи.
- 166. Метод Фурье для уравнений гиперболического типа.
- 167. Предельная задача для сферы.
- 168. Колебания внутренней части сферы.
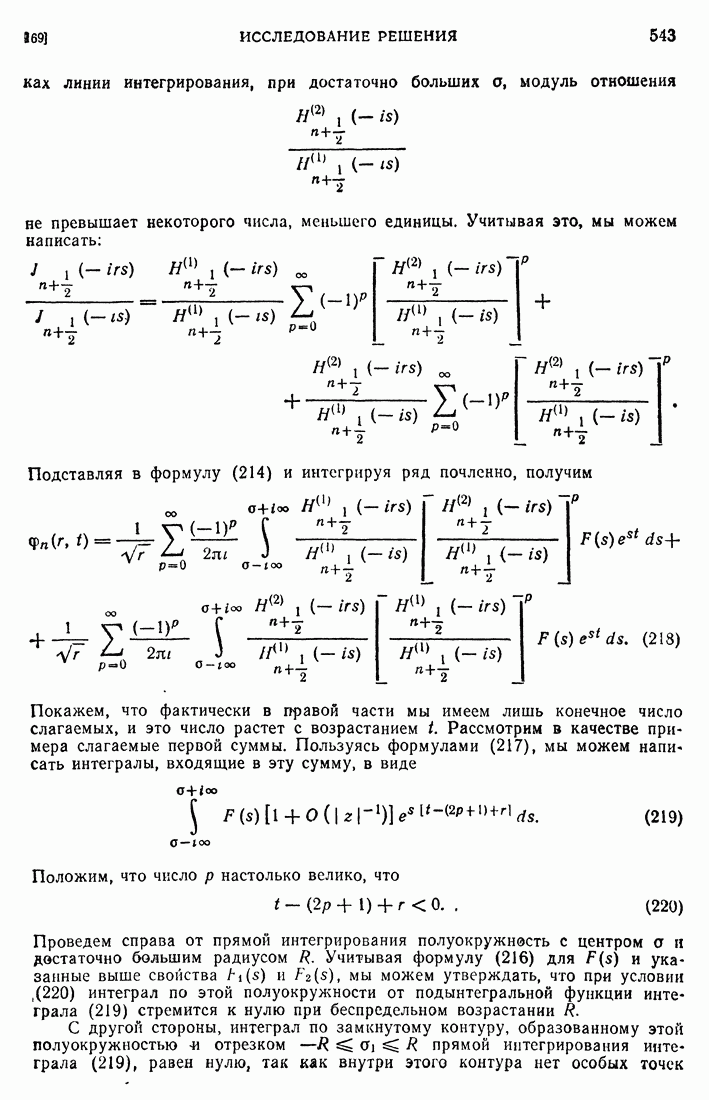
- 169 Исследование решения.
- 170. Предельная задача для телеграфного уравнения.