18.3. Теорема Римана — Роха для алгебраических схем

В этом разделе мы работаем в категории алгебраических схем (отделимых и локально конечного типа) над фиксированным основным полем.

Теорема 18.3. Для любой схемы X существует гомоморфизм

удовлетворяющий следующим условиям:

(1) (ковариантность). Если - собственный морфизм, а то

(3) Если замкнутое вложение в гладкую схему локально свободная резольвента на то

(4) Пусть морфизм, причем обладают вложениями в гладкие схемы. Тогда для всех а

(5) (старший член). Пусть V — замкнутое n-мерное подмногообразие в Тогда

Кроме того, однозначно определяется свойствами (1), (4) (для открытых вложений квазипроективных схем) и

Доказательство, будет дано в конце параграфа. Сначала мы сообщим некоторые следствия. Для любой схемы X ее класс Тодда задается формулой

Следствие 18.3.1. (а) Если X полна, то для любого векторного расслоения над X

В частности,

(b) Если X регулярно вкладывается в гладкую схему, то

Здесь виртуальное касательное расслоение к В частности, это так для гладких схем.

(c) Пусть собственный морфизм и Предположим, что существует элемент такой, что

Например, это так для любого л.п.п. морфизма или, более общо, для любого совершенного морфизма (ср. пример 15.1.8). Тогда

В частности, если гладкие, то

Доказательство, (а) следует из ковариантности для отображения X в точку и свойства (2). Если X гладкая, (b) следует из свойства (3) теоремы 18.3, где для вычисления вкладывается в себя. Если регулярное вложение X в гладкую схему то по свойству (4)

(с) следует из свойств (1) и (2):

Следствие 18.3.2. Для любой схемы X гомоморфизм индуцирует изоморфизм

Доказательство. Если каноническая сюръекция (пример 15.1.5), композиция индуцирует изоморфизм ассоциированной градуированной группы что следует из свойства (5).

В частности, для неособого многообразия X характер Чженя определяет изоморфизм

Доказательство теоремы 18.3 опирается на следующие два предложения. Пусть замкнутое вложение схемы X в гладкую схему когерентный пучок на Положим

где резольвента на Это определяет гомоморфизм

Предложение 18.3.1. Пусть замкнутые вложения схемы X в гладкие схемы Тогда

Доказательство. Достаточно показать, что

где X диагонально вложена в когерентный пучок на Рассмотрим диаграмму

где проекции. Заметим, что регулярное вложение с нормальным расслоением Пусть резольвента пучка на Тогда резольвента на так как плоский морфизм. Поэтому по теореме 18.1

Применим теперь теорему 18.2(3) к регулярному вложению А, которое рассматривается как морфизм схем, проективных над базисной схемой Это дает равенство

для любого Применим эту формулу к Тогда так что по (ii) и (iii)

Умножая на мы получаем (i).

Предложение 18.3.2. Пусть

— расслоенный квадрат с замкнутым вложением и проективным морфизмом причем индуцирует изоморфизм на Тогда точна последовательность

Доказательство. Положим и пусть -индуцированный изоморфизм. Тогда получается коммутативная диаграмма с точными строками

где первая высшая - группа Квиллена § 7, предл. 3.2, [Fulton - Gillet 1]). Заключение следует из простого диаграммного поиска.

Гомоморфизм был построен в § 18.2 для квазипроективных схем. Чтобы распространить его на произвольные схемы, воспользуемся понятием развертки Чжоу.

Определение 18.3. Разверткой схемы X назовем собственный морфизм такой, что для любого подмногообразия

ществует подмногообразие , бирационально проектирующееся на при Если X квазипроективна над назовем разверткой Чжоу.

Нам нужна будет следующая элементарная лемма.

Лемма 18.3. (1) Если развертки, то развертка.

(2) Если развертка и произвольный морфизм, то индуцированный морфизм также является разверткой.

(3) Для любой схемы X существуют развертка Чжоу и открытое плотное подмножество , такие, что изоморфизм над

(4) Если развертки, то существует развертка Чжоу доминирующая

(5) Для любого морфизма и любой развертки Чжоу существуют развертка Чжоу и морфизм такие, что Если собственный, можно считать собственным.

(6) Если развертка, то гомоморфизмы

сюръективны.

Доказательство. (1) очевидно. пусть - подмногообразие и -замыкание Пусть отображается бирационально на Существуют открытые такие, что изоморфно отображает на Тогда замыкание является подмногообразием в которое бирационально проектируется на по лемме Чжоу (ср. существует собственный морфизм с квазипроективной схемой являющийся изоморфизмом над некоторым открытым плотным подмножеством По нётеровой индукции имеется развертка Чжоу Тогда

будет разверткой Чжоу для

В ситуации (4) выберем развертку Чжоу Согласно (1) и (2), композиция также развертка Чжоу.

В (5) надо взять любую развертку Чжоу

Наконец в (6) обозначим через подгруппу в порожденную пучками с носителями размерности Тогда порождается

массами где V пробегает подмногообразия размерности Если отображает V бирационально на V, то где а. из Все завершается нётеровой индукцией. В случае А, утверждение тривиально в силу сюръективности на уровне циклов.

Теперь можно приступить к доказательству теоремы Римана — Роха. Для любой квазипроективной схемы X обозначим через гомоморфизм, построенный в § 18.2. Распространение его на произвольную схему X проводится в несколько шагов.

Шаг 1. Пусть - развертка Чжоу. Тогда имеется не более одного гомоморфизма делающего коммутативной диаграмму

Это следует из леммы Таким образом, допускает не более одного распространения с квазипроективных схем на произвольные схемы с сохранением свойства ковариантности. Если коммутативна, мы говорим, что согласовано с

Шаг 2. Пусть гомоморфизм, согласованный с разверткой Чжоу Тогда для любого собственного морфизма с квазипроективной схемой диаграмма

коммутативна. В частности, гомоморфизм если он существует, не зависит от используемой развертки Чжоу. Чтобы показать это, выберем

как в лемме Ковариантность для будет следовать из ковариантности для (§ 18.2), предполагаемой ковариантности для и сюръективности для В самом деле, пусть а для Тогда

Шаг 3. Докажем существование индукцией по размерности Для данной схемы X выберем развертку Чжоу являющуюся изоморфизмом над и образуем расслоенный квадрат

Так как замкнутое вложение, квазипроективна. По нётеровой индукции существует гомоморфизм согласованный с разверткой Чжоу Рассмотрим диаграмму

где определены, как в предложении 18.3.2. Согласно предположению и известной ковариантности для морфизма квазипроективных схем, квадрат в этой диаграмме коммутативен. Согласно предложению 18.3.2, верхняя строка точна, как, впрочем, и нижняя (пример 1.8.1), хотя нам это и не понадобится. Поэтому существует единственный гомоморфизм делающий диаграмму коммутативной. В частности, согласован с

Шаг 4. Согласно шагам 2 и 3, для каждой схемы X имеется гомоморфизм

согласованный с любой разверткой Чжоу Докажем теперь свойство ковариантности. Пусть собственный морфизм, и выберем как в лемме 18.3(5). Равенство получается так же, как в шаге 2.

Шаг 5. Докажем свойство (2). Пусть Выберем развертку Чжоу Тогда

по результату, известному для X из теоремы 18.2, и формуле проекции.

Шаг 6. Для доказательства свойства (3) рассмотрим замкнутое вложение в гладкую схему, и пусть развертка Чжоу. Пусть замкнутое вложение в открытый кусок

проективного пространства. Тогда замкнутое вложение. Пусть а и положим

По теореме 18.2, применяемой в категории схем, квазипроективных над

(Точнее, теорема 18.2 дает равенство до умножения обеих частей на Но, согласно предложению 18.3.1, совпадает с классом, полученным при вложении т. е.

Поэтому и по шагу что и требовалось установить.

Шаг 7. Пусть морфизм, как в свойстве (4). Образуем коммутативную диаграмму

Для проекции доказательство (4) такое же, как в шаге 4 доказательства теоремы 18.2. Для регулярного вложения следует из теоремы 18.2(3), где рассматриваются как квазипроективные схемы над гладкой базой

Шаг 8. При доказательстве свойства (5) в силу ковариантности можно предполагать, что а взяв развертку Чжоу — что X квазипроективно. Так как согласован с ограничениями на открытые подмногообразия, можно считать X проективным. Выберем конечный сюръективный морфизм степени d. Тогда и

где По ковариантности

где класс размерности Здесь используется справедливость (5) для которая следует из свойства (3), и ковариантность относительно вложения подмногообразий пространства Если старший член то

с Сравнение этих двух выражений дает нужное заключение, что

Что касается единственности, то предположим, что также обладает указанными свойствами. Так как — изоморфизм (следствие 18.3.2), можно рассмотреть композицию Тогда есть преобразование в себя, которое ковариантно для собственных морфизмов, контравариантно для открытых вложений квазипроективных схем, и размерности Согласно примеру тождественное преобразование, что и требовалось доказать.

Пример 18.3.1. Декартовы произведения. Пусть -алгебраические схемы. Тогда диаграмма

коммутативна. В частности, (Если квазипроективны, это доказано в работе [Baum - Fulton - MacPherson 1], III.2. Общий случай получается из разверток Чжоу Это эквивалентно мультипликативности локализованного характера Чженя (пример

Пример 18.3.2. Единственность. На категории полных схем однозначно определяется свойством ковариантности (1), свойством (2) и нормализацией где точка. (См. [Baum - Fulton - MacPherson 1], III.2.) На категории всех алгебраических схем требуется еще свойство согласованности с открытыми вложениями.

Пример 18.3.3. Пусть собственный бирациональный морфизм, являющийся изоморфизмом вне Тогда

где а расположен на В частности,

Например, пусть X есть -мерное многообразие с конечным числом особых точек и X — разрешение особенностей. Тогда

при где сумма берется

по особым точкам и

Здесь обозначает длину слоя пучка в точке Если X нормально, последний член равен нулю.

Пример 18.3.4. (а) Пусть X — проективная кривая и разрешение особенностей. Тогда

где В частности,

Если векторное расслоение ранга над X, то

(b) Пусть -нормальная поверхность, а -разрешение особенностей. Тогда

где В частности,

Если векторное расслоение ранга над X, то

Пример 18.3.5. Пусть — регулярное вложение коразмерности с нормальным расслоением Предположим, что вкладывается в неособое многообразие. Тогда

Если X — полное пересечение гиперповерхностей на У, то

где

В частности, если -дивизор Картье на то

Если -гладкое многообразие размерности то

Существуют особые проективные многообразия X, такие, что не поднимается в когомологии. В статье [Baum - Fulton - MacPherson 1], IV.6, построено нормальное -мерное проективное многообразие X с одной особой точкой, такое, что образ нельзя представить в виде ни для какого

Пример 18.3.6. Пусть X есть -мерная полная схема, когерентный пучок на линейные расслоения над X с Тогда

где компоненты Это многочлен степени от старший член которого равен

Это придает конкретный вид многочленам, рассмотренным в [Snapper 1], см. также [Kleiman 1] и [Mumford 6].

Пример 18.3.7. (а) Пусть векторное расслоение ранга над полной схемой X размерности Тогда

(По формуле Хирцебруха — Римана — Роха и примеру

Остается заметить, что и совпадают в размерности

Пусть имеет регулярное сечение с конечной схемой нулей Тогда равенство из (а) принимает вид

(ср. § 14.1). Если имеет регулярное сечение для некоторого линейного расслоения например, если X— проективное многообразие — то, как заметил Лазарсфельд, (а) можно вывести прямо из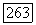

Если X — неособое полное многообразие, то

есть его топологическая эйлерова характеристика.

Пример 18.3.8. Плоские семейства. Пусть 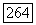- неособая база, а 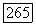—квазипроективный морфизм. Для 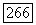пусть 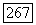слой над 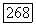отображение специализации (§ 10.1). Пусть 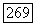когерентный пучок на X, плоский над 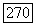Тогда

где 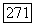-слой 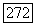над 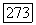(Надо использовать теорему 18.1 и тот факт, что нормальное расслоение 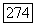Ттривиально.) Это обобщает (и передоказывает) утверждение о локальном постоянстве 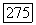как функции от 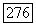В частности, если X плоско над 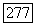то 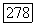Это частный случай теоремы, обсуждаемой в примере 18.3.16.

Пример 18.3.9. Пусть 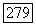конечный этальный морфизм. Тогда 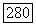о ту. (Взяв развертку Чжоу 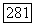редуцируем к случаю квазипроективных 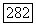Тогда это частный случай теоремы 18.2(3).) Отсюда следует, что

Поэтому 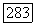В частности, если полные, то 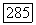(Клейман дал элементарное доказательство этого равенства для арифметического рода.)

Пример 18.3.10. Пусть 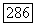- собственный л.п.п. морфизм. Предположим, что 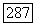разлагается на регулярное вложение и гладкий собственный морфизм 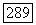Тогда для любого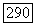

(Достаточно доказать это для регулярного вложения и гладкого морфизма. Первый случай покрывается теоремой 18.2. Для гладкого 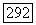мы должны показать, что обе стороны одинаково действуют на 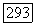квазипроективно. Запишем 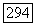Нужное равенство формально следует из применения теоремы 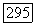к морфизму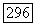

Пример 18.3.11. Пусть когерентный пучок на схеме X с 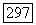Определим -цикл пучка

где сумма берется по всем -мерным компонентам носителя а длина слоя над локальным кольцом Тогда

Если подгруппа в порожденная пучками с носителями размерности то определяет гомоморфизм

(На самом деле по модулю совпадает с градуированным гомоморфизмом, ассоциированным с Так как образующие группы могут быть связаны пучками более высокой размерности, этот факт не очевиден из определений. Заметим, что для корректности мы должны тензорно умножить на

Пример 18.3.12. Формула Римана — Роха. Пусть комплекс векторных расслоений над схемой точный вне замкнутой подсхемы Пусть когерентный пучок на Тогда пучки гомологий комплекса расположены на X, так что определены классы Имеет место формула

Если гладкая, и резольвента пучка на X, то мы получаем свойство (3) теоремы 18.3. Свойство (4) также можно получить из (ср. пример 18.3.10). Обратно, имея разрешение особенностей, можно вывести из теоремы Римана — Роха. Заметим, что в случае формула следует из свойства (2) теоремы 18.3. Наметим кратко общее доказательство

При фиксированном комплексе обе части аддитивны по и определяют гомоморфизмы из Пусть обозначает значение левой части на элементе Тогда эквивалентна формуле

для Доказательство разобьем на четыре шага.

1. Пусть - собственный морфизм, индуцированный морфизм и Предположим, что

Тогда выполняется для (Применим к обеим частям и воспользуемся ковариантностью Нужна также формула

вытекающая из спектральной последовательности

2. Пусть точная последовательность комплексов векторных расслоений над точных вне Если выполняется для и она выполняется для (предложение

3. Пусть квазипроективное многообразие и элементарный комплекс, т. е. при линейные расслоения. Предположим также, что Тогда верна. (Сдвигая и подкручивая, можно считать, что где эффективный дивизор на естественное вложение. Тогда вытекает из теоремы и следствия 18.1.2.)

4. В общем случае в силу леммы Чжоу и шага 1 можно считать, что квазипроективное многообразие. Проведем индукцию по сумме рангов расслоений Пусть комплекс

Можно считать, что Применим шаг 1 к проекции так как сюръективно отображается на Ко можно считать, что содержит линейное подрасслоение В этой ситуации будем вести индукцию по размерности носителя Можно считать, что Согласно шагам 1 и 2 и предположениям индукции достаточно найти собственный бирациональный морфизм такой, что содержит элементарный подкомплекс точный вне

Пусть проекция, и универсальные подрасслоение и факторрасслоение для Пусть схемное пересечение множеств зануления отображений расслоений

Ограничение на имеет элементарный подкомплекс где ограничения на На дифференциал инъективен, так что прямая в для Это определяет сечение такое, что комплекс точен. Замыкание образа в является требуемым многообразием, индуцируется проекцией и

Пример 18.3.13. (а) Пусть - регулярное вложение коразмерности d с нормальным расслоением предположим, что вкладывается в гладкую схему.. Тогда для любого когерентного пучка на

Если то равенство старших членов дает

(Применим теорему или пример 18.3.12.)

(b) Пусть X — неособое многообразие, замкнутые подмногообразия в Тогда

где (Применим (а) к диагональному вложению

Обсуждение роли функторов для определения произведения-пересечения см. в § 20.4.

Пример 18.3.14. Пусть комплекс векторных расслоений над схемой точный вне точки Для когерентного пучка на У

Пусть обозначает член степени класса Пусть и предположим, что

Пусть двойственный комплекс векторных расслоений. Тогда

(Надо использовать примеры 18.3.12 и 18.1.2.) Условие выполнено, если обратный образ комплекса векторных расслоений над неособым многообразием. В работе [Dutta - Hochster - McLaughlin 1] недавно построен комплекс на трехмерном многообразии, резольвента модуля конечной длины, такой, что принимает как положительные, так и отрицательные значения, где структурный пучок подходящей поверхности в таким образом, Обсуждение связей теоремы Римана — Роха с локальной алгеброй см.

Пример 18.3.15. Пусть замкнутое вложение, такое, что для имеется локально свободная резольвента над Таким образом, -совершенный морфизм (ср. пример 15.1.8) и где отображение Гизина. В этом случае пример 18.3.12 читается так:

В частности, если - регулярное вложение, то (следствие 18.1.2)

где нормальное расслоение к Это передоказывает теорему 18.3(4). (Жилле сообщает, что использование скрученных комплексов, как в статье [Toledo - Tong 1], позволяет избавиться от предположения о существовании глобальной резольвенты

Пример 18.3.16. Бивариантная теорема Римана — Роха. Все схемы предполагаются квазипроективными над фиксированной неособой базой Для морфизма определим

как группу Гротендика - совершенных комплексов на Если разложен на замкнутое вложение и гладкий морфизм то комплекс пучков на X называется -совершенным, когда квазиизоморфен ограниченному локально свободному комплексу называемому резольвентой комплекса на Существуют естественные понятия прямого образа (для собственного морфизма) и обратного образа (для независимых квадратов) и умножение, превращающие К в бивариантную теорию (ср. [Fulton - MacPherson 3]).

Если разлагается, как выше, то В частности, если гладкая, то тогда как Определим гомоморфизм

Для этого разложим как выше. Для -совершенного комплекса на X возьмем его резольвенту на и положим

где .

Теорема. Гомоморфизм не зависит от разложения и согласован с прямыми образами, обратными образами и умножением.

(За исключением согласованности с умножением, доказательство проводится в основном, как для теоремы 18.2. Существенная часть для умножения состоит в следующем. Пусть

— замкнутые вложения, есть -совершенный комплекс, а есть -совершенный комплекс. Пусть резольвента на резольвента на Предположим, что комплекс локально свободный, хотя, быть может, неограниченный сверху. Тогда произведение представляется комплексом Пусть резольвента на Согласованность с умножением означает, что для любого

На первый взгляд это представляется трудным, так как мы не знаем, как алгебраически связан с суть в работе [Fulton - MacPherson 3] заключалась в доказательстве такой топологической связи для комплексных многообразий. Имеется, однако, простая уловка. Элемент определяет гомоморфизм для любого если есть -совершенный комплекс на X и когерентный пучок на У, то переводит [3] в

Если - замкнутое вложение и резольвента на то

Из примера 18.3.12 мы получаем

Аналогом для является равенство

которое следует из спектральной последовательности для Отсюда получается так как сюръективно.)

Пример 18.3.17. Пусть -совершенный морфизм равноразмерных квазипроективных схем, Определим как член степени где определяется предыдущей процедурой.

(a) Если - плоский л.п.п. морфизм или -гладкая схема, то образ целочисленного класса из определенного в § 17.4. Члены степени меньше равны нулю.

(b) Пусть морфизмы, причем можно разложить в последовательность плоских морфизмов, л.п.п. морфизмов или морфизмов в гладкие схемы. Тогда

Неизвестно, верно ли это для целых коэффициентов (ср. пример 17.4.6). Для общего совершенного морфизма неизвестно, исчезают ли члены степени, меньшей и будет ли член степени d целочисленным. Если замкнутое вложение и резольвента 0? на это превращается в вопросы об исчезновении и целочисленности для локальных классов что кажется сомнительным, пример 18.3.14.

Пример 18.3.18. Для комплексных алгебраических схем имеются гомоморфизмы

где обозначает теорию гомологий (с локально замкнутыми носителями) топологической АТ-теории. Эти гомоморфизмы обладают свойством ковариантности и другими свойствами из теоремы 18.3. Если схема X неособа, образ есть класс ориентации Если

— характер Чженя в гомологиях, то композиция удовлетворяет тем же условиям и формулам, что и (В квазипроективном случае требуемое отображение построено в работе [Baum - Fulton - MacPherson 2]. Распространение на произвольные схемы делается, как в этом параграфе.)

Пример 18.3.19. Теорема Римана — Роха и двойственность Гротендика. Пусть ограниченный комплекс пучков на схеме X с когерентными пучками когомологий Предположим, что X вкладывается в гладкую схему. Пусть

где дуализирующий комплекс на X (ср. [Hartshorne 2]). Тогда для всех к

Если -схема Коэна — Маколея с дуализирующим пучком локально свободен, то

где

что следует также из двойственности Серра — Гротендика. (Если X вложено в гладкую схему резольвента на то резольвета , ср. [Fulton - MacPherson 3], §7.)

Пример 18.3.20. Для алгебраической схемы X пусть группа Гротендика пучков на X с полными носителями. Существует гомоморфизм

как в примере 10.2.8, обладающий ковариантностью для любых морфизмов и другими свойствами из теоремы 18.3. В частности, индуцирует изоморфизм