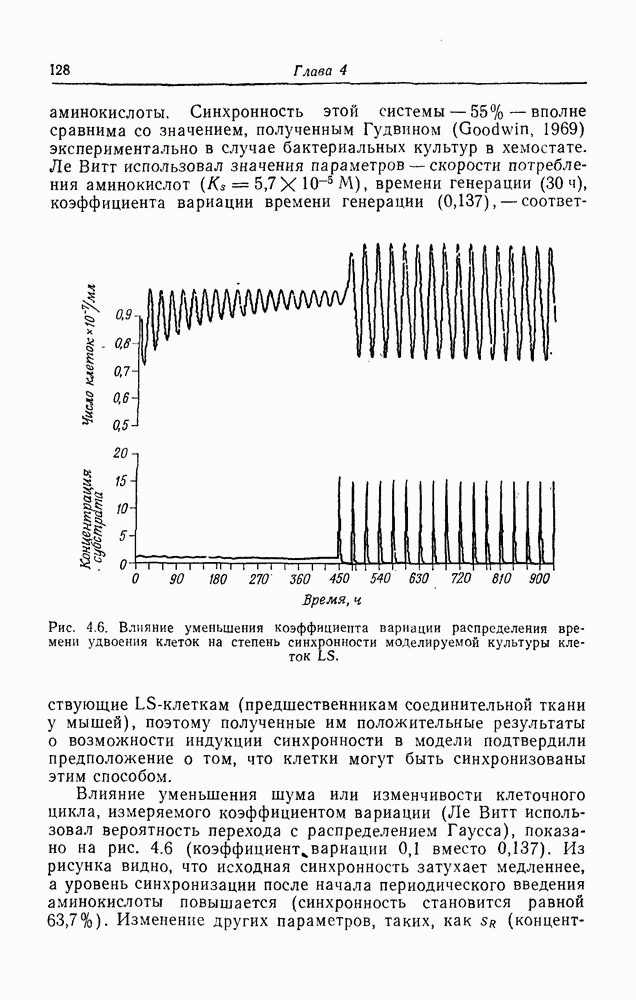
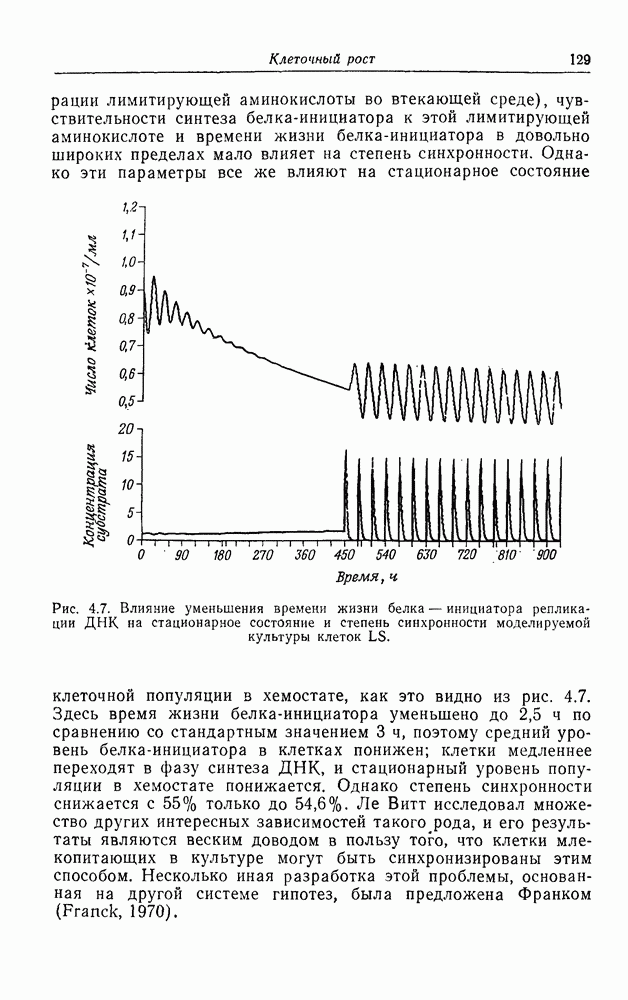
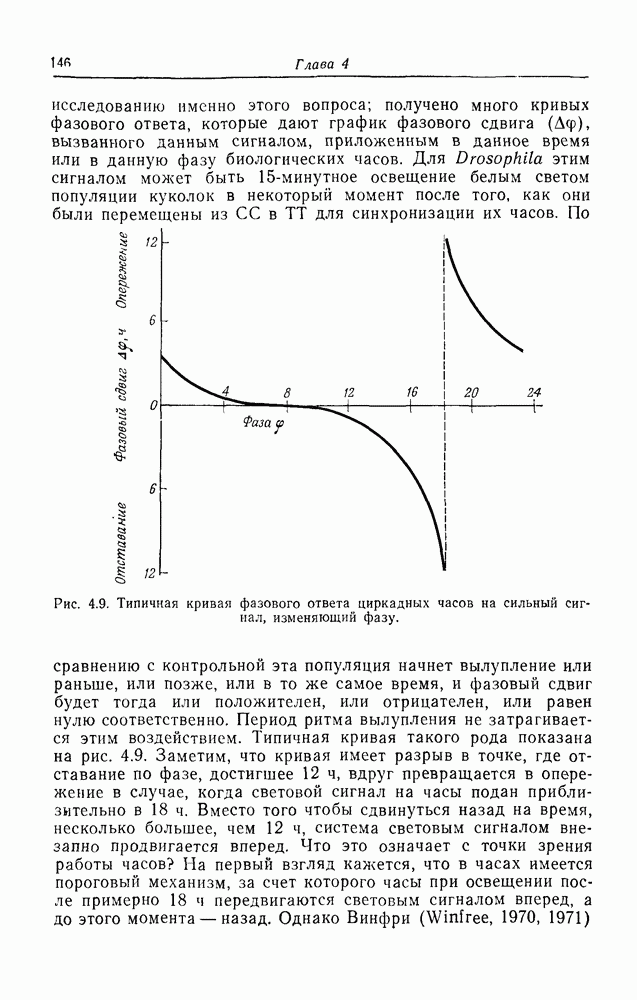
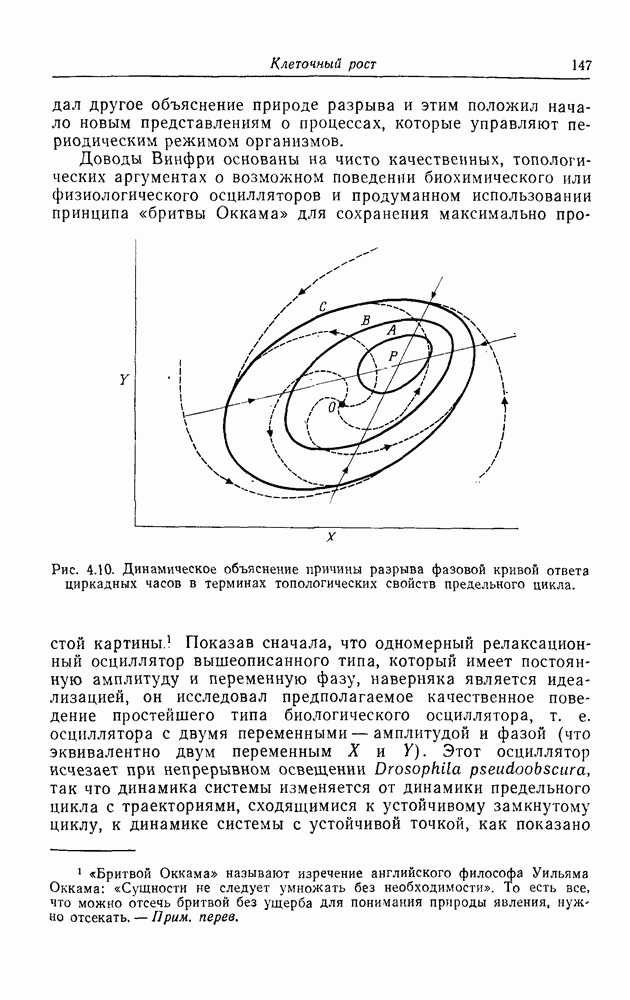
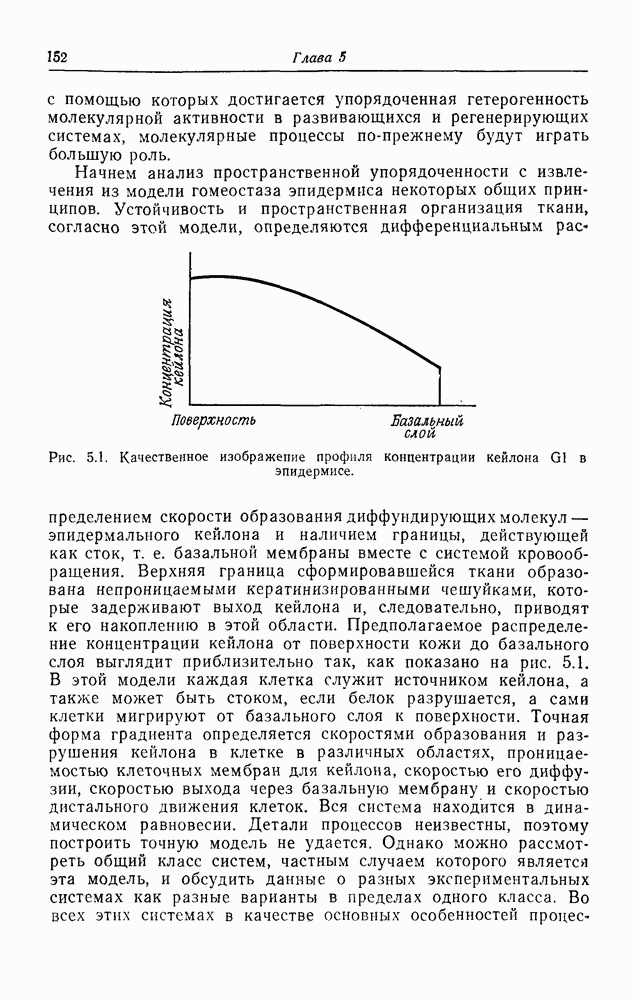
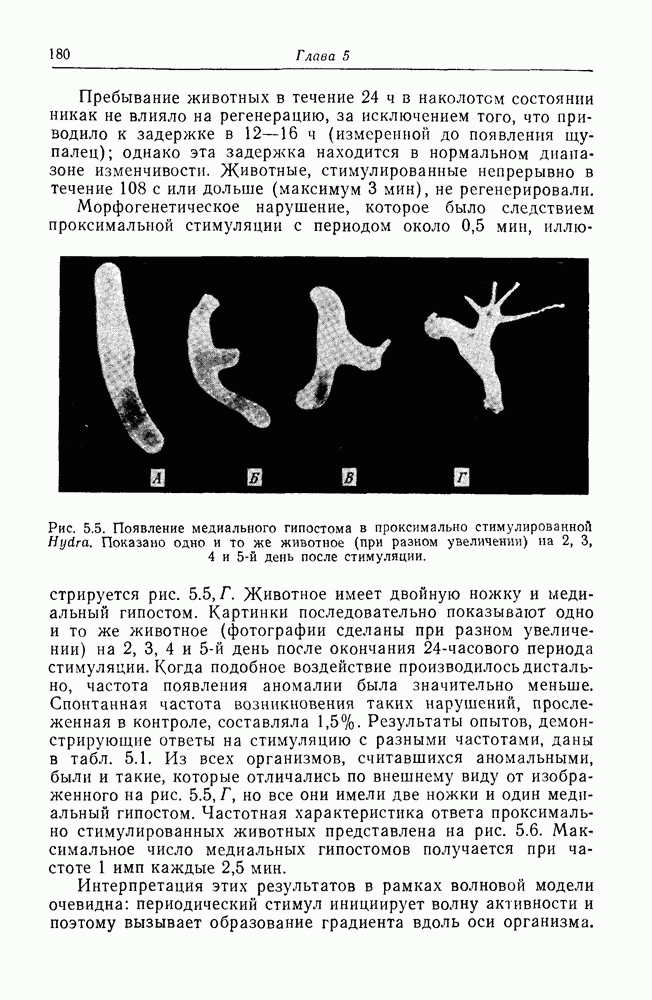
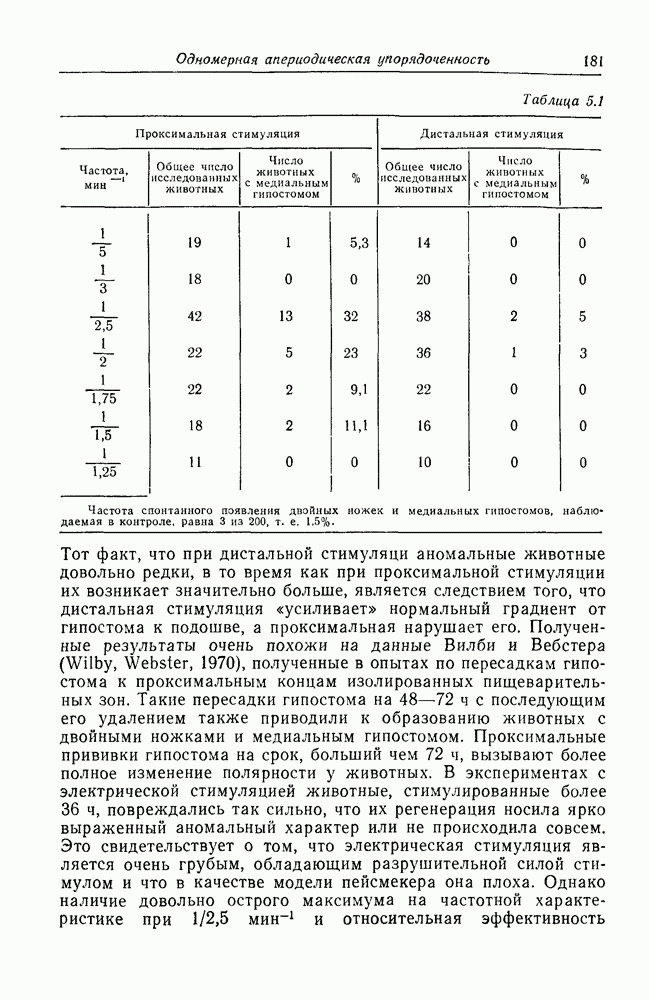
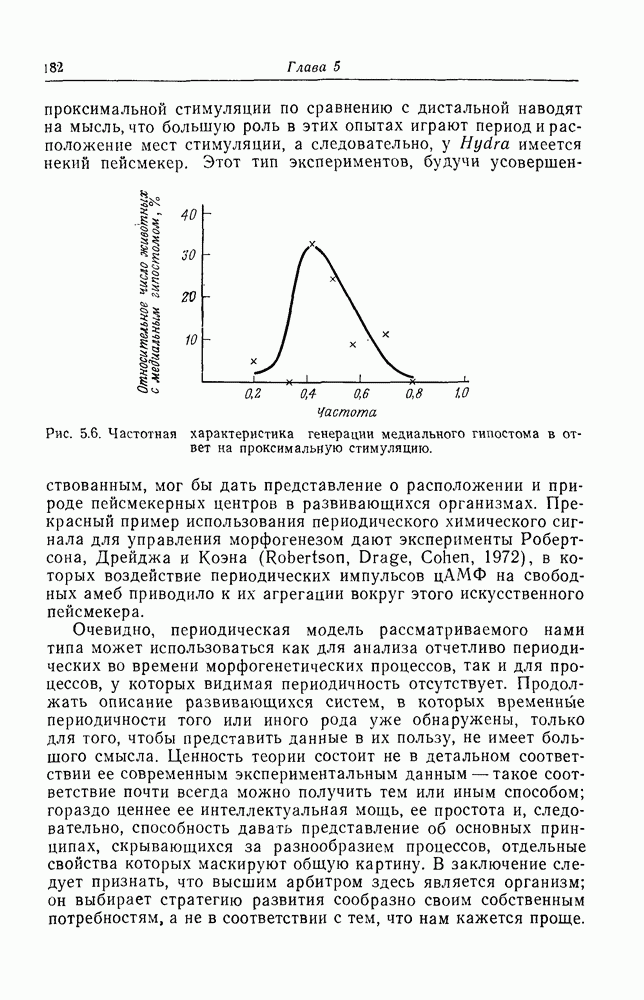
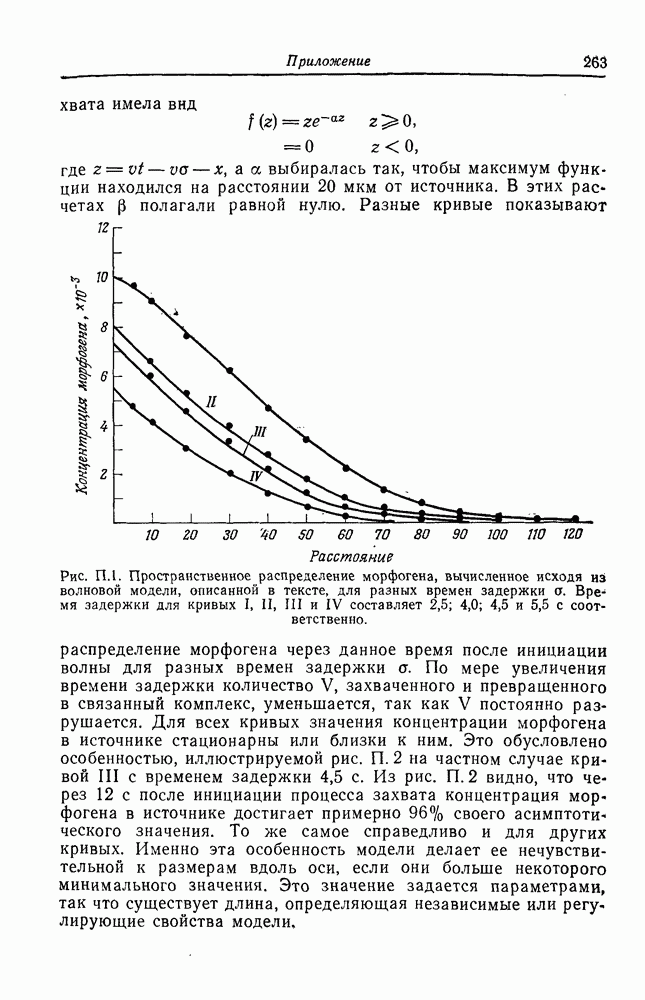
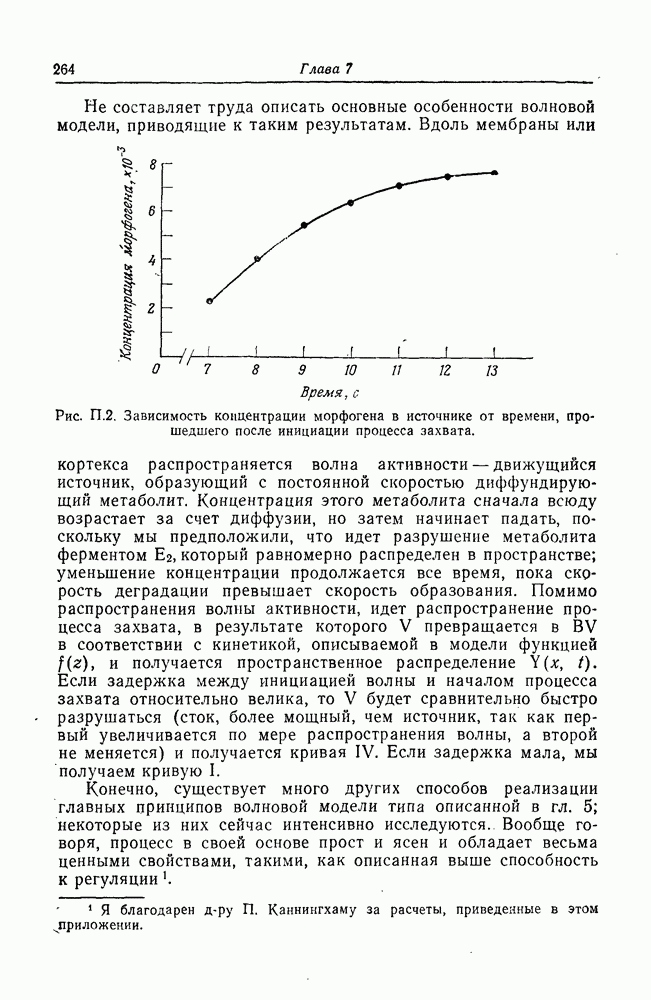
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Вероятностные модели клеточного цикла и его управления
Как отмечалось ранее, какую бы модель мы ни выбрали для описания поведения клеток во время клеточного цикла, в нее должен быть каким-то образом введен стохастический (вероятностный) фактор. Простейший вариант — это предположение, что молекулярные осцилляторы, ответственные за ритмическое поведение отдельной клетки, имеют различные фазы и частоты, так что суммарным результатом их активности оказывается «шумовой» цикл (Engleberg, 1968). Такая модель была бы детерминированной на молекулярном уровне и не рассматривала бы случайных процессов, таких, как спонтанная диссоциация комплексов репрессор — оператор или других молекулярных ассоциаций, участвующих в регуляции, флуктуаций скоростей реакций, обусловленных изменениями температуры, частоты столкновений, ориентации реагирующих молекул и т.д. Поскольку на молекулярном уровне картина биохимических процессов, происходящих в клетке, оказывается по своей природе «шумовой» (особенно если в этих процессах участвует мало молекул, как в случае процессов, регулирующих активность генов), то, по-видимому, наиболее естественно предположить, что стохастический фактор вводится главным образом на этом уровне. Согласно крайней точке зрения, детерминированные элементы клеточного поведения отсутствуют вообще в том смысле, что на осциллятор не накладывается никаких динамических ограничений, детерминирующих определенную форму колебаний с данной частотой и амплитудой. Можно считать, например, что клетка разделится, когда произойдет ряд событий, каждое из которых имеет данную вероятность появления как функцию времени, и что эти события могут происходить в любом порядке. Такая модель не предполагает существования причинного цикла в клетках, так как не налагает никаких ограничений на упорядоченность событий. Подобный поход был использован Раном (Rahn, 1932), что дало распределение вероятностей для времени генерации клеток, не очень хорошо соответствующее экспериментальным данным; такое соответствие можно было бы получить, сделав ряд дальнейших допущений, например присвоив разные вероятности разным событиям. Наиболее серьезным возражением против данного подхода представляется отсутствие в такой модели определенной S-фазы, за которой следует фаза 
что противоречит подавляющему большинству экспериментов. Кендолл (Kendall, 1948) модифицировал эту модель, предположив, что события, составляющие цикл, хотя и определяются зависящими от времени вероятностями, происходят тем не менее последовательно. Тогда действительно появляется цикл, но корреляция между одним циклом и следующим не обязана существовать, так как после окончания цикла процесс каждый раз начинается заново и никакого влияния одного цикла на другой не существует. Для динамического осциллятора это не так, поскольку его поведение зависит от начальных условий и степени устойчивости процесса. Известно, что времена генерации материнских и дочерних клеток скоррелированы, и поэтому, как показано рядом авторов (Schaechter et al., 1962; Powell, Errington, 1963; Kubitschek, 1966), требуется ввести некоторую связь между генерациями. Это может быть сделано различными способами, как описано Марром, Пэйнтером и Нильсоном (Магг, Painter, Nilson, 1959) в статье, где построена очень общая вероятностная модель, весьма удачно описывающая клеточный цикл.
Все имеющиеся модели клеточного цикла, за исключением модели Рана (Rahn, 1932), явно или неявно предполагают существование каких-то часов — постулат, который выводится из последовательного характера процесса, происходящего от одного клеточного деления до другого. Однако если решающий шаг в этой последовательности управляется чисто случайным событием, то можно задать вполне законный вопрос: проходят ли растущие и делящиеся клетки цикл? Доказательство того, что в эукариотическом ядре это действительно так, представлено в интересной статье Смита и Мартина (Smith, Martin, 1973). Согласно этим авторам, данные, полученные для распределения времен генерации в культурах различных типов клеток, решительно указывают на то, что действительно имеется случайное событие, которое управляет переходом клеток из некоторой стадии фазы  в детерминированную последовательность событий, ведущих к окончанию митоза. Хотя сама эта последовательность и стохастическая, она значительно более организована во времени, чем случайные инициирующие события, определяющие переход, на основании чего авторы считают необходимым ввести в фазу
в детерминированную последовательность событий, ведущих к окончанию митоза. Хотя сама эта последовательность и стохастическая, она значительно более организована во времени, чем случайные инициирующие события, определяющие переход, на основании чего авторы считают необходимым ввести в фазу  недетерминированное состояние А. Такое предположение очень интересно видоизменяет основную концепцию клеточного цикла, локализуя практически весь шум в одном событии, вместо того чтобы распределять его равномерно по всему циклу. Однако проблема построения модели, которая объясняла бы как устойчивость роста и процесса деления, так и их стохастические свойства, по-прежнему остается нерешенной. Я снова вкратце остановлюсь на этом вопросе в последней главе в связи с феноменологическим подходом к описанию клеточного цикла.
недетерминированное состояние А. Такое предположение очень интересно видоизменяет основную концепцию клеточного цикла, локализуя практически весь шум в одном событии, вместо того чтобы распределять его равномерно по всему циклу. Однако проблема построения модели, которая объясняла бы как устойчивость роста и процесса деления, так и их стохастические свойства, по-прежнему остается нерешенной. Я снова вкратце остановлюсь на этом вопросе в последней главе в связи с феноменологическим подходом к описанию клеточного цикла.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ЛИТЕРАТУРА
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ МЕТАБОЛИЧЕСКОЙ СИСТЕМЫ
- Устойчивость и закон действующих масс в метаболической системе
- Ингибирование по типу обратной связи в метаболических системах
- Аллостерические свойства ферментов
- Кооперативная ферментативная кинетика
- Цепи управления метаболизмом и их динамика
- Заключение
- Глава 2. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ ЭПИГЕНЕТИЧЕСКОЙ СИСТЕМЫ
- Индукция и репрессия генов
- Репрессия путей биосинтеза по типу обратной связи
- Контроль синтеза рибосомной РНК
- Динамика эпигенетических сетей
- Аналогия со статистической термодинамикой
- Аналогия с вычислительными машинами: клетка как конечный автомат
- Глава 3. МИТОТИЧЕСКИЙ И КЛЕТОЧНЫЙ ЦИКЛЫ
- Репликон и гипотеза инициатора
- Гипотеза репрессора инициации
- Эукариоты
- Представление клеточного цикла в виде последовательности стадий
- Клеточный цикл млекопитающих
- Управление скоростью цикла и клеточная дифференцировка
- Эпидермис млекопитающих и кейлонная теория
- Вероятностные модели клеточного цикла и его управления
- Глава 4. КЛЕТОЧНЫЙ РОСТ, СИНХРОННОСТЬ КЛЕТОЧНЫХ ЦИКЛОВ И БИОЛОГИЧЕСКИЕ ЧАСЫ
- Хемостат
- Адаптивное поведение хемостата
- Системы восстановления клеток
- Синхронизация клеток
- Суточные ритмы деления клеток в тканях млекопитающих
- Контактное торможение
- Клеточные часы
- Физиология клеточных часов
- Динамика часов, контролирующих вылупление личинок у Drosophila
- Глава 5. МОРФОГЕНЕЗ: ОДНОМЕРНАЯ АПЕРИОДИЧЕСКАЯ УПОРЯДОЧЕННОСТЬ
- Полярность и осевые градиенты
- Пейсмекеры и волны активности
- Морфогенез одноклеточных
- Мембраны и морфогенез
- Регуляция и устойчивость
- Периодические режимы у гидроидов
- Глава 6. МОРФОГЕНЕЗ: ПРОСТРАНСТВЕННЫЕ ПЕРИОДИЧНОСТИ И МНОГОМЕРНАЯ УПОРЯДОЧЕННОСТЬ
- Распространение волн и пространственные периодичности
- Эпидермис насекомых
- Мембрана и эпидермис насекомых
- Эпиморфоз: крыло цыпленка
- Волновая модель и эпиморфоз
- Локальная и глобальная упорядоченность: имагинальный диск и конечность таракана
- Ретино-тектальная проекция в зрительной системе амфибий
- Механизм образования двумерной проекции
- Глава 7. ОРГАНИЗМ КАК ПОЗНАЮЩАЯ И КООПЕРАТИВНАЯ СИСТЕМА
- Функциональная иерархия
- Обратные предельные системы
- Кооперативные взаимодействия и фазовые переходы в познающих системах
- Фазовые переходы и теория катастроф
- Коллективные моды в ритмических процессах
- Процессы генерации в познающих системах
- ПРИЛОЖЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ