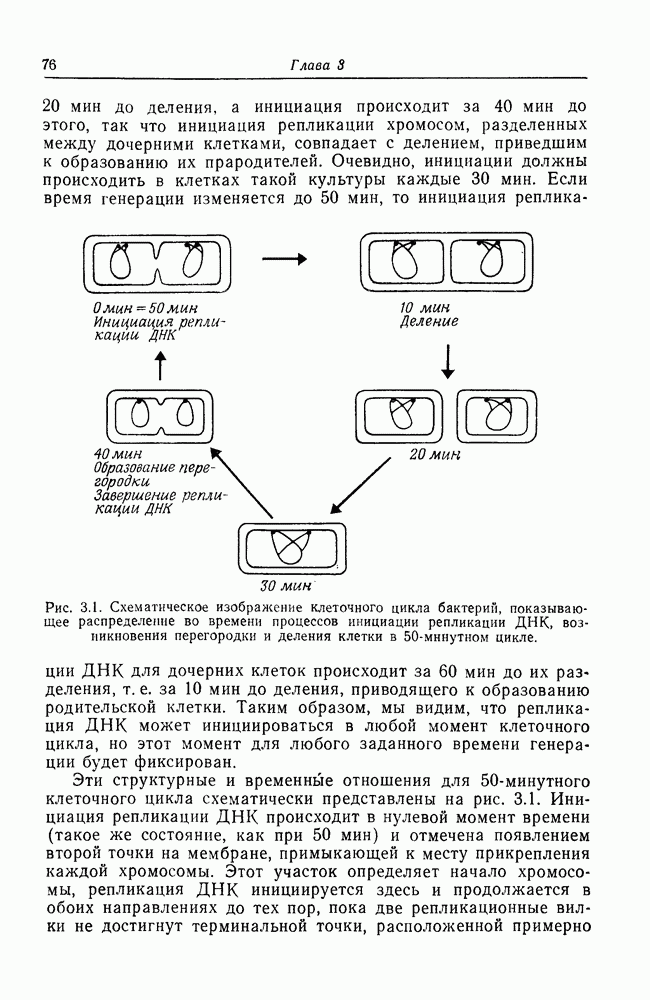
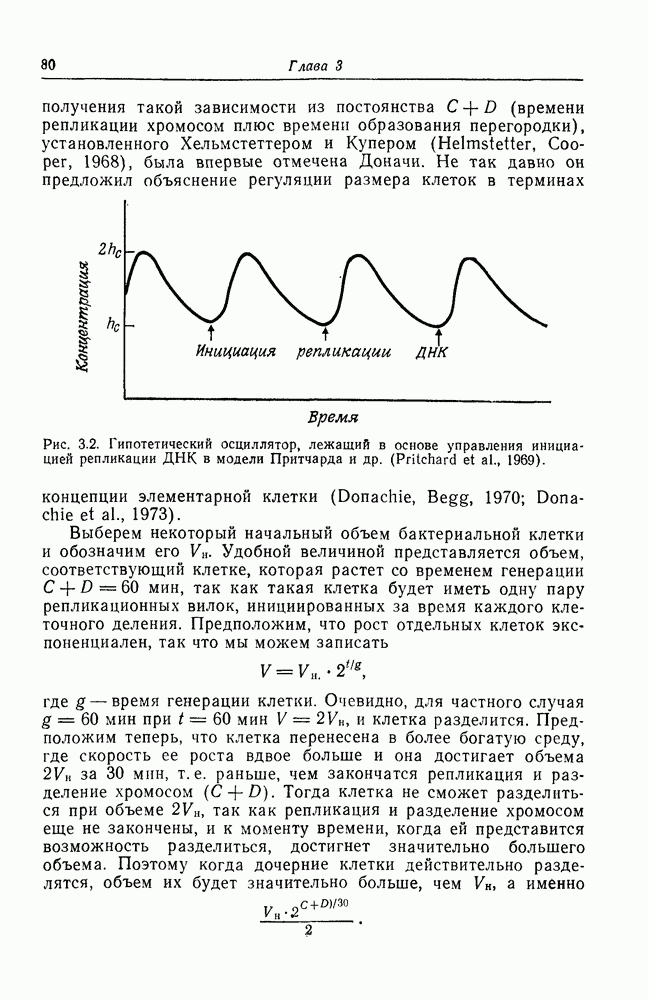
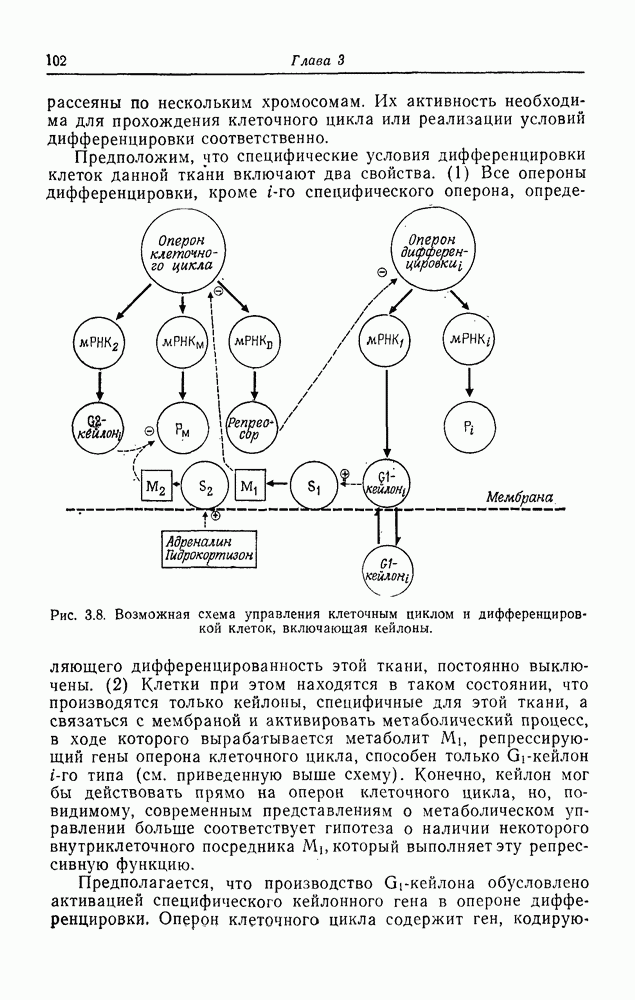
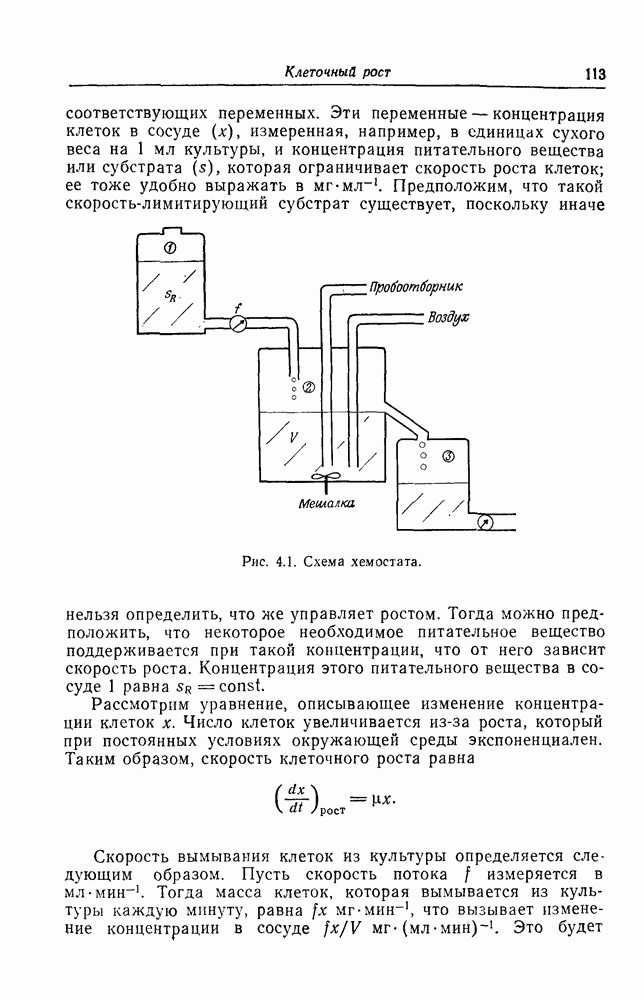
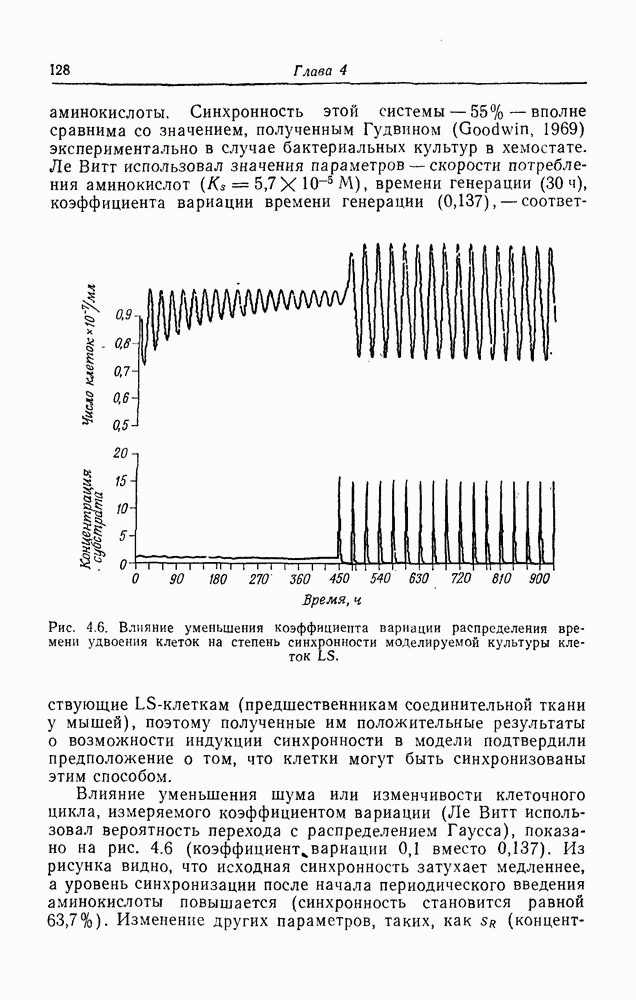
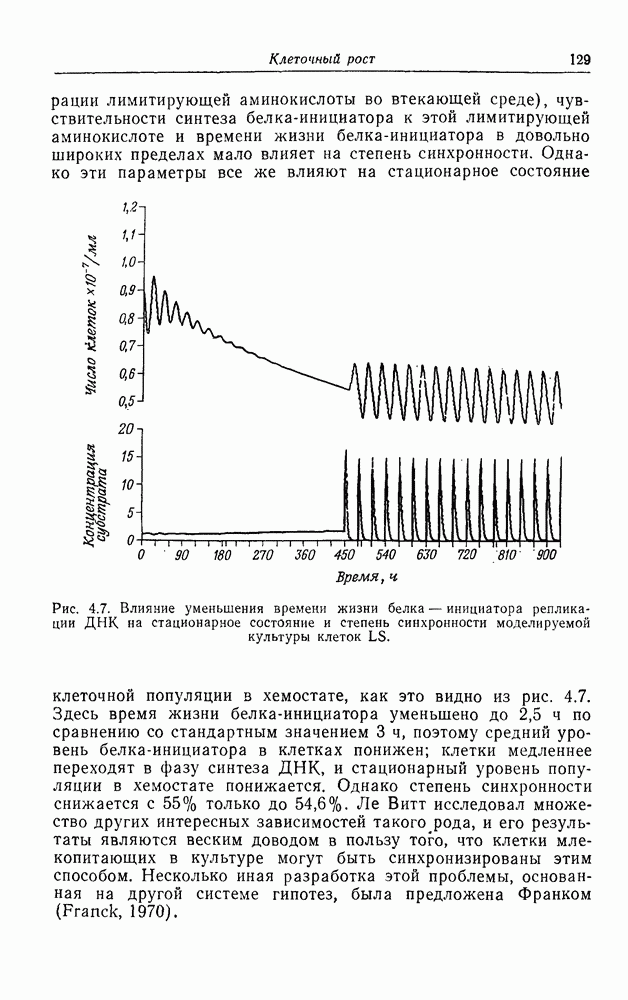
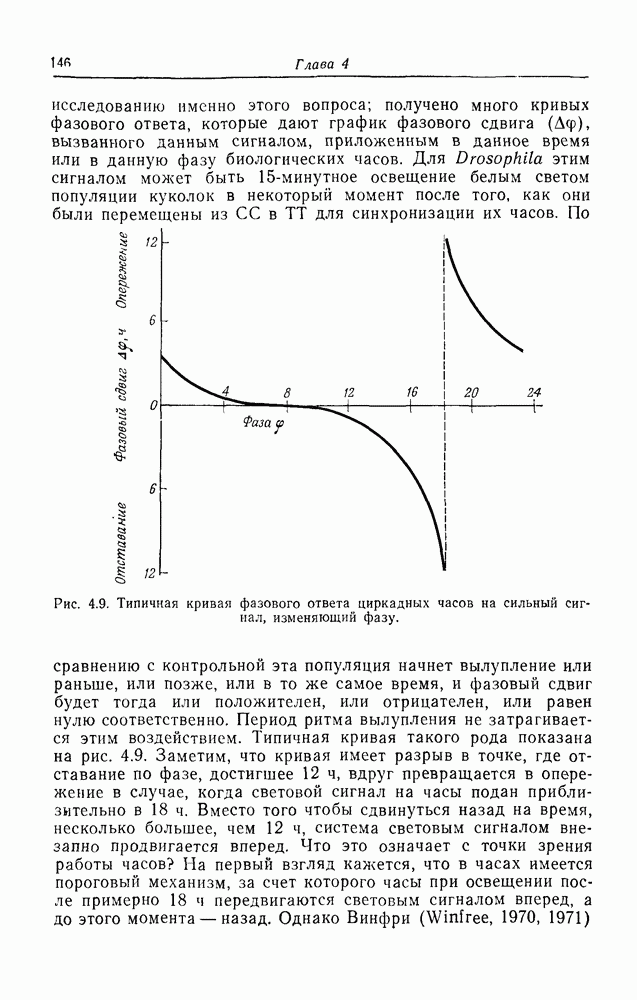
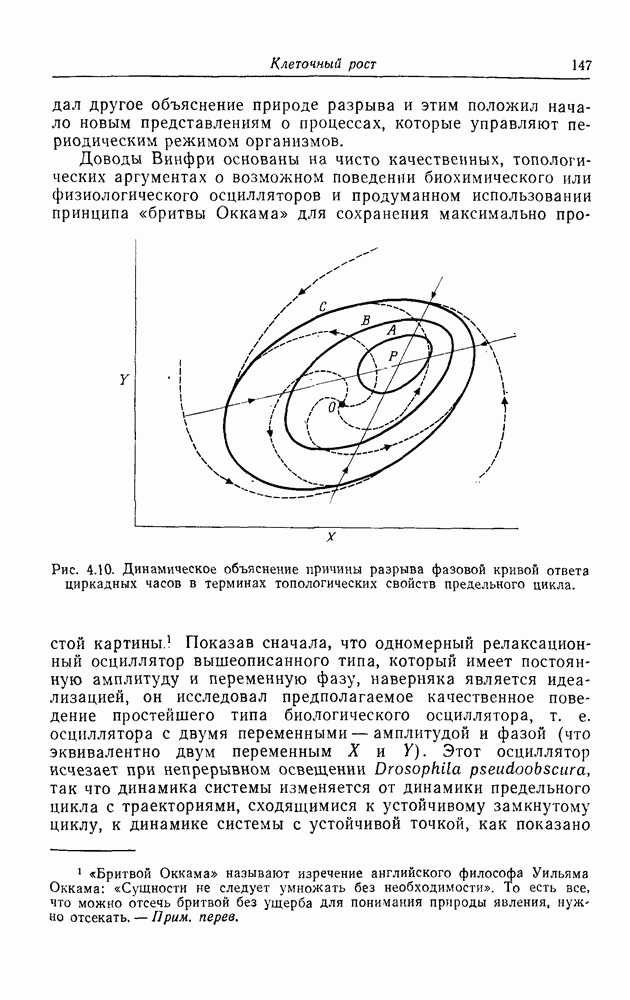
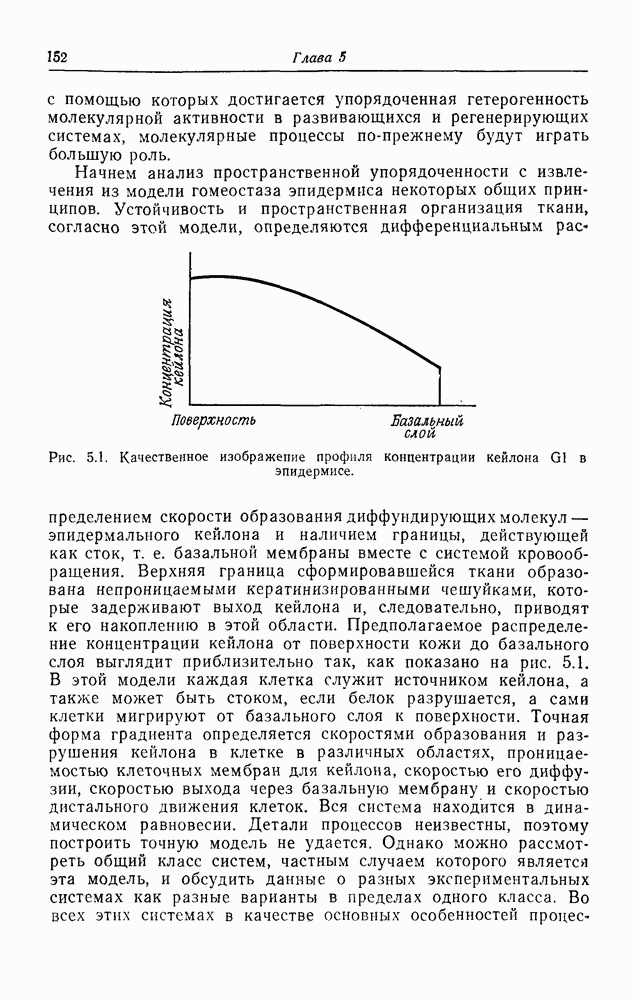
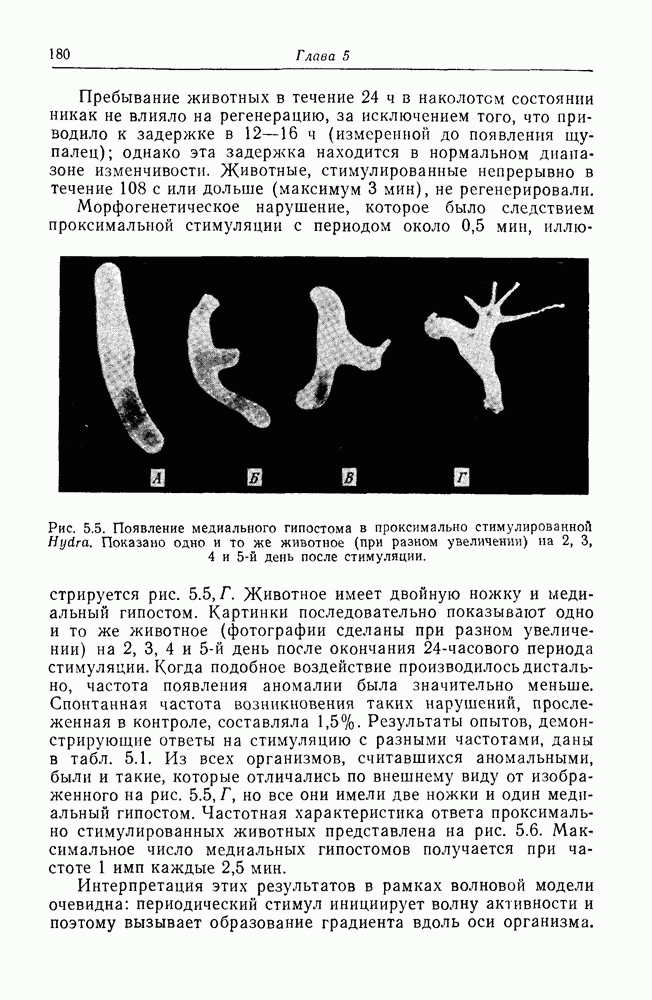
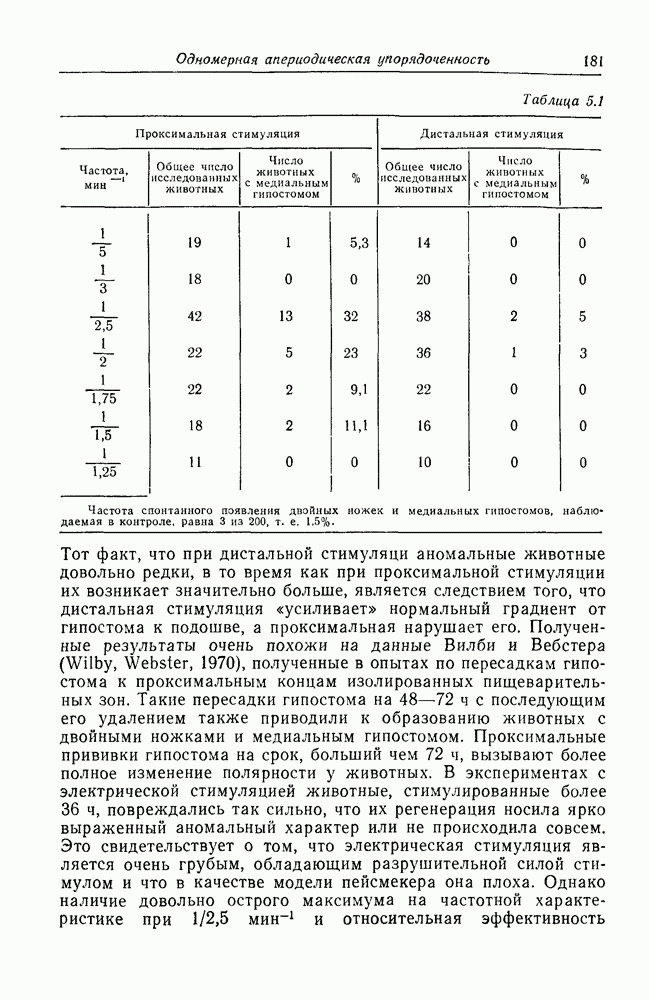
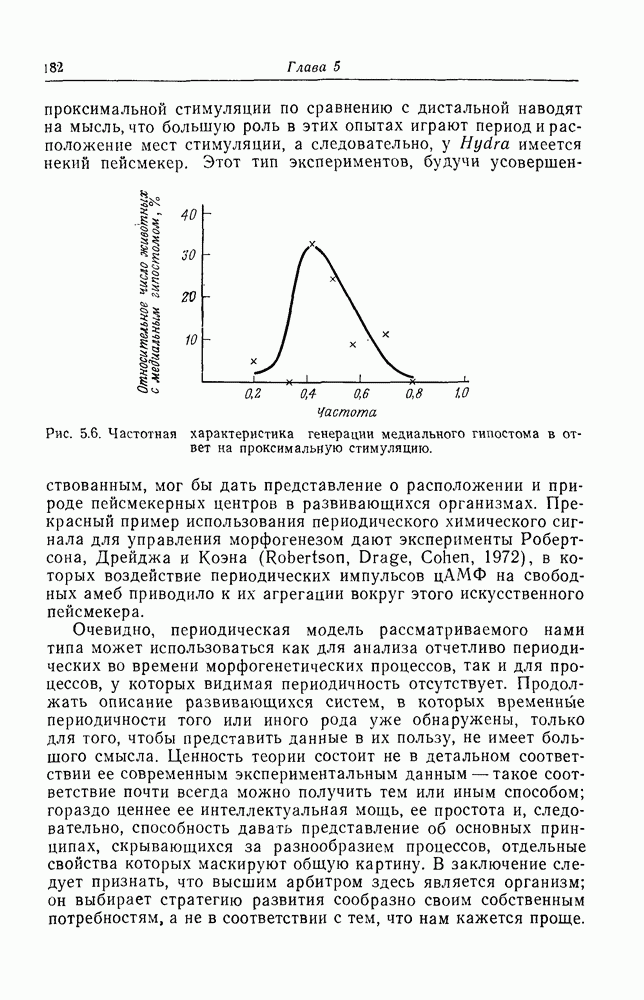
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Регуляция и устойчивость
Какова же биохимическая природа молекул, фигурирующих в волновой модели? Наиболее интересной из них является V — молекула, которая, будучи связана с активными центрами на мембране, играет роль неуловимого морфогена. Поскольку мы предположили, что эта молекула влияет на ионное равновесие и, следовательно, причастна к управлению свойствами мембран, нам нужно рассмотреть те метаболиты, которые могут оказывать такое действие. Трудность состоит в том, что таких метаболитов очень много. Однако наш выбор несколько ограничивается требованием, предъявляемым к модели, — она должна быть достаточно универсальной. Интересным кандидатом на роль V представляется сам циклический АМФ; в этом случае  будет аденилатциклазой, которая, как известно, в значительной степени связана с мембранными фракциями, а
будет аденилатциклазой, которая, как известно, в значительной степени связана с мембранными фракциями, а  — фосфодиэстеразой, растворимым ферментом. Вместо того чтобы действовать прямо на проницаемость мембраны, цАМФ сначала будет активировать протеинкиназы и таким образом создаст на мембране вторичный градиент ковалентно связанного фосфата. Это приведет к двум важным следствиям. Первое — в результате фос-форилирования и последующего электростатического взаимодействия и образования водородных связей между составными частями мембраны возрастет устойчивость распределения белков в мембране. Это уменьшит подвижность мембранных белков и стабилизирует градиент против диффузионного размывания, согласно жидкой мозаичной модели мембраны (Frye, Edidin, 1970; Nicolson, Singer, 1971; Gitler, 1972). Второе — фосфатные группы на связанных с мембраной белках будут стремиться связать двухвалентные катионы, такие, как
— фосфодиэстеразой, растворимым ферментом. Вместо того чтобы действовать прямо на проницаемость мембраны, цАМФ сначала будет активировать протеинкиназы и таким образом создаст на мембране вторичный градиент ковалентно связанного фосфата. Это приведет к двум важным следствиям. Первое — в результате фос-форилирования и последующего электростатического взаимодействия и образования водородных связей между составными частями мембраны возрастет устойчивость распределения белков в мембране. Это уменьшит подвижность мембранных белков и стабилизирует градиент против диффузионного размывания, согласно жидкой мозаичной модели мембраны (Frye, Edidin, 1970; Nicolson, Singer, 1971; Gitler, 1972). Второе — фосфатные группы на связанных с мембраной белках будут стремиться связать двухвалентные катионы, такие, как  , которые в свою очередь могут вызвать открывание каналов, по которым через мембраны проходят
, которые в свою очередь могут вызвать открывание каналов, по которым через мембраны проходят  или
или  с помощью механизма, аналогичного механизму действия родопсина в колбочках сетчатки (Наgins, 1972) и тропонина в мышце (Bremel, Weber, 1972, Hitchcock, 1973). Сейчас метаболическим последствиям локальных изменений ионных концентраций, вызванных связанными с мембраной
с помощью механизма, аналогичного механизму действия родопсина в колбочках сетчатки (Наgins, 1972) и тропонина в мышце (Bremel, Weber, 1972, Hitchcock, 1973). Сейчас метаболическим последствиям локальных изменений ионных концентраций, вызванных связанными с мембраной
белками, придается большое значение, так как это, по-видимому, один из первичных актов действия гормонов.
Циклический АМФ является только одним из возможных кандидатов на роль вещества V; другие кандидаты — циклический ГМФ, серотонин ( -окситриптамин), у-аминобутират и т. д. Все они — простые метаболиты, которые могут играть важную морфогенетическую роль в качестве модуляторов мембран и, следовательно, воздействовать на локальный метаболизм специфическими способами, приводящими к упорядоченной физиологической и структурной гетерогенности в клетках или развивающихся тканях. Это элементы универсального языка формирования структур в организмах.
-окситриптамин), у-аминобутират и т. д. Все они — простые метаболиты, которые могут играть важную морфогенетическую роль в качестве модуляторов мембран и, следовательно, воздействовать на локальный метаболизм специфическими способами, приводящими к упорядоченной физиологической и структурной гетерогенности в клетках или развивающихся тканях. Это элементы универсального языка формирования структур в организмах.
Особенность данной модели, предположительно обладающей регулирующими свойствами, состоит в том, что процессы, участвующие в образовании градиента, являются по существу локальными, т. е. метаболит V диффундирует из центра образования на связанных с мембраной ферментах  и захватывается белками В, расположенными в мембране по соседству. Как только волновой фронт уйдет на некоторое расстояние от любой данной области мембраны, так сразу в этой области будет захватываться очень мало диффундирующего метаболита, потому что центры связывания релаксируют к исходному неактивному состоянию. Таким образом, можно предположить, что, как только волна удалится на некоторое расстояние, уровень морфогена в источнике приблизится к своему максимальному значению. Это будет, конечно, зависеть от значений v и
и захватывается белками В, расположенными в мембране по соседству. Как только волновой фронт уйдет на некоторое расстояние от любой данной области мембраны, так сразу в этой области будет захватываться очень мало диффундирующего метаболита, потому что центры связывания релаксируют к исходному неактивному состоянию. Таким образом, можно предположить, что, как только волна удалится на некоторое расстояние, уровень морфогена в источнике приблизится к своему максимальному значению. Это будет, конечно, зависеть от значений v и  чем меньше D, тем более локальным будет процесс.
чем меньше D, тем более локальным будет процесс.
Важным моментом для всего процесса является природа функции захвата, описывающей, на каком расстоянии активируются центры связывания, а затем релаксируют к неактивному состоянию. В приложении, используя функцию

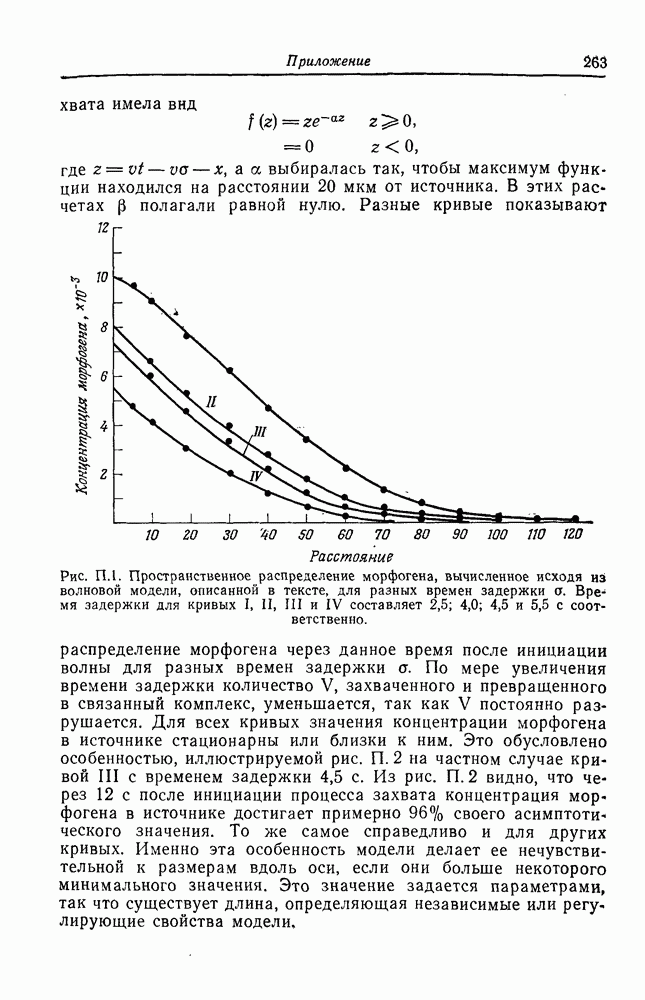
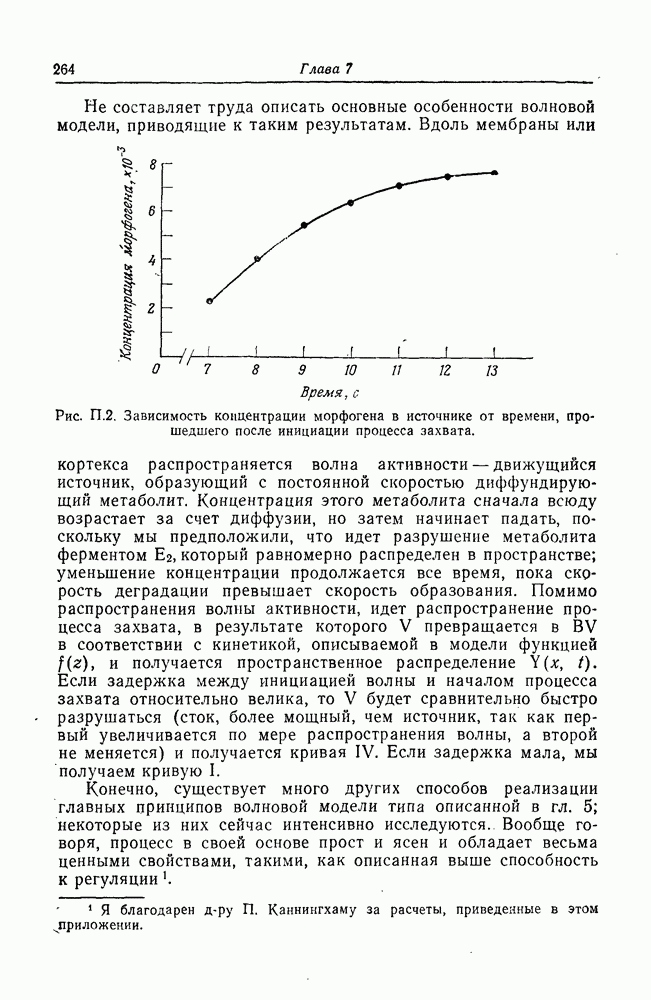
где а такова, что процесс связывания достигает максимума в 20 мкм позади того места, где начинается активация В, и затем спадает экспоненциально, мы покажем, что при  и задержке между возникновением волны и захватом в 4,5 с уровень морфогена достигает 96% своего максимального значения в точке, являющейся источником волны, после того как волна ушла на 60 мкм. Произвольно предположив, что 96% нормального диапазона значений уровня морфогена функционально эквивалентны всему диапазону, можно сделать вывод, что в волновой модели для приведенных выше значений параметров все осевые расстояния больше 60 мкм будут иметь одинаковый эффективный
и задержке между возникновением волны и захватом в 4,5 с уровень морфогена достигает 96% своего максимального значения в точке, являющейся источником волны, после того как волна ушла на 60 мкм. Произвольно предположив, что 96% нормального диапазона значений уровня морфогена функционально эквивалентны всему диапазону, можно сделать вывод, что в волновой модели для приведенных выше значений параметров все осевые расстояния больше 60 мкм будут иметь одинаковый эффективный
диапазон значений уровня морфогена. Меньшие расстояния будут недостаточными, т. е. регуляции не произойдет. Для разных организмов характерные значения параметров будут, конечно, различаться, так что расстояние, на котором нарушается независимость от размера, для них тоже будет разным. Мы видим, что волновая модель дает нам регуляцию как подарок: для того чтобы получить это биологически важное свойство, к основным постулатам не нужно добавлять никаких специальных предположений. Таким образом, в классе моделей, описываемых уравнениями (5.1), модель, основанная на процессах распространения волн, имеет то преимущество, что регуляция получается как естественное следствие основных постулатов. Кроме того, мембранная волновая модель объясняет, почему информация морфогенетического поля устойчива к возмущениям (центрифугированию цитоплазмы, удалению, гомогенизации и замене цитоплазмы) и каким образом на это поле можно воздействовать поворотом или трансплантацией сегментов кортикального слоя. Объяснить все эти данные с помощью моделей, включающих ферментативную активность и диффузию метаболитов в объеме типа модели Тьюринга (Turing, 1952) или Гирера и Мейнарта (Gierer, Meinhardt, 1972), довольно трудно.
Обратимся теперь к вопросу применения волновой модели к процессу морфогенеза гидроидов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ЛИТЕРАТУРА
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ МЕТАБОЛИЧЕСКОЙ СИСТЕМЫ
- Устойчивость и закон действующих масс в метаболической системе
- Ингибирование по типу обратной связи в метаболических системах
- Аллостерические свойства ферментов
- Кооперативная ферментативная кинетика
- Цепи управления метаболизмом и их динамика
- Заключение
- Глава 2. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ ЭПИГЕНЕТИЧЕСКОЙ СИСТЕМЫ
- Индукция и репрессия генов
- Репрессия путей биосинтеза по типу обратной связи
- Контроль синтеза рибосомной РНК
- Динамика эпигенетических сетей
- Аналогия со статистической термодинамикой
- Аналогия с вычислительными машинами: клетка как конечный автомат
- Глава 3. МИТОТИЧЕСКИЙ И КЛЕТОЧНЫЙ ЦИКЛЫ
- Репликон и гипотеза инициатора
- Гипотеза репрессора инициации
- Эукариоты
- Представление клеточного цикла в виде последовательности стадий
- Клеточный цикл млекопитающих
- Управление скоростью цикла и клеточная дифференцировка
- Эпидермис млекопитающих и кейлонная теория
- Вероятностные модели клеточного цикла и его управления
- Глава 4. КЛЕТОЧНЫЙ РОСТ, СИНХРОННОСТЬ КЛЕТОЧНЫХ ЦИКЛОВ И БИОЛОГИЧЕСКИЕ ЧАСЫ
- Хемостат
- Адаптивное поведение хемостата
- Системы восстановления клеток
- Синхронизация клеток
- Суточные ритмы деления клеток в тканях млекопитающих
- Контактное торможение
- Клеточные часы
- Физиология клеточных часов
- Динамика часов, контролирующих вылупление личинок у Drosophila
- Глава 5. МОРФОГЕНЕЗ: ОДНОМЕРНАЯ АПЕРИОДИЧЕСКАЯ УПОРЯДОЧЕННОСТЬ
- Полярность и осевые градиенты
- Пейсмекеры и волны активности
- Морфогенез одноклеточных
- Мембраны и морфогенез
- Регуляция и устойчивость
- Периодические режимы у гидроидов
- Глава 6. МОРФОГЕНЕЗ: ПРОСТРАНСТВЕННЫЕ ПЕРИОДИЧНОСТИ И МНОГОМЕРНАЯ УПОРЯДОЧЕННОСТЬ
- Распространение волн и пространственные периодичности
- Эпидермис насекомых
- Мембрана и эпидермис насекомых
- Эпиморфоз: крыло цыпленка
- Волновая модель и эпиморфоз
- Локальная и глобальная упорядоченность: имагинальный диск и конечность таракана
- Ретино-тектальная проекция в зрительной системе амфибий
- Механизм образования двумерной проекции
- Глава 7. ОРГАНИЗМ КАК ПОЗНАЮЩАЯ И КООПЕРАТИВНАЯ СИСТЕМА
- Функциональная иерархия
- Обратные предельные системы
- Кооперативные взаимодействия и фазовые переходы в познающих системах
- Фазовые переходы и теория катастроф
- Коллективные моды в ритмических процессах
- Процессы генерации в познающих системах
- ПРИЛОЖЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ