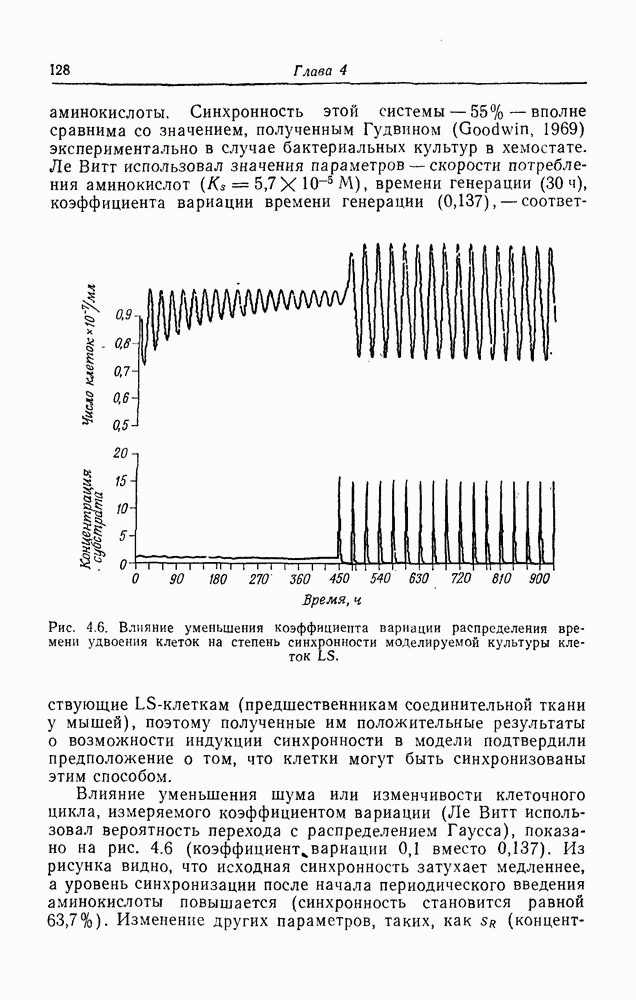
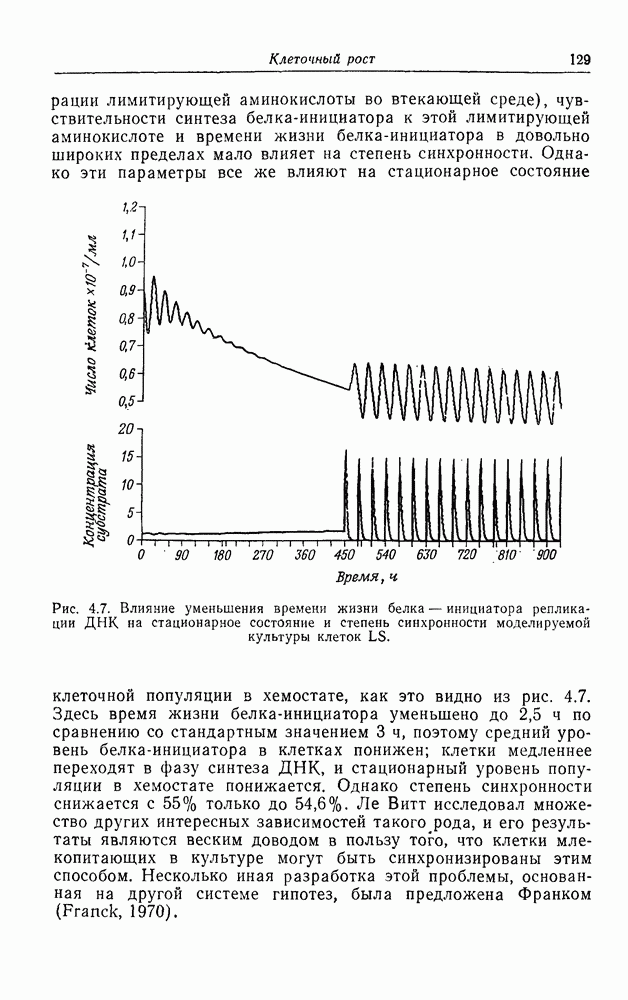
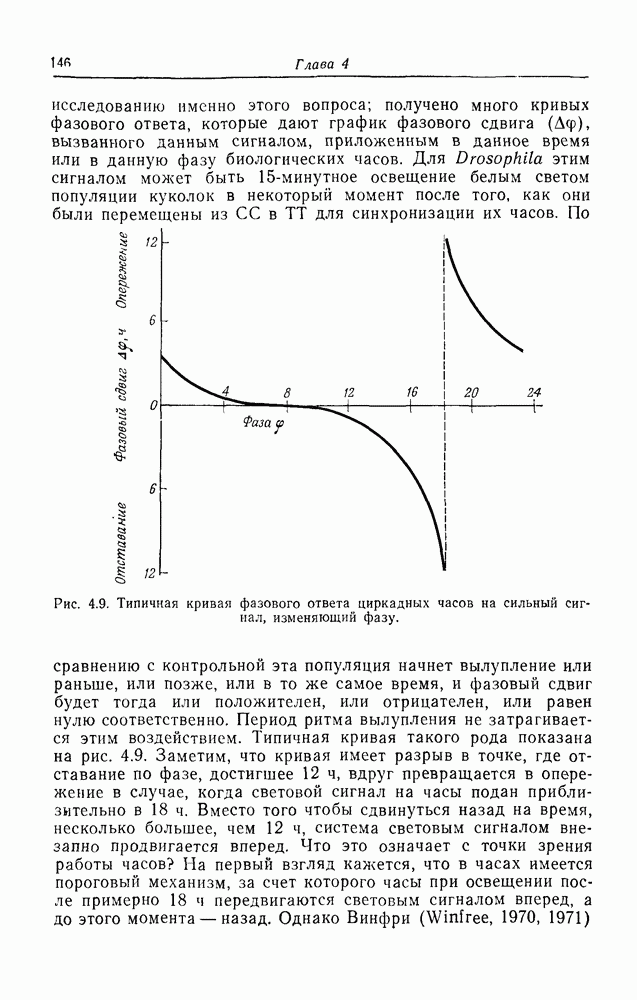
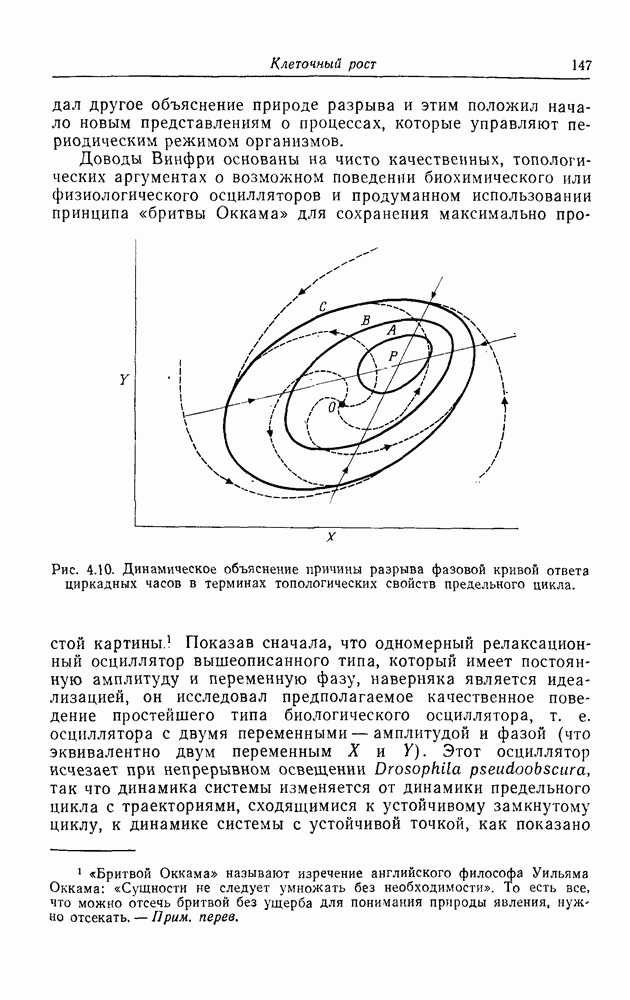
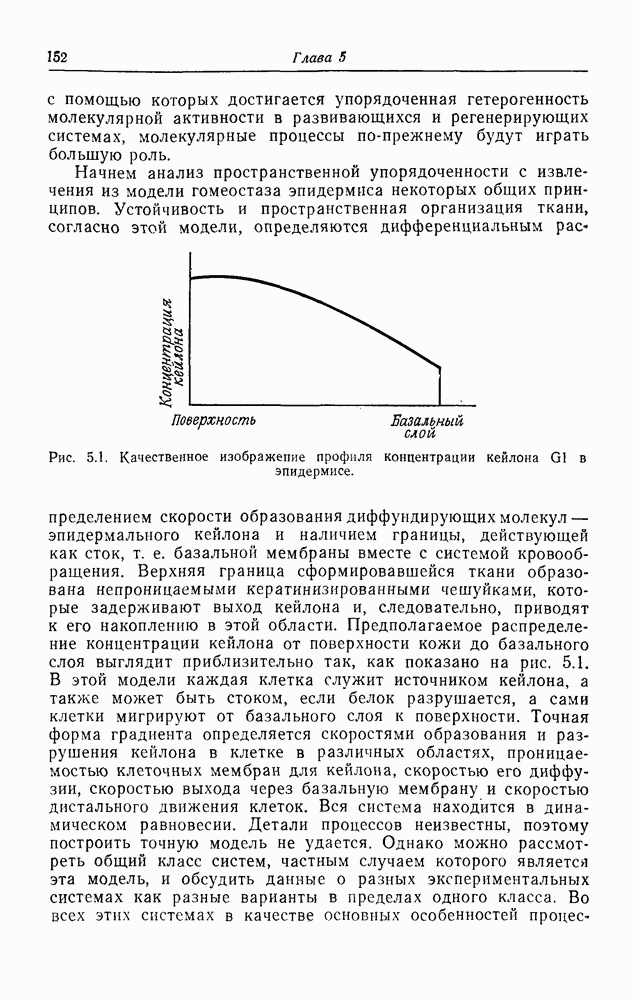
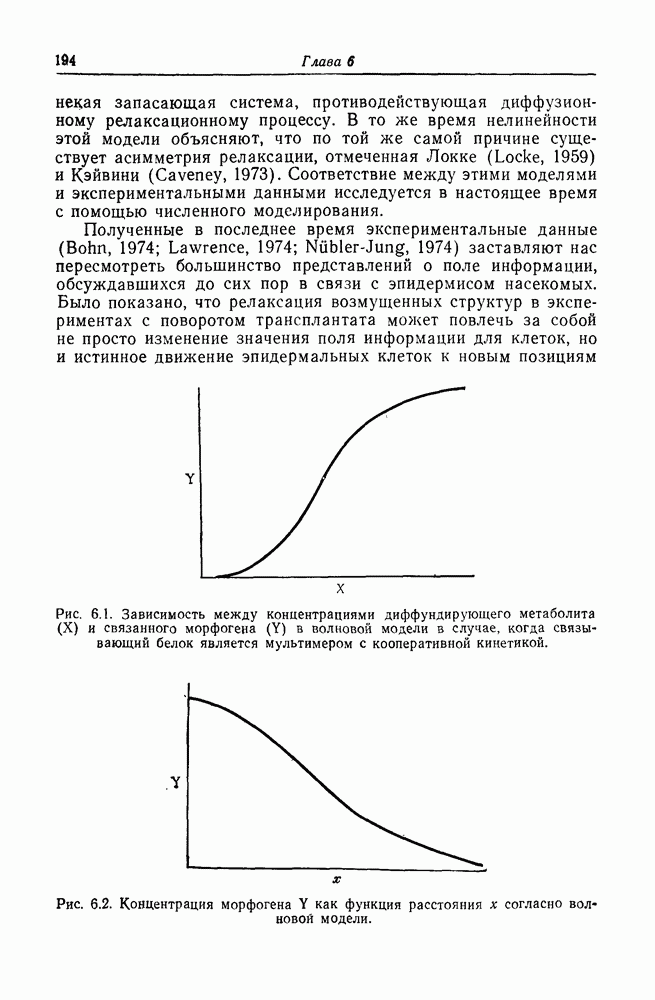
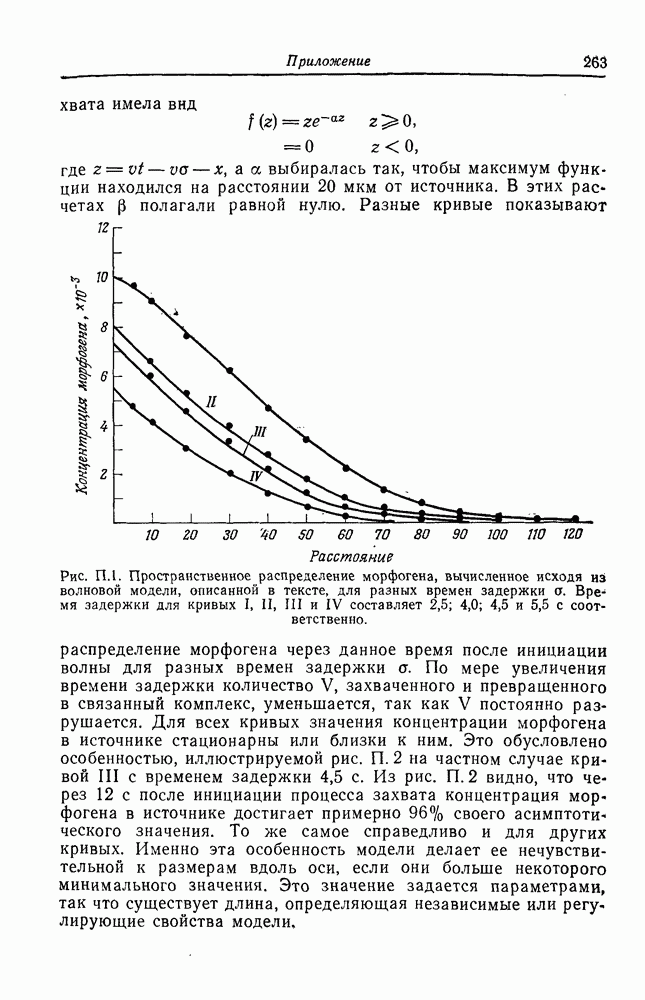
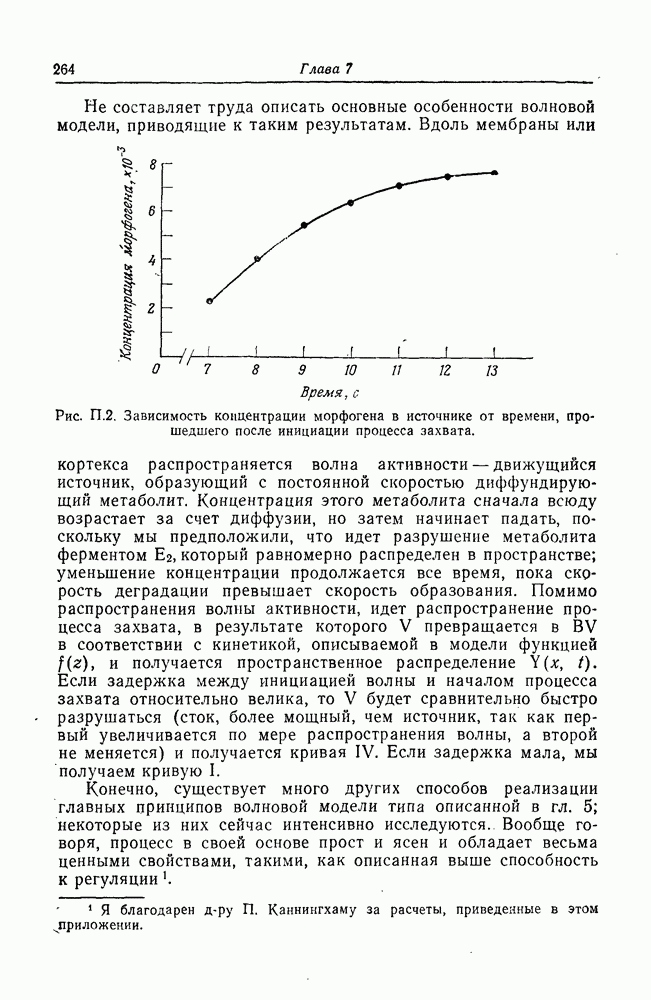
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Фазовые переходы и теория катастроф
Описанная выше модель перехода от невозбудимого состояния мембраны к возбудимому по существу идентична модели, используемой для описания конденсации газа. Она дает простейшее «микроскопическое» описание этого процесса. Существует более феноменологический, или макроскопический, подход к этой проблеме, основанный на законе Ван-дер-Ваальса для неидеального газа, где вводится малый поправочный член для учета несжимаемости молекул газа. Уравнение состояния для неидеального газа имеет вид

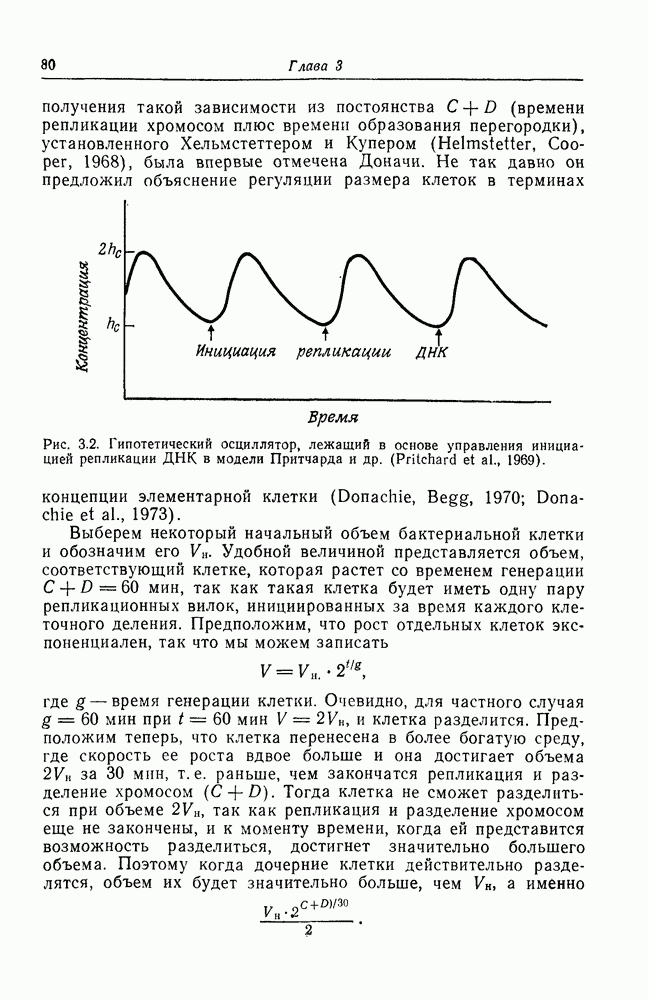
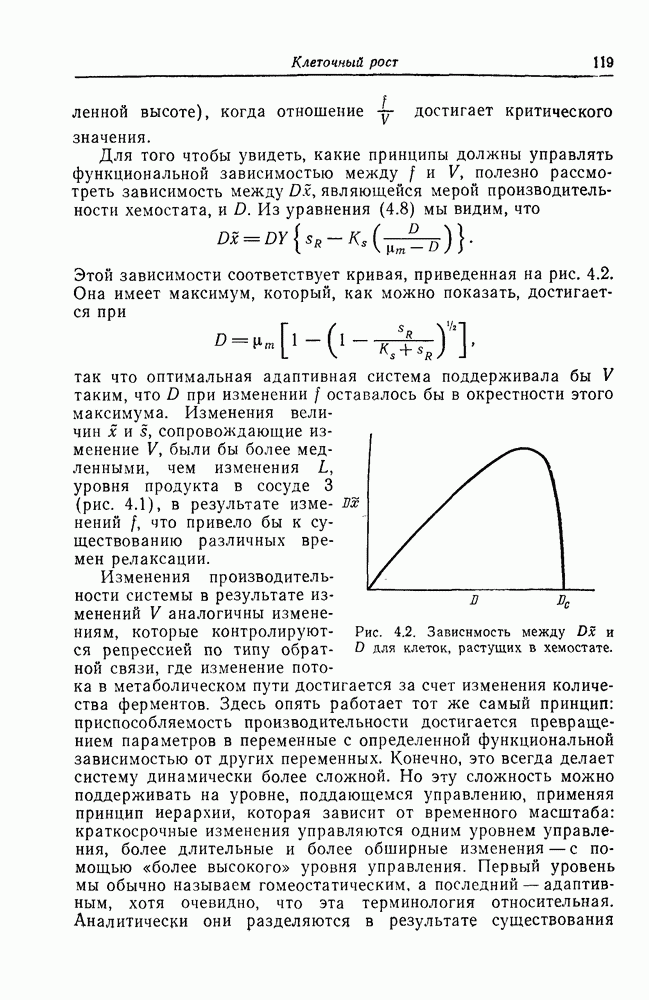
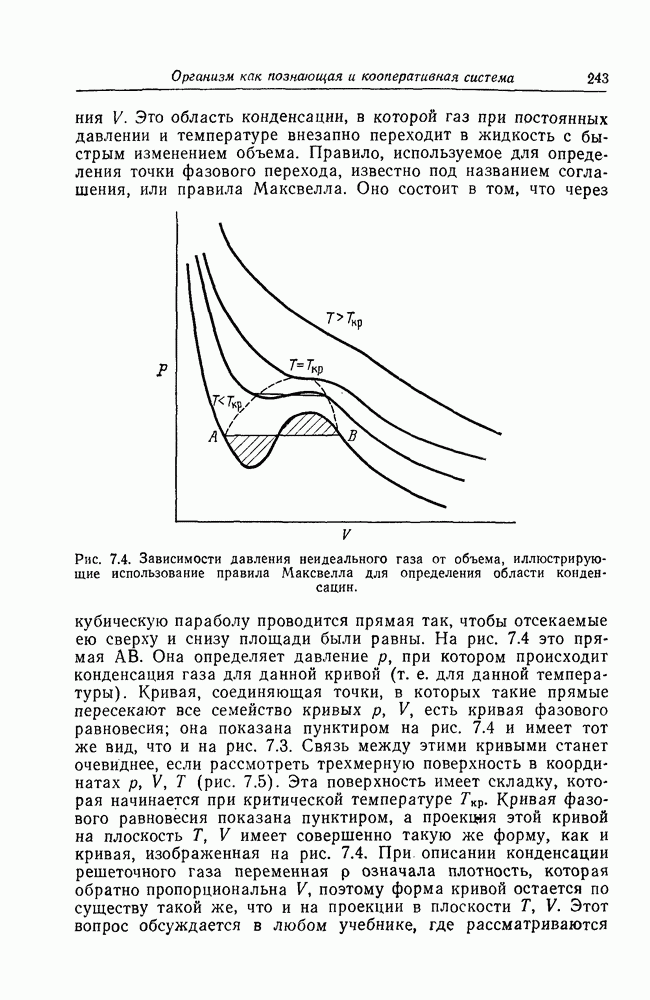
Зависимости  от V при различных значениях Т графически представлены на рис. 7.4. При некотором значении Т, названном критической температурой
от V при различных значениях Т графически представлены на рис. 7.4. При некотором значении Т, названном критической температурой  наклон кривой в точке перегиба равен нулю. Выше этой температуры существует однозначная зависимость между
наклон кривой в точке перегиба равен нулю. Выше этой температуры существует однозначная зависимость между  и V, а ниже ее для любого заданного в некоторой области значения
и V, а ниже ее для любого заданного в некоторой области значения  существуют три значения
существуют три значения
V. Это область конденсации, в которой газ при постоянных давлении и температуре внезапно переходит в жидкость с быстрым изменением объема. Правило, используемое для определения точки фазового перехода, известно под названием соглашения, или правила Максвелла. Оно состоит в том, что через кубическую параболу проводится прямая так, чтобы отсекаемые ею сверху и снизу площади были равны.

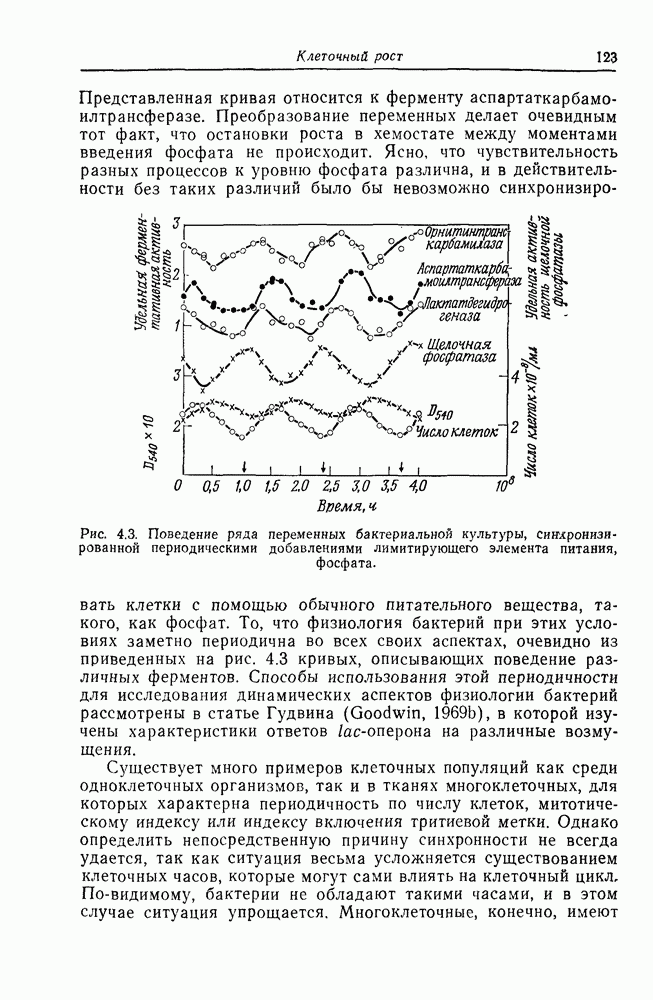
Рис. 7.4. Зависимости давления неидеального газа от объема, иллюстрирующие использование правила Максвелла для определения области конденсации.
На рис. 7.4 это прямая АВ. Она определяет давление  , при котором происходит конденсация газа для данной кривой (т. е. для данной температуры). Кривая, соединяющая точки, в которых такие прямые пересекают все семейство кривых
, при котором происходит конденсация газа для данной кривой (т. е. для данной температуры). Кривая, соединяющая точки, в которых такие прямые пересекают все семейство кривых  , есть кривая фазового равновесия; она показана пунктиром на рис. 7.4 и имеет тот же вид, что и на рис. 7.3. Связь между этими кривыми станет очевиднее, если рассмотреть трехмерную поверхность в координатах
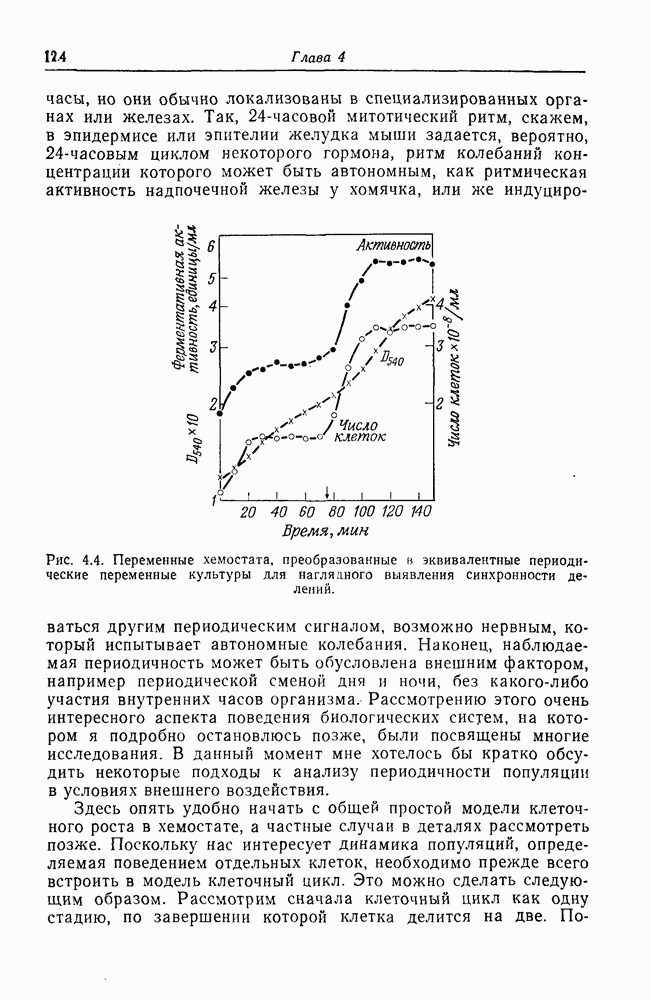
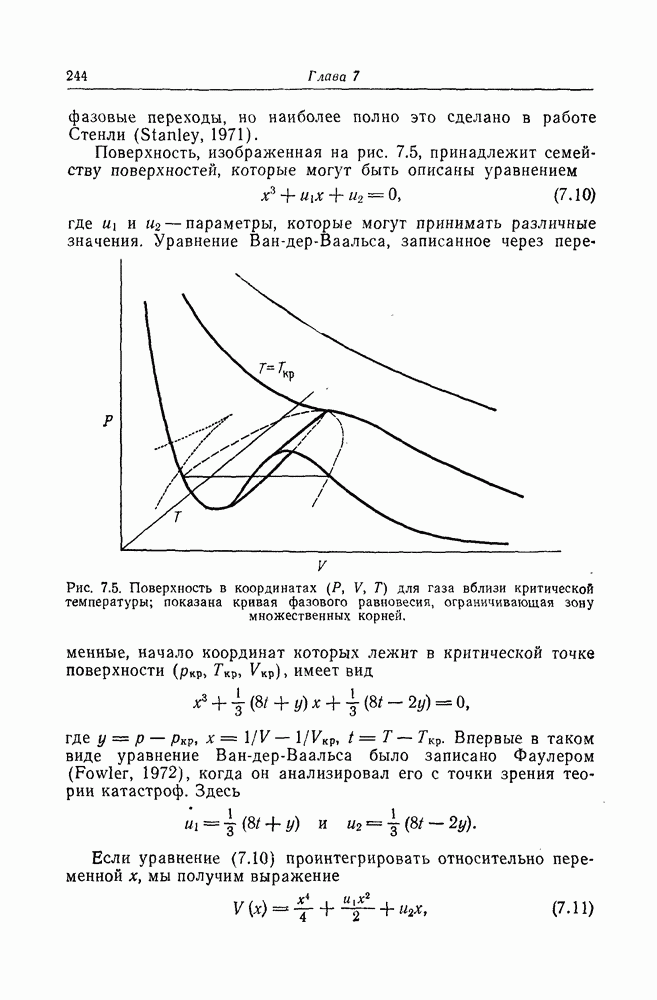
, есть кривая фазового равновесия; она показана пунктиром на рис. 7.4 и имеет тот же вид, что и на рис. 7.3. Связь между этими кривыми станет очевиднее, если рассмотреть трехмерную поверхность в координатах  (рис. 7.5). Эта поверхность имеет складку, которая начинается при критической температуре
(рис. 7.5). Эта поверхность имеет складку, которая начинается при критической температуре  Кривая фазового равновесия показана пунктиром, а проекция этой кривой на плоскость Т, V имеет совершенно такую же форму, как и кривая, изображенная на рис. 7.4. При описании конденсации решеточного газа переменная
Кривая фазового равновесия показана пунктиром, а проекция этой кривой на плоскость Т, V имеет совершенно такую же форму, как и кривая, изображенная на рис. 7.4. При описании конденсации решеточного газа переменная  означала плотность, которая обратно пропорциональна V, поэтому форма кривой остается по существу такой же, что и на проекции в плоскости Т, V. Этот вопрос обсуждается в любом учебнике, где рассматриваются
означала плотность, которая обратно пропорциональна V, поэтому форма кривой остается по существу такой же, что и на проекции в плоскости Т, V. Этот вопрос обсуждается в любом учебнике, где рассматриваются
фазовые переходы, но наиболее полно это сделано в работе Стенли (Stanley, 1971).
Поверхность, изображенная на рис. 7.5, принадлежит семейству поверхностей, которые могут быть описаны уравнением

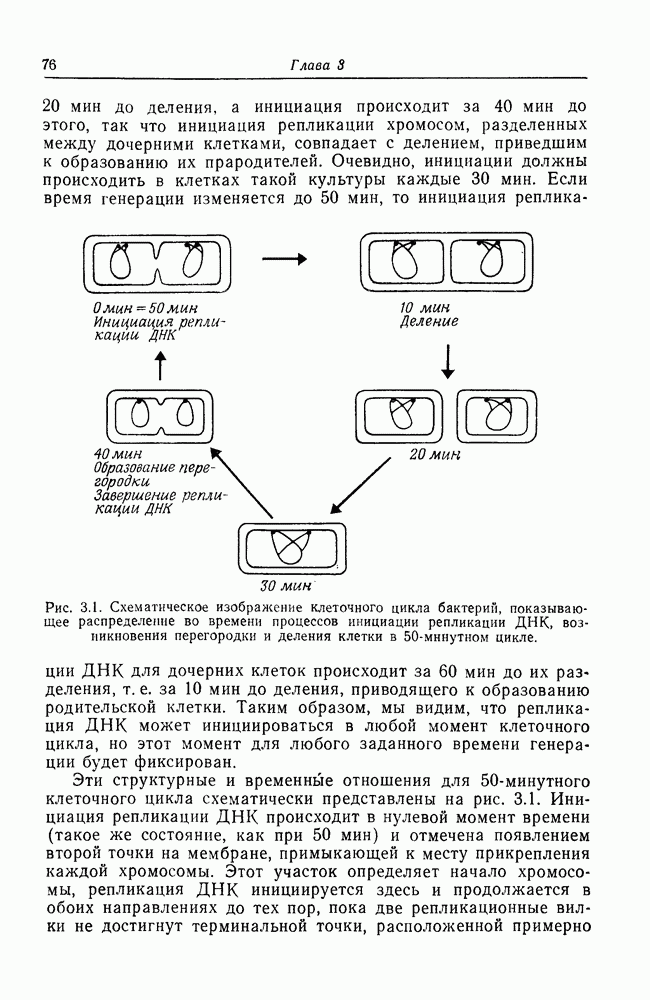
где  параметры, которые могут принимать различные значения.
параметры, которые могут принимать различные значения.

Рис. 7.5. Поверхность в координатах (Р, V, Т) для газа вблизи критической температуры; показана кривая фазового равновесия, ограничивающая зону множественных корней.
Уравнение Ван-дер-Ваальса, записанное через переменные, начало координат которых лежит в критической точке поверхности  , имеет вид
, имеет вид

где  . Впервые в таком виде уравнение Ван-дер-Ваальса было записано Фаулером (Fowler, 1972), когда он анализировал его с точки зрения теории катастроф. Здесь
. Впервые в таком виде уравнение Ван-дер-Ваальса было записано Фаулером (Fowler, 1972), когда он анализировал его с точки зрения теории катастроф. Здесь

Если уравнение (7.10) проинтегрировать относительно переменной  мы получим выражение
мы получим выражение

считая, что постоянная интегрирования равна нулю. Эта функция была названа Томом (Thom, 1970, b) универсальной деформацией сборки или катастрофой Римана—Гюгонио, зародыш или организующий центр которой равен  . В теории Тома существуют семь элементарных катастроф; каждая из них определяется в терминах потенциальной функции, аналогичной функции V в уравнении (7.11), и приводит к своей особой поверхности. Основное утверждение этой теории сводится к тому, что определенные биологические процессы могут быть описаны в терминах работы сил, приводящих систему к минимуму потенциальной поверхности, как это обычно делается в физике. Поверхность, изображенная на рис. 7.5, представляет собой поверхность, по которой «движется» газ при изменении параметров, т. е. на этой поверхности газ находится в состоянии равновесия. При изменении одной из переменных другие меняются согласно уравнению (7.10), полученному из уравнения (7.11) дифференцированием по х и приравниванием этой производной нулю для определения экстремумов
. В теории Тома существуют семь элементарных катастроф; каждая из них определяется в терминах потенциальной функции, аналогичной функции V в уравнении (7.11), и приводит к своей особой поверхности. Основное утверждение этой теории сводится к тому, что определенные биологические процессы могут быть описаны в терминах работы сил, приводящих систему к минимуму потенциальной поверхности, как это обычно делается в физике. Поверхность, изображенная на рис. 7.5, представляет собой поверхность, по которой «движется» газ при изменении параметров, т. е. на этой поверхности газ находится в состоянии равновесия. При изменении одной из переменных другие меняются согласно уравнению (7.10), полученному из уравнения (7.11) дифференцированием по х и приравниванием этой производной нулю для определения экстремумов

что возвращает нас к уравнению (7.10). Таким образом, Том представляет динамический процесс, например поведение газа при различных значениях давления, объема и температуры, как процесс, описываемый поверхностью, полученной из универсальной деформации элементарной катастрофы. Все приведенные выше рассуждения были не более чем описанием известных в физике фактов в новых математических терминах. Мы увидели, что на поверхностях состояний существуют некие представляющие особый интерес области, такие, которые определяют зоны сосуществования критических явлений, например зоны фазовых переходов. Это области, где имеются множественные корни (в данном случае три). Математически они определяются экстремумами поверхности, изображенной на рис. 7.5. Существование множественных корней V имеет место везде, где  и Т лежат в области сборки, которая получается при проецировании экстремумов поверхности на плоскость
и Т лежат в области сборки, которая получается при проецировании экстремумов поверхности на плоскость  , как это показано на рис. 7.5. Это область, в пределах которой могут происходить фазовые переходы типа ударной волны согласно терминологии Тома. Такие ударные волны он рассматривает как необходимую основу формообразования, точно так же как фазовый переход газ — жидкость описывает изменение в морфологии газа.
, как это показано на рис. 7.5. Это область, в пределах которой могут происходить фазовые переходы типа ударной волны согласно терминологии Тома. Такие ударные волны он рассматривает как необходимую основу формообразования, точно так же как фазовый переход газ — жидкость описывает изменение в морфологии газа.
Одной из проблем этой теории является вопрос о том, как интерпретировать поведение системы в окрестности математической особой точки. Мы уже видели подобный пример — правило Максвелла, но известны и другие рассмотренные Фаулером
(Fowler, 1972) примеры. Том (Thorn, 1970 а) также обсуждает правило Максвелла, его недостатки и возможность другой физической интерпретации математических особенностей. Им рассмотрен вопрос о флуктуациях и об их представлении в терминах теории катастроф. Весьма интересная работа о чисто динамической интерпретации теории катастроф опубликована Зиманом (Zeeman, 1972). Однако наибольшая трудность в приложении теории катастроф к морфогенетическим процессам, мне кажется, состоит в проблеме интерпретации не динамических аспектов теории, а ее пространственных результатов. Том (Thom, 1970 b) дает и пространственную, и временною интерпретации элементарных катастроф. Они основаны на предположении, что пространственные переменные входят в параметры, описывающие деформацию, характерную для данной катастрофы. При этом не вводится никаких правил интерпретации и существует полная свобода выбора, хотя сама пространственная интерпретация подразумевает некоторые ограничения на способ, которым пространственные переменные включаются в функции. Так, например, Том (Thom, 1970 b) использует катастрофу ласточкина хвоста для описания процесса гаструляции у амфибий, однако можно показать, что в этом случае для описания процесса вполне достаточна катастрофа сборки, развертывающаяся в рамках определенной пространственной геометрии. Именно это и было показано позже Зиманом (Zeeman, 1974).
Я думаю, что единственный способ подойти к решению этой проблемы состоит в том, чтобы применить теорию катастроф к некоторым биологическим процессам и посмотреть, действительно ли они дают полезные описания (т. е. посмотреть, помогают ли они нашей собственной познавательной деятельности). Тогда оценка ситуации, в которой они используются, может дать соответствующие правила их интерпретации. Отметим, что название «теория катастроф» не очень удачно; оно отражает небиологические последствия динамических разрывов, а все дело в том, что разрывы приводят к беспорядку, а не сопутствуют увеличению упорядоченности. В инженерном смысле это название кажется вполне уместным, что и показали очень интересные исследования Томпсона (Thompson, 1975), но в биологии разрывы состояния, лежащие в основе морфогенеза, ни в каком смысле не являются катастрофичными. До тех пор пока биологи будут применять теории, являющиеся результатом небиологических исследований, они будут испытывать эти терминологические неудобства. Те же замечания относятся и к теории диссипативных структур, разработанной Глансдорфом и Пригожиным (Glansdorff, Prigogine, 1971). Термин «диссипативный» возник в результате применения термодинамического подхода, для которого
объектом исследования является замкнутая система, к открытой, далекой от равновесия системе, для которой необходимо «диссипативное» описание. Все реальные системы в действительности открытые; замкнутость — это удобный способ описания, а биологические системы не только открытые, но и упорядоченные. Диссипация энергии — аксиоматическое свойство открытой системы, но оно не дает понимания причин биологической упорядоченности. Я надеюсь, что при построении теории процессов генерации в познающих системах удастся найти более подходящий язык для описания биологической организации и освободиться от нечеткой терминологии теории катастроф и диссипативных структур.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ЛИТЕРАТУРА
- ПРЕДИСЛОВИЕ АВТОРА
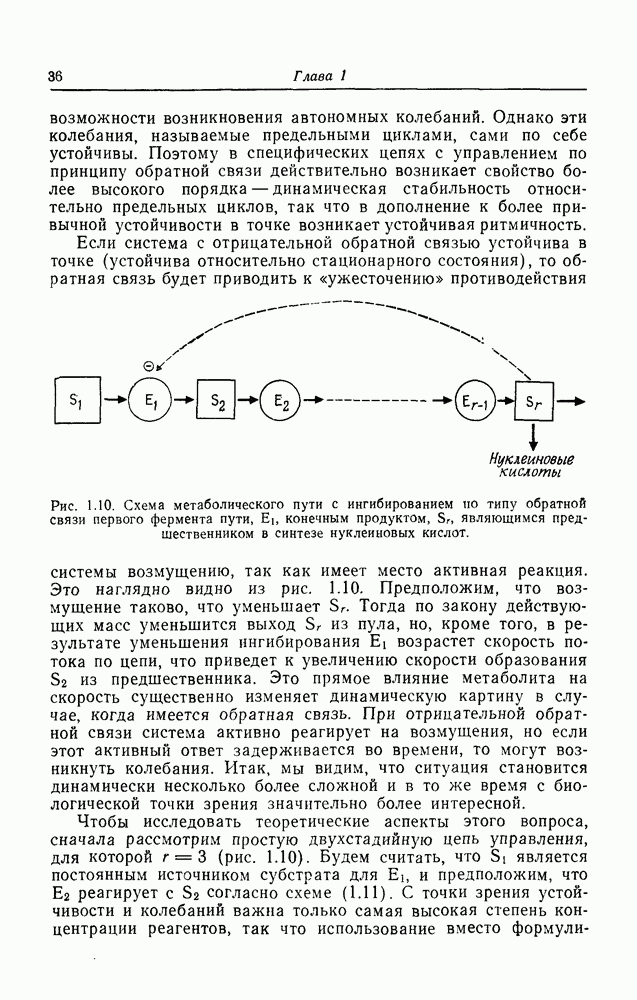
- Глава 1. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ МЕТАБОЛИЧЕСКОЙ СИСТЕМЫ
- Устойчивость и закон действующих масс в метаболической системе
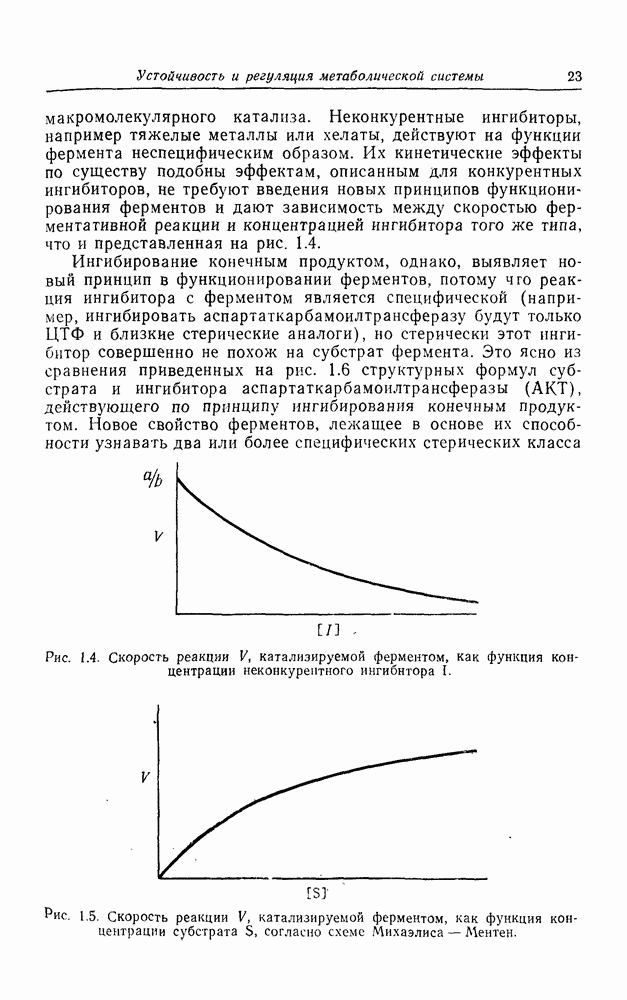
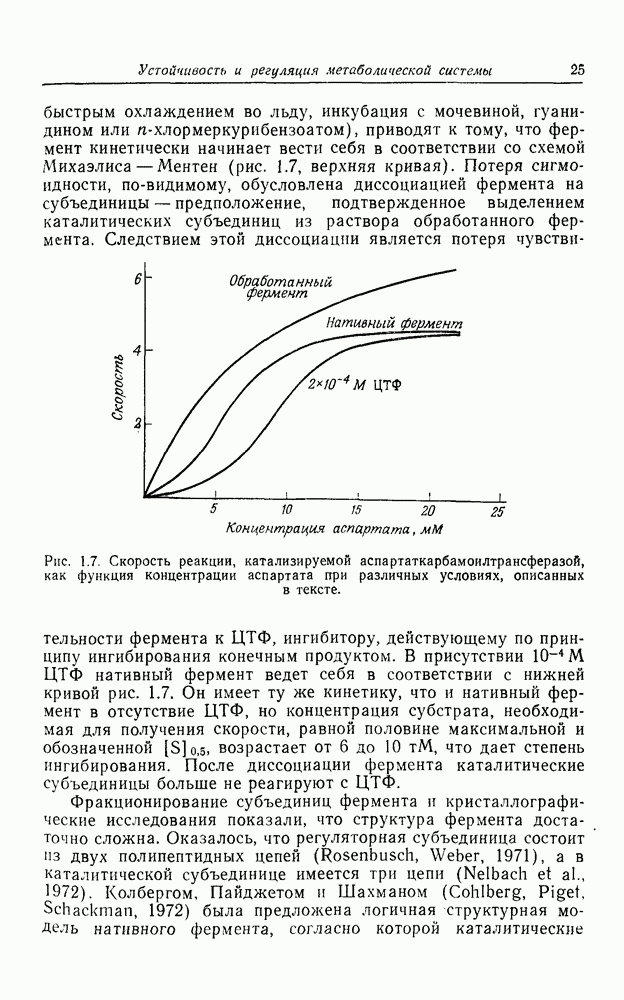
- Ингибирование по типу обратной связи в метаболических системах
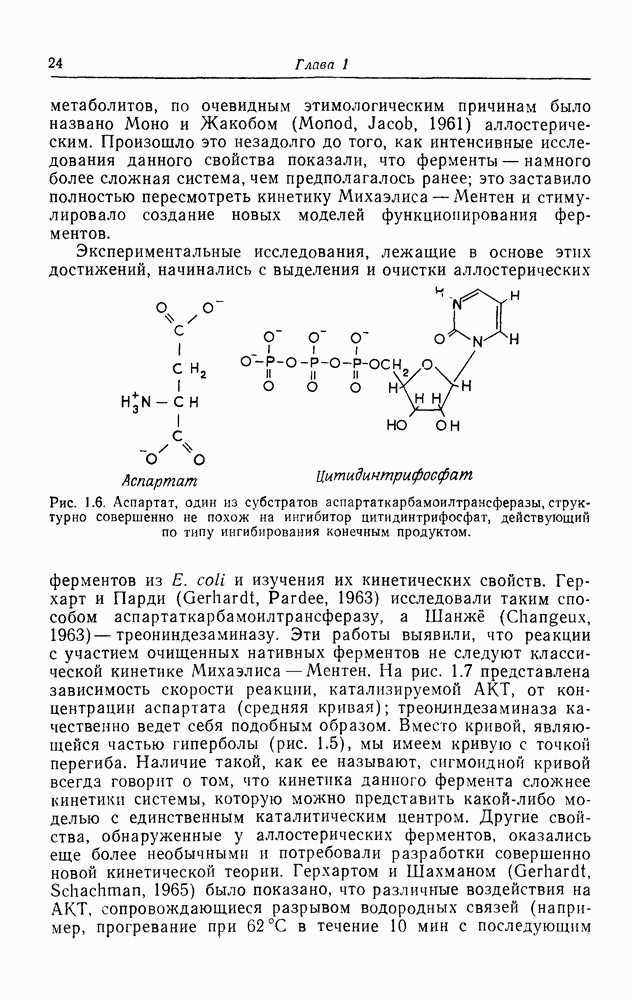
- Аллостерические свойства ферментов
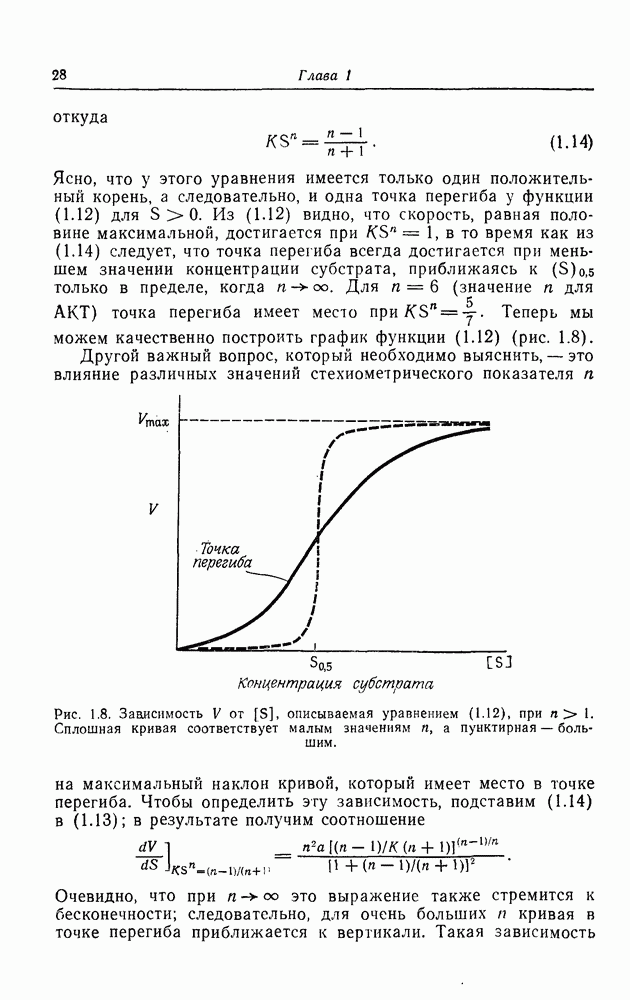
- Кооперативная ферментативная кинетика
- Цепи управления метаболизмом и их динамика
- Заключение
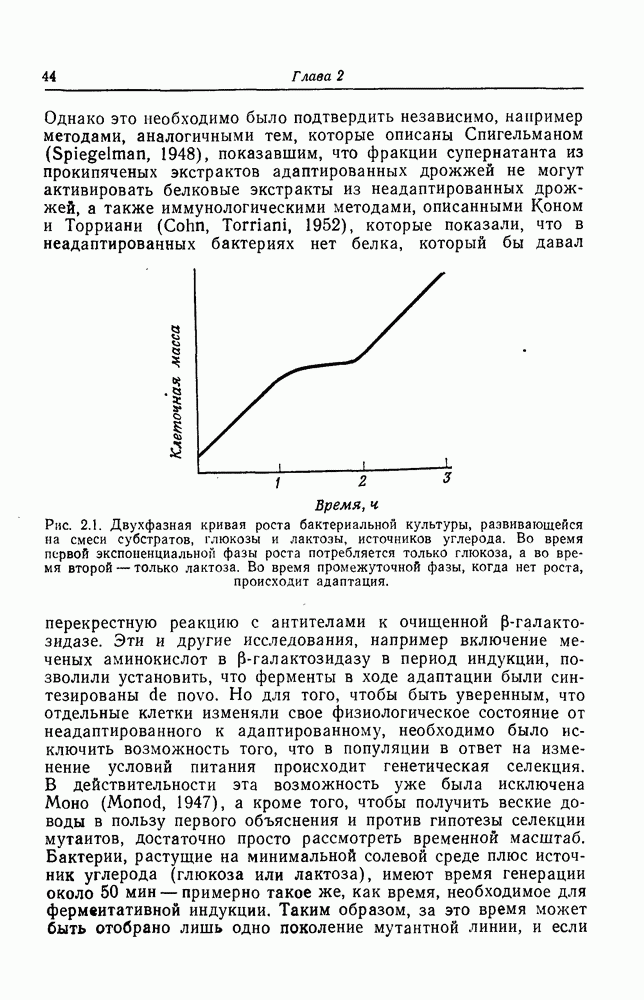
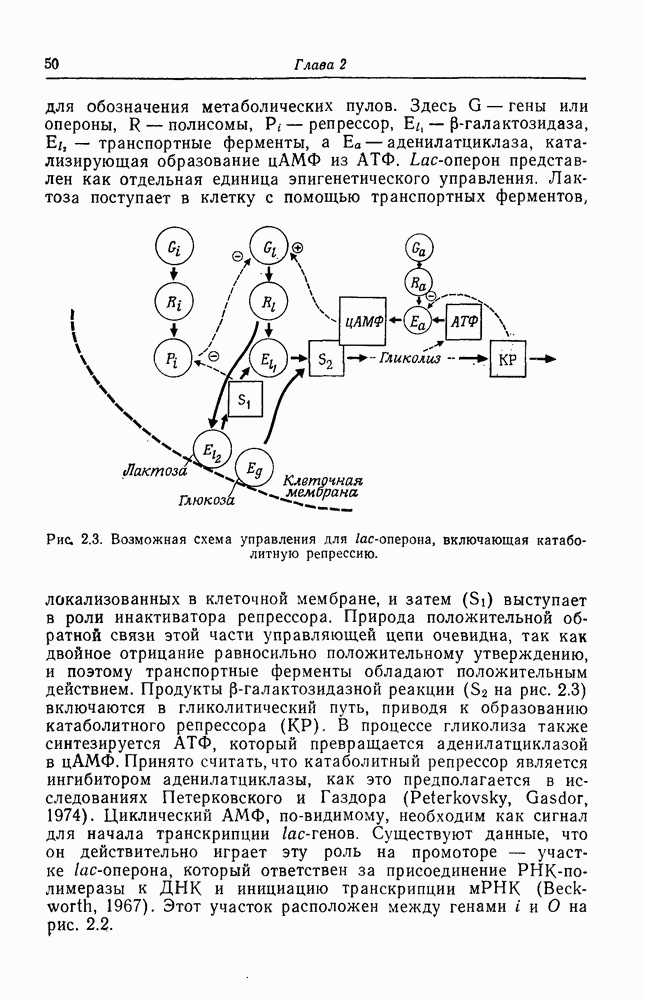
- Глава 2. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ ЭПИГЕНЕТИЧЕСКОЙ СИСТЕМЫ
- Индукция и репрессия генов
- Репрессия путей биосинтеза по типу обратной связи
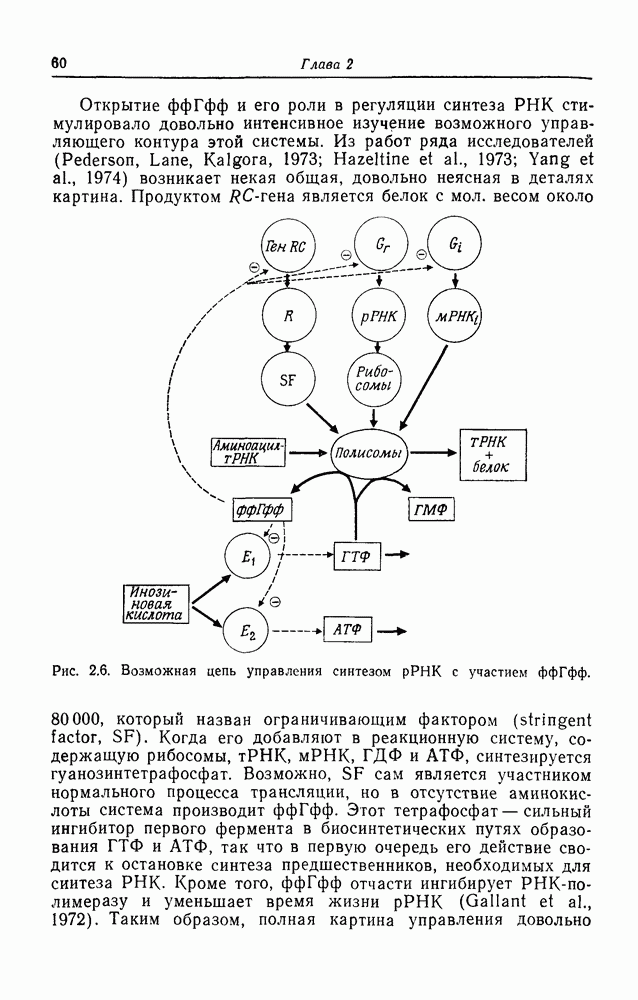
- Контроль синтеза рибосомной РНК
- Динамика эпигенетических сетей
- Аналогия со статистической термодинамикой
- Аналогия с вычислительными машинами: клетка как конечный автомат
- Глава 3. МИТОТИЧЕСКИЙ И КЛЕТОЧНЫЙ ЦИКЛЫ
- Репликон и гипотеза инициатора
- Гипотеза репрессора инициации
- Эукариоты
- Представление клеточного цикла в виде последовательности стадий
- Клеточный цикл млекопитающих
- Управление скоростью цикла и клеточная дифференцировка
- Эпидермис млекопитающих и кейлонная теория
- Вероятностные модели клеточного цикла и его управления
- Глава 4. КЛЕТОЧНЫЙ РОСТ, СИНХРОННОСТЬ КЛЕТОЧНЫХ ЦИКЛОВ И БИОЛОГИЧЕСКИЕ ЧАСЫ
- Хемостат
- Адаптивное поведение хемостата
- Системы восстановления клеток
- Синхронизация клеток
- Суточные ритмы деления клеток в тканях млекопитающих
- Контактное торможение
- Клеточные часы
- Физиология клеточных часов
- Динамика часов, контролирующих вылупление личинок у Drosophila
- Глава 5. МОРФОГЕНЕЗ: ОДНОМЕРНАЯ АПЕРИОДИЧЕСКАЯ УПОРЯДОЧЕННОСТЬ
- Полярность и осевые градиенты
- Пейсмекеры и волны активности
- Морфогенез одноклеточных
- Мембраны и морфогенез
- Регуляция и устойчивость
- Периодические режимы у гидроидов
- Глава 6. МОРФОГЕНЕЗ: ПРОСТРАНСТВЕННЫЕ ПЕРИОДИЧНОСТИ И МНОГОМЕРНАЯ УПОРЯДОЧЕННОСТЬ
- Распространение волн и пространственные периодичности
- Эпидермис насекомых
- Мембрана и эпидермис насекомых
- Эпиморфоз: крыло цыпленка
- Волновая модель и эпиморфоз
- Локальная и глобальная упорядоченность: имагинальный диск и конечность таракана
- Ретино-тектальная проекция в зрительной системе амфибий
- Механизм образования двумерной проекции
- Глава 7. ОРГАНИЗМ КАК ПОЗНАЮЩАЯ И КООПЕРАТИВНАЯ СИСТЕМА
- Функциональная иерархия
- Обратные предельные системы
- Кооперативные взаимодействия и фазовые переходы в познающих системах
- Фазовые переходы и теория катастроф
- Коллективные моды в ритмических процессах
- Процессы генерации в познающих системах
- ПРИЛОЖЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ