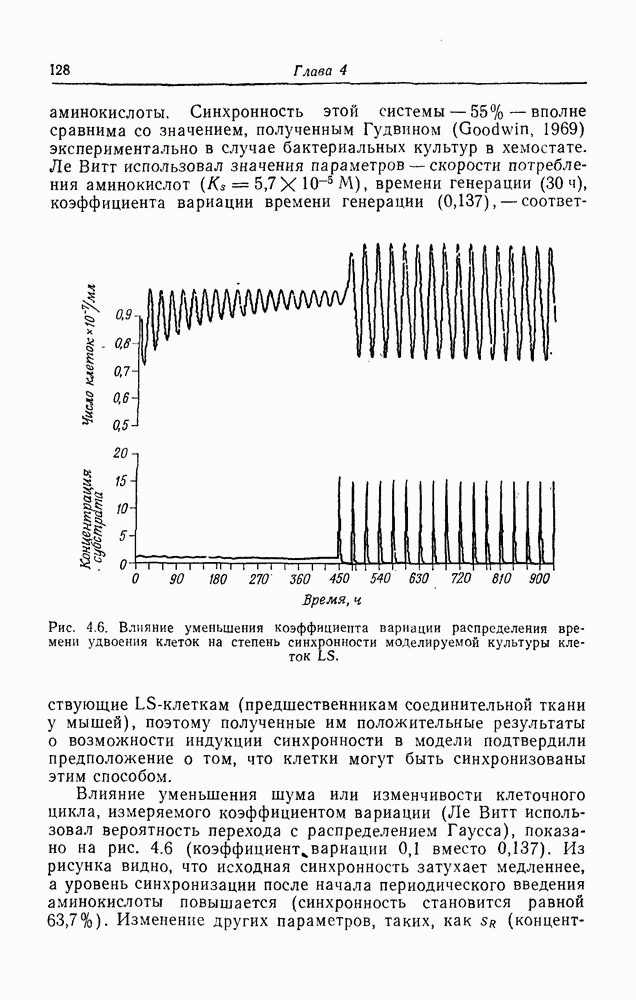
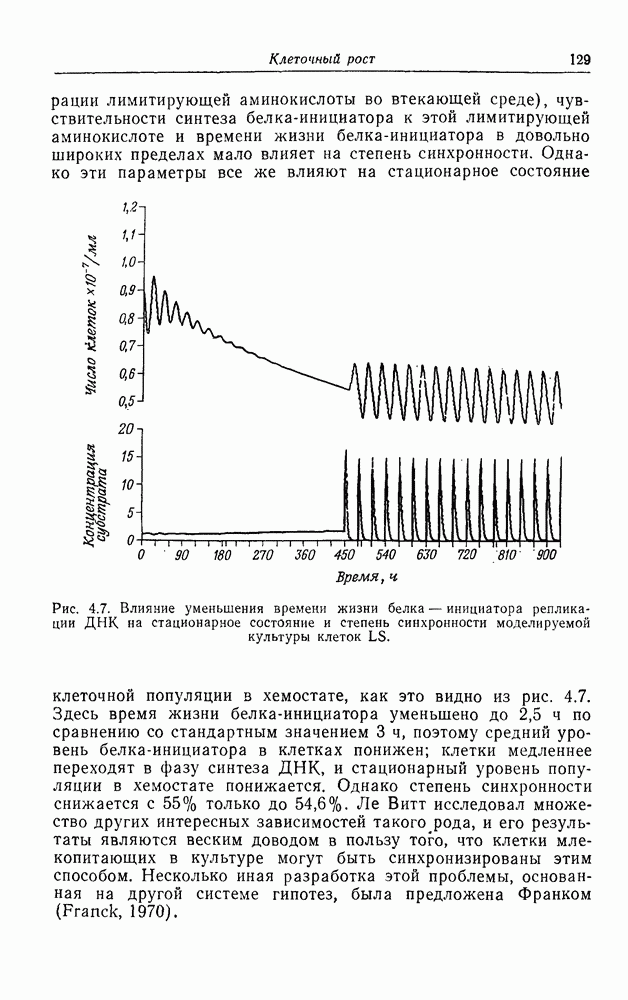
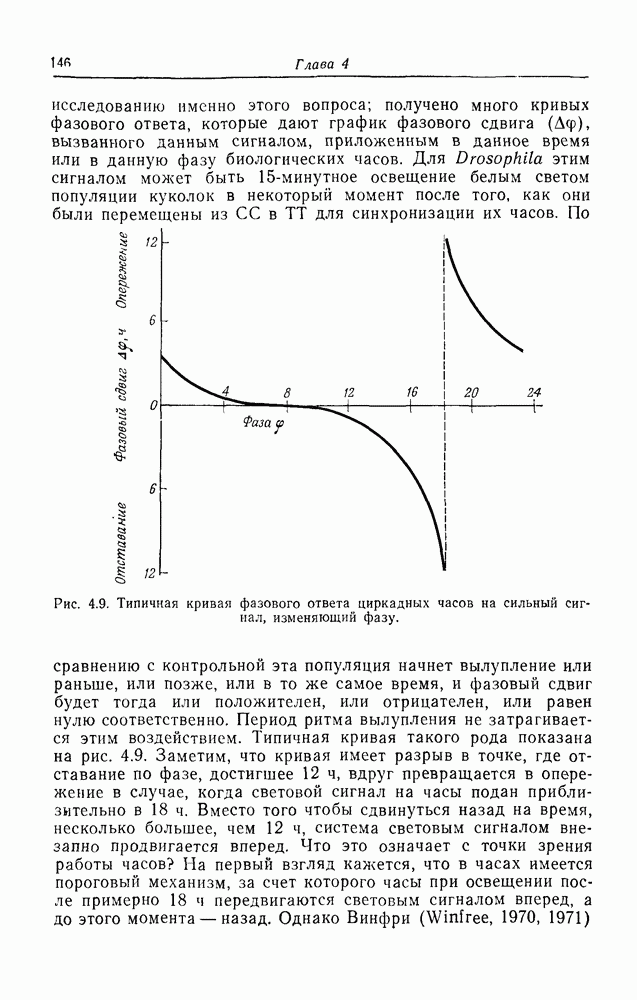
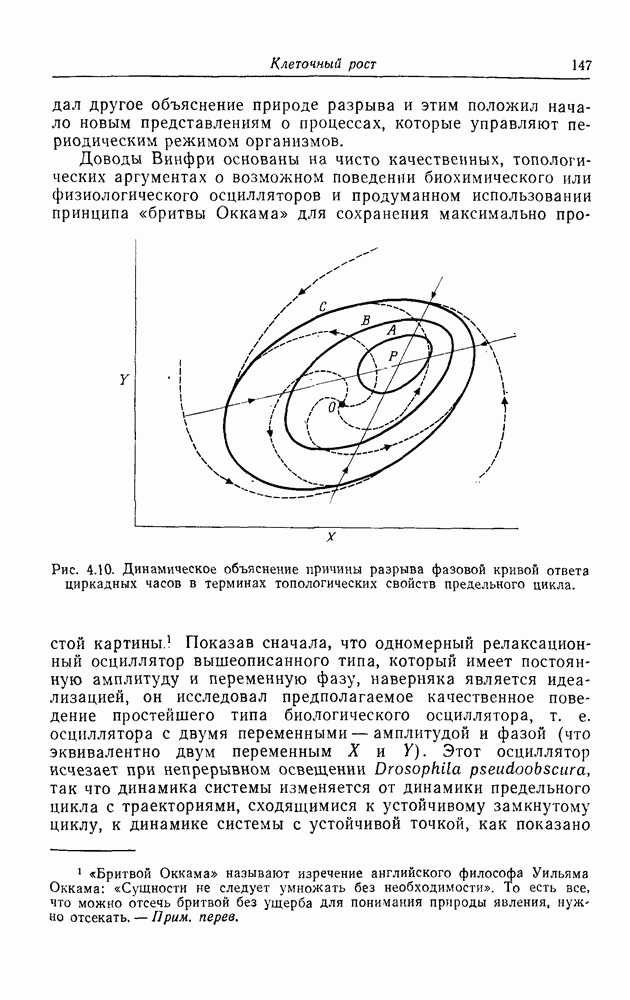
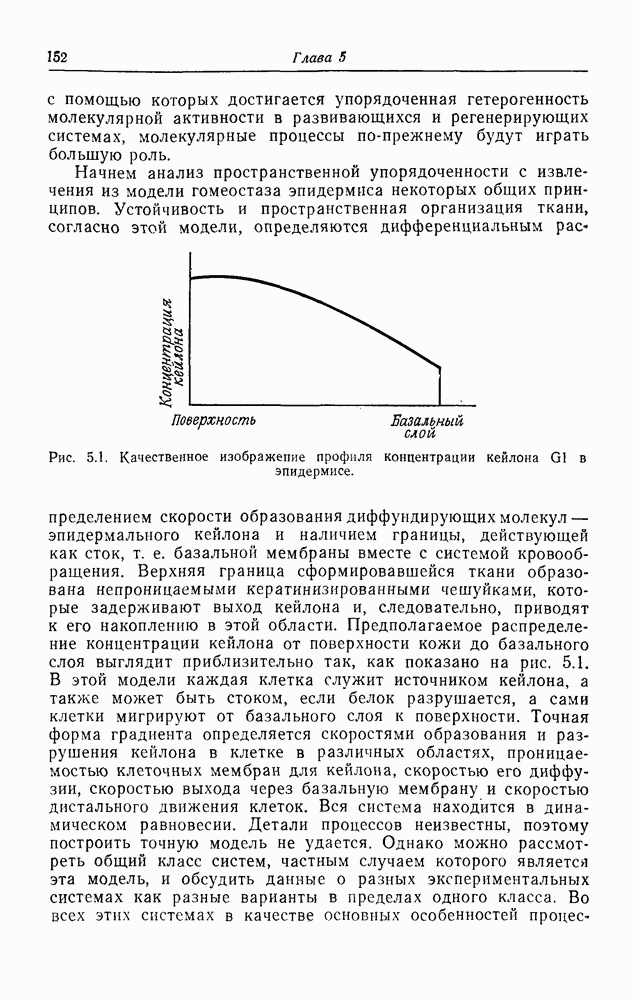
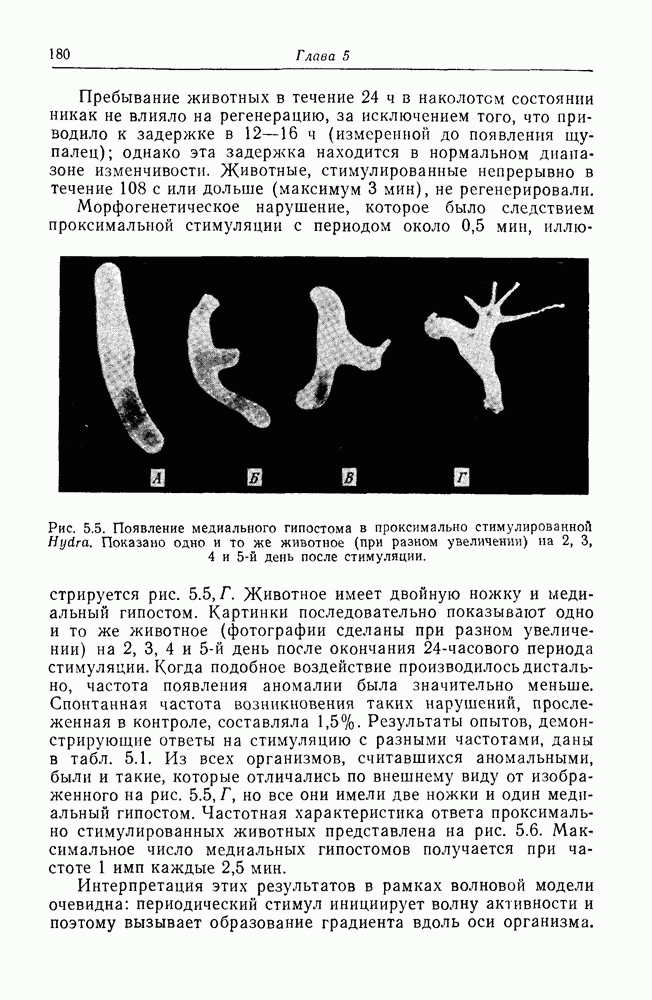
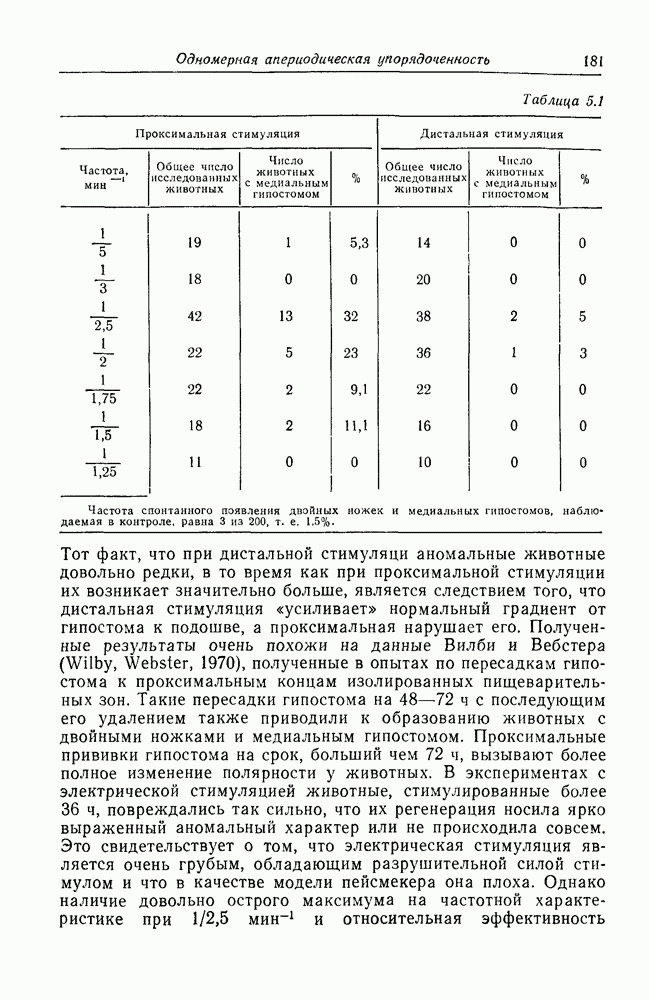
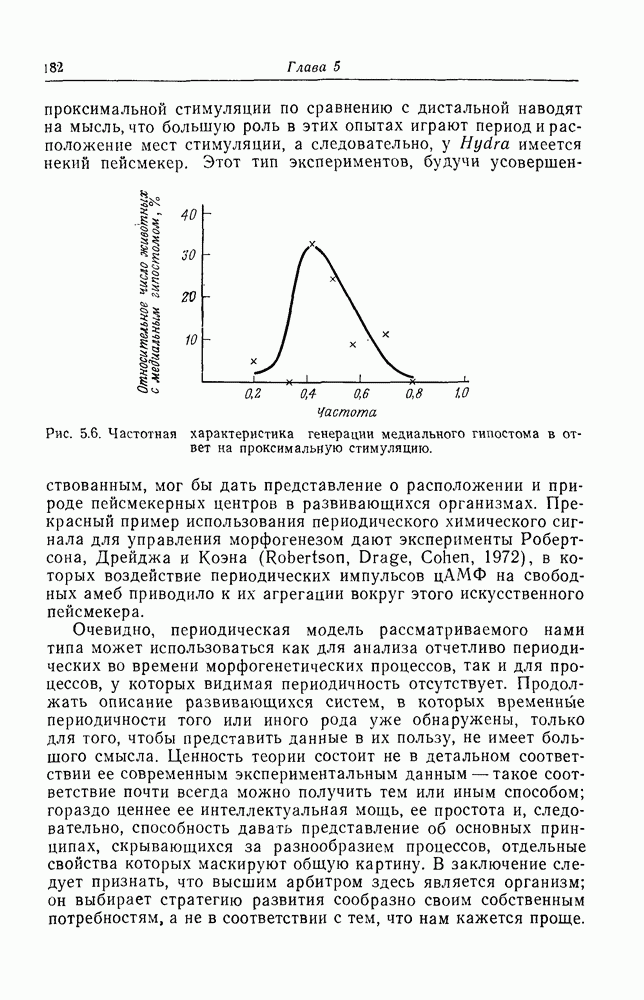
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРИЛОЖЕНИЕ
Некоторые основные черты волновой модели, построенной для анализа образования морфогенетического градиента, даны в этом приложении в виде результатов численных расчетов на частной реализации модели. Проведен анализ пространственно-одномерной системы двух дифференциальных уравнений вида

где  — концентрация диффундирующего метаболита V (см. гл. 5), а
— концентрация диффундирующего метаболита V (см. гл. 5), а  — концентрация комплекса BV, который, как считается, представляет собой недиффундирующий морфоген. Другие параметры и функции в системе уравнений имеют следующий смысл: D — константа диффузии метаболита V;
— концентрация комплекса BV, который, как считается, представляет собой недиффундирующий морфоген. Другие параметры и функции в системе уравнений имеют следующий смысл: D — константа диффузии метаболита V;  — постоянная распада морфогена
— постоянная распада морфогена  —
—  -функция, умноженная на константу (этот член описывает распространение фронта волны метаболической активности, движущейся со скоростью v, где t — время,
-функция, умноженная на константу (этот член описывает распространение фронта волны метаболической активности, движущейся со скоростью v, где t — время,  расстояние вдоль оси);
расстояние вдоль оси);  —
—  -функция, характеризующая процесс захвата, который распространяется позади волнового фронта (с той же скоростью, но с задержкой
-функция, характеризующая процесс захвата, который распространяется позади волнового фронта (с той же скоростью, но с задержкой  );
);  — константа распада метаболита V, описывающая в модели скорость превращения V в W. При расчетах дельта-функция была представлена узким распределением Гаусса, описывающим мгновенное «включение» фермента
— константа распада метаболита V, описывающая в модели скорость превращения V в W. При расчетах дельта-функция была представлена узким распределением Гаусса, описывающим мгновенное «включение» фермента  и образование V при распространении волны активности. Вычисления проводились в безразмерных переменных, так что D, t и
и образование V при распространении волны активности. Вычисления проводились в безразмерных переменных, так что D, t и  — это относительные величины. Волна распространяется в обоих направлениях, но вследствие симметрии процесса относительно источника можно рассматривать лишь Одно направление.
— это относительные величины. Волна распространяется в обоих направлениях, но вследствие симметрии процесса относительно источника можно рассматривать лишь Одно направление.
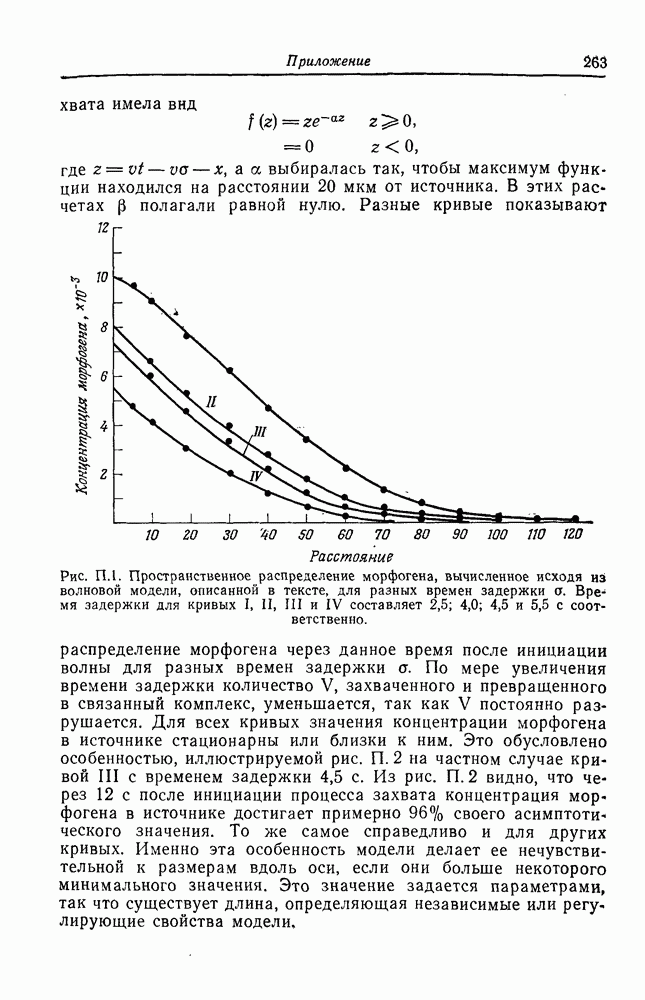
На рис. П.1 показаны кривые распределения морфогена после прохождения единичной волны для разных времен задержки а. Скорость волны всюду была равна  . Функция захвата
. Функция захвата
имела вид

где  выбиралась так, чтобы максимум функции находился на расстоянии 20 мкм от источника. В этих расчетах
выбиралась так, чтобы максимум функции находился на расстоянии 20 мкм от источника. В этих расчетах  полагали равной нулю. Разные кривые показывают распределение морфогена через данное время после инициации волны для разных времен задержки а.
полагали равной нулю. Разные кривые показывают распределение морфогена через данное время после инициации волны для разных времен задержки а.

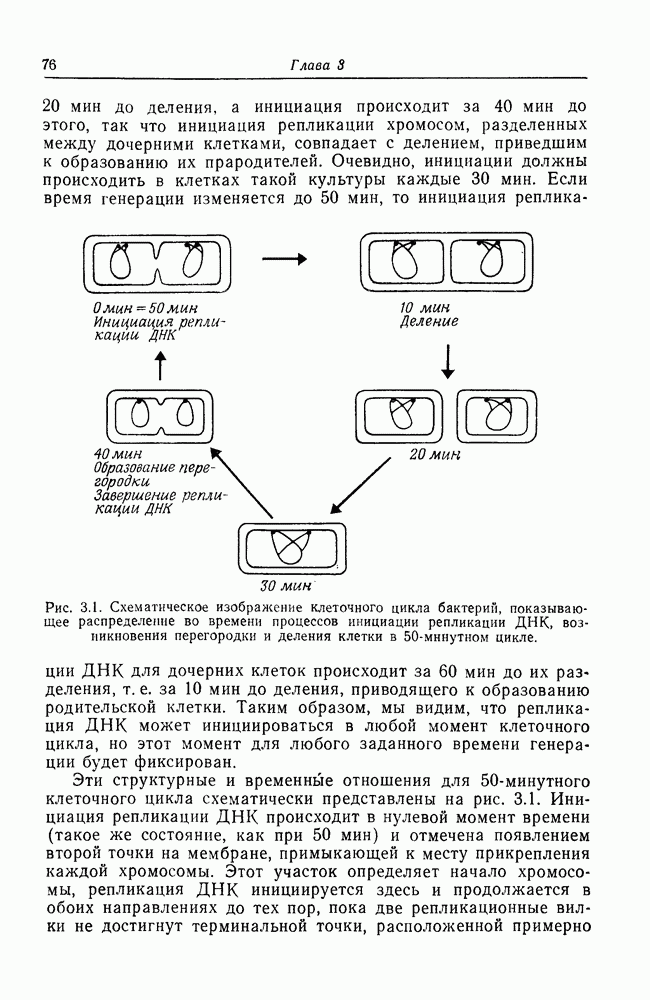
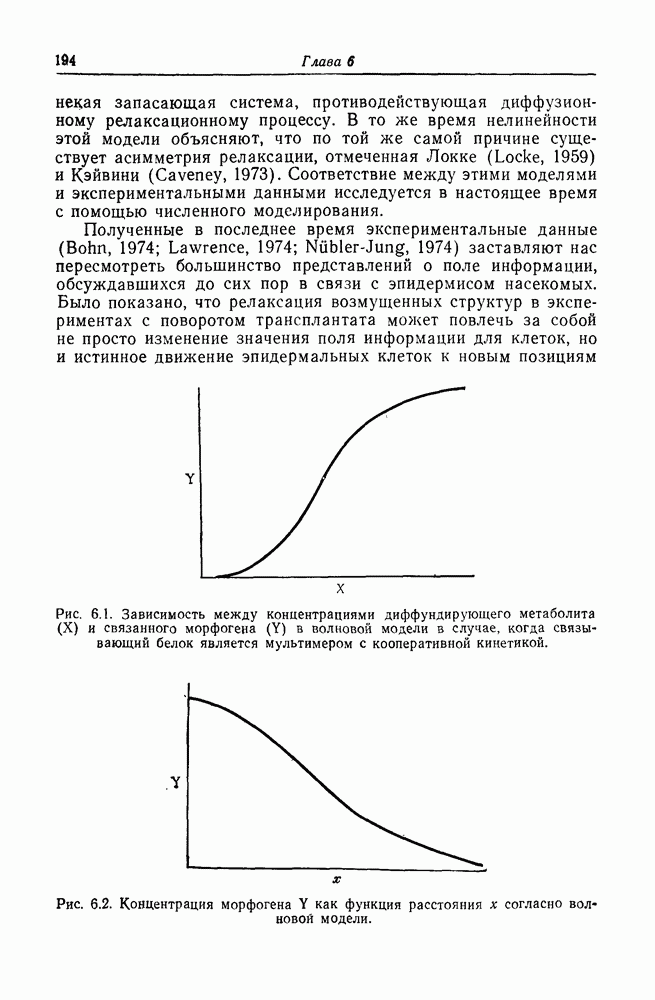
Рис. П. 1. Пространственное распределение морфогена, вычисленное исходя из волновой модели, описанной в тексте, для разных времен задержки а. Время задержки для кривых I, II, III и IV составляет 2,5; 4,0; 4,5 и 5,5 с соответственно.
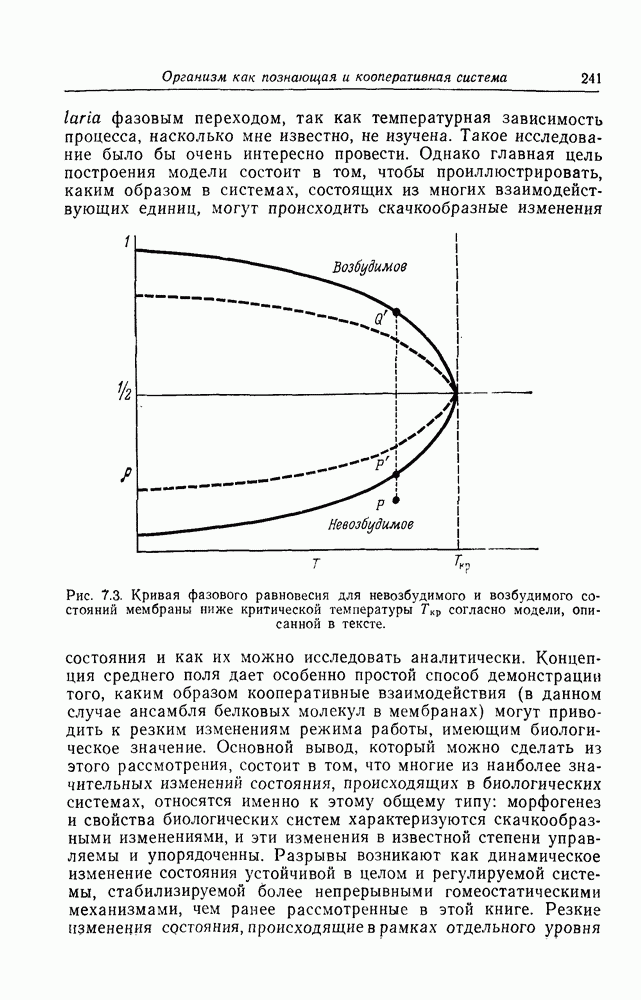
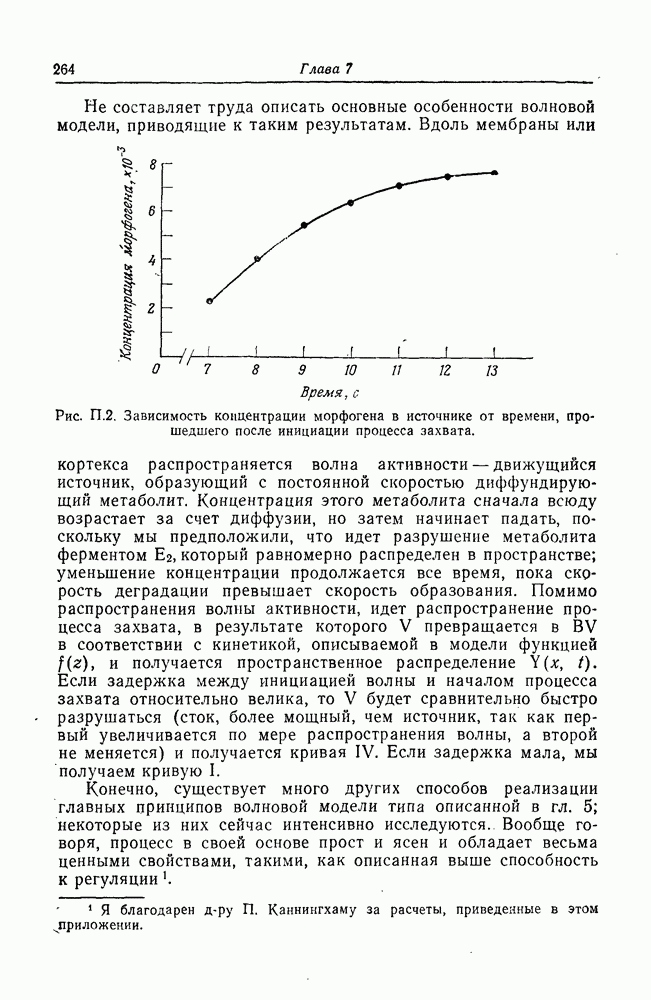
По мере увеличения времени задержки количество V, захваченного и превращенного в связанный комплекс, уменьшается, так как V постоянно разрушается. Для всех кривых значения концентрации морфогена в источнике стационарны или близки к ним. Это обусловлено особенностью, иллюстрируемой рис. П. 2 на частном случае кривой III с временем задержки 4,5 с. Из рис. П. 2 видно, что через 12 с после инициации процесса захвата концентрация морфогена в источнике достигает примерно 96% своего асимптотического значения. То же самое справедливо и для других кривых. Именно эта особенность модели делает ее нечувствительной к размерам вдоль оси, если они больше некоторого минимального значения. Это значение задается параметрами, так что существует длина, определяющая независимые или регулирующие свойства модели,
Не составляет труда описать основные особенности волновой модели, приводящие к таким результатам.

Рис. П. 2. Зависимость концентрации морфогена в источнике от времени, прошедшего после инициации процесса захвата.
Вдоль мембраны или кортекса распространяется волна активности — движущийся источник, образующий с постоянной скоростью диффундирующий метаболит. Концентрация этого метаболита сначала всюду возрастает за счет диффузии, но затем начинает падать, поскольку мы предположили, что идет разрушение метаболита ферментом  который равномерно распределен в пространстве; уменьшение концентрации продолжается все время, пока скорость деградации превышает скорость образования. Помимо распространения волны активности, идет распространение процесса захвата, в результате которого V превращается в BV в соответствии с кинетикой, описываемой в модели функцией
который равномерно распределен в пространстве; уменьшение концентрации продолжается все время, пока скорость деградации превышает скорость образования. Помимо распространения волны активности, идет распространение процесса захвата, в результате которого V превращается в BV в соответствии с кинетикой, описываемой в модели функцией  и получается пространственное распределение
и получается пространственное распределение  Если задержка между инициацией волны и началом процесса захвата относительно велика, то V будет сравнительно быстро - разрушаться (сток, более мощный, чем источник, так как первый увеличивается по мере распространения волны, а второй не меняется) и получается кривая IV. Если задержка мала, мы получаем кривую I.
Если задержка между инициацией волны и началом процесса захвата относительно велика, то V будет сравнительно быстро - разрушаться (сток, более мощный, чем источник, так как первый увеличивается по мере распространения волны, а второй не меняется) и получается кривая IV. Если задержка мала, мы получаем кривую I.
Конечно, существует много других способов реализации главных принципов волновой модели типа описанной в гл. 5; некоторые из них сейчас интенсивно исследуются. Вообще говоря, процесс в своей основе прост и ясен и обладает весьма ценными свойствами, такими, как описанная выше способность к регуляции
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ЛИТЕРАТУРА
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ МЕТАБОЛИЧЕСКОЙ СИСТЕМЫ
- Устойчивость и закон действующих масс в метаболической системе
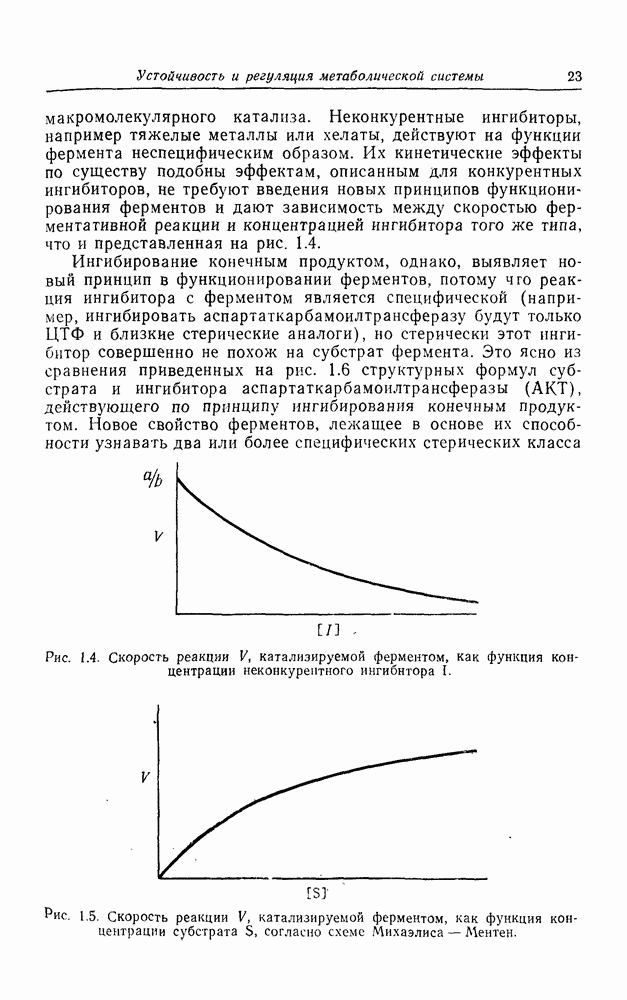
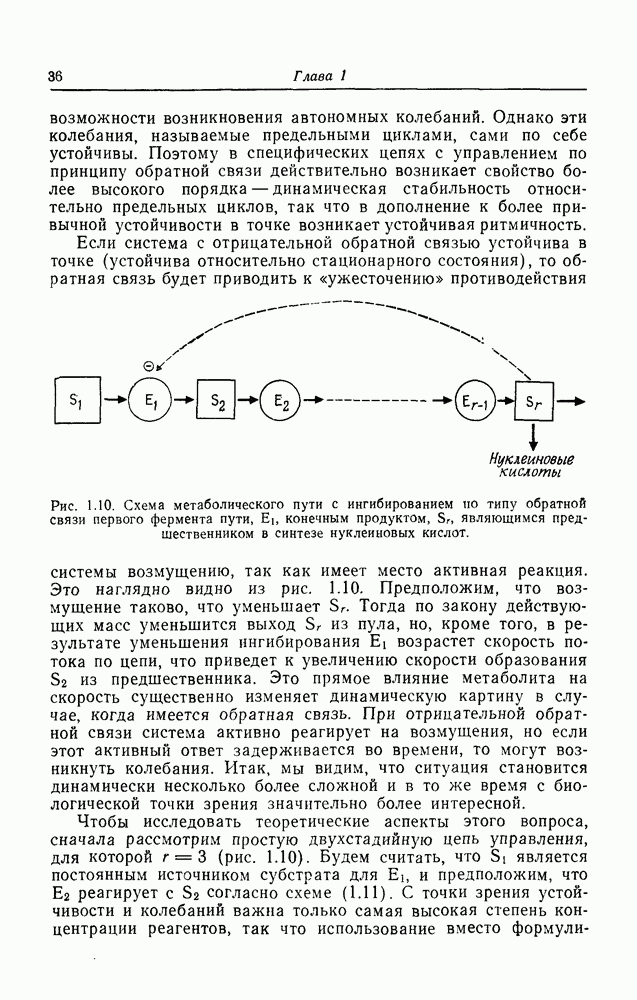
- Ингибирование по типу обратной связи в метаболических системах
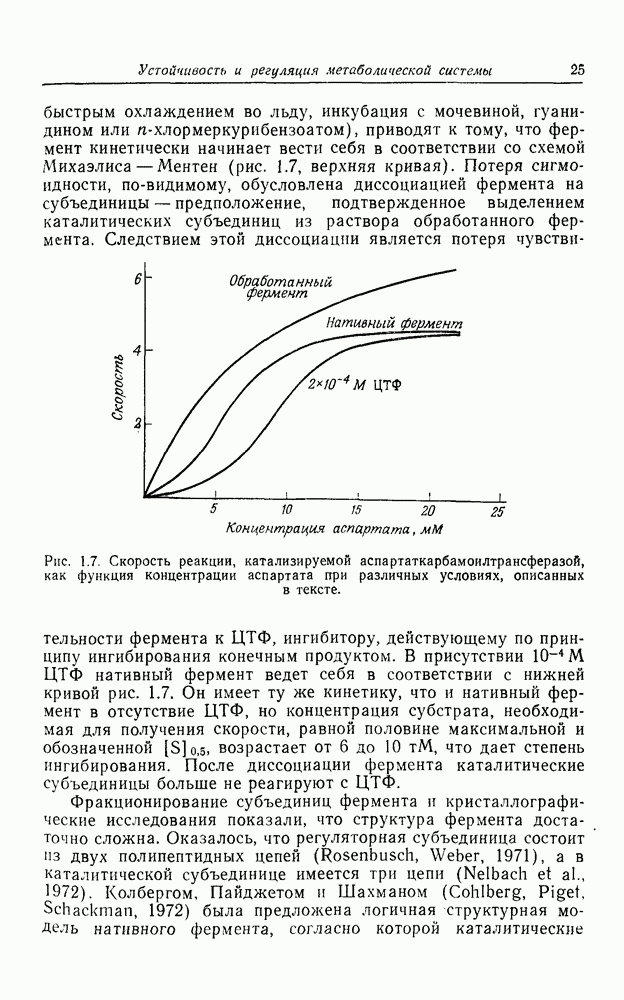
- Аллостерические свойства ферментов
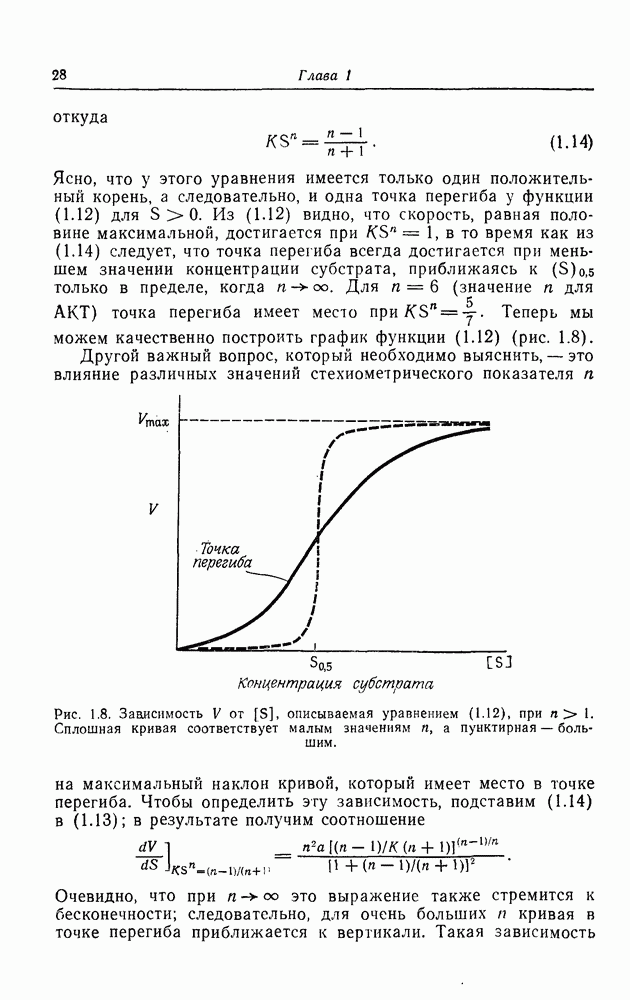
- Кооперативная ферментативная кинетика
- Цепи управления метаболизмом и их динамика
- Заключение
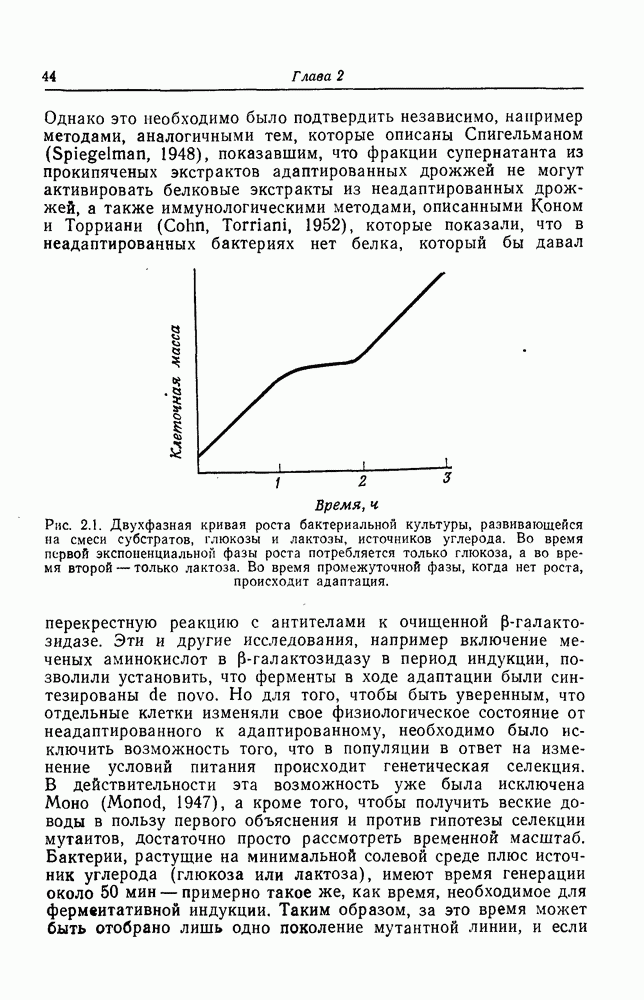
- Глава 2. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ ЭПИГЕНЕТИЧЕСКОЙ СИСТЕМЫ
- Индукция и репрессия генов
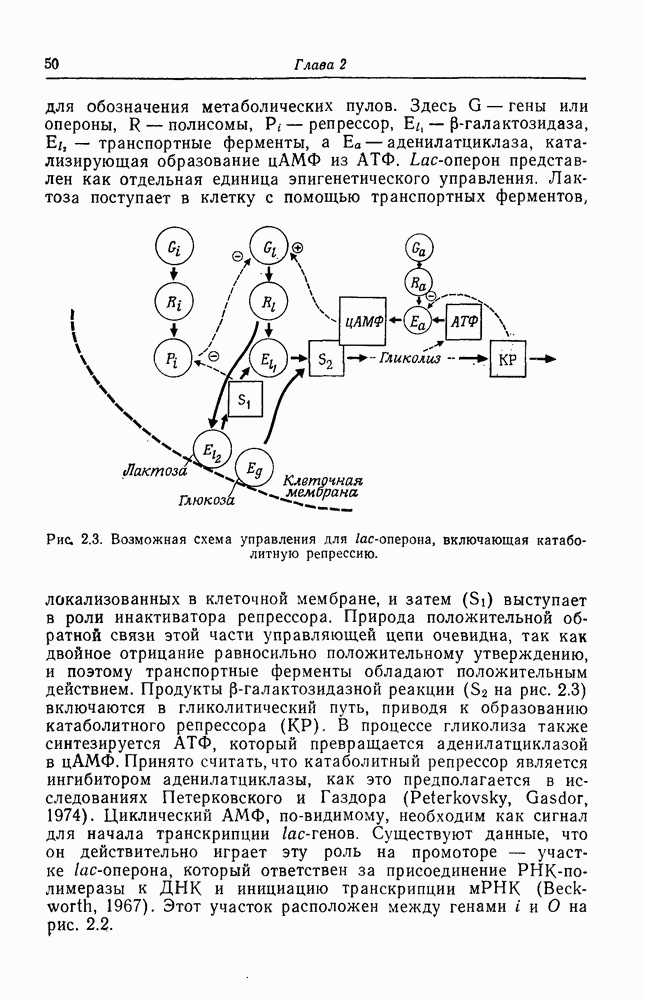
- Репрессия путей биосинтеза по типу обратной связи
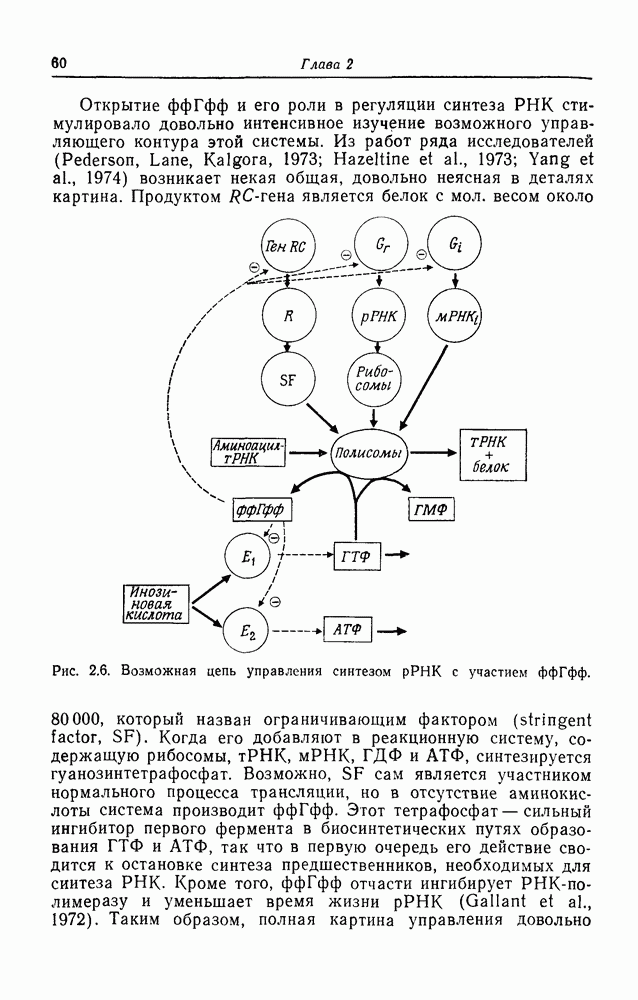
- Контроль синтеза рибосомной РНК
- Динамика эпигенетических сетей
- Аналогия со статистической термодинамикой
- Аналогия с вычислительными машинами: клетка как конечный автомат
- Глава 3. МИТОТИЧЕСКИЙ И КЛЕТОЧНЫЙ ЦИКЛЫ
- Репликон и гипотеза инициатора
- Гипотеза репрессора инициации
- Эукариоты
- Представление клеточного цикла в виде последовательности стадий
- Клеточный цикл млекопитающих
- Управление скоростью цикла и клеточная дифференцировка
- Эпидермис млекопитающих и кейлонная теория
- Вероятностные модели клеточного цикла и его управления
- Глава 4. КЛЕТОЧНЫЙ РОСТ, СИНХРОННОСТЬ КЛЕТОЧНЫХ ЦИКЛОВ И БИОЛОГИЧЕСКИЕ ЧАСЫ
- Хемостат
- Адаптивное поведение хемостата
- Системы восстановления клеток
- Синхронизация клеток
- Суточные ритмы деления клеток в тканях млекопитающих
- Контактное торможение
- Клеточные часы
- Физиология клеточных часов
- Динамика часов, контролирующих вылупление личинок у Drosophila
- Глава 5. МОРФОГЕНЕЗ: ОДНОМЕРНАЯ АПЕРИОДИЧЕСКАЯ УПОРЯДОЧЕННОСТЬ
- Полярность и осевые градиенты
- Пейсмекеры и волны активности
- Морфогенез одноклеточных
- Мембраны и морфогенез
- Регуляция и устойчивость
- Периодические режимы у гидроидов
- Глава 6. МОРФОГЕНЕЗ: ПРОСТРАНСТВЕННЫЕ ПЕРИОДИЧНОСТИ И МНОГОМЕРНАЯ УПОРЯДОЧЕННОСТЬ
- Распространение волн и пространственные периодичности
- Эпидермис насекомых
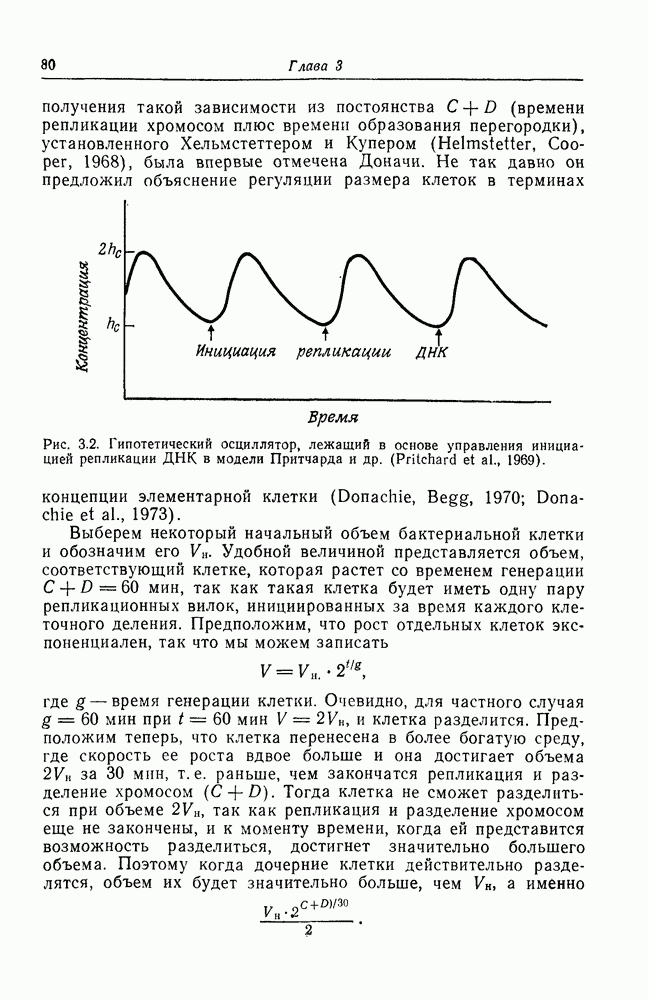
- Мембрана и эпидермис насекомых
- Эпиморфоз: крыло цыпленка
- Волновая модель и эпиморфоз
- Локальная и глобальная упорядоченность: имагинальный диск и конечность таракана
- Ретино-тектальная проекция в зрительной системе амфибий
- Механизм образования двумерной проекции
- Глава 7. ОРГАНИЗМ КАК ПОЗНАЮЩАЯ И КООПЕРАТИВНАЯ СИСТЕМА
- Функциональная иерархия
- Обратные предельные системы
- Кооперативные взаимодействия и фазовые переходы в познающих системах
- Фазовые переходы и теория катастроф
- Коллективные моды в ритмических процессах
- Процессы генерации в познающих системах
- ПРИЛОЖЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ