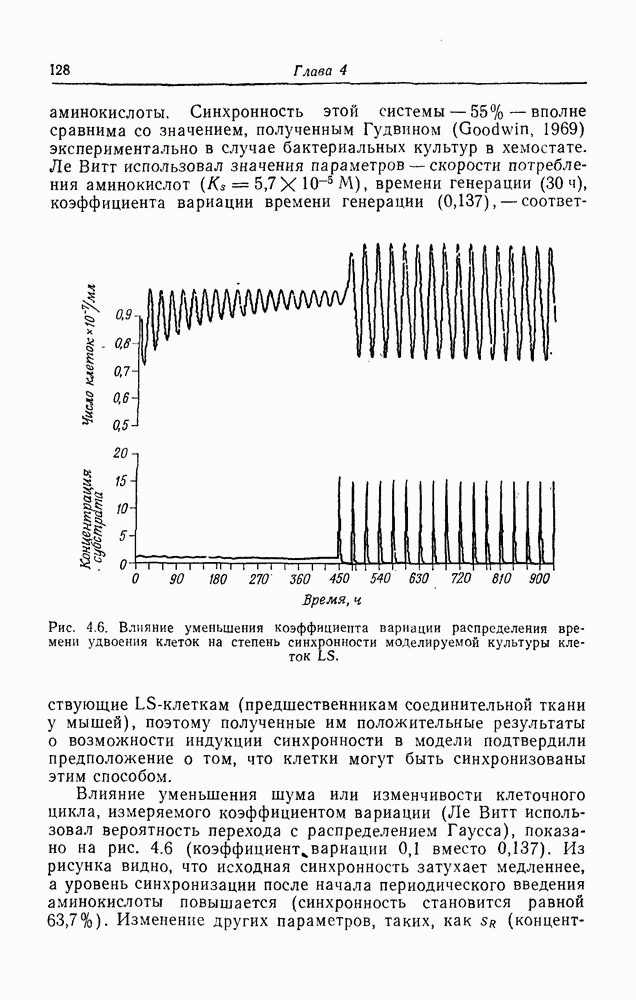
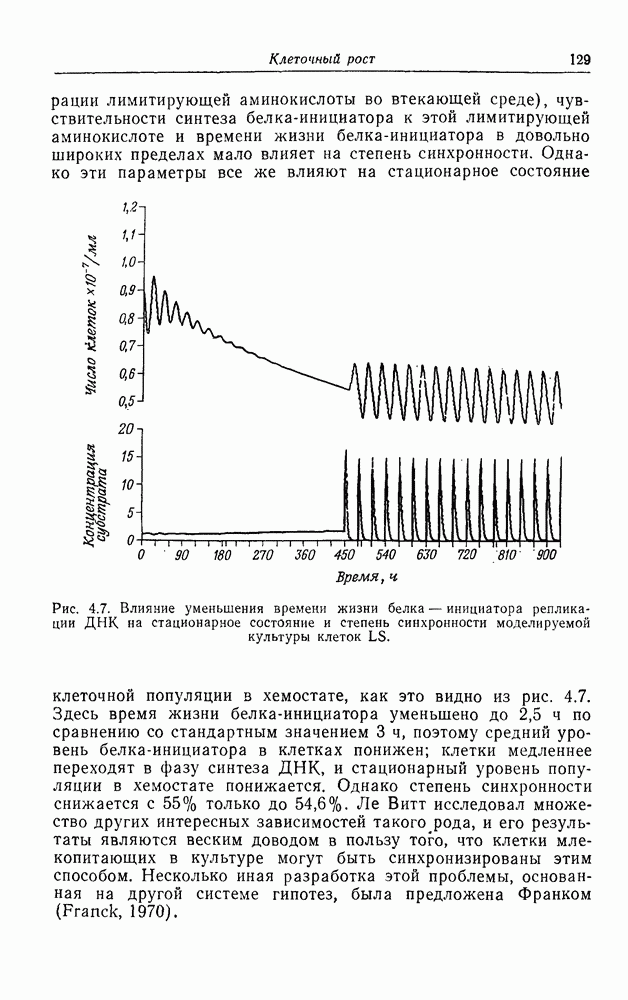
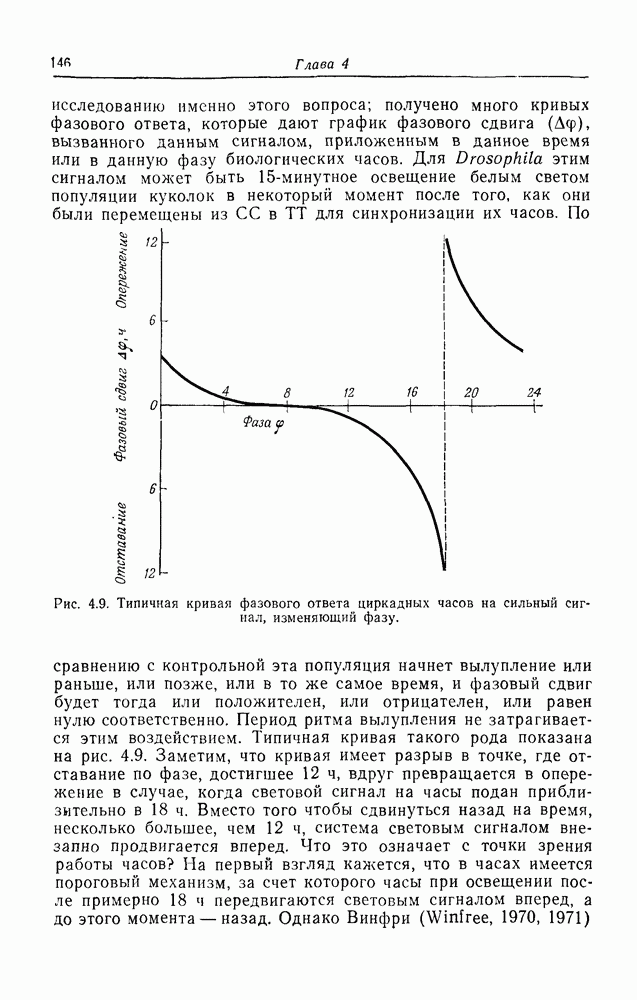
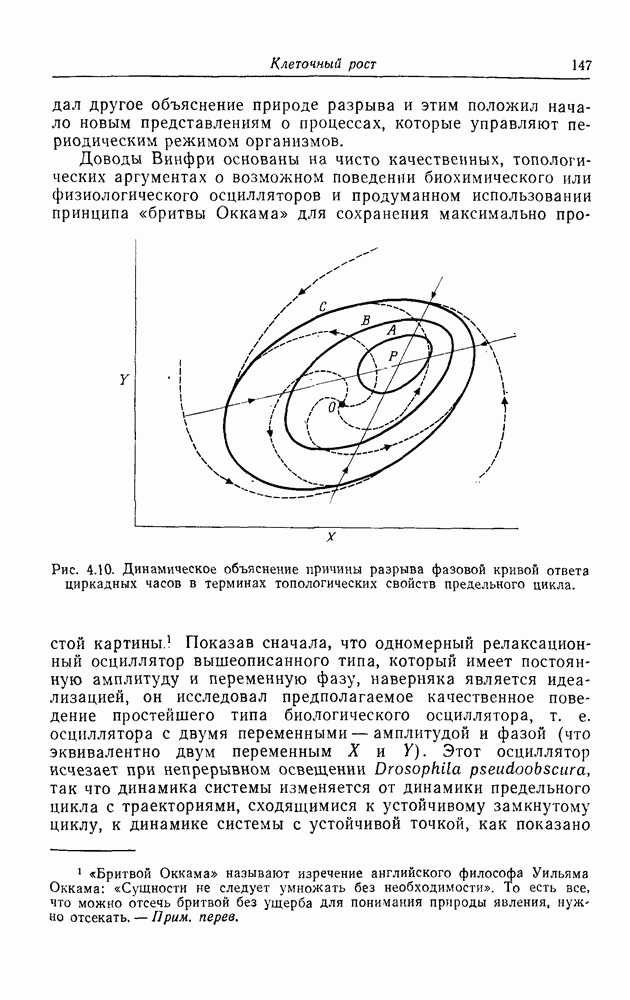
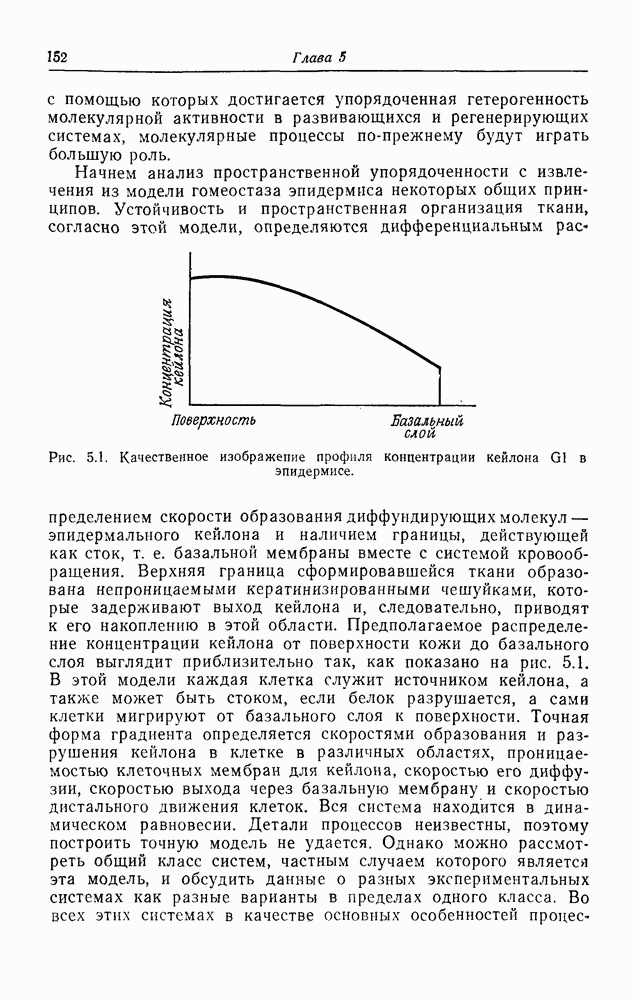
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Кооперативные взаимодействия и фазовые переходы в познающих системах
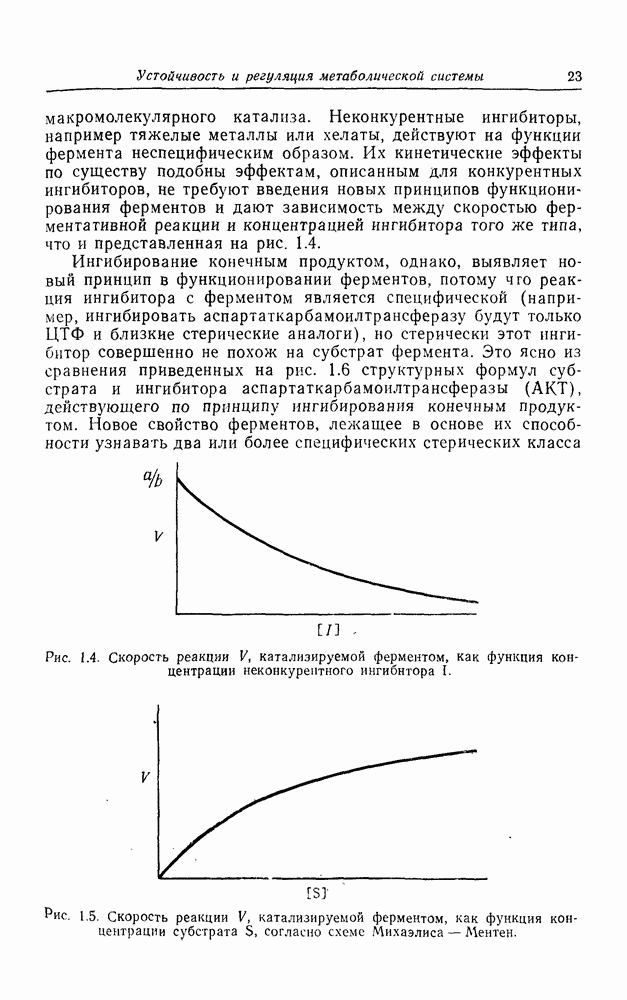
Любой уровень организации, представленный на рис. 7.1 как категория  является, вообще говоря, очень сложным функциональным пространством. Однако замечательное свойство организмов заключается в том, что из этой сложности возникает относительно простое упорядоченное поведение. Можно описать появление согласованности и простого поведения из многочисленных взаимодействий, которые имеют место на данном уровне организации, используя представление о кооперативных процессах или коллективных явлениях. Мы уже рассмотрели очень простой случай кооперативного поведения при изучении взаимодействия субъединиц в мультимерном белке в гл. 1. Теперь я опишу несколько более сложный и интересный пример
является, вообще говоря, очень сложным функциональным пространством. Однако замечательное свойство организмов заключается в том, что из этой сложности возникает относительно простое упорядоченное поведение. Можно описать появление согласованности и простого поведения из многочисленных взаимодействий, которые имеют место на данном уровне организации, используя представление о кооперативных процессах или коллективных явлениях. Мы уже рассмотрели очень простой случай кооперативного поведения при изучении взаимодействия субъединиц в мультимерном белке в гл. 1. Теперь я опишу несколько более сложный и интересный пример
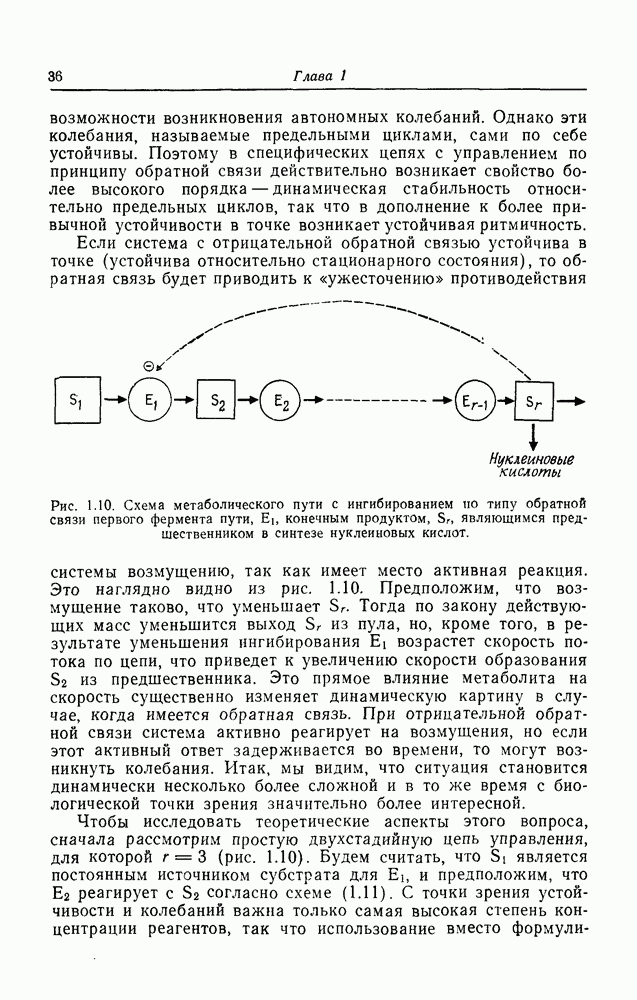
кооперативного процесса, который иллюстрирует, как взаимодействия между единицами могут приводить к скачкообразным изменениям состояния, известным как фазовые переходы. Это послужит естественным введением к более общему описанию таких разрывов, известному под названием теории катастроф, которая была построена математиком Рене Томом и применяется для описания биологических процессов, особенно морфогенеза. Включение этой теории в общие рамки описания с помощью обратных предельных систем и процессов познавания позволяет весьма полно рассмотреть процессы, протекающие в организмах. Конечная цель нашего анализа — понять суть процессов регенерации, в результате которых упорядоченные в пространстве и времени системы появляются в правильной последовательности из значительно более простых систем, обладающих потенциальной возможностью развития (например, развитие головастика из икринки). Эта возможность воплощена в полезных описаниях себя и окружающей среды, — описаниях, проявляющихся в пространстве и во времени при развитии.
Процесс, который я рассмотрю как пример фазового перехода, — это развитие возбудимости в биологических мембранах. Чтобы сделать пример конкретным и связать его с материалом, обсуждавшимся ранее, я остановлюсь на развитии метаболической возбудимости в мембране, аналогичной рассмотренной в волновой модели. (Этот вопрос исследован в работе Goodwin, 1974.) Из рис. 5.4 видно, что если плотность фермента  слишком низка, волна активности не сможет распространяться, поскольку активности одной молекулы фермента будет недостаточно для возбуждения своих соседей. Точные соотношения между ферментами зависят от стехиометрии метаболической реакциии, в ходе которой V превращается в U, от влияния V на равновесие между связанными и свободными ионами, от концентрации ионов, температуры и т. д. Плотность ферментов в мембране зависит от равновесия между скоростью их включения в структуру мембраны и скоростью деградации или разбавления (если формируется новая мембрана). Мы можем представить все эти факторы с помощью химического потенциала (а, так что плотность фермента будет определяться этой величиной.
слишком низка, волна активности не сможет распространяться, поскольку активности одной молекулы фермента будет недостаточно для возбуждения своих соседей. Точные соотношения между ферментами зависят от стехиометрии метаболической реакциии, в ходе которой V превращается в U, от влияния V на равновесие между связанными и свободными ионами, от концентрации ионов, температуры и т. д. Плотность ферментов в мембране зависит от равновесия между скоростью их включения в структуру мембраны и скоростью деградации или разбавления (если формируется новая мембрана). Мы можем представить все эти факторы с помощью химического потенциала (а, так что плотность фермента будет определяться этой величиной.
Предположим, что в мембране имеются центры связывания фермента  и что среднее их число на единицу площади постоянно. О природе таких центров и их распределении мы знаем очень мало. Как они расположены — упорядоченным образом, определяемым другими структурами в мембране, или случайно, — неизвестно. По-видимому, на самом деле центры расположены неким промежуточным образом между этими двумя крайними случаями; не случайно, но и не строго упорядоченно.
и что среднее их число на единицу площади постоянно. О природе таких центров и их распределении мы знаем очень мало. Как они расположены — упорядоченным образом, определяемым другими структурами в мембране, или случайно, — неизвестно. По-видимому, на самом деле центры расположены неким промежуточным образом между этими двумя крайними случаями; не случайно, но и не строго упорядоченно.
Такие соображения не влияют на качественную модель, которую мы строим, но они определяют геометрию распространения волны по возбудимой мембране, например влияют на то, как будут распространяться волны от точки возбуждения — в виде концентрических окружностей или в виде спиралей. Эти альтернативные следствия здесь не будут рассматриваться.
Для обозначения состояния участка мембраны i используем бинарную переменную  Эта переменная принимает значения 0 или 1 в зависимости от того, свободен участок или занят соответственно. Модель аналогична известному в физике описанию конденсации решеточного газа, которое в свою очередь основано на модели ферромагнетизма Изинга, использующей приближение среднего поля. Это предполагает, что каждая единица в рассматриваемой системе (в нашем случае — фермент) находится в усредненном поле сил, обусловленном присутствием других единиц, и сущность метода заключается в том, чтобы найти уравнение, которое описывает это поле через его собственные компоненты (уравнение самосогласованного поля). Рассматриваемое нами поле обусловлено взаимодействиями, которые, как предполагается, имеют место между ферментами, связанными с мембраной, и ферментами, встраивающимися в нее, так как присутствие фермента на некотором участке способствует встраиванию другой молекулы фермента в мембрану на
Эта переменная принимает значения 0 или 1 в зависимости от того, свободен участок или занят соответственно. Модель аналогична известному в физике описанию конденсации решеточного газа, которое в свою очередь основано на модели ферромагнетизма Изинга, использующей приближение среднего поля. Это предполагает, что каждая единица в рассматриваемой системе (в нашем случае — фермент) находится в усредненном поле сил, обусловленном присутствием других единиц, и сущность метода заключается в том, чтобы найти уравнение, которое описывает это поле через его собственные компоненты (уравнение самосогласованного поля). Рассматриваемое нами поле обусловлено взаимодействиями, которые, как предполагается, имеют место между ферментами, связанными с мембраной, и ферментами, встраивающимися в нее, так как присутствие фермента на некотором участке способствует встраиванию другой молекулы фермента в мембрану на  соседнем участке. Введем величину
соседнем участке. Введем величину  — усредненную по всем центрам занятость центра. Пусть общее число занятых центров, т. е. молекул фермента в мембране, равно N, так что
— усредненную по всем центрам занятость центра. Пусть общее число занятых центров, т. е. молекул фермента в мембране, равно N, так что

т. е. сумма по всем центрам. И наконец, пусть взаимодействие между двумя ферментами  есть
есть 
При определении средних значений в такой системе удобно использовать большое каноническое распределение, которое учитывает вариации и N, общего числа активных молекул фермента на мембране, и энергии системы, определяемой взаимодействиями. Для ознакомления с этими вопросами читатель может обратиться к книгам, рассматривающим модель Изинга и решеточный газ (например, Brout, 1965; Huang, 1963), где показано, что гамильтониан этой системы имеет вид

Самосогласованное уравнение для  , которое получается из этого выражения с помощью большого канонического распределения, есть
, которое получается из этого выражения с помощью большого канонического распределения, есть

где  - преобразование Фурье суммы
- преобразование Фурье суммы  взятое в точке 0. Здесь сделано допущение, что поле взаимодействий везде одинаково, т. е.
взятое в точке 0. Здесь сделано допущение, что поле взаимодействий везде одинаково, т. е.  инвариантно относительно трансляции. Параметр
инвариантно относительно трансляции. Параметр  есть
есть  , где k — постоянная Больцмана, а Т — абсолютная температура. Он входит в уравнение из-за принятого допущения, что средняя энергия постоянна, а следовательно, система находится при определенной температуре. Именно это допущение означает, что здесь мы имеем дело с системой, которая относительно рассматриваемых процессов равновесна. Таким образом, хотя известно, что мембраны в живых системах поддерживаются в нативном состоянии активным потоком энергии, мы тем не менее игнорируем это и трактуем процессы ассоциации и диссоциации ферментов с мембраной и взаимодействия между ферментами так, как если бы эти процессы были простыми химическими реакциями, характеризующимися определенным химическим потенциалом и тем, что члены, описывающие взаимодействия, постоянны. Таким образом, мы рассматриваем весь процесс с точки зрения химического равновесия. При условии, что потоки в системе достаточно малы, это приближение вполне приемлемо.
, где k — постоянная Больцмана, а Т — абсолютная температура. Он входит в уравнение из-за принятого допущения, что средняя энергия постоянна, а следовательно, система находится при определенной температуре. Именно это допущение означает, что здесь мы имеем дело с системой, которая относительно рассматриваемых процессов равновесна. Таким образом, хотя известно, что мембраны в живых системах поддерживаются в нативном состоянии активным потоком энергии, мы тем не менее игнорируем это и трактуем процессы ассоциации и диссоциации ферментов с мембраной и взаимодействия между ферментами так, как если бы эти процессы были простыми химическими реакциями, характеризующимися определенным химическим потенциалом и тем, что члены, описывающие взаимодействия, постоянны. Таким образом, мы рассматриваем весь процесс с точки зрения химического равновесия. При условии, что потоки в системе достаточно малы, это приближение вполне приемлемо.
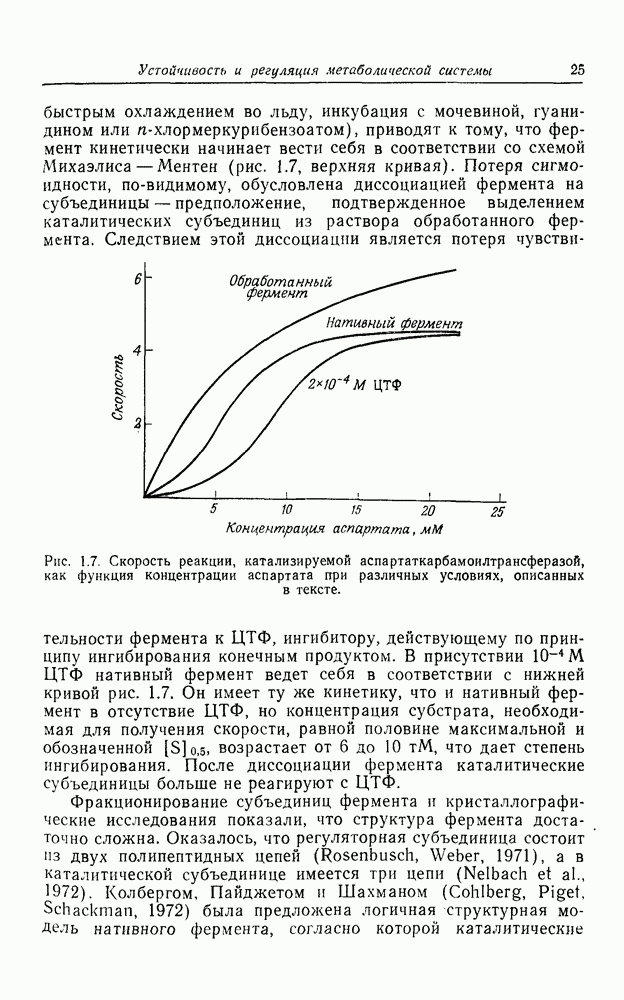
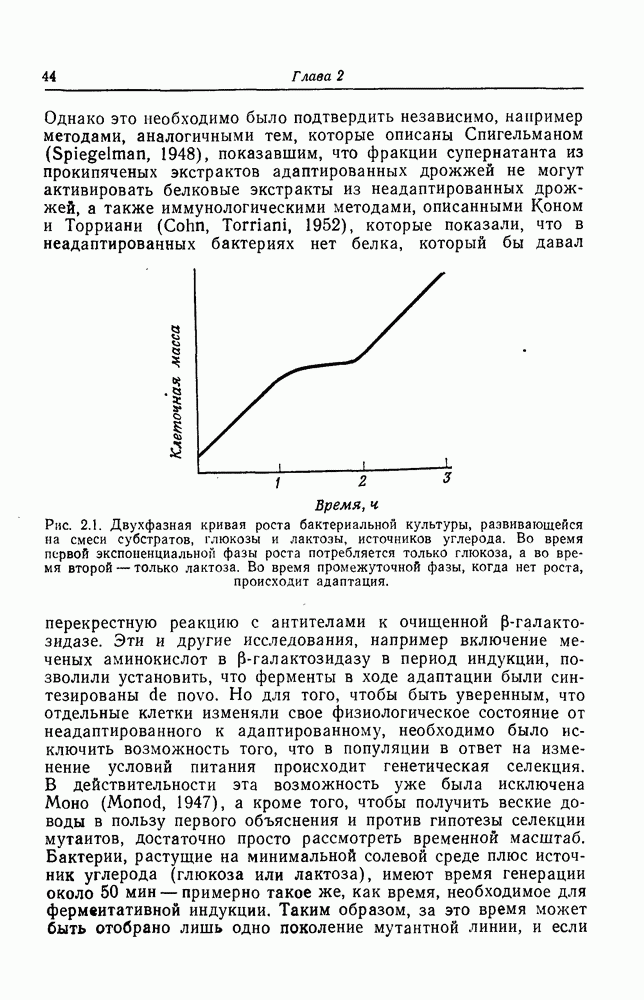
Остановимся теперь на следствиях, вытекающих из этой модели. Можно ли исходя из нее получить довольно резкий переход от состояния невозбудимости к состоянию возбудимости при данных значениях температуры Т и химического потенциала  , который определяет плотность молекул фермента на мембране? Пример перехода этого типа в развивающейся системе дают регенерирующие растения Acetabularia. Исследуя их электро-физиологическими методами, Новак и Бентрап (Novak, Bentrup, 1972) обнаружили, что спустя приблизительно 8-10 ч после начала процесса появляются спонтанные потенциалы действия, которые существуют затем на протяжении всего периода регенерации. Это проявление некой возбудимости в системе, хотя такая возбудимость может отличаться от описанной здесь.
, который определяет плотность молекул фермента на мембране? Пример перехода этого типа в развивающейся системе дают регенерирующие растения Acetabularia. Исследуя их электро-физиологическими методами, Новак и Бентрап (Novak, Bentrup, 1972) обнаружили, что спустя приблизительно 8-10 ч после начала процесса появляются спонтанные потенциалы действия, которые существуют затем на протяжении всего периода регенерации. Это проявление некой возбудимости в системе, хотя такая возбудимость может отличаться от описанной здесь.
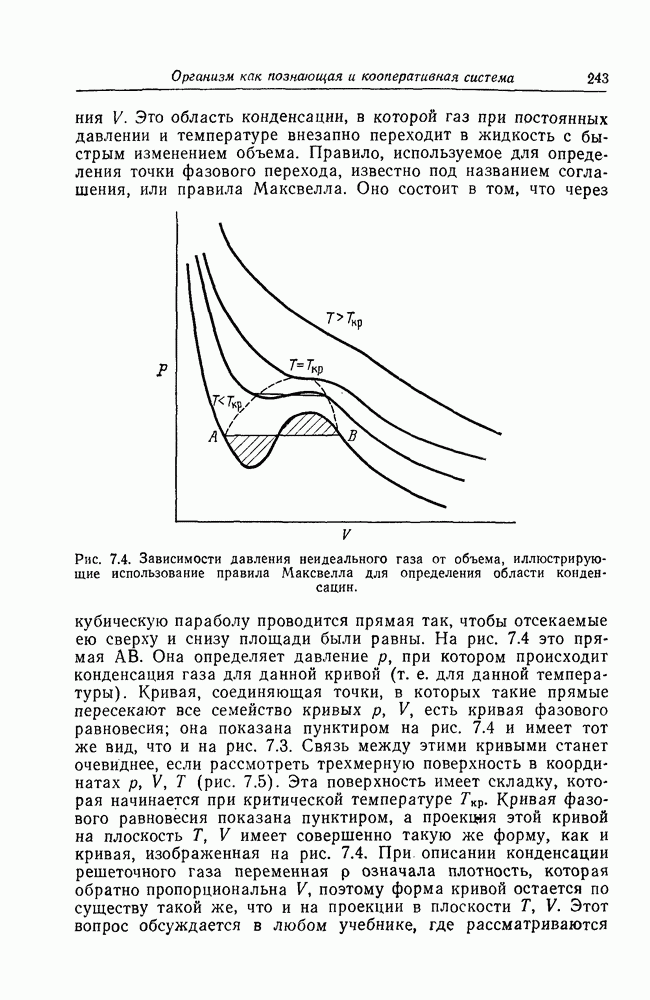
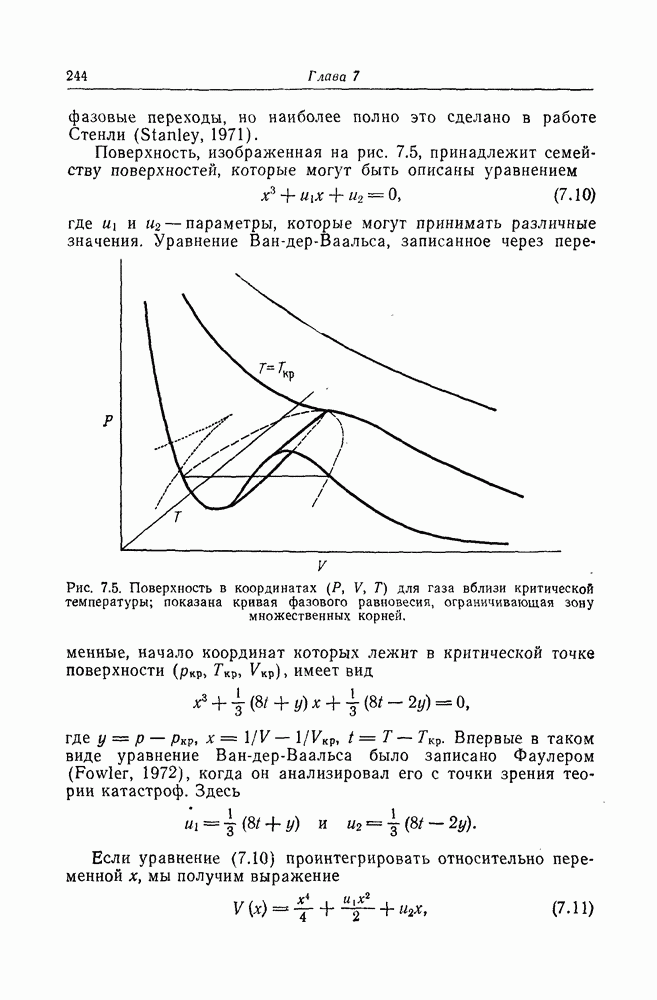
Область на диаграмме состояния, описываемой уравнением (7.7), которая представляет интерес при изучении переходов такого типа между состояниями, известна под названием области сосуществования фаз. В газах это область, где может происходить переход от газа к жидкости, а в ферромагнетиках — где может появляться спонтанное намагничивание. Значение потенциала, при котором возможен переход в нашем случае, равно  Поскольку
Поскольку  определяется с точностью до произвольной постоянной, отрицательный знак здесь не существен. Это значение при подстановке в (7.7) дает нам уравнение
определяется с точностью до произвольной постоянной, отрицательный знак здесь не существен. Это значение при подстановке в (7.7) дает нам уравнение

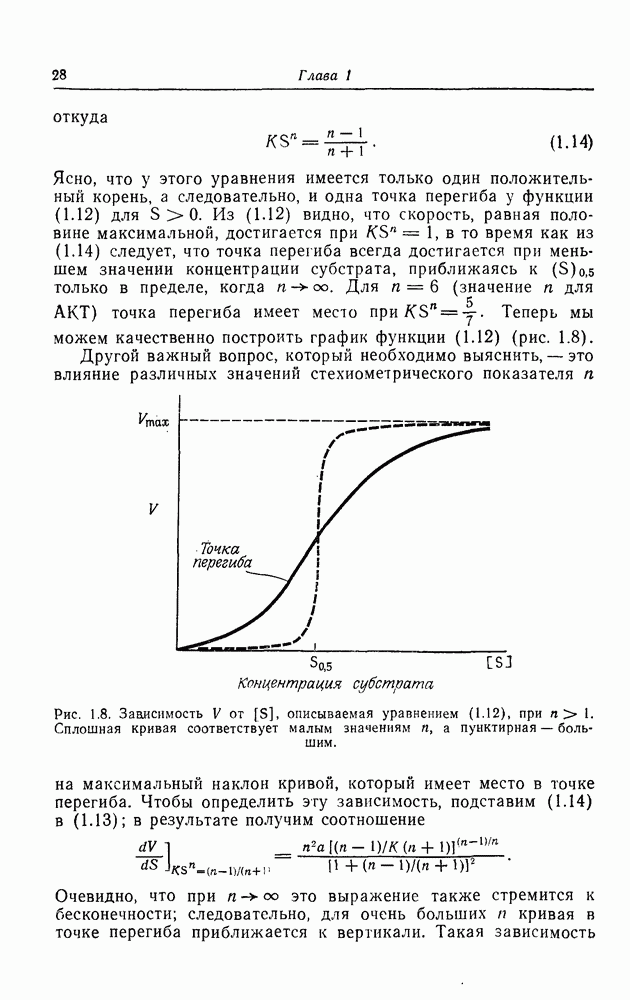
Если  достаточно велико (
достаточно велико ( достаточно мало), то это уравнение
достаточно мало), то это уравнение
имеет три корня, а при малых  оно имеет единственный корень, который является тривиальным решением,
оно имеет единственный корень, который является тривиальным решением,  . Это ясно из рис. 7.2, где прямая
. Это ясно из рис. 7.2, где прямая  и кривая
и кривая  построены в одних и тех же координатах. Для кривой I значение
построены в одних и тех же координатах. Для кривой I значение  , которое определяет наклон гиперболического тангенса, при
, которое определяет наклон гиперболического тангенса, при  больше 2, в то время как для кривой II ситуация обратная. Критическое значение
больше 2, в то время как для кривой II ситуация обратная. Критическое значение  (назовем его
(назовем его  а соответствующее значение Т—Ткр) дает значение наклона в этой точке, равное 2.
а соответствующее значение Т—Ткр) дает значение наклона в этой точке, равное 2.

Рис. 7.2. Графики функций  показывающие, как изменения Р вызывают появление множественных решений для
показывающие, как изменения Р вызывают появление множественных решений для  согласно уравнению (7.8).
согласно уравнению (7.8).
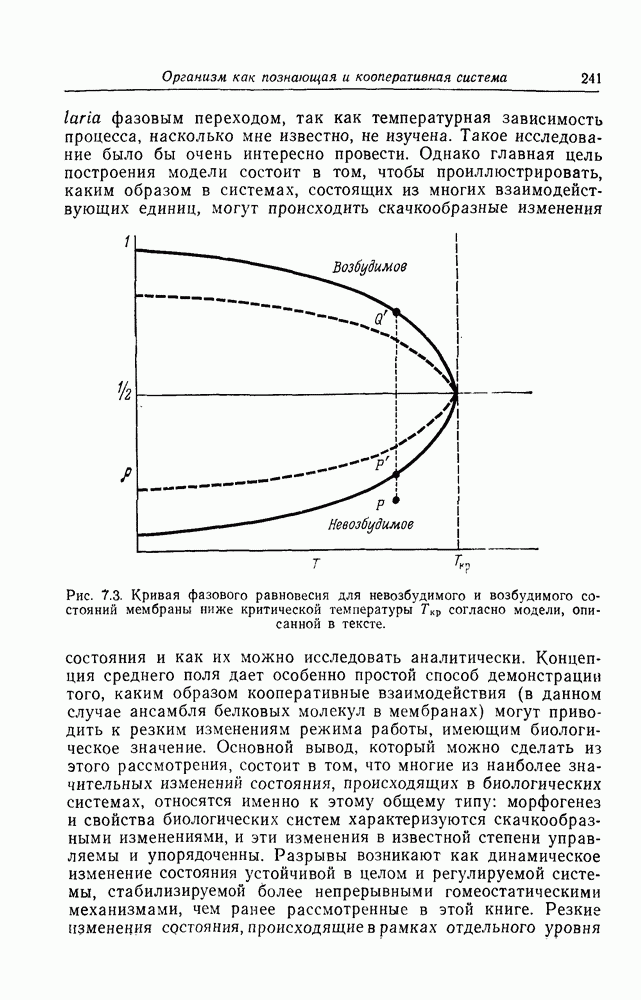
Если теперь мы отложим  как функцию Т, то получим кривую, показанную на рис. 7.3. Выше критической температуры
как функцию Т, то получим кривую, показанную на рис. 7.3. Выше критической температуры  существует только один корень
существует только один корень  представляет неопределенное состояние мембраны: ни возбудимое, ни невозбудимое. А ниже
представляет неопределенное состояние мембраны: ни возбудимое, ни невозбудимое. А ниже  состояние мембраны может изменяться от возбудимого до невозбудимого в зависимости от
состояние мембраны может изменяться от возбудимого до невозбудимого в зависимости от  , среднего поля взаимодействия. Таким образом, если система вначале находится в точке Р в невозбудимой области и
, среднего поля взаимодействия. Таким образом, если система вначале находится в точке Р в невозбудимой области и  увеличивается (с мембраной связывается все больше молекул фермента), то система окажется в точке Р на кривой фазового равновесия. Это неустойчивая точка, и система быстро перейдет в Q, оказавшись при этом в области возбудимости. Когда температура уменьшается, переход от невозбудимости к возбудимости совершается при все меньших и меньших значениях
увеличивается (с мембраной связывается все больше молекул фермента), то система окажется в точке Р на кривой фазового равновесия. Это неустойчивая точка, и система быстро перейдет в Q, оказавшись при этом в области возбудимости. Когда температура уменьшается, переход от невозбудимости к возбудимости совершается при все меньших и меньших значениях  среднего поля возбудимости, т. е. тепловой шум все меньше и меньше влияет на процессы, приводящие к возбуждению.
среднего поля возбудимости, т. е. тепловой шум все меньше и меньше влияет на процессы, приводящие к возбуждению.
Ясно, что в биологической системе имеется также и нижняя температурная граница зоны возбудимости, т. е. кривая фазового равновесия должна быть замкнутой, если процесс потери возбудимости тоже является фазовым переходом. Это можно смоделировать, вводя дополнительные предположения, скажем о зависимости величин  от температуры при низких значениях Т, однако большого смысла в этом нет, поскольку экспериментальные данные по таким переходам в биологических системах весьма немногочисленны; возможно, здесь начинают играть роль факторы совершенно иной природы, чем рассмотренные выше. В действительности мы не знаем, можно ли считать спонтанное появление потенциалов действия в Acetabularia
от температуры при низких значениях Т, однако большого смысла в этом нет, поскольку экспериментальные данные по таким переходам в биологических системах весьма немногочисленны; возможно, здесь начинают играть роль факторы совершенно иной природы, чем рассмотренные выше. В действительности мы не знаем, можно ли считать спонтанное появление потенциалов действия в Acetabularia
фазовым переходом, так как температурная зависимость процесса, насколько мне известно, не изучена. Такое исследование было бы очень интересно провести. Однако главная цель построения модели состоит в том, чтобы проиллюстрировать, каким образом в системах, состоящих из многих взаимодействующих единиц, могут происходить скачкообразные изменения состояния и как их можно исследовать аналитически.

Рис. 7.3. Кривая фазового равновесия для невозбудимого и возбудимого состояний мембраны ниже критической температуры  согласно модели, описанной в тексте.
согласно модели, описанной в тексте.
Концепция среднего поля дает особенно простой способ демонстрации того, каким образом кооперативные взаимодействия (в данном случае ансамбля белковых молекул в мембранах) могут приводить к резким изменениям режима работы, имеющим биологическое значение. Основной вывод, который можно сделать из этого рассмотрения, состоит в том, что многие из наиболее значительных изменений состояния, происходящих в биологических системах, относятся именно к этому общему типу: морфогенез и свойства биологических систем характеризуются скачкообразными изменениями, и эти изменения в известной степени управляемы и упорядоченны. Разрывы возникают как динамическое изменение состояния устойчивой в целом и регулируемой системы, стабилизируемой более непрерывными гомеостатическими механизмами, чем ранее рассмотренные в этой книге. Резкие изменения состояния, происходящие в рамках отдельного уровня
иерархии  приведут на этом уровне к образованию новых коллективных переменных, так что «сигналы», переданные с помощью функции
приведут на этом уровне к образованию новых коллективных переменных, так что «сигналы», переданные с помощью функции  изменятся. В рассмотренном выше примере до появления у мембраны возбудимости в системе не может распространяться никаких метаболических волн и, следовательно, на языке волновой модели гл. 5 не образуется никаких градиентов. Таким образом, до тех пор, пока не произойдет этот фазовый переход, в системе не может генерироваться никакого пространственно-упорядоченного сигнала, и в ней существует только некое пространственное распределение, соответствующее изначально имеющемуся в системе распределению сигнала. Это распределение может быть весьма существенным, но оно носиг мозаичный характер и не сможет осуществлять регуляцию. Однако, когда мембраны становятся возбудимыми, поведение метаболической системы становится качественно иным — в ней распространяется метаболическая волна, несущая регулирующую пространственно-упорядоченную информацию в форме связанных с мембраной градиентов, которая способна управлять изменениями эпигенетического состояния. Итак, теперь понятно, каким образом фазовые переходы могут сформировать важную особенность генеративного процесса, который мы называем развитием, и как они вписываются в рамки схемы рис. 7.1: это переходы между дискретными состояниями в пределах отдельных уровней или всей иерархии, что в результате кооперативных взаимодействий между единицами приводит к упрощению динамики.
изменятся. В рассмотренном выше примере до появления у мембраны возбудимости в системе не может распространяться никаких метаболических волн и, следовательно, на языке волновой модели гл. 5 не образуется никаких градиентов. Таким образом, до тех пор, пока не произойдет этот фазовый переход, в системе не может генерироваться никакого пространственно-упорядоченного сигнала, и в ней существует только некое пространственное распределение, соответствующее изначально имеющемуся в системе распределению сигнала. Это распределение может быть весьма существенным, но оно носиг мозаичный характер и не сможет осуществлять регуляцию. Однако, когда мембраны становятся возбудимыми, поведение метаболической системы становится качественно иным — в ней распространяется метаболическая волна, несущая регулирующую пространственно-упорядоченную информацию в форме связанных с мембраной градиентов, которая способна управлять изменениями эпигенетического состояния. Итак, теперь понятно, каким образом фазовые переходы могут сформировать важную особенность генеративного процесса, который мы называем развитием, и как они вписываются в рамки схемы рис. 7.1: это переходы между дискретными состояниями в пределах отдельных уровней или всей иерархии, что в результате кооперативных взаимодействий между единицами приводит к упрощению динамики.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ЛИТЕРАТУРА
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ МЕТАБОЛИЧЕСКОЙ СИСТЕМЫ
- Устойчивость и закон действующих масс в метаболической системе
- Ингибирование по типу обратной связи в метаболических системах
- Аллостерические свойства ферментов
- Кооперативная ферментативная кинетика
- Цепи управления метаболизмом и их динамика
- Заключение
- Глава 2. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ ЭПИГЕНЕТИЧЕСКОЙ СИСТЕМЫ
- Индукция и репрессия генов
- Репрессия путей биосинтеза по типу обратной связи
- Контроль синтеза рибосомной РНК
- Динамика эпигенетических сетей
- Аналогия со статистической термодинамикой
- Аналогия с вычислительными машинами: клетка как конечный автомат
- Глава 3. МИТОТИЧЕСКИЙ И КЛЕТОЧНЫЙ ЦИКЛЫ
- Репликон и гипотеза инициатора
- Гипотеза репрессора инициации
- Эукариоты
- Представление клеточного цикла в виде последовательности стадий
- Клеточный цикл млекопитающих
- Управление скоростью цикла и клеточная дифференцировка
- Эпидермис млекопитающих и кейлонная теория
- Вероятностные модели клеточного цикла и его управления
- Глава 4. КЛЕТОЧНЫЙ РОСТ, СИНХРОННОСТЬ КЛЕТОЧНЫХ ЦИКЛОВ И БИОЛОГИЧЕСКИЕ ЧАСЫ
- Хемостат
- Адаптивное поведение хемостата
- Системы восстановления клеток
- Синхронизация клеток
- Суточные ритмы деления клеток в тканях млекопитающих
- Контактное торможение
- Клеточные часы
- Физиология клеточных часов
- Динамика часов, контролирующих вылупление личинок у Drosophila
- Глава 5. МОРФОГЕНЕЗ: ОДНОМЕРНАЯ АПЕРИОДИЧЕСКАЯ УПОРЯДОЧЕННОСТЬ
- Полярность и осевые градиенты
- Пейсмекеры и волны активности
- Морфогенез одноклеточных
- Мембраны и морфогенез
- Регуляция и устойчивость
- Периодические режимы у гидроидов
- Глава 6. МОРФОГЕНЕЗ: ПРОСТРАНСТВЕННЫЕ ПЕРИОДИЧНОСТИ И МНОГОМЕРНАЯ УПОРЯДОЧЕННОСТЬ
- Распространение волн и пространственные периодичности
- Эпидермис насекомых
- Мембрана и эпидермис насекомых
- Эпиморфоз: крыло цыпленка
- Волновая модель и эпиморфоз
- Локальная и глобальная упорядоченность: имагинальный диск и конечность таракана
- Ретино-тектальная проекция в зрительной системе амфибий
- Механизм образования двумерной проекции
- Глава 7. ОРГАНИЗМ КАК ПОЗНАЮЩАЯ И КООПЕРАТИВНАЯ СИСТЕМА
- Функциональная иерархия
- Обратные предельные системы
- Кооперативные взаимодействия и фазовые переходы в познающих системах
- Фазовые переходы и теория катастроф
- Коллективные моды в ритмических процессах
- Процессы генерации в познающих системах
- ПРИЛОЖЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ