| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
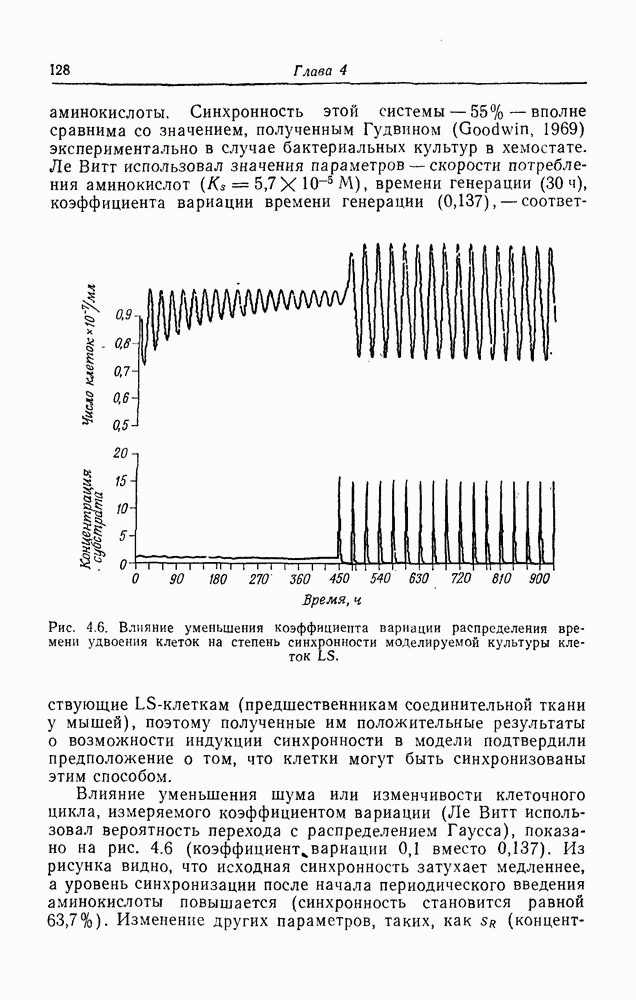
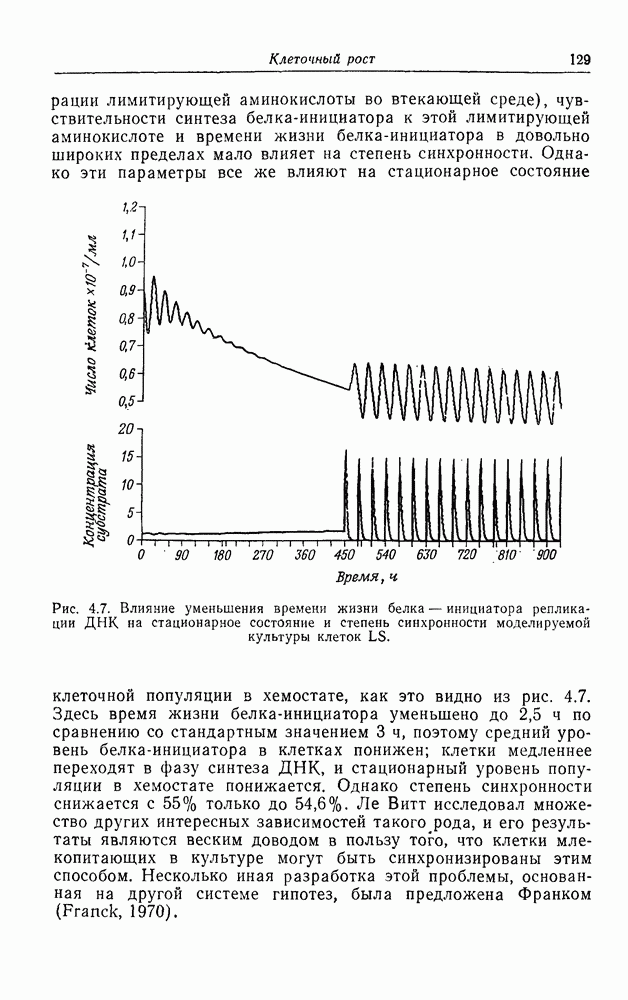
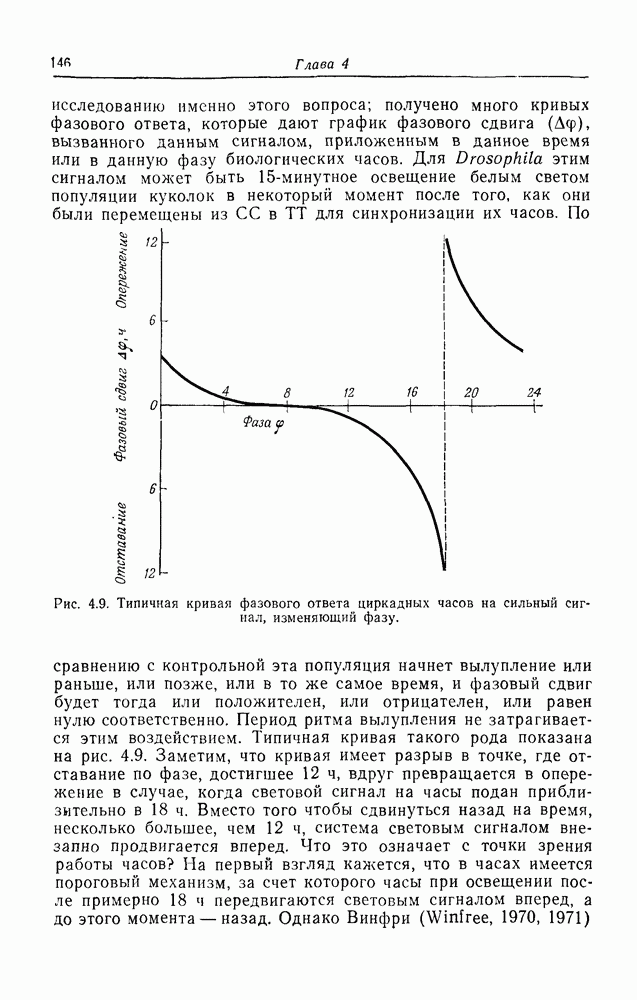
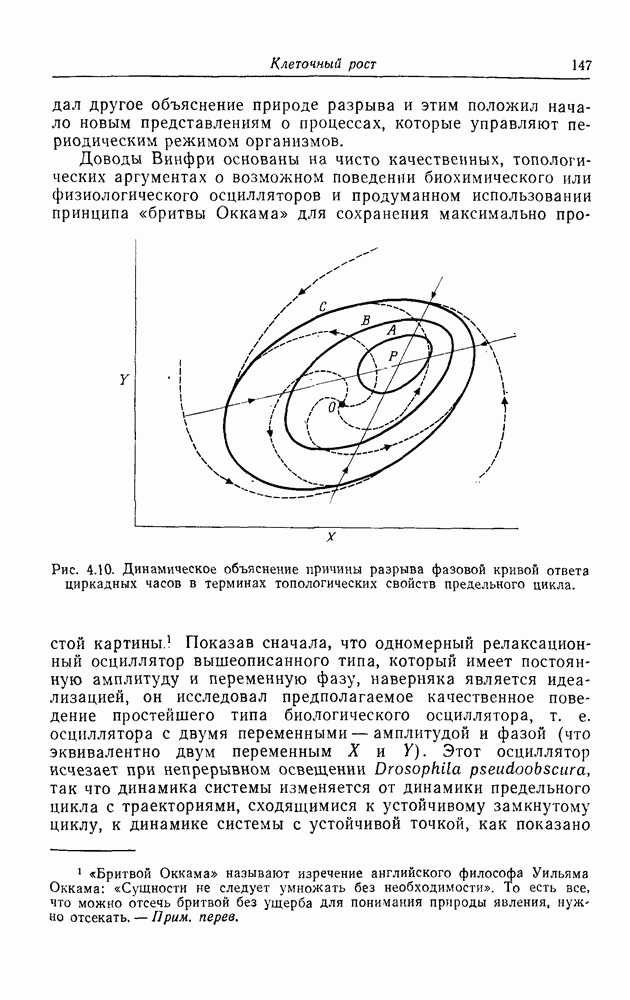
Хемостат
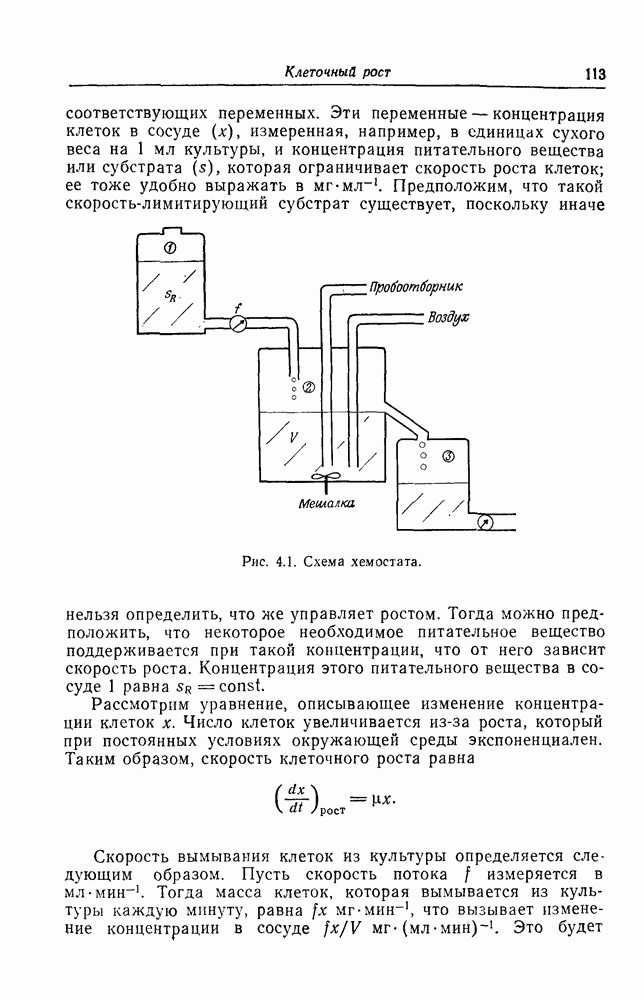
Устройство, предназначенное для выращивания клеточных популяций в постоянных химических условиях, было описано в 1950 г. Новиком и Сциллардом (Novick, Szilard, 1950) и Моно (Monod, 1950), причем для объяснения его функционирования в обеих работах использовалась по существу одна и та же теория. Прибор в своей основе очень прост и со времени появления с большим успехом применяется при изучении клеточной физиологии и поведения популяций. Схема его представлена на рис. 4.1. Сосуд 1 содержит питательную среду, необходимую для роста клеток (таких, как бактерии, дрожжи, LS-клетки и т. д.), которые могут расти в суспензионных культурах. Скорость поступления f питательных веществ в сосуд 2, где происходит рост, регулируется с помощью специального устройства. Это устройство изображено здесь в виде кружка со стрелкой. Сосуд 2 содержит объем V культуры клеток; быстрое перемешивание поступающей среды осуществляется с помощью мешалки, поддерживающей содержимое сосуда однородным. Объем сохраняется постоянным с помощью сливного рукава, через который культура вытекает в сосуд 3 с той же скоростью, с какой из сосуда 1 поступает среда. В сосуд 2 подается также воздух, и имеется устройство для отбора проб. Сосуд 3 служит для сбора клеток, которые могут быть использованы затем для получения биологических продуктов (лекарств, витаминов, белка, спирта и т. д.).
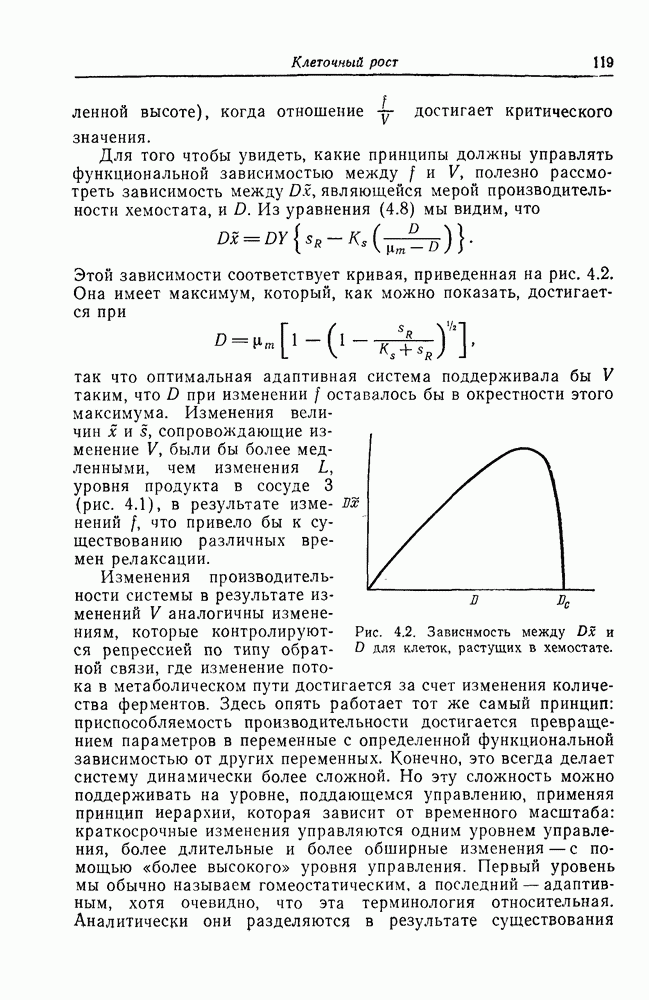
Интуитивно ясно, что, если скорость потока через сосуд 2 не превышает максимальную скорость роста клеток внутри него, в системе установится стационарное состояние роста, которое будет устойчивым к малым возмущениям клеточной плотности или концентрации питательных веществ. Чтобы показать это, выведем дифференциальные уравнения, описывающие поведение
соответствующих переменных. Эти переменные — концентрация клеток в сосуде  измеренная, например, в единицах сухого веса на 1 мл культуры, и концентрация питательного вещества или субстрата (s), которая ограничивает скорость роста клеток; ее тоже удобно выражать в
измеренная, например, в единицах сухого веса на 1 мл культуры, и концентрация питательного вещества или субстрата (s), которая ограничивает скорость роста клеток; ее тоже удобно выражать в  . Предположим, что такой скорость-лимитирующий субстрат существует, поскольку иначе нельзя определить, что же управляет ростом.
. Предположим, что такой скорость-лимитирующий субстрат существует, поскольку иначе нельзя определить, что же управляет ростом.

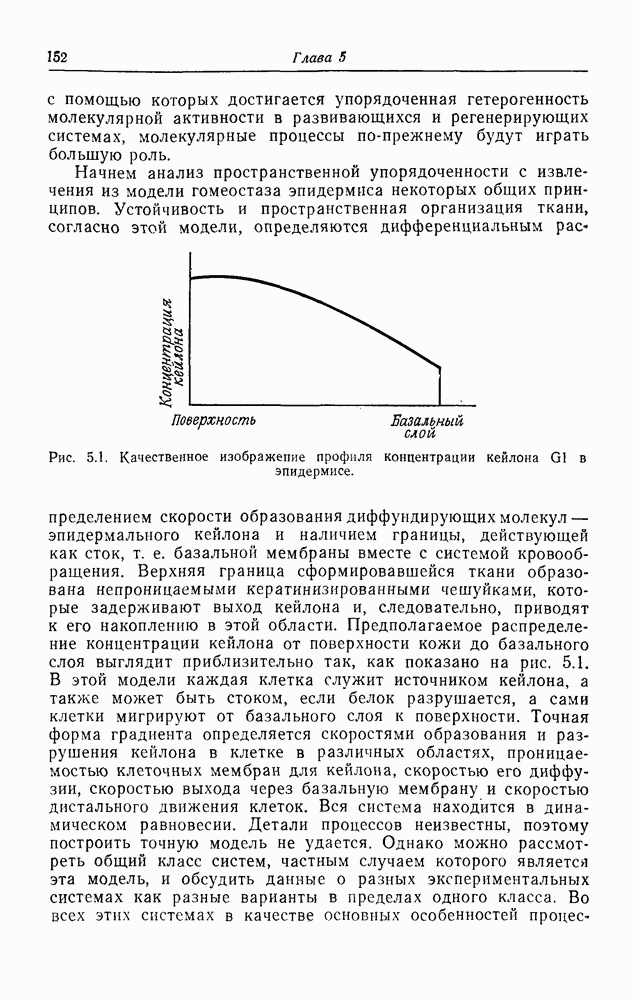
Рис. 4.1. Схема хемостата.
Тогда можно предположить, что некоторое необходимое питательное вещество поддерживается при такой концентрации, что от него зависит скорость роста. Концентрация этого питательного вещества в сосуде 1 равна  .
.
Рассмотрим уравнение, описывающее изменение концентрации клеток  Число клеток увеличивается из-за роста, который при постоянных условиях окружающей среды экспоненциален. Таким образом, скорость клеточного роста равна
Число клеток увеличивается из-за роста, который при постоянных условиях окружающей среды экспоненциален. Таким образом, скорость клеточного роста равна

Скорость вымывания клеток из культуры определяется следующим образом. Пусть скорость потока f измеряется в  . Тогда масса клеток, которая вымывается из культуры каждую минуту, равна
. Тогда масса клеток, которая вымывается из культуры каждую минуту, равна  , что вызывает изменение концентрации в сосуде
, что вызывает изменение концентрации в сосуде  Это будет
Это будет
разбавление за счет выведения клеток. Следовательно, изменение концентрации клеток имеет вид

Введя  получим
получим

Далее нам необходимо найти уравнение для s. Субстрат поступает в сосуд со скоростью  , что вызывает изменение концентрации его в сосуде
, что вызывает изменение концентрации его в сосуде  , где
, где  измеряется в
измеряется в  . Скорость выведения равна
. Скорость выведения равна  , где s — концентрация лимитирующего скорость субстрата в сосуде 2. Третий член, который необходимо учесть в выражении для ds/dt, описывает потребление субстрата клетками. Введем величину Y, равную весу клеток, образованных на единицу субстрата. Эта величина известна как константа выхода. Например, для бактерии Aerobacter cloacae, растущей на среде, где лимитирующим субстратом является глицерин, У принимает значение 0,5, т. е. на каждые 0,5 мг прироста бактерий потребляется 1 мг глицерина. Конечно, бактерии поглощают из среды и множество других соединений, таких, как N, Р, S, К, Na, Mg и т. д., в виде различных солей, но они присутствуют в количествах, не ограничивающих скорость, и поэтому не входят в систему уравнений как переменные. Уравнение для s, таким образом, примет вид
, где s — концентрация лимитирующего скорость субстрата в сосуде 2. Третий член, который необходимо учесть в выражении для ds/dt, описывает потребление субстрата клетками. Введем величину Y, равную весу клеток, образованных на единицу субстрата. Эта величина известна как константа выхода. Например, для бактерии Aerobacter cloacae, растущей на среде, где лимитирующим субстратом является глицерин, У принимает значение 0,5, т. е. на каждые 0,5 мг прироста бактерий потребляется 1 мг глицерина. Конечно, бактерии поглощают из среды и множество других соединений, таких, как N, Р, S, К, Na, Mg и т. д., в виде различных солей, но они присутствуют в количествах, не ограничивающих скорость, и поэтому не входят в систему уравнений как переменные. Уравнение для s, таким образом, примет вид

Поскольку мы предположили, что s — переменная, которая ограничивает скорость роста, то тейерь необходимо определить [i как функцию s. Из рассмотрения работы lac-оперона мы знаем, что поступление источника углерода в бактерии регулируется особым ферментом, пермеазой, локализованной в клеточной мембране. Поэтому скорость роста будет зависеть от катализируемой ферментом реакции. Это утверждение, конечно, было бы справедливым, даже если бы специальная пермеазная система отсутствовала, потому что скорость утилизации питательного вещества все равно зависела бы от активности некоторого фермента. Поэтому разумно взять функциональную зависимость  от s в виде выражения для скорости реакции, катализируемой ферментом, с s в качестве субстрата. Сейчас, записывая вид этой зависимости, мы имеем возможность выбора: можно воспользоваться уравнением Михаэлиса — Ментен (1.9) с
от s в виде выражения для скорости реакции, катализируемой ферментом, с s в качестве субстрата. Сейчас, записывая вид этой зависимости, мы имеем возможность выбора: можно воспользоваться уравнением Михаэлиса — Ментен (1.9) с  или взять одно из более сложных уравнений (1.11) или (1.23), описывающих ферменты с сигмоидной кинетикой. Естественно,
или взять одно из более сложных уравнений (1.11) или (1.23), описывающих ферменты с сигмоидной кинетикой. Естественно,
что Новик и Сцилард (Novick, Szilard, 1950) и Моно (Monod, 1950) использовали более простое выражение Михаэлиса — Ментен, так как в то время кооперативность ферментов еще не была обнаружена. Итак, следуя им, примем

где  — максимальная скорость роста, аналог максимальной ферментативной активности, a
— максимальная скорость роста, аналог максимальной ферментативной активности, a  -аналог константы Михаэлиса
-аналог константы Михаэлиса  в уравнении (1.9). Величина определяется собственной скоростью роста клеток и, следовательно, зависит только от их наследственной структуры.
в уравнении (1.9). Величина определяется собственной скоростью роста клеток и, следовательно, зависит только от их наследственной структуры.
Подстановка выражения (4.3) в уравнения (4.1) и (4.2) дает нам пару уравнений:

Стационарное состояние (если оно существует) определяется некоторой парой значений s их, при которых производные обращаются в 0. Обозначим эти значения как х и s; они должны определяться уравнениями

Очевидным решением уравнения (4.6) является  тогда из уравнения (4.7) мы находим, что
тогда из уравнения (4.7) мы находим, что  . Это соответствует такому состоянию хемостата, когда клетки не введены в сосуд 2. так что концентрация субстрата в нем такая же, как и в сосуде 1, т. е.
. Это соответствует такому состоянию хемостата, когда клетки не введены в сосуд 2. так что концентрация субстрата в нем такая же, как и в сосуде 1, т. е.  . Другое решение этой системы уравнений:
. Другое решение этой системы уравнений:

Из уравнений (4.8) видно, что при некотором значении D, назовем его  выражение в квадратных скобках будет равно 0, т. е.
выражение в квадратных скобках будет равно 0, т. е.

или

В этом случае уравнение (4.4) примет вид

Пока в хемостате существуют клетки, s меньше, чем  потому что клетки используют некоторое количество субстрата; таким образом, из уравнения (4.10) мы видим, что, когда
потому что клетки используют некоторое количество субстрата; таким образом, из уравнения (4.10) мы видим, что, когда  до тех пор, пока при
до тех пор, пока при  не обратится в 0. Это соответствует решению
не обратится в 0. Это соответствует решению  . Следовательно,
. Следовательно,  есть критическая скорость разведения, при которой клетки не могут расти достаточно быстро для того, чтобы скомпенсировать выведение, и поэтому сосуд с культурой медленно, но неуклонно освобождается от клеток. Эта ситуация, а также условия, при которых происходит вымывание, были рассмотрены в интересном и информативном исследовании теории и экспериментального поведения клеток, растущих в хемостате, Хербертом, Эллсвортом и Теллингом (Herbert, Ellsworth, Telling, 1956). Они обсудили также многие другие аспекты соотношений между теорией и экспериментом, выявив как соответствия, так и ряд несоответствий, которые помогают определить, какие допущения модели неверны. Несоответствия теории эксперименту возникают главным образом при исследовании поведения системы в окрестности критической точки
есть критическая скорость разведения, при которой клетки не могут расти достаточно быстро для того, чтобы скомпенсировать выведение, и поэтому сосуд с культурой медленно, но неуклонно освобождается от клеток. Эта ситуация, а также условия, при которых происходит вымывание, были рассмотрены в интересном и информативном исследовании теории и экспериментального поведения клеток, растущих в хемостате, Хербертом, Эллсвортом и Теллингом (Herbert, Ellsworth, Telling, 1956). Они обсудили также многие другие аспекты соотношений между теорией и экспериментом, выявив как соответствия, так и ряд несоответствий, которые помогают определить, какие допущения модели неверны. Несоответствия теории эксперименту возникают главным образом при исследовании поведения системы в окрестности критической точки  При высоких скоростях разбавления выживаемость клеток выше, чем это предсказывает теория; поэтому предположение о гомогенности, означающее, что смешивание новых объемов питательного вещества с культурой происходит мгновенно, по-видимому, неверно. Меньшую выживаемость клеток, чем ожидается при критической скорости разбавления, может объяснить именно гетерогенность. Конечно, при любом D большем, чем
При высоких скоростях разбавления выживаемость клеток выше, чем это предсказывает теория; поэтому предположение о гомогенности, означающее, что смешивание новых объемов питательного вещества с культурой происходит мгновенно, по-видимому, неверно. Меньшую выживаемость клеток, чем ожидается при критической скорости разбавления, может объяснить именно гетерогенность. Конечно, при любом D большем, чем  клетки тем более будут удаляться.
клетки тем более будут удаляться.
Теперь мы можем исследовать устойчивость стационарных решений уравнений (4.4) и (4.5). Используем тот же метод, что и при изучении устойчивости стационарного решения системы уравнений (1.25). Сначала введем новые переменные,  и допустим, что
и допустим, что  малы, так что всеми членами, степень которых выше единицы, можно пренебречь. Тогда система уравнений примет вид
малы, так что всеми членами, степень которых выше единицы, можно пренебречь. Тогда система уравнений примет вид

где

Характеристическое уравнение системы уравнений (4.11) и

Его корни равны

Поскольку а, b и с положительны, действительная часть корней отрицательна, и поэтому стационарное состояние для  устойчиво. Подставляя в выражение для с
устойчиво. Подставляя в выражение для с  из уравнения (4.6), можно также показать, что
из уравнения (4.6), можно также показать, что  поэтому корни не имеют мнимых частей, и, следовательно, в работе хемостата не может существовать никакого овершута с затухающими колебаниями. Однако экспериментально это явление обнаружено, т. е. опять имеется несоответствие между теорией и экспериментом, требующее модификации модели. Этот случай был рассмотрен Мозером (Moser, 1958).
поэтому корни не имеют мнимых частей, и, следовательно, в работе хемостата не может существовать никакого овершута с затухающими колебаниями. Однако экспериментально это явление обнаружено, т. е. опять имеется несоответствие между теорией и экспериментом, требующее модификации модели. Этот случай был рассмотрен Мозером (Moser, 1958).
Если  , то можно показать, что решение
, то можно показать, что решение  неустойчиво, подставляя эти значения в уравнения (4.11) и (4.12). В этом случае характеристическое уравнение имеет вид
неустойчиво, подставляя эти значения в уравнения (4.11) и (4.12). В этом случае характеристическое уравнение имеет вид  , где
, где  так что существует положительное собственное значение, дающее неустойчивость. Но если
так что существует положительное собственное значение, дающее неустойчивость. Но если  то решение
то решение  будет устойчиво. Выяснения влияния параметра D на поведение этой системы интересно с той точки зрения, что оно показывает зависимость устойчивости от выполнения некоторых ограничений, определяемых параметрами.
будет устойчиво. Выяснения влияния параметра D на поведение этой системы интересно с той точки зрения, что оно показывает зависимость устойчивости от выполнения некоторых ограничений, определяемых параметрами.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ЛИТЕРАТУРА
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ МЕТАБОЛИЧЕСКОЙ СИСТЕМЫ
- Устойчивость и закон действующих масс в метаболической системе
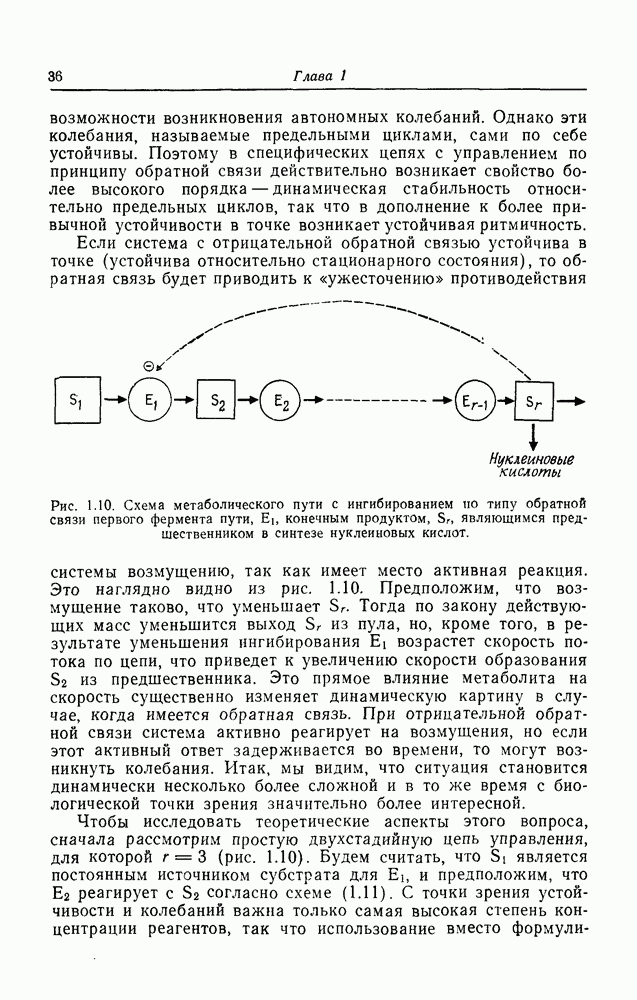
- Ингибирование по типу обратной связи в метаболических системах
- Аллостерические свойства ферментов
- Кооперативная ферментативная кинетика
- Цепи управления метаболизмом и их динамика
- Заключение
- Глава 2. УСТОЙЧИВОСТЬ И РЕГУЛЯЦИЯ ЭПИГЕНЕТИЧЕСКОЙ СИСТЕМЫ
- Индукция и репрессия генов
- Репрессия путей биосинтеза по типу обратной связи
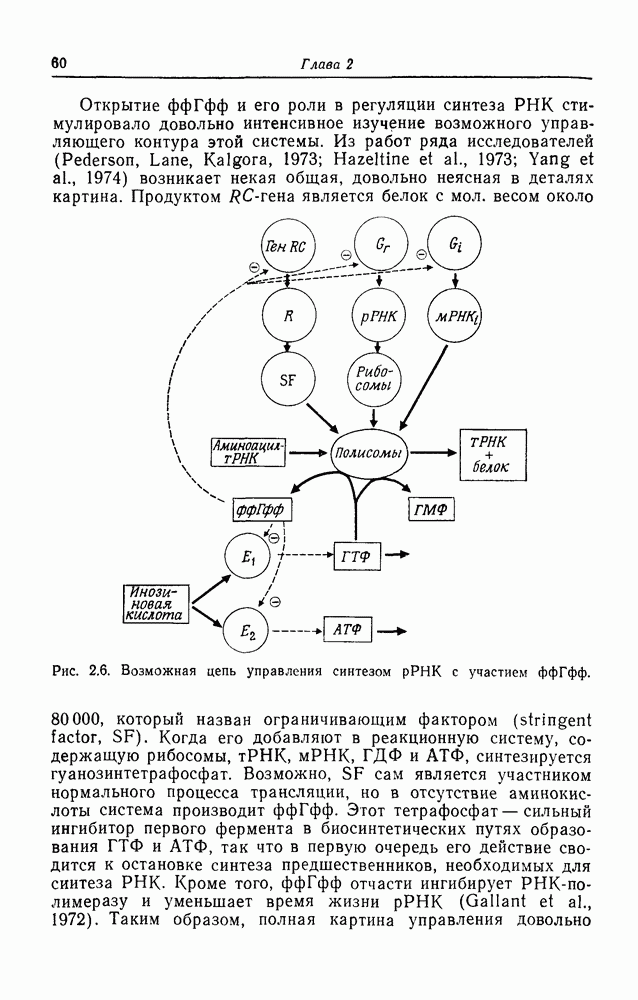
- Контроль синтеза рибосомной РНК
- Динамика эпигенетических сетей
- Аналогия со статистической термодинамикой
- Аналогия с вычислительными машинами: клетка как конечный автомат
- Глава 3. МИТОТИЧЕСКИЙ И КЛЕТОЧНЫЙ ЦИКЛЫ
- Репликон и гипотеза инициатора
- Гипотеза репрессора инициации
- Эукариоты
- Представление клеточного цикла в виде последовательности стадий
- Клеточный цикл млекопитающих
- Управление скоростью цикла и клеточная дифференцировка
- Эпидермис млекопитающих и кейлонная теория
- Вероятностные модели клеточного цикла и его управления
- Глава 4. КЛЕТОЧНЫЙ РОСТ, СИНХРОННОСТЬ КЛЕТОЧНЫХ ЦИКЛОВ И БИОЛОГИЧЕСКИЕ ЧАСЫ
- Хемостат
- Адаптивное поведение хемостата
- Системы восстановления клеток
- Синхронизация клеток
- Суточные ритмы деления клеток в тканях млекопитающих
- Контактное торможение
- Клеточные часы
- Физиология клеточных часов
- Динамика часов, контролирующих вылупление личинок у Drosophila
- Глава 5. МОРФОГЕНЕЗ: ОДНОМЕРНАЯ АПЕРИОДИЧЕСКАЯ УПОРЯДОЧЕННОСТЬ
- Полярность и осевые градиенты
- Пейсмекеры и волны активности
- Морфогенез одноклеточных
- Мембраны и морфогенез
- Регуляция и устойчивость
- Периодические режимы у гидроидов
- Глава 6. МОРФОГЕНЕЗ: ПРОСТРАНСТВЕННЫЕ ПЕРИОДИЧНОСТИ И МНОГОМЕРНАЯ УПОРЯДОЧЕННОСТЬ
- Распространение волн и пространственные периодичности
- Эпидермис насекомых
- Мембрана и эпидермис насекомых
- Эпиморфоз: крыло цыпленка
- Волновая модель и эпиморфоз
- Локальная и глобальная упорядоченность: имагинальный диск и конечность таракана
- Ретино-тектальная проекция в зрительной системе амфибий
- Механизм образования двумерной проекции
- Глава 7. ОРГАНИЗМ КАК ПОЗНАЮЩАЯ И КООПЕРАТИВНАЯ СИСТЕМА
- Функциональная иерархия
- Обратные предельные системы
- Кооперативные взаимодействия и фазовые переходы в познающих системах
- Фазовые переходы и теория катастроф
- Коллективные моды в ритмических процессах
- Процессы генерации в познающих системах
- ПРИЛОЖЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ