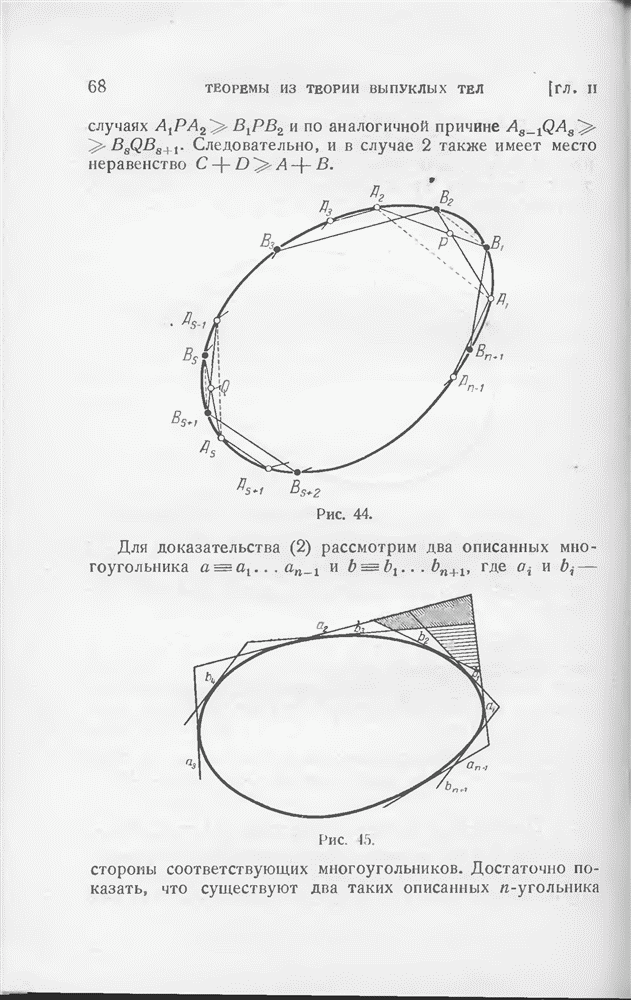
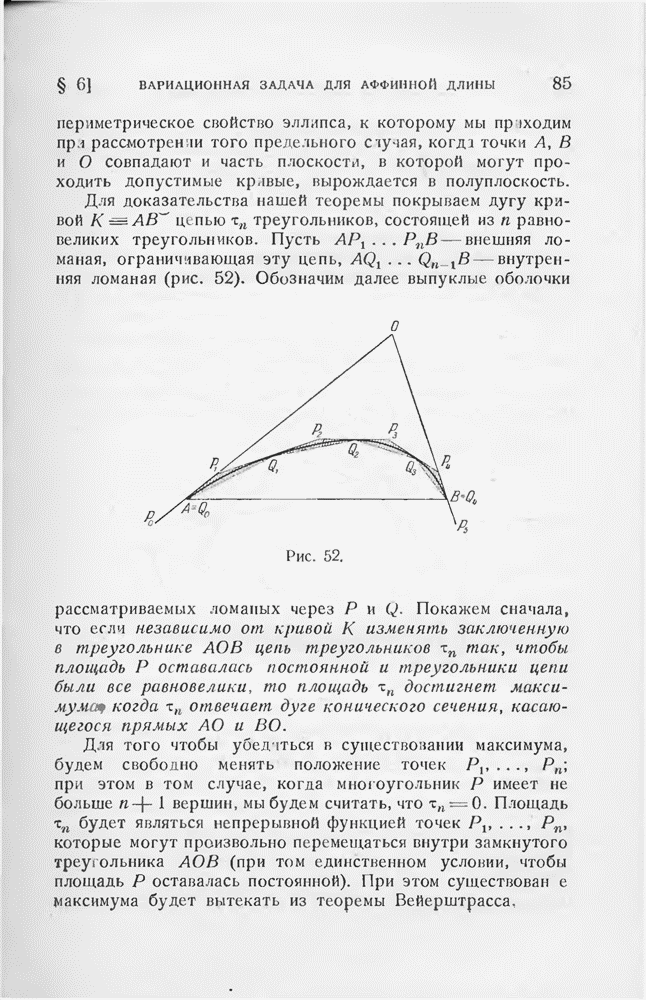
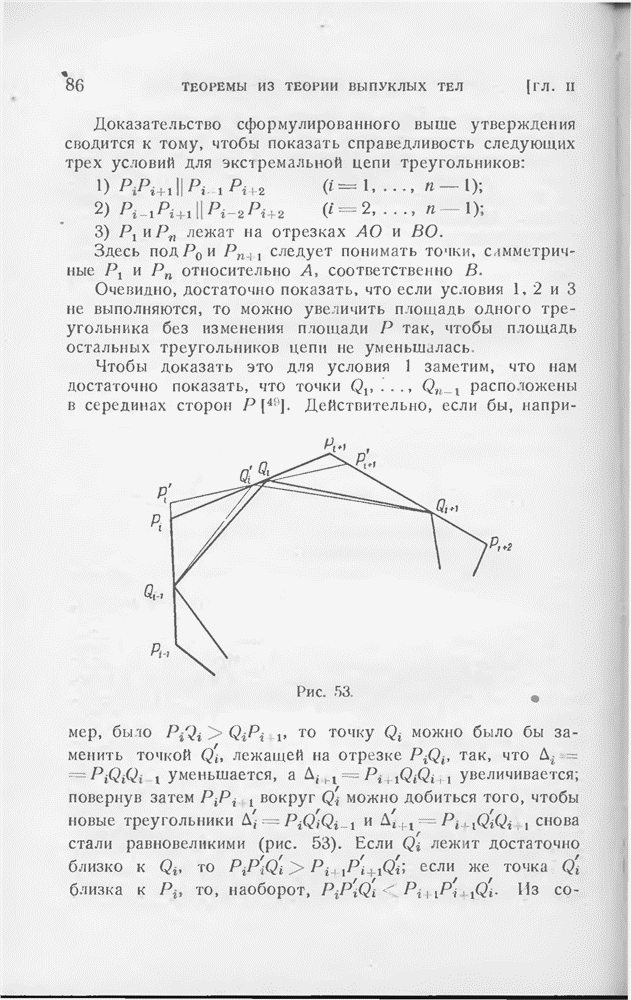
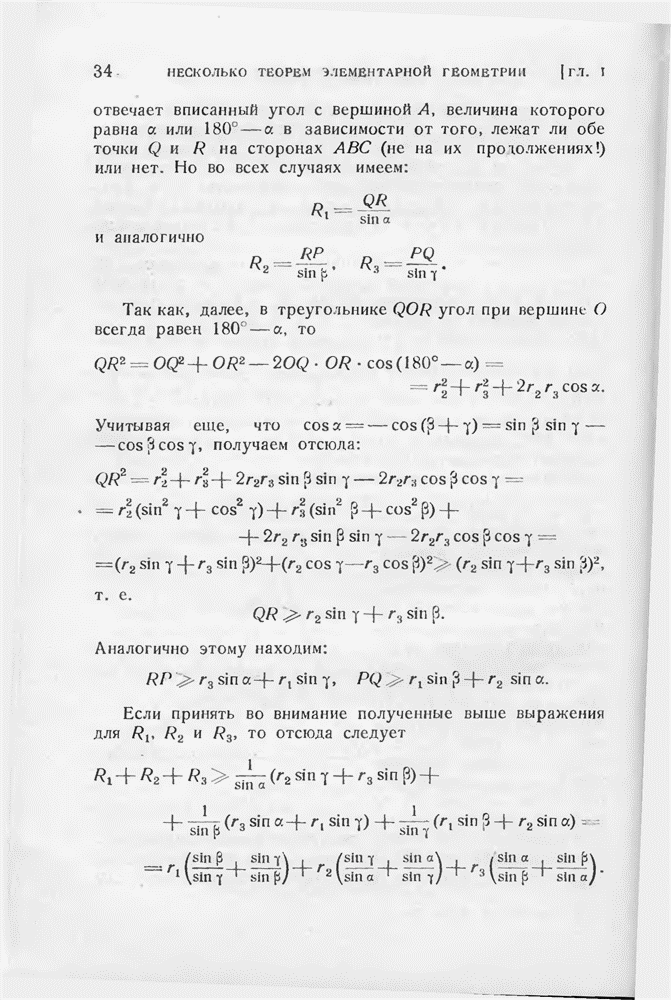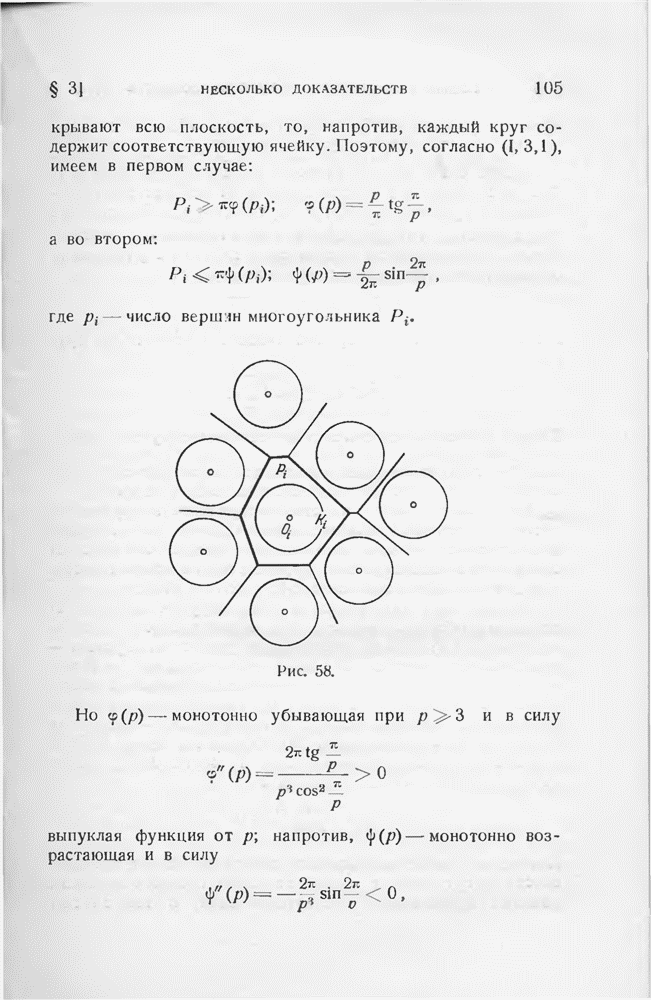| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
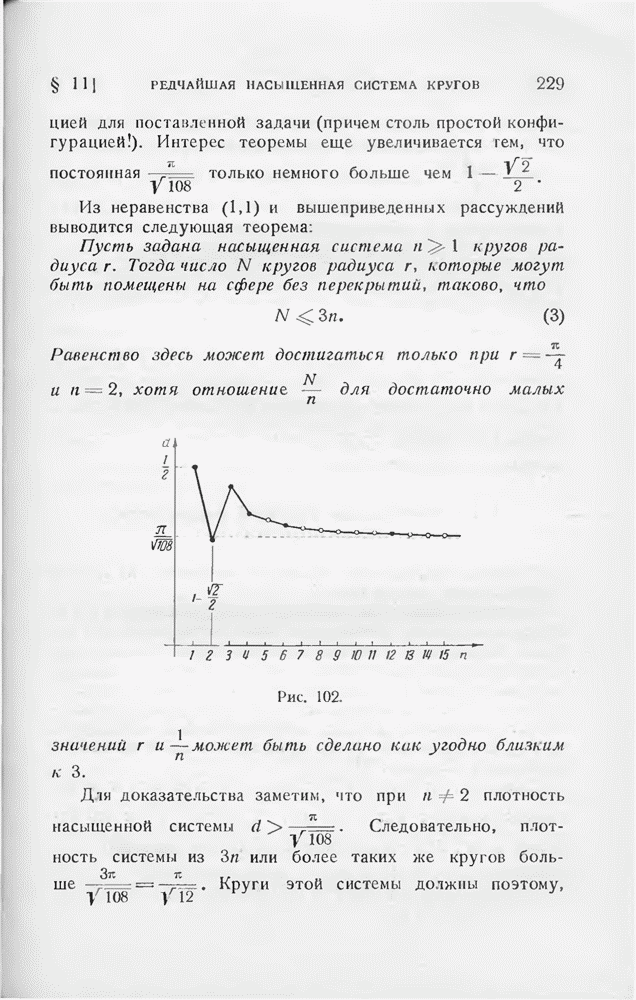
§ 2. Центрально-симметричные фигуры
Докажем сначала следующую теорему:
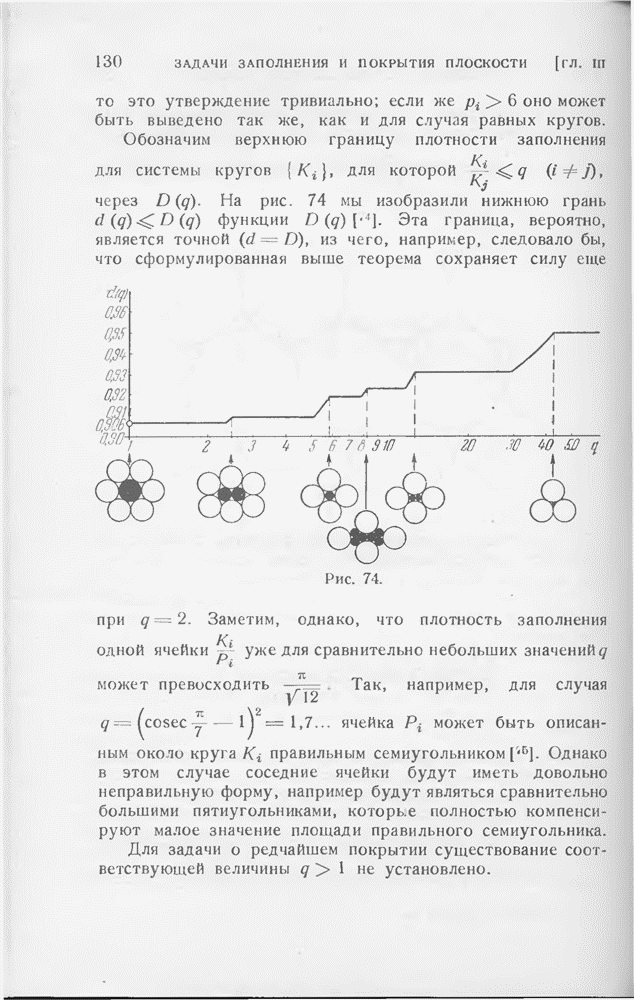
Если  есть плотность редчайшей покрывающей решетки центрально-симметричной выпуклой фигуры М, то
есть плотность редчайшей покрывающей решетки центрально-симметричной выпуклой фигуры М, то

равенство здесь достигается в том и только в том случае, когда М — эллипс.
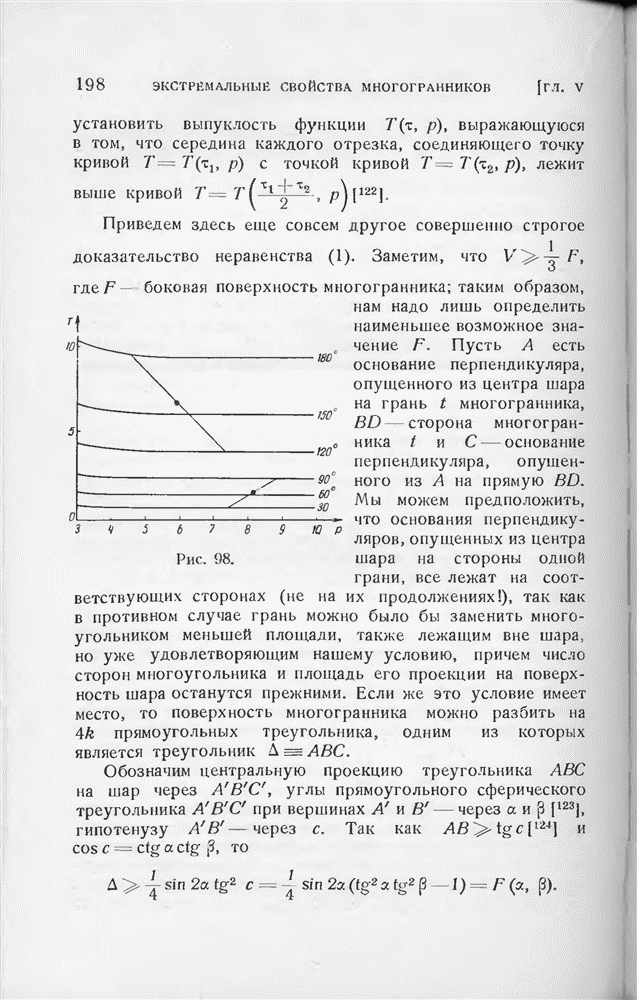
Эта теорема решает в основном упомянутую во введении к этой главе вторую основную задачу для случая центрально-симметричной фигуры: при помощи каждой центрально-симметричной выпуклой фигуры, не являющейся эллипсом, можно более экономно покрыть плоскость, чем при помощи кругов. После этого остается еще только разобрать вопрос о единственности соответствующей экстремальной задачи, т. е. показать, что эллипсы действительно являются экстремальными фигурами. Для этого надо доказать, что редчайшее покрытие плоскости равными эллипсами обязательно должно быть решетчатым; рассуждения § 10 гл. III делают этот результат весьма правдоподобным.
То, что в соотношении (1) для эллипса достигается равенство, очевидно  Поэтому достаточно показать, что из неэллиптических центрально-симметричных выпуклых фигур можно образовать покрывающую решетку с плотностью, меньшей
Поэтому достаточно показать, что из неэллиптических центрально-симметричных выпуклых фигур можно образовать покрывающую решетку с плотностью, меньшей 
Это, однако, непосредственно следует из построения Саса (§ 4, гл. II), позволяющего вписать в неэллиптическую центрально-симметричную выпуклую фигуру М центрально-симметричный шестиугольник площади, большей М; искомое решетчатое покрытие плоскости получается в процессе замощения плоскости такими шестиугольниками
Обратимся теперь к двойственной задаче: для какой из центрально-симметричных выпуклых фигур плотнейшая разделенная решетка является наиболее редкой?
Напрашивающееся предположение, что экстремальной фигурой и здесь является эллипс, было опровергнуто Рейнгардтом [1] и Малером [1]. А именно, они указали на тот замечательный факт, что можно найти центрально-симметричную выпуклую фигуру М, для которой плотность  плотнейшей разделенной решетки меньше
плотнейшей разделенной решетки меньше  . Малер показал, что такой фигурой является, например, правильный восьмиугольник А, для которого эта плотность равна
. Малер показал, что такой фигурой является, например, правильный восьмиугольник А, для которого эта плотность равна

Исследования Рейнгардта и Малера заставляют предположить, что экстремальной фигурой является сглаженный восьмиугольник, который получается из аффинно правильного восьмиугольника, если закруглить каждую вершину с помощью гиперболы, касающейся обеих смежных сторон и имеющей асимптотами стороны, смежные к этим последним (рис. 94). Если это предположение верно, то для произвольной центрально-симметричной выпуклой фигуры М

причем равенство достигается только в том случае, если М есть сглаженный восьмиугольник. Доказательство этого предположения решило бы (в силу результатов § 10 гл III) для центрально-симметричных фигур также и первую основную задачу, сформулированную во введении к этой главе.
Укажем теперь следующий более слабый результат, который зато можно получить с помощью совсем элементарных и простых рассуждений:
Для каждой центрально-симметричной выпуклой фигуры можно построить разделенную решетку, плотность которой

Стоящая справа постоянная всего лишь приблизительно на  меньше, чем предполагаемая наилучшая постоянная
меньше, чем предполагаемая наилучшая постоянная 
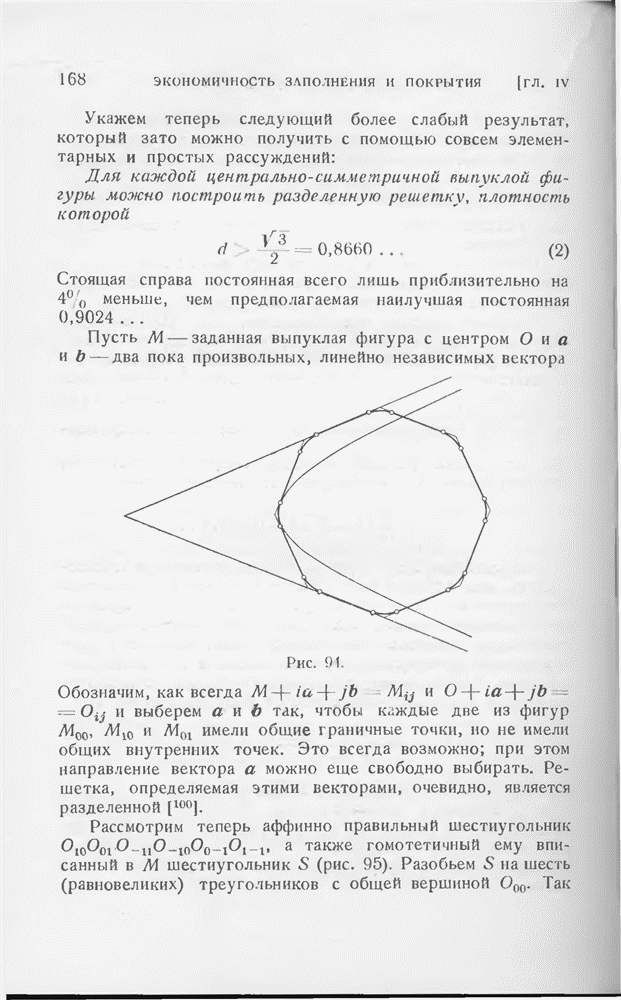
Пусть М — заданная выпуклая фигура с центром Она и b — два пока произвольных, линейно независимых вектора

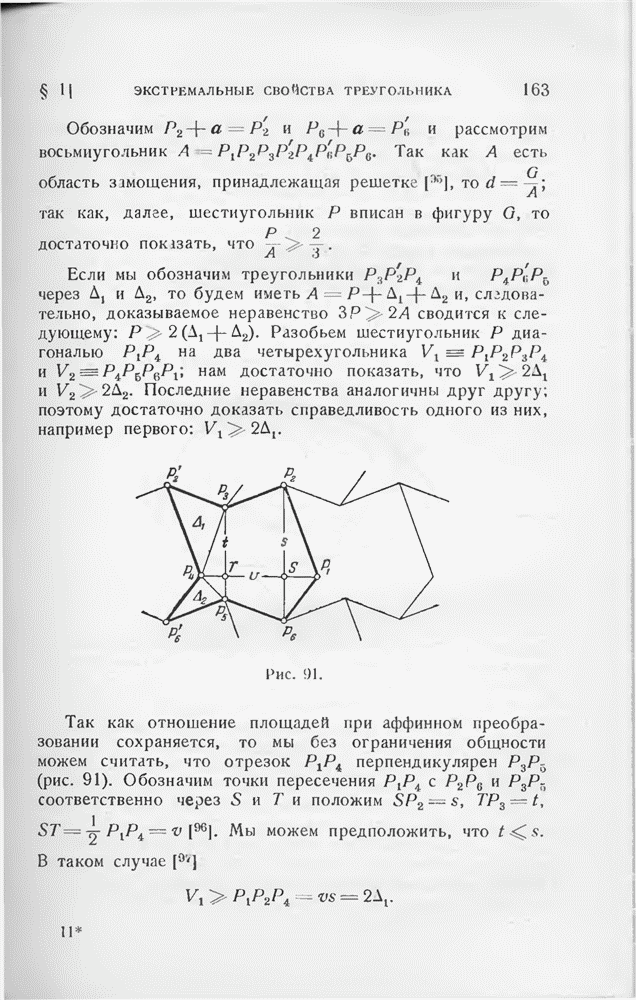
Рис. 91.
Обозначим, как всегда  и выберем а и b так, чтобы каждые две из фигур
и выберем а и b так, чтобы каждые две из фигур  имели общие граничные точки, но не имели общих внутренних точек. Это всегда возможно; при этом направление вектора а можно еще свободно выбирать. Решетка, определяемая этими векторами, очевидно, является разделенной
имели общие граничные точки, но не имели общих внутренних точек. Это всегда возможно; при этом направление вектора а можно еще свободно выбирать. Решетка, определяемая этими векторами, очевидно, является разделенной 
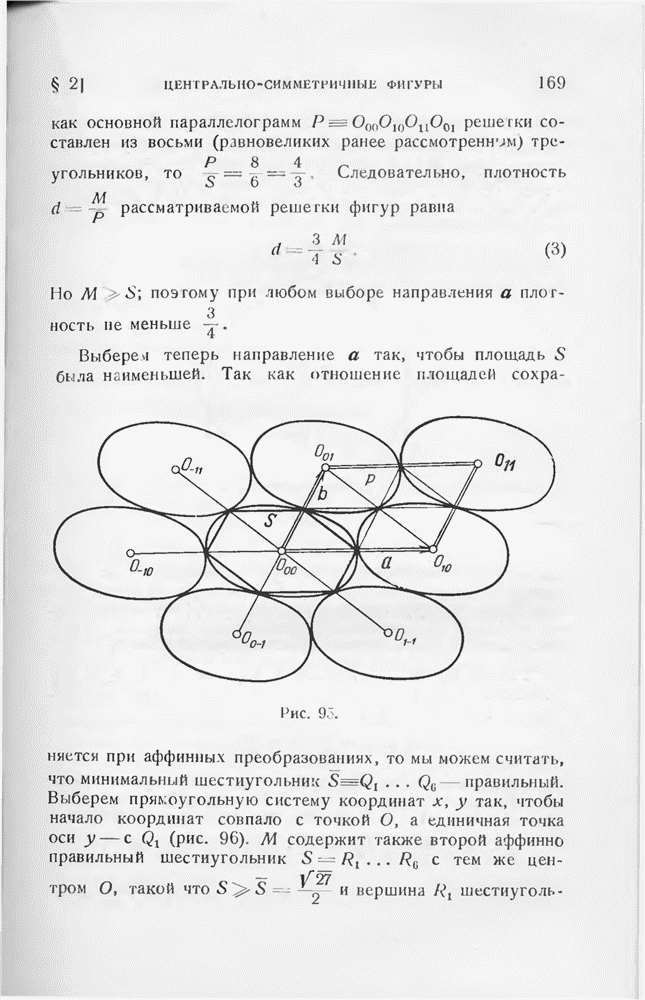
Рассмотрим теперь аффинно правильный шестиугольник  а также гомотетичный ему вписанный в М шестиугольник S (рис. 95). Разобьем S на шесть (равновеликих) треугольников с общей вершиной
а также гомотетичный ему вписанный в М шестиугольник S (рис. 95). Разобьем S на шесть (равновеликих) треугольников с общей вершиной 
Так как основной параллелограмм  решетки составлен из восьми (равновеликих ранее рассмотренном) треугольников, то
решетки составлен из восьми (равновеликих ранее рассмотренном) треугольников, то  . Следовательно, плотность
. Следовательно, плотность  рассматриваемой решетки фигур равна
рассматриваемой решетки фигур равна

Но  поэтому при любом выборе направления а плотность не меньше
поэтому при любом выборе направления а плотность не меньше 
Выберем теперь направление а так, чтобы площадь S была наименьшей.

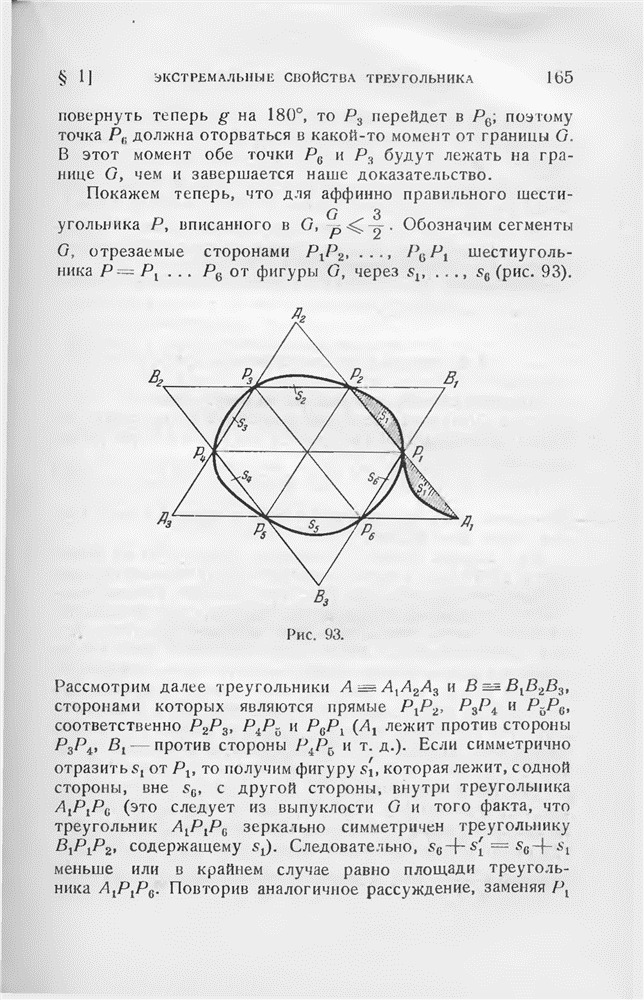
Рис. 95.
Так как отношение площадей сохраняется при аффинных преобразованиях, то мы можем считать, что минимальный шестиугольник  правильный. Выберем прямоугольную систему координат х, у так, чтобы начало координат совпало с точкой О, а единичная точка оси
правильный. Выберем прямоугольную систему координат х, у так, чтобы начало координат совпало с точкой О, а единичная точка оси  (рис. 96). М содержит также второй аффинно правильный шестиугольник
(рис. 96). М содержит также второй аффинно правильный шестиугольник  с тем же центром О, такой что
с тем же центром О, такой что  и вершина
и вершина  шестиугольника S принадлежит оси
шестиугольника S принадлежит оси 
При этом все вершины S лежат вне шестиугольника  и наоборот [101].
и наоборот [101].
Выпуклую оболочку шестиугольников S и S обозначим через И. Если сдвинуть отрезки  вдоль прямых, на которых они лежат, так, чтобы эти отрезки стали симметричны относительно оси у, то площадь Н не изменится; поэтому мы можем считать, что ось у является осью симметрии для
вдоль прямых, на которых они лежат, так, чтобы эти отрезки стали симметричны относительно оси у, то площадь Н не изменится; поэтому мы можем считать, что ось у является осью симметрии для  .
.

Рис. 96.
Положим  [102]; в этом случае условие
[102]; в этом случае условие  можно будет записать в виде
можно будет записать в виде 
Теперь имеем  где
где  и
и  - треугольники
- треугольники  Так как нормальное уравнение прямой
Так как нормальное уравнение прямой  имеет вид
имеет вид

то расстояние от точки  до этой прямой равно
до этой прямой равно  Учитывая, что получаем:
Учитывая, что получаем:

Равенство в обоих последних неравенствах достигается только в том случае, если  , т. е. если Н есть правильный двенадцатиугольник. В этом случае, однако,
, т. е. если Н есть правильный двенадцатиугольник. В этом случае, однако,  так как иначе
так как иначе  не будет наименьшим аффинно правильным шестиугольником, вписанным в
не будет наименьшим аффинно правильным шестиугольником, вписанным в  Следовательно, во всяком случае,
Следовательно, во всяком случае,  и вследствие этого
и вследствие этого

что и требовалось доказать.
Заметим еще, что замощение плоскости равными экземплярами шестиугольника  приводит к покрывающей решетке плотности
приводит к покрывающей решетке плотности  В силу равенства (3) отсюда вытекает следующая точная оценка:
В силу равенства (3) отсюда вытекает следующая точная оценка:

имеющая место для каждой центрально-симметричной выпуклой фигуры М.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ АВТОРА
- ГЛАВА I. НЕСКОЛЬКО ТЕОРЕМ ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ
- § 1. Выпуклые фигуры
- § 2. Аффинное преобразование и полярное преобразование
- § 3. Экстремальные свойства правильных многоугольников
- § 4. Изопериметрическая задача
- § 5. Некоторые неравенства, относящиеся к треугольнику
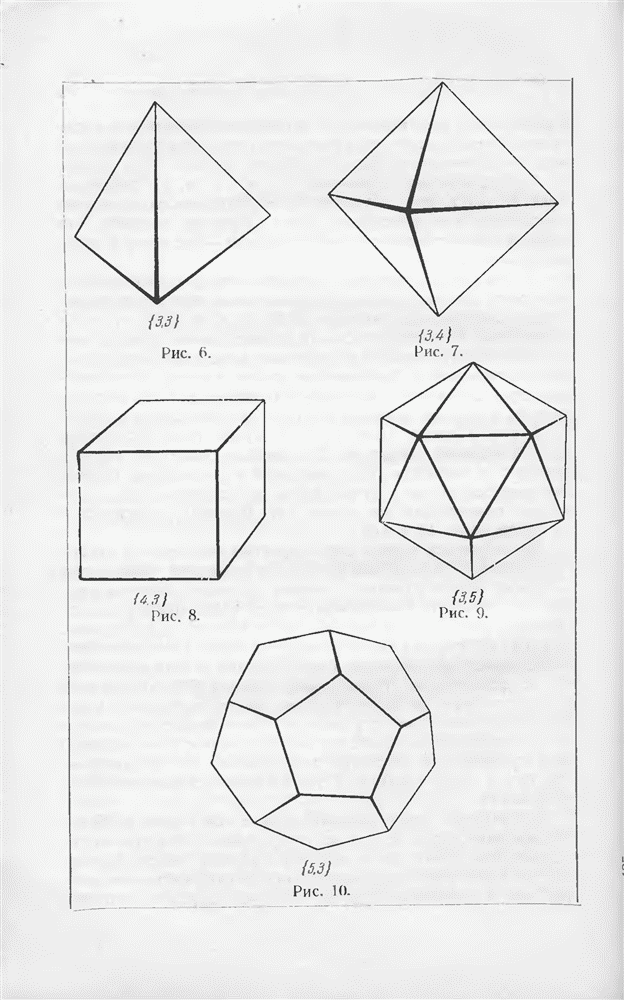
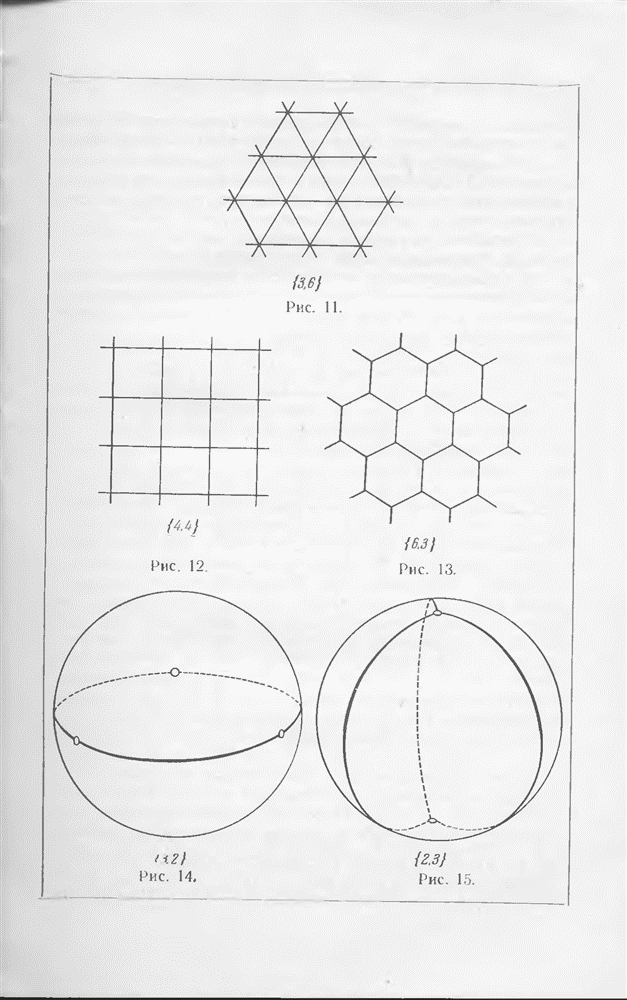
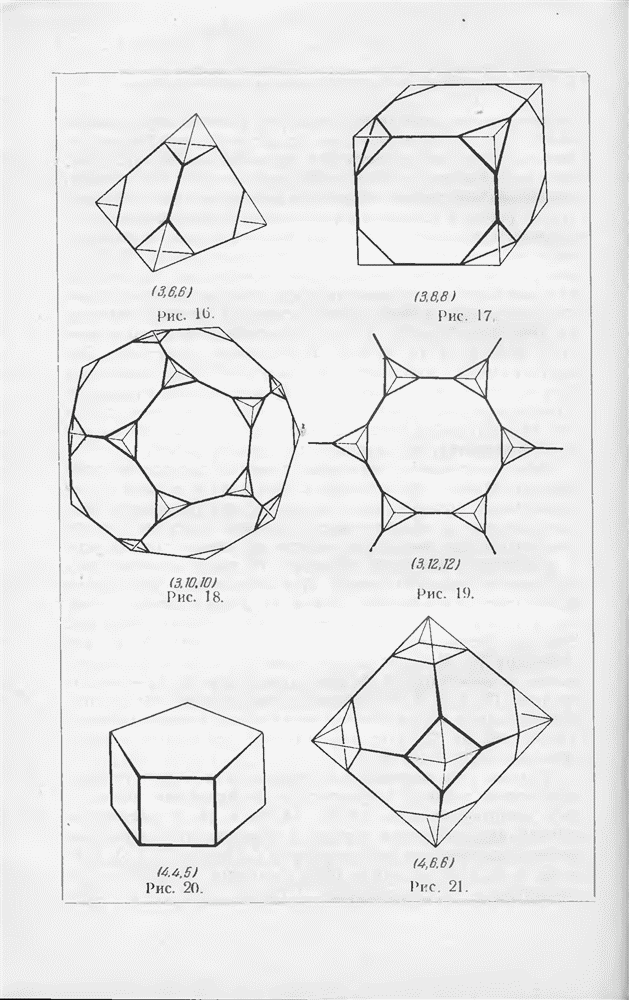
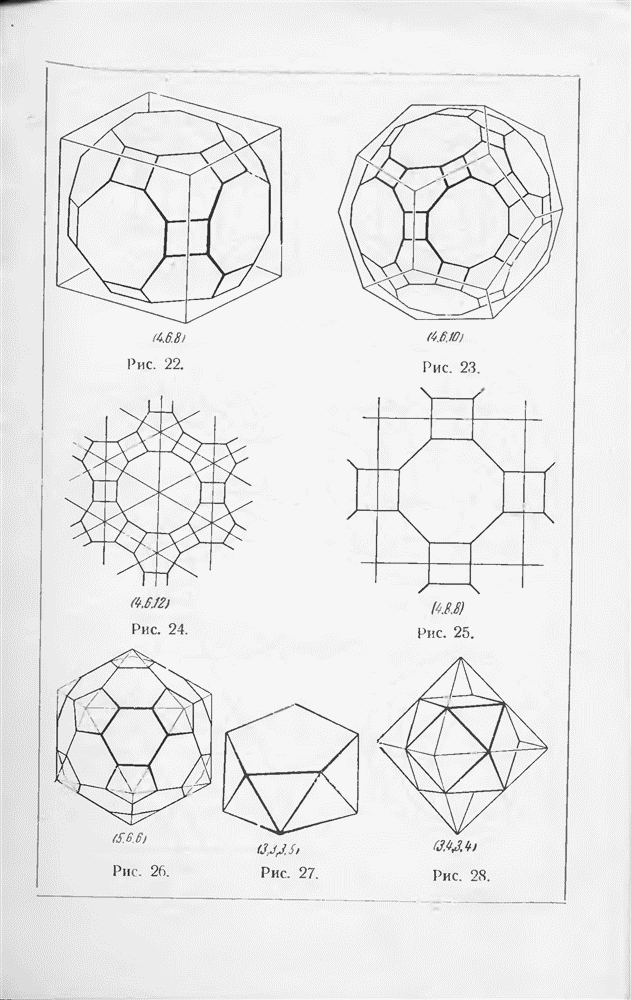
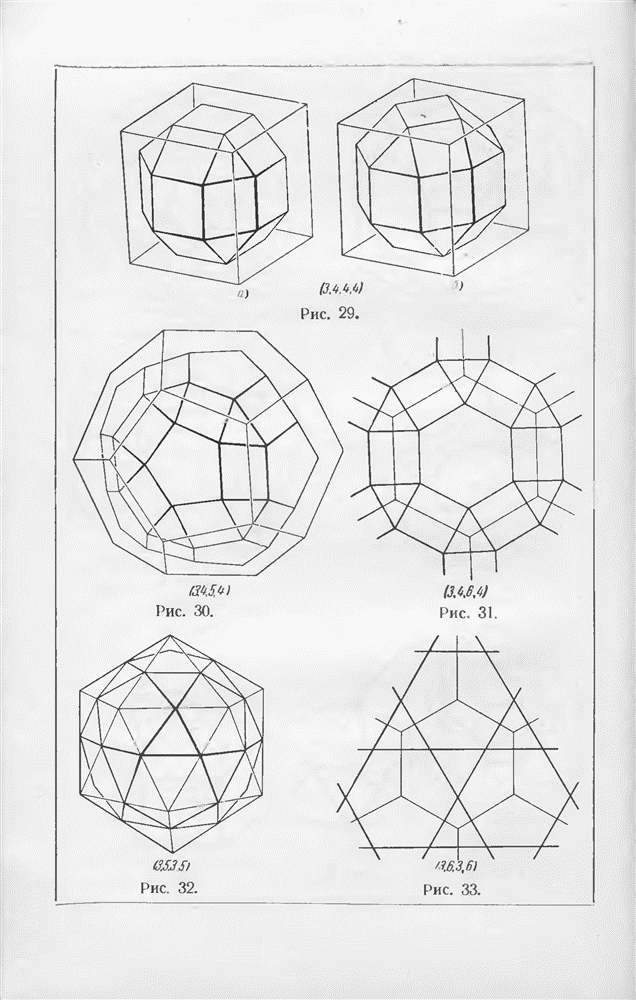
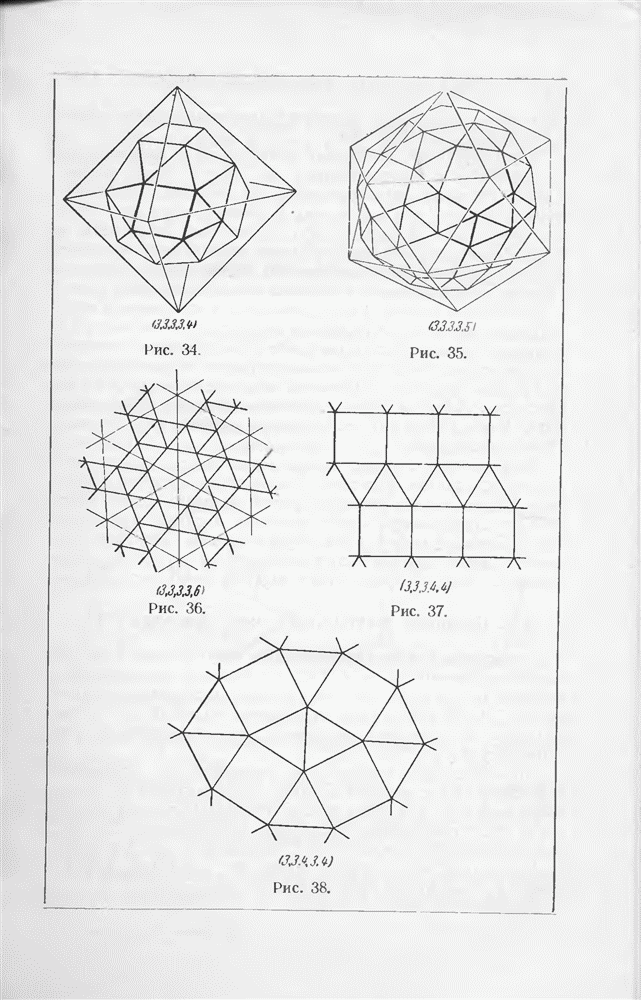
- § 6. Теорема Эйлера о многогранниках
- § 7. Правильные и полуправильные многогранники
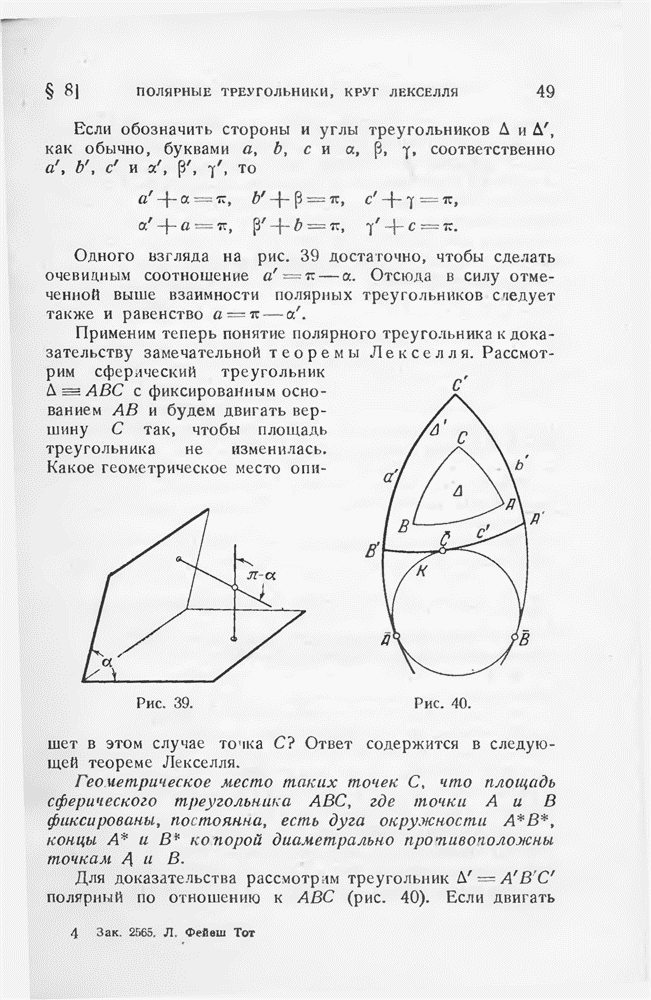
- § 8. Полярные треугольники, круг Лекселля
- § 9. Некоторые тождества из векторной алгебры
- § 10. Некоторые формулы сферической тригонометрии
- § 11. Исторические замечания
- ГЛАВА II. ТЕОРЕМЫ ИЗ ТЕОРИИ ВЫПУКЛЫХ ТЕЛ
- § 1. «Теорема выбора» Бляшке
- § 2. Неравенство Иенсена
- § 3. Теоремы Доукера
- § 4. Одно экстремальное свойство эллипса
- § 5. Об аффинной длине
- § 6. Вариационная задача для аффинной длины
- § 7. Основные факты интегральной геометрии
- § 8. Исторические замечания
- ГЛАВА III. ЗАДАЧА ЗАПОЛНЕНИЯ И ЗАДАЧА ПОКРЫТИЯ ДЛЯ СЛУЧАЯ ПЛОСКОСТИ
- § 1. Плотность системы фигур
- § 2. Задачи о плотнейшем заполнении плоскости кругами и о редчайшем покрытии плоскости кругами
- § 3. Несколько доказательств
- § 4. Заполнение и покрытие выпуклой области равными кругами
- § 5. Разбиение выпуклой области на выпуклые подобласти
- § 6. Заполнение выпуклой области кругами n различных размеров
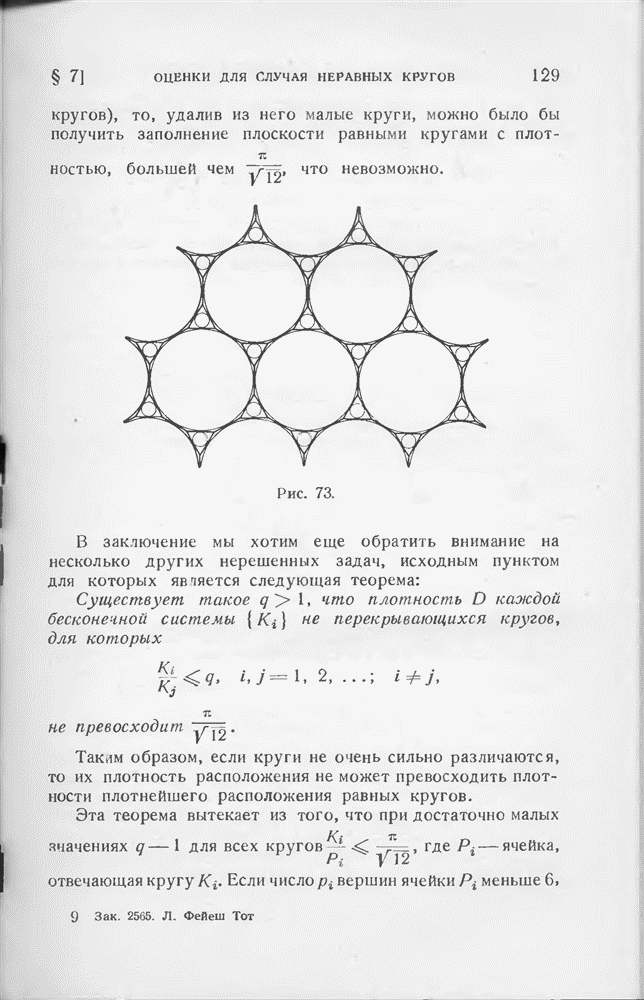
- § 7. Оценки для случая неравных кругов
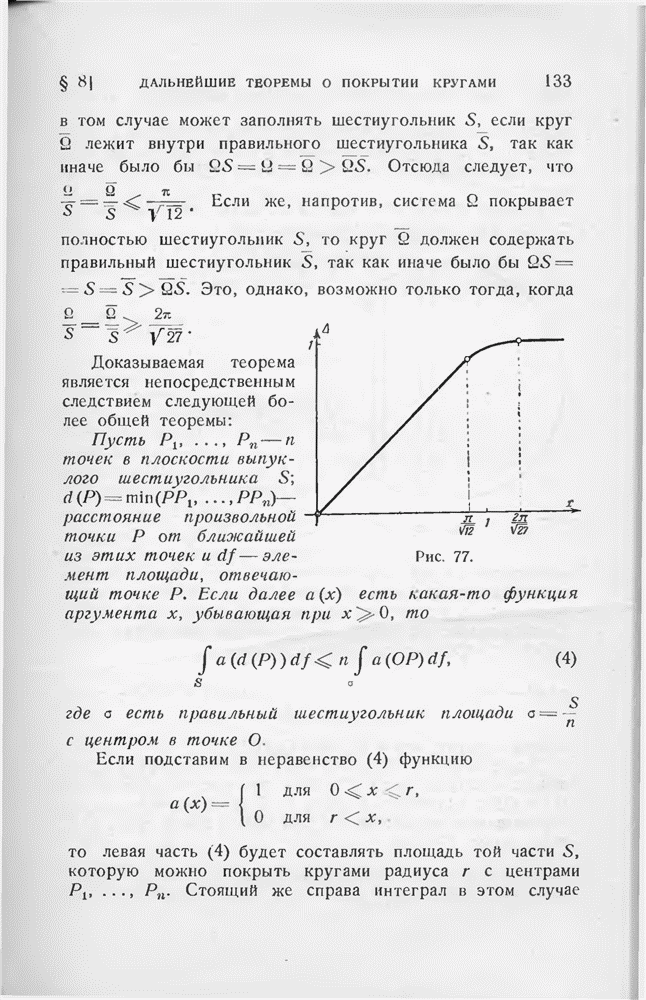
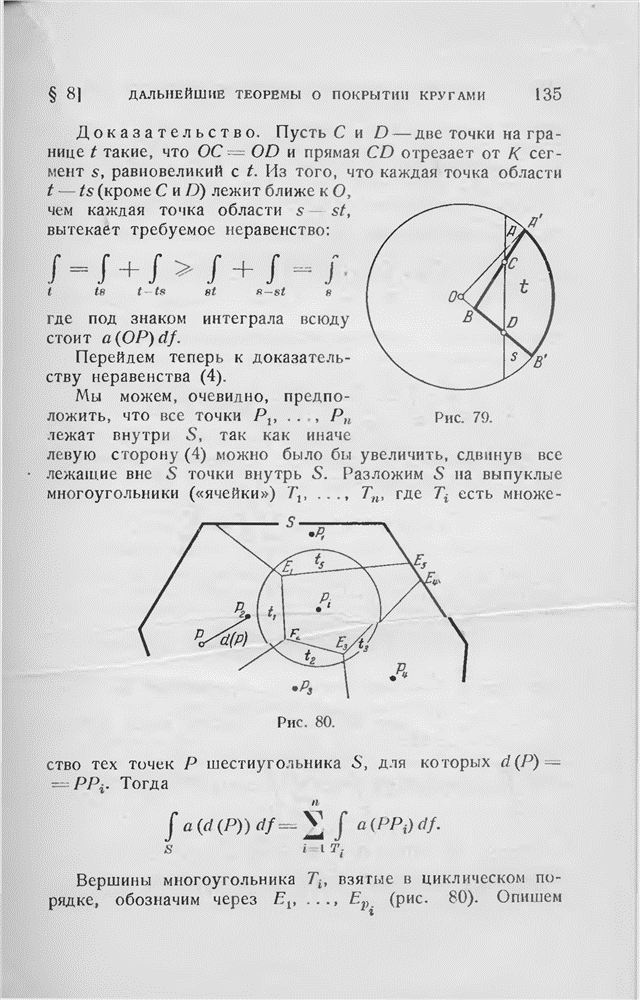
- § 8. Дальнейшие теоремы о покрытии кругами
- § 9. Разбиение выпуклого шестиугольника на выпуклые многоугольники
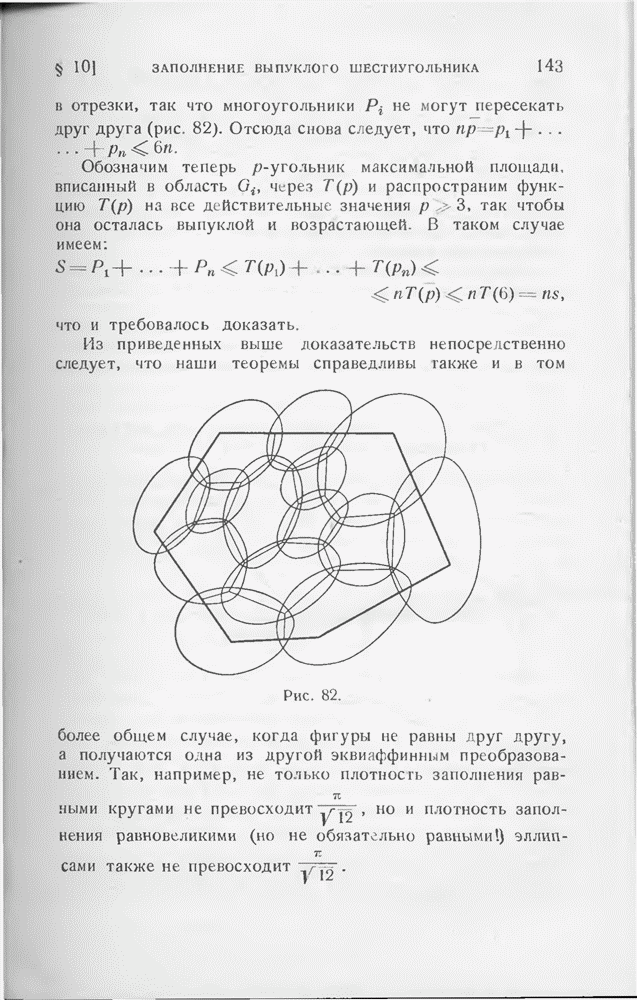
- § 10. Заполнение и покрытие выпуклого шестиугольника равными выпуклыми фигурами
- § 11. Одна задача о заполнении выпуклыми фигурами, связанная с понятием аффинной длины
- § 12. О формуле осреднения
- § 13. Исторические замечания
- ГЛАВА IV. ЭКОНОМИЧНОСТЬ ЗАПОЛНЕНИЯ и ПОКРЫТИЯ ФИГУРАМИ ДАННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 1. Экстремальные свойства треугольника
- § 2. Центрально-симметричные фигуры
- § 3. Экономичность заполнения и покрытия фигурами данной последовательности
- § 4. Покрытие разрезанными на куски выпуклыми фигурами
- § 5. Исторические замечания
- ГЛАВА V. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
- § 1. Заполнение и покрытие сферы равными кругами
- § 2. Некоторые другие доказательства
- § 3. Приближение шара многогранниками
- § 4. Объем описанного многогранника
- § 5. Объем вписанного многогранника
- § 6. Неравенства, связывающие радиусы вписанного и описанного шаров выпуклого многогранника
- § 7. Изопериметрическая задача для многогранников
- § 8. Одно общее неравенство
- § 9. О кратчайшей сети, разбивающей сферу на равновеликие выпуклые части
- § 10. О сумме длин ребер многогранника
- § 11. Редчайшая насыщенная система сферических кругов
- § 12. Приближение выпуклой поверхности многогранниками
- § 13. Исторические замечания
- ГЛАВА VI. НЕПРАВИЛЬНЫЕ РАСПОЛОЖЕНИЯ НА СФЕРЕ
- § 1. Граф, отвечающий заданной системе точек
- § 2. Максимальная фигура для n = 7
- § 3. Максимальная фигура для n = 8 и n = 9
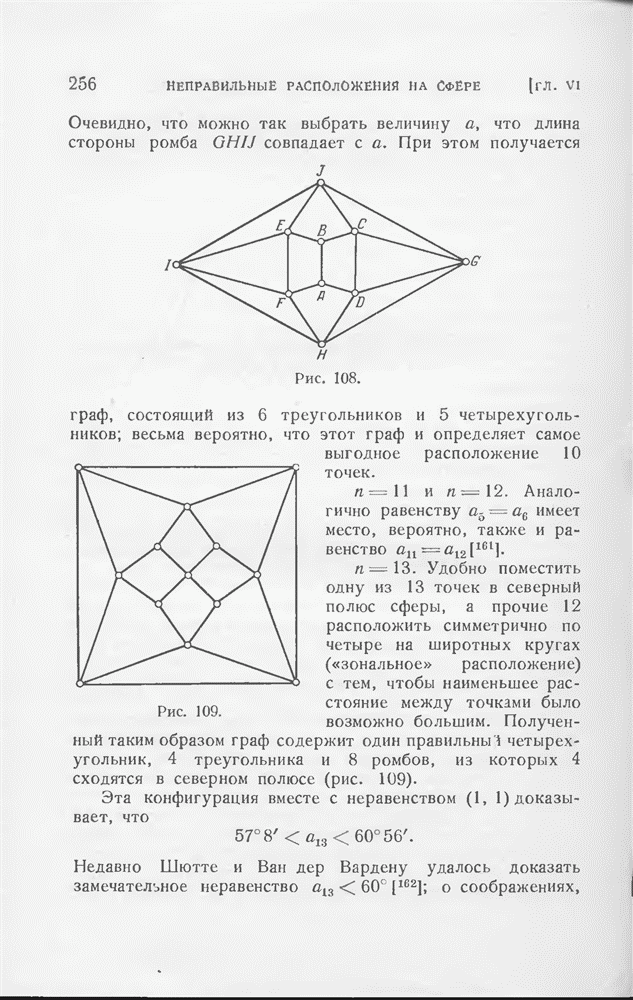
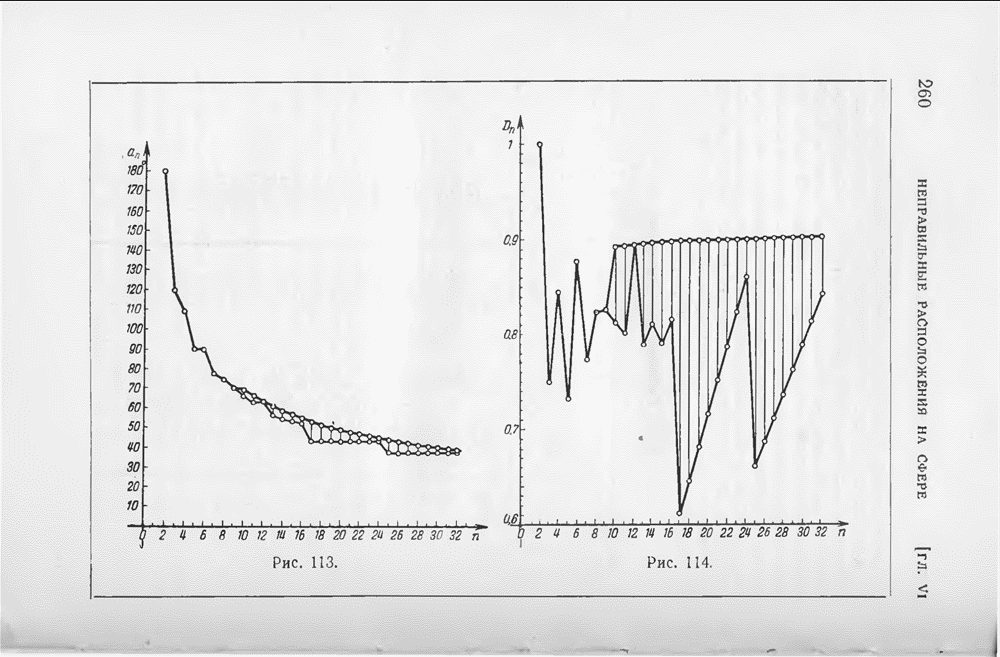
- § 4. Несколько расположений более чем 9 точек
- § 5. Таблица результатов
- § 6. Исторические замечания
- ГЛАВА VII. РАСПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ
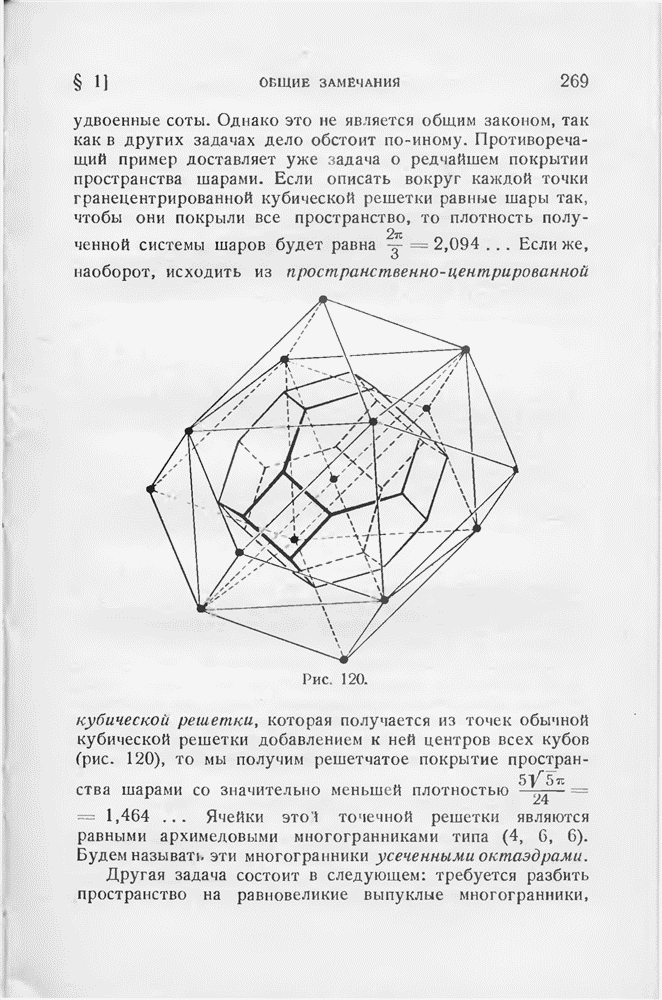
- § 2. Задача о теснейшей упаковке шаров
- § 3. Об одном экстремальном разбиении пространства
- § 4. Формула осреднения для пространства
- § 5. Исторические замечания
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ПРИЛОЖЕНИЕ I. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ, КАСАЮЩИЕСЯ РАСПОЛОЖЕНИЙ В n-МЕРНОМ ПРОСТРАНСТВЕ
- ПРИЛОЖЕНИЕ II. НЕСКОЛЬКО ОПРЕДЕЛЕНИЙ РАЗМЕРНОСТИ
- БИБЛИОГРАФИЯ