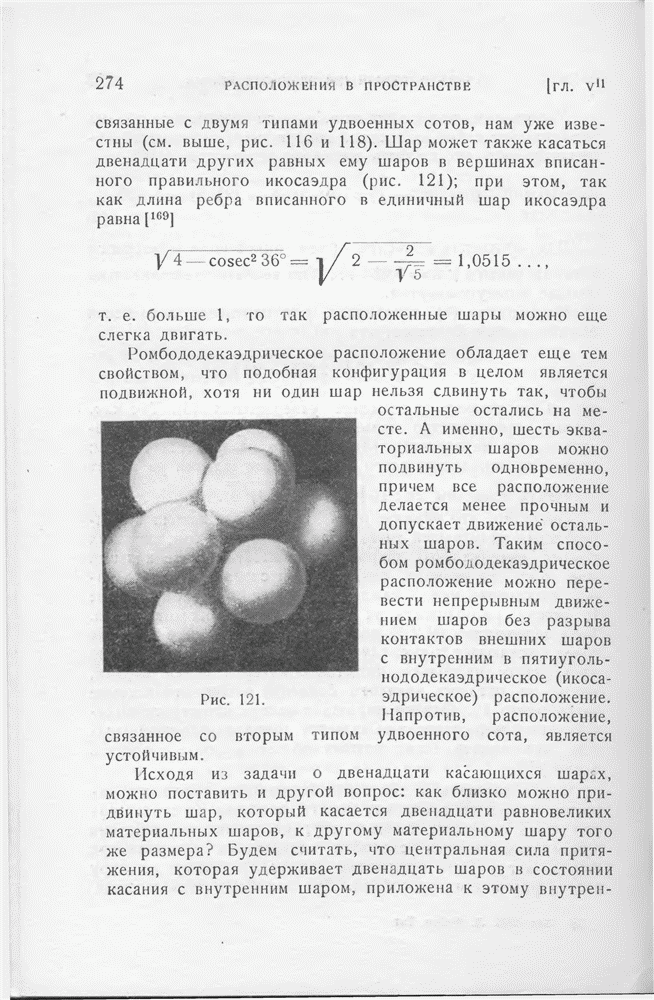
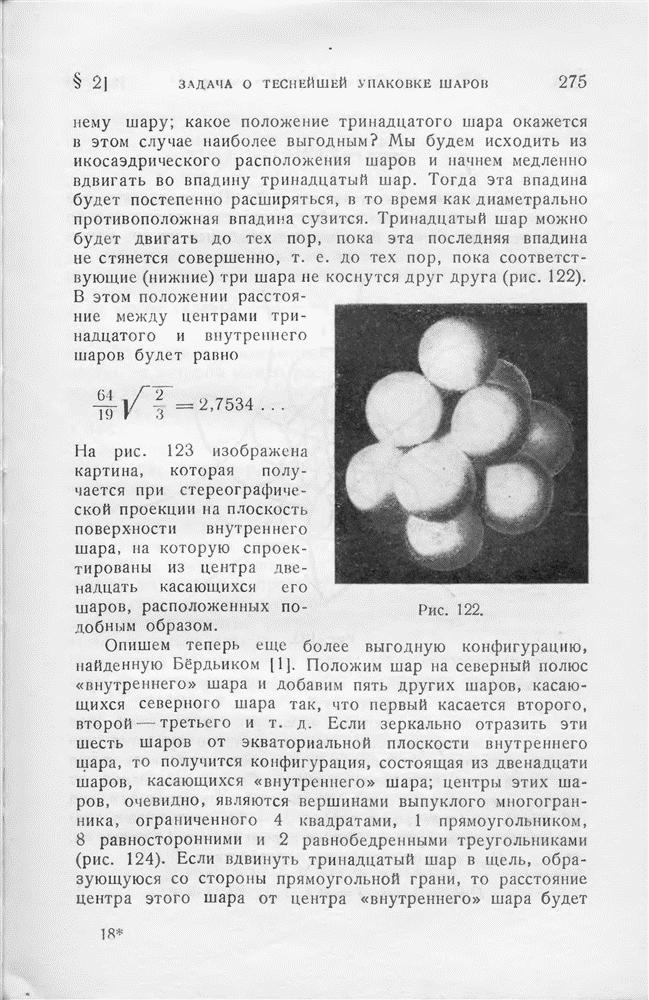
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
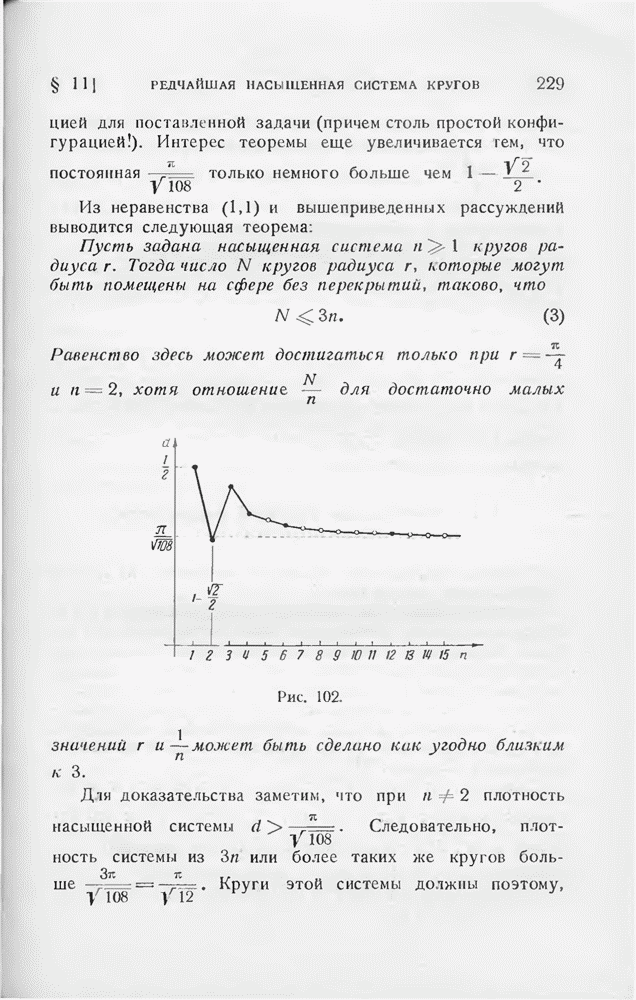
§ 5. Объем вписанного многогранника
Этот параграф мы начнем с доказательства следующей теоремы:
Если многогранник  с
с  вершинами целиком содержится внутри единичного шара, то
вершинами целиком содержится внутри единичного шара, то

Учитывая, что

получаем отсюда:

где точками обозначен член порядка К сожалению, этот член отрицательный, так что здесь нельзя получить точную асимптотическую оценку, аналогичную неравенствам (4,4).
Для доказательства неравенства (1) мы можем положить, что  есть вписанный в единичный шар с центром О многогранник, все грани которого являются треугольными.
есть вписанный в единичный шар с центром О многогранник, все грани которого являются треугольными.
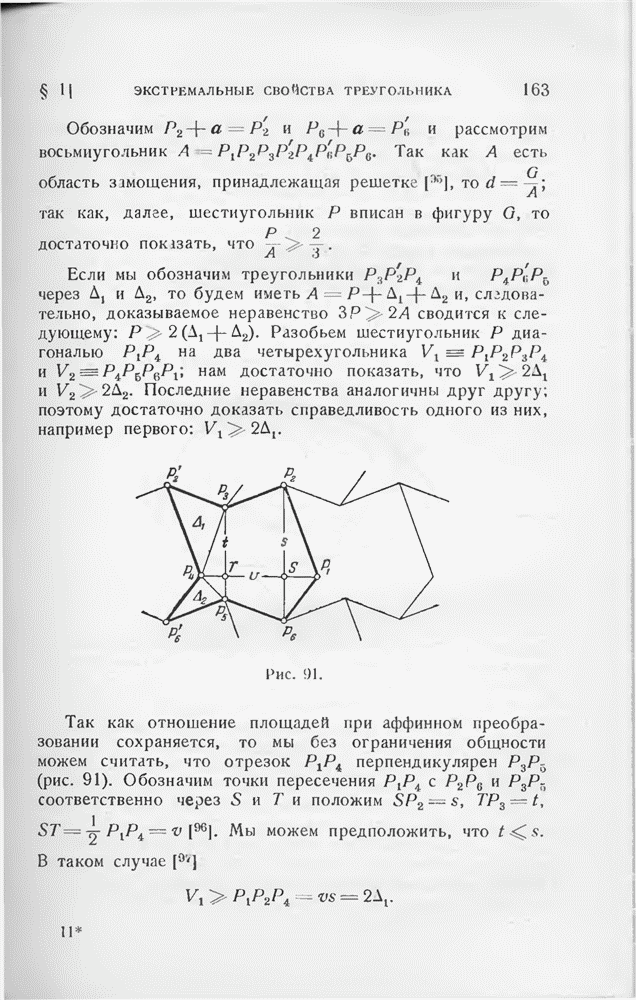
Возьмем грань  и рассмотрим тетраэдр
и рассмотрим тетраэдр  и сферический треугольник
и сферический треугольник  . Мы покажем, что объем v при данной величине
. Мы покажем, что объем v при данной величине  достигает своего максимума в случае равностороннего треугольника
достигает своего максимума в случае равностороннего треугольника  . Достаточно показать, что у тетраэдра наибольшего объема
. Достаточно показать, что у тетраэдра наибольшего объема  Чтобы пояснить это, будем считать плоскость
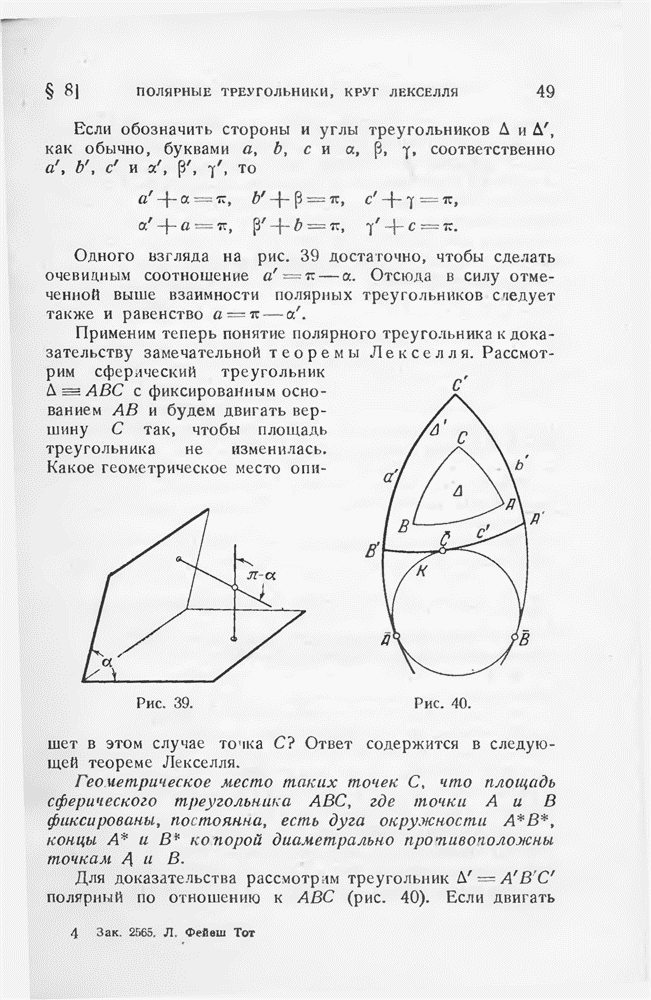
Чтобы пояснить это, будем считать плоскость  горизонтальной и рассмотрим круг Лекселля, проходящий через
горизонтальной и рассмотрим круг Лекселля, проходящий через  и точки
и точки  диаметрально противоположные
диаметрально противоположные 
При движении  по дуге
по дуге  этого круга, площадь
этого круга, площадь  остается постоянной. С другой стороны, v достигает своего максимума, если высота тетраэдра, опущенная из
остается постоянной. С другой стороны, v достигает своего максимума, если высота тетраэдра, опущенная из  будет наибольшей, т. е. если
будет наибольшей, т. е. если  — наивысшая точка круга Лекселля. Эта точка как раз и характеризуется тем, что
— наивысшая точка круга Лекселля. Эта точка как раз и характеризуется тем, что  .
.
Только что доказанное экстремальное свойство можно записать так:

Но функция  вогнута, так как
вогнута, так как

поэтому имеем:

что и требовалось доказать.
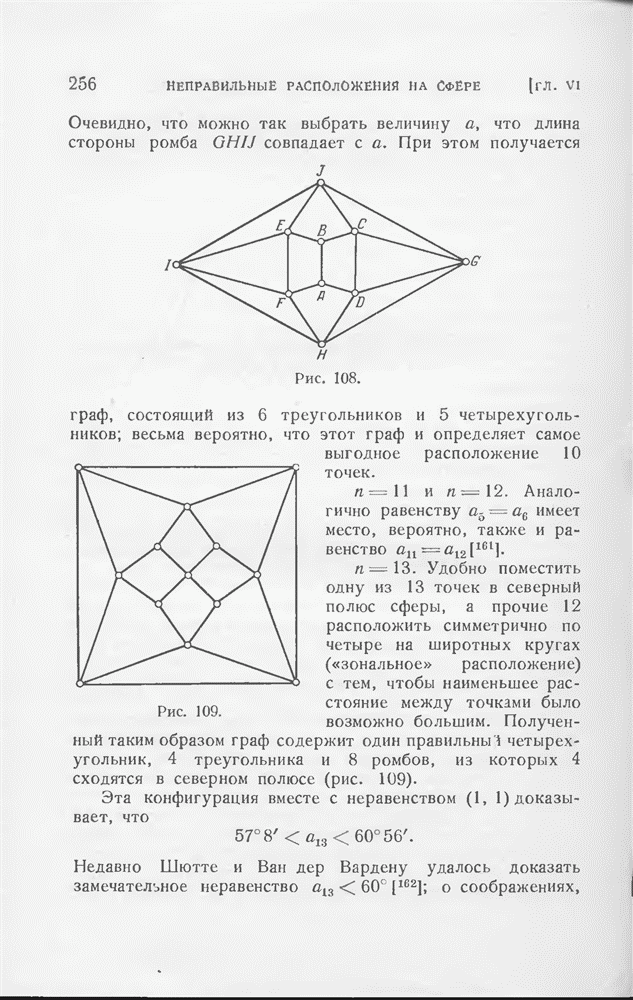
Повернем одну грань куба W вокруг ее центра на 45° и рассмотрим выпуклую оболочку Н новой грани и грани куба, противолежащей рассматриваемой. Нетрудно показать, что  . Следовательно, среди всех вписанных в шар многогранников с 8 вершинами куб не будет наибольшим по объему. Анатогично и додекаэдр не является экстремальным многогранником. Вообще можно показать, что экстремальный многогранник может иметь только треугольные грани, лежащие в различных плоскостях; такой многогранник естественно называть истинным многогранником с треугольными гранями. Мы докажем здесь даже гораздо более общее предложение: многогранник, имеющий самый большой объем среди всех многогранников с данным числом вершин, вписанных в какую-то фиксированную гладкую выпуклую поверхность (т. е. в выпуклую поверхность, не имеющую особых точек), обязательно является истинным многогранником с треугольными гранями.
. Следовательно, среди всех вписанных в шар многогранников с 8 вершинами куб не будет наибольшим по объему. Анатогично и додекаэдр не является экстремальным многогранником. Вообще можно показать, что экстремальный многогранник может иметь только треугольные грани, лежащие в различных плоскостях; такой многогранник естественно называть истинным многогранником с треугольными гранями. Мы докажем здесь даже гораздо более общее предложение: многогранник, имеющий самый большой объем среди всех многогранников с данным числом вершин, вписанных в какую-то фиксированную гладкую выпуклую поверхность (т. е. в выпуклую поверхность, не имеющую особых точек), обязательно является истинным многогранником с треугольными гранями.
Под «гладкой поверхностью» (поверхностью без особенностей) мы здесь понимаем такую выпуклую поверхность, через каждую точку которой можно провести только одну опорную плоскость.
Эта теорема с определенной точки зрения представляет значительный интерес. Поясним это следующим примером. Очевидно, что среди всех многогранников с 8 вершинами, вписанных в куб W, наибольший объем имеет сам куб. Покроем теперь W тонким слоем воска так, чтобы вершины W остались на поверхности полученного тела К; при этом К может иметь те же симметрии, что и куб W, но может быть также и несимметричным. Надо только позаботиться о том, чтобы грани и углы W были закруглены, т. е. чтобы тело К было уже гладким. При этом вписанный в К многогранник с 8 вершинами, имеющий наибольший возможный объем, уже не будет совпадать с кубом W, как бы не был тонок слой воска.
Для доказательства нашей теоремы рассмотрим систему точек  не лежащих в одной плоскости. Постараемся сначала определить геометрическое место G таких точек Р, что объем выпуклой оболочки Н точек
не лежащих в одной плоскости. Постараемся сначала определить геометрическое место G таких точек Р, что объем выпуклой оболочки Н точек  и Р является постоянным.
и Р является постоянным.
Временно предположим, что в вершине Рмногогранника Н сходятся лишь треугольные грани  Каждой треугольной грани
Каждой треугольной грани  сопоставим вектор имеющий направление внешней нормали к грани и величину
сопоставим вектор имеющий направление внешней нормали к грани и величину  положим еще
положим еще 
Если сдвинуть точку Р на вектор  в новое положение Р так, чтобы новый многогранник Н остался изоморфным первоначальному многограннику Н, то
в новое положение Р так, чтобы новый многогранник Н остался изоморфным первоначальному многограннику Н, то

Поэтому есля желать, чтобы площадь Н осталась неизменной, то Р следует двигать в плоскости, перпендикулярной к вектору V. Однако дело будет обстоять таким образом только до тех пор, пока Р не попадет в плоскость грани  выпуклой оболочки точек
выпуклой оболочки точек 
При таком положении Р не все сходящиеся в этом вершине грани Н будут треугольниками. Если Р пересечет плоскость  , то в Р будут сходиться уже другие треугольные грани; стало быть, точка Р должна будет двигаться в другой плоскости чем прежде. Один взгляд на рис. 99, который изображает аналогичную ситуацию для двумерного случая, убеждает в том, что О должно быть поверхностью выпуклого многогранника.
, то в Р будут сходиться уже другие треугольные грани; стало быть, точка Р должна будет двигаться в другой плоскости чем прежде. Один взгляд на рис. 99, который изображает аналогичную ситуацию для двумерного случая, убеждает в том, что О должно быть поверхностью выпуклого многогранника.

Рис. 99.
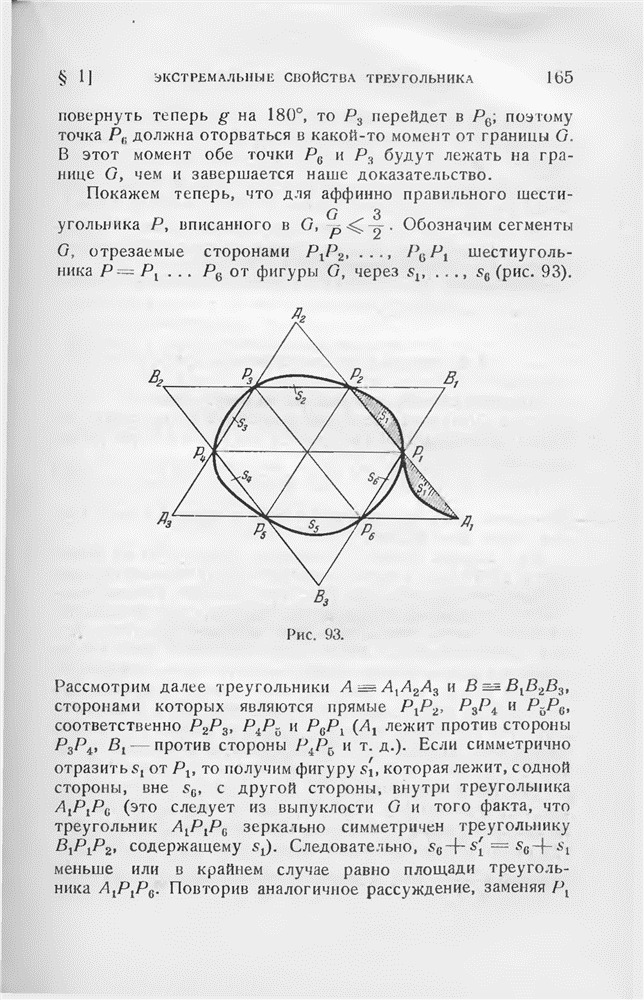
Рассмотрим теперь  точек
точек  гладкой выпуклой поверхности Е и предположим, что, например, в точке
гладкой выпуклой поверхности Е и предположим, что, например, в точке  сходятся не только трехугольные грани выпуклой оболочки Н этих точек. Если фиксировать все остальные точки и двигать
сходятся не только трехугольные грани выпуклой оболочки Н этих точек. Если фиксировать все остальные точки и двигать  так, чтобы объем Н оставался постоянным, то
так, чтобы объем Н оставался постоянным, то  будет пробегать границу выпуклого многогранника. Так как первоначальное положе-» ние точки
будет пробегать границу выпуклого многогранника. Так как первоначальное положе-» ние точки  принадлежит ребру этого многогранника, то многогранник в окрестности точки
принадлежит ребру этого многогранника, то многогранник в окрестности точки  будет пересекать поверхность Е. Но так как всякий многогранник наибольшего объема обязательно должен быть вписан в Е, то отсюда вытекает, что Н не может быть таким многогранником.
будет пересекать поверхность Е. Но так как всякий многогранник наибольшего объема обязательно должен быть вписан в Е, то отсюда вытекает, что Н не может быть таким многогранником.
Наши рассуждения одновременно показывают, что многогранник наибольшего объема обладает тем свойством, что если векторы  определяют взятые в циклической последовательности ребра, исходящие из одной вершины, то вектор
определяют взятые в циклической последовательности ребра, исходящие из одной вершины, то вектор  имеет направление нормали к поверхности Е в этой вершине.
имеет направление нормали к поверхности Е в этой вершине.
Оставим теперь на время нашу общую выпуклую поверхность и вернемся к случаю сферы. Последующие рассуждения можно рассматривать как попытку доказательства неравенства
 (3)
(3)
где e, f и k число вершин, граней и ребер выпуклого многогранника V, содержащегося внутри единичного
По-видимому, это неравенство во всех случаях имеет место, однако пока еще мы не имеем оснований утверждать это совсем определенно [126].
Пусть  - грань V, имеющая
- грань V, имеющая  сторон, v выпуклая оболочка многоугольника t и центра шара О их проекция t из О на поверхность шара. По-видимому, имеет место следующее неравенство:
сторон, v выпуклая оболочка многоугольника t и центра шара О их проекция t из О на поверхность шара. По-видимому, имеет место следующее неравенство:

означающее, что при заданном числе сторон  и площади проекции
и площади проекции  основания t пирамиды v объем этой пирамиды достигает максимума в том случае, когда t есть правильный
основания t пирамиды v объем этой пирамиды достигает максимума в том случае, когда t есть правильный  -угольник, вписанный в шар. Однако доказательство этого факта, вероятно, не так просто, как доказательство аналогичного эстремального свойства правильного
-угольник, вписанный в шар. Однако доказательство этого факта, вероятно, не так просто, как доказательство аналогичного эстремального свойства правильного  -угольпика в предыдущем параграфе.
-угольпика в предыдущем параграфе.
Функция  при
при  при постоянном
при постоянном  представляет собой вогнутую функцию
представляет собой вогнутую функцию  и, наоборот, при постоянном
и, наоборот, при постоянном  вогнутую функцию
вогнутую функцию  . Если бы она являлась также вогнутой функцией двух переменных
. Если бы она являлась также вогнутой функцией двух переменных  , то можно было бы утверждать, что
, то можно было бы утверждать, что

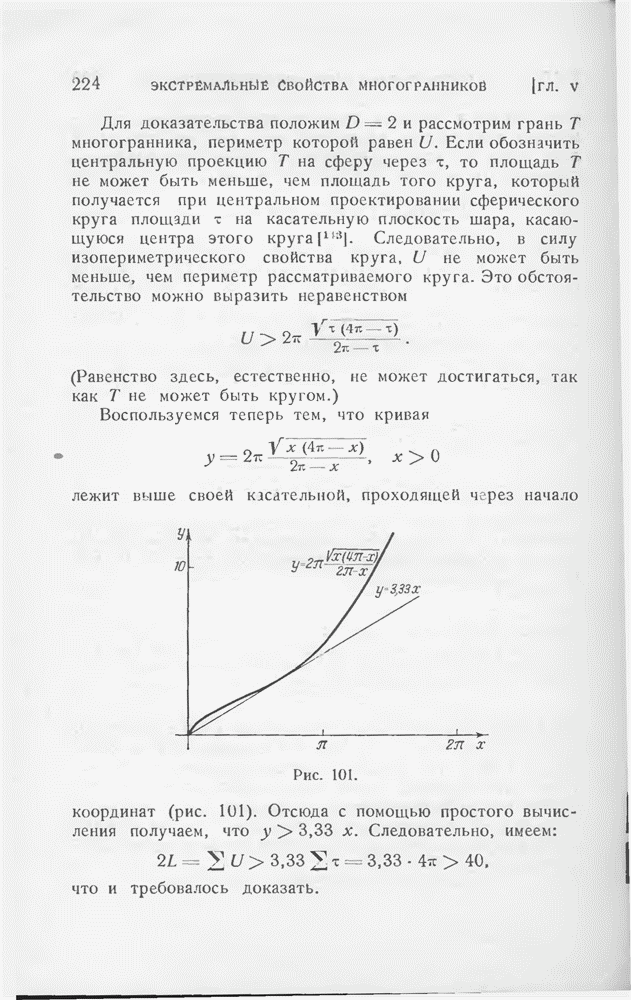
чем было бы доказано неравенство  Однако
Однако  во всей полосе
во всей полосе  не является вогнутой функцией. Достаточно, однако, воспользоваться вогнутостью ее только в области Охтг; здесь же вогнутость, по-видимому, действительно имеет место, что подтверждается изображенными на рис. 100 графиками функций
не является вогнутой функцией. Достаточно, однако, воспользоваться вогнутостью ее только в области Охтг; здесь же вогнутость, по-видимому, действительно имеет место, что подтверждается изображенными на рис. 100 графиками функций  ), отвечающих ряду значений
), отвечающих ряду значений  .
.
Мы ограничимся сначала случаем  и заметим, что для произвольного
и заметим, что для произвольного 

Если заменить теперь каждую величину  на
на  и обозначить новые значения величин через
и обозначить новые значения величин через  , то для
, то для 

Вместо детального обсуждения случая  мы ограничимся одним простым примером.
мы ограничимся одним простым примером.

Рис. 100.
Рассмотрим многогранник типа пятигранной призмы  или, более обще, многогранник, для которого
или, более обще, многогранник, для которого  . Здесь достаточно заметить, что для постоянного
. Здесь достаточно заметить, что для постоянного  функция
функция  является возрастающей функцией
является возрастающей функцией  не только для 0 но и для следовательно, на этот случай можно перенести все предшествующие рассуждения
не только для 0 но и для следовательно, на этот случай можно перенести все предшествующие рассуждения 
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ АВТОРА
- ГЛАВА I. НЕСКОЛЬКО ТЕОРЕМ ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ
- § 1. Выпуклые фигуры
- § 2. Аффинное преобразование и полярное преобразование
- § 3. Экстремальные свойства правильных многоугольников
- § 4. Изопериметрическая задача
- § 5. Некоторые неравенства, относящиеся к треугольнику
- § 6. Теорема Эйлера о многогранниках
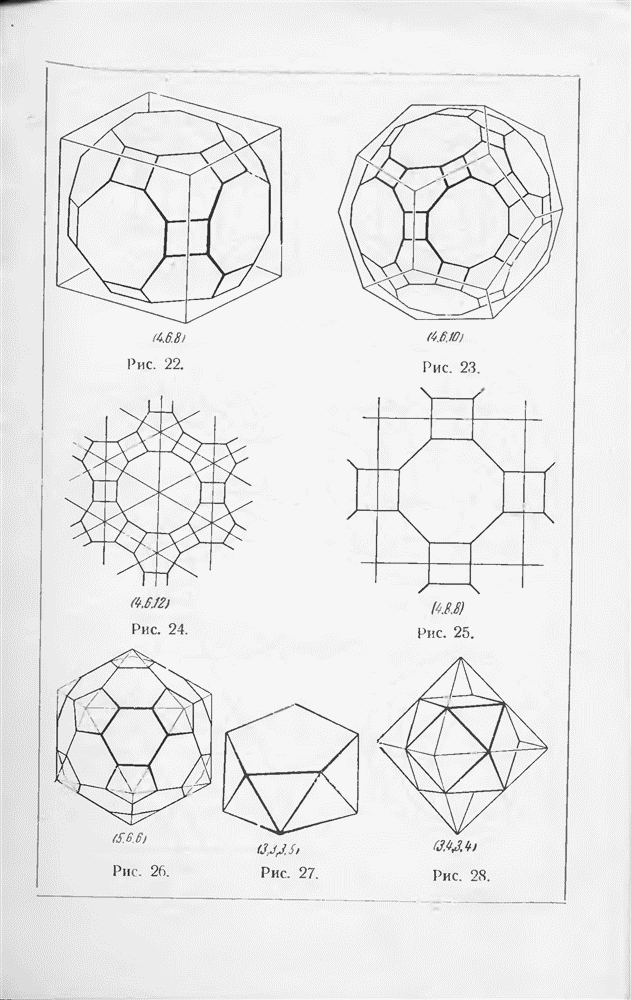
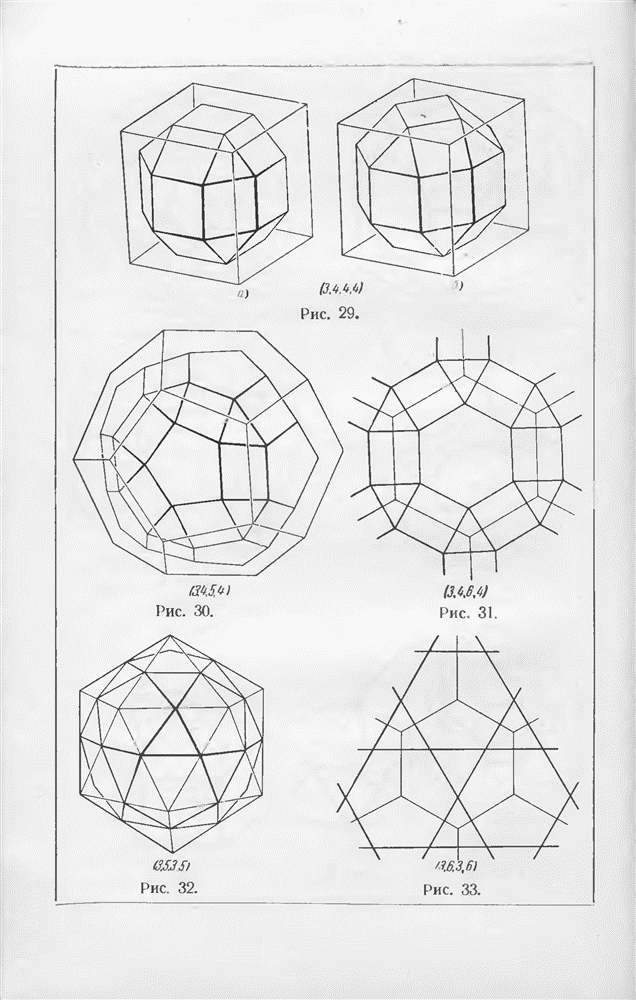
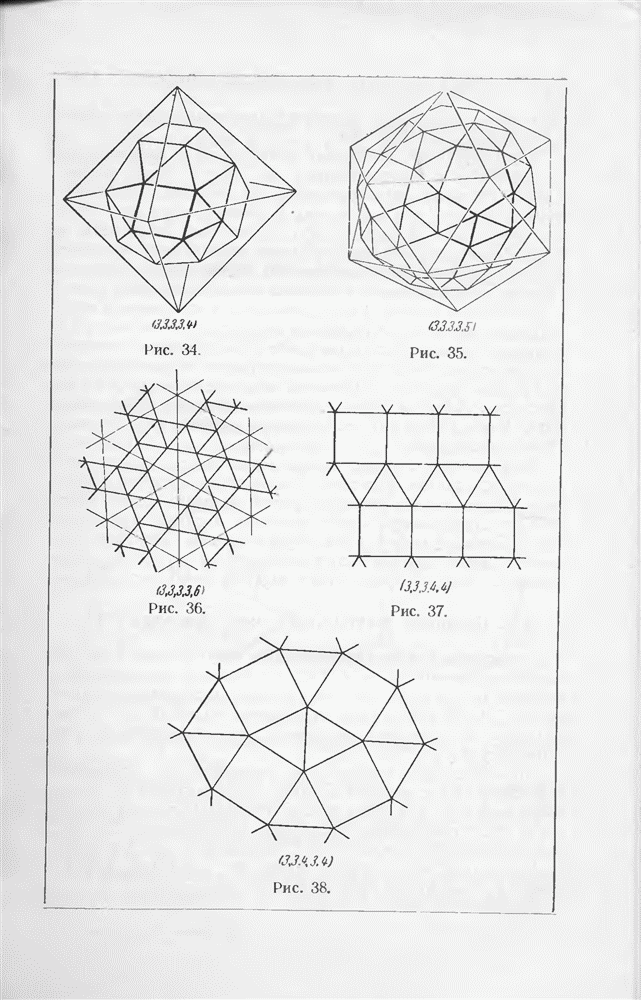
- § 7. Правильные и полуправильные многогранники
- § 8. Полярные треугольники, круг Лекселля
- § 9. Некоторые тождества из векторной алгебры
- § 10. Некоторые формулы сферической тригонометрии
- § 11. Исторические замечания
- ГЛАВА II. ТЕОРЕМЫ ИЗ ТЕОРИИ ВЫПУКЛЫХ ТЕЛ
- § 1. «Теорема выбора» Бляшке
- § 2. Неравенство Иенсена
- § 3. Теоремы Доукера
- § 4. Одно экстремальное свойство эллипса
- § 5. Об аффинной длине
- § 6. Вариационная задача для аффинной длины
- § 7. Основные факты интегральной геометрии
- § 8. Исторические замечания
- ГЛАВА III. ЗАДАЧА ЗАПОЛНЕНИЯ И ЗАДАЧА ПОКРЫТИЯ ДЛЯ СЛУЧАЯ ПЛОСКОСТИ
- § 1. Плотность системы фигур
- § 2. Задачи о плотнейшем заполнении плоскости кругами и о редчайшем покрытии плоскости кругами
- § 3. Несколько доказательств
- § 4. Заполнение и покрытие выпуклой области равными кругами
- § 5. Разбиение выпуклой области на выпуклые подобласти
- § 6. Заполнение выпуклой области кругами n различных размеров
- § 7. Оценки для случая неравных кругов
- § 8. Дальнейшие теоремы о покрытии кругами
- § 9. Разбиение выпуклого шестиугольника на выпуклые многоугольники
- § 10. Заполнение и покрытие выпуклого шестиугольника равными выпуклыми фигурами
- § 11. Одна задача о заполнении выпуклыми фигурами, связанная с понятием аффинной длины
- § 12. О формуле осреднения
- § 13. Исторические замечания
- ГЛАВА IV. ЭКОНОМИЧНОСТЬ ЗАПОЛНЕНИЯ и ПОКРЫТИЯ ФИГУРАМИ ДАННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 1. Экстремальные свойства треугольника
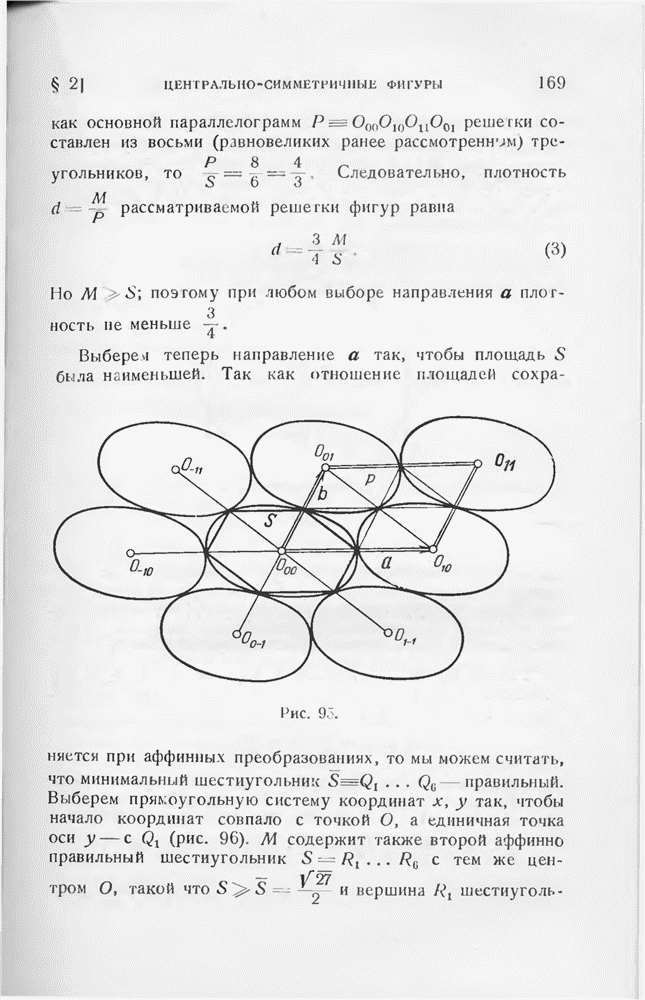
- § 2. Центрально-симметричные фигуры
- § 3. Экономичность заполнения и покрытия фигурами данной последовательности
- § 4. Покрытие разрезанными на куски выпуклыми фигурами
- § 5. Исторические замечания
- ГЛАВА V. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
- § 1. Заполнение и покрытие сферы равными кругами
- § 2. Некоторые другие доказательства
- § 3. Приближение шара многогранниками
- § 4. Объем описанного многогранника
- § 5. Объем вписанного многогранника
- § 6. Неравенства, связывающие радиусы вписанного и описанного шаров выпуклого многогранника
- § 7. Изопериметрическая задача для многогранников
- § 8. Одно общее неравенство
- § 9. О кратчайшей сети, разбивающей сферу на равновеликие выпуклые части
- § 10. О сумме длин ребер многогранника
- § 11. Редчайшая насыщенная система сферических кругов
- § 12. Приближение выпуклой поверхности многогранниками
- § 13. Исторические замечания
- ГЛАВА VI. НЕПРАВИЛЬНЫЕ РАСПОЛОЖЕНИЯ НА СФЕРЕ
- § 1. Граф, отвечающий заданной системе точек
- § 2. Максимальная фигура для n = 7
- § 3. Максимальная фигура для n = 8 и n = 9
- § 4. Несколько расположений более чем 9 точек
- § 5. Таблица результатов
- § 6. Исторические замечания
- ГЛАВА VII. РАСПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ
- § 2. Задача о теснейшей упаковке шаров
- § 3. Об одном экстремальном разбиении пространства
- § 4. Формула осреднения для пространства
- § 5. Исторические замечания
- ПРИМЕЧАНИЯ РЕДАКТОРА
- ПРИЛОЖЕНИЕ I. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ, КАСАЮЩИЕСЯ РАСПОЛОЖЕНИЙ В n-МЕРНОМ ПРОСТРАНСТВЕ
- ПРИЛОЖЕНИЕ II. НЕСКОЛЬКО ОПРЕДЕЛЕНИЙ РАЗМЕРНОСТИ
- БИБЛИОГРАФИЯ