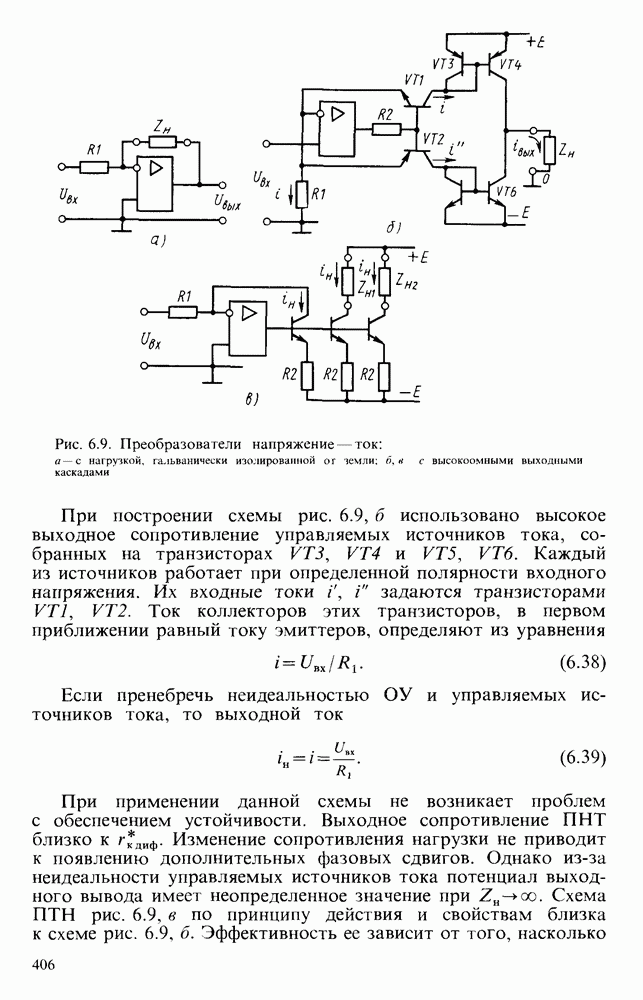
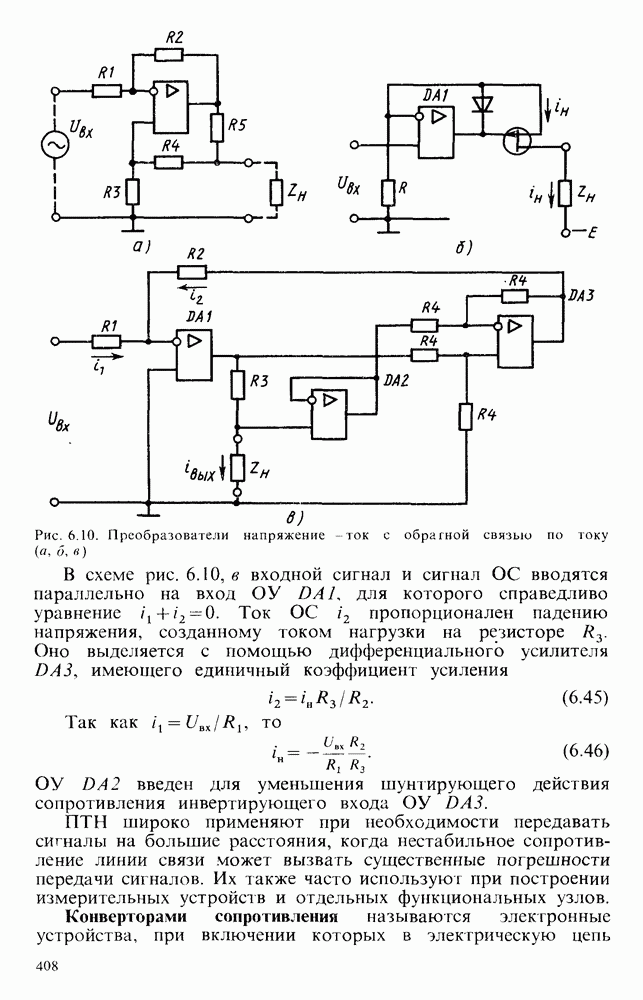
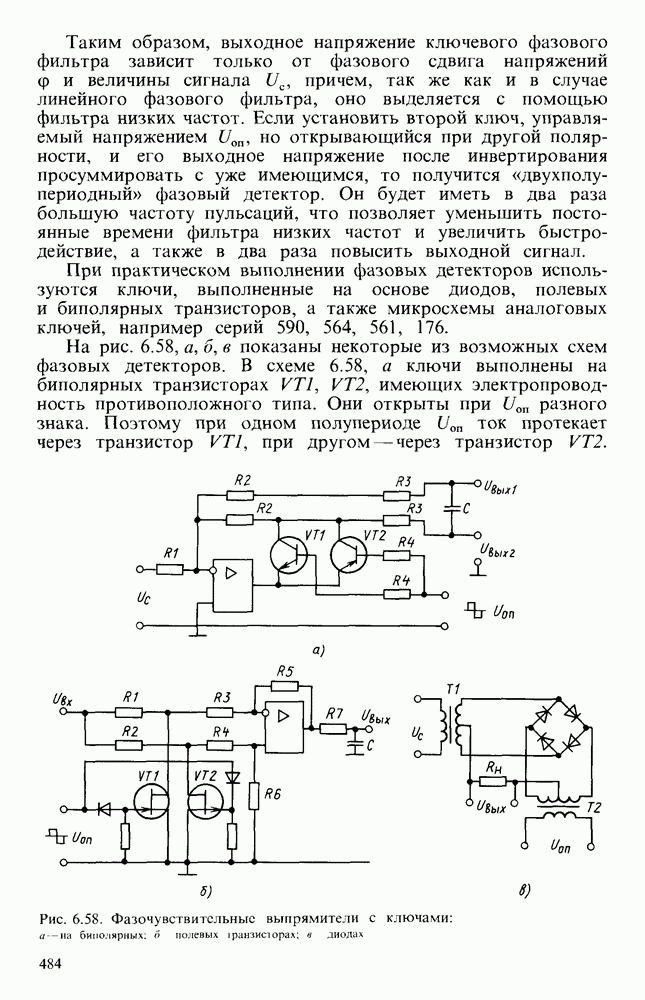
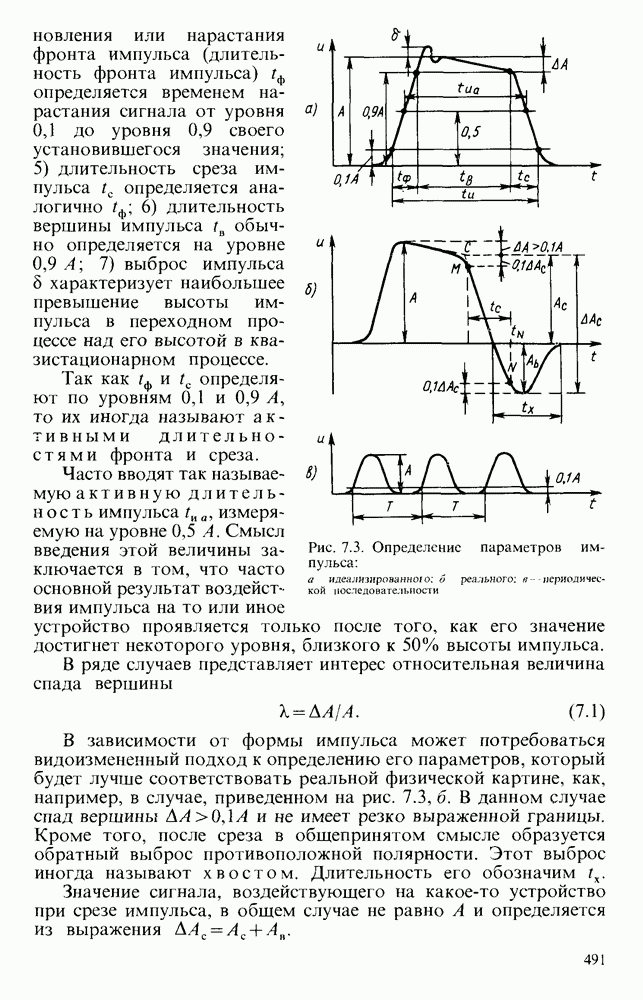
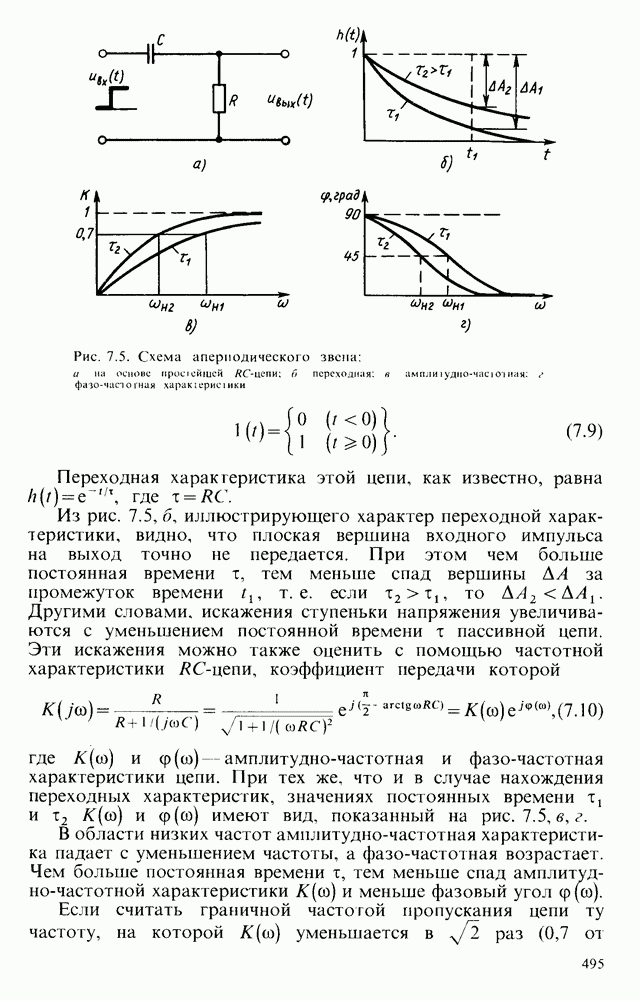
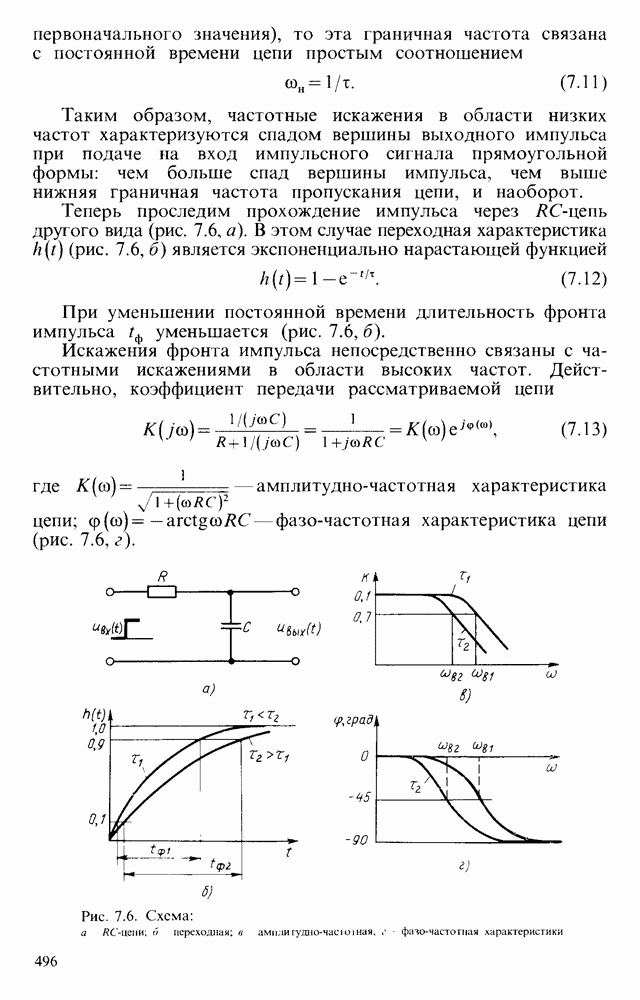
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
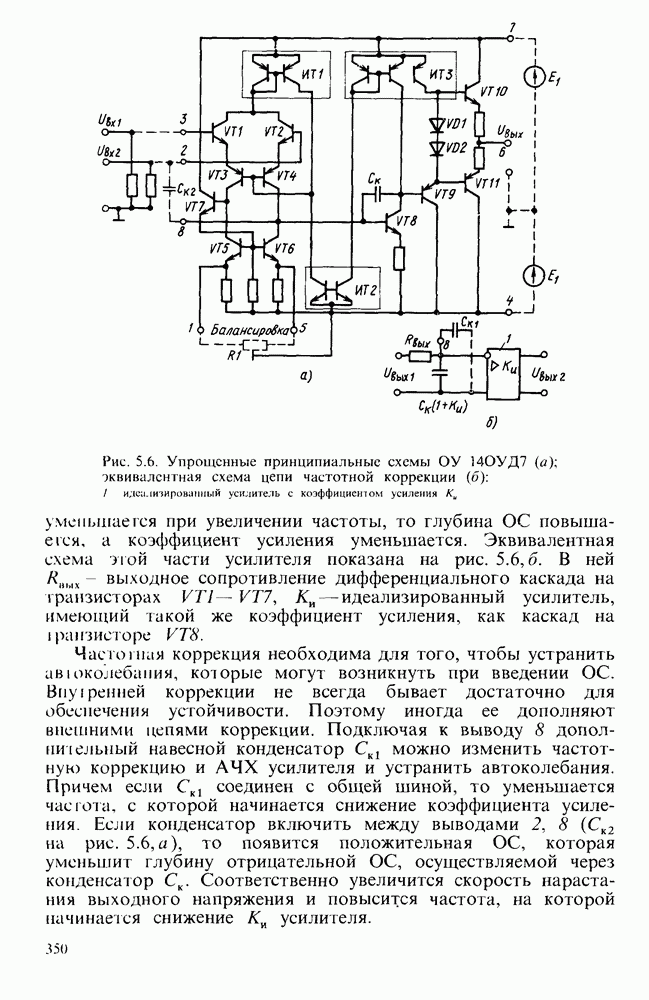
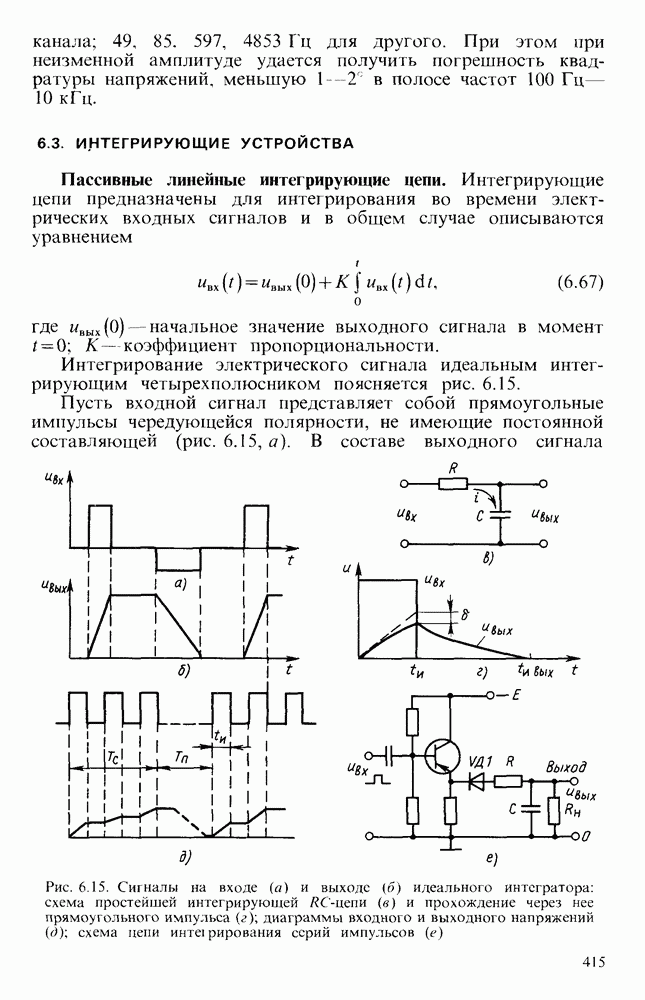
Интеграторы на основе операционных усилителей.
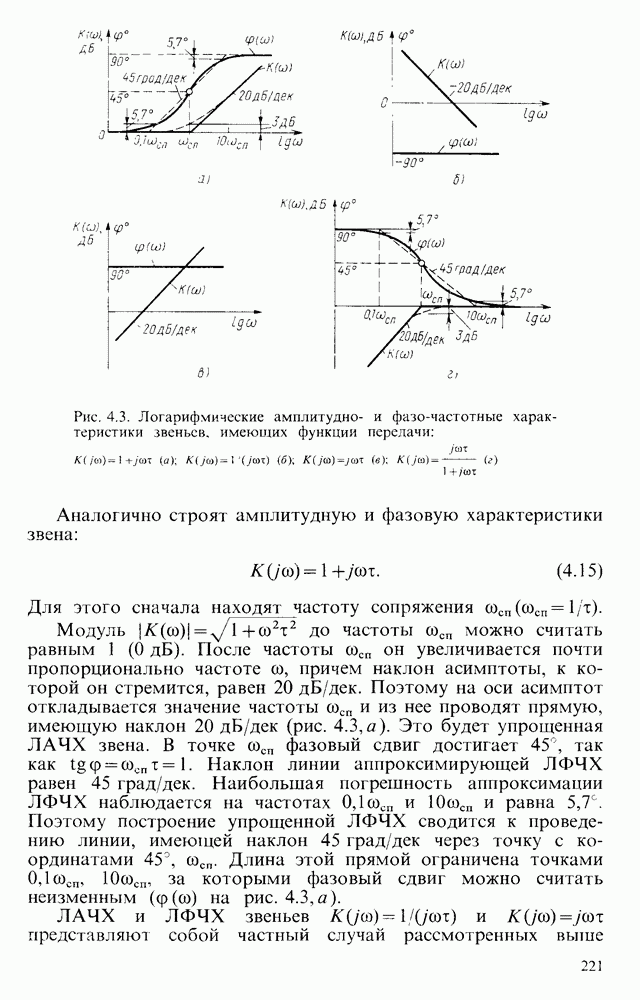
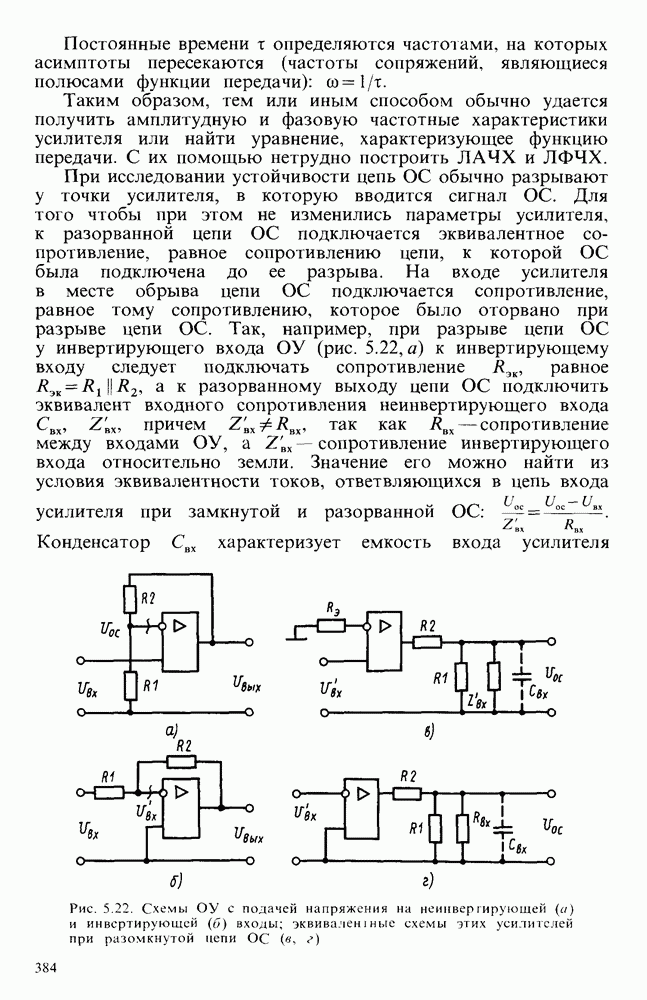
Простейшая схема интегратора на ОУ показана на рис. 6.16, а. Если операционный усилитель считать идеальным  , то коэффициент передачи при таком включении может быть найден на основании следующих рассуждений. Так как коэффициент усиления ОУ велик, то при работе в линейном режиме разность потенциалов между его входами стремится к нулю. Вход, не инвертирующий входной сигнал, соединен с общей шиной.
, то коэффициент передачи при таком включении может быть найден на основании следующих рассуждений. Так как коэффициент усиления ОУ велик, то при работе в линейном режиме разность потенциалов между его входами стремится к нулю. Вход, не инвертирующий входной сигнал, соединен с общей шиной.

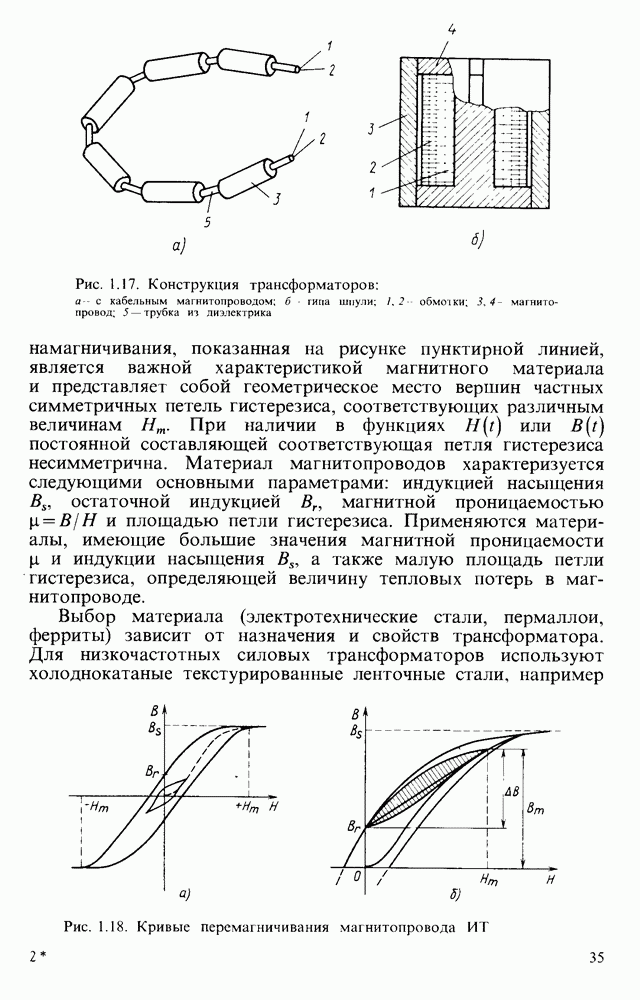
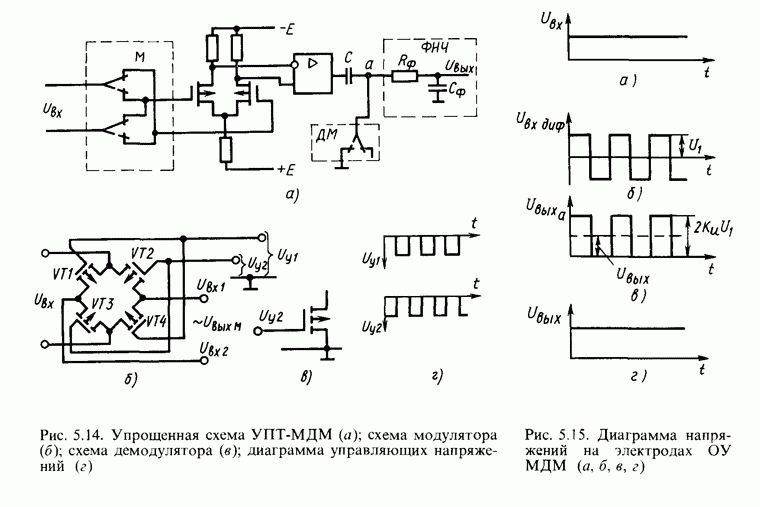
Рис. 6.16. Схема интегратора на ОУ  его эквивалентная схема (б); ЛАЧХ интегратора (в)
его эквивалентная схема (б); ЛАЧХ интегратора (в)
Следовательно, и потенциал инвертирующего входа близок к потенциалу обтцей тины. Входной ток

Этот ток при высоком входном сопротивлении ОУ полностью протекает через конденсатор С:

Напряжение на конденсаторе  и выходное напряжение усилителя изменяются по закону
и выходное напряжение усилителя изменяются по закону

При подаче на вход скачка напряжения постоянного значения  выходное напряжение
выходное напряжение

Таким образом, если ОУ близок к идеальному, то данная схема обеспечивает прецизионное интегрирование входного сигнала. При этом, как видно из полученного выражения, выходное напряжение не зависит от коэффициента усиления ОУ.
В реальном ОУ имеется смещение нуля выходного напряжения, что учитывается введением во входную цепь ОУ источника напряжения  . Кроме того, в цепи каждого входа протекают токи
. Кроме того, в цепи каждого входа протекают токи  напряжения и токи учтены в эквивалентной схеме, показанной на рис.
напряжения и токи учтены в эквивалентной схеме, показанной на рис.  .
.
Входные токи вызывают появление на входе усилителя дифференциального напряжения

которое усиливается в К раз и создает в цепи резистора R и конденсатора С дополнительный ток  , который уменьшает
, который уменьшает  до нуля (при работе в линейном режиме, при
до нуля (при работе в линейном режиме, при  , дифференциальный входной сигнал всегда стремится к нулю).
, дифференциальный входной сигнал всегда стремится к нулю).
Найдем его значение из уравнения

откуда -  .
.
Для поддержания этого постоянного тока, который заряжает конденсатор С, выходное напряжение должно изменяться по закону

Появление дополнительного выходного напряжения  вызывает ошибку интегрирования, которая зависит от дифференциального входного сигнала, вызванного разностью входных токов. Для уменьшения ее следует подбирать резистор
вызывает ошибку интегрирования, которая зависит от дифференциального входного сигнала, вызванного разностью входных токов. Для уменьшения ее следует подбирать резистор  так, чтобы
так, чтобы  .
.
При выполнении условия

ошибка интегрирования, вызванная наличием входных гоков, ничтожно мала.
Напряжение смещения нуля  также вызывает в цепи резистора R и конденсатора С ток
также вызывает в цепи резистора R и конденсатора С ток

Для обеспечения этого постоянного тока выходное напряжение должно изменяться по закону
 (6.85)
(6.85)
Таким образом, неидеальность ОУ приводит к тому, что выходное напряжение изменяется в соответствии с уравнением 

Последний член появился потому, что при  потенциал точки а отличается от нуля на величину
потенциал точки а отличается от нуля на величину  . Действительно, в момент начала интегрирования, когда конденсатор С разряжен и
. Действительно, в момент начала интегрирования, когда конденсатор С разряжен и  , потенциал выхода ОУ равен потенциалу точки а, т. е.
, потенциал выхода ОУ равен потенциалу точки а, т. е.  . В связи с тем что дифференциальное напряжение на входе ОУ близко к нулю, потенциал точки а уравновешивает напряжение смещения нуля:
. В связи с тем что дифференциальное напряжение на входе ОУ близко к нулю, потенциал точки а уравновешивает напряжение смещения нуля:  .
.
Следовательно, в момент начала интегрирования на выходе ОУ имеется напряжение, значение которого равно напряжению смещения нуля ОУ. Поэтому в уравнение выходного напряжения и добавлен этот член.
Наличие напряжения смещения нуля  и входных токов приводит к ограничению максимальной длительности интегрирования полезного сигнала, так как с течением времени напряжение ошибки постепенно нарастает. В итоге при неблагоприятных условиях ОУ может попасть в режим насыщения по одной из полярностей.
и входных токов приводит к ограничению максимальной длительности интегрирования полезного сигнала, так как с течением времени напряжение ошибки постепенно нарастает. В итоге при неблагоприятных условиях ОУ может попасть в режим насыщения по одной из полярностей.
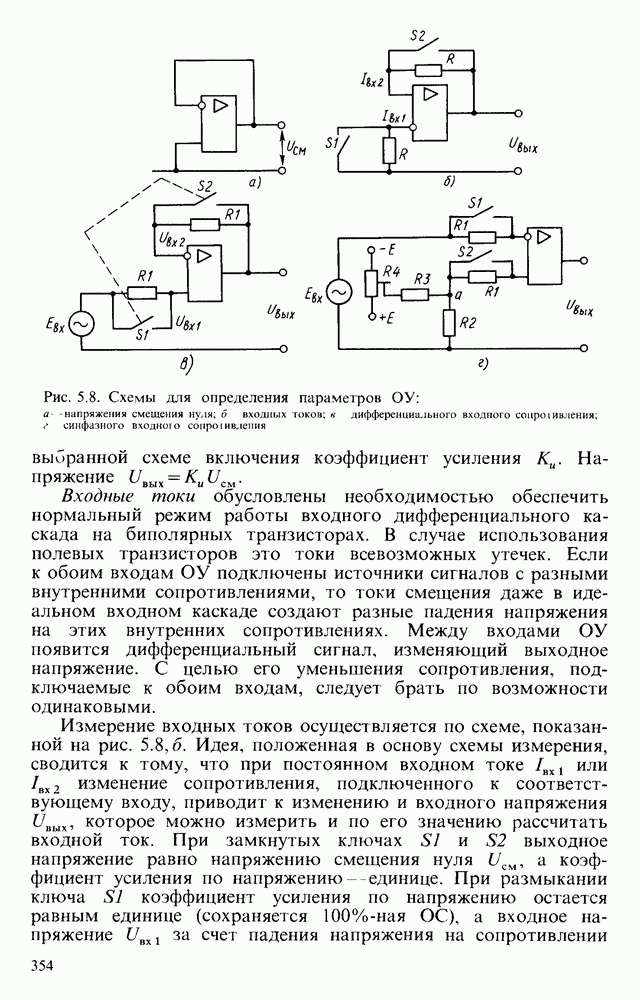
Реальный ОУ имеет конечное значение коэффициента усиления и для него справедливы эквивалентная схема рис. 5.18, в и результаты, полученные в § 5.6.
Из них следует, что данный интегратор эквивалентен обычной  -цепи, у которой значение емкости конденсатора С увеличено в
-цепи, у которой значение емкости конденсатора С увеличено в  раз, а падение напряжения на нем усилено в
раз, а падение напряжения на нем усилено в  раз. Так, например, при подаче на вход импульса прямоугольной формы и постоянной величины выходное напряжение
раз. Так, например, при подаче на вход импульса прямоугольной формы и постоянной величины выходное напряжение

Соответственно частота  на
на  (рис. 6.16, в) равна
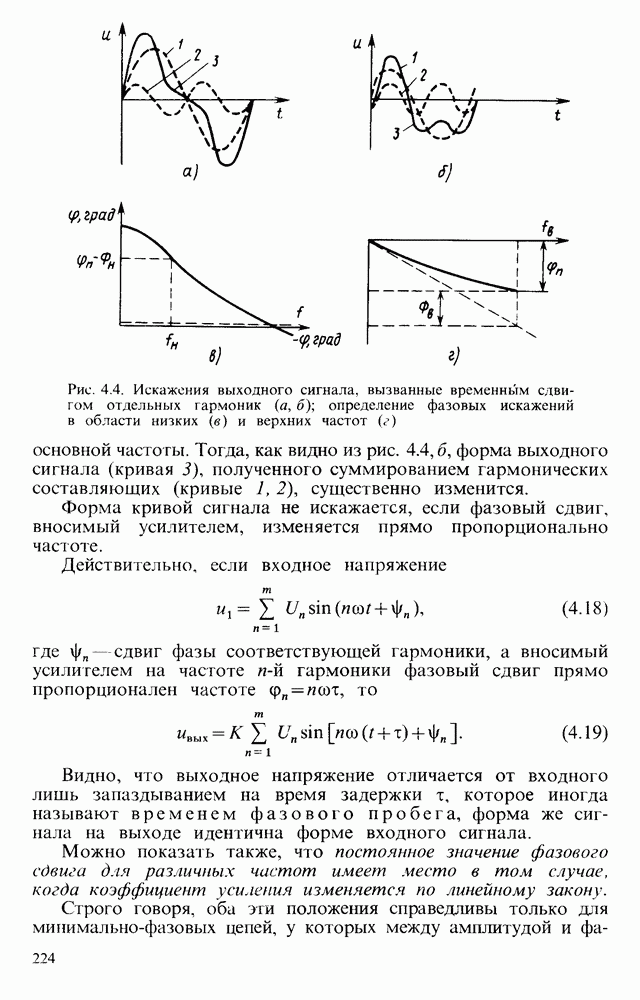
(рис. 6.16, в) равна  , где
, где  . Так же как и в пассивной
. Так же как и в пассивной  -цепи, при подаче на вход интегратора скачка напряжения выходной сигнал изменяется по экспоненциальному закону (рис. 6.17, а)
-цепи, при подаче на вход интегратора скачка напряжения выходной сигнал изменяется по экспоненциальному закону (рис. 6.17, а)

а относительная ошибка интегрирования

Из (6.88) следует, что погрешность интегрирования приблизительно в  раз меньше по сравнению с простой
раз меньше по сравнению с простой  -цепью при тех же номиналах R и С.
-цепью при тех же номиналах R и С.
Таким образом, из-за конечного значения коэффициента усиления ОУ интегратор в полосе низких частот работает как усилитель. Только с частоты  начинают проявляться его интегрирующие свойства. Хорошие характеристики получаются на частотах не менее чем в 10—50 раз больших, чем
начинают проявляться его интегрирующие свойства. Хорошие характеристики получаются на частотах не менее чем в 10—50 раз больших, чем  .
.
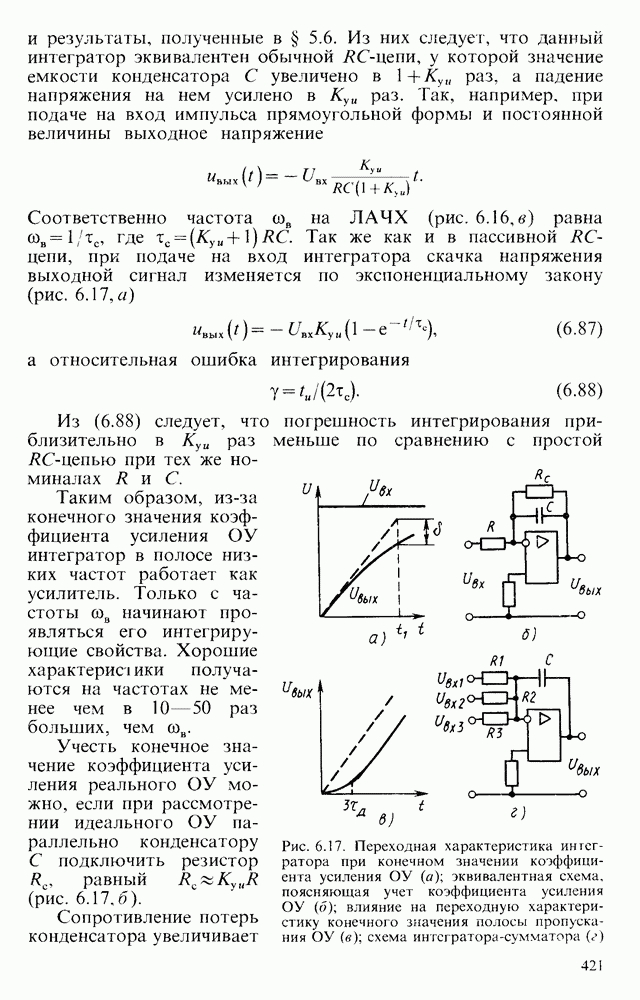
Учесть конечное значение коэффициента усиления реального ОУ можно, если при рассмотрении идеального ОУ параллельно конденсатору С подключить резистор  , равный
, равный  (рис.
(рис.  ).
).

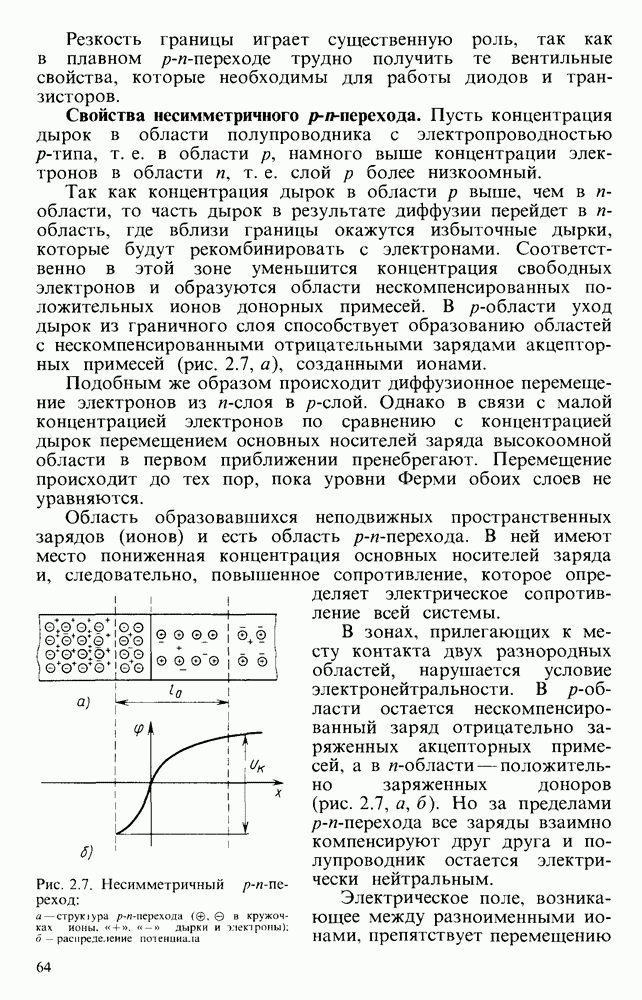
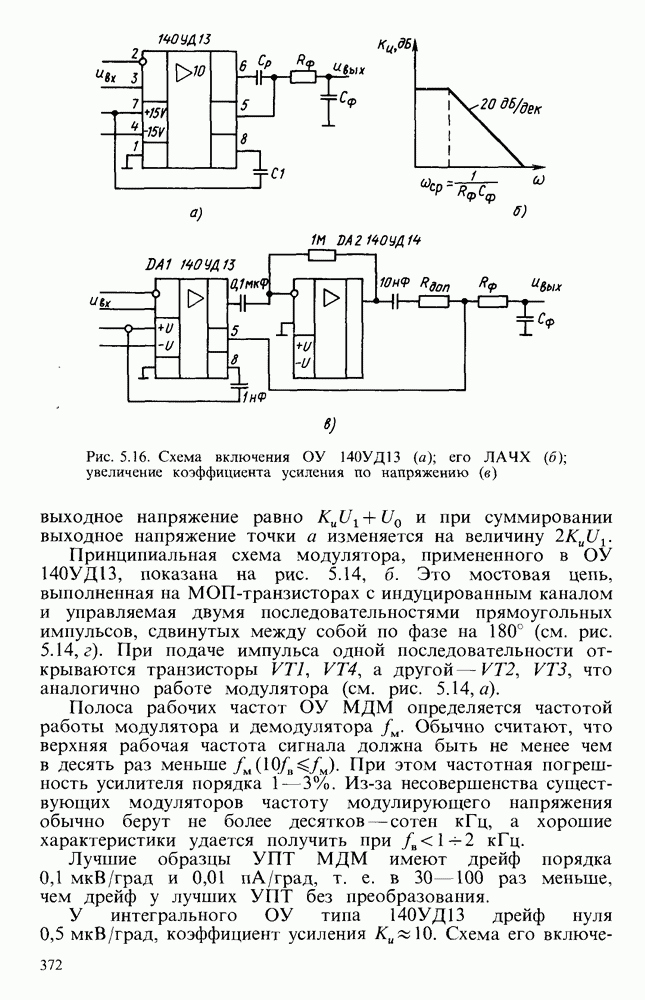
Рис. 6.17. Переходная характеристика интегратора при конечном значении коэффициента усиления ОУ (а); эквивалентная схема, поясняющая учет коэффициента усиления ОУ (б); влияние на переходную характеристику конечного значения полосы пропускания ОУ (в); схема интегратора-сумматора (г)
Сопротивление потерь конденсатора увеличивает погрешность интегрирования, поэтому в точных интеграторах следует применять конденсаторы с минимальными потерями.
Так как полоса пропускания реального ОУ имеет конечное значение, то при интегрировании ступенчатого сигнала появляется дополнительная погрешность, выражающаяся в запаздывании выходного сигнала (рис. 6.17, в). Оно характеризуется постоянной времени  и обусловлено ограниченной полосой пропускания ОУ в области высоких частот:
и обусловлено ограниченной полосой пропускания ОУ в области высоких частот:  (
( - верхняя граничная частота ОУ, определенная на уровне 0,7).
- верхняя граничная частота ОУ, определенная на уровне 0,7).
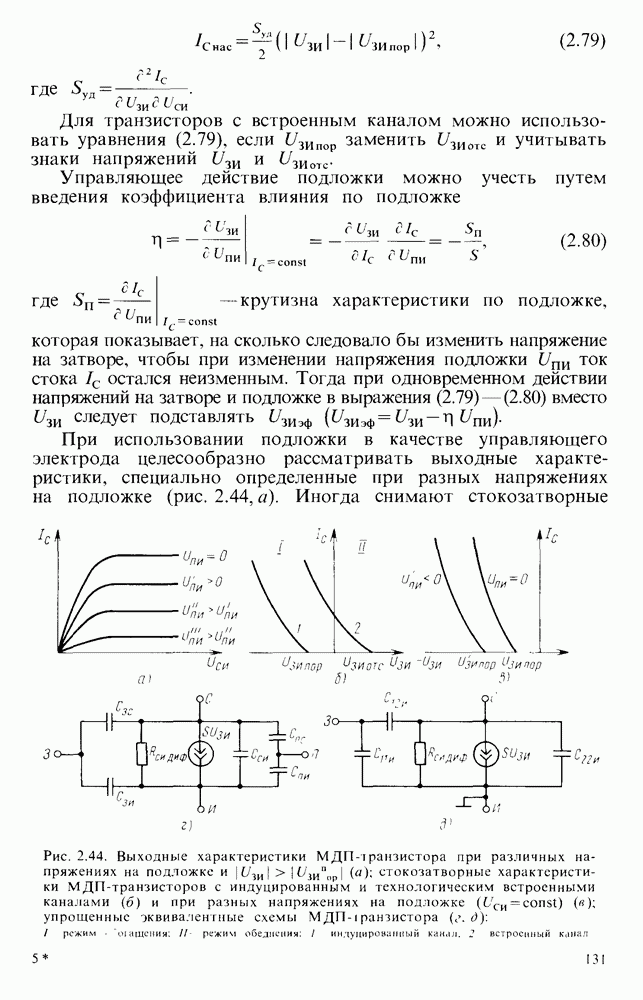
Иногда используют интеграторы-сумматоры (рис. 6.17, г), интегрирующие несколько сигналов, поступающих от разных источников. В этом случае выходное напряжение находят из упрощенного уравнения

Если конденсатор, осуществляющий интегрирование сигнала, должен иметь «заземленную» обкладку,  можно применять интеграторы, выполненные на основе схем ПНТ (например, см. рис. 6.10, а). В
можно применять интеграторы, выполненные на основе схем ПНТ (например, см. рис. 6.10, а). В  устройствах (рис. 6.18, а, б) ток заряда конденсатора не зависит от напряжения на нем, что позволяет интегрировать входной сигнал. При этом имеется возможность создать дифференциальный вход и интегрировать разность входных сигналов.
устройствах (рис. 6.18, а, б) ток заряда конденсатора не зависит от напряжения на нем, что позволяет интегрировать входной сигнал. При этом имеется возможность создать дифференциальный вход и интегрировать разность входных сигналов.

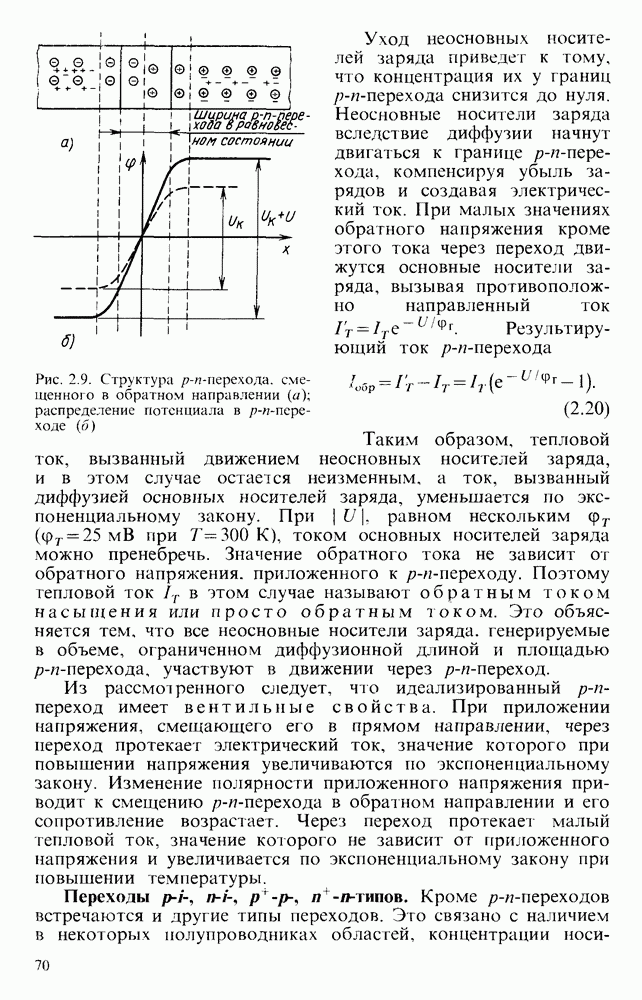
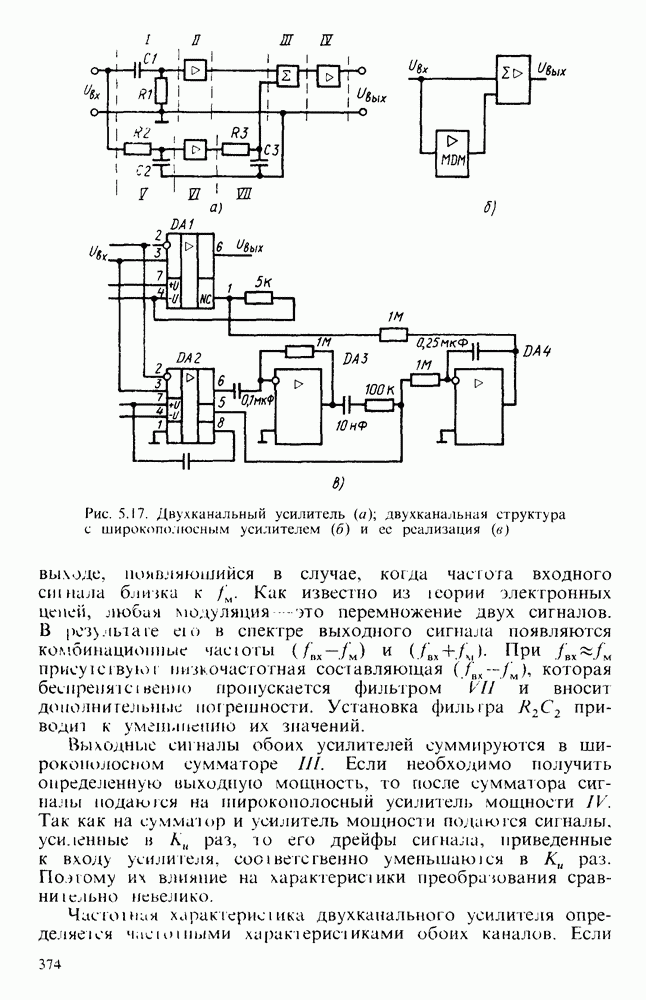
Рис. 6.18. Интеграторы: а - с дифференциальным входом. б - повышенной точности: в - со сбросом начального заряда
Ток конденсатора С определяют из (6.40, 6.43), а выходное напряжение

Однако значительный синфазный сигнал и необходимость иметь источники входных напряжений с малыми внутренними сопротивлениями ухудшают характеристики данного интегратора.
Значительно лучшие результаты можно получить с помощью схемы рис.  . В ней имеется возможность применять конденсатор С малой емкости, что позволяет использовать высокостабильные конденсаторы с малыми потерями и незначительной адсорбцией. Идея работы интегратора заключается в следующем. Входное напряжение заряжает конденсатор С. При увеличении напряжения на нем ток должен уменьшаться. Но это уменьшение тока компенсируется благодаря тому, что напряжение
. В ней имеется возможность применять конденсатор С малой емкости, что позволяет использовать высокостабильные конденсаторы с малыми потерями и незначительной адсорбцией. Идея работы интегратора заключается в следующем. Входное напряжение заряжает конденсатор С. При увеличении напряжения на нем ток должен уменьшаться. Но это уменьшение тока компенсируется благодаря тому, что напряжение  через усилитель
через усилитель  с единичным коэффициентом усиления и усилитель
с единичным коэффициентом усиления и усилитель  с коэффициентом усиления
с коэффициентом усиления  через резистор
через резистор  прикладывается к точке а. При
прикладывается к точке а. При  ток
ток  , приходящий в точку а, разветвляется на два тока:
, приходящий в точку а, разветвляется на два тока:  . При
. При  составляющая тока
составляющая тока  уменьшается из-за того, что на выходе ОУ
уменьшается из-за того, что на выходе ОУ  появляется напряжение ивых. При правильно выбранных параметрах схемы можно обеспечить неизменное значение тока
появляется напряжение ивых. При правильно выбранных параметрах схемы можно обеспечить неизменное значение тока  , а следовательно, идеальное интегрирование входного сигнала. В общем случае передаточную функцию интегратора записывают в виде
, а следовательно, идеальное интегрирование входного сигнала. В общем случае передаточную функцию интегратора записывают в виде

где  примет вид
примет вид

Это уравнение идеального интегратора. Коэффициент передачи изменяется подбором номиналов резистора  . При использовании ОУ с малыми входными токами и точно подобранными резисторами
. При использовании ОУ с малыми входными токами и точно подобранными резисторами  на основе данной схемы можно получить прецизионные интеграторы при емкости С в несколько сотен
на основе данной схемы можно получить прецизионные интеграторы при емкости С в несколько сотен  и более.
и более.
Перед началом интегрирования интеграторы надо «сбросить» на ноль. Это обусловлено тем, что вследствие неидеальности ОУ на конденсаторе С может быть накоплен значительный заряд, который вызывает появление выходного напряжения, близкого к максимально достижимому.
Для сброса на ноль параллельно с конденсатором С включают электронный ключ, выполненный на микросхеме или на MOП-транзисторе.
Длительность стадии разрядки конденсатора С зависит от его емкости и внутреннего сопротивления включенного электронного ключа  . Изменение напряжения на конденсаторе С происходит по экспоненциальному закону
. Изменение напряжения на конденсаторе С происходит по экспоненциальному закону

где  .
.
Введение ключа увеличивает погрешности интегрирования из-за появления дополнительных токов утечек и отличия от нуля начального значения выходного напряжения. Так, например, в схеме 6.18, в начальное значение выходного напряжения  . В режиме интегрирования погрешность вносит ток утечки истока закрытого транзистора. Постоянная времени разрядки в этой схеме вследствие действия цепи ОС оказывается уменьшенной в
. В режиме интегрирования погрешность вносит ток утечки истока закрытого транзистора. Постоянная времени разрядки в этой схеме вследствие действия цепи ОС оказывается уменьшенной в  раз и равна
раз и равна  . Аналогично рассмотренному осуществляется сброс и в других схемах интеграторов.
. Аналогично рассмотренному осуществляется сброс и в других схемах интеграторов.
Интеграторы широко применяют при создании генераторов линейно изменяющегося и синусоидального напряжений, точных фазосдвигающих устройств, обеспечивающих получение 90° фазового сдвига напряжения с погрешностями минуты — десятки минут, в качестве фильтров низких частот и пр.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПАССИВНЫЕ КОМПОНЕНТЫ ЭЛЕКТРОННЫХ УСТРОЙСТВ
- § 1.1. РЕЗИСТОРЫ
- Основные параметры резисторов
- § 1.2. КОНДЕНСАТОРЫ
- Основные параметры постоянных конденсаторов
- 1.3. КАТУШКИ ИНДУКТИВНОСТИ
- Основные параметры катушки индуктивности (ГОСТ 20718—75)
- § 1.4. ТРАНСФОРМАТОРЫ ЭЛЕКТРОННОЙ АППАРАТУРЫ
- Основные параметры трансформаторов питания
- ГЛАВА 2. ПОЛУПРОВОДНИКОВЫЕ КОМПОНЕНТЫ ЭЛЕКТРОННЫХ ЦЕПЕЙ
- § 2.1. ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
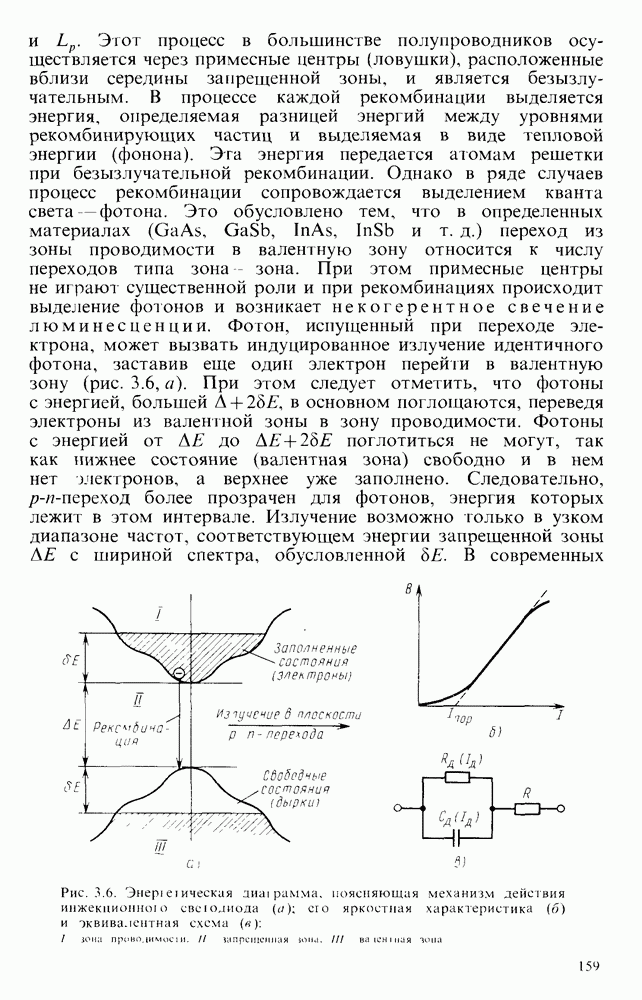
- Основные положения теории электропроводности.
- Примесная электропроводность.
- § 2.2. ОСНОВНЫЕ СВОЙСТВА И ХАРАКТЕРИСТИКИ ПОЛУПРОВОДНИКОВ
- Концентрация носителей зарядов.
- Уравнения непрерывности.
- § 2.3. ЭЛЕКТРИЧЕСКИЕ ПЕРЕХОДЫ
- Контакт металл — полупроводник.
- Контакт двух полупроводников p- и n-типов.
- Свойства несимметричного p-n-перехода.
- p-n-переход смещен в прямом направлении
- Переход, смещенный в обратном направлении.
- Переходы p-i, n-i-, p+-p-, n+-n-типов.
- 2.4. ОСОБЕННОСТИ РЕАЛЬНЫХ p-n-ПЕРЕХОДОВ
- Пробой p-n-перехода.
- § 2.5. ОСНОВНЫЕ ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ, ИСПОЛЬЗУЕМЫЕ ПРИ ИЗГОТОВЛЕНИИ ПОЛУПРОВОДНИКОВЫХ ПРИБОРОВ И ИНТЕГРАЛЬНЫХ МИКРОСХЕМ
- § 2.6. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
- Выпрямительные диоды.
- Основные параметры выпрямительных диодов и их значения у маломощных диодов
- Импульсные диоды.
- Полупроводниковые стабилитроны.
- Варикапы.
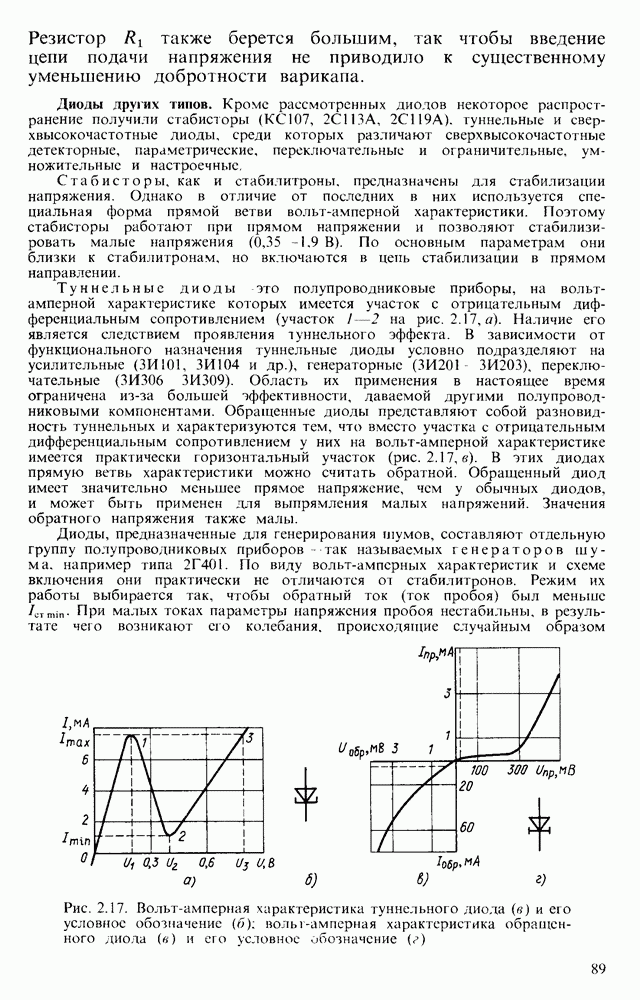
- Диоды других типов.
- § 2.7. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ
- Математическая модель транзистора.
- Три схемы включения транзистора.
- Инерционные свойства транзистора.
- Шумы транзистора.
- Н-параметры транзисторов.
- § 2.8. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ С ИНЖЕКЦИОННЫМ ПИТАНИЕМ
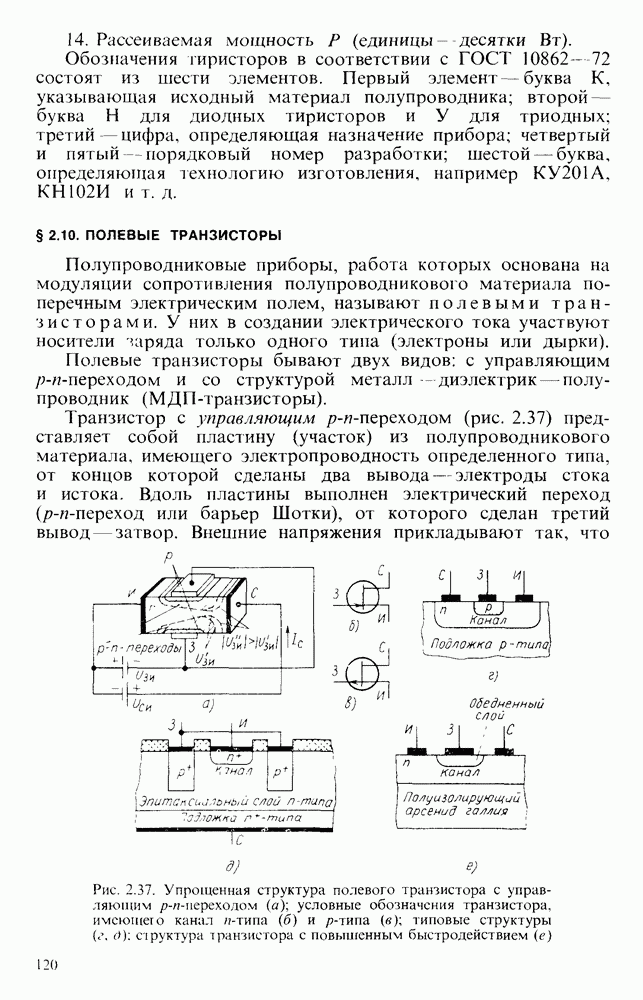
- § 2.9. ТИРИСТОРЫ
- Симметричные тиристоры.
- Основные параметры тиристоров и их ориентировочные значения
- § 2.10. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
- Основные параметры полевых транзисторов и их ориентировочные значения
- § 2.11. ОСОБЕННОСТИ КОМПОНЕНТОВ ЭЛЕКТРОННЫХ ЦЕПЕЙ В МИКРОМИНИАТЮРНОМ ИСПОЛНЕНИИ
- Пассивные компоненты ИС.
- Конденсаторы.
- Индуктивности.
- Транзисторы ИС.
- Изоляция компонентов в монолитных интегральных узлах.
- ГЛАВА 3. КОМПОНЕНТЫ ОПТОЭЛЕКТРОНИКИ И ТЕХНИЧЕСКИЕ СРЕДСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.1. ОБЩИЕ СВЕДЕНИЯ О КОМПОНЕНТАХ ОПТОЭЛЕКТРОНИКИ
- § 3.2. УПРАВЛЯЕМЫЕ ИСТОЧНИКИ СВЕТА
- Основные параметры и характеристики светодиодов
- § 3.3. ФОТОПРИЕМНИКИ
- Основные характеристики и параметры фоторезистора
- Фотодиоды.
- Основные характеристики и параметры фотодиода
- Фототранзисторы.
- Основные характеристики и параметры фототранзистора
- Фототиристоры.
- Многоэлементные фотоприемники.
- Фотоприемники с внешним фотоэффектом.
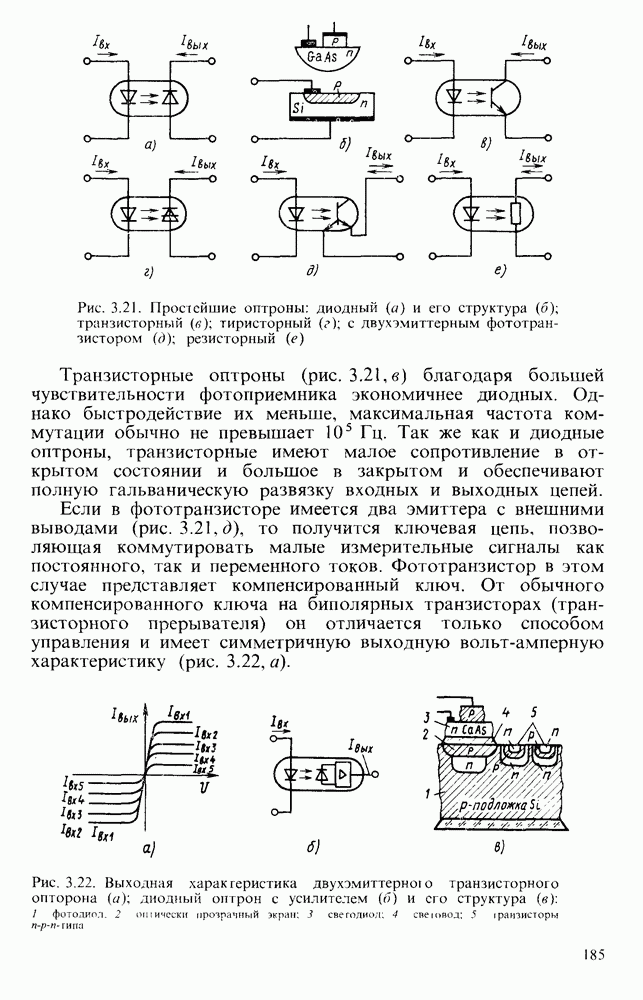
- § 3.4. СВЕТОВОДЫ И ПРОСТЕЙШИЕ ОПТРОНЫ
- § 3 5. ОБЩИЕ СВЕДЕНИЯ О КОМПОНЕНТАХ УСТРОЙСТВ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.6. ЖИДКОКРИСТАЛЛИЧЕСКИЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.7. ГАЗОНАПОЛНЕННЫЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- Основные параметры газонаполненных матричных панелей неременного тока
- § 3.8. ВАКУУМНЫЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.9. ПОЛУПРОВОДНИКОВЫЕ И ЭЛЕКТРОЛЮМИНЕСЦЕНТНЫЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- ГЛАВА 4. УСИЛИТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- § 4.1. ОБЩИЕ СВЕДЕНИЯ ОБ УСИЛИТЕЛЯХ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ, ИХ ОСНОВНЫХ ПАРАМЕТРАХ И ХАРАКТЕРИСТИКАХ
- § 4.2. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ОБРАТНОЙ СВЯЗИ ПРИМЕНИТЕЛЬНО К УСИЛИТЕЛЯМ
- § 4.3. СТАТИЧЕСКИЙ РЕЖИМ РАБОТЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ
- § 4.4. УСИЛИТЕЛЬНЫЕ КАСКАДЫ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- Каскад с общим стоком.
- § 4.5. УСИЛИТЕЛЬНЫЙ КАСКАД НА БИПОЛЯРНОМ ТРАНЗИСТОРЕ С ОБЩИМ ЭМИТТЕРОМ
- Входное сопротивление.
- § 4.6. УСИЛИТЕЛЬНЫЙ КАСКАД НА БИПОЛЯРНОМ ТРАНЗИСТОРЕ С ОБЩЕЙ БАЗОЙ
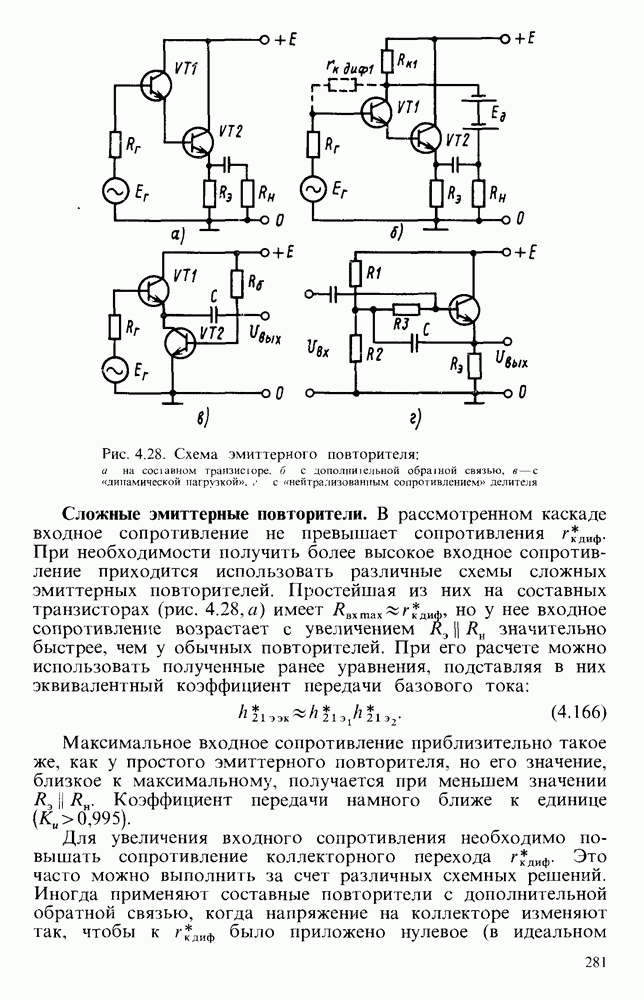
- § 4.7. УСИЛИТЕЛЬНЫЙ КАСКАД НА БИПОЛЯРНОМ ТРАНЗИСТОРЕ С ОБЩИМ КОЛЛЕКТОРОМ
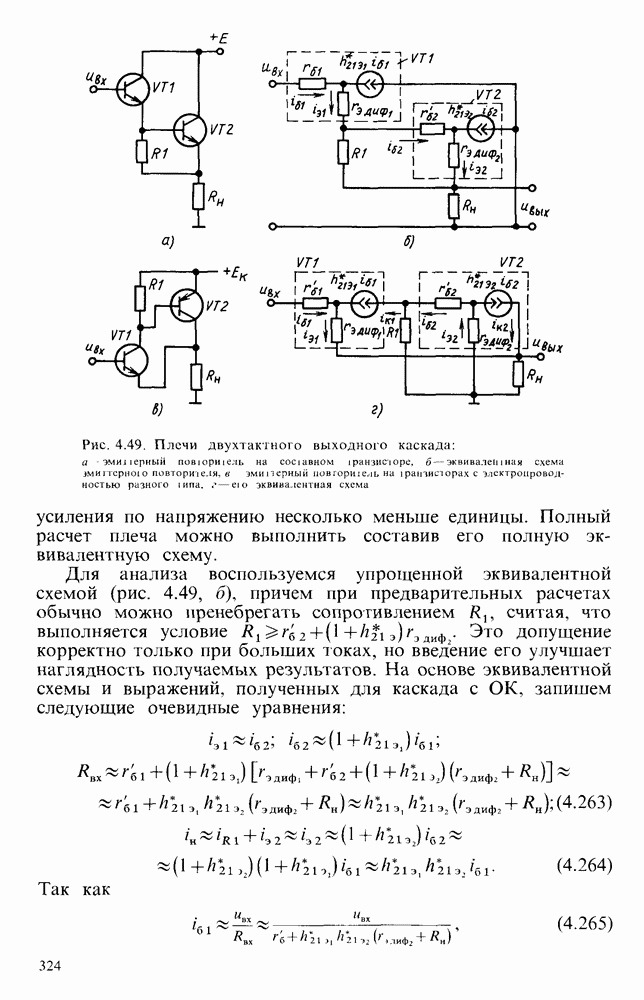
- Сложные эмиттерные повторители.
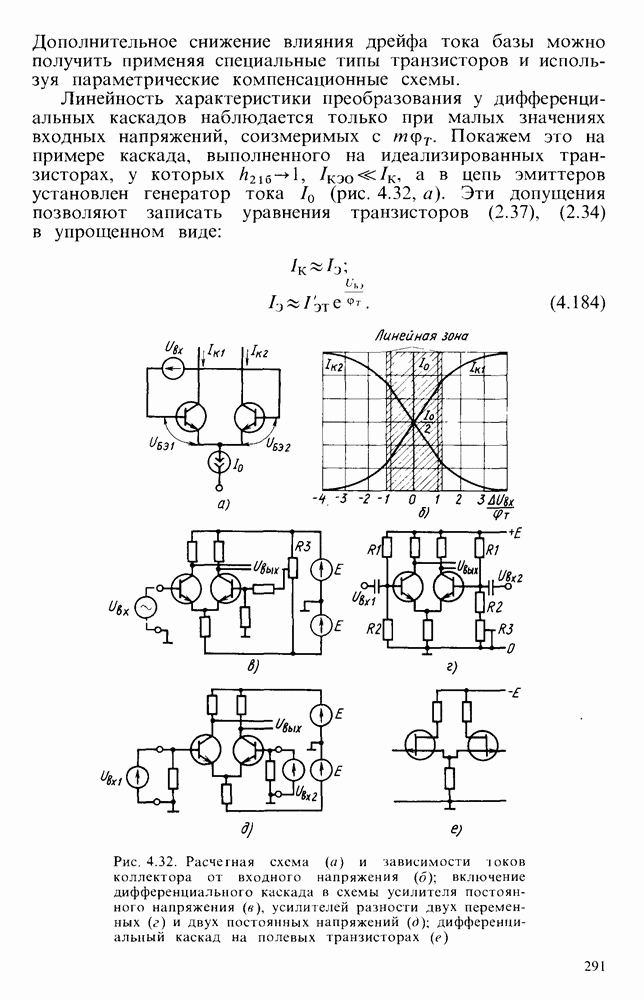
- § 4.8. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
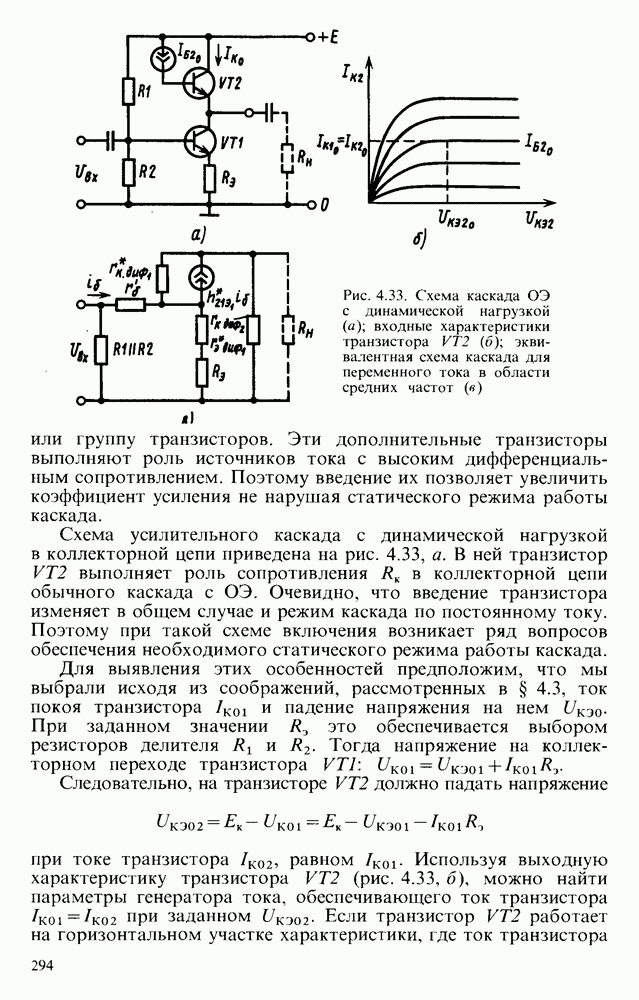
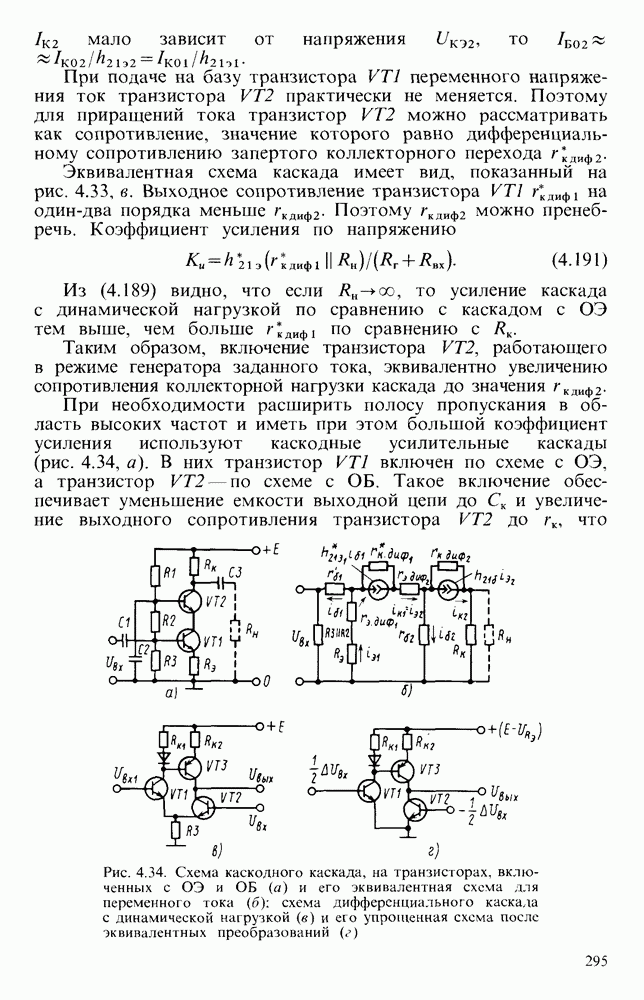
- § 4.9. УСИЛИТЕЛЬНЫЕ КАСКАДЫ С ДИНАМИЧЕСКОЙ НАГРУЗКОЙ И С КАСКОДНЫМ ВКЛЮЧЕНИЕМ ТРАНЗИСТОРОВ
- § 4.10. УПРАВЛЯЕМЫЕ ИСТОЧНИКИ ТОКА И УСИЛИТЕЛЬНЫЕ КАСКАДЫ НА ИХ ОСНОВЕ
- 4.11. УСИЛИТЕЛЬНЫЕ КАСКАДЫ С ТРАНСФОРМАТОРНОЙ СВЯЗЬЮ
- 4.12. МОЩНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- Каскад с ОБ трансформаторным входом и трансформаторным выходом.
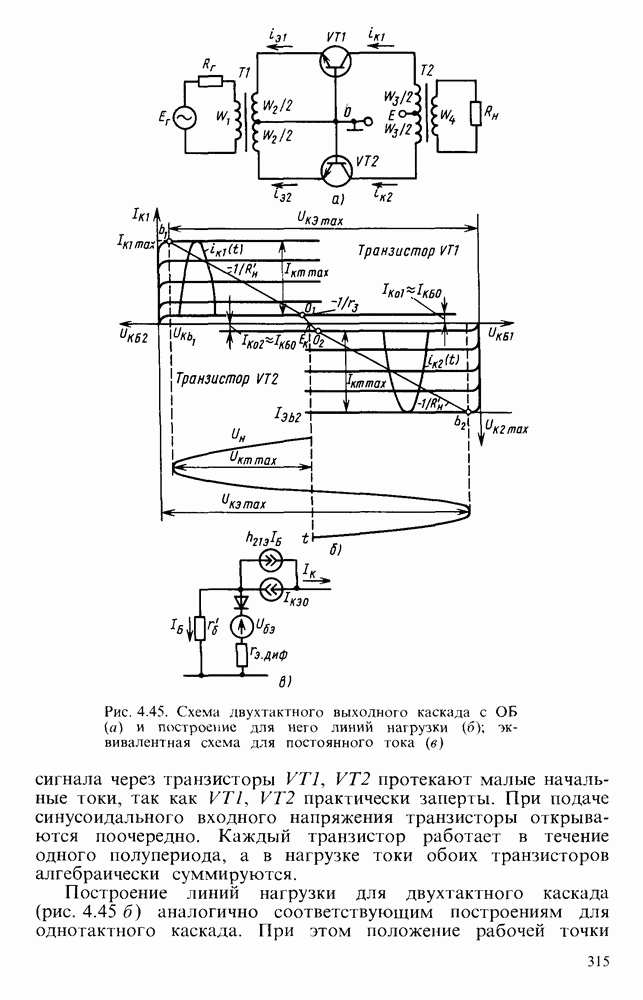
- Двухтактные выходные каскады.
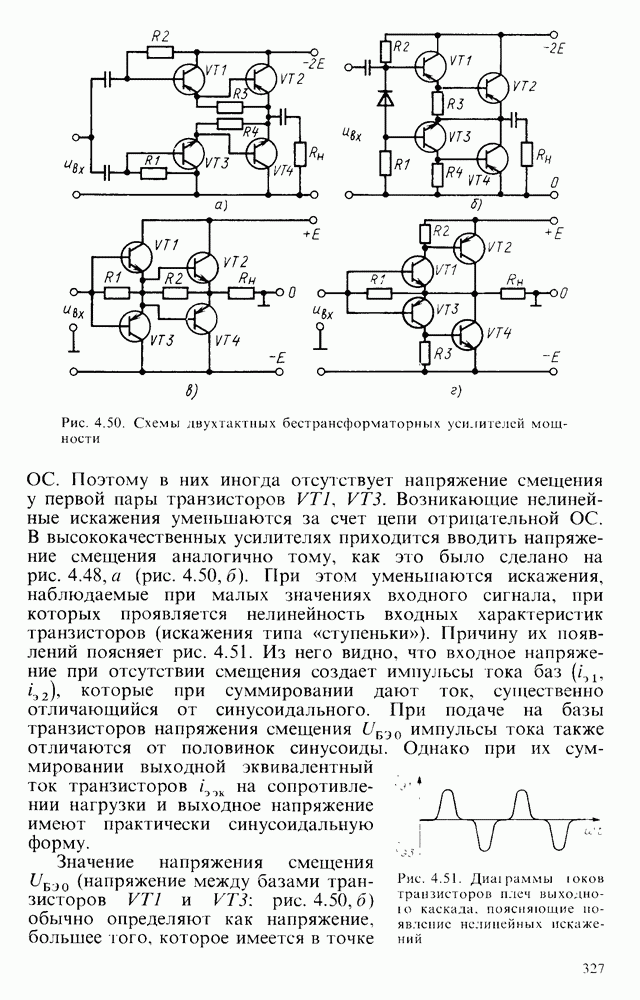
- § 4.13. БЕСТРАНСФОРМАТОРНЫЕ МОЩНЫЕ ВЫХОДНЫЕ КАСКАДЫ
- ГЛАВА 5. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- § 5.1. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- Параметры RC-цепи связи.
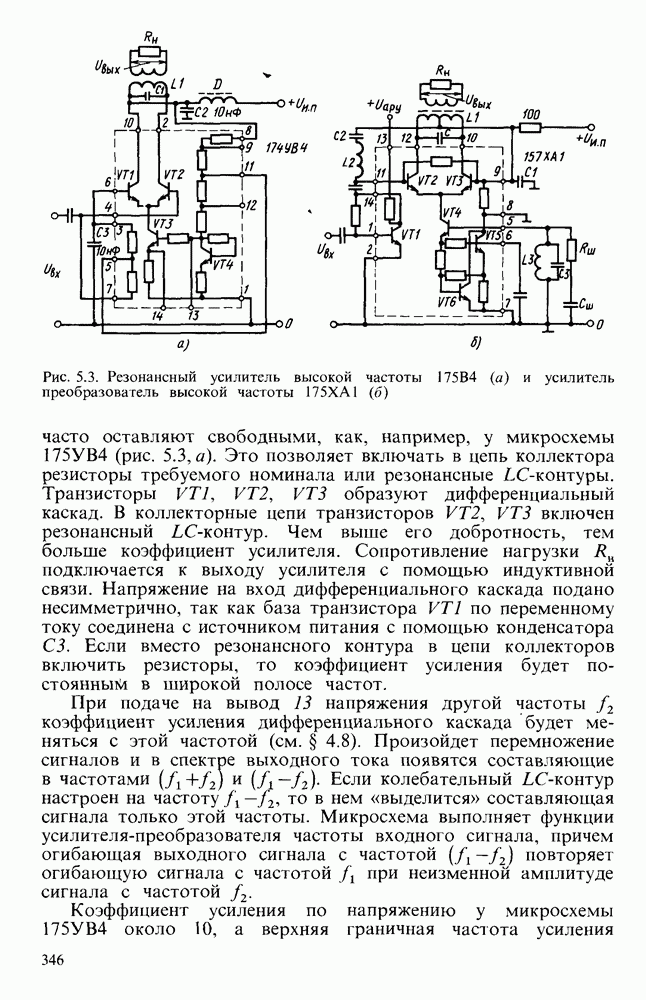
- § 5.2. УСИЛИТЕЛИ В ИНТЕГРАЛЬНОМ ИСПОЛНЕНИИ
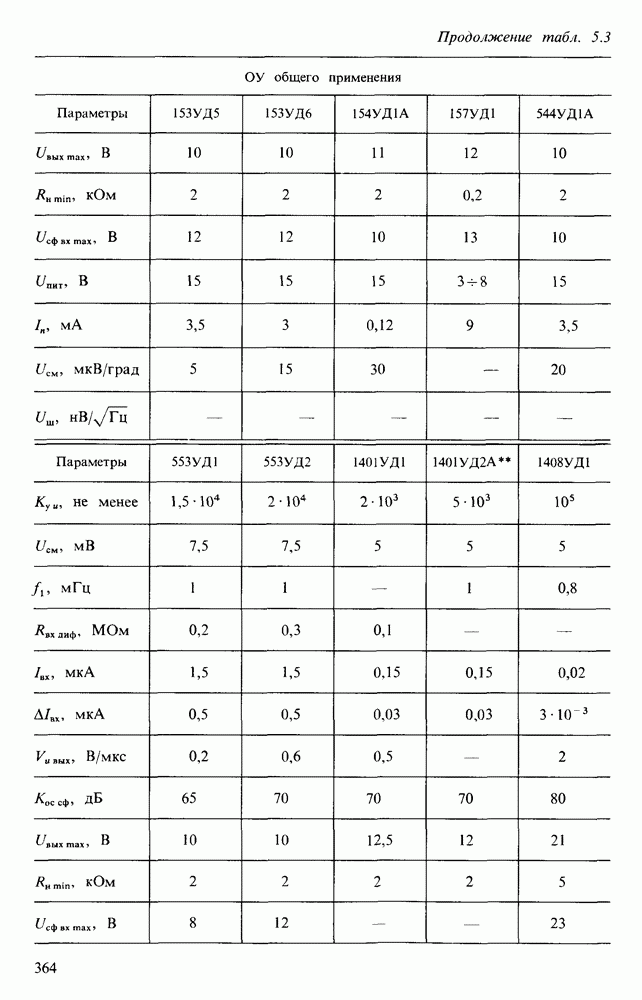
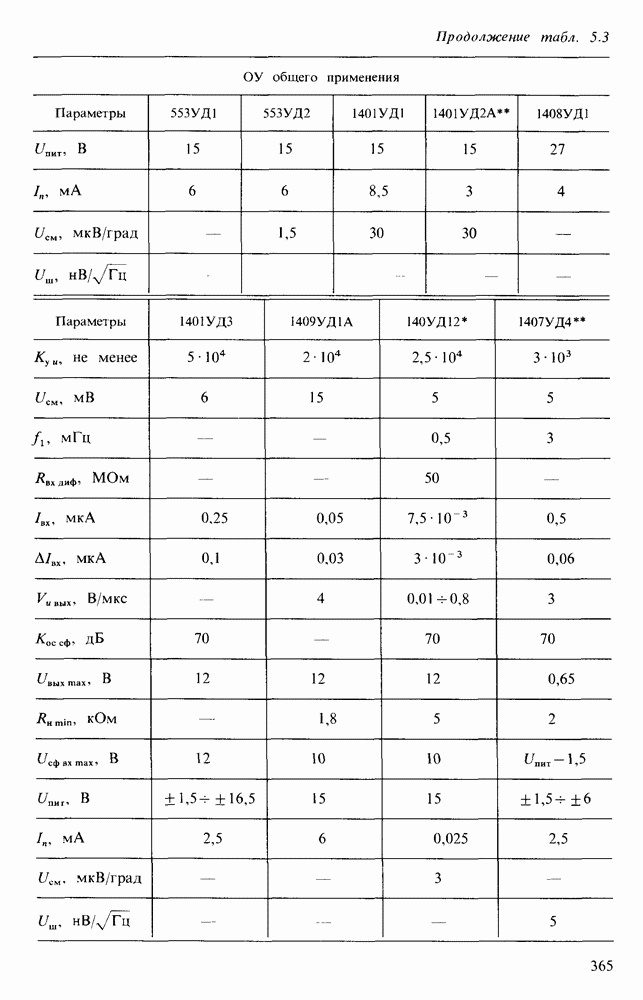
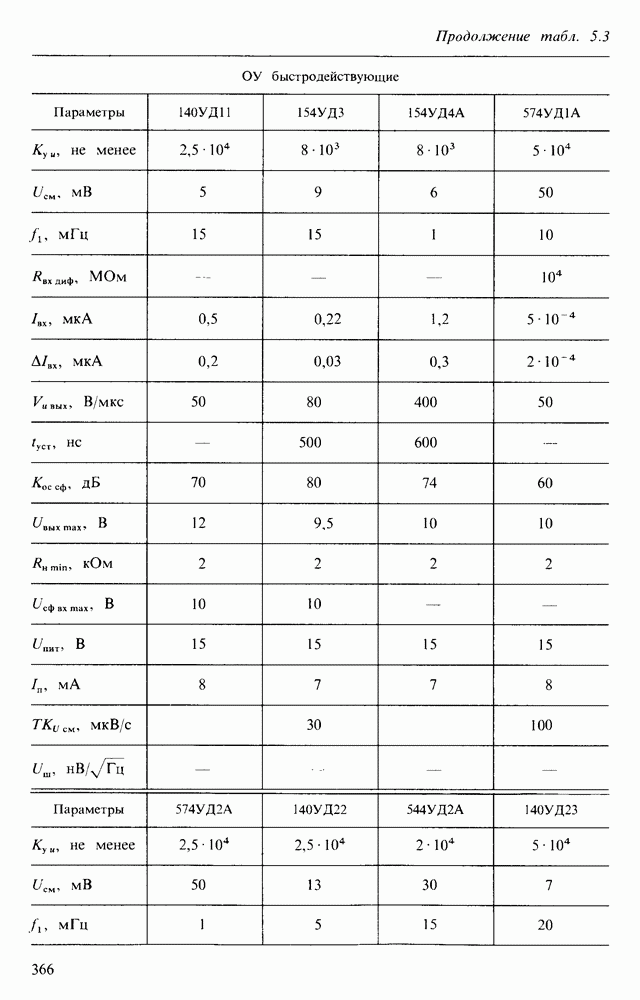
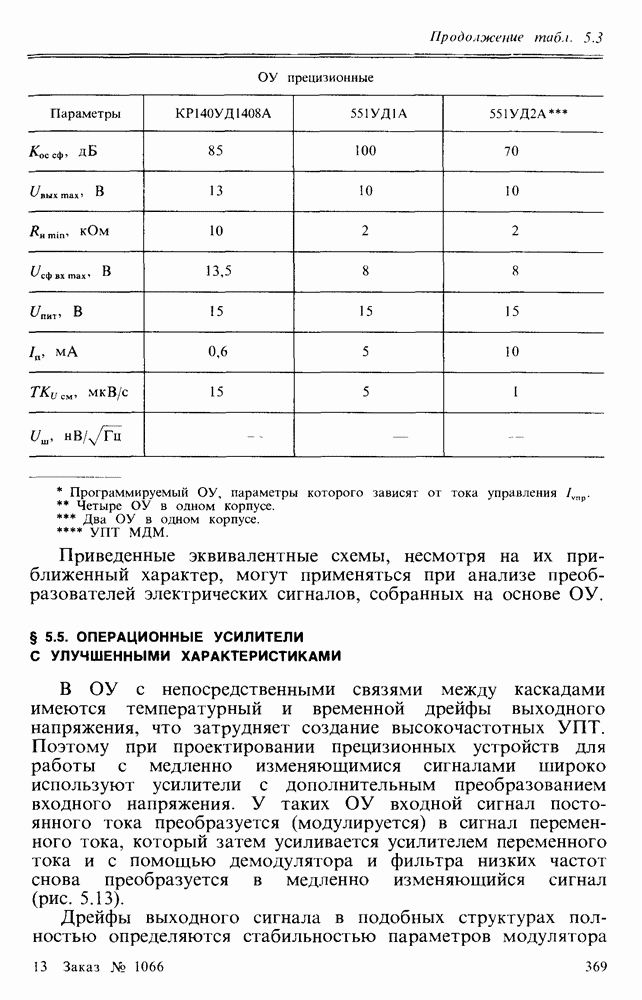
- 5.3. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- § 5.4. ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- § 5.5. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ С УЛУЧШЕННЫМИ ХАРАКТЕРИСТИКАМИ
- § 5.6. ОСОБЕННОСТИ ВКЛЮЧЕНИЯ И СВОЙСТВА ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ, ОХВАЧЕННЫХ ОБРАТНОЙ СВЯЗЬЮ
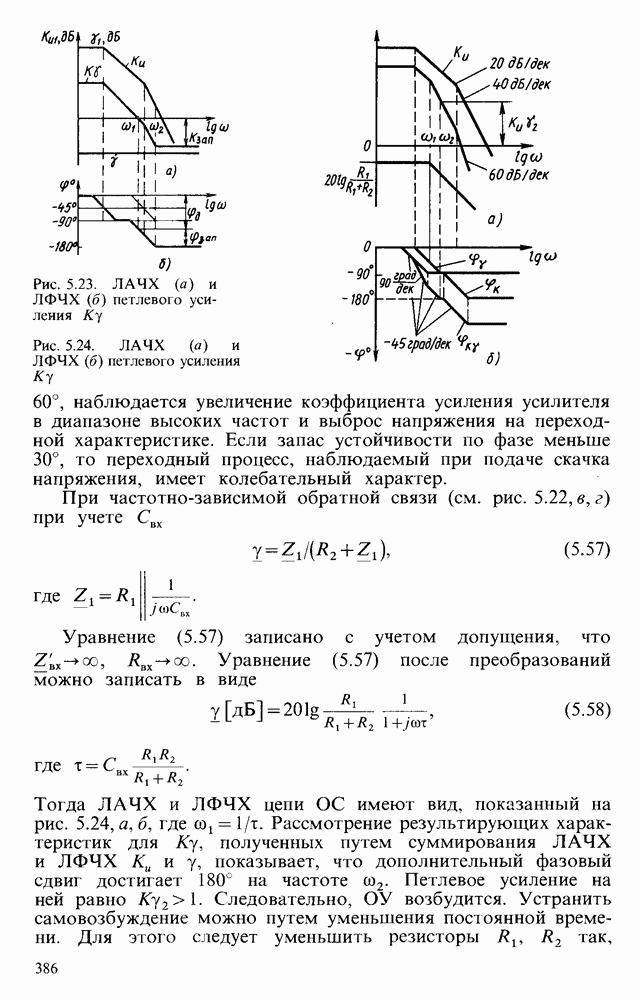
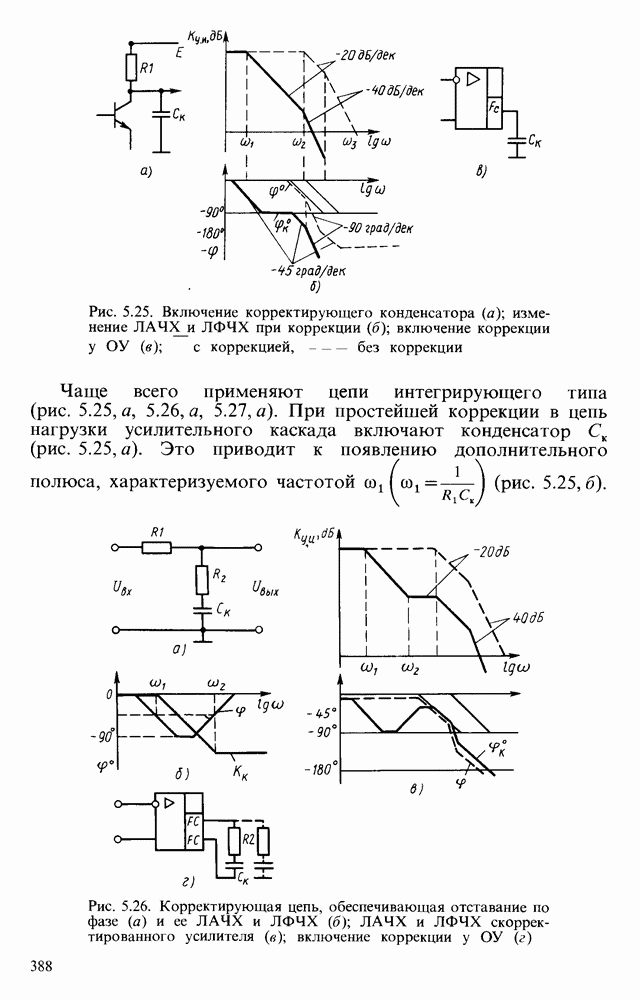
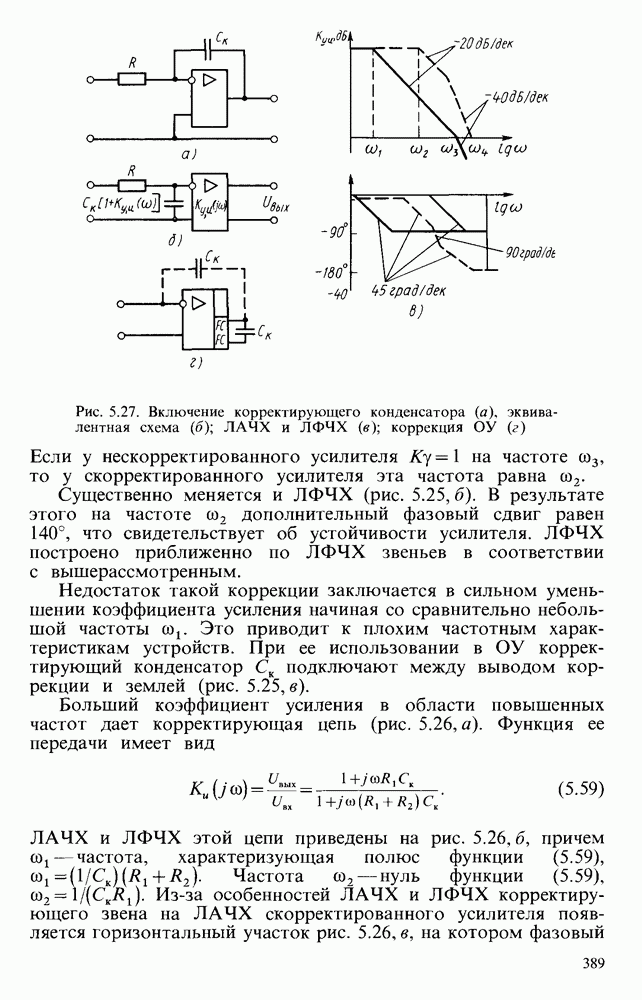
- § 5.7. УСТОЙЧИВОСТЬ УСИЛИТЕЛЕЙ И КОРРЕКЦИЯ ИХ ХАРАКТЕРИСТИК
- ГЛАВА 6. АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- § 6.1. МАСШТАБНЫЕ УСИЛИТЕЛИ
- 6.2. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 6.3. ИНТЕГРИРУЮЩИЕ УСТРОЙСТВА
- Интеграторы на основе операционных усилителей.
- § 6.4. ДИФФЕРЕНЦИРУЮЩИЕ УСТРОЙСТВА
- Активные дифференцирующие устройства.
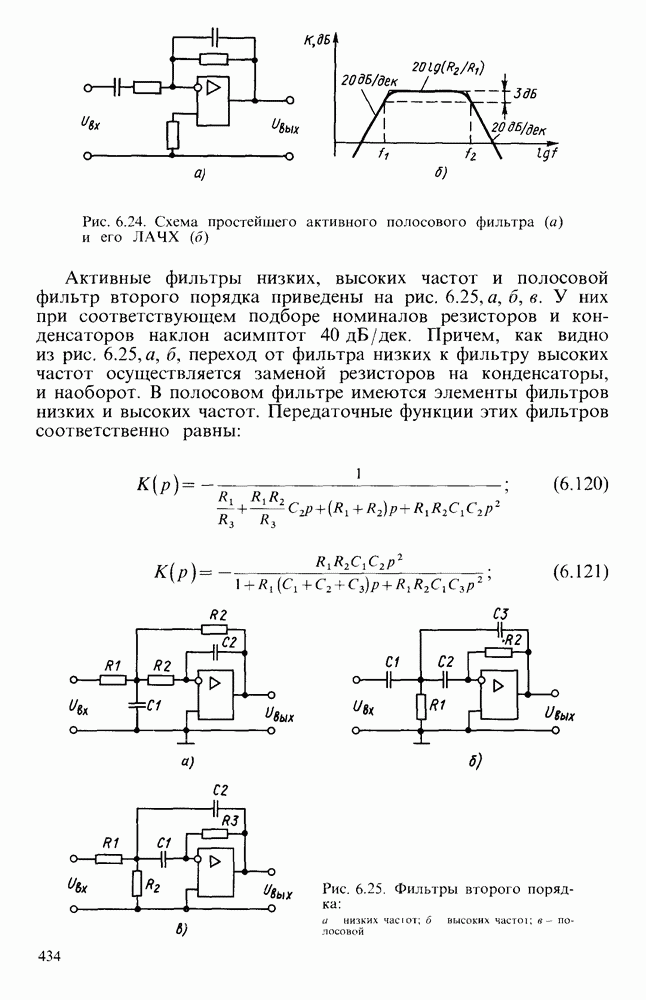
- § 6.5. АКТИВНЫЕ ФИЛЬТРЫ
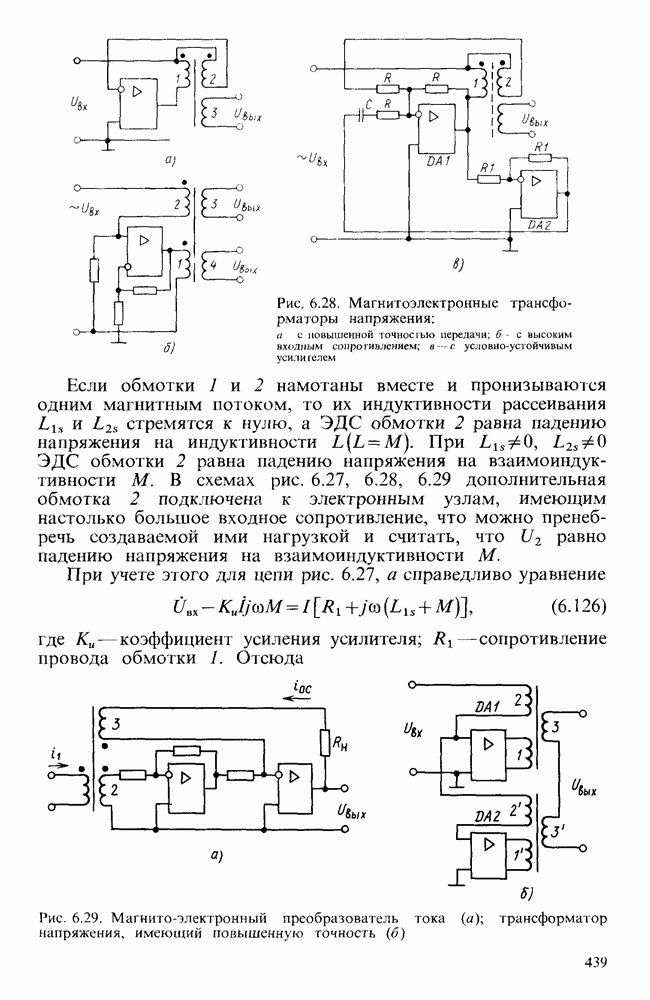
- § 6.6. МАГНИТОЭЛЕКТРОННЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
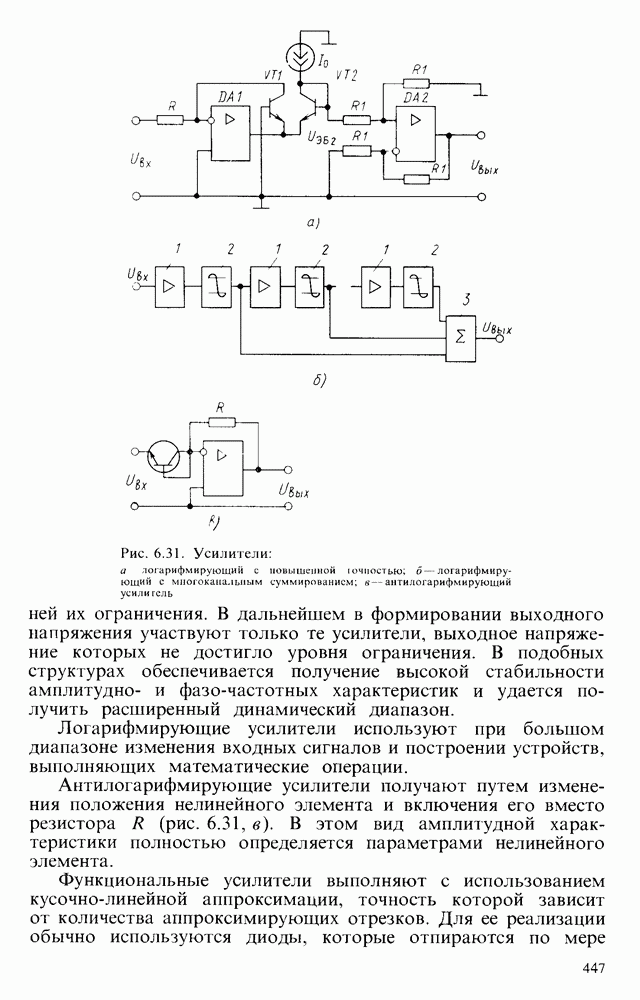
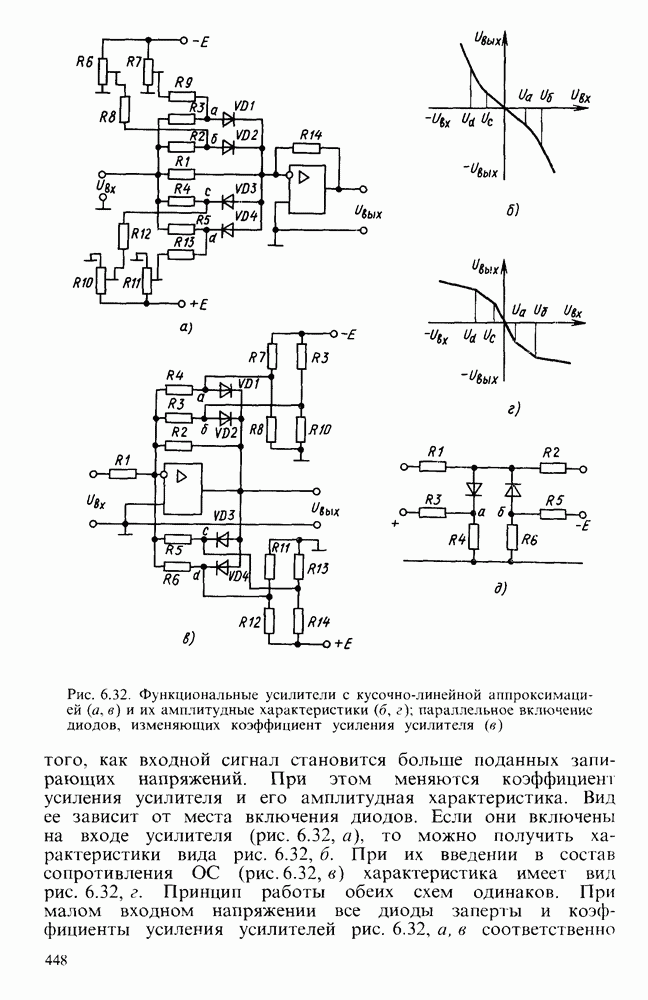
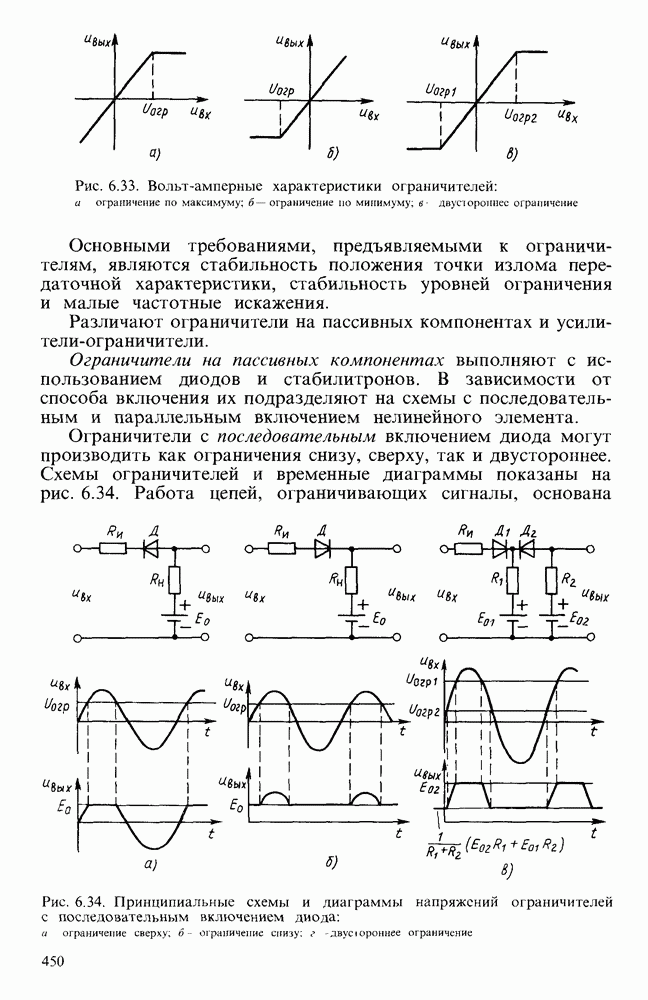
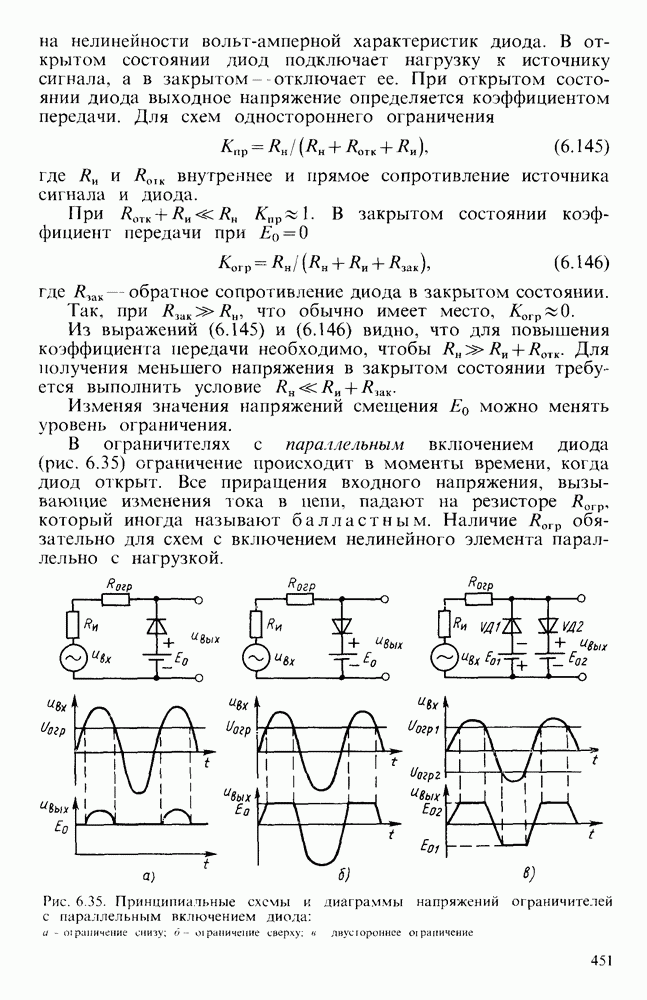
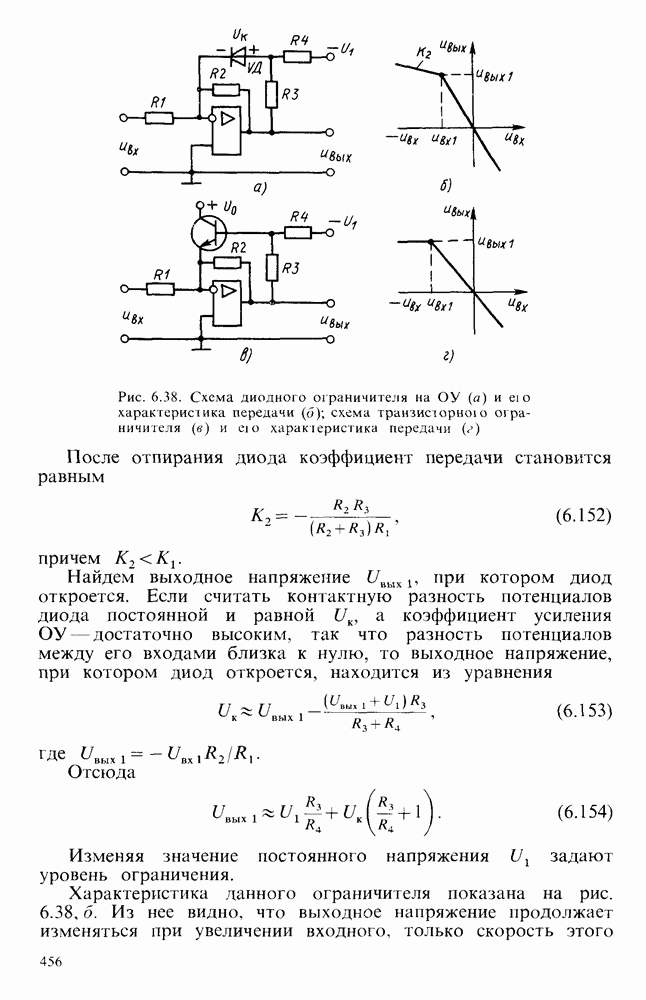
- § 6.7. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
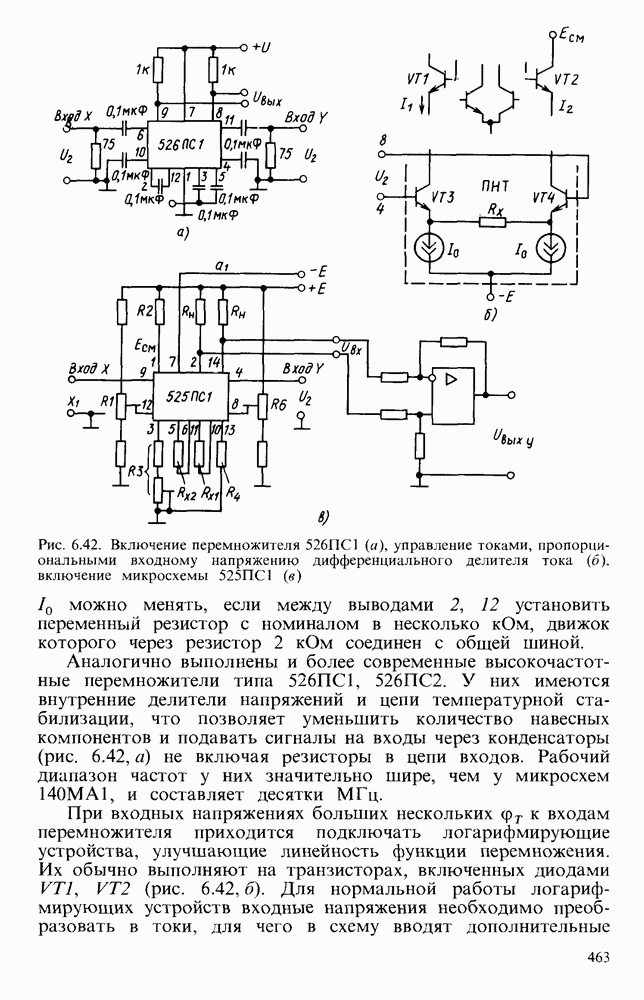
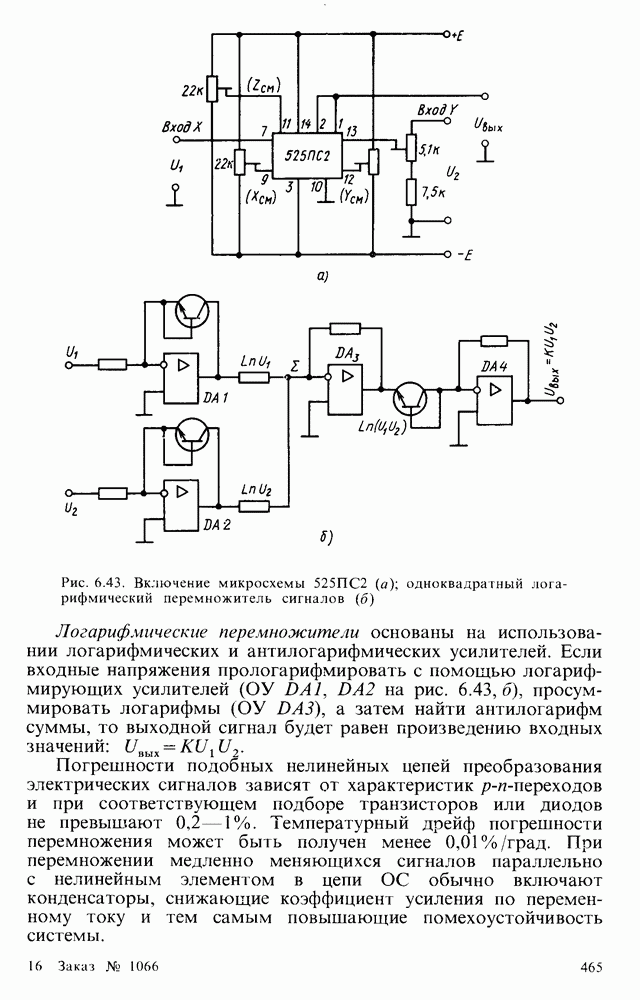
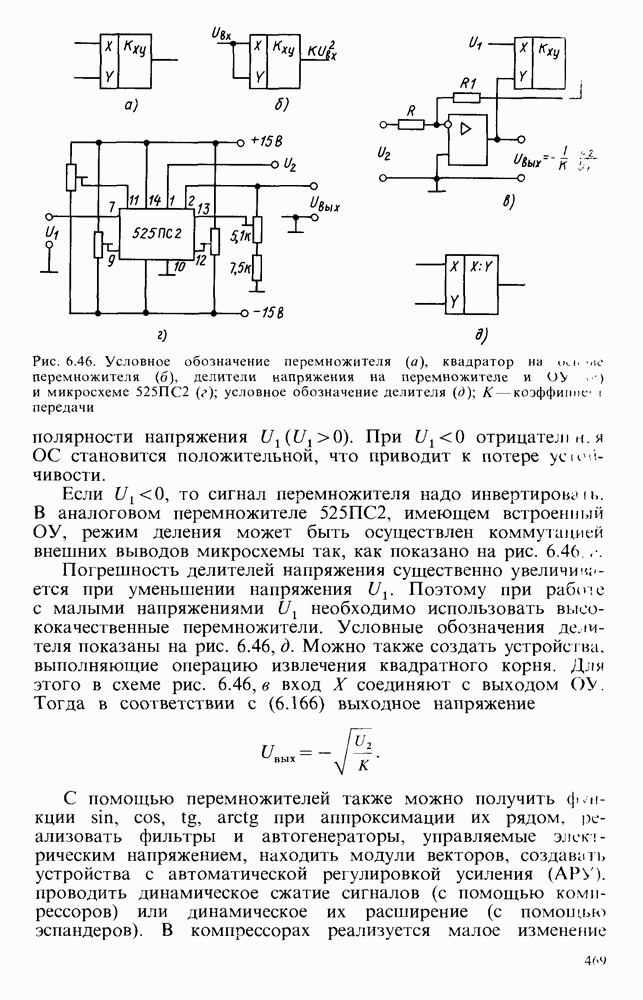
- § 6.8. ПЕРЕМНОЖИТЕЛИ СИГНАЛОВ И УСТРОЙСТВА, ВЫПОЛНЯЮЩИЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ
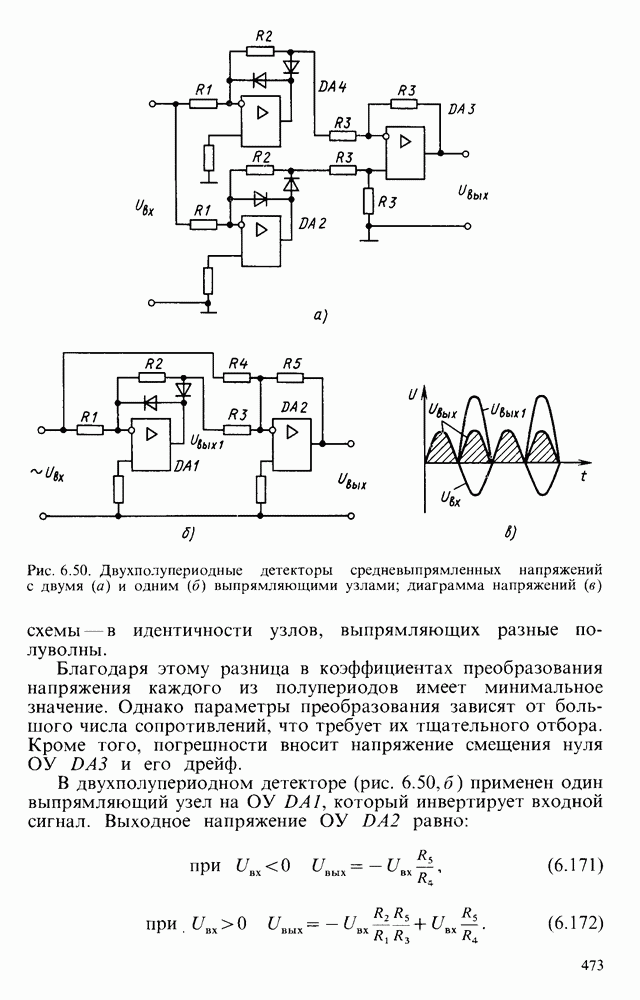
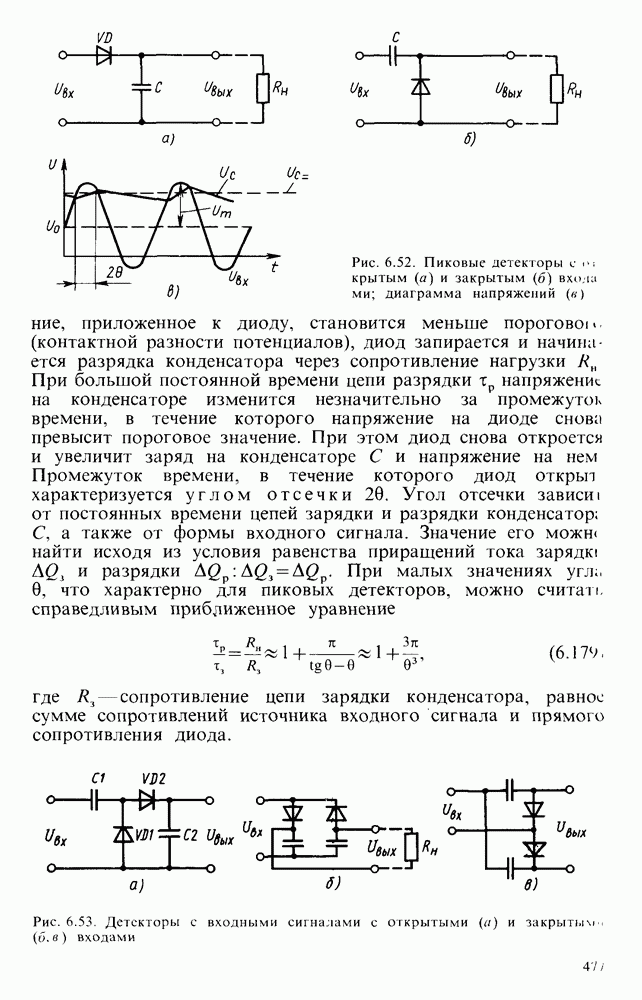
- § 6.9. ДЕТЕКТОРЫ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- ГЛАВА 7. ЭЛЕКТРОННЫЕ КЛЮЧИ
- § 7.1. ОБЩИЕ СВЕДЕНИЯ ОБ ИМПУЛЬСНЫХ ПРОЦЕССАХ И УСТРОЙСТВАХ
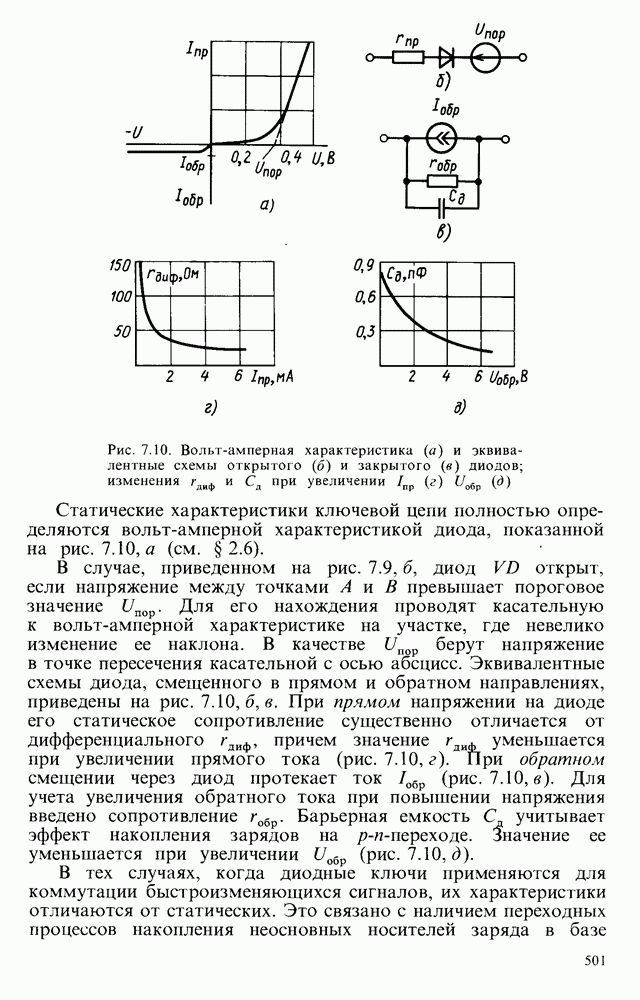
- § 7.2. ДИОДНЫЕ КЛЮЧИ
- § 7.3. КЛЮЧИ НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ
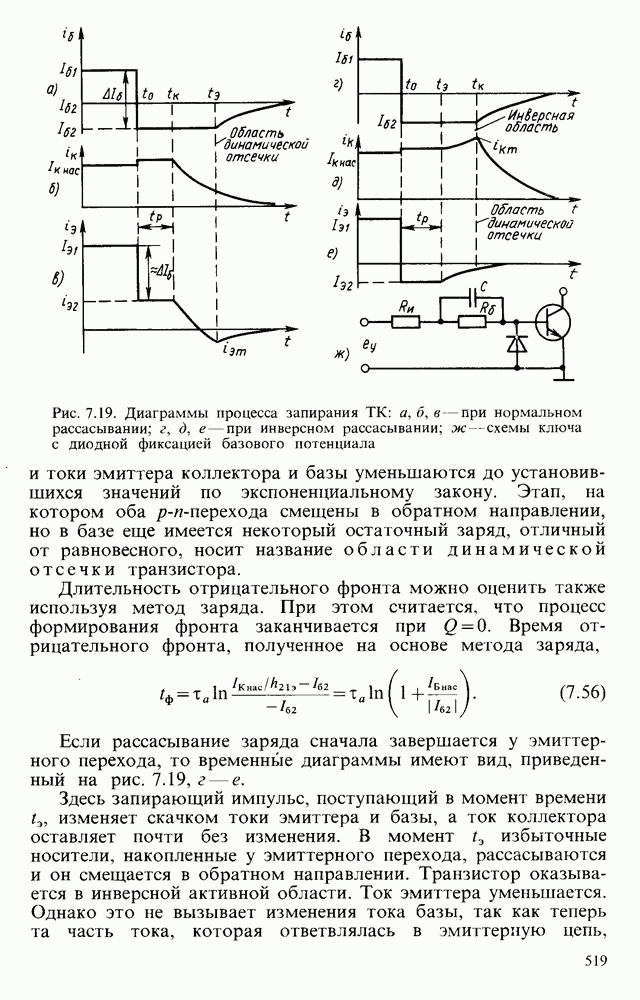
- § 7.4. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В КЛЮЧЕВЫХ ЦЕПЯХ С БИПОЛЯРНЫМИ ТРАНЗИСТОРАМИ
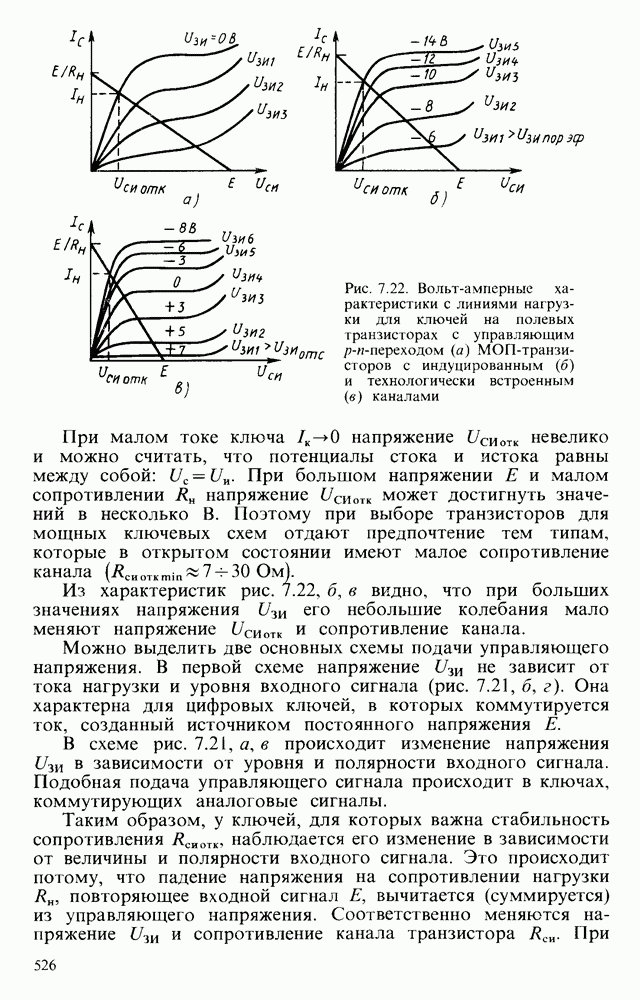
- 7.5. КЛЮЧИ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- § 7.6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В КЛЮЧАХ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- ГЛАВА 8. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ, ТРИГГЕРЫ, АВТОГЕНЕРАТОРЫ
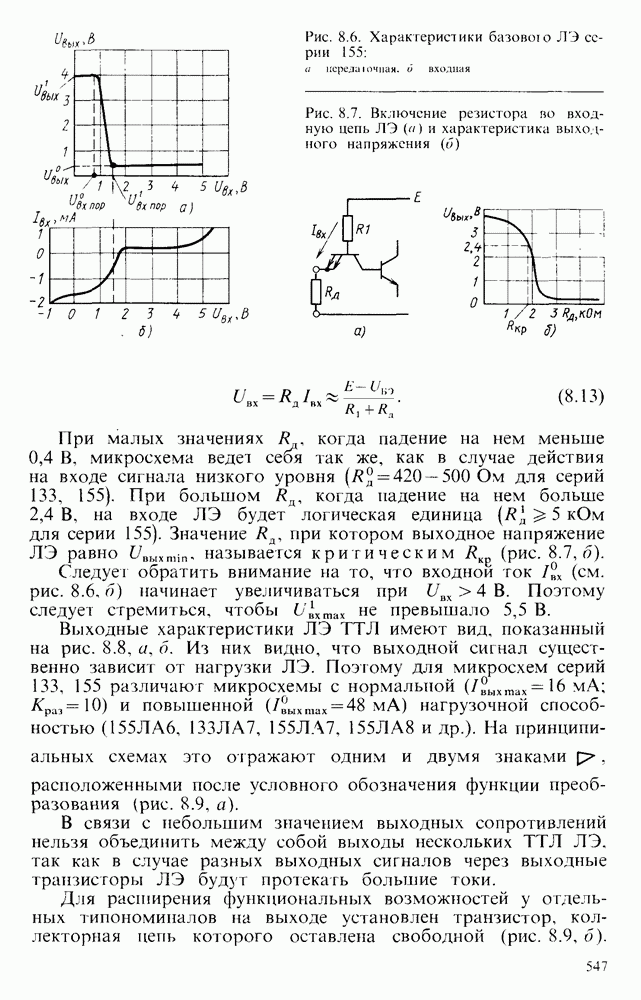
- § 8.1. ОБЩИЕ СВЕДЕНИЯ О ЛОГИЧЕСКИХ ЭЛЕМЕНТАХ
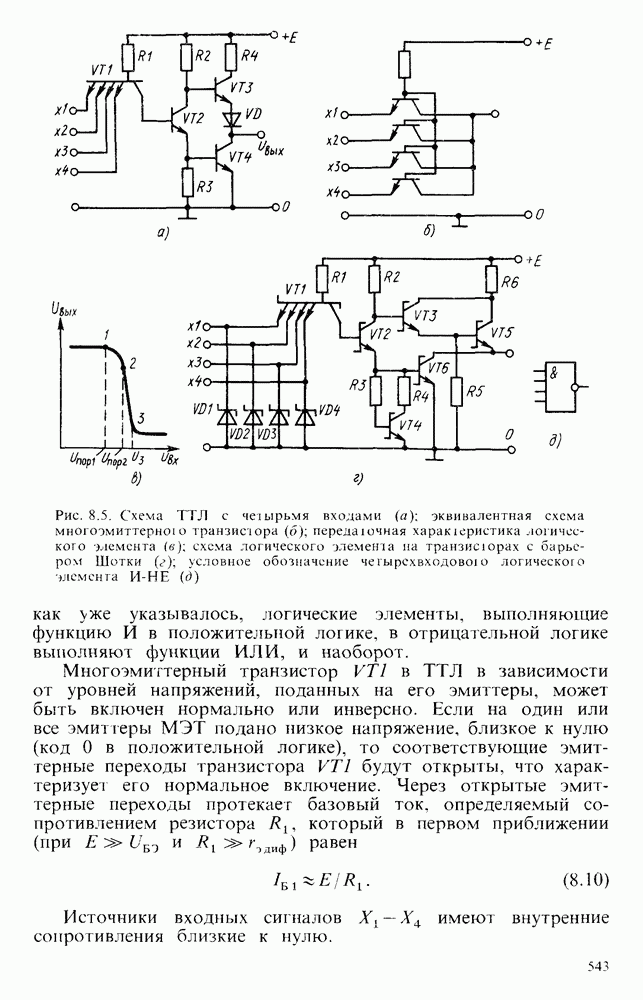
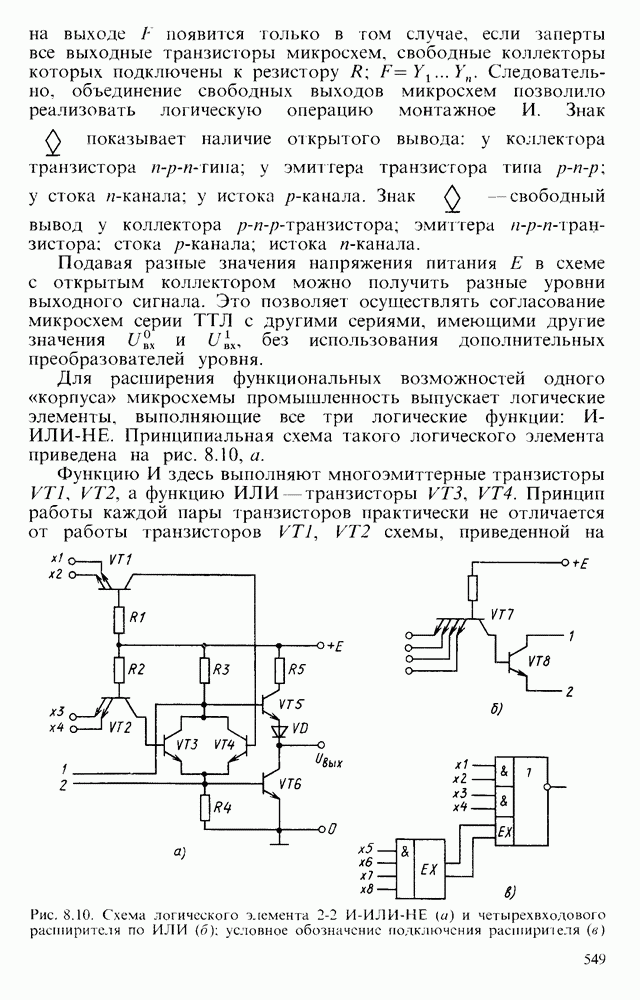
- § 8.2. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
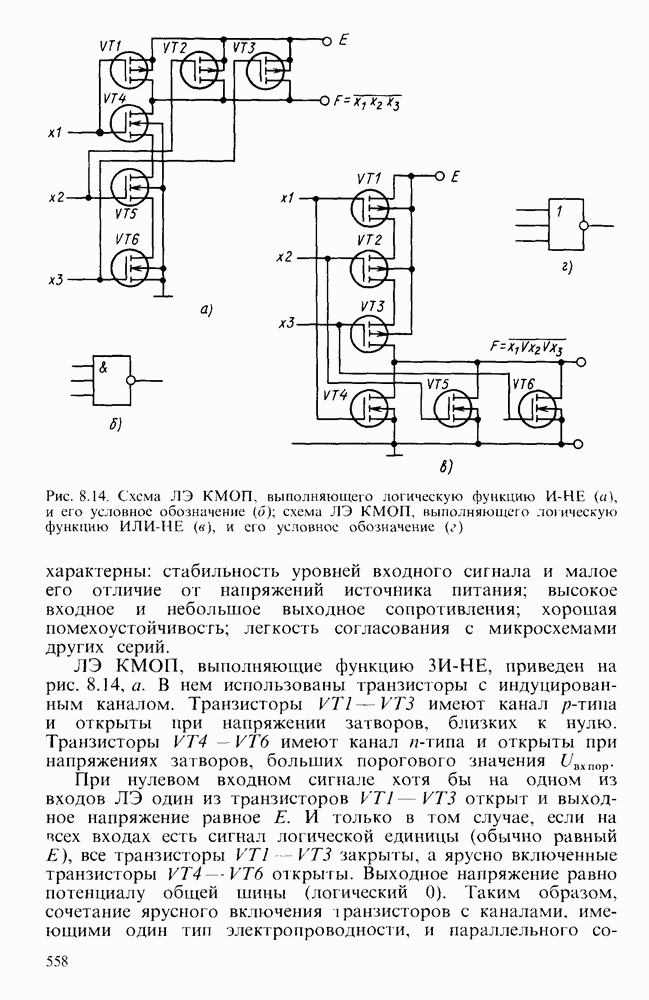
- 8.3. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МОП-ТРАНЗИСТОРАХ
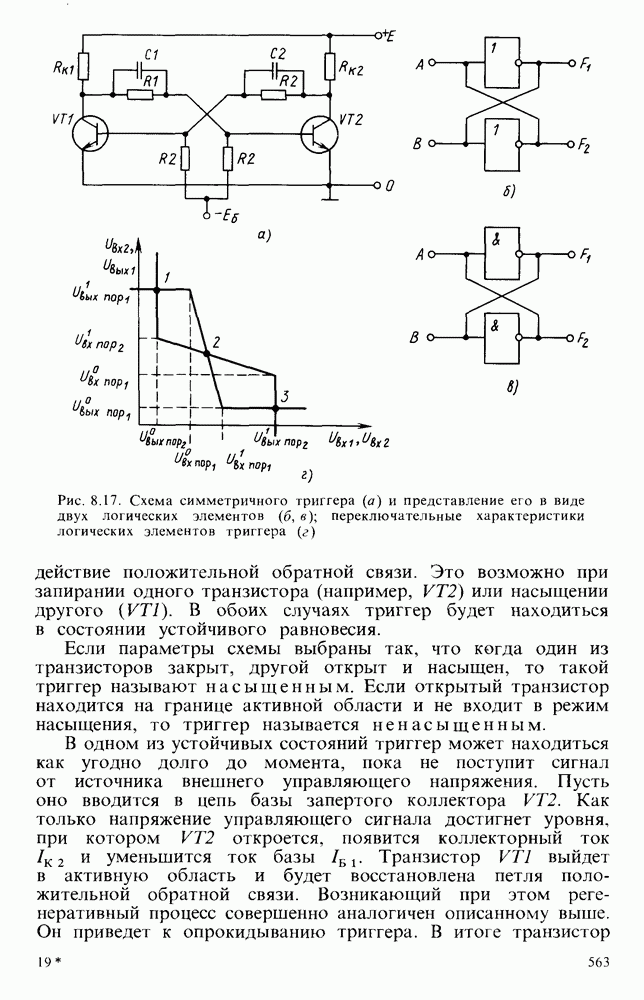
- § 8.4. ТРИГГЕРЫ
- § 8.5. НЕСИММЕТРИЧНЫЕ ТРИГГЕРЫ
- § 8.6. ГЕНЕРАТОРЫ КОЛЕБАНИЙ
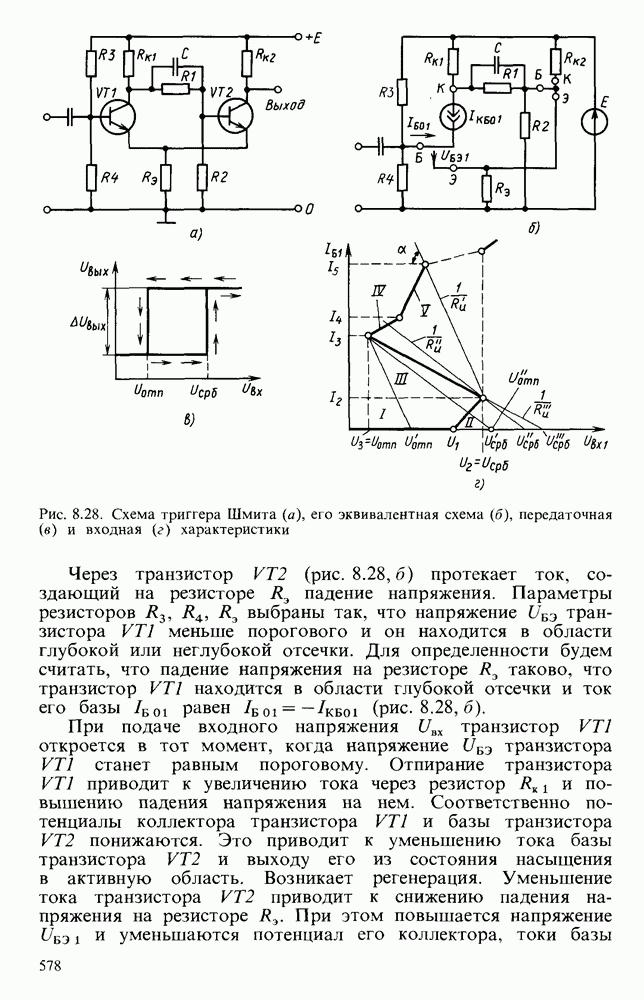
- Генераторы напряжения прямоугольной формы.
- Генераторы линейно изменяющегося напряжения (ГЛИН).
- Генераторы напряжения треугольной формы.
- Генераторы синусоидальных колебаний.
- Генераторы LC-типа.
- Генераторы с кварцевыми резонаторами и электромеханическими резонансными системами.
- ЗАКЛЮЧЕНИЕ
- Приложение
- Схемы включения операционных усилителей
- ЛИТЕРАТУРА