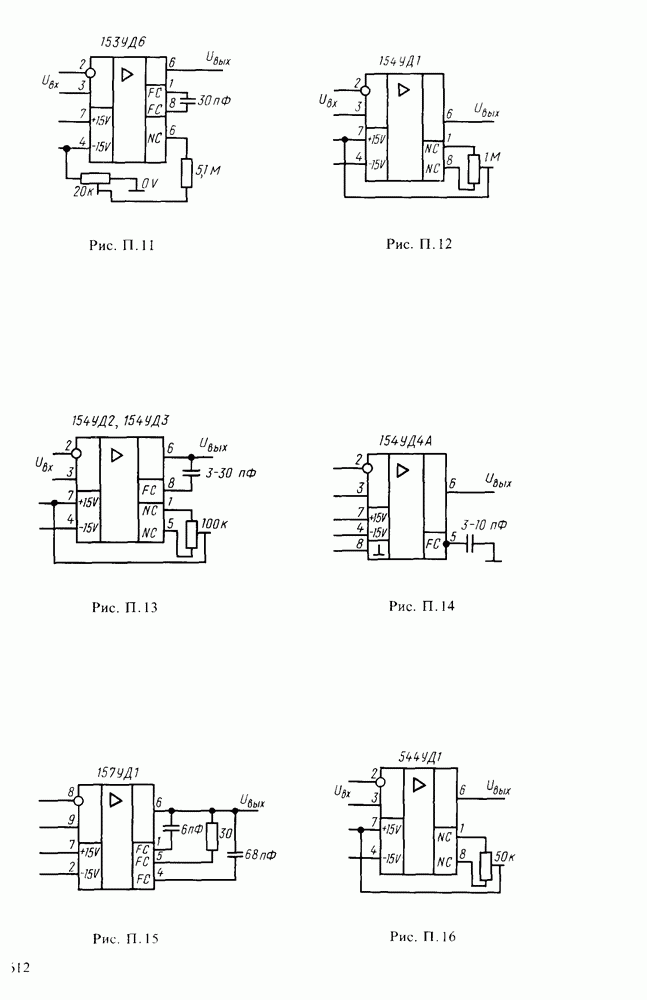
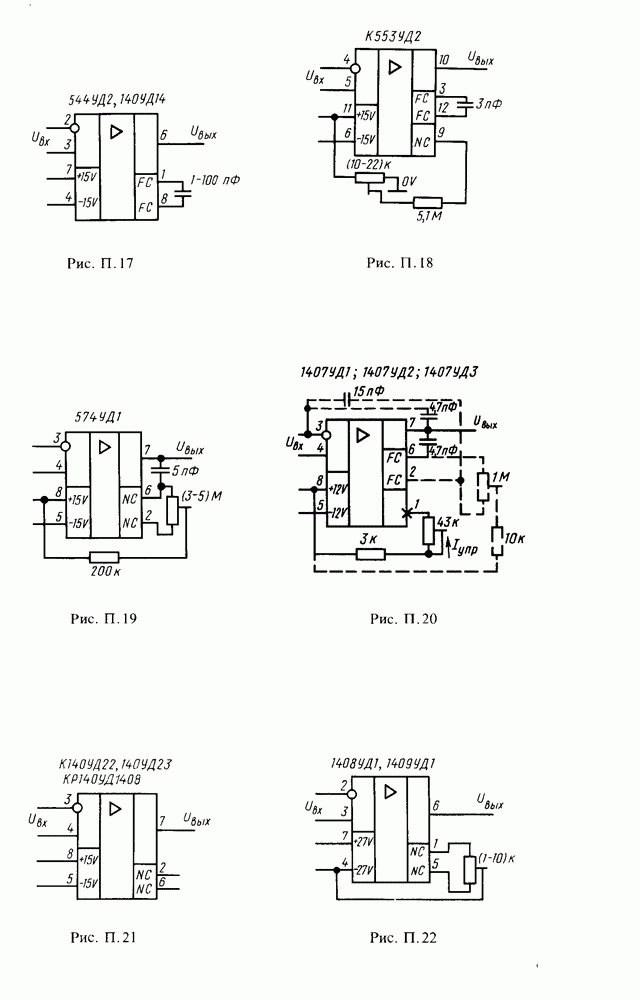
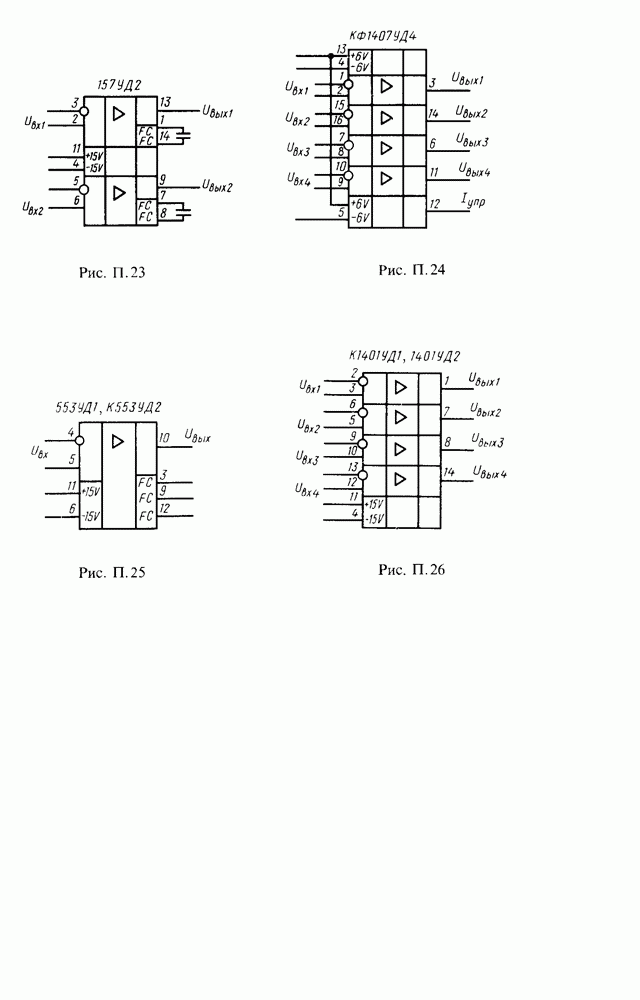
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 7. ЭЛЕКТРОННЫЕ КЛЮЧИ
§ 7.1. ОБЩИЕ СВЕДЕНИЯ ОБ ИМПУЛЬСНЫХ ПРОЦЕССАХ И УСТРОЙСТВАХ
Импульсными называются устройства, предназначенные для генерирования, формирования, преобразования и неискаженной передачи импульсных сигналов (импульсов).
Электрическим импульсом называют напряжение или ток, отличающиеся от нуля или постоянного значения только в течение короткого промежутка времени, который меньше или сравним с длительностью установления процессов в электрической системе, в которой они действуют. В случае следующих друг за другом импульсов обычно предполагается, что интервал между ними существенно превышает длительность процессов установления. В противном случае этот сигнал называют несинусоидальным напряжением или током. Такое определение не отличается строгостью, ибо переходные процессы протекают, как известно, бесконечно долго.

Рис. 7.1. Видеоимпульс (а) и радиоимпульс (б)
Однако оно позволяет отличать импульсы в общепринятом смысле от напряжения сложной формы.
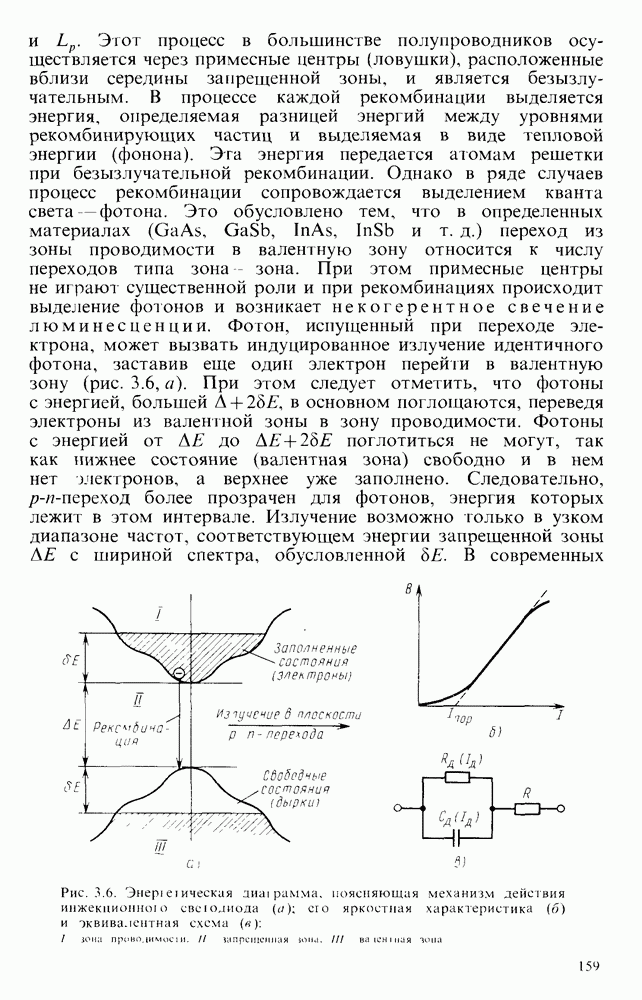
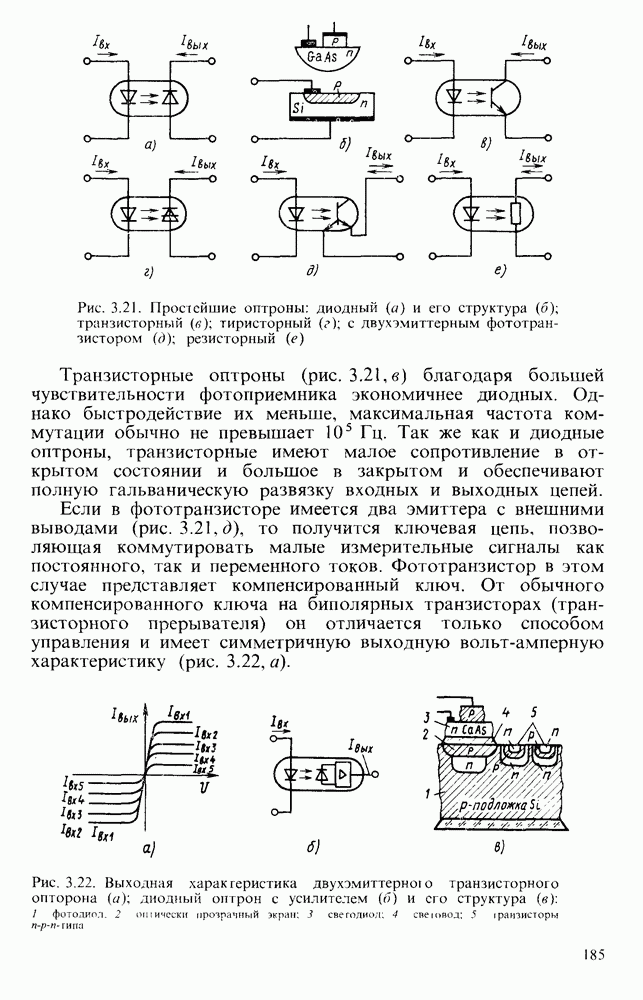
Все многообразие электрических импульсов принято подразделять на видеоимпульсы (рис. 7.1, а) и радиоимпульсы (рис.  ). Связь между этими двумя типами импульсов состоит в том, что огибающая радиоимпульса представляют собой видеоимпульс. Частота синусоиды, которой заполнен видеоимпульс, называется частотой заполнения. Обычно рассматривают только видеоимпульсы и их преобразования, так как радиоимпульсы, с помощью которых ведут передачу информации в радиотехнических трактах, после детектирования становятся видеоимпульсами. Поэтому в дальнейшем рассматриваются только видеоимпульсы, которые названы просто импульсами.
). Связь между этими двумя типами импульсов состоит в том, что огибающая радиоимпульса представляют собой видеоимпульс. Частота синусоиды, которой заполнен видеоимпульс, называется частотой заполнения. Обычно рассматривают только видеоимпульсы и их преобразования, так как радиоимпульсы, с помощью которых ведут передачу информации в радиотехнических трактах, после детектирования становятся видеоимпульсами. Поэтому в дальнейшем рассматриваются только видеоимпульсы, которые названы просто импульсами.
Формы импульсов, используемых в импульсных устройствах различного назначения, разнообразны. Наиболее распространенные из них приведены на рис.  .
.
Принято различать следующие участки импульса: фронт  , вершина (ВС), срез (CD), основание
, вершина (ВС), срез (CD), основание  .
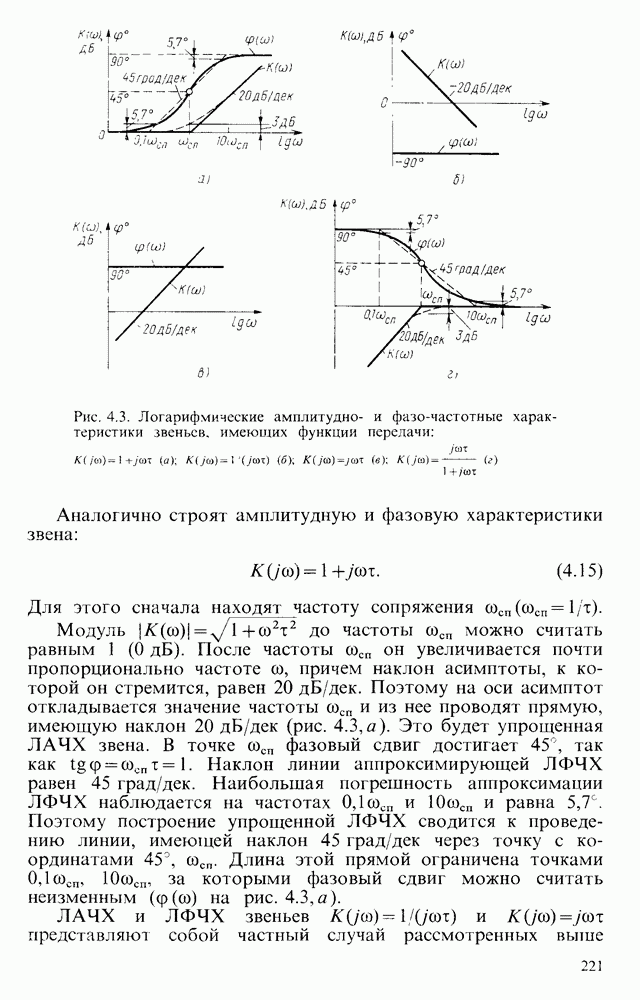
.
Фронт соответствует быстрому возрастанию сигнала; вершина — медленному его изменению; срез  быстрому убыванию сигнала. Иногда срез называют задним фронтом в отличие от переднего фронта.
быстрому убыванию сигнала. Иногда срез называют задним фронтом в отличие от переднего фронта.
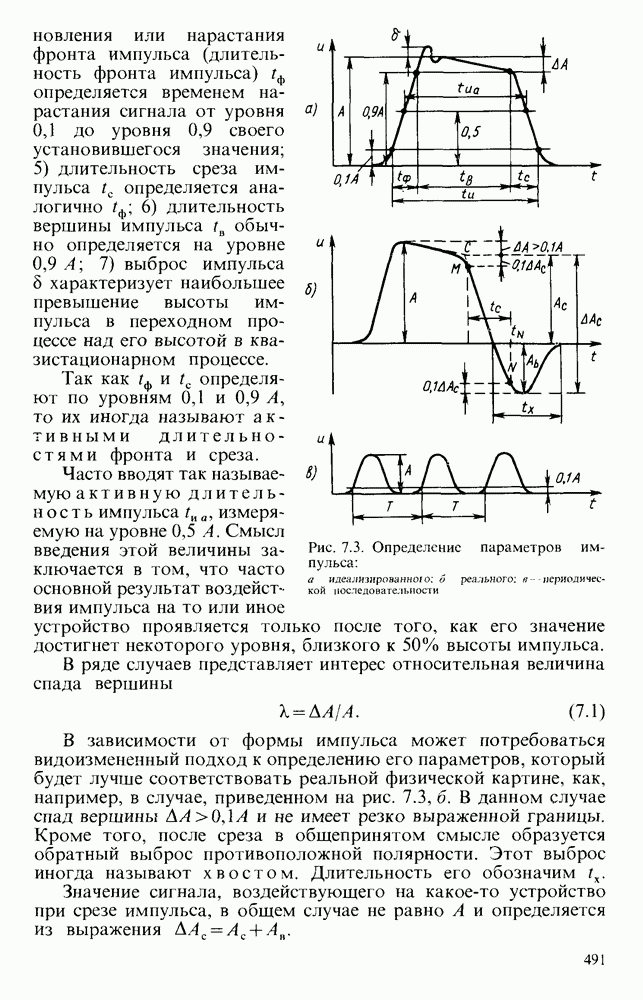
Основными параметрами импульса являются следующие (рис. 7.3, а, б, в): 1) высота импульса — А; 2) спад вершины импульса А А находится как разность высоты импульса в момент окончания переходного процесса и в момент окончания вершины импульса; 3) длительность импульса  определяют на уровне 0,1 А; 4) время установления или нарастания фронта импульса (длительность фронта импульса)
определяют на уровне 0,1 А; 4) время установления или нарастания фронта импульса (длительность фронта импульса)  определяется временем нарастания сигнала от уровня 0,1 до уровня 0,9 своего установившегося значения;
определяется временем нарастания сигнала от уровня 0,1 до уровня 0,9 своего установившегося значения;

Рис. 7.2. Идеализированные импульсы: а прямоугольный; б трапецеидальный; в - треугольный: г - с экспоненциальным фронтом и срезом; д - колоколообразпый; е - с экспоненциальным фронтом и срезом
5) длительность среза импульса  определяется аналогично
определяется аналогично  длительность вершины импульса
длительность вершины импульса  обычно определяется на уровне 0,9 А; 7) выброс импульса 8 характеризует наибольшее превышение высоты импульса в переходном процессе над его высотой в квазистационарном процессе.
обычно определяется на уровне 0,9 А; 7) выброс импульса 8 характеризует наибольшее превышение высоты импульса в переходном процессе над его высотой в квазистационарном процессе.
Так как  определяют по уровням 0,1 и 0,9 А, то их иногда называют активными длительностями фронта и среза.
определяют по уровням 0,1 и 0,9 А, то их иногда называют активными длительностями фронта и среза.
Часто вводят так называемую активную длительность импульса  а, измеряемую на уровне 0,5 А. Смысл введения этой величины заключается в том, что часто основной результат воздействия импульса на то или иное устройство проявляется только после того, как его значение достигнет некоторого уровня, близкого к 50% высоты импульса.
а, измеряемую на уровне 0,5 А. Смысл введения этой величины заключается в том, что часто основной результат воздействия импульса на то или иное устройство проявляется только после того, как его значение достигнет некоторого уровня, близкого к 50% высоты импульса.
В ряде случаев представляет интерес относительная величина спада вершины

В зависимости от формы импульса может потребоваться видоизмененный подход к определению его параметров, который будет лучше соответствовать реальной физической картине, как, например, в случае, приведенном на рис. 7.3, б. В данном случае спад вершины  и не имеет резко выраженной границы. Кроме того, после среза в общепринятом смысле образуется обратный выброс противоположной полярности. Этот выброс иногда называют хвостом. Длительность его обозначим
и не имеет резко выраженной границы. Кроме того, после среза в общепринятом смысле образуется обратный выброс противоположной полярности. Этот выброс иногда называют хвостом. Длительность его обозначим  .
.
Значение сигнала, воздействующего на какое-то устройство при срезе импульса, в общем случае не равно А и определяется из выражения  .
.

Рис. 7.3. Определение параметров импульса: а - идеализированного; б - реального; в - периодической последовательности
Для определения параметров импульса в случаях, аналогичных показанному на рис. 7.3, б, следует провести касательные к вершине импульса и его срезу, на пересечении касательных найти точку С и вычислить  , затем найти точки М и N, определяемые при
, затем найти точки М и N, определяемые при  , расстояние между которыми будет характеризовать длительность (активную) среза
, расстояние между которыми будет характеризовать длительность (активную) среза  .
.
При наличии периодической последовательности импульсов (рис. 7.3, в) вводят параметры, характеризующие эту последовательность: период повторения импульсов Т; частоту повторения импульсов  скважность импульсов
скважность импульсов  коэффициент заполнения
коэффициент заполнения  .
.
Частоту повторения выражают в герцах, а скважность и коэффициент заполнения — в относительных единицах.
Анализ импульсных процессов представляет собой довольно сложную задачу, особенно при наличии существенных нелинейностей у цепи, преобразующей импульсы. Поэтому чаще всего эту цепь стремятся свести к линейной. Исследование ее проводят следующими методами: «классическим» методом анализа переходных процессов, который заключается в составлении дифференциальных уравнений, характеризующих процессы в цепи, с последующим их решением; спектральным (частотным); методом суперпозиции (с использованием интеграла Дюамеля); операторным.
Если импульсная цепь по условиям ее работы не может быть линеаризована, то анализ ее сводится к решению нелинейных дифференциальных уравнений, причем вид решения зависит от характера нелинейности цепи.
Во многих практически важных случаях нарастание и срез импульса происходят по экспоненциальному закону или закону, который может быть аппроксимирован экспонентой. В этом случае анализ импульсных цепей существенно упрощается, так как мгновенные значения импульса во время его нарастания и среза описываются уравнениями

где  — постоянная времени экспоненты.
— постоянная времени экспоненты.
Зная мгновенное значение импульса, можно найти время t, в течение которого импульс достиг этого значения:

Так как активную длительность фронта (время установления) и среза определяем как промежуток времени между значениями, равными 0,1 и  , то
, то

Если длительности  определять по уровням 0,1 А и А, то аналогично (7.4) можно получить
определять по уровням 0,1 А и А, то аналогично (7.4) можно получить

Любую периодическую последовательность импульсов произвольной формы можно представить в виде ряда Фурье, т. е. в виде суммы гармонических колебаний, имеющих разные амплитуды и частоты, кратные частоте повторения и импульсов  :
:

где  — фазы отдельных гармоник.
— фазы отдельных гармоник.
Спектр периодической последовательности импульсов является линейчатым, так как отдельные составляющие его отстоят друг от друга на расстоянии, равном частоте следования импульсов (рис. 7.4, а)  . Амплитуды гармоник зависят как от длительности импульсов, так и от частоты их повторения.
. Амплитуды гармоник зависят как от длительности импульсов, так и от частоты их повторения.
Амплитуды гармоник, имеющих частоты  , где
, где  — целое число, равны нулю. С уменьшением длительности импульса
— целое число, равны нулю. С уменьшением длительности импульса  частоты, при которых амплитуды гармоник становятся равными нулю, смещаются в сторону больших частот. При этом число гармоник, имеющих амплитуду, большую какого-либо наперед заданного значения, существенно увеличивается и спектр импульса расширяется. Следовательно, уменьшение длительности импульса приводит к расширению его спектра, а увеличение длительности — к его сужению. При
частоты, при которых амплитуды гармоник становятся равными нулю, смещаются в сторону больших частот. При этом число гармоник, имеющих амплитуду, большую какого-либо наперед заданного значения, существенно увеличивается и спектр импульса расширяется. Следовательно, уменьшение длительности импульса приводит к расширению его спектра, а увеличение длительности — к его сужению. При  спектр импульса стремится к бесконечности.
спектр импульса стремится к бесконечности.
При увеличении частоты следования импульсов амплитуды гармоник увеличиваются. Огибающая спектра сохраняет свою форму, а расстояние между спектральными линиями возрастает. В итоге в том же диапазоне частот оказывается меньшее число линий спектра, что говорит об обеднении его гармониками.
Если частота следования импульсов уменьшается, то уменьшаются амплитуды гармоник и расстояние между линиями спектра (рис. 7.4, б). Уменьшение частоты следования импульсов обогащает спектр гармониками. В пределе, когда частота следования импульсов мала  расстояние между линиями спектра стремится к нулю и спектр из линейчатого превращается в сплошной (непрерывный).
расстояние между линиями спектра стремится к нулю и спектр из линейчатого превращается в сплошной (непрерывный).

Рис. 7.4. Линейчатый спектр периодических импульсов прямоугольной формы (а) и сплошной спектр единичного импульса (б)
Амплитуды гармоник также стремятся к нулю.
Энергия импульса равна сумме энергий всех его гармоник, причем основная часть энергии видеоимпульсов лежит в низкочастотной части спектра и только сравнительно малая — в высокочастотной. Так, для прямоугольных импульсов 95% всей энергии импульса сосредоточена в полосе частот  .
.
В связи с тем что обычно важно знать поведение системы в том диапазоне частот, в котором передается основная часть энергии, вводят понятие активной ширины спектра, под которой понимают диапазон частот от  до некоторой граничной частоты
до некоторой граничной частоты  в котором сосредоточено 95% полной энергии импульса. Использование активной ширины спектра позволяет ограничить полосу пропускания устройств, на которые воздействуют импульсы, имеющие достаточно широкий спектр, и выбирать ее равной или несколько большей активной ширины спектра.
в котором сосредоточено 95% полной энергии импульса. Использование активной ширины спектра позволяет ограничить полосу пропускания устройств, на которые воздействуют импульсы, имеющие достаточно широкий спектр, и выбирать ее равной или несколько большей активной ширины спектра.
Так как прямоугольный импульс имеет один из наиболее широких спектров, активная ширина которого лежит в пределах от 0 до  , то для импульсов с более узким спектром, не анализируя детально их спектральный состав, можно задавать верхнюю частоту полосы пропускания в пределах
, то для импульсов с более узким спектром, не анализируя детально их спектральный состав, можно задавать верхнюю частоту полосы пропускания в пределах

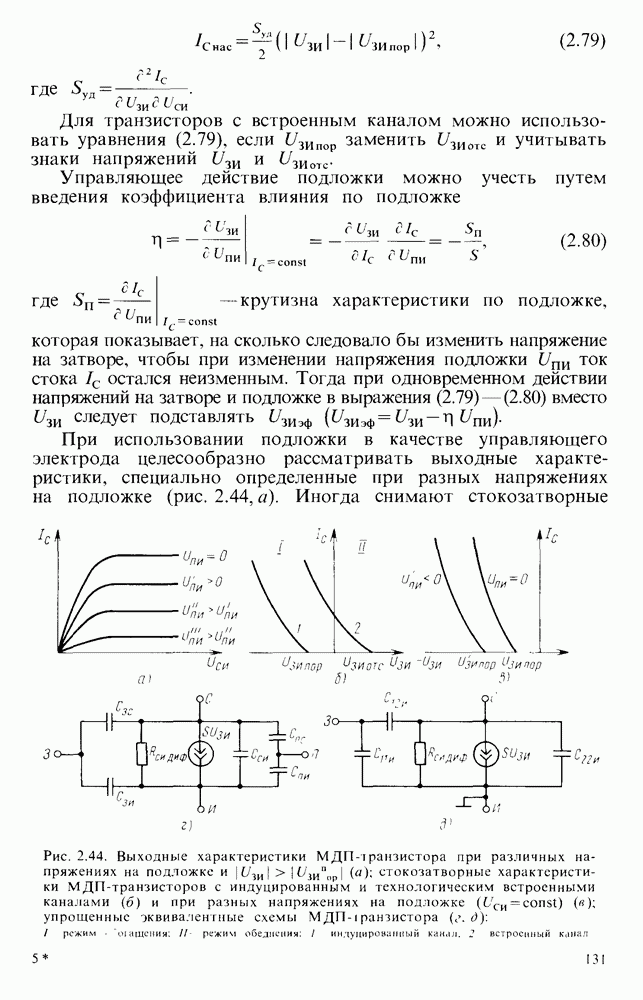
Для импульсов, у которых  , при ориентированном определении
, при ориентированном определении  часто используют уравнение
часто используют уравнение

где.
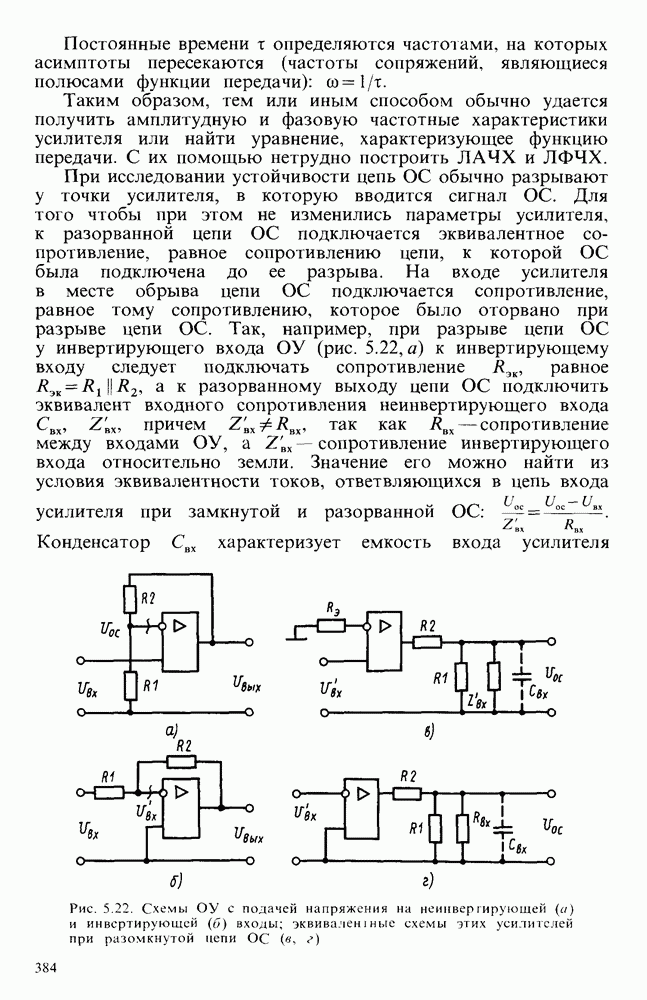
Одну и ту же цепь, используемую для преобразования импульсных сигналов, можно исследовать различными методами. Наиболее часто получают или переходную характеристику, показывающую, как изменяется выходной сигнал при изменении скачком входного, или частотную характеристику цепи. Так как разными методами исследуют одни и те же цепи, то эти характеристики однозначно связаны между собой. В общем случае эту связь находят путем решения интегрального уравнения, причем она оказывается достаточно сложной.
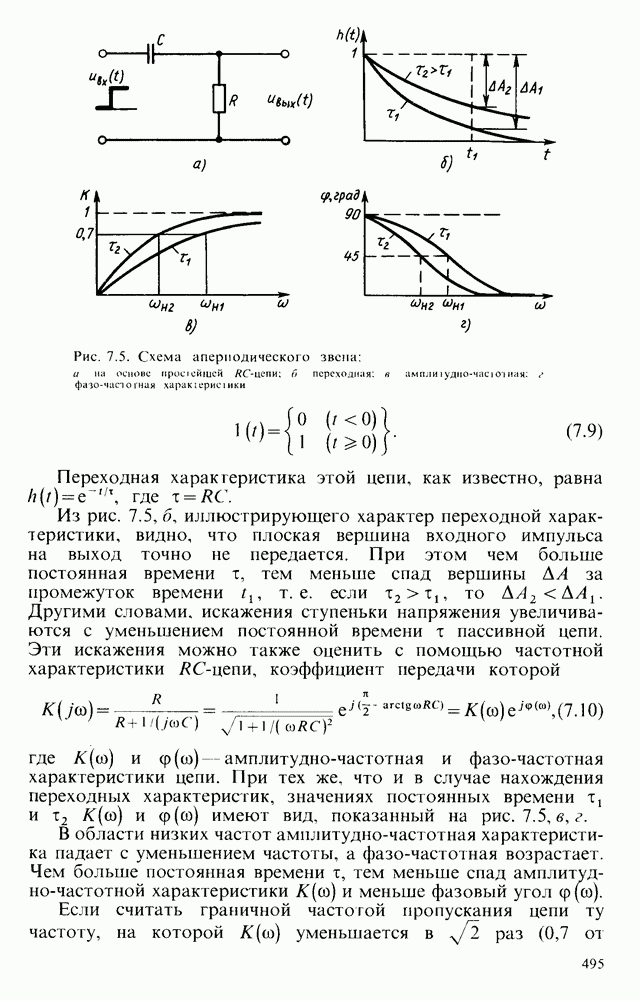
Поэтому рассмотрим взаимосвязь между переходной и частотной характеристиками на примере простейшего апериодического звена. У звена этого типа переходная характеристика определяется постоянной времени  , а частотная — граничными частотами пропускания, определяемыми на уровне 0,7 (3 дБ) от установившегося значения.
, а частотная — граничными частотами пропускания, определяемыми на уровне 0,7 (3 дБ) от установившегося значения.
Проследим прохождение импульсного сигнала через простейшую линейную  -цепь (рис. 7.5, а). Пусть на ее вход подана единичная ступенька напряжения
-цепь (рис. 7.5, а). Пусть на ее вход подана единичная ступенька напряжения

Рис. 7.5. Схема апериодического звена: а - на основе простейшей  -цепи; б - переходная: в - амплитудно-частотная: г - фазочастотная характеристики
-цепи; б - переходная: в - амплитудно-частотная: г - фазочастотная характеристики

Переходная характеристика этой цегш, как известно, равна  , где
, где  .
.
Из рис. 7.5, б, иллюстрирующего характер переходной характеристики, видно, что плоская вершина входного импульса на выход точно не передается. При этом чем больше постоянная времени  , тем меньше спад вершины
, тем меньше спад вершины  за промежуток времени
за промежуток времени  , т. е. если
, т. е. если  то
то  . Другими словами, искажения ступеньки напряжения увеличиваются с уменьшением постоянной времени
. Другими словами, искажения ступеньки напряжения увеличиваются с уменьшением постоянной времени  пассивной цепи. Эти искажения можно также оценить с помощью частотной характеристики RС-цепи, коэффициент передачи которой
пассивной цепи. Эти искажения можно также оценить с помощью частотной характеристики RС-цепи, коэффициент передачи которой

где  — амплитудно-частотная и фазо-частотная характеристики цепи. При тех же, что и в случае нахождения переходных характеристик, значениях постоянных времени
— амплитудно-частотная и фазо-частотная характеристики цепи. При тех же, что и в случае нахождения переходных характеристик, значениях постоянных времени  и
и  имеют вид, показанный на рис. 7.5, б, г.
имеют вид, показанный на рис. 7.5, б, г.
В области низких частот амплитудно-частотная характеристика падает с уменьшением частоты, а фазо-частотная возрастает. Чем больше постоянная времени  , тем меньше спад амплитудно-частотной характеристики
, тем меньше спад амплитудно-частотной характеристики  и меньше фазовый угол
и меньше фазовый угол  .
.
Если считать граничной частотой пропускания цепи ту частоту, на которой  уменьшается в
уменьшается в  раз (0,7 от первоначального значения), то эта граничная частота связана с постоянной времени цепи простым соотношением
раз (0,7 от первоначального значения), то эта граничная частота связана с постоянной времени цепи простым соотношением

Таким образом, частотные искажения в области низких частот характеризуются спадом вершины выходного импульса при подаче на вход импульсного сигнала прямоугольной формы: чем больше спад вершины импульса, чем выше нижняя граничная частота пропускания цепи, и наоборот.
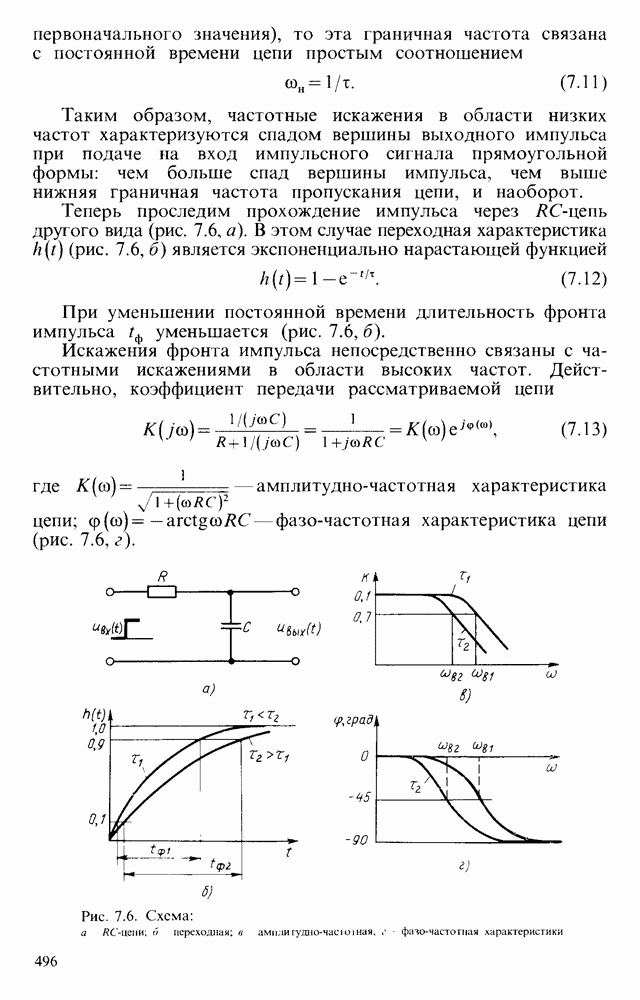
Теперь проследим прохождение импульса через  -цепь другого вида (рис. 7.6, а). В этом случае переходная характеристика
-цепь другого вида (рис. 7.6, а). В этом случае переходная характеристика  (рис. 7.6, б) является экспоненциально нарастающей функцией
(рис. 7.6, б) является экспоненциально нарастающей функцией

При уменьшении постоянной времени длительность фронта импульса  уменьшается (рис. 7.6, б).
уменьшается (рис. 7.6, б).
Искажения фронта импульса непосредственно связаны с частотными искажениями в области высоких частот. Действительно, коэффициент передачи рассматриваемой цепи

где  — амплитудно-частотная характеристика
— амплитудно-частотная характеристика  цепи;
цепи;  — фазо-частотная характеристика цепи (рис. 7.6, г).
— фазо-частотная характеристика цепи (рис. 7.6, г).

Рис. 7.6. Схема: а - RC-цепи; б - переходная; в - амплитудно-частотная, г - фазо-частотная характеристики

Рис. 7.7. Схемы апериодических  -цепей
-цепей
Если верхнюю граничную частоту определять как  , на которой
, на которой  уменьшается в 1,41 раза, то связь граничной частоты
уменьшается в 1,41 раза, то связь граничной частоты  с постоянной времени цепи имеет вид, аналогичный рассмотренному ранее:
с постоянной времени цепи имеет вид, аналогичный рассмотренному ранее:

Искажения фронта нарастания импульсного сигнала характеризуют частотные искажения в области высоких частот. Чем меньше  цепи, тем быстрее нарастает импульс выходного напряжения и тем больше верхняя граничная частота.
цепи, тем быстрее нарастает импульс выходного напряжения и тем больше верхняя граничная частота.
Таким же образом форму импульса искажают  -цепи, показанные на рис. 7.7, а, б. Постоянная времени
-цепи, показанные на рис. 7.7, а, б. Постоянная времени  .
.
Из сказанного ясно, почему в качестве граничных частот пропускания различных систем берут частоты, на которых  уменьшается в 1,41 раза (на 3 дБ), а не какие-либо другие значения.
уменьшается в 1,41 раза (на 3 дБ), а не какие-либо другие значения.
Следует отметить, что такая простая связь справедлива для простейших цепей первого порядка. В сложных цепях, где имеется несколько соизмеримых постоянных времени, связь между частотными и переходными характеристиками значительно сложнее.
При передаче импульсов через разделительные цепи с реактивными компонентами частот требуется получить минимальные искажения формы сигнала. Так, например, если между каскадами импульсного усилителя установлены RС-цепи (см. рис. 7.5, а) и они искажают импульс, то такой усилитель не выполняет своей основной функции.
При определении параметров разделительных цепей, предназначенных для неискаженной передачи сигналов, обычно ориентируются на отрицательный спад плоской вершины импульса прямоугольной формы X. Он равен

где  — длительность импульса
— длительность импульса  .
.
Постоянную времени разделительной цепи, передающей импульсы без искажений, определяют пользуясь формулой

Следует обратить внимание на потерю постоянной составляющей при передаче через разделительную RC-цепь последовательности импульсов. Пусть на вход цепи (рис. 7.5, а) поступают однополярные прямоугольные импульсы длительностью  с периодом следования Т (рис. 7.8, а). При переходе первого импульса произойдет зарядка конденсатора С, а после его окончания — разрядка. При этом напряжение на конденсаторе изменится в соответствии с уравнениями (7.2). Если
с периодом следования Т (рис. 7.8, а). При переходе первого импульса произойдет зарядка конденсатора С, а после его окончания — разрядка. При этом напряжение на конденсаторе изменится в соответствии с уравнениями (7.2). Если  , то при приходе второго импульса напряжение на конденсаторе С отлично от нуля:
, то при приходе второго импульса напряжение на конденсаторе С отлично от нуля:  . Это напряжение вычитается из входного сигнала, а следовательно, перепад напряжения и ток зарядки конденсатора меньше, чем при первом импульсе. Ток разрядки после второго импульса окажется больше в связи с большим значением напряжения на конденсаторе. Процесс уменьшения тока зарядки и увеличения тока разрядки продолжается до тех пор, пока приращения заряда на обкладках конденсатора за время действия импульса и во время паузы не будут равны между собой. На этом процесс установления режима работы цепи (переходный процесс) заканчивается, что на диаграммах рис. 7.8, а, 6 характеризуется равенством площадей и
. Это напряжение вычитается из входного сигнала, а следовательно, перепад напряжения и ток зарядки конденсатора меньше, чем при первом импульсе. Ток разрядки после второго импульса окажется больше в связи с большим значением напряжения на конденсаторе. Процесс уменьшения тока зарядки и увеличения тока разрядки продолжается до тех пор, пока приращения заряда на обкладках конденсатора за время действия импульса и во время паузы не будут равны между собой. На этом процесс установления режима работы цепи (переходный процесс) заканчивается, что на диаграммах рис. 7.8, а, 6 характеризуется равенством площадей и  . То, что
. То, что  , свидетельствует об отсутствии в выходном сигнале постоянной составляющей и равенстве нулю среднего напряжения на сопротивлении R. Длительность переходного процесса оценивается как
, свидетельствует об отсутствии в выходном сигнале постоянной составляющей и равенстве нулю среднего напряжения на сопротивлении R. Длительность переходного процесса оценивается как  .
.
Аналогично рассмотренному, постоянная составляющая импульсов теряется при их передаче через трансформаторы. Для восстановления постоянной составляющей приходится вводить фиксаторы уровня, рассмотренные в § 6.7. Таким образом, при работе с импульсными сигналами приходится учитывать ряд факторов, не характерных для ранее рассмотренных аналоговых цепей.

Рис. 7.8. Диаграмма изменения напряжений в разделительной RС-цепи (а, б); диаграмма передачи через RС-цепи последовательности импульсов (в, г)
Устройства, в которых выполняются основные виды преобразований импульсных сигналов или используются эти сигналы, можно подразделить на несколько видов:
1) электрические цепи, обеспечивающие неискаженную передачу импульсов; к ним обычно относят кабели и трансформаторы для передачи импульсов, линии задержки, усилители импульсов (видеоусилители) и 
2) устройства преобразования импульсов, обеспечивающие получение импульсов одной формы из импульсов другой формы или получение импульсов той же формы, но с другими параметрами; в этой группе различают линейные преобразователи импульсов (интегрирующие и дифференцирующие устройства, контуры ударного возбуждения и  ); нелинейные формирующие устройства (электронные цепи, основное назначение которых — сформировать сигнал нужной формы из сигнала, имеющего форму, не удобную для дальнейшего преобразования), к ним относят: ограничители, фиксаторы уровня, компараторы, триггеры Шмита; формирователи импульсов из перепадов сигнала и
); нелинейные формирующие устройства (электронные цепи, основное назначение которых — сформировать сигнал нужной формы из сигнала, имеющего форму, не удобную для дальнейшего преобразования), к ним относят: ограничители, фиксаторы уровня, компараторы, триггеры Шмита; формирователи импульсов из перепадов сигнала и  преобразователи импульсов цифровых устройств (их основное назначение — в выполнении логических функций и преобразовании по определенным законам одной последовательности импульсов в другие), к ним относят логические элементы, триггеры, счетчики, регистры, различные комбинационные устройства, выполненные на основе логических элементов, и
преобразователи импульсов цифровых устройств (их основное назначение — в выполнении логических функций и преобразовании по определенным законам одной последовательности импульсов в другие), к ним относят логические элементы, триггеры, счетчики, регистры, различные комбинационные устройства, выполненные на основе логических элементов, и 
3) устройства, генерирующие импульсы, или импульсные генераторы. В зависимости от режима работы их подразделяют на автоколебательные (автогенераторы), заторможенные и на генераторы, работающие в режиме синхронизации или деления частоты.
Автогенераторы вырабатывают импульсы, параметры которых определяются внутренними параметрами его компонентов. Заторможенные (ждущие) генераторы генерируют импульсы, период повторения которых определяется периодом повторения запускающих импульсов. Их форма и другие параметры зависят от внутренних параметров схем. В режиме синхронизации или деления частоты генераторы вырабатывают импульсы, частота повторения которых кратна частоте синхронизирующего сигнала. Генераторы, вырабатывающие несколько последовательностей импульсов, называют многофазными.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПАССИВНЫЕ КОМПОНЕНТЫ ЭЛЕКТРОННЫХ УСТРОЙСТВ
- § 1.1. РЕЗИСТОРЫ
- Основные параметры резисторов
- § 1.2. КОНДЕНСАТОРЫ
- Основные параметры постоянных конденсаторов
- 1.3. КАТУШКИ ИНДУКТИВНОСТИ
- Основные параметры катушки индуктивности (ГОСТ 20718—75)
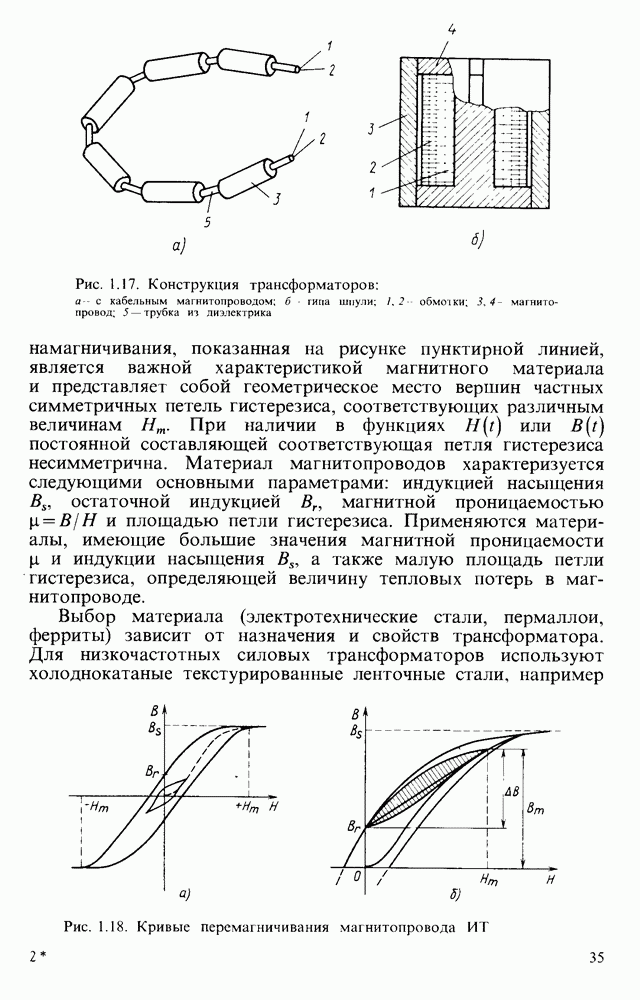
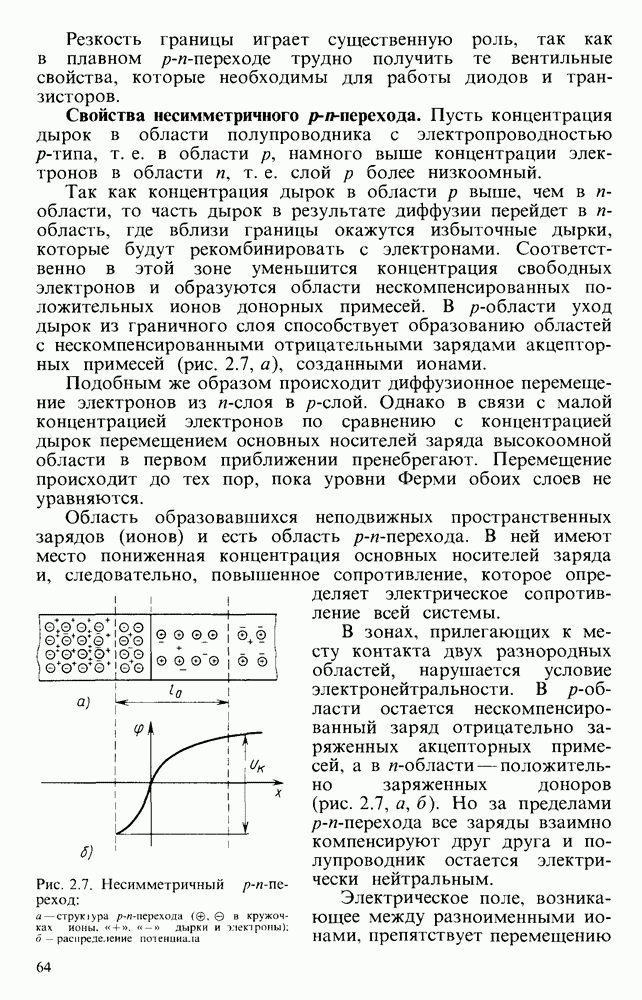
- § 1.4. ТРАНСФОРМАТОРЫ ЭЛЕКТРОННОЙ АППАРАТУРЫ
- Основные параметры трансформаторов питания
- ГЛАВА 2. ПОЛУПРОВОДНИКОВЫЕ КОМПОНЕНТЫ ЭЛЕКТРОННЫХ ЦЕПЕЙ
- § 2.1. ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
- Основные положения теории электропроводности.
- Примесная электропроводность.
- § 2.2. ОСНОВНЫЕ СВОЙСТВА И ХАРАКТЕРИСТИКИ ПОЛУПРОВОДНИКОВ
- Концентрация носителей зарядов.
- Уравнения непрерывности.
- § 2.3. ЭЛЕКТРИЧЕСКИЕ ПЕРЕХОДЫ
- Контакт металл — полупроводник.
- Контакт двух полупроводников p- и n-типов.
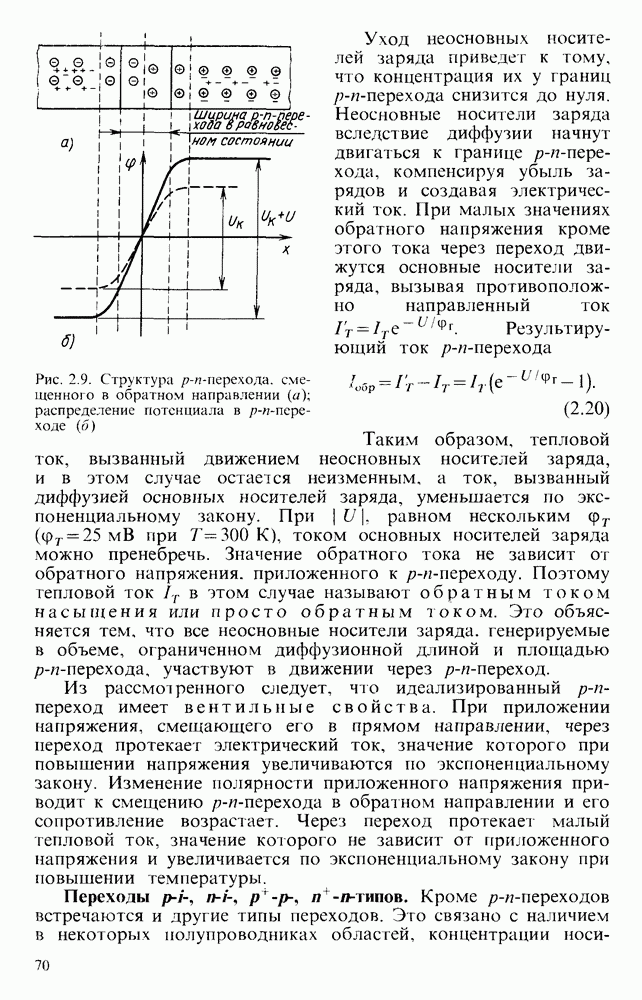
- Свойства несимметричного p-n-перехода.
- p-n-переход смещен в прямом направлении
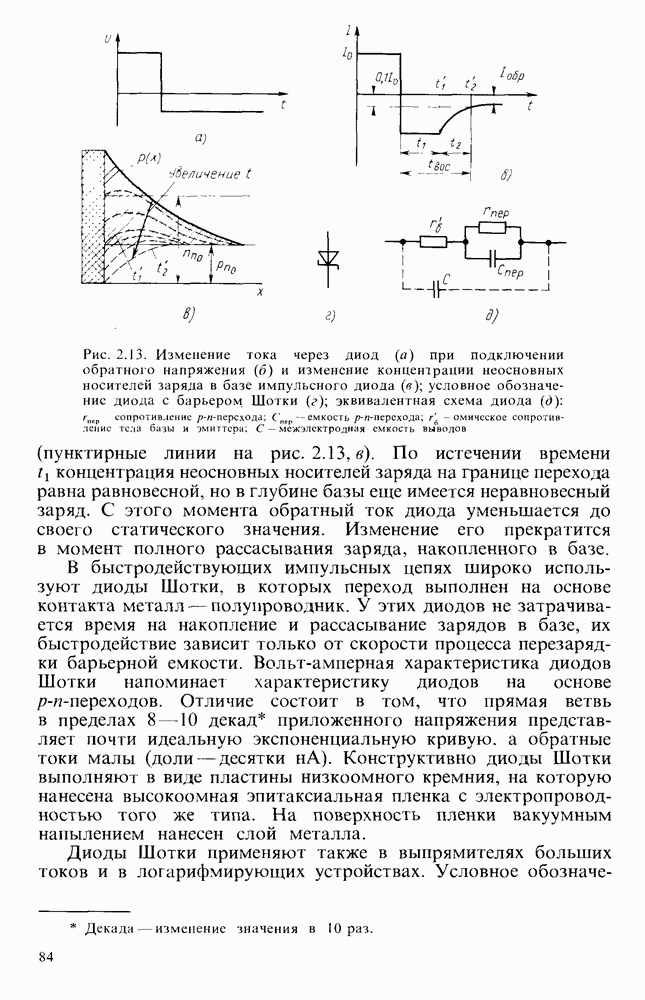
- Переход, смещенный в обратном направлении.
- Переходы p-i, n-i-, p+-p-, n+-n-типов.
- 2.4. ОСОБЕННОСТИ РЕАЛЬНЫХ p-n-ПЕРЕХОДОВ
- Пробой p-n-перехода.
- § 2.5. ОСНОВНЫЕ ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ, ИСПОЛЬЗУЕМЫЕ ПРИ ИЗГОТОВЛЕНИИ ПОЛУПРОВОДНИКОВЫХ ПРИБОРОВ И ИНТЕГРАЛЬНЫХ МИКРОСХЕМ
- § 2.6. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
- Выпрямительные диоды.
- Основные параметры выпрямительных диодов и их значения у маломощных диодов
- Импульсные диоды.
- Полупроводниковые стабилитроны.
- Варикапы.
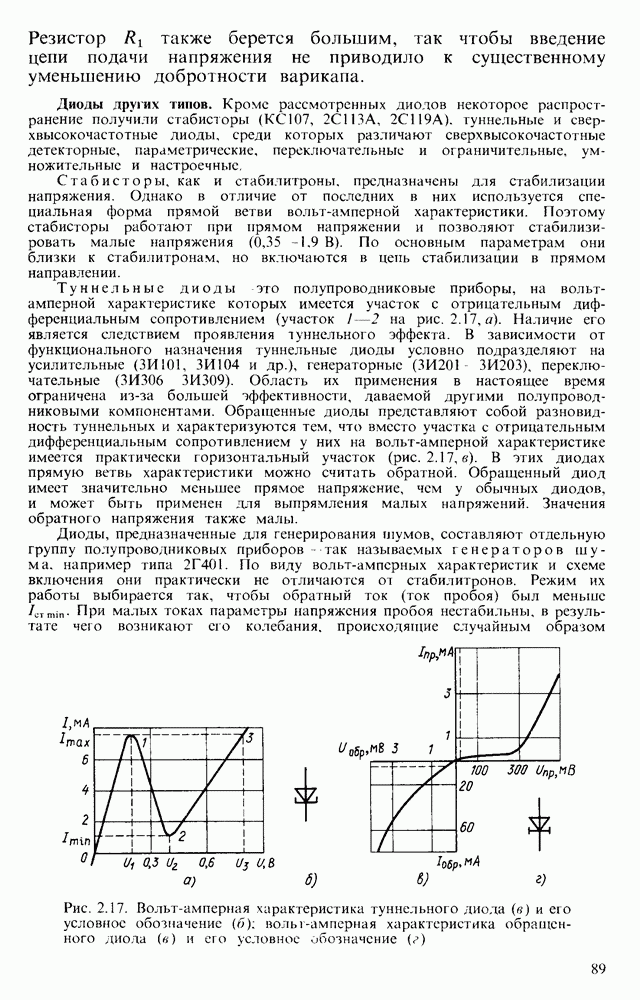
- Диоды других типов.
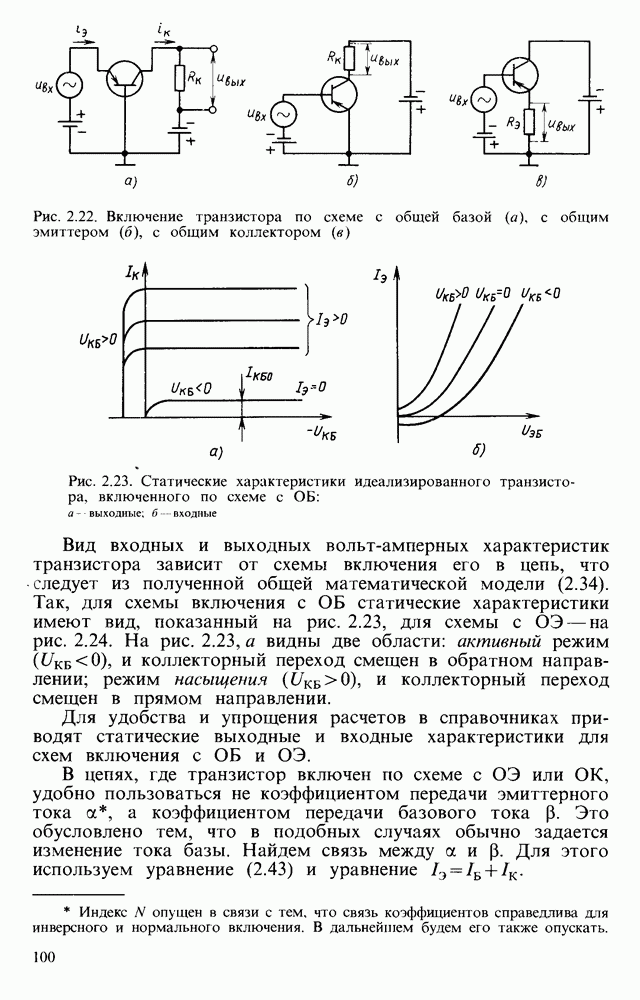
- § 2.7. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ
- Математическая модель транзистора.
- Три схемы включения транзистора.
- Инерционные свойства транзистора.
- Шумы транзистора.
- Н-параметры транзисторов.
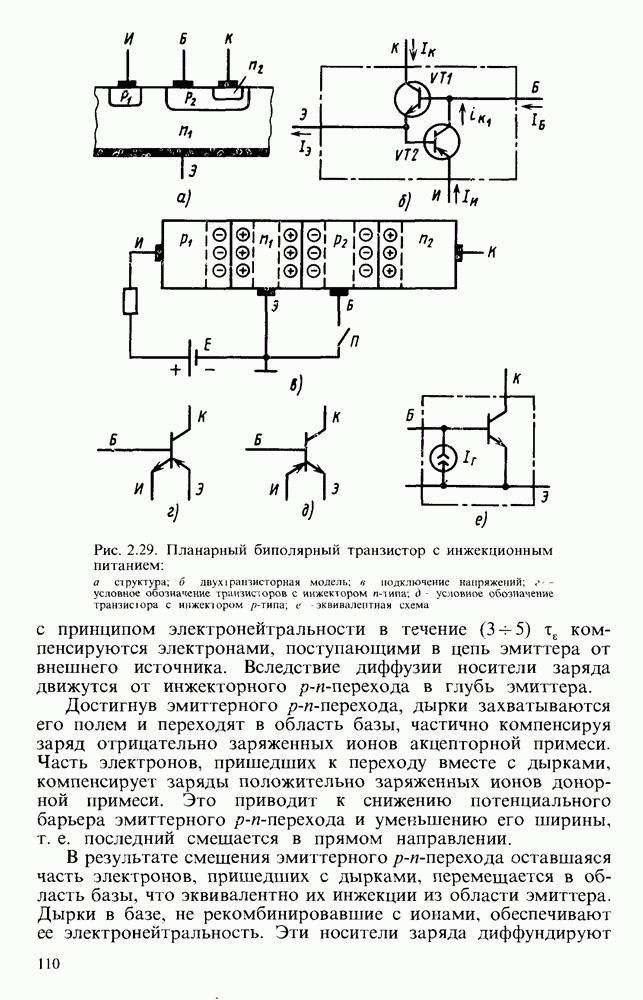
- § 2.8. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ С ИНЖЕКЦИОННЫМ ПИТАНИЕМ
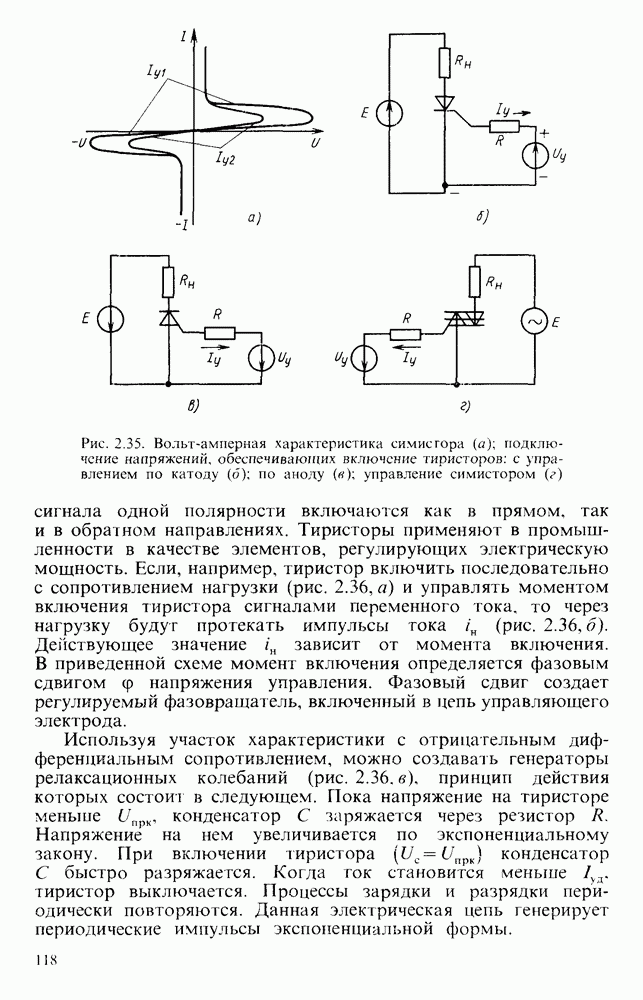
- § 2.9. ТИРИСТОРЫ
- Симметричные тиристоры.
- Основные параметры тиристоров и их ориентировочные значения
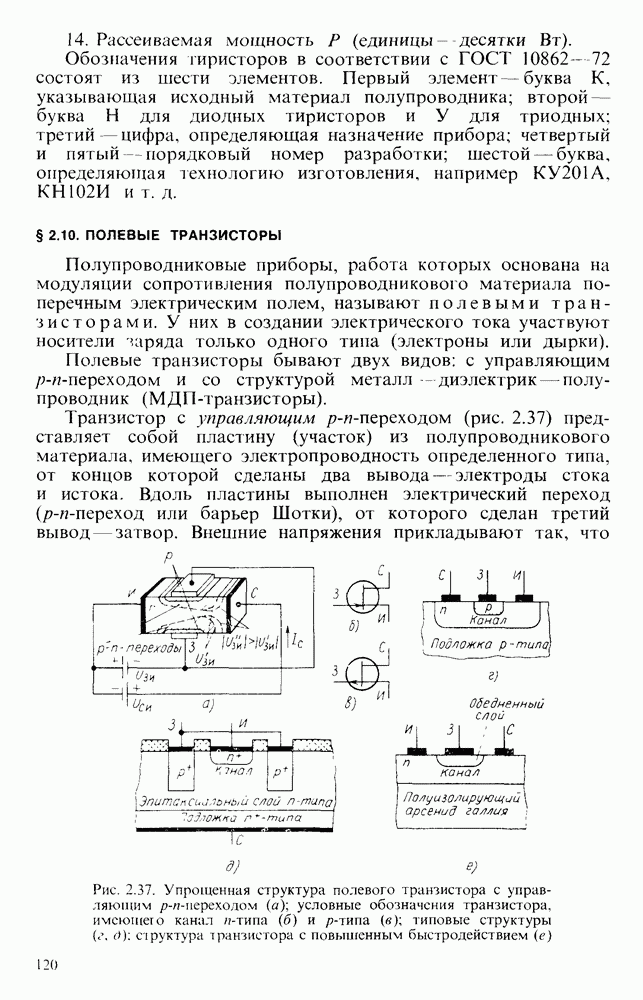
- § 2.10. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
- Основные параметры полевых транзисторов и их ориентировочные значения
- § 2.11. ОСОБЕННОСТИ КОМПОНЕНТОВ ЭЛЕКТРОННЫХ ЦЕПЕЙ В МИКРОМИНИАТЮРНОМ ИСПОЛНЕНИИ
- Пассивные компоненты ИС.
- Конденсаторы.
- Индуктивности.
- Транзисторы ИС.
- Изоляция компонентов в монолитных интегральных узлах.
- ГЛАВА 3. КОМПОНЕНТЫ ОПТОЭЛЕКТРОНИКИ И ТЕХНИЧЕСКИЕ СРЕДСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.1. ОБЩИЕ СВЕДЕНИЯ О КОМПОНЕНТАХ ОПТОЭЛЕКТРОНИКИ
- § 3.2. УПРАВЛЯЕМЫЕ ИСТОЧНИКИ СВЕТА
- Основные параметры и характеристики светодиодов
- § 3.3. ФОТОПРИЕМНИКИ
- Основные характеристики и параметры фоторезистора
- Фотодиоды.
- Основные характеристики и параметры фотодиода
- Фототранзисторы.
- Основные характеристики и параметры фототранзистора
- Фототиристоры.
- Многоэлементные фотоприемники.
- Фотоприемники с внешним фотоэффектом.
- § 3.4. СВЕТОВОДЫ И ПРОСТЕЙШИЕ ОПТРОНЫ
- § 3 5. ОБЩИЕ СВЕДЕНИЯ О КОМПОНЕНТАХ УСТРОЙСТВ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.6. ЖИДКОКРИСТАЛЛИЧЕСКИЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.7. ГАЗОНАПОЛНЕННЫЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- Основные параметры газонаполненных матричных панелей неременного тока
- § 3.8. ВАКУУМНЫЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.9. ПОЛУПРОВОДНИКОВЫЕ И ЭЛЕКТРОЛЮМИНЕСЦЕНТНЫЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- ГЛАВА 4. УСИЛИТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- § 4.1. ОБЩИЕ СВЕДЕНИЯ ОБ УСИЛИТЕЛЯХ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ, ИХ ОСНОВНЫХ ПАРАМЕТРАХ И ХАРАКТЕРИСТИКАХ
- § 4.2. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ОБРАТНОЙ СВЯЗИ ПРИМЕНИТЕЛЬНО К УСИЛИТЕЛЯМ
- § 4.3. СТАТИЧЕСКИЙ РЕЖИМ РАБОТЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ
- § 4.4. УСИЛИТЕЛЬНЫЕ КАСКАДЫ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- Каскад с общим стоком.
- § 4.5. УСИЛИТЕЛЬНЫЙ КАСКАД НА БИПОЛЯРНОМ ТРАНЗИСТОРЕ С ОБЩИМ ЭМИТТЕРОМ
- Входное сопротивление.
- § 4.6. УСИЛИТЕЛЬНЫЙ КАСКАД НА БИПОЛЯРНОМ ТРАНЗИСТОРЕ С ОБЩЕЙ БАЗОЙ
- § 4.7. УСИЛИТЕЛЬНЫЙ КАСКАД НА БИПОЛЯРНОМ ТРАНЗИСТОРЕ С ОБЩИМ КОЛЛЕКТОРОМ
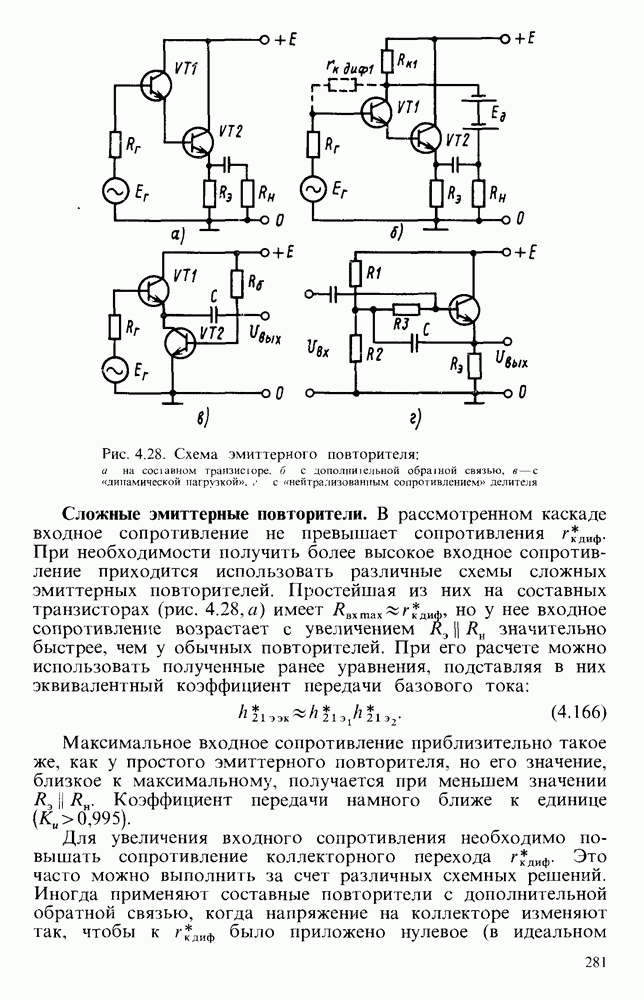
- Сложные эмиттерные повторители.
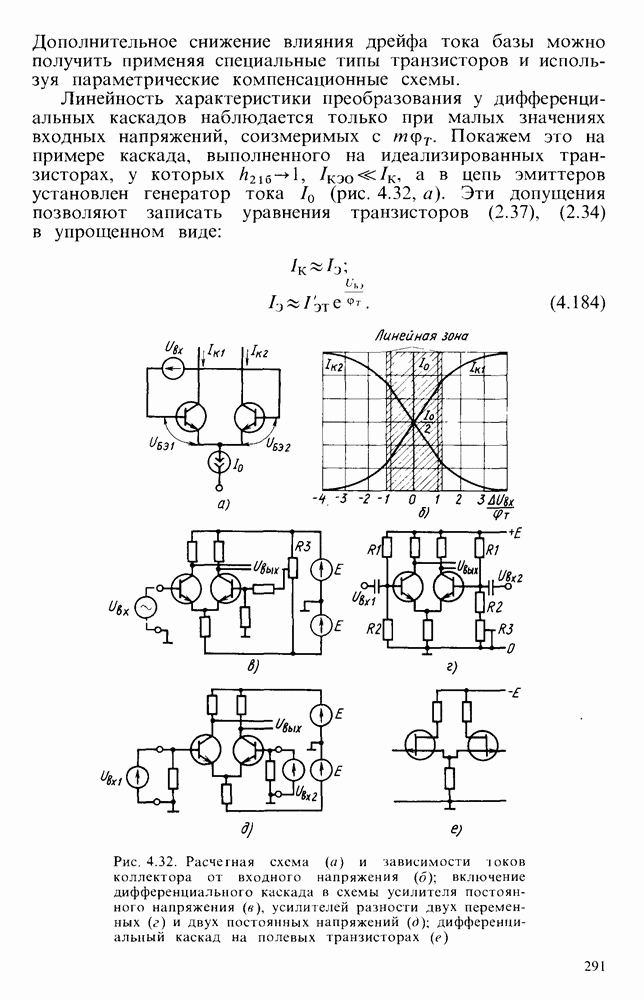
- § 4.8. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
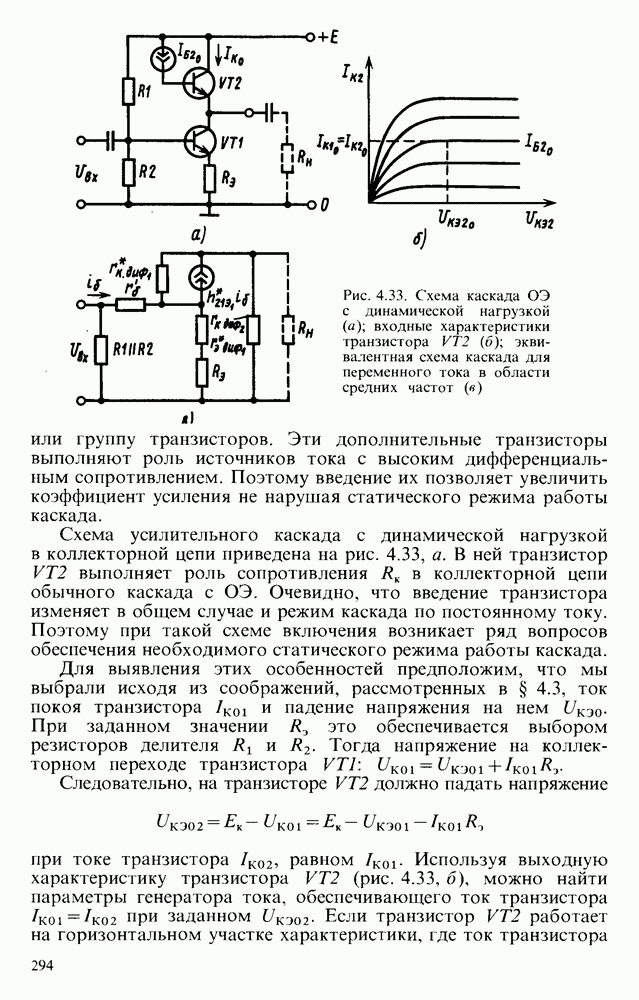
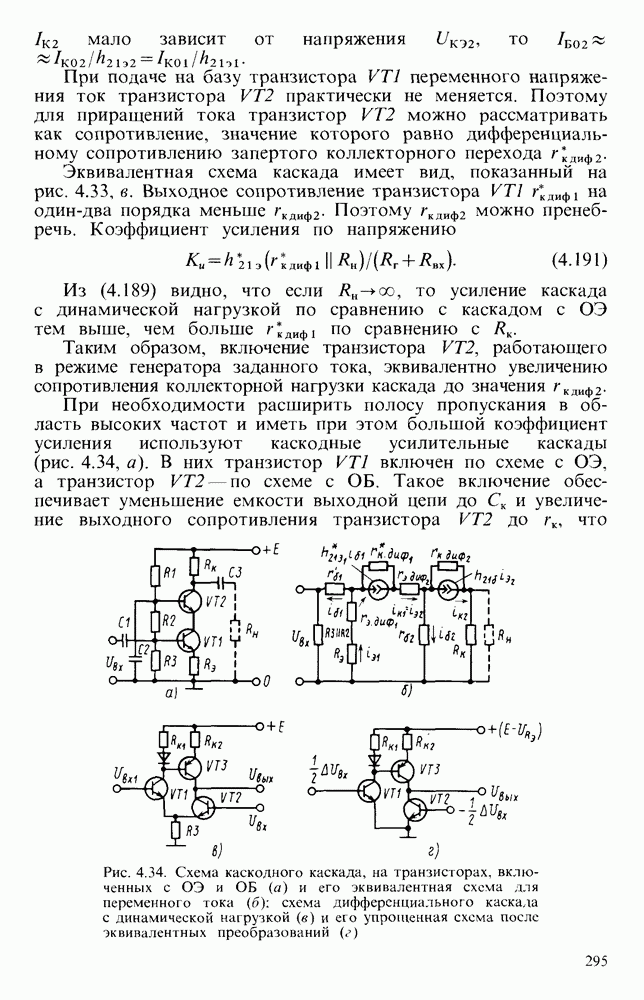
- § 4.9. УСИЛИТЕЛЬНЫЕ КАСКАДЫ С ДИНАМИЧЕСКОЙ НАГРУЗКОЙ И С КАСКОДНЫМ ВКЛЮЧЕНИЕМ ТРАНЗИСТОРОВ
- § 4.10. УПРАВЛЯЕМЫЕ ИСТОЧНИКИ ТОКА И УСИЛИТЕЛЬНЫЕ КАСКАДЫ НА ИХ ОСНОВЕ
- 4.11. УСИЛИТЕЛЬНЫЕ КАСКАДЫ С ТРАНСФОРМАТОРНОЙ СВЯЗЬЮ
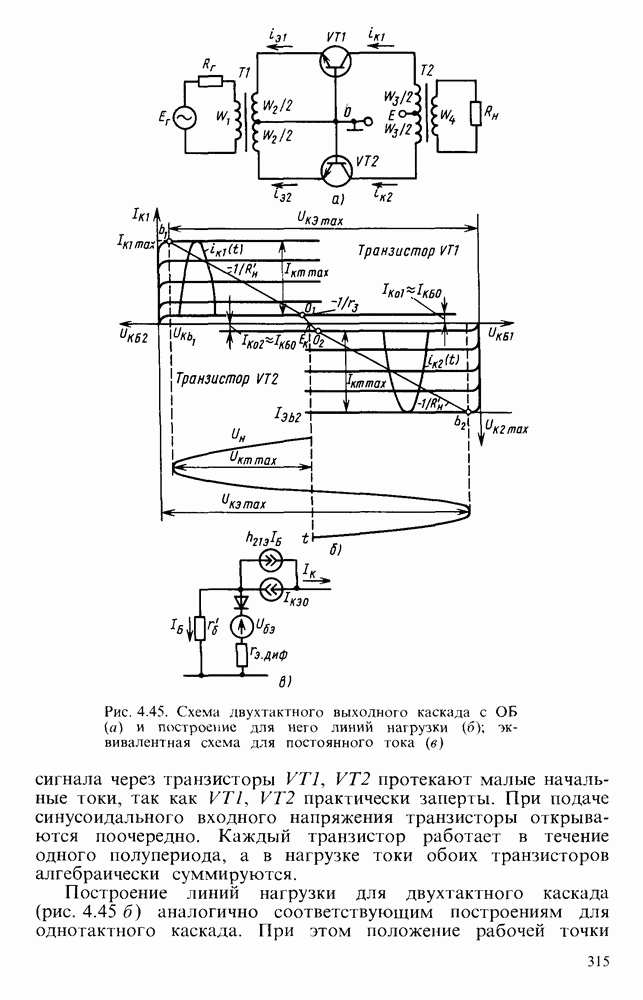
- 4.12. МОЩНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- Каскад с ОБ трансформаторным входом и трансформаторным выходом.
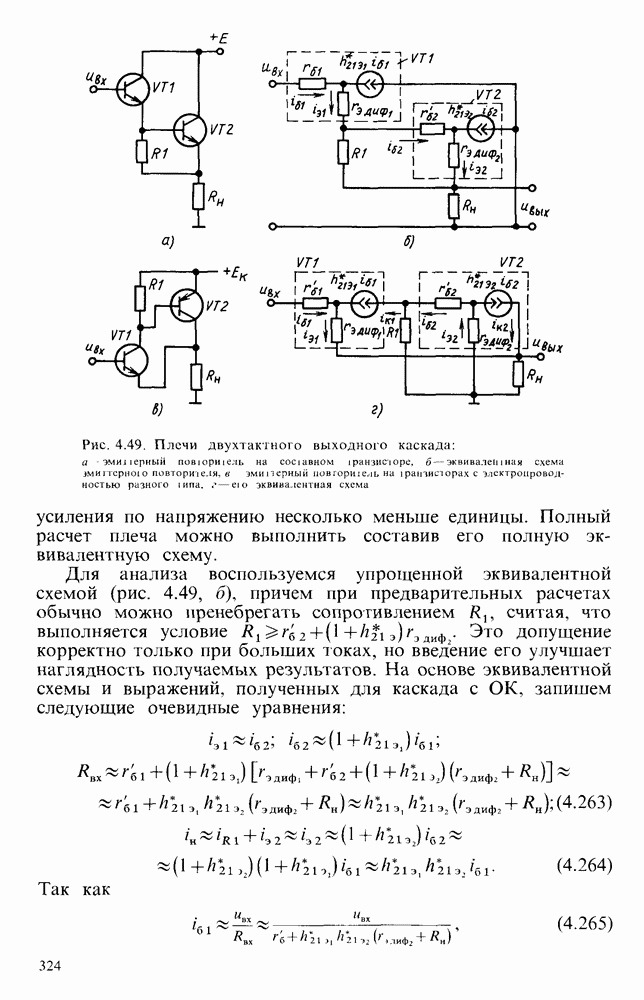
- Двухтактные выходные каскады.
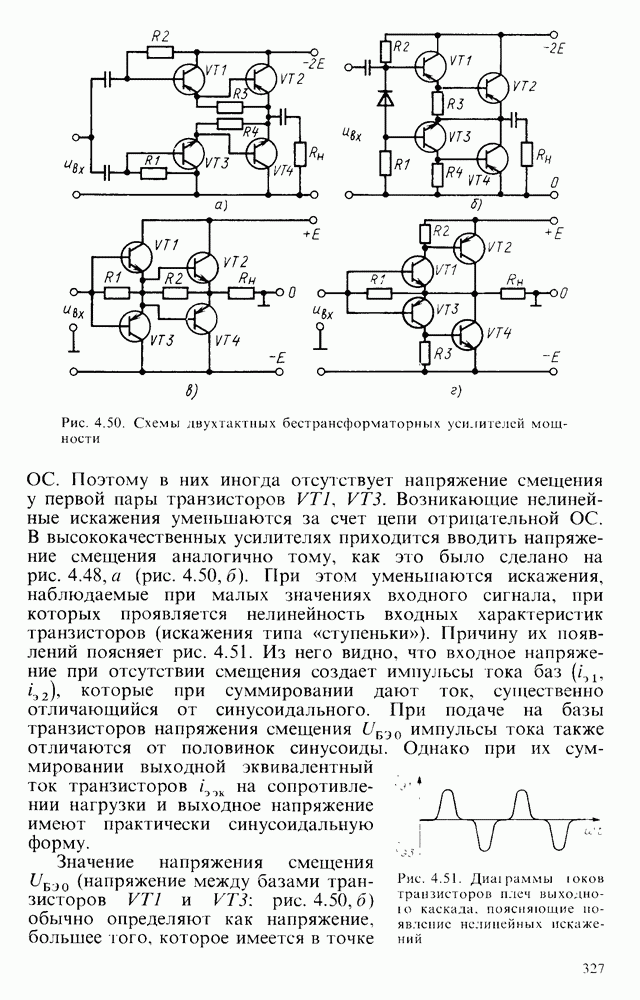
- § 4.13. БЕСТРАНСФОРМАТОРНЫЕ МОЩНЫЕ ВЫХОДНЫЕ КАСКАДЫ
- ГЛАВА 5. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- § 5.1. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- Параметры RC-цепи связи.
- § 5.2. УСИЛИТЕЛИ В ИНТЕГРАЛЬНОМ ИСПОЛНЕНИИ
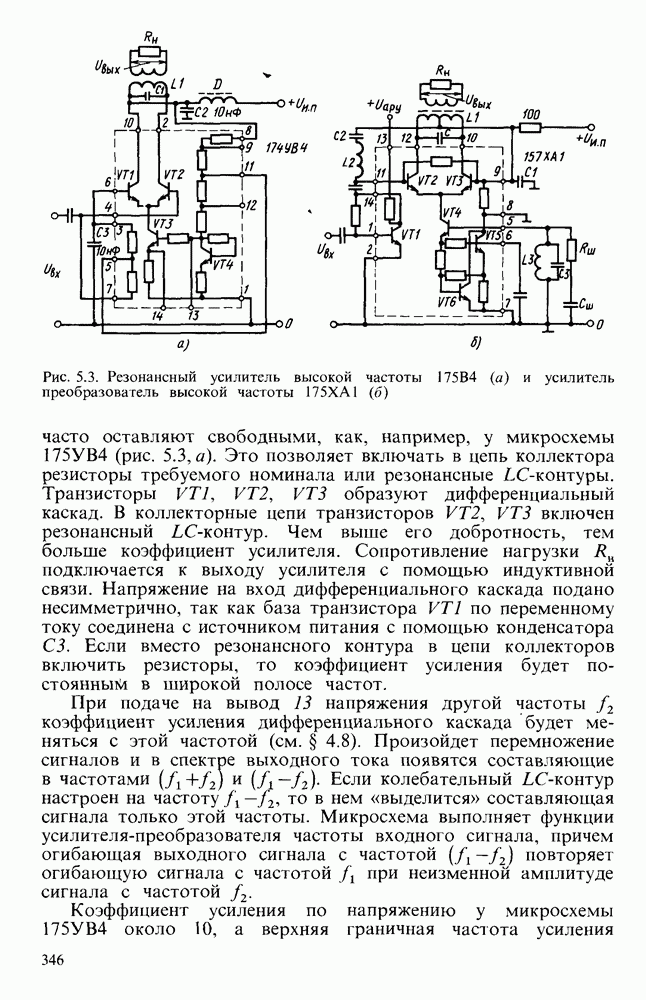
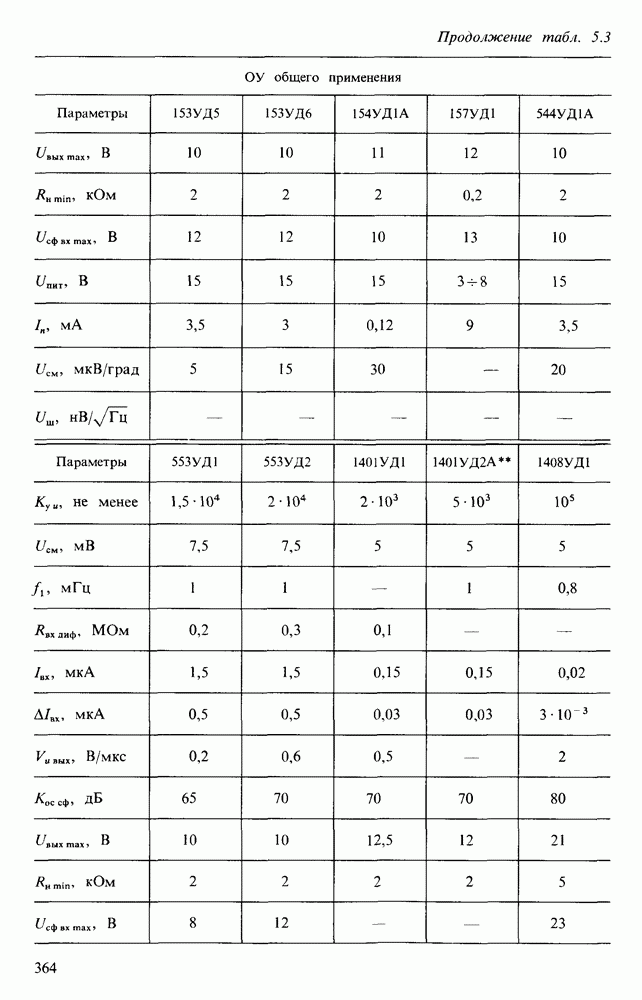
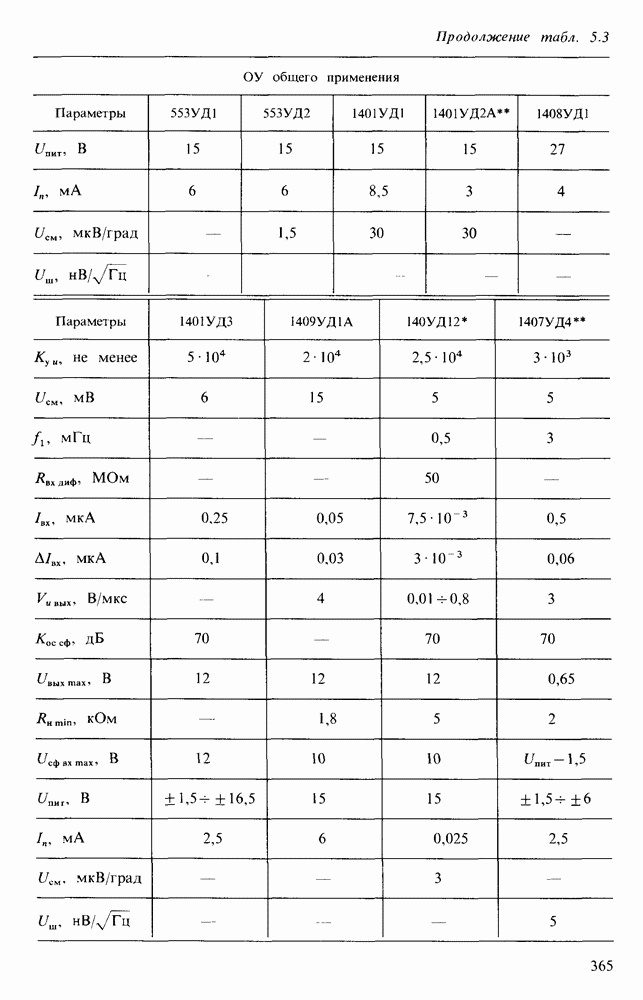
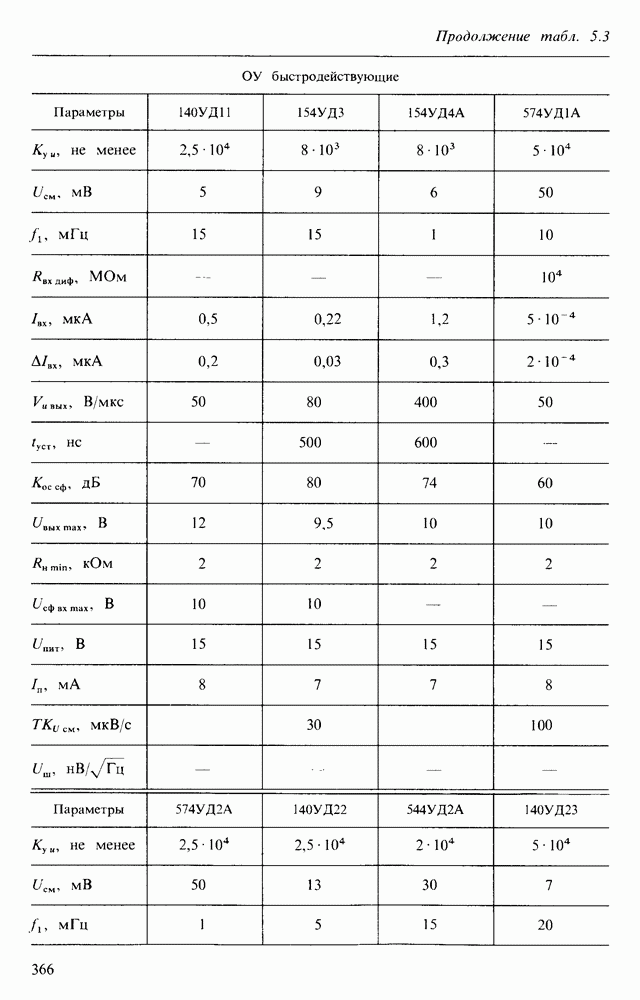
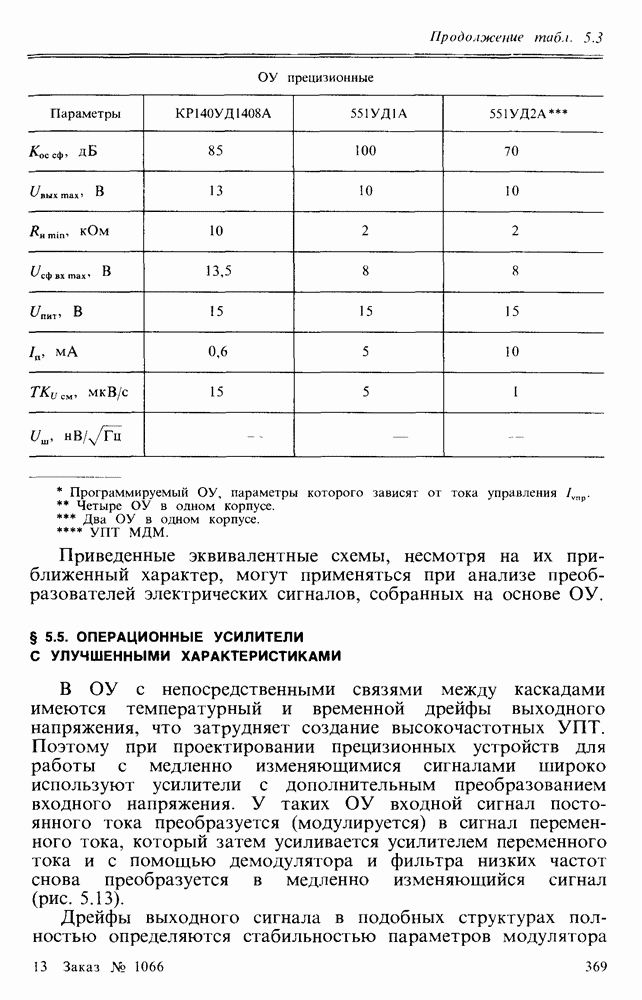
- 5.3. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- § 5.4. ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- § 5.5. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ С УЛУЧШЕННЫМИ ХАРАКТЕРИСТИКАМИ
- § 5.6. ОСОБЕННОСТИ ВКЛЮЧЕНИЯ И СВОЙСТВА ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ, ОХВАЧЕННЫХ ОБРАТНОЙ СВЯЗЬЮ
- § 5.7. УСТОЙЧИВОСТЬ УСИЛИТЕЛЕЙ И КОРРЕКЦИЯ ИХ ХАРАКТЕРИСТИК
- ГЛАВА 6. АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- § 6.1. МАСШТАБНЫЕ УСИЛИТЕЛИ
- 6.2. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 6.3. ИНТЕГРИРУЮЩИЕ УСТРОЙСТВА
- Интеграторы на основе операционных усилителей.
- § 6.4. ДИФФЕРЕНЦИРУЮЩИЕ УСТРОЙСТВА
- Активные дифференцирующие устройства.
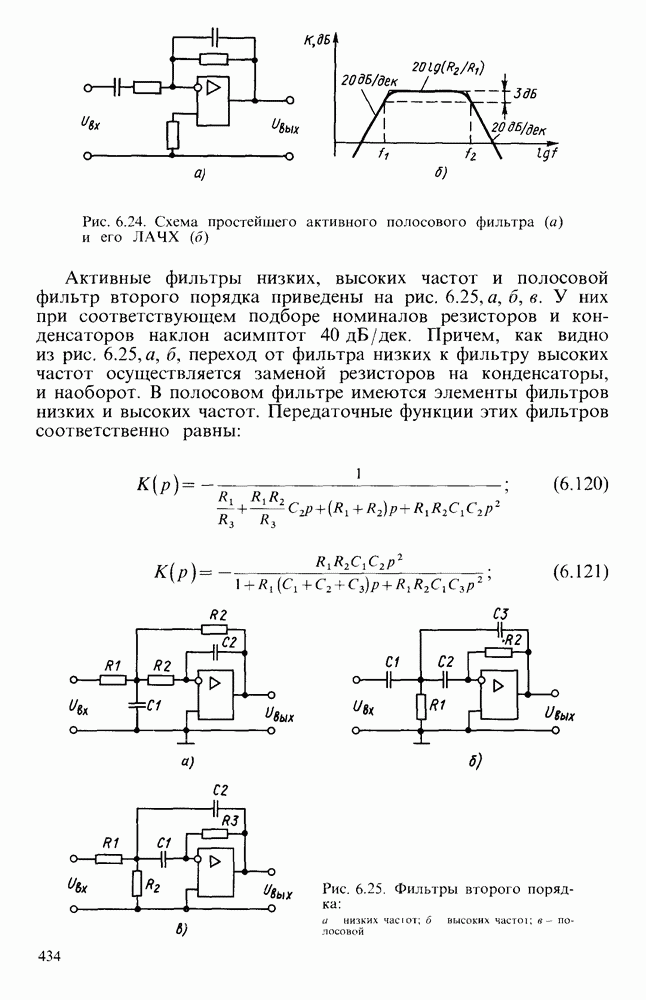
- § 6.5. АКТИВНЫЕ ФИЛЬТРЫ
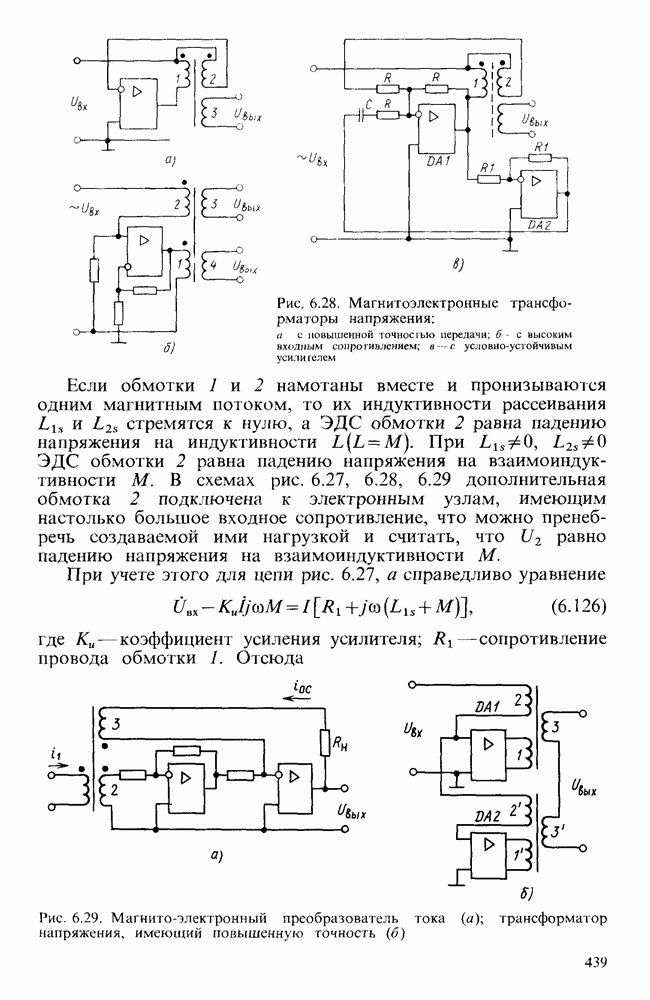
- § 6.6. МАГНИТОЭЛЕКТРОННЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
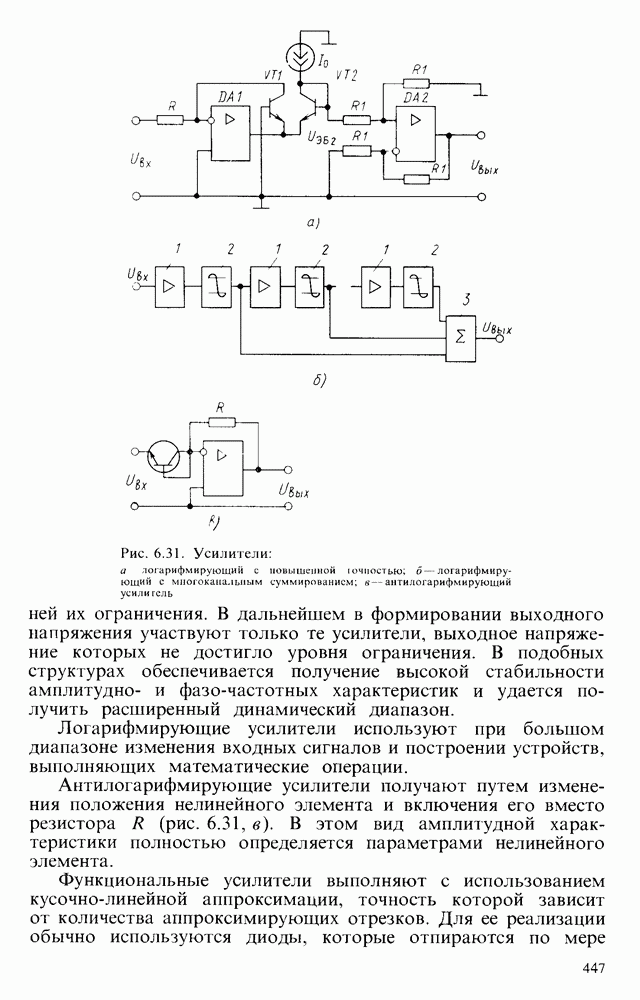
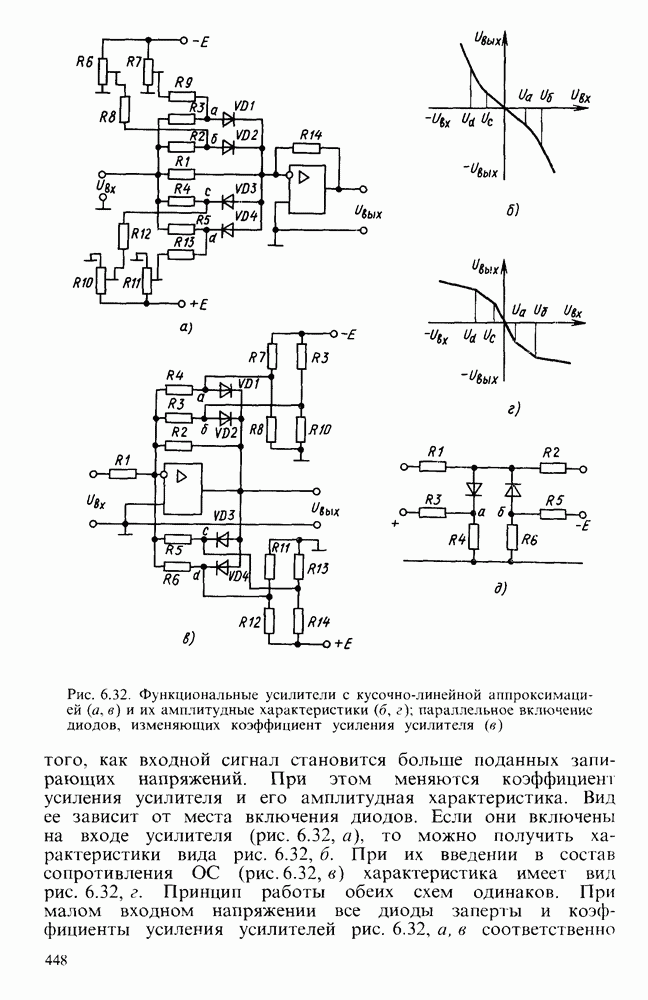
- § 6.7. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- § 6.8. ПЕРЕМНОЖИТЕЛИ СИГНАЛОВ И УСТРОЙСТВА, ВЫПОЛНЯЮЩИЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ
- § 6.9. ДЕТЕКТОРЫ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- ГЛАВА 7. ЭЛЕКТРОННЫЕ КЛЮЧИ
- § 7.1. ОБЩИЕ СВЕДЕНИЯ ОБ ИМПУЛЬСНЫХ ПРОЦЕССАХ И УСТРОЙСТВАХ
- § 7.2. ДИОДНЫЕ КЛЮЧИ
- § 7.3. КЛЮЧИ НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ
- § 7.4. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В КЛЮЧЕВЫХ ЦЕПЯХ С БИПОЛЯРНЫМИ ТРАНЗИСТОРАМИ
- 7.5. КЛЮЧИ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- § 7.6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В КЛЮЧАХ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- ГЛАВА 8. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ, ТРИГГЕРЫ, АВТОГЕНЕРАТОРЫ
- § 8.1. ОБЩИЕ СВЕДЕНИЯ О ЛОГИЧЕСКИХ ЭЛЕМЕНТАХ
- § 8.2. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 8.3. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МОП-ТРАНЗИСТОРАХ
- § 8.4. ТРИГГЕРЫ
- § 8.5. НЕСИММЕТРИЧНЫЕ ТРИГГЕРЫ
- § 8.6. ГЕНЕРАТОРЫ КОЛЕБАНИЙ
- Генераторы напряжения прямоугольной формы.
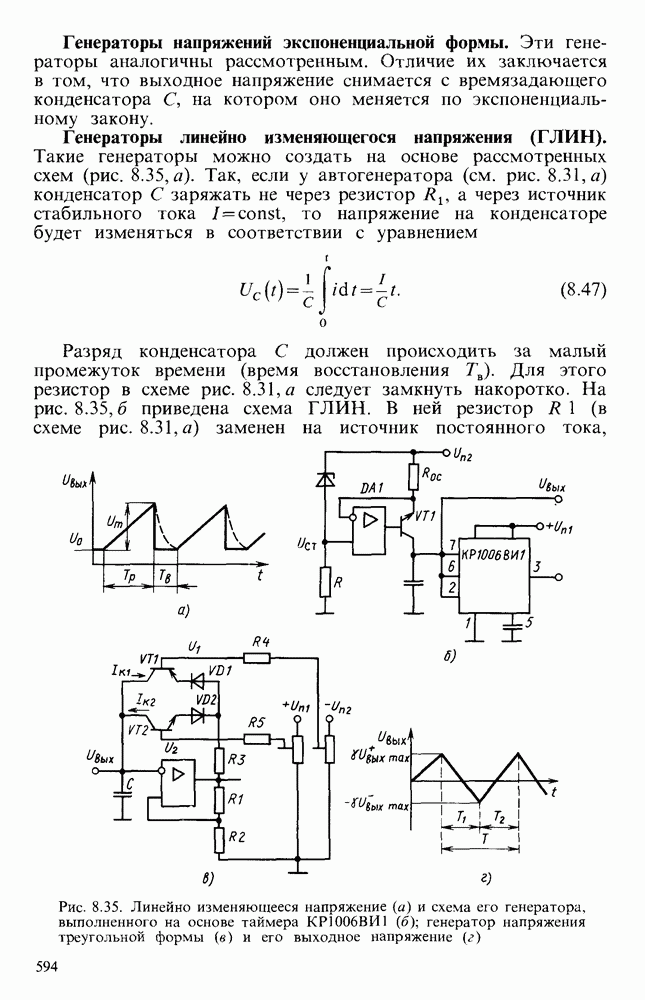
- Генераторы линейно изменяющегося напряжения (ГЛИН).
- Генераторы напряжения треугольной формы.
- Генераторы синусоидальных колебаний.
- Генераторы LC-типа.
- Генераторы с кварцевыми резонаторами и электромеханическими резонансными системами.
- ЗАКЛЮЧЕНИЕ
- Приложение
- Схемы включения операционных усилителей
- ЛИТЕРАТУРА