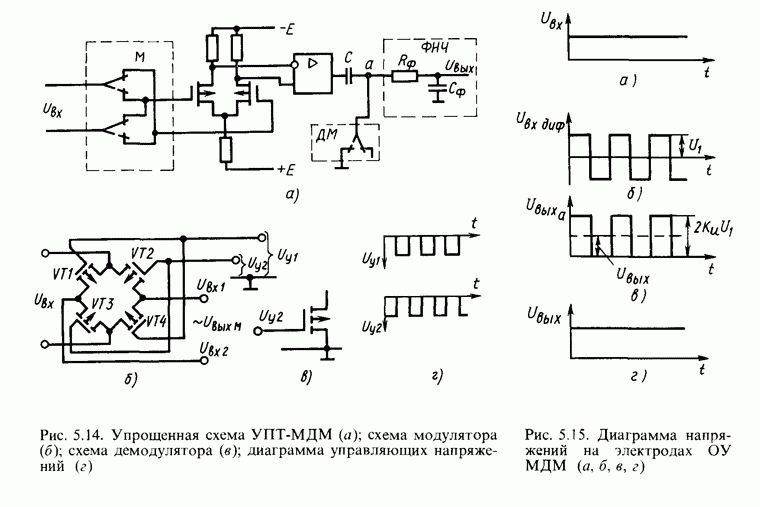
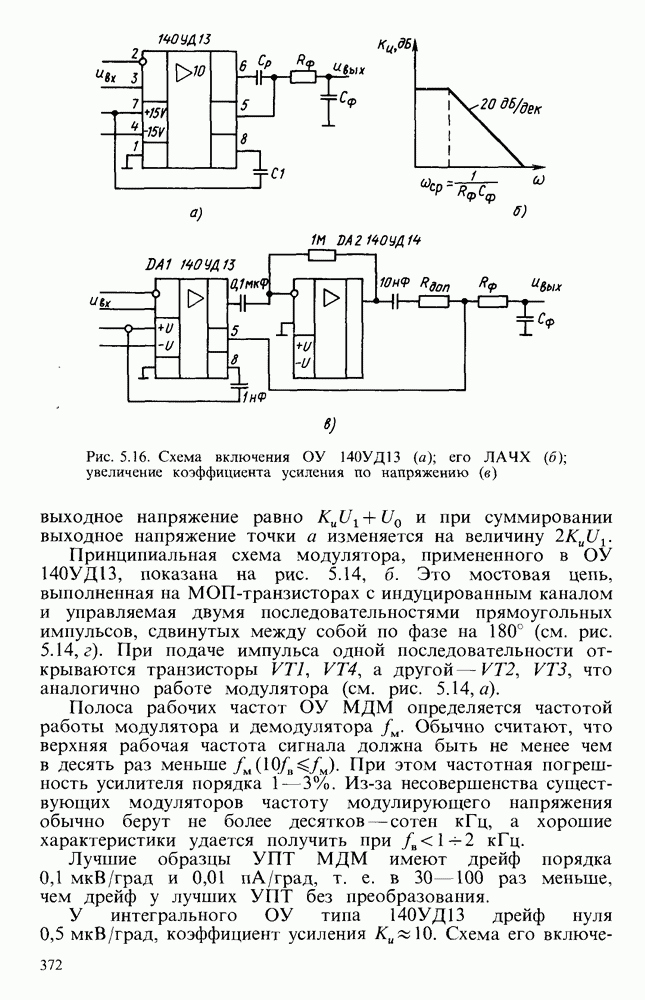
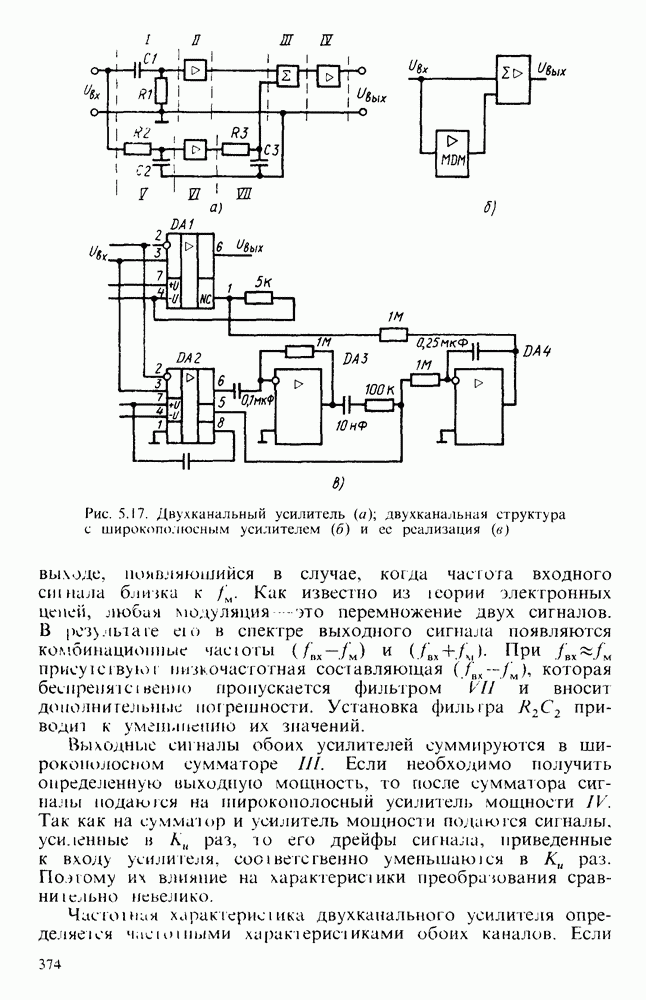
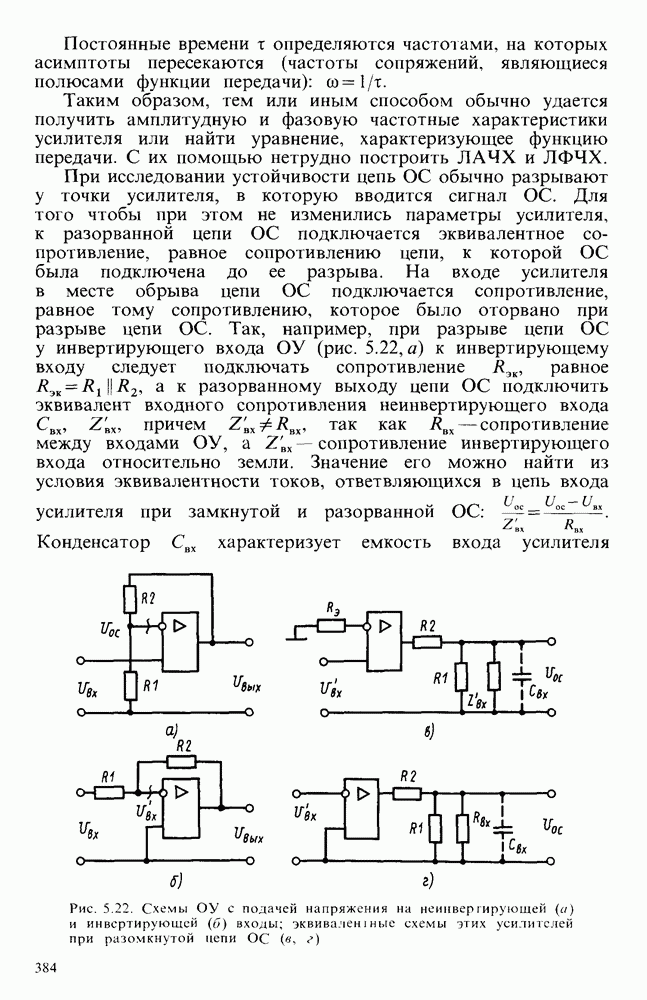
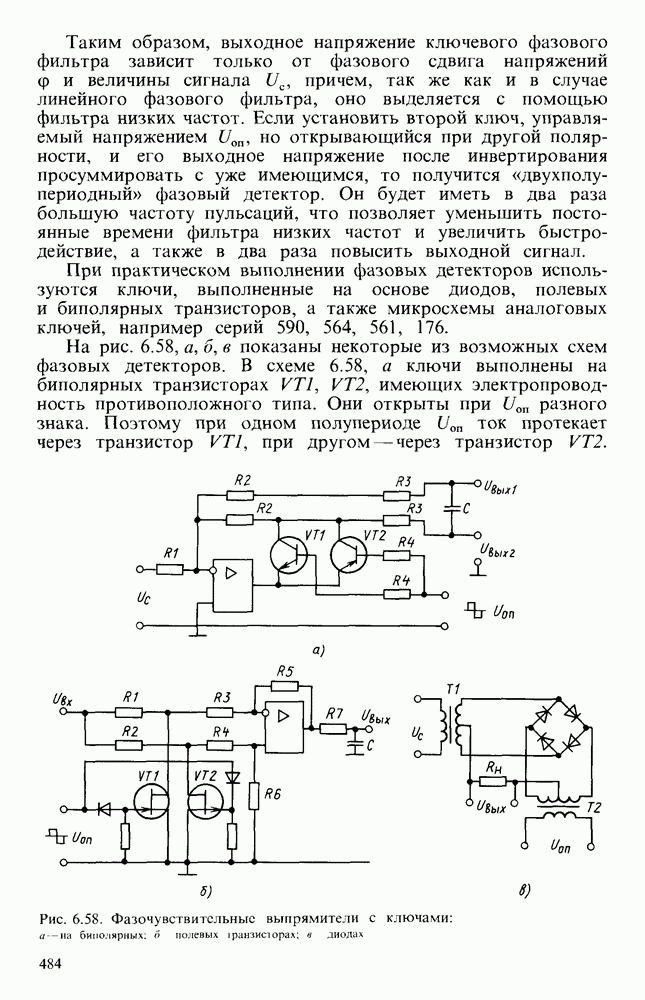
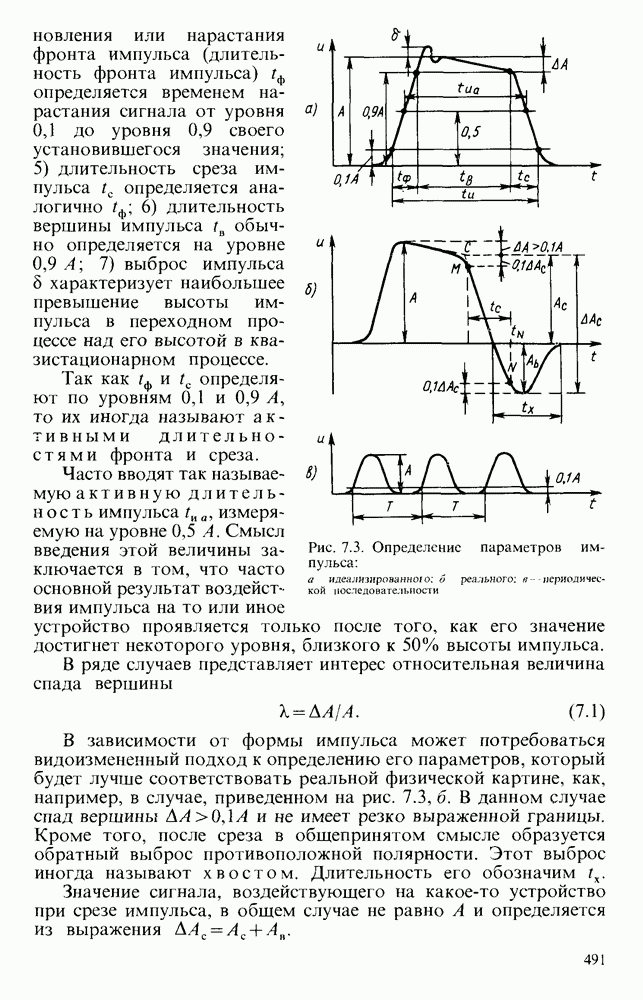
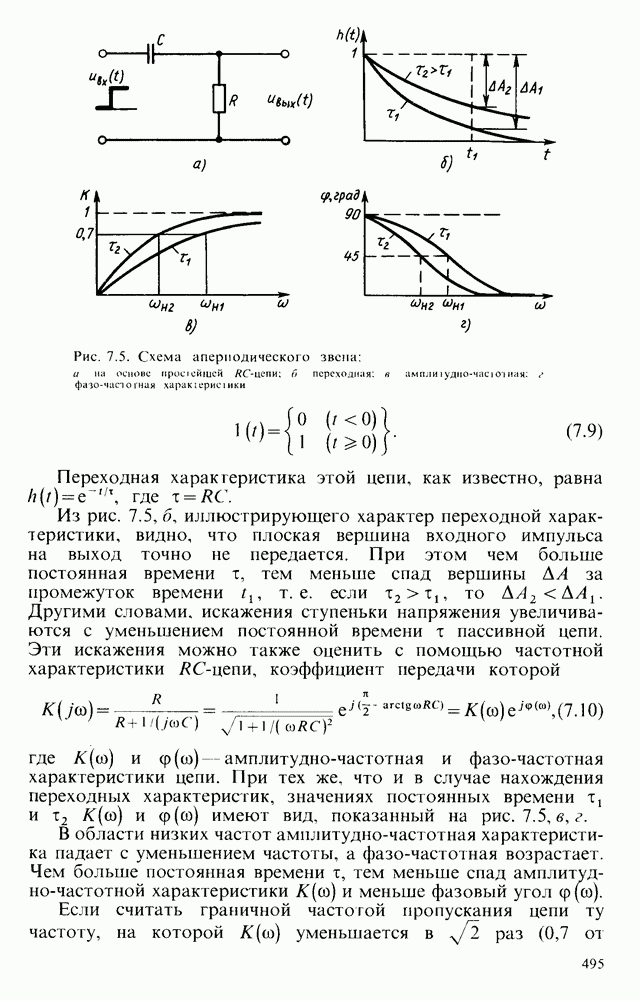
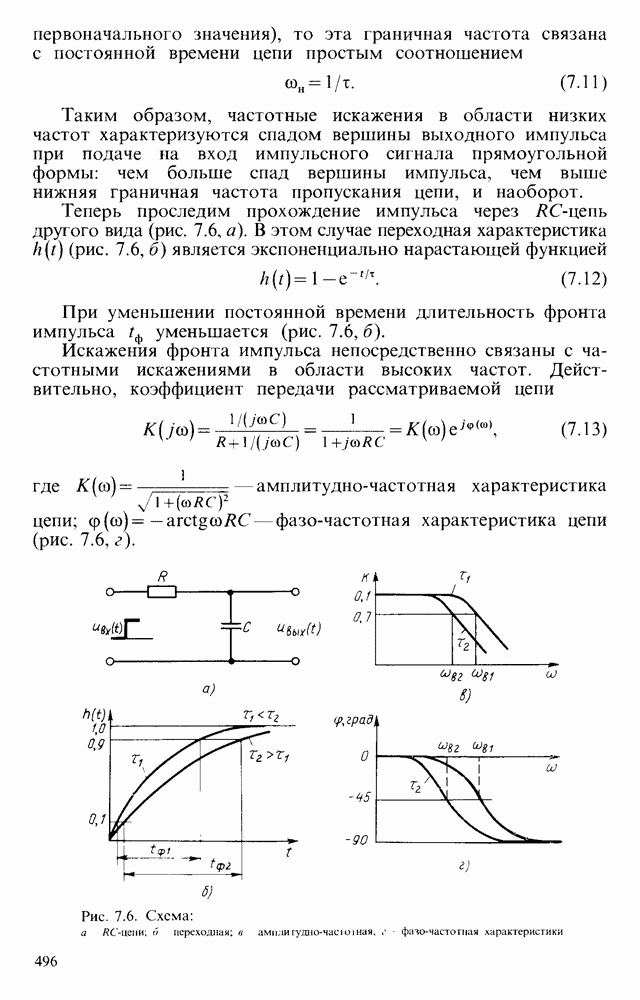
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6.5. АКТИВНЫЕ ФИЛЬТРЫ
Усилители, имеющие избирательные свойства, условно подразделяют на фильтры низких и высоких частот, а также полосовые и режекторные (заграждающие). Фильтры низких и высоких частот соответственно пропускают только низкие или только высокие частоты, полосовые и режекторные обеспечивают пропускание или непропускание сигналов определенных частот.
Для получения у усилителей избирательных свойств в области низких частот (ниже  ) преимущественно применяют
) преимущественно применяют  -цепи интегрирующего или дифференцирующего типа. Они включаются на входе или выходе усилителя и охватывают его частотно-зависимой обратной связью.
-цепи интегрирующего или дифференцирующего типа. Они включаются на входе или выходе усилителя и охватывают его частотно-зависимой обратной связью.
В области высоких частот в качестве фильтров низких частот широко применяют высокочастотные дроссели, а полосовые и режекторные фильтры выполняют на основе использования катушек индуктивности ( -фильтры).
-фильтры).
В отдельных случаях применяют электромеханические фильтры, которые относятся к числу полосовых и имеют резонансную частоту, равную частоте собственных механических колебаний системы. Добротность таких фильтров обычно высокая (сотни — тысячи единиц), но перестройка частоты затруднена. Поэтому электромеханические фильтры в основном применяют в технике связи или радиовещании, где имеются стандартные определенные рабочие частоты.
Под активными фильтрами обычно понимают электронные усилители, содержащие RС-цепи, включенные так, что у усилителя появляются избирательные свойства. При их применении удается обойтись без громоздких, дорогостоящих и нетехнологичных катушек индуктивности и создать низкочастотные фильтры в микроэлектронном исполнении, в которых основные параметры могут быть изменены с помощью навесных резисторов и конденсаторов.
Простейшие фильтры высоких и низких частот показаны на рис. 6.23, а, в. В них конденсатор, определяющий частотную характеристику, включен в цепь ОС.
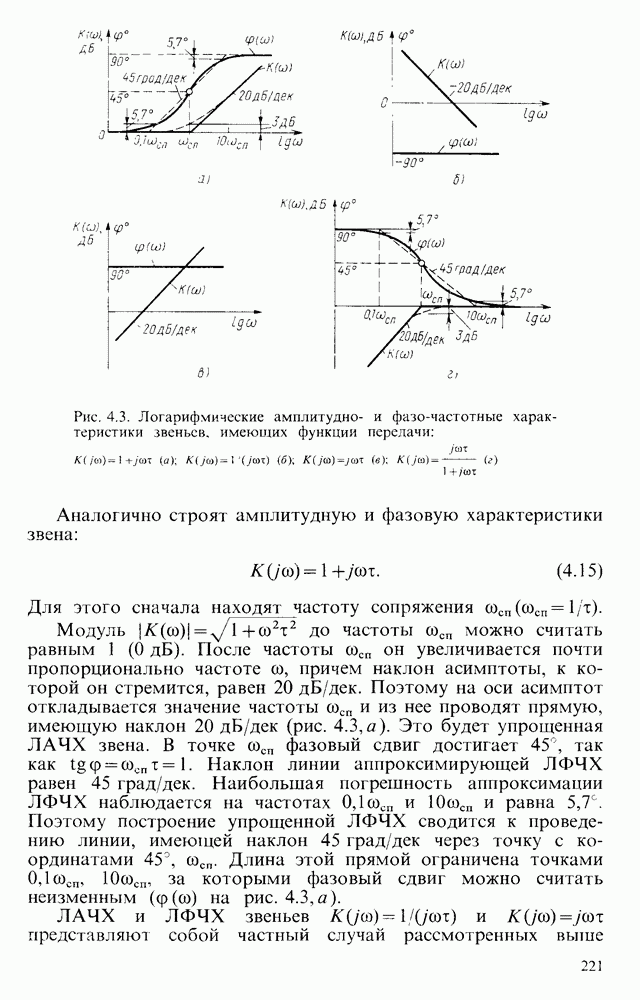
Для фильтра высоких частот, который часто используется в качестве дифференцирующего устройства, коэффициент передачи
 (6.116)
(6.116)
Переходя к операторной записи, получим передаточную функцию
 (6.117)
(6.117)
где  .
.
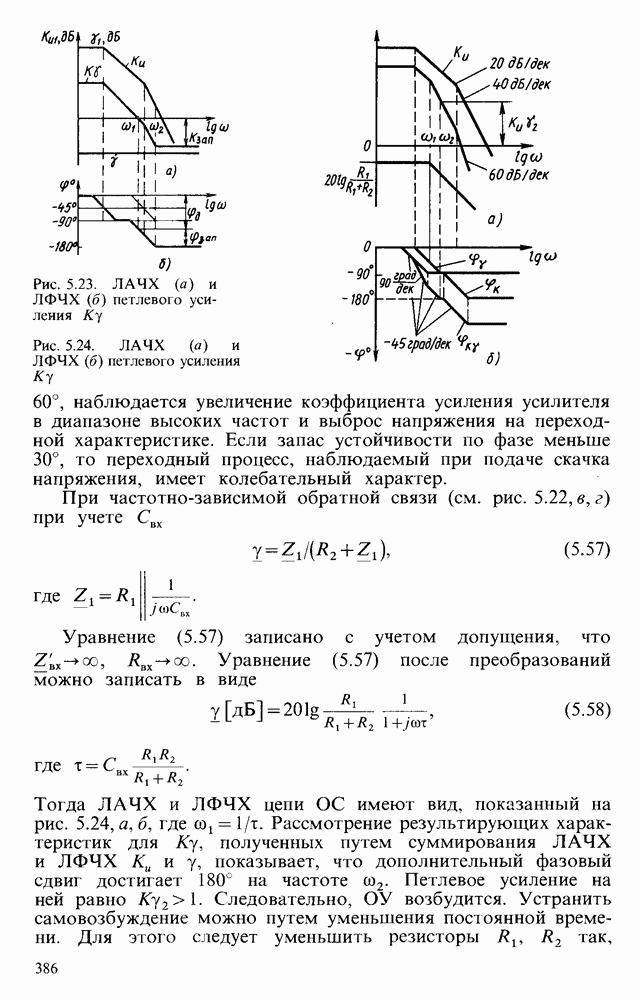
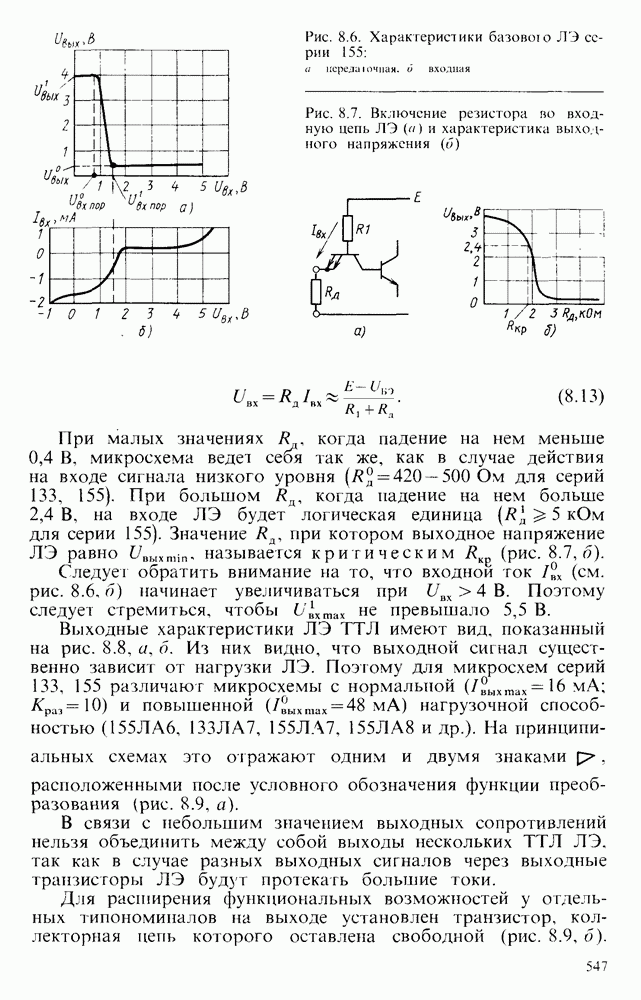
ЛАЧХ данного фильтра приведена на рис.  . Частоту сопряжения асимптот находят из условия
. Частоту сопряжения асимптот находят из условия  , откуда
, откуда

Для фильтра низких частот (рис. 6.23,в) аналогично рассмотренному имеем

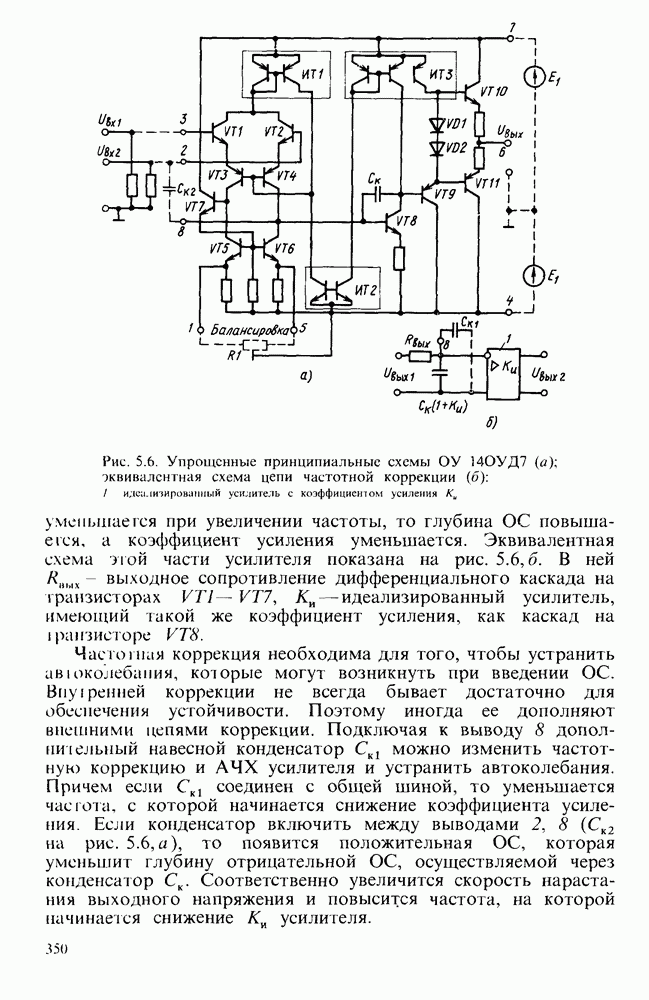
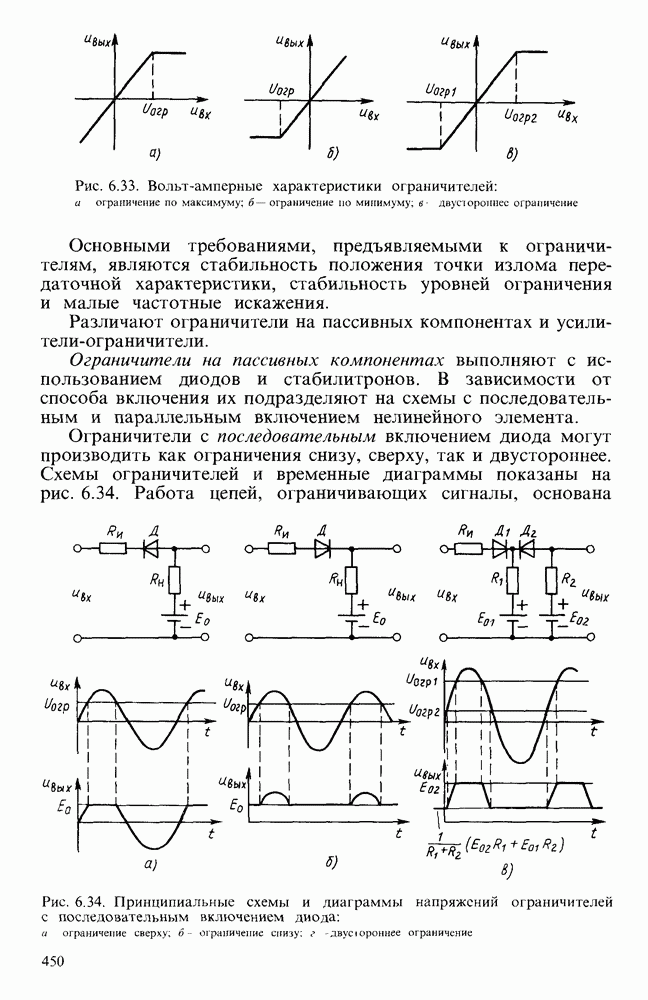
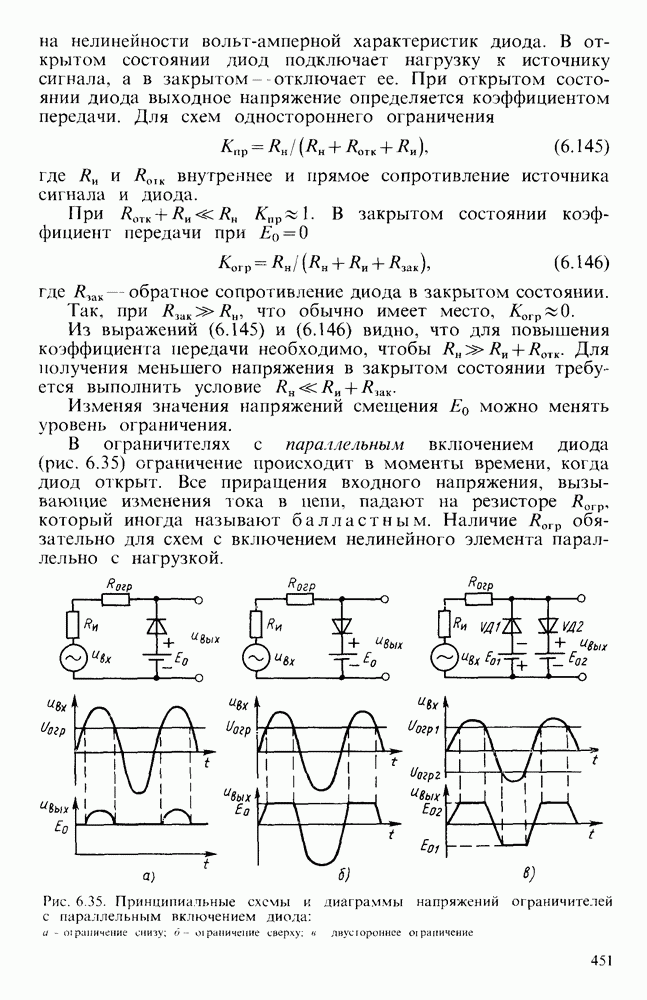
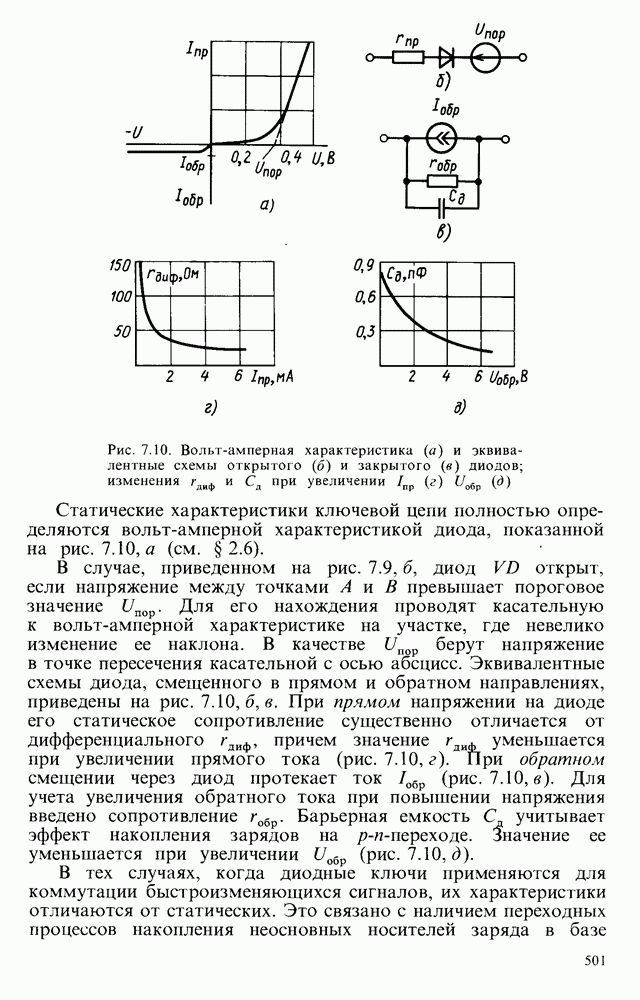
Рис. 6.23. Схемы фильтров: а — высоких частот, б - его ЛАЧХ; в — низких частот; г — его ЛАЧХ

или в операторном виде
 (6-119)
(6-119)
где  .
.
ЛАЧХ фильтра низких частот показана на рис. 6.23, г. Так как на частоте сопряжения асимптот выполняется условие  , то частота сопряжения
, то частота сопряжения  .
.
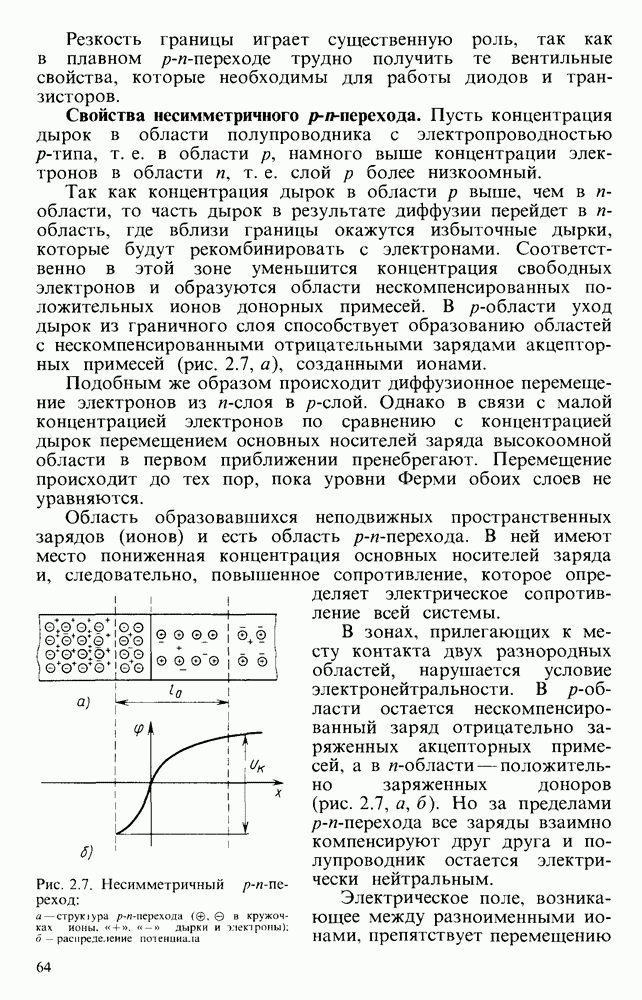
Передаточные функции приведенных простейших фильтров представляют собой уравнения первого порядка, поэтому и фильтры называются фильтрами первого порядка. Коэффициент усиления у них уменьшается с частотой на  .
.
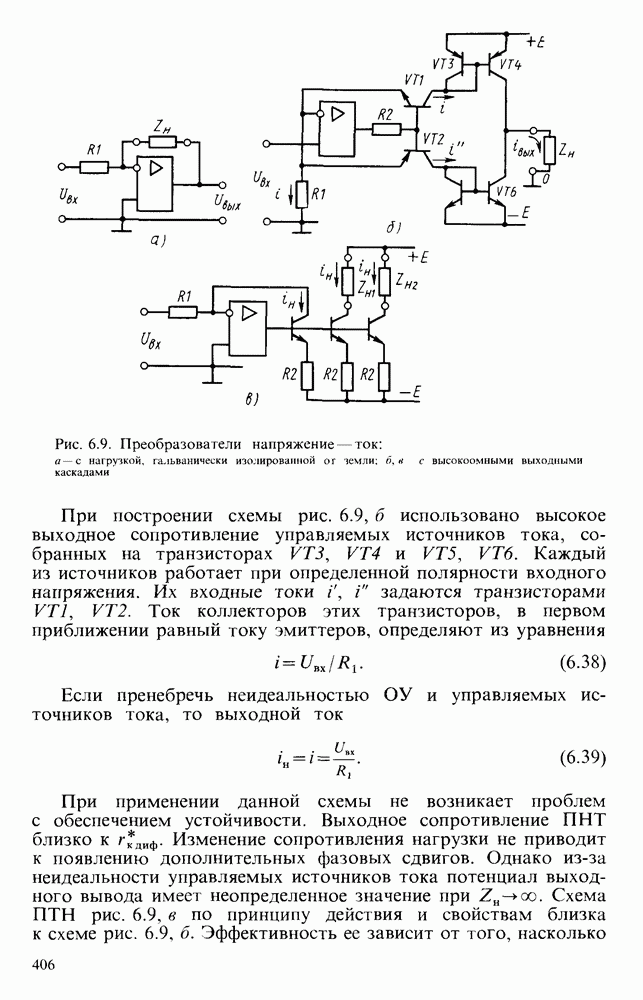
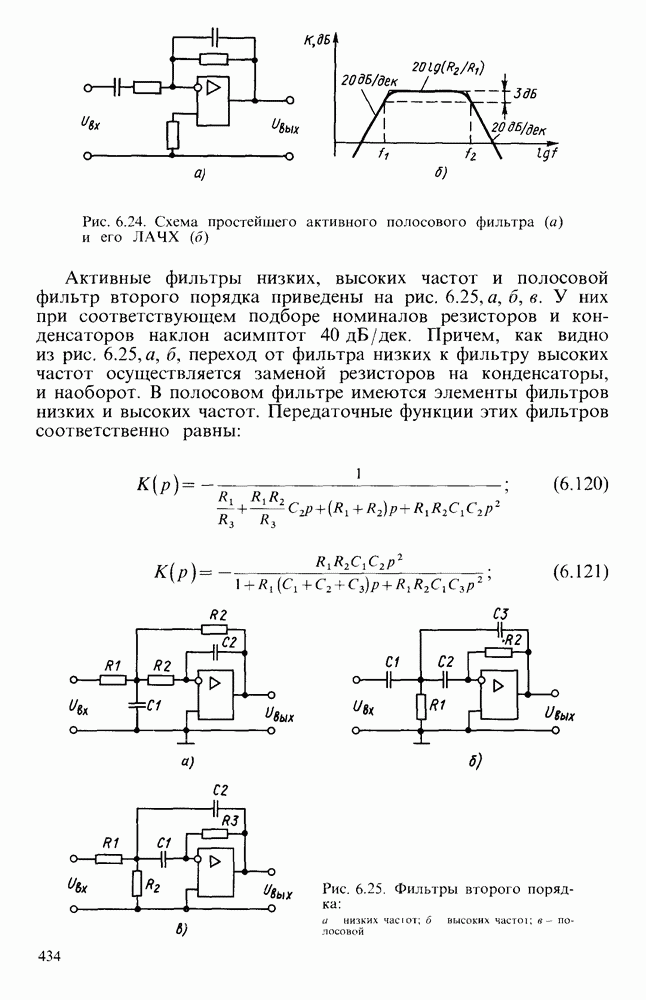
При объединении фильтров низких и высоких частот (рис. 6.23, а, в) получается полосовой фильтр (рис. 6.24, а), имеющий ЛАЧХ (рис. 6.24,б).
Простейшие активные фильтры имеют малую крутизну спада ЛАЧХ, что свидетельствует о плохих избирательских свойствах. Для улучшения избирательности нужно повышать порядок передаточных функций за счет введения дополнительных  -цепей или последовательного включения идентичных активных фильтров. На практике наиболее часто используют ОУ с цепями ОС, работа которых описывается уравнениями второго порядка. При необходимости повысить избирательность системы отдельные фильтры второго порядка включают последовательно.
-цепей или последовательного включения идентичных активных фильтров. На практике наиболее часто используют ОУ с цепями ОС, работа которых описывается уравнениями второго порядка. При необходимости повысить избирательность системы отдельные фильтры второго порядка включают последовательно.

Рис. 6.24. Схема простейшего активного полосового фильтра (а) и его ЛАЧХ (б)
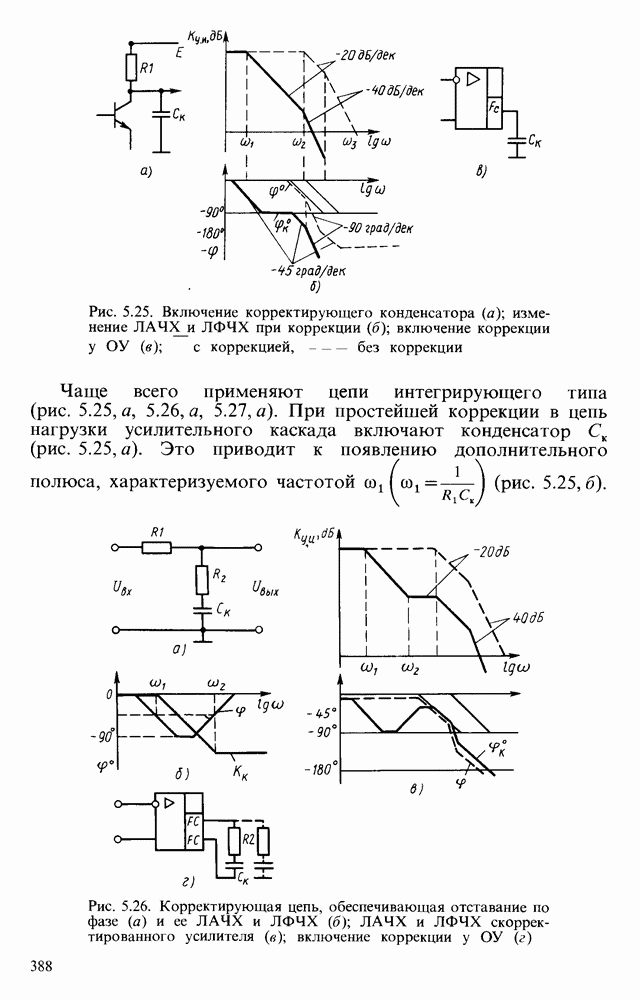
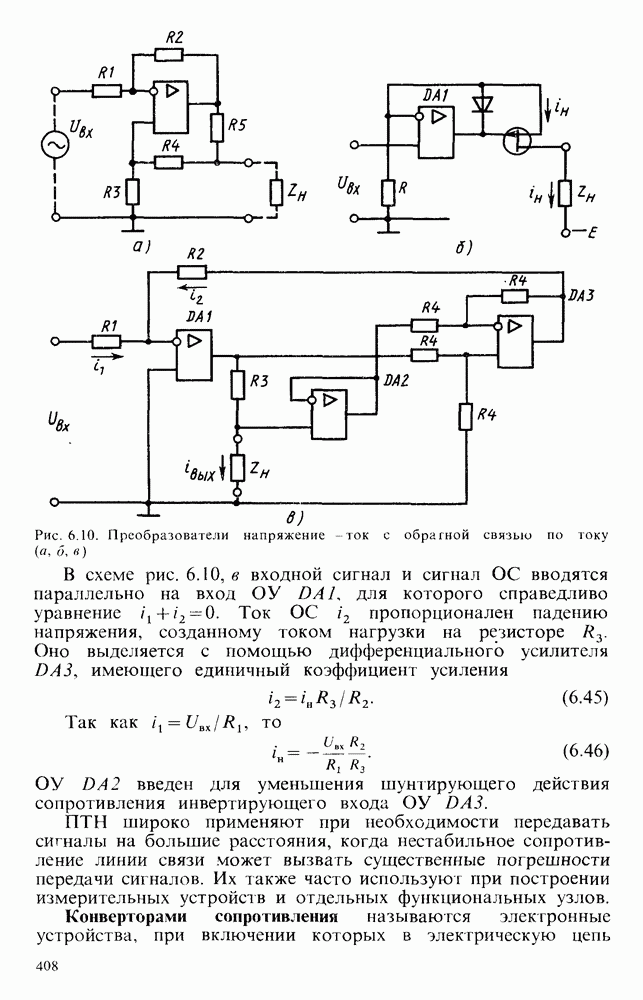
Активные фильтры низких, высоких частот и полосовой фильтр второго порядка приведены на рис. 6.25, а, б, в. У них при соответствующем подборе номиналов резисторов и конденсаторов наклон асимптот  . Причем, как видно из рис. 6.25, а, б, переход от фильтра низких к фильтру высоких частот осуществляется заменой резисторов на конденсаторы, и наоборот. В полосовом фильтре имеются элементы фильтров низких и высоких частот. Передаточные функции этих фильтров соответственно равны:
. Причем, как видно из рис. 6.25, а, б, переход от фильтра низких к фильтру высоких частот осуществляется заменой резисторов на конденсаторы, и наоборот. В полосовом фильтре имеются элементы фильтров низких и высоких частот. Передаточные функции этих фильтров соответственно равны:
 (6.120)
(6.120)

Рис. 6.25. Фильтры второго порядка: а - низких частот; б - высоких частот; в - полосовой
 (6.122)
(6.122)
Для полосового фильтра рис. 6.25, в резонансная частота

Для фильтров низких и высоких частот частоты, характеризующие «начало» среза или его окончание, равны
 (6.124)
(6.124)
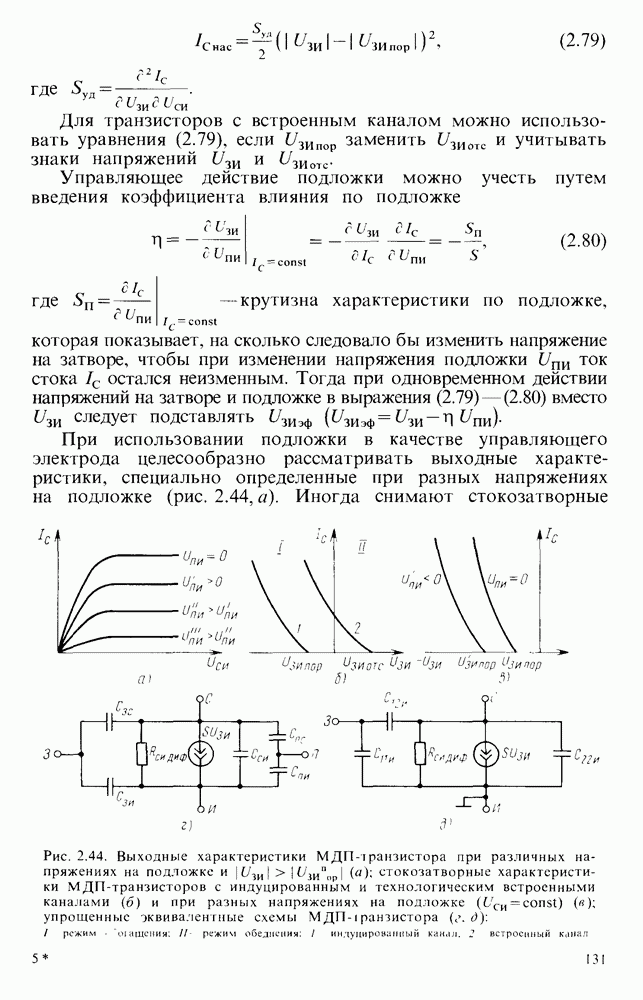
Вид их частотной характеристики зависит от параметров компонентов. Она может быть монотонно убывающей или возрастающей или иметь немонотонный вид и подъемы вблизи частоты  .
.
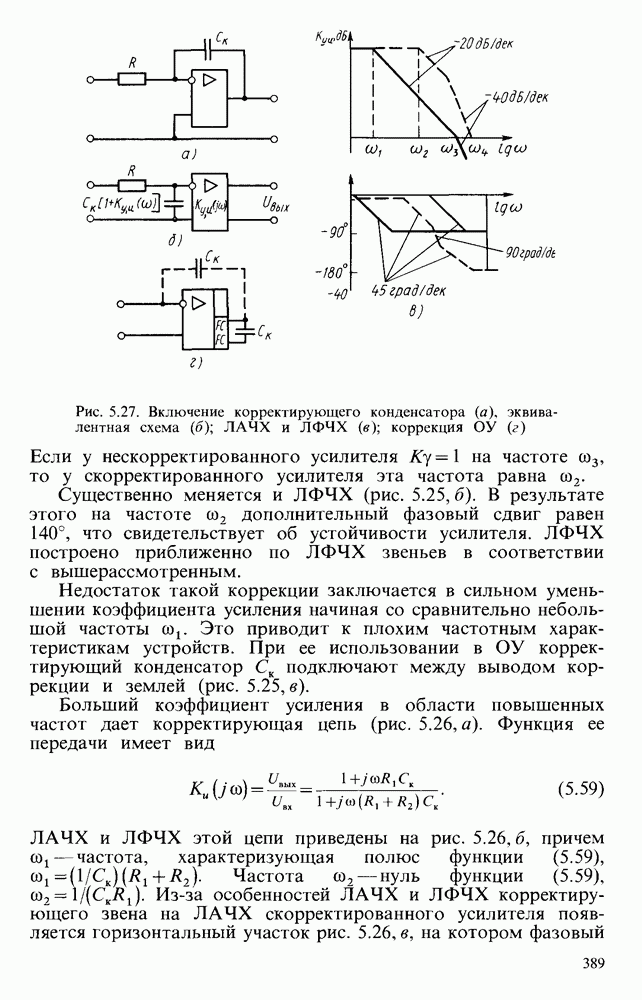
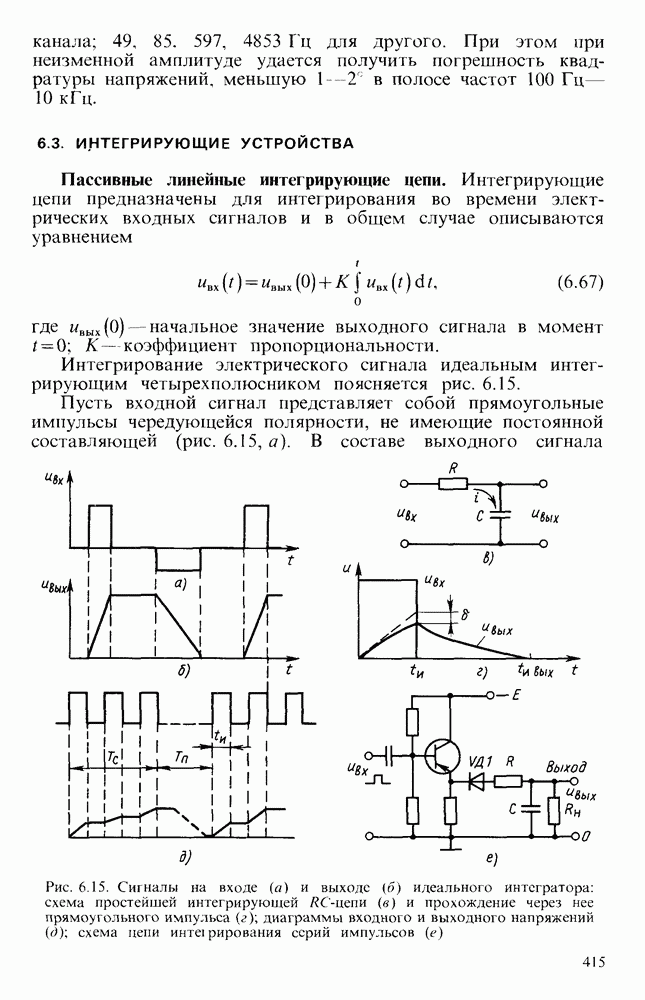
Достаточно часто полосовые фильтры второго порядка реализуют с помощью мостовых цепей. Наиболее распространены двойные Т-образные мосты, которые «не пропускают» сигнал на частоте резонанса (рис. 6.26, а) и мосты Вина, имеющие максимальный коэффициент передачи на резонансной частоте  (рис. 6.26. б).
(рис. 6.26. б).
Мостовые цепи включены в цепи отрицательной и положительной ОС. В случае двойного Т-образного моста глубина отрицательной ОС минимальна на частоте резонанса. Коэффициент усиления на этой частоте имеет максимальное значение. При использовании моста Вина на частоте резонанса получается максимальная глубина положительной ОС и наибольшее усиление. При этом для сохранения устойчивости глубина отрицательной ОС, созданной с помощью резисторов  , должна быть больше положительной. Если коэффициенты положительной и отрицательной ОС близки, то данный активный фильтр может иметь эквивалентную добротность 2 да 2000.
, должна быть больше положительной. Если коэффициенты положительной и отрицательной ОС близки, то данный активный фильтр может иметь эквивалентную добротность 2 да 2000.
Резонансную частоту двойного Т-образного моста при  и моста Вина при
и моста Вина при  выбирают исходя из условия устойчивости
выбирают исходя из условия устойчивости  , так как коэффициент передачи моста Вина на частоте
, так как коэффициент передачи моста Вина на частоте  равен 1/3.
равен 1/3.
Для получения режекторного фильтра двойной Т-образный мост можно включить так, как показано на рис. 6.26, в, или мост Вина включить в цепь отрицательной ОС.

Рис. 6.26. Полосовые фильтры: а с двойным Т-образным мостом,  мостом Випа; в — режекторный фильтр; г — схема сложного активного фильтра; д — его ЛАЧХ при снятии сигнала с ВЧ выхода, е - ЛАЧХ при снятии сигнала с НЧ-выхода,
мостом Випа; в — режекторный фильтр; г — схема сложного активного фильтра; д — его ЛАЧХ при снятии сигнала с ВЧ выхода, е - ЛАЧХ при снятии сигнала с НЧ-выхода,  - ЛАЧХ при снятии сигнала с НЧ-выхода
- ЛАЧХ при снятии сигнала с НЧ-выхода
Если активный фильтр требуется перестраивать в широких пределах, то обычно используют мост Вина, у которого резисторы  и
и  выполняют в виде сдвоенного переменного резистора.
выполняют в виде сдвоенного переменного резистора.
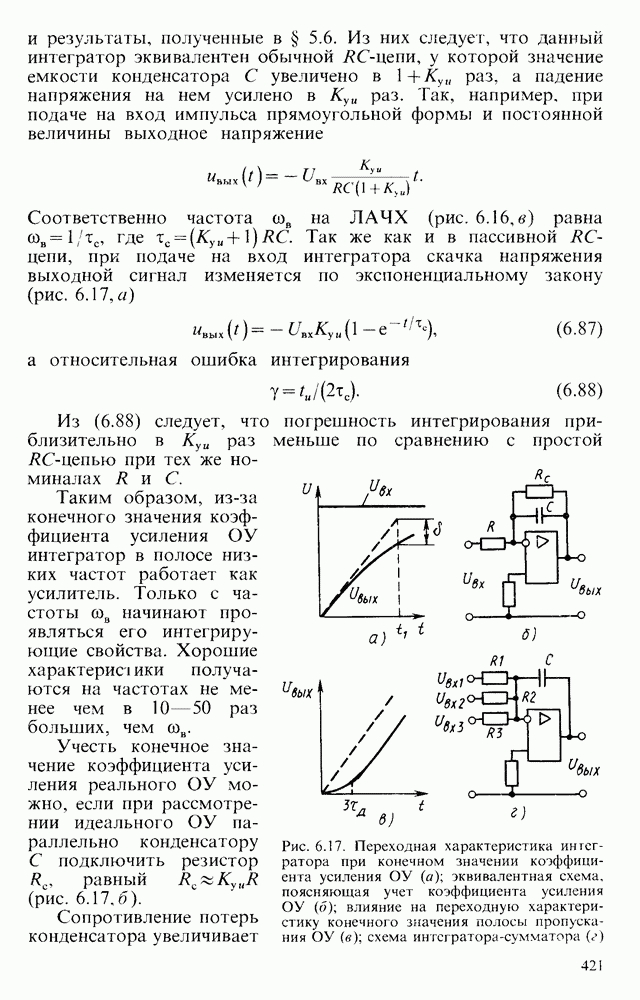
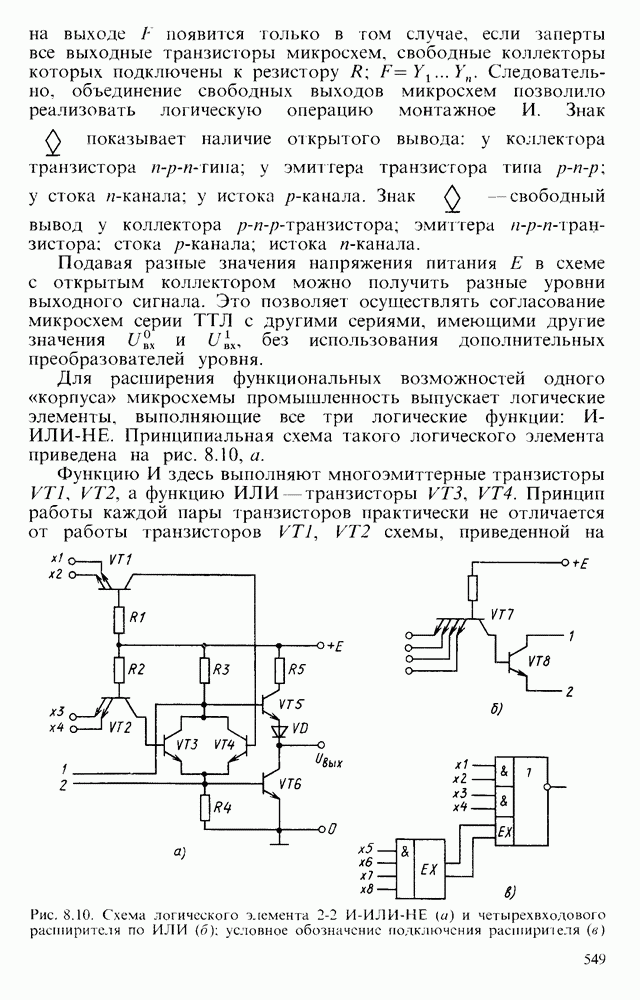
С удешевлением и выпуском нескольких ОУ в одном корпусе начали широко применять несколько активных фильтров низких порядков, объединенных между собой в единую замкнутую систему. Пример построения такого фильтра показан на рис. 6.26, г.
В его состав входят сумматор на ОУ  и два фильтра низких частот первого порядка на ОУ
и два фильтра низких частот первого порядка на ОУ  . Сумматор и активные фильтры включены последовательно. Если
. Сумматор и активные фильтры включены последовательно. Если  , то частота сопряжения
, то частота сопряжения  .
.
Асимптоты имеют наклон  (рис. 6.26, д, е, ж). В подобном сложном фильтре удается одновременно реализовать фильтры низких и высоких частот, а также полосовой фильтр, который имеет сравнительно низкую чувствительность к отклонениям параметров отдельных компонентов, что бывает важно при практической реализации избирательных устройств. Структура, близкая к разобранной, использована в микросхеме типа
(рис. 6.26, д, е, ж). В подобном сложном фильтре удается одновременно реализовать фильтры низких и высоких частот, а также полосовой фильтр, который имеет сравнительно низкую чувствительность к отклонениям параметров отдельных компонентов, что бывает важно при практической реализации избирательных устройств. Структура, близкая к разобранной, использована в микросхеме типа  .
.
В электронных цепях кроме рассмотренных используют фазовые фильтры. Они имеют не зависящий от частоты коэффициент передачи и пропорциональный ей фазовый сдвиг выходного сигнала. В качестве фазовых фильтров можно использовать фазосдвигающие устройства (рис. 6.14,а, б), работа которых рассмотрена ранее.
Наиболее важным его параметром является групповое время задержки, под ним понимают промежуток времени, на который сигнал задерживается фазовым фильтром:  . Групповое время задержки в общем случае меняется при изменении частоты сигнала и зависит от порядка уравнения, характеризующего математическую модель фильтра.
. Групповое время задержки в общем случае меняется при изменении частоты сигнала и зависит от порядка уравнения, характеризующего математическую модель фильтра.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПАССИВНЫЕ КОМПОНЕНТЫ ЭЛЕКТРОННЫХ УСТРОЙСТВ
- § 1.1. РЕЗИСТОРЫ
- Основные параметры резисторов
- § 1.2. КОНДЕНСАТОРЫ
- Основные параметры постоянных конденсаторов
- 1.3. КАТУШКИ ИНДУКТИВНОСТИ
- Основные параметры катушки индуктивности (ГОСТ 20718—75)
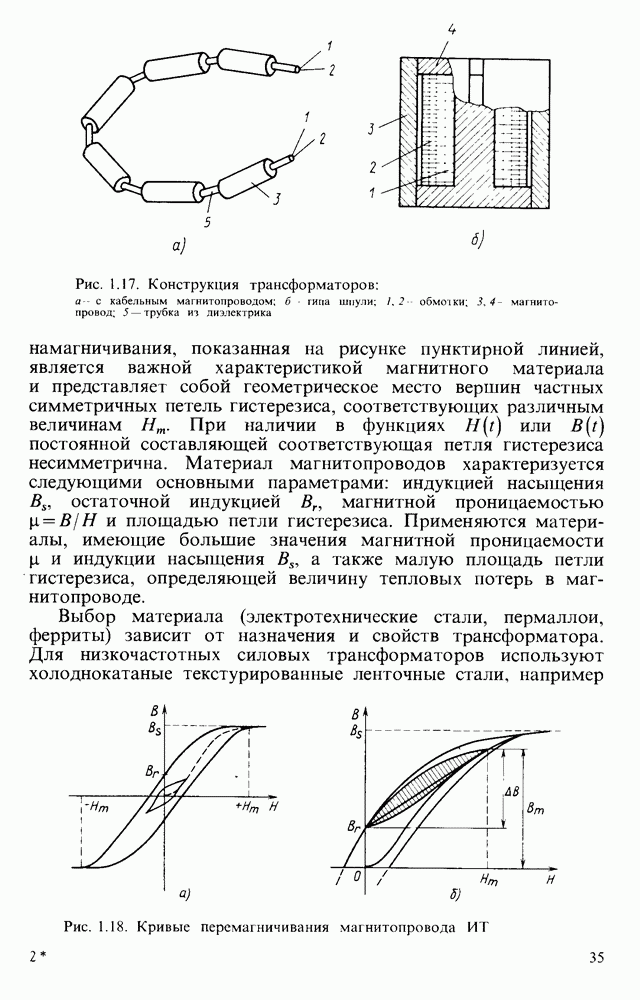
- § 1.4. ТРАНСФОРМАТОРЫ ЭЛЕКТРОННОЙ АППАРАТУРЫ
- Основные параметры трансформаторов питания
- ГЛАВА 2. ПОЛУПРОВОДНИКОВЫЕ КОМПОНЕНТЫ ЭЛЕКТРОННЫХ ЦЕПЕЙ
- § 2.1. ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
- Основные положения теории электропроводности.
- Примесная электропроводность.
- § 2.2. ОСНОВНЫЕ СВОЙСТВА И ХАРАКТЕРИСТИКИ ПОЛУПРОВОДНИКОВ
- Концентрация носителей зарядов.
- Уравнения непрерывности.
- § 2.3. ЭЛЕКТРИЧЕСКИЕ ПЕРЕХОДЫ
- Контакт металл — полупроводник.
- Контакт двух полупроводников p- и n-типов.
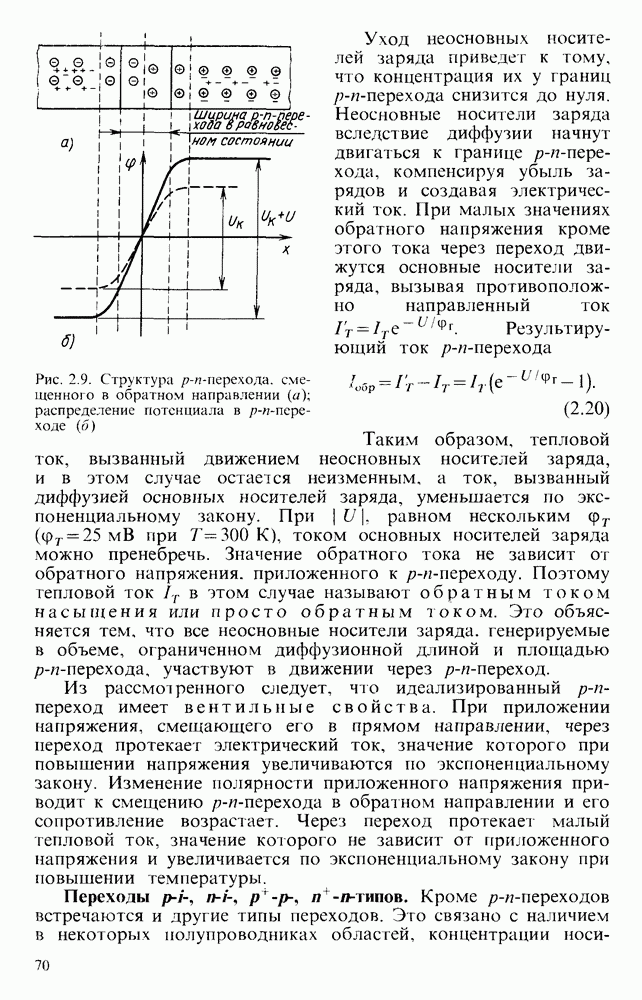
- Свойства несимметричного p-n-перехода.
- p-n-переход смещен в прямом направлении
- Переход, смещенный в обратном направлении.
- Переходы p-i, n-i-, p+-p-, n+-n-типов.
- 2.4. ОСОБЕННОСТИ РЕАЛЬНЫХ p-n-ПЕРЕХОДОВ
- Пробой p-n-перехода.
- § 2.5. ОСНОВНЫЕ ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ, ИСПОЛЬЗУЕМЫЕ ПРИ ИЗГОТОВЛЕНИИ ПОЛУПРОВОДНИКОВЫХ ПРИБОРОВ И ИНТЕГРАЛЬНЫХ МИКРОСХЕМ
- § 2.6. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
- Выпрямительные диоды.
- Основные параметры выпрямительных диодов и их значения у маломощных диодов
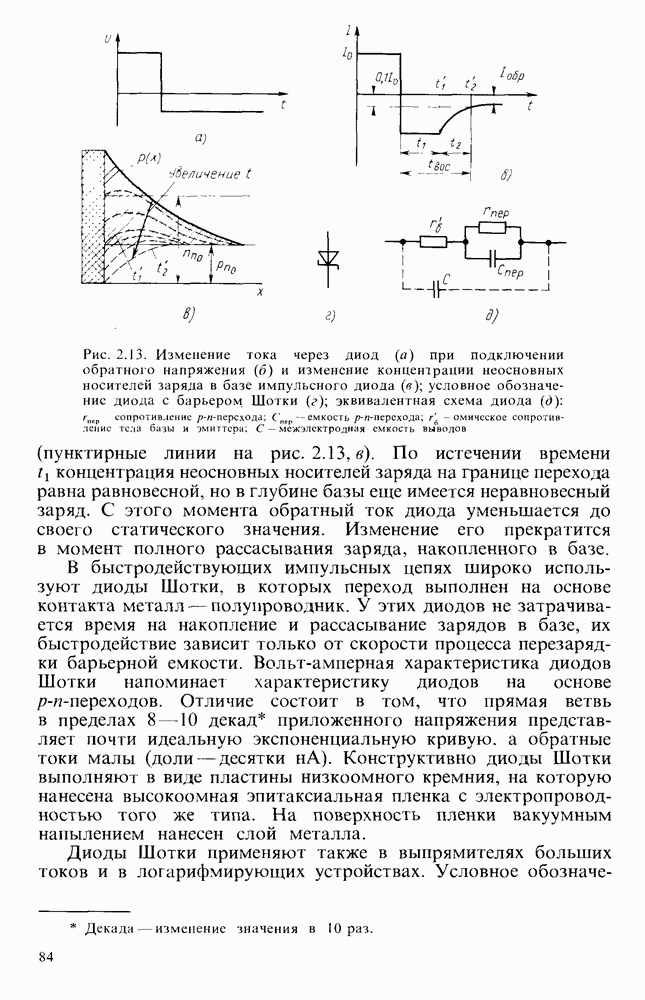
- Импульсные диоды.
- Полупроводниковые стабилитроны.
- Варикапы.
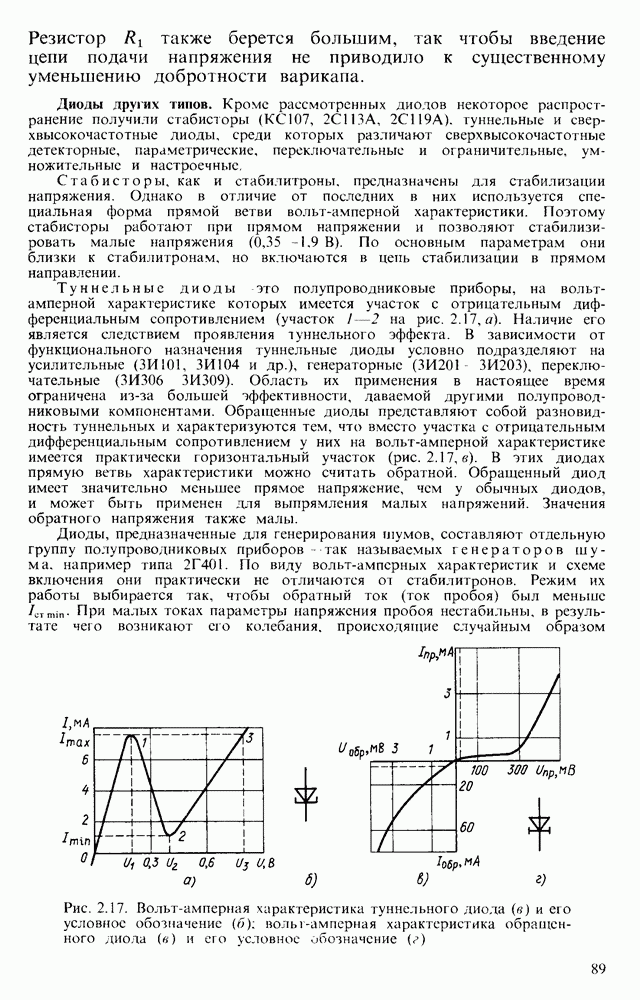
- Диоды других типов.
- § 2.7. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ
- Математическая модель транзистора.
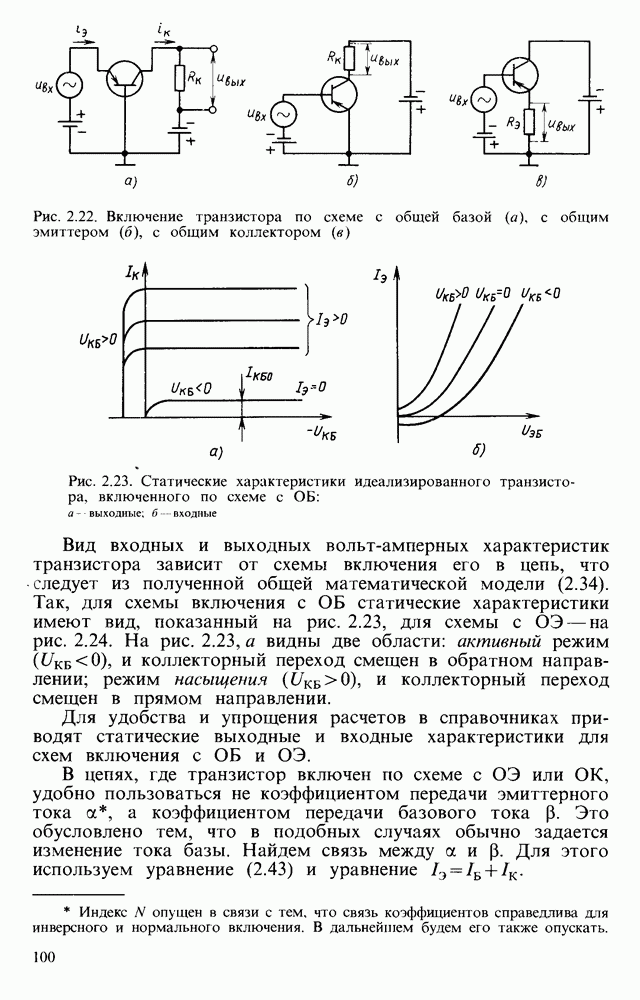
- Три схемы включения транзистора.
- Инерционные свойства транзистора.
- Шумы транзистора.
- Н-параметры транзисторов.
- § 2.8. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ С ИНЖЕКЦИОННЫМ ПИТАНИЕМ
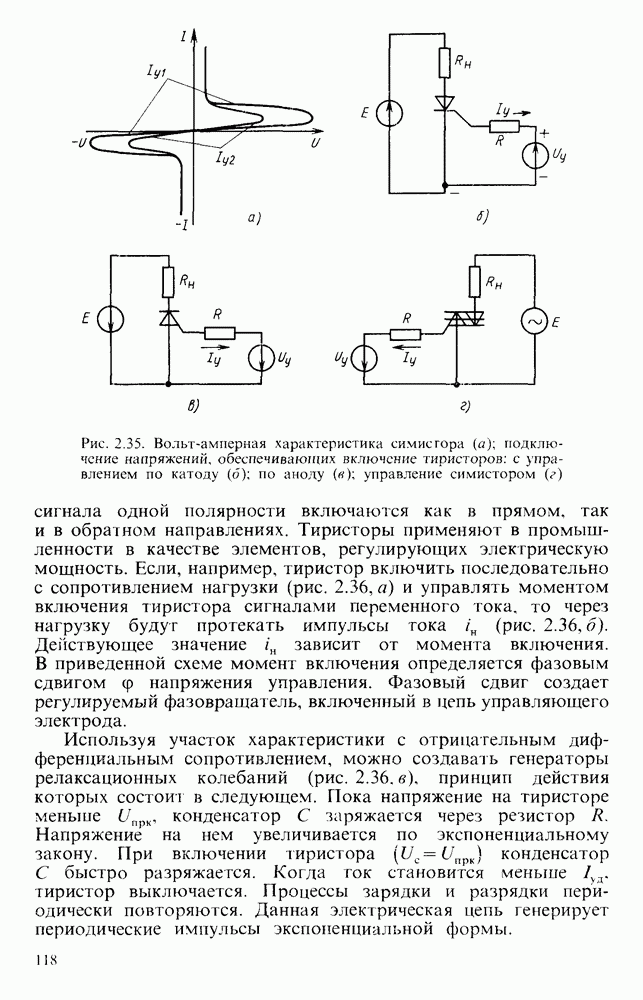
- § 2.9. ТИРИСТОРЫ
- Симметричные тиристоры.
- Основные параметры тиристоров и их ориентировочные значения
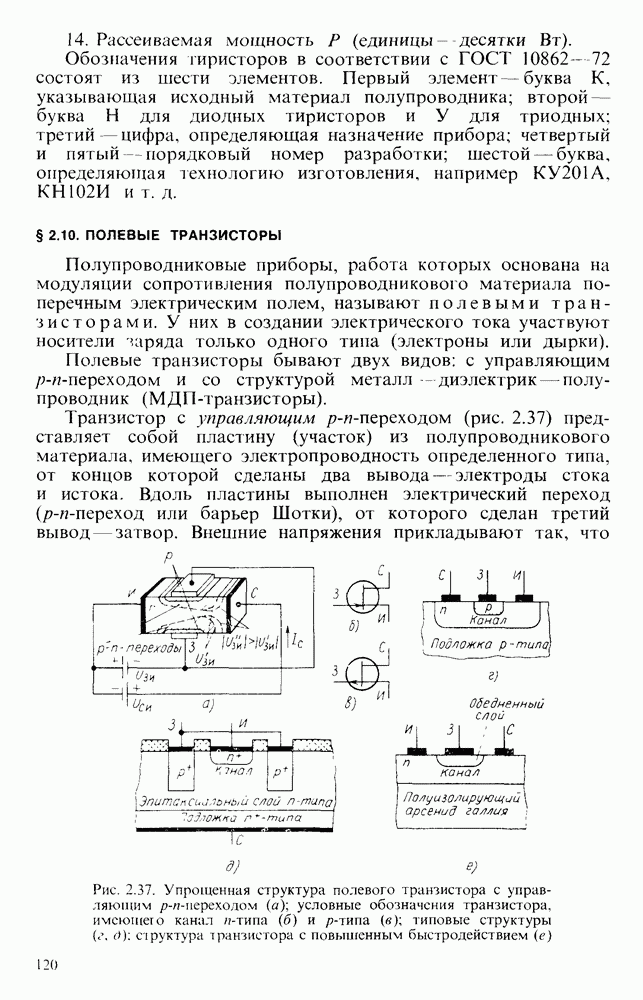
- § 2.10. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
- Основные параметры полевых транзисторов и их ориентировочные значения
- § 2.11. ОСОБЕННОСТИ КОМПОНЕНТОВ ЭЛЕКТРОННЫХ ЦЕПЕЙ В МИКРОМИНИАТЮРНОМ ИСПОЛНЕНИИ
- Пассивные компоненты ИС.
- Конденсаторы.
- Индуктивности.
- Транзисторы ИС.
- Изоляция компонентов в монолитных интегральных узлах.
- ГЛАВА 3. КОМПОНЕНТЫ ОПТОЭЛЕКТРОНИКИ И ТЕХНИЧЕСКИЕ СРЕДСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.1. ОБЩИЕ СВЕДЕНИЯ О КОМПОНЕНТАХ ОПТОЭЛЕКТРОНИКИ
- § 3.2. УПРАВЛЯЕМЫЕ ИСТОЧНИКИ СВЕТА
- Основные параметры и характеристики светодиодов
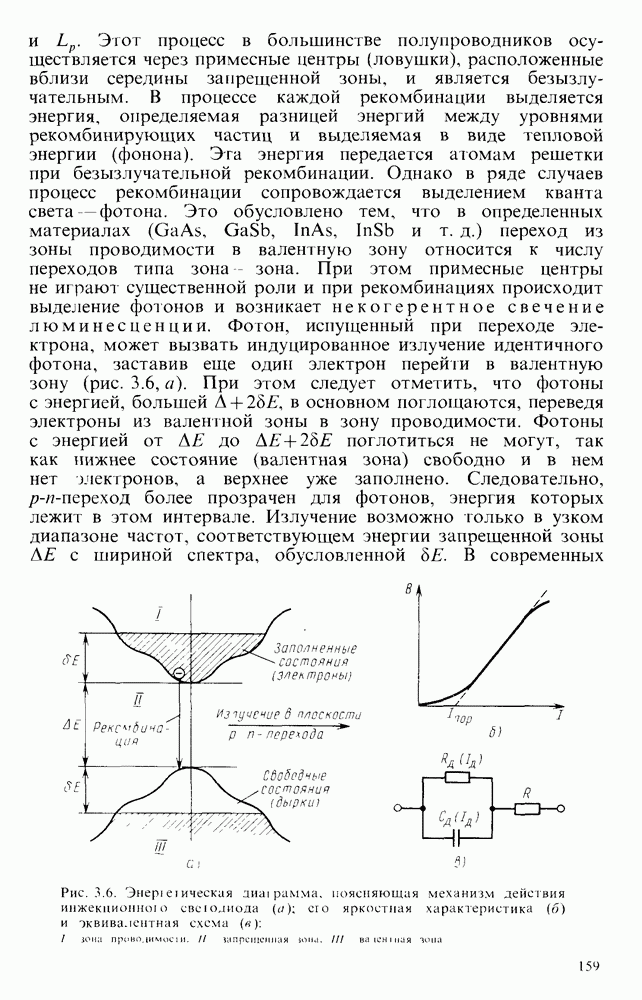
- § 3.3. ФОТОПРИЕМНИКИ
- Основные характеристики и параметры фоторезистора
- Фотодиоды.
- Основные характеристики и параметры фотодиода
- Фототранзисторы.
- Основные характеристики и параметры фототранзистора
- Фототиристоры.
- Многоэлементные фотоприемники.
- Фотоприемники с внешним фотоэффектом.
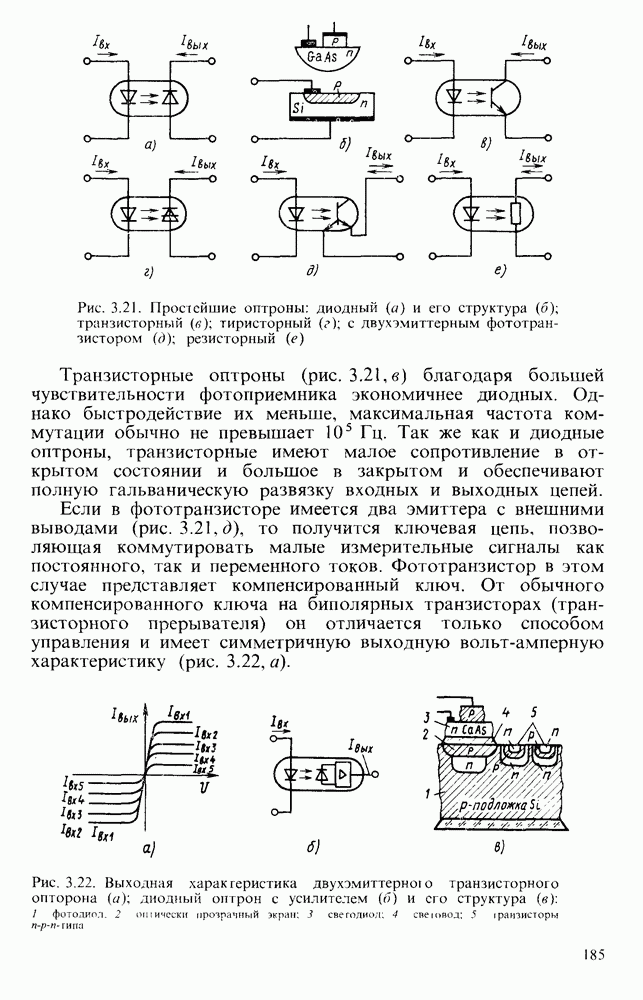
- § 3.4. СВЕТОВОДЫ И ПРОСТЕЙШИЕ ОПТРОНЫ
- § 3 5. ОБЩИЕ СВЕДЕНИЯ О КОМПОНЕНТАХ УСТРОЙСТВ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.6. ЖИДКОКРИСТАЛЛИЧЕСКИЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
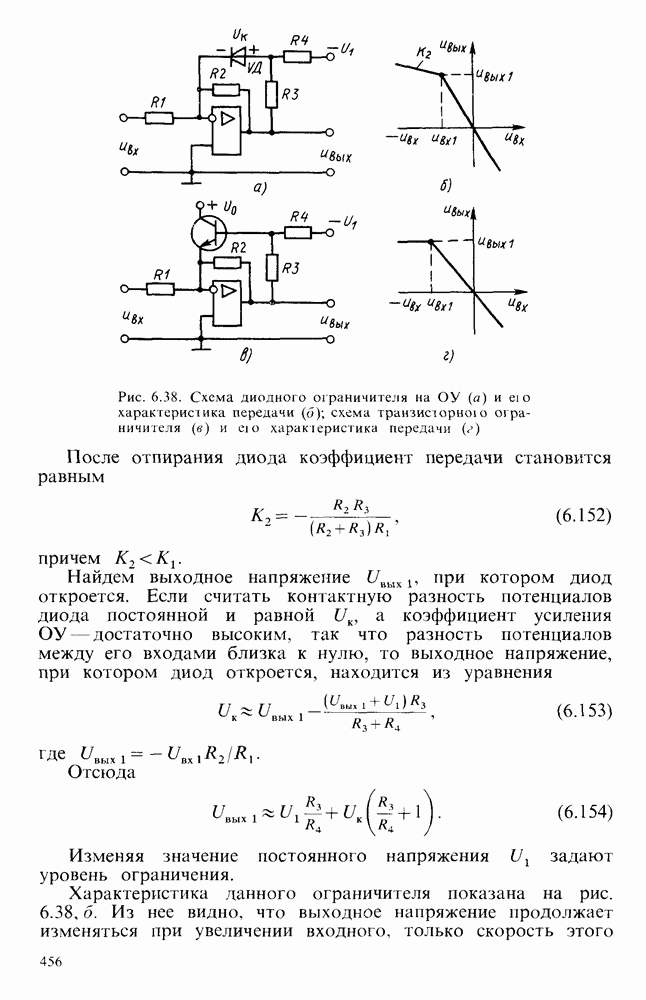
- § 3.7. ГАЗОНАПОЛНЕННЫЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- Основные параметры газонаполненных матричных панелей неременного тока
- § 3.8. ВАКУУМНЫЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- § 3.9. ПОЛУПРОВОДНИКОВЫЕ И ЭЛЕКТРОЛЮМИНЕСЦЕНТНЫЕ ПРИБОРЫ ДЛЯ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- ГЛАВА 4. УСИЛИТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- § 4.1. ОБЩИЕ СВЕДЕНИЯ ОБ УСИЛИТЕЛЯХ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ, ИХ ОСНОВНЫХ ПАРАМЕТРАХ И ХАРАКТЕРИСТИКАХ
- § 4.2. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ОБРАТНОЙ СВЯЗИ ПРИМЕНИТЕЛЬНО К УСИЛИТЕЛЯМ
- § 4.3. СТАТИЧЕСКИЙ РЕЖИМ РАБОТЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ
- § 4.4. УСИЛИТЕЛЬНЫЕ КАСКАДЫ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- Каскад с общим стоком.
- § 4.5. УСИЛИТЕЛЬНЫЙ КАСКАД НА БИПОЛЯРНОМ ТРАНЗИСТОРЕ С ОБЩИМ ЭМИТТЕРОМ
- Входное сопротивление.
- § 4.6. УСИЛИТЕЛЬНЫЙ КАСКАД НА БИПОЛЯРНОМ ТРАНЗИСТОРЕ С ОБЩЕЙ БАЗОЙ
- § 4.7. УСИЛИТЕЛЬНЫЙ КАСКАД НА БИПОЛЯРНОМ ТРАНЗИСТОРЕ С ОБЩИМ КОЛЛЕКТОРОМ
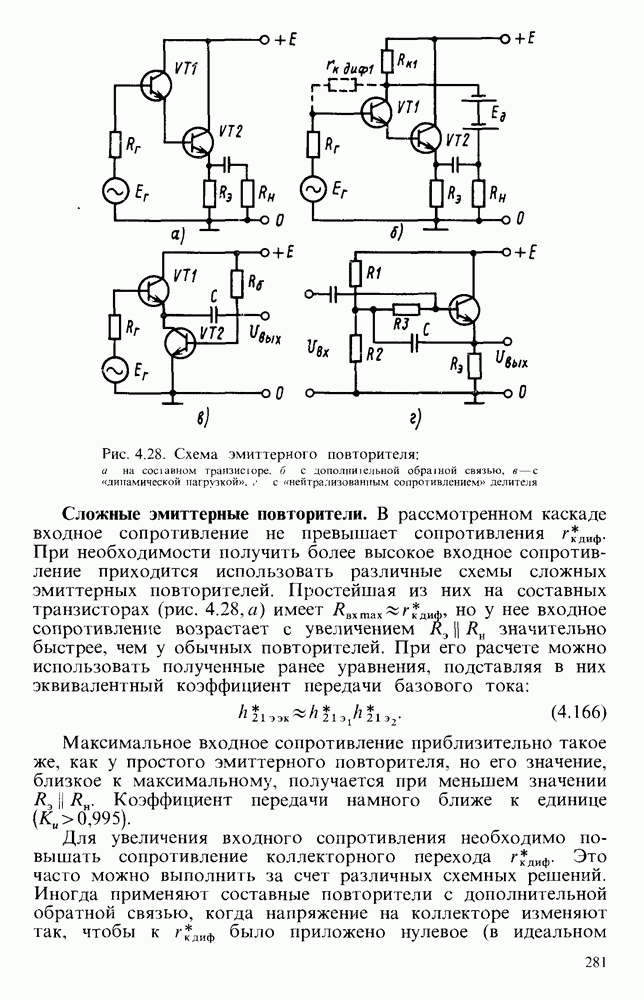
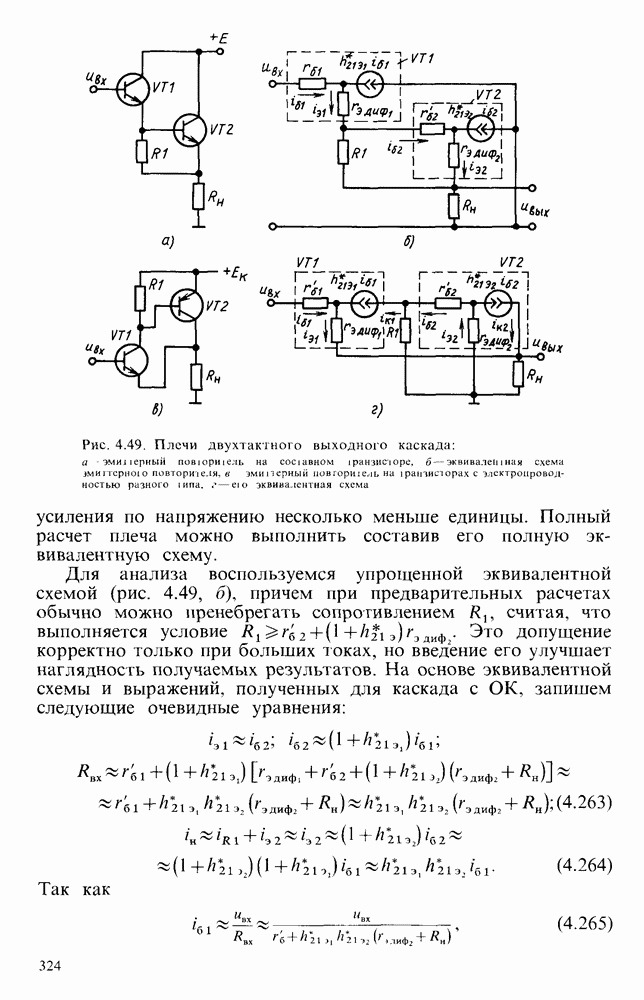
- Сложные эмиттерные повторители.
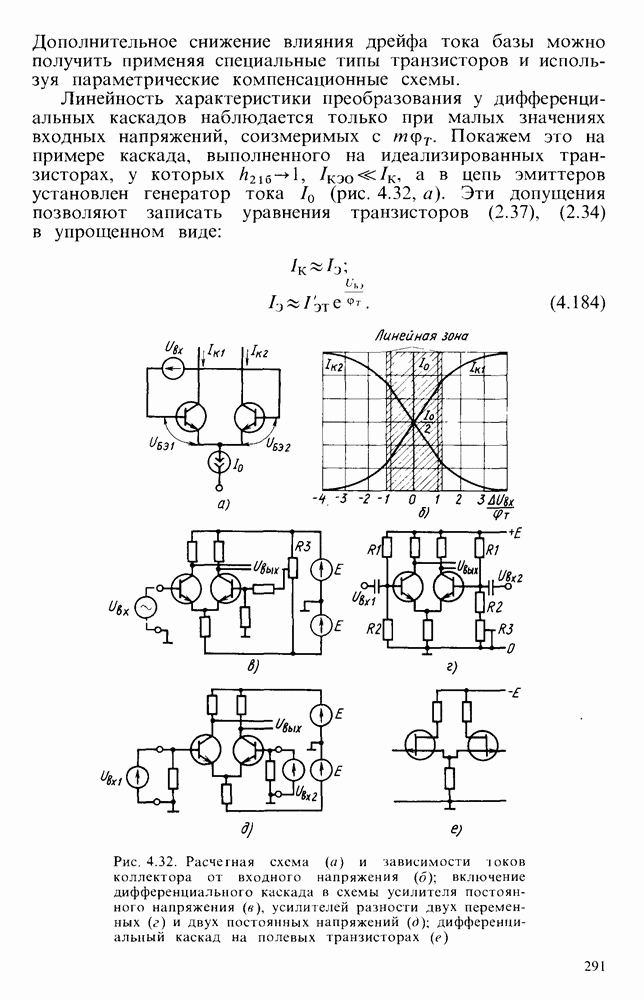
- § 4.8. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
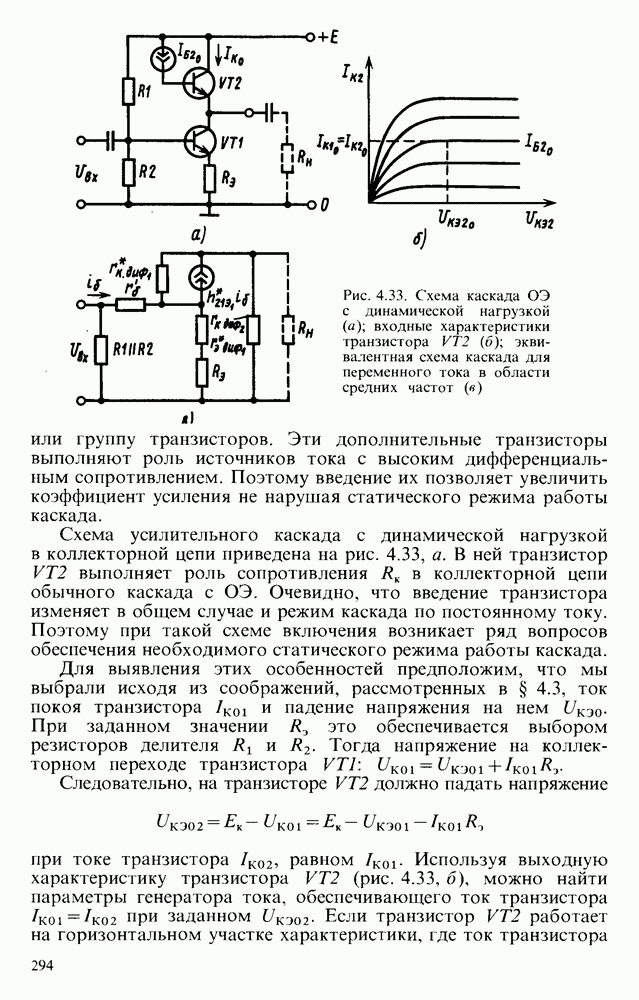
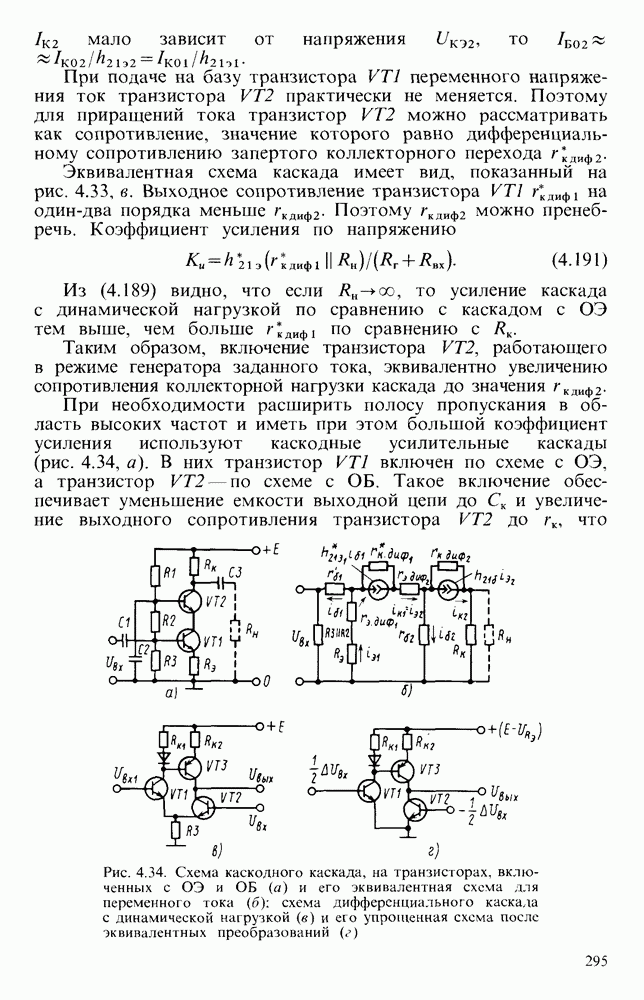
- § 4.9. УСИЛИТЕЛЬНЫЕ КАСКАДЫ С ДИНАМИЧЕСКОЙ НАГРУЗКОЙ И С КАСКОДНЫМ ВКЛЮЧЕНИЕМ ТРАНЗИСТОРОВ
- § 4.10. УПРАВЛЯЕМЫЕ ИСТОЧНИКИ ТОКА И УСИЛИТЕЛЬНЫЕ КАСКАДЫ НА ИХ ОСНОВЕ
- 4.11. УСИЛИТЕЛЬНЫЕ КАСКАДЫ С ТРАНСФОРМАТОРНОЙ СВЯЗЬЮ
- 4.12. МОЩНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- Каскад с ОБ трансформаторным входом и трансформаторным выходом.
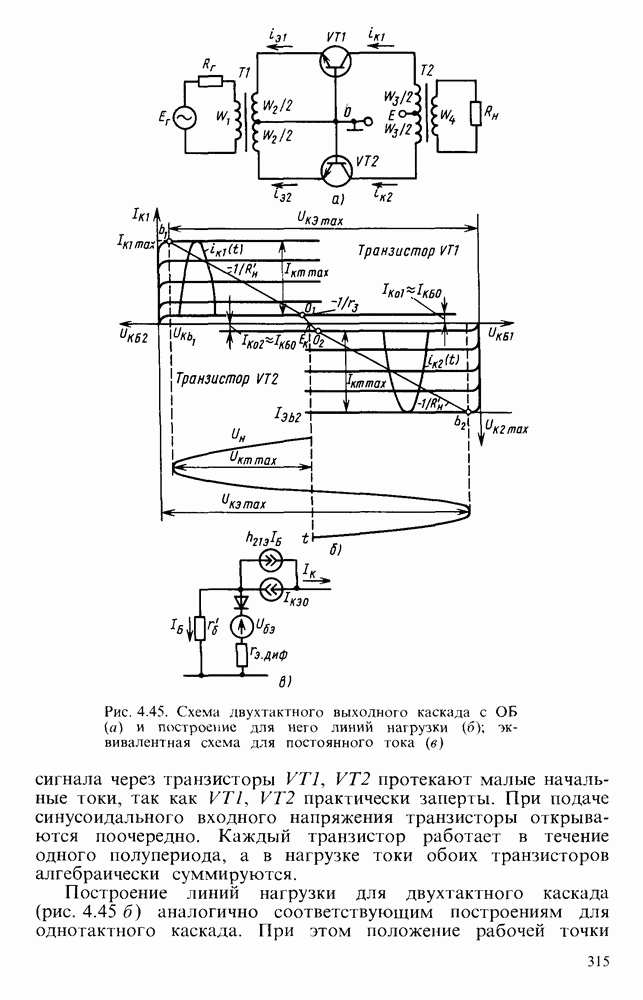
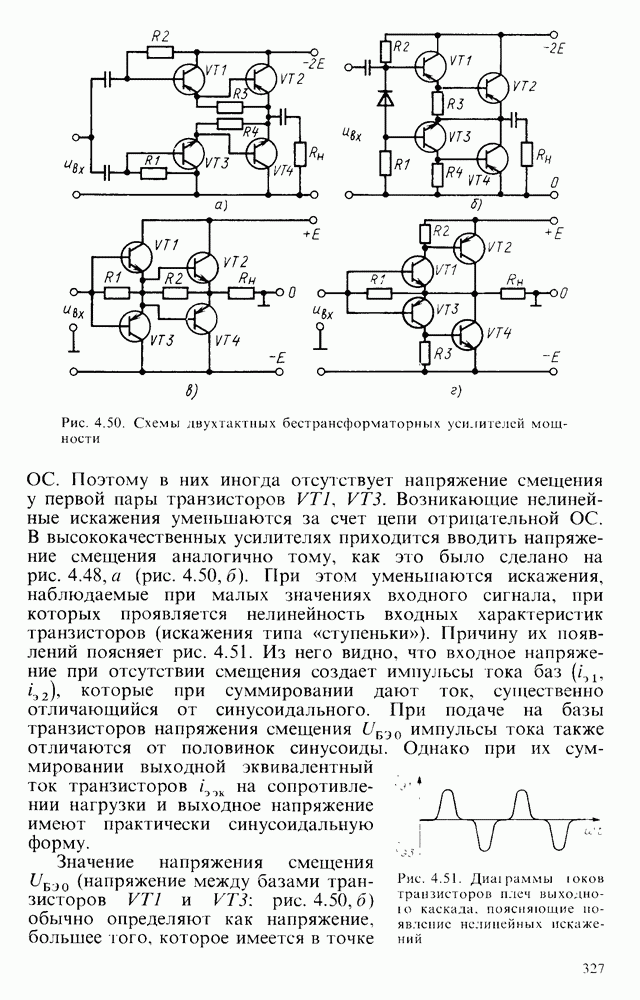
- Двухтактные выходные каскады.
- § 4.13. БЕСТРАНСФОРМАТОРНЫЕ МОЩНЫЕ ВЫХОДНЫЕ КАСКАДЫ
- ГЛАВА 5. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- § 5.1. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- Параметры RC-цепи связи.
- § 5.2. УСИЛИТЕЛИ В ИНТЕГРАЛЬНОМ ИСПОЛНЕНИИ
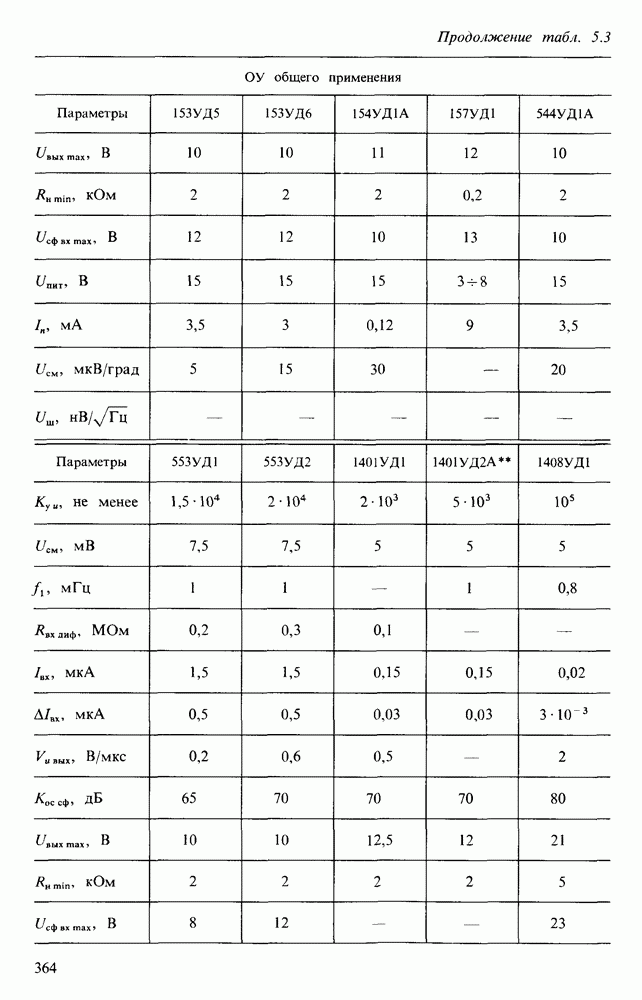
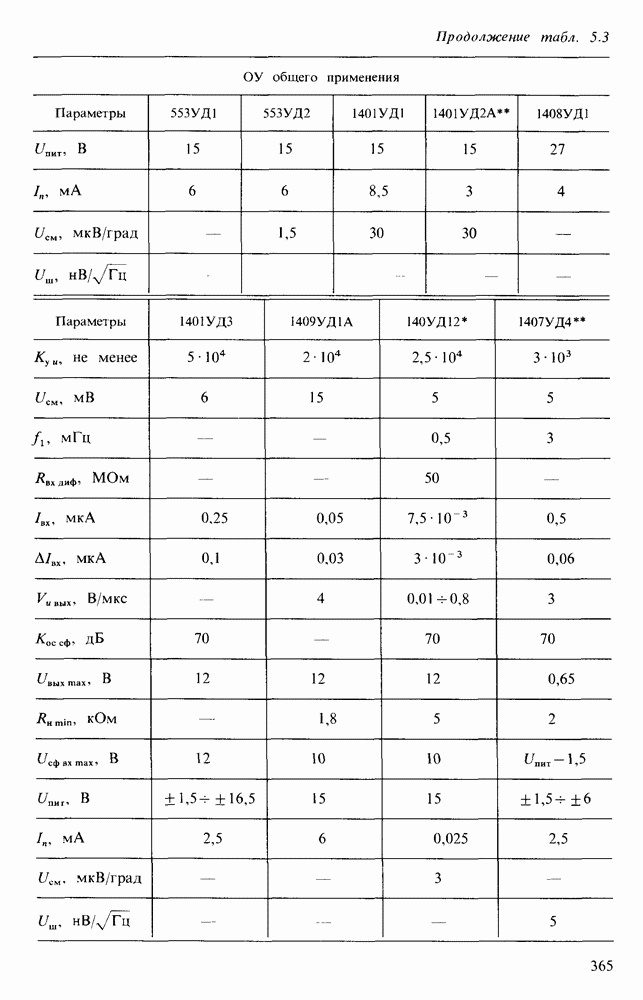
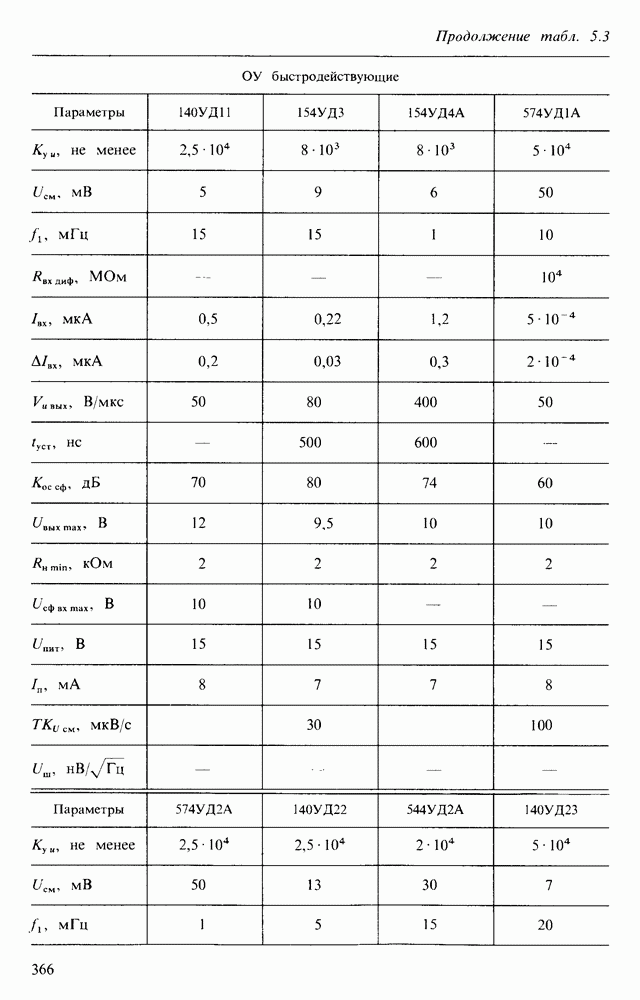
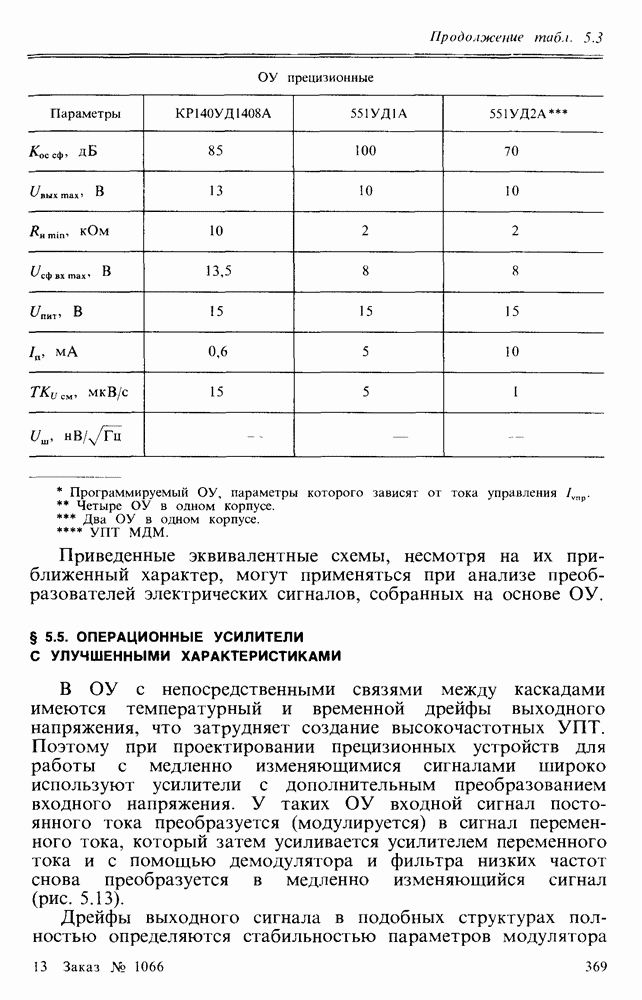
- 5.3. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- § 5.4. ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- § 5.5. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ С УЛУЧШЕННЫМИ ХАРАКТЕРИСТИКАМИ
- § 5.6. ОСОБЕННОСТИ ВКЛЮЧЕНИЯ И СВОЙСТВА ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ, ОХВАЧЕННЫХ ОБРАТНОЙ СВЯЗЬЮ
- § 5.7. УСТОЙЧИВОСТЬ УСИЛИТЕЛЕЙ И КОРРЕКЦИЯ ИХ ХАРАКТЕРИСТИК
- ГЛАВА 6. АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- § 6.1. МАСШТАБНЫЕ УСИЛИТЕЛИ
- 6.2. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 6.3. ИНТЕГРИРУЮЩИЕ УСТРОЙСТВА
- Интеграторы на основе операционных усилителей.
- § 6.4. ДИФФЕРЕНЦИРУЮЩИЕ УСТРОЙСТВА
- Активные дифференцирующие устройства.
- § 6.5. АКТИВНЫЕ ФИЛЬТРЫ
- § 6.6. МАГНИТОЭЛЕКТРОННЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- § 6.7. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
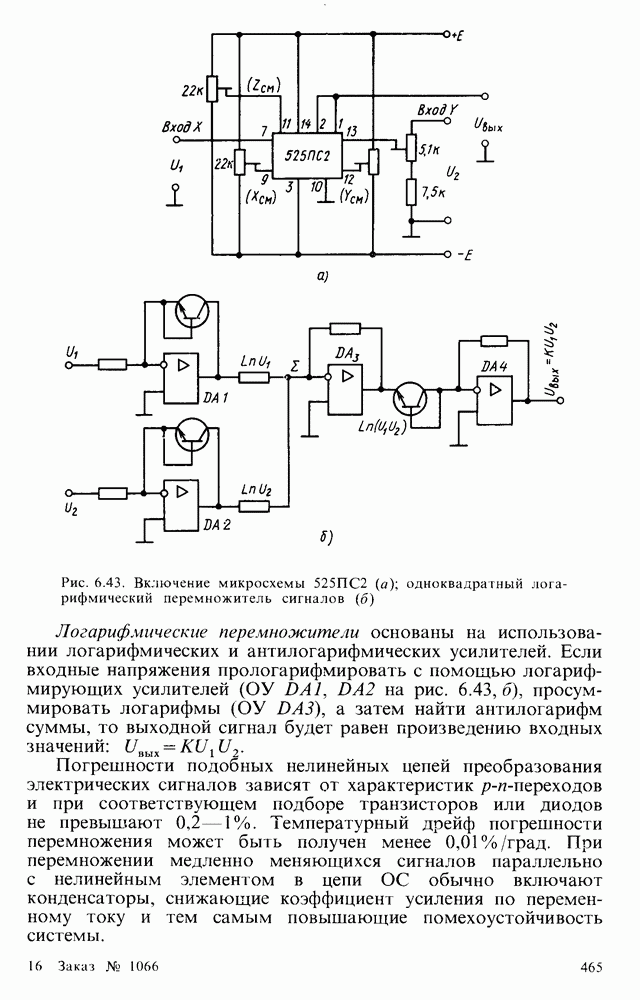
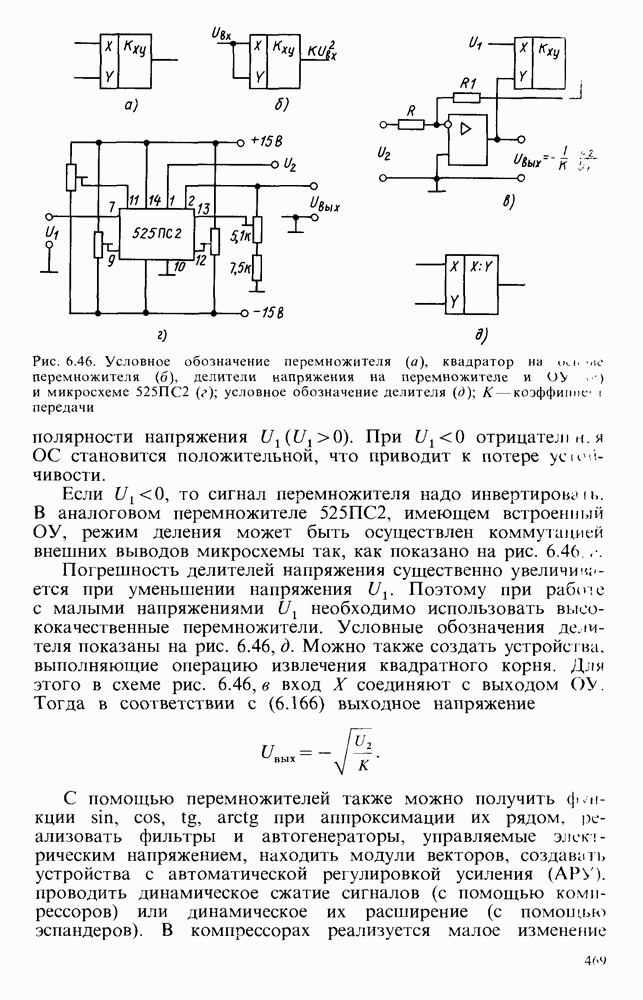
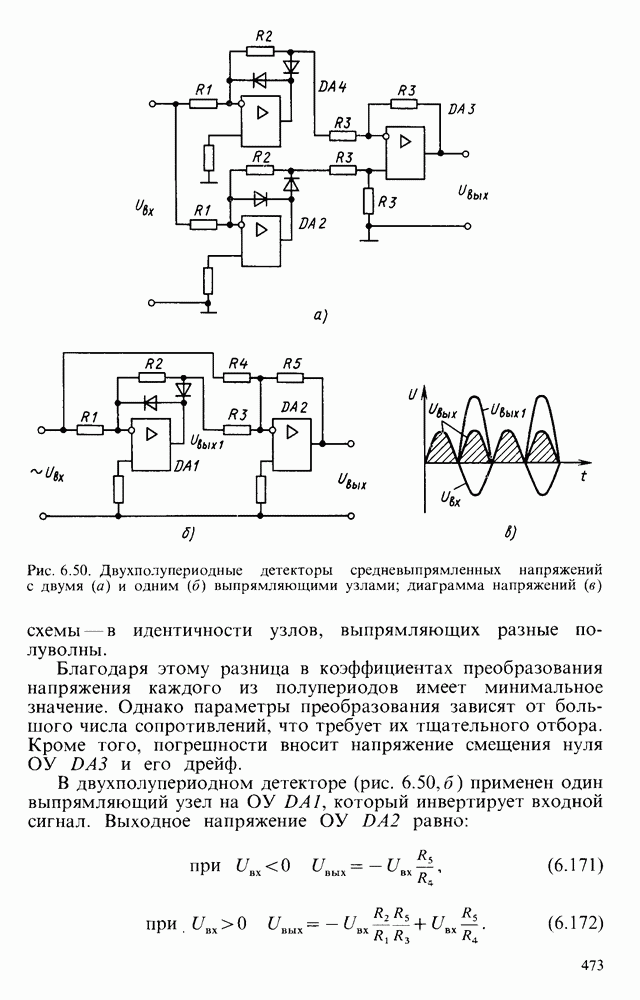
- § 6.8. ПЕРЕМНОЖИТЕЛИ СИГНАЛОВ И УСТРОЙСТВА, ВЫПОЛНЯЮЩИЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ
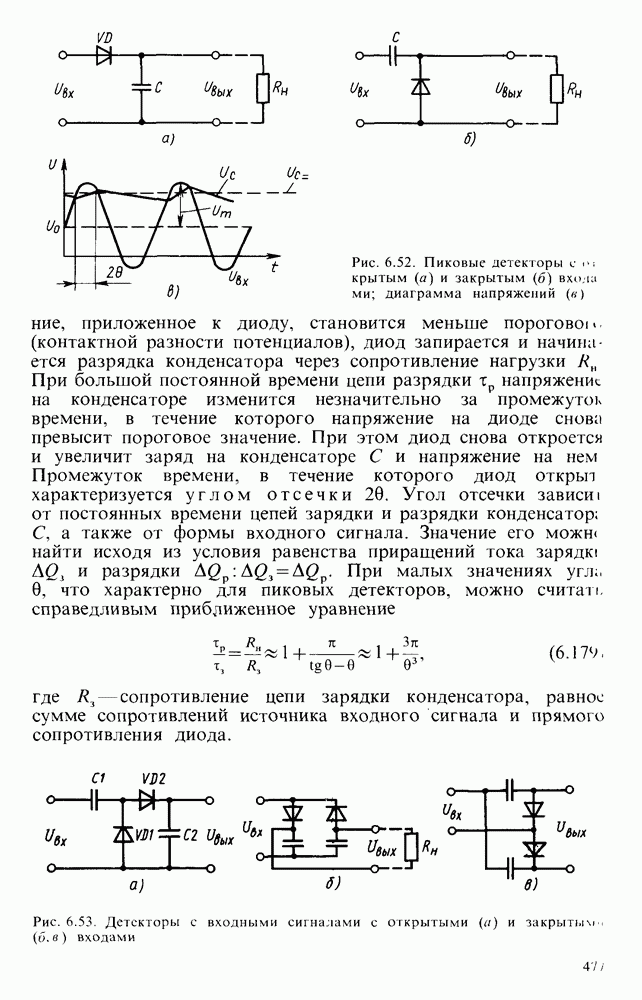
- § 6.9. ДЕТЕКТОРЫ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- ГЛАВА 7. ЭЛЕКТРОННЫЕ КЛЮЧИ
- § 7.1. ОБЩИЕ СВЕДЕНИЯ ОБ ИМПУЛЬСНЫХ ПРОЦЕССАХ И УСТРОЙСТВАХ
- § 7.2. ДИОДНЫЕ КЛЮЧИ
- § 7.3. КЛЮЧИ НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ
- § 7.4. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В КЛЮЧЕВЫХ ЦЕПЯХ С БИПОЛЯРНЫМИ ТРАНЗИСТОРАМИ
- 7.5. КЛЮЧИ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- § 7.6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В КЛЮЧАХ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- ГЛАВА 8. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ, ТРИГГЕРЫ, АВТОГЕНЕРАТОРЫ
- § 8.1. ОБЩИЕ СВЕДЕНИЯ О ЛОГИЧЕСКИХ ЭЛЕМЕНТАХ
- § 8.2. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 8.3. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МОП-ТРАНЗИСТОРАХ
- § 8.4. ТРИГГЕРЫ
- § 8.5. НЕСИММЕТРИЧНЫЕ ТРИГГЕРЫ
- § 8.6. ГЕНЕРАТОРЫ КОЛЕБАНИЙ
- Генераторы напряжения прямоугольной формы.
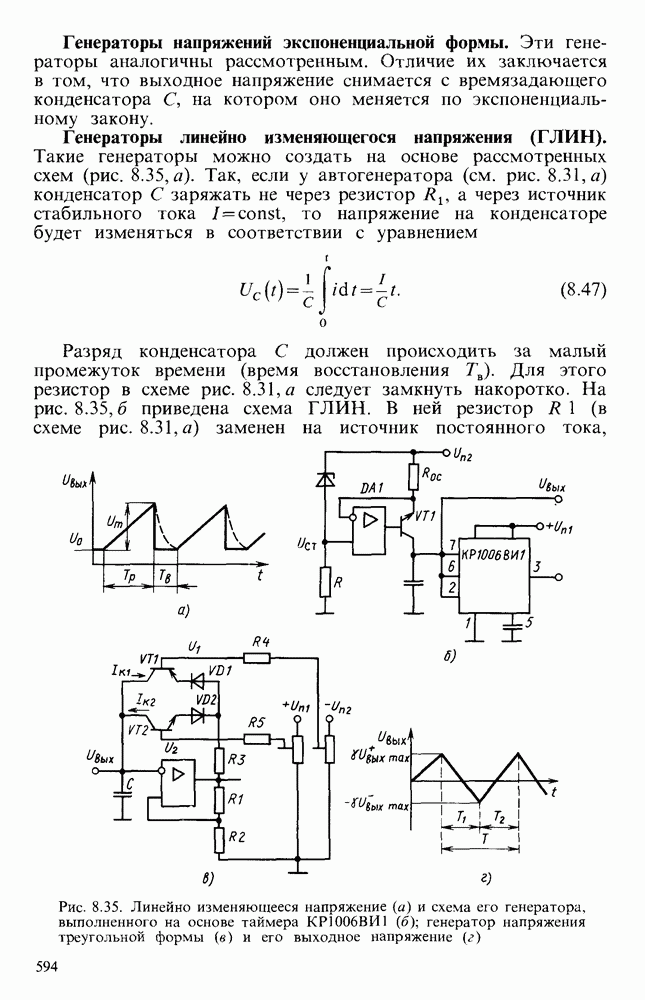
- Генераторы линейно изменяющегося напряжения (ГЛИН).
- Генераторы напряжения треугольной формы.
- Генераторы синусоидальных колебаний.
- Генераторы LC-типа.
- Генераторы с кварцевыми резонаторами и электромеханическими резонансными системами.
- ЗАКЛЮЧЕНИЕ
- Приложение
- Схемы включения операционных усилителей
- ЛИТЕРАТУРА