| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
11.6.3. Авторегрессивное моделирование для задачи спектрального анализа
Авторегрессивное моделирование широко используется в обработке речи, подводной акустики, сонарах, радарах и обработке сейсмических сигналов. Авторегрессивное моделирование эквивалентно одномерному случаю линейного прогнозирования исходов, методу максимальной энтропии и является особым случаем оптимального поиска по методу наименьших квадратов или винеровской фильтрации. Цель этого моделирования заключается в представлении временных последовательностей сигналов в виде малого числа параметров авторегрессии (чисто полярная модель), с помощью которых временные последовательности сигналов могли бы быть восстановлены с точностью, определяемой методом наименьших квадратов, при пропускании белого шума через модель. Пропускание временных последовательностей через обратный фильтр удалило бы, следовательно, информацию о самих временных последовательностях сигналов и оставило бы на выходе белый шум. Поэтому параметры авторегрессии содержат информацию, необходимую для вычислений спектра временных последовательностей сигнала, т. е. его цвет. Параметры авторегрессии можно также рассматривать как коэффициенты линейного прогнозирования исходов (ЛПИ) из-за того, что конечный импульсный отклик или «пересылка среднего», рассмотренные для фильтра с этими коэффициентами, позволяют предсказать следующие значения временной последовательности сигналов исходя из предыдущих значений. Вычитание предсказанных значений из имеющихся величин дает белый шум, как и в случае применения инверсного авторегрессивного фильтра. Коэффициенты ЛПИ, а именно  позволяют предсказать значение временных последовательностей в момент времени
позволяют предсказать значение временных последовательностей в момент времени  на основании их предшествующих значений
на основании их предшествующих значений

и вычисляются при помощи минимизации выражения

В связи с этим уместно упомянуть три возможных практических применения. Например, в геофизике отраженные от земли сигналы рассматриваются как случайные. Измеренные датчиками на поверхности земли сигналы представляют свертку слабых волн, испускаемых от источника, и последовательности случайных сигналов, отражаемых от земли. Влияние источника слабых сигналов исключается из данных, снимаемых с датчиков, посредством обратного преобразования свертки от
прогнозируемых данных, т. е. в спектре сигналов исключается информация о цвете [40].
В случае обработки речи фрагмент речи, состоящий из 200 образцов, может быть представлен в виде  коэффициентов ЛПИ (параметров авторегрессии), поскольку это число полюсов приемлемо для моделирования спектра и для распознавания указанного фрагмента. В этом случае уплотнение данных размерности 200 до 16 чисел позволяет в последующих стадиях провести быстрые вычисления. Обычно для меньших словарных запасов используется 10 коэффициентов ЛПИ.
коэффициентов ЛПИ (параметров авторегрессии), поскольку это число полюсов приемлемо для моделирования спектра и для распознавания указанного фрагмента. В этом случае уплотнение данных размерности 200 до 16 чисел позволяет в последующих стадиях провести быстрые вычисления. Обычно для меньших словарных запасов используется 10 коэффициентов ЛПИ.
Третий пример относится к определению спектра  с помощью параметров авторегрессии
с помощью параметров авторегрессии  и энергии
и энергии  с помощью выражения
с помощью выражения

При вычислении быстрого преобразования Фурье используют предположение о том, что за пределами измеренной области данные являются либо нулевыми, либо имеют повторяющиеся значения. В случае обработки коротких образцов данных это может приводить к зацикливанию вычислений. Избежать зацикливания удается путем вычисления спектра с помощью авторегрессионных моделей.
Ранее упомянутые подходы, такие, как авторегрессия, линейное прогнозирование исходов, метод максимальной энтропии, приводят к необходимости выполнения следующих шагов по определению параметров авторегрессии или ЛПИ. Для временных последовательностей вычисляют автокорреляционную функцию

Далее, для нахождения параметров авторегрессии или ЛПИ находят решения для  с помощью уравнения
с помощью уравнения

где  — автокорреляционная матрица Теплица, образованная из
— автокорреляционная матрица Теплица, образованная из  Эта процедура обычно выполняется на последовательном процессоре, использующем алгоритм Левинсона или Левинсона—Дарбина. Для параллельной машины [41, 62] более подходящим является алгоритм Шура. Реализация алгоритма Левинсона на основе описанного в гл. 11 процессора описана в [43], а алгоритма Левинсона—Дарбина — в [44, 42]. В данном случае используется алгоритм Шура.
Эта процедура обычно выполняется на последовательном процессоре, использующем алгоритм Левинсона или Левинсона—Дарбина. Для параллельной машины [41, 62] более подходящим является алгоритм Шура. Реализация алгоритма Левинсона на основе описанного в гл. 11 процессора описана в [43], а алгоритма Левинсона—Дарбина — в [44, 42]. В данном случае используется алгоритм Шура.
Матрицу  представляют в виде произведения двух «треугольных» матриц (взятых сверху и снизу от диагонали)
представляют в виде произведения двух «треугольных» матриц (взятых сверху и снизу от диагонали)

Подстановка в уравнение (11.7) позволяет получить решение за два шага. Решение для  получается из
получается из

и решение для а находят из

Автокорреляционная функция в уравнении (11.6) может быть вычислена с использованием древовидной структуры нахождения корреляционной функции, показанной на рис. 11.9, и системы, представленной на рис. 11.2. В этом случае данные вводятся в умножители (предполагают, что имеется достаточное число процессоров), и затем копия этих данных, задержанная на интервал времени, равный максимальной требуемой задержке, вводится начиная с вершины древовидной структуры. На каждом шаге корреляция выполняется с задержкой на один шаг, до тех пор пока задержанный поток данных точно не установлен по отношению к оригинальным данным. Это обеспечивает нулевое значение задержки коэффициента автокорреляции.
Коэффициенты автокорреляции вводятся в систолическую матрицу, показанную на рис. 11.10, по мере их вычисления. В этой матрице для вычисления параметров авторегрессии или ЛПИ временных последовательностей сигналов используется алгоритм Шура. Вычисляется верхняя «треугольная» матрица  которая затем используется в нижней систолической матрице для вычислений
которая затем используется в нижней систолической матрице для вычислений  . В то время как вычисляются
. В то время как вычисляются  , два верхних столбца процессора начинают вычисление соответствующего разложения для следующей временной последовательности сигналов.
, два верхних столбца процессора начинают вычисление соответствующего разложения для следующей временной последовательности сигналов.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ПРОСТРАНСТВЕННЫЕ МОДУЛЯТОРЫ СВЕТА
- Глава 1. МАГНИТООПТИЧЕСКИЕ МОДУЛЯТОРЫ СВЕТА
- 1.2. Принцип действия магнитооптических модуляторов
- 1.3. Магнитные свойства ферримагнитных гранатов и механизмы переключения
- 1.3.2. Формирование магнитных доменов
- 1.3.3. Подвод внешнего магнитного поля и петля гистерезиса
- 1.4. Оптические свойства магнитооптических гранатовых пленок
- 1.4.2. Спектральная зависимость коэффициента пропускания
- 1.4.3. Практические ограничения полной эффективности
- 1.4.4. Ограничения величины контраста
- 1.5. Конструкция магнитооптических модуляторов
- 1.5.2. Модуляторы с термомагнитным переключением
- 1.5.3. Модулятор света «лайтмод» с магнитной адресацией
- 1.5.4. Способ переключения с помощью магнитного поля смещения
- 1.6. Обсуждение результатов и перспектив
- Глава 2. ОПТИЧЕСКИЕ БИСТАБИЛЬНЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 2.2. Принципы работы бистабильных устройств
- 2.3. Требования к характеристикам нелинейных устройств и материалам
- 2.4. Причины возникновения нелинейных оптических эффектов в полупроводниках
- 2.5. Современное состояние работ по оптическим бистабильным устройствам
- 2.6. Оптические логические элементы Фабри — Перо (ОЛЭФП)
- 2.7. Устройства на собственном электрооптическом эффекте (СЭОУ)
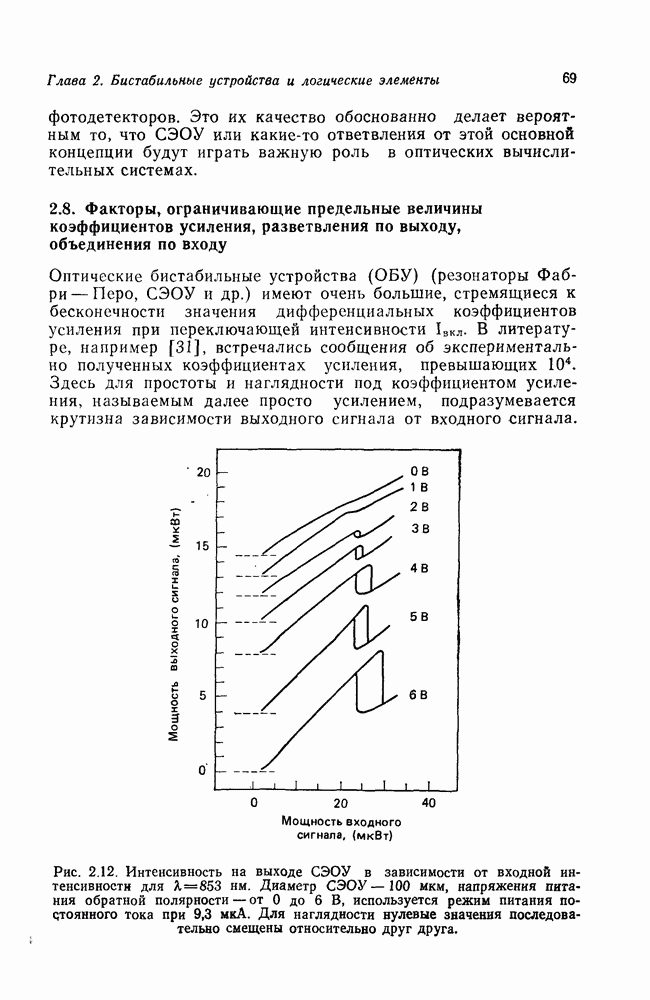
- 2.8. Факторы, ограничивающие предельные величины коэффициентов усиления, разветвления по выходу, объединения по входу
- 2.9. Концепции архитектуры
- 2.10. Предельные параметры и вычислительные возможности ОБУ
- 2.11. Три-стабильность и многозначная логика
- 2.12. Выводы
- Глава 3. КОМПОНЕНТЫ ОПТИЧЕСКОГО ПРОЦЕССОРА НА ОСНОВЕ ПРИБОРОВ С ЗАРЯДОВОЙ СВЯЗЬЮ (ПЗС)
- 3.2. Примеры электрооптической обработки сигналов (ЭООС)
- 3.3. Принципы работы ПЗС
- 3.3.1. Обсуждение конструкций с высоким быстродействием
- 3.4. Применение ПЗС в качестве выходных устройств ЭООС
- 3.5. Адресуемые ПЗС-пространственные модуляторы света (ПЗС-ПМС)
- 3.5.2. Устройство и характеристики ПЗС-модулятора
- 3.5.3. Эффект выбеливания
- 3.5.4. Эффект электропоглощения в квантовых ямах
- 3.6. Выводы
- Часть II. МНОГОЗНАЧНАЯ И ПОРОГОВАЯ ЛОГИКА
- Глава 4. МНОГОЗНАЧНАЯ ЛОГИКА В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 4.2. Проблема полноты в двоичной логике
- 4.3. Многозначные логические схемы, основанные на системе счисления в остаточных классах (ССОК)
- 4.4. Оптические многозначные логические ССОК-процессоры
- 4.5. Проблема полноты в многозначной логике
- 4.6. Краткое изложение и выводы
- Глава 5. ПОРОГОВОЕ КОДИРОВАНИЕ И ВЗВЕШИВАНИЕ В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 5.1.2. Определения взвешивания и порогового кодирования
- 5.1.3. Стандартная и нестандартная пороговые логики
- 5.2. Устройства с внешним пороговым кодированием
- 5.2.2. Пример 2-разрядного перестраиваемого устройства
- 5.3. Устройства с внутренним пороговым кодированием
- 5.4. Заключение
- Глава 6. МНОГОЗНАЧНАЯ ПОРОГОВАЯ ЛОГИКА
- 6.2. Многозначная пороговая логика
- 6.2.2. Критические оценки возможностей
- 6.2.3. Многозначная пороговая логика и электрооптические устройства
- 6.3. Мультилинейные разделяющиеся функции
- 6.4. Перспективные разработки
- ЧАСТЬ III. СИСТОЛИЧЕСКИЕ ПРОЦЕССОРЫ И ОПТИЧЕСКИЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 7. ОПТИЧЕСКОЕ УМНОЖЕНИЕ МАТРИЦ
- 7.2. Цифровая оптика
- 7.2.2. Оптические устройства, выполняющие свертку при операциях умножения
- 7.2.2.2. Временная свертка
- 7.3. Рабочие характеристики
- 7.3.1. Быстродействие процессора
- 7.3.2. Проблемы разработки систем и возможности их приборной реализации
- 7.4. Заключение
- Глава 8. АРХИТЕКТУРЫ КЛЕТОЧНОЙ ЛОГИКИ
- 8.2. Клеточная логика
- 8.2.1. Клеточные компьютеры
- 8.2.2. Структуры матриц
- 8.2.3. Клеточный автомат
- 8.2.4. Клеточная матрица Минника и синтез логических функций
- 8.2.5. Перестраиваемые матрицы
- 8.2.6. Классификация методов обработки данных
- 8.3. Оптическая двоичная логика и архитектура МКМД
- 8.4. Оптическая реализация
- 8.4.2. Локальная клеточная логика
- 8.4.2.2. Алгоритм перекодированных таблиц и согласованная фильтрация
- 8.4.2.3. Клеточная логика, использующая матрицы согласованных фильтров
- 8.5. Заключение
- Глава 9. ВОЛОКОННО-ОПТИЧЕСКИЕ ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- 9.2. Характеристики волоконно-оптических ПЛМ
- 9.2.2. Рассеиваемая мощность
- 9.2.3. Производительность и возможность изменения масштабов устройства
- 9.2.4. Сравнение возможностей различных методик реализации комбинационной логики
- 9.3. Проблемы создания логических схем для волоконно-оптических систем
- 9.3.2. Роль свойств декодеров высоких порядков
- 9.3.3. Производительность, функциональная сложность и затраты энергии
- 9.4. Перестраиваемые волоконные системы
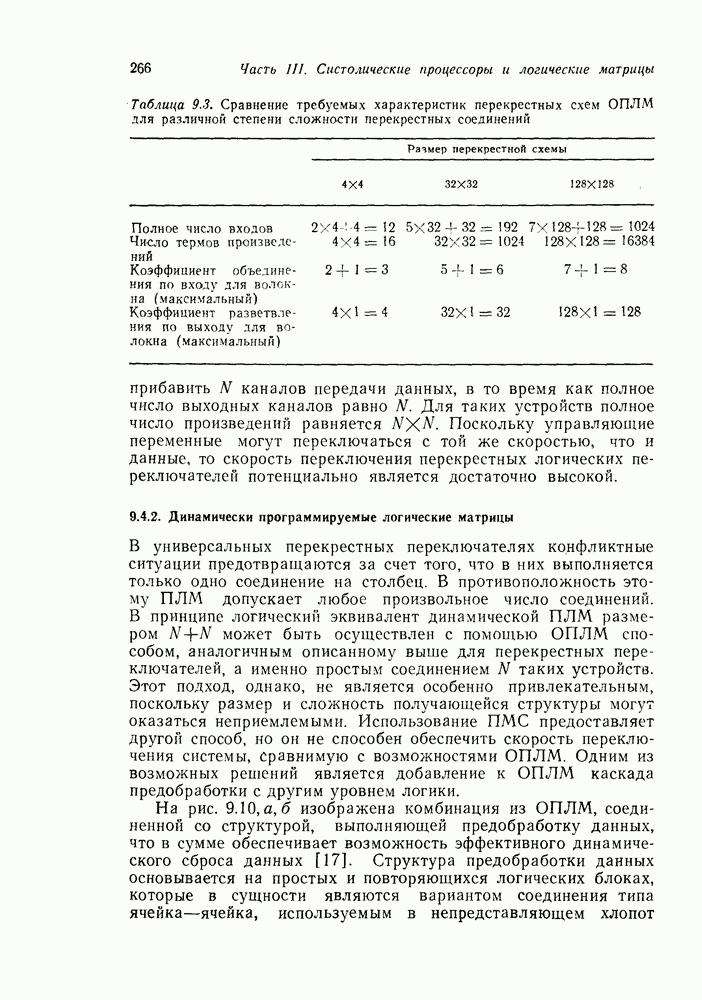
- 9.4.2. Динамически программируемые логические матрицы
- 9.5. Выводы
- Часть IV. СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- Глава 10. ОПТИКА И СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
- 10.2. Что такое искусственный интеллект?
- 10.2.1. Характеристики знаний
- 10.2.2. Представление знаний
- 10.2.3. Поиск
- 10.2.4. Сравнительные характеристики символьных и цифровых вычислений
- 10.3. Функциональные возможности символьных вычислений
- 10.3.2. Понимание речи
- 10.3.3. Техническое зрение
- 10.3.4. Понимание естественного языка
- 10.3.5. Экспертные системы
- 10.4. Архитектуры символьных вычислений
- 10.4.2. Архитектуры параллельной обработки
- 10.4.3. Оптическая реализация мультипроцессорных архитектур
- 10.4.4. Чисто оптические архитектуры
- 10.4.5. Гибридные оптоэлектрониые системы
- Глоссарий
- Глава 11. ОПТИЧЕСКИЕ МЕЖЭЛЕМЕНТНЫЕ СОЕДИНЕНИЯ ДЛЯ СИМВОЛЬНОЙ И ЦИФРОВОЙ ОБРАБОТКИ И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 11.2. Роль параллелизма и символьной обработки в вычислениях, проводимых в реальном времени
- 11.2.2. Необходимость вычислений в реальном времени
- 11.2.3. Необходимость параллельной обработки
- 11.2.4. Требования, предъявляемые к структуре процессоров
- 11.3. Преимущества перекрестных оптических схем
- 11.3.2. Преимущества оптических межэлементных соединений
- 11.3.3. Возможность реконфигурации сетей с оптическими переключателями
- 11.3.4. Получение запрограммированного потока данных с помощью оптических переключателей
- 11.4. Оптический процессор с перекрестной схемой
- 11.4.2. Описание элементов обработки
- 11.4.3. Оптический перекрестный переключатель и устройства с деформируемыми зеркалами
- 11.4.4. Программирование и функциональные операции
- 11.5. Получение логических выводов с помощью оптического процессора с перекрестной схемой
- 11.5.2. Схема «от фактов к цели» и ее реализация
- 11.5.3. Схема «от цели к фактам» и ее реализация
- 11.6. Цифровая обработка сигналов с помощью оптического мультипроцессора с перекрестной схемой
- 11.6.2. Коррелятор и матрично-векторный умножитель
- 11.6.3. Авторегрессивное моделирование для задачи спектрального анализа
- 11.7. Случай одновременного выполнения символьных и цифровых вычислений, пример речевой системы
- 11.7.2. Символьно-цифровое распознавание речи и система синтаксического анализа
- 11.7.3. Распознавание речи с помощью динамического изменения масштаба времени
- 11.7.4. Синтаксический анализ речи с помощью экспертной системы синтаксического анализа типа «ситуация — действие», «жди и смотри»
- 11.8. Выводы
- ЛИТЕРАТУРА