| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.1.3. Стандартная и нестандартная пороговые логики
Пороговая логика — это область, тесно связанная с операциями порогового кодирования и взвешивания в вычислениях. Эта область активно исследовалась в 1960-е и начале 1970-х гг. [9-11], но с тех пор и до настоящего времени [12] интерес к ней спал в основном ,потому, что общепринятой во всех чисто электронных ИС стала традиционная булева логика.
Пример стандартной, или построенной на линейных неравенствах пороговой логики наглядно показан на рис. 5.1. Здесь логическая функция  (для которой дана таблица истинности) реализуется с помощью пороговых логических элементов, у которых
(для которой дана таблица истинности) реализуется с помощью пороговых логических элементов, у которых  — входные двоичные сигналы, у — двоичный выходной сигнал, знак
— входные двоичные сигналы, у — двоичный выходной сигнал, знак  обозначает операцию ИЛИ, подразумеваемое умножение является операцией И, а черта — операцией НЕ. Элемент умножает каждый двоичный входной сигнал на действительное число, являющееся весовым коэффициентом
обозначает операцию ИЛИ, подразумеваемое умножение является операцией И, а черта — операцией НЕ. Элемент умножает каждый двоичный входной сигнал на действительное число, являющееся весовым коэффициентом  или
или 
суммирует результаты и сравнивает их с пороговым действительным значением Т. Если сумма меньше порогового значения, то выходной сигнал равняется 0, в противном случае — 1. В приведенном примере следует обратить внимание на то, что единственный пороговый элемент реализует логическую функцию, которая потребовала бы нескольких обычных булевых вентилей и двух уровней логики , (трех уровней в том случае, если присутствует операция НЕ). Следует также заметить, что, во-первых, пороговый элемент будет правильно срабатывать в случае, если порог является любым числом, удовлетворяющим условию  , во-вторых, если допустимое отклонение значения порога ограничено, тогда могут быть определены ненулевые допустимые отклонения весовых коэффициентов.
, во-вторых, если допустимое отклонение значения порога ограничено, тогда могут быть определены ненулевые допустимые отклонения весовых коэффициентов.
В общем пороговые логические элементы с линейными неравенствами имеют несколько двоичных входов, один двоичный выход и встроенное аналоговое устройство, пригодное для работы с оптикой (некоторые конструкции элементов допускают применение дискретных встроенных устройств [13] и несколько двоичных выходов [14]). Как показано на рис. 5.1, можно добиться, чтобы пороговый элемент работал корректно даже в случае отклонения значения порога и веса от номинальных величин, что возникает вследствие внешних условий, погрешностей при изготовлении прибора и т. д. Из таблицы истинности на рис. 5.1 видно, что соответствующие величины веса и порога могут быть получены путем решения системы линейных неравенств. Например,  строка таблицы истинности требует, чтобы
строка таблицы истинности требует, чтобы


Рис. 5.1. Пример порогового логического элемента, выполняющего функцию  а — пороговый элемент; б — таблица истинности,
а — пороговый элемент; б — таблица истинности,
Обычно число неравенств превышает число неизвестных (в приведенном примере 16 неравенств, или строк таблицы истинности приходится на  неизвестных
неизвестных  и Г), однако решения будут существовать не всегда. Тем не менее существующие решения, определяющие максимальные допустимые отклонения различных порогов и весов, могут быть определены с помощью методов линейного программирования. Большинство ранних работ по пороговой логике было посвящено нахождению таких решений или их характеристик без явного применения методов линейного программирования, часто требующих проведения обширных вычислений. Совершенствование вычислительной техники и алгоритмов, однако, сделало использование линейного программирования для разработки пороговых логических элементов и схем более привлекательным [15].
и Г), однако решения будут существовать не всегда. Тем не менее существующие решения, определяющие максимальные допустимые отклонения различных порогов и весов, могут быть определены с помощью методов линейного программирования. Большинство ранних работ по пороговой логике было посвящено нахождению таких решений или их характеристик без явного применения методов линейного программирования, часто требующих проведения обширных вычислений. Совершенствование вычислительной техники и алгоритмов, однако, сделало использование линейного программирования для разработки пороговых логических элементов и схем более привлекательным [15].
Как показано выше, не все логические функции могут быть реализованы с помощью пороговых логических элементов с одним линейным неравенством; те из них, которые могут быть реализованы, называются пороговыми, или линейно-разделяемыми функциями. В целом существует  логических функций
логических функций  двоичных переменных (каждая из
двоичных переменных (каждая из  входных строк таблицы истинности может иметь любой двоичный выход), но число пороговых функций обычно намного меньше — верхний предел их числа составляет
входных строк таблицы истинности может иметь любой двоичный выход), но число пороговых функций обычно намного меньше — верхний предел их числа составляет  Например, если
Например, если  полное число функций равняется 256, верхнее предельное значение составляет 170, а фактическое число функций оказывается равным
полное число функций равняется 256, верхнее предельное значение составляет 170, а фактическое число функций оказывается равным  Для
Для  (простейший случай) можно легко показать, что 14 из 16 возможных булевых логических вентилей с двумя входами, включая И и ИЛИ, могут быть реализованы с помощью единственного порогового элемента; таким образом, линейные неравенства пороговой логики можно рассматривать как более общий случай булевой логики. Поскольку любые комбинационные логические функции
(простейший случай) можно легко показать, что 14 из 16 возможных булевых логических вентилей с двумя входами, включая И и ИЛИ, могут быть реализованы с помощью единственного порогового элемента; таким образом, линейные неравенства пороговой логики можно рассматривать как более общий случай булевой логики. Поскольку любые комбинационные логические функции  таблицей истинности из постоянных значений) можно реализовать на основе системы вентилей или элементов с не более чем двумя уровнями булевой логики (т. е. сигнал в системе не должен проходить более двух последовательно соединенных логических вентилей, исключая вентиль НЕ), то оказывается, что то же самое справедливо для пороговой логики. Однако (булевы логические схемы для сложных функций (например,
таблицей истинности из постоянных значений) можно реализовать на основе системы вентилей или элементов с не более чем двумя уровнями булевой логики (т. е. сигнал в системе не должен проходить более двух последовательно соединенных логических вентилей, исключая вентиль НЕ), то оказывается, что то же самое справедливо для пороговой логики. Однако (булевы логические схемы для сложных функций (например,  -разрядный умножитель) обычно требуют более двух логических уровней, чтобы избежать соединений на одном и том же уровне неоправданно большого числа логических элементов [16]. Пороговая логика, в частности реализация пороговой логики в оптике, может смягчить эти требования. Данная характеристика и пример на рис. 5.1 показывают, что пороговая логика имеет потенциальные преимущества, обеспечивая
-разрядный умножитель) обычно требуют более двух логических уровней, чтобы избежать соединений на одном и том же уровне неоправданно большого числа логических элементов [16]. Пороговая логика, в частности реализация пороговой логики в оптике, может смягчить эти требования. Данная характеристика и пример на рис. 5.1 показывают, что пороговая логика имеет потенциальные преимущества, обеспечивая
меньшее число логических уровней (что приводит ,к большему быстродействию), логических элементов (что уменьшает энергопотребление) и соединений (что уменьшает сложность системы) 
Данные преимущества обычно сильнее выражены для более общих случаев нестандартных типов пороговой логики, или логик с нелинейными неравенствами. Элемент в подобной логической схеме производит сравнение пороговой величины с нелинейной функцией Двоичного входного сигнала, такой как квадратичный полином, коэффициенты которого рассматривают в качестве весовых коэффициентов [17]. Как утверждается в разд. 5.2, когерентные оптические системы реализуют нелинейную функцию пропорционально возведенной в квадрат сумме двоичных входных сигналов, умноженных на комплексные значения весовых множителей, где последние представляют амплитуды и фазы световой волны. С помощью исчерпывающего, но имеющего ограниченную точность численного расчета было показано, что число логических функций при  двоичных переменных для случая одного порогового элемента с комплексными весами и как инвертированными, так и неинвертированными выходами составляет по меньшей мере 246 [18]. По сравнению
двоичных переменных для случая одного порогового элемента с комплексными весами и как инвертированными, так и неинвертированными выходами составляет по меньшей мере 246 [18]. По сравнению  такими/функциями, которые реализуются с помощью стандартной пороговой логики, это число показывает увеличение вычислительных возможностей одного из вариантов нестандартной пороговой логики. Некоторые архитектуры. Оптических вычислительных схем [4, 5, 19, 20] описываются с помощью общепринятых систем пороговой логики, а в случае использования на практике их рабочие характеристики могут быть улучшены. Например, если число разновидностей
такими/функциями, которые реализуются с помощью стандартной пороговой логики, это число показывает увеличение вычислительных возможностей одного из вариантов нестандартной пороговой логики. Некоторые архитектуры. Оптических вычислительных схем [4, 5, 19, 20] описываются с помощью общепринятых систем пороговой логики, а в случае использования на практике их рабочие характеристики могут быть улучшены. Например, если число разновидностей  двоичных элементов, которые необходимо классифицировать по одному или двум признакам, составляет величину менее
двоичных элементов, которые необходимо классифицировать по одному или двум признакам, составляет величину менее  тогда хорошо известные адаптивные методы, основанные на алгоритме Видрова — Хоффа или на архитектуре персептрона, обычно могут идентифицировать линейноразделяемую функцию или отдельный стандартный пороговый элемент, выполняющий классификацию [10]. Однако при наличии возможности использования одиночного нелинейного порогового элемента (имеющего эффективное приложение в оптике) можйо надлежащим образом классифицировать более чем
тогда хорошо известные адаптивные методы, основанные на алгоритме Видрова — Хоффа или на архитектуре персептрона, обычно могут идентифицировать линейноразделяемую функцию или отдельный стандартный пороговый элемент, выполняющий классификацию [10]. Однако при наличии возможности использования одиночного нелинейного порогового элемента (имеющего эффективное приложение в оптике) можйо надлежащим образом классифицировать более чем  разновидностей элементов [21].
разновидностей элементов [21].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ПРОСТРАНСТВЕННЫЕ МОДУЛЯТОРЫ СВЕТА
- Глава 1. МАГНИТООПТИЧЕСКИЕ МОДУЛЯТОРЫ СВЕТА
- 1.2. Принцип действия магнитооптических модуляторов
- 1.3. Магнитные свойства ферримагнитных гранатов и механизмы переключения
- 1.3.2. Формирование магнитных доменов
- 1.3.3. Подвод внешнего магнитного поля и петля гистерезиса
- 1.4. Оптические свойства магнитооптических гранатовых пленок
- 1.4.2. Спектральная зависимость коэффициента пропускания
- 1.4.3. Практические ограничения полной эффективности
- 1.4.4. Ограничения величины контраста
- 1.5. Конструкция магнитооптических модуляторов
- 1.5.2. Модуляторы с термомагнитным переключением
- 1.5.3. Модулятор света «лайтмод» с магнитной адресацией
- 1.5.4. Способ переключения с помощью магнитного поля смещения
- 1.6. Обсуждение результатов и перспектив
- Глава 2. ОПТИЧЕСКИЕ БИСТАБИЛЬНЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 2.2. Принципы работы бистабильных устройств
- 2.3. Требования к характеристикам нелинейных устройств и материалам
- 2.4. Причины возникновения нелинейных оптических эффектов в полупроводниках
- 2.5. Современное состояние работ по оптическим бистабильным устройствам
- 2.6. Оптические логические элементы Фабри — Перо (ОЛЭФП)
- 2.7. Устройства на собственном электрооптическом эффекте (СЭОУ)
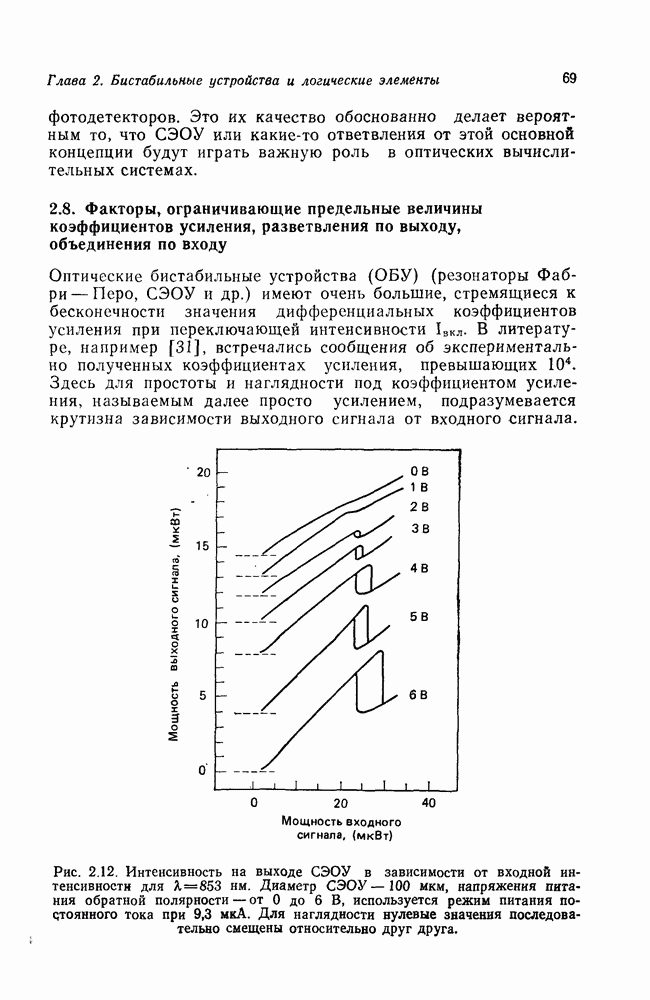
- 2.8. Факторы, ограничивающие предельные величины коэффициентов усиления, разветвления по выходу, объединения по входу
- 2.9. Концепции архитектуры
- 2.10. Предельные параметры и вычислительные возможности ОБУ
- 2.11. Три-стабильность и многозначная логика
- 2.12. Выводы
- Глава 3. КОМПОНЕНТЫ ОПТИЧЕСКОГО ПРОЦЕССОРА НА ОСНОВЕ ПРИБОРОВ С ЗАРЯДОВОЙ СВЯЗЬЮ (ПЗС)
- 3.2. Примеры электрооптической обработки сигналов (ЭООС)
- 3.3. Принципы работы ПЗС
- 3.3.1. Обсуждение конструкций с высоким быстродействием
- 3.4. Применение ПЗС в качестве выходных устройств ЭООС
- 3.5. Адресуемые ПЗС-пространственные модуляторы света (ПЗС-ПМС)
- 3.5.2. Устройство и характеристики ПЗС-модулятора
- 3.5.3. Эффект выбеливания
- 3.5.4. Эффект электропоглощения в квантовых ямах
- 3.6. Выводы
- Часть II. МНОГОЗНАЧНАЯ И ПОРОГОВАЯ ЛОГИКА
- Глава 4. МНОГОЗНАЧНАЯ ЛОГИКА В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 4.2. Проблема полноты в двоичной логике
- 4.3. Многозначные логические схемы, основанные на системе счисления в остаточных классах (ССОК)
- 4.4. Оптические многозначные логические ССОК-процессоры
- 4.5. Проблема полноты в многозначной логике
- 4.6. Краткое изложение и выводы
- Глава 5. ПОРОГОВОЕ КОДИРОВАНИЕ И ВЗВЕШИВАНИЕ В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 5.1.2. Определения взвешивания и порогового кодирования
- 5.1.3. Стандартная и нестандартная пороговые логики
- 5.2. Устройства с внешним пороговым кодированием
- 5.2.2. Пример 2-разрядного перестраиваемого устройства
- 5.3. Устройства с внутренним пороговым кодированием
- 5.4. Заключение
- Глава 6. МНОГОЗНАЧНАЯ ПОРОГОВАЯ ЛОГИКА
- 6.2. Многозначная пороговая логика
- 6.2.2. Критические оценки возможностей
- 6.2.3. Многозначная пороговая логика и электрооптические устройства
- 6.3. Мультилинейные разделяющиеся функции
- 6.4. Перспективные разработки
- ЧАСТЬ III. СИСТОЛИЧЕСКИЕ ПРОЦЕССОРЫ И ОПТИЧЕСКИЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 7. ОПТИЧЕСКОЕ УМНОЖЕНИЕ МАТРИЦ
- 7.2. Цифровая оптика
- 7.2.2. Оптические устройства, выполняющие свертку при операциях умножения
- 7.2.2.2. Временная свертка
- 7.3. Рабочие характеристики
- 7.3.1. Быстродействие процессора
- 7.3.2. Проблемы разработки систем и возможности их приборной реализации
- 7.4. Заключение
- Глава 8. АРХИТЕКТУРЫ КЛЕТОЧНОЙ ЛОГИКИ
- 8.2. Клеточная логика
- 8.2.1. Клеточные компьютеры
- 8.2.2. Структуры матриц
- 8.2.3. Клеточный автомат
- 8.2.4. Клеточная матрица Минника и синтез логических функций
- 8.2.5. Перестраиваемые матрицы
- 8.2.6. Классификация методов обработки данных
- 8.3. Оптическая двоичная логика и архитектура МКМД
- 8.4. Оптическая реализация
- 8.4.2. Локальная клеточная логика
- 8.4.2.2. Алгоритм перекодированных таблиц и согласованная фильтрация
- 8.4.2.3. Клеточная логика, использующая матрицы согласованных фильтров
- 8.5. Заключение
- Глава 9. ВОЛОКОННО-ОПТИЧЕСКИЕ ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- 9.2. Характеристики волоконно-оптических ПЛМ
- 9.2.2. Рассеиваемая мощность
- 9.2.3. Производительность и возможность изменения масштабов устройства
- 9.2.4. Сравнение возможностей различных методик реализации комбинационной логики
- 9.3. Проблемы создания логических схем для волоконно-оптических систем
- 9.3.2. Роль свойств декодеров высоких порядков
- 9.3.3. Производительность, функциональная сложность и затраты энергии
- 9.4. Перестраиваемые волоконные системы
- 9.4.2. Динамически программируемые логические матрицы
- 9.5. Выводы
- Часть IV. СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- Глава 10. ОПТИКА И СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
- 10.2. Что такое искусственный интеллект?
- 10.2.1. Характеристики знаний
- 10.2.2. Представление знаний
- 10.2.3. Поиск
- 10.2.4. Сравнительные характеристики символьных и цифровых вычислений
- 10.3. Функциональные возможности символьных вычислений
- 10.3.2. Понимание речи
- 10.3.3. Техническое зрение
- 10.3.4. Понимание естественного языка
- 10.3.5. Экспертные системы
- 10.4. Архитектуры символьных вычислений
- 10.4.2. Архитектуры параллельной обработки
- 10.4.3. Оптическая реализация мультипроцессорных архитектур
- 10.4.4. Чисто оптические архитектуры
- 10.4.5. Гибридные оптоэлектрониые системы
- Глоссарий
- Глава 11. ОПТИЧЕСКИЕ МЕЖЭЛЕМЕНТНЫЕ СОЕДИНЕНИЯ ДЛЯ СИМВОЛЬНОЙ И ЦИФРОВОЙ ОБРАБОТКИ И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 11.2. Роль параллелизма и символьной обработки в вычислениях, проводимых в реальном времени
- 11.2.2. Необходимость вычислений в реальном времени
- 11.2.3. Необходимость параллельной обработки
- 11.2.4. Требования, предъявляемые к структуре процессоров
- 11.3. Преимущества перекрестных оптических схем
- 11.3.2. Преимущества оптических межэлементных соединений
- 11.3.3. Возможность реконфигурации сетей с оптическими переключателями
- 11.3.4. Получение запрограммированного потока данных с помощью оптических переключателей
- 11.4. Оптический процессор с перекрестной схемой
- 11.4.2. Описание элементов обработки
- 11.4.3. Оптический перекрестный переключатель и устройства с деформируемыми зеркалами
- 11.4.4. Программирование и функциональные операции
- 11.5. Получение логических выводов с помощью оптического процессора с перекрестной схемой
- 11.5.2. Схема «от фактов к цели» и ее реализация
- 11.5.3. Схема «от цели к фактам» и ее реализация
- 11.6. Цифровая обработка сигналов с помощью оптического мультипроцессора с перекрестной схемой
- 11.6.2. Коррелятор и матрично-векторный умножитель
- 11.6.3. Авторегрессивное моделирование для задачи спектрального анализа
- 11.7. Случай одновременного выполнения символьных и цифровых вычислений, пример речевой системы
- 11.7.2. Символьно-цифровое распознавание речи и система синтаксического анализа
- 11.7.3. Распознавание речи с помощью динамического изменения масштаба времени
- 11.7.4. Синтаксический анализ речи с помощью экспертной системы синтаксического анализа типа «ситуация — действие», «жди и смотри»
- 11.8. Выводы
- ЛИТЕРАТУРА