| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
9.3.3. Производительность, функциональная сложность и затраты энергии
Для каждого значения переменных входных сигналов, показанных в табл. 9.1, связанная с ним программируемая униполярная пороговая функция представляет определенный уровень функциональной сложности. Использование декодеров высших порядков обеспечивает наличие механизма уменьшения сложности вычислений, требуемой для получения пороговых функций. В действительности это приводит к увеличению относительного коэффициента объединения по входу ПЛМ, уменьшая между тем коэффициент разветвления по выходу. Фактически именно произведение коэффициентов разветвления и объединения имеет критическое значение. При постоянной ширине полосы частот это произведение пропорционально производительности, а также мощности входного сигнала, или энергии, необходимой для полного завершения всей процедуры вычислений. Для того чтобы минимизировать соотношение между коэффициентами объединения по входу и коэффициентами разветвления по выходу, необходимо более детально рассмотреть относительный коэффициент объединения по входу ПЛМ.
Оценка относительных коэффициентов объединения по входу ПЛМ как функции сложности декодера начинается с установления того факта, что число выходных каналов для  -разрядного декодера равняется
-разрядного декодера равняется  . Относительный коэффициент объединения по входу ПЛМ может быть определен путем установления числа переменных входного сигнала и последующего вычисления произведения соответствующего числа декодеров и числа выходных каналов, приходящихся на декодер. Таким образом, функция восьми переменных требует 2-разрядного декодера или двух 4-разрядных декодеров. Относительный коэффициент объединения по входу ПЛМ, следовательно, будет больше в случае 4-разрядных декодеров, чем для случая 2-раз-рядных декодеров. По мере увеличения сложности декодеров входного сигнала относительный коэффициент объединения по входу ПЛМ также возрастает. Единственным исключением из этого случая является переход от
. Относительный коэффициент объединения по входу ПЛМ может быть определен путем установления числа переменных входного сигнала и последующего вычисления произведения соответствующего числа декодеров и числа выходных каналов, приходящихся на декодер. Таким образом, функция восьми переменных требует 2-разрядного декодера или двух 4-разрядных декодеров. Относительный коэффициент объединения по входу ПЛМ, следовательно, будет больше в случае 4-разрядных декодеров, чем для случая 2-раз-рядных декодеров. По мере увеличения сложности декодеров входного сигнала относительный коэффициент объединения по входу ПЛМ также возрастает. Единственным исключением из этого случая является переход от  -разрядных декодеров к 2-разрядным декодерам, где относительный коэффициент объединения по входу остается постоянным.
-разрядных декодеров к 2-разрядным декодерам, где относительный коэффициент объединения по входу остается постоянным.
В табл. 9.1 суммируются относительные коэффициенты объединения по входу для четырех уровней функциональной сложности, начиная с четырех переменных и кончая шестнадцатью. Относительные произведения коэффициентов разветвления по выходу и объединения по входу для каждого уровня функциональной сложности и для каждого уровня сложности декодеров вычислены и представлены в последнем столбце табл. 9.1. На рис. 9.8 представлены зависимости относительного
произведения коэффициентов разветвления по выходу и объединения по входу от числа переменных входного сигнала. Из данного рисунка следует, что применение декодеров высшего порядка значительно снижает требования к относительному произведению коэффициентов разветвления и объединения, или, что эквивалентно, относительной производительности, требуемой на каждом уровне функциональной сложности. Во всех случаях требуемая производительность вычислений экспоненциально возрастает при увеличении функциональной сложности, но скорость возрастания тем не менее является значительно меньшей, чем в случае, когда используются декодеры высших порядков.
Рисунок 9.8 вводит читателя в заблуждение в том смысле, что он выполнен в предположении, что требуемая производительность для определенного уровня функциональной сложности уменьшается монотонно с увеличением сложности декодеров. Тщательный анализ последнего столбца в табл. 9.1 показывает, что относительное произведение коэффициентов

Рис. 9.8. Зависимость произведения относительных коэффициентов объединения в по входу и разветвления по выходу от числа разрядов (числа переменных) входного сигнала, приведенная для ОПЛМ с декодерами высших порядков. Указанная зависимость эквивалентна зависимости относительной производительности вычислений от степени функциональной сложности.
разветвления по выходу и объединения по входу, рассматриваемое в качестве функции сложности декодера, фактически проходит через минимум. Из этих данных становится очевидным, что существует оптимальный уровень сложности декодеров, необходимый для минимизации требуемой производительности. Следовательно, при постоянной ширине полосы частот мощность и энергия, необходимые для проведения конкретного вычисления, также могут быть минимизированы за счет соответствующего подбора сложности декодера. Фактический коэффициент на практике зависит от распределения нулей и единиц в отдельных термах произведения. В результате этого требования к реальным коэффициентам могут быть значительно снижены по сравнению с представленными здесь номинальными пределами. Различие между номинальными и фактическими коэффициентами обсуждается в следующем подразделе.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ПРОСТРАНСТВЕННЫЕ МОДУЛЯТОРЫ СВЕТА
- Глава 1. МАГНИТООПТИЧЕСКИЕ МОДУЛЯТОРЫ СВЕТА
- 1.2. Принцип действия магнитооптических модуляторов
- 1.3. Магнитные свойства ферримагнитных гранатов и механизмы переключения
- 1.3.2. Формирование магнитных доменов
- 1.3.3. Подвод внешнего магнитного поля и петля гистерезиса
- 1.4. Оптические свойства магнитооптических гранатовых пленок
- 1.4.2. Спектральная зависимость коэффициента пропускания
- 1.4.3. Практические ограничения полной эффективности
- 1.4.4. Ограничения величины контраста
- 1.5. Конструкция магнитооптических модуляторов
- 1.5.2. Модуляторы с термомагнитным переключением
- 1.5.3. Модулятор света «лайтмод» с магнитной адресацией
- 1.5.4. Способ переключения с помощью магнитного поля смещения
- 1.6. Обсуждение результатов и перспектив
- Глава 2. ОПТИЧЕСКИЕ БИСТАБИЛЬНЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 2.2. Принципы работы бистабильных устройств
- 2.3. Требования к характеристикам нелинейных устройств и материалам
- 2.4. Причины возникновения нелинейных оптических эффектов в полупроводниках
- 2.5. Современное состояние работ по оптическим бистабильным устройствам
- 2.6. Оптические логические элементы Фабри — Перо (ОЛЭФП)
- 2.7. Устройства на собственном электрооптическом эффекте (СЭОУ)
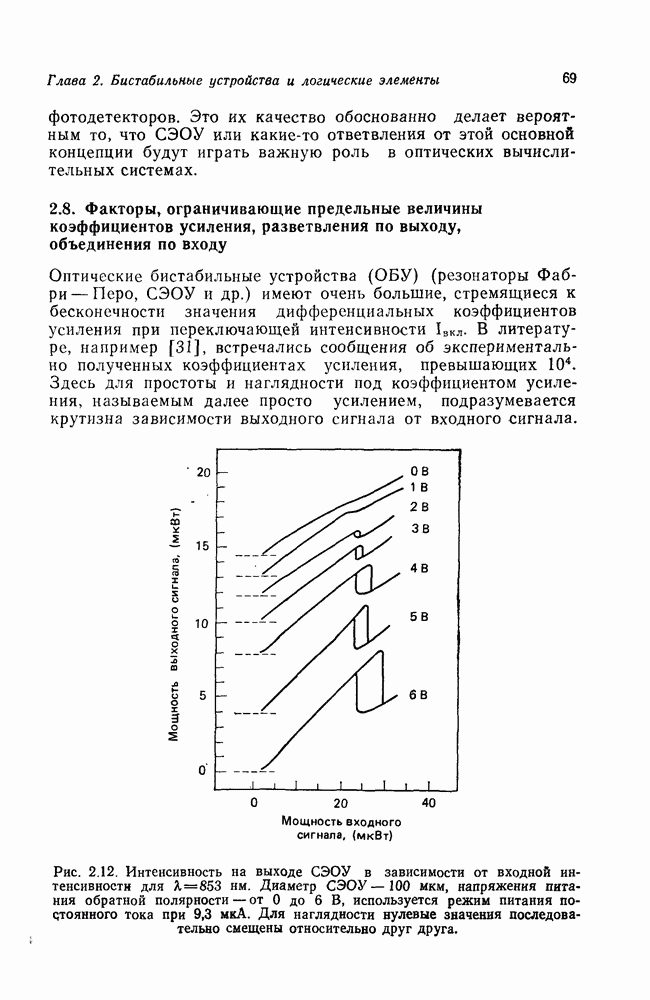
- 2.8. Факторы, ограничивающие предельные величины коэффициентов усиления, разветвления по выходу, объединения по входу
- 2.9. Концепции архитектуры
- 2.10. Предельные параметры и вычислительные возможности ОБУ
- 2.11. Три-стабильность и многозначная логика
- 2.12. Выводы
- Глава 3. КОМПОНЕНТЫ ОПТИЧЕСКОГО ПРОЦЕССОРА НА ОСНОВЕ ПРИБОРОВ С ЗАРЯДОВОЙ СВЯЗЬЮ (ПЗС)
- 3.2. Примеры электрооптической обработки сигналов (ЭООС)
- 3.3. Принципы работы ПЗС
- 3.3.1. Обсуждение конструкций с высоким быстродействием
- 3.4. Применение ПЗС в качестве выходных устройств ЭООС
- 3.5. Адресуемые ПЗС-пространственные модуляторы света (ПЗС-ПМС)
- 3.5.2. Устройство и характеристики ПЗС-модулятора
- 3.5.3. Эффект выбеливания
- 3.5.4. Эффект электропоглощения в квантовых ямах
- 3.6. Выводы
- Часть II. МНОГОЗНАЧНАЯ И ПОРОГОВАЯ ЛОГИКА
- Глава 4. МНОГОЗНАЧНАЯ ЛОГИКА В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 4.2. Проблема полноты в двоичной логике
- 4.3. Многозначные логические схемы, основанные на системе счисления в остаточных классах (ССОК)
- 4.4. Оптические многозначные логические ССОК-процессоры
- 4.5. Проблема полноты в многозначной логике
- 4.6. Краткое изложение и выводы
- Глава 5. ПОРОГОВОЕ КОДИРОВАНИЕ И ВЗВЕШИВАНИЕ В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 5.1.2. Определения взвешивания и порогового кодирования
- 5.1.3. Стандартная и нестандартная пороговые логики
- 5.2. Устройства с внешним пороговым кодированием
- 5.2.2. Пример 2-разрядного перестраиваемого устройства
- 5.3. Устройства с внутренним пороговым кодированием
- 5.4. Заключение
- Глава 6. МНОГОЗНАЧНАЯ ПОРОГОВАЯ ЛОГИКА
- 6.2. Многозначная пороговая логика
- 6.2.2. Критические оценки возможностей
- 6.2.3. Многозначная пороговая логика и электрооптические устройства
- 6.3. Мультилинейные разделяющиеся функции
- 6.4. Перспективные разработки
- ЧАСТЬ III. СИСТОЛИЧЕСКИЕ ПРОЦЕССОРЫ И ОПТИЧЕСКИЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 7. ОПТИЧЕСКОЕ УМНОЖЕНИЕ МАТРИЦ
- 7.2. Цифровая оптика
- 7.2.2. Оптические устройства, выполняющие свертку при операциях умножения
- 7.2.2.2. Временная свертка
- 7.3. Рабочие характеристики
- 7.3.1. Быстродействие процессора
- 7.3.2. Проблемы разработки систем и возможности их приборной реализации
- 7.4. Заключение
- Глава 8. АРХИТЕКТУРЫ КЛЕТОЧНОЙ ЛОГИКИ
- 8.2. Клеточная логика
- 8.2.1. Клеточные компьютеры
- 8.2.2. Структуры матриц
- 8.2.3. Клеточный автомат
- 8.2.4. Клеточная матрица Минника и синтез логических функций
- 8.2.5. Перестраиваемые матрицы
- 8.2.6. Классификация методов обработки данных
- 8.3. Оптическая двоичная логика и архитектура МКМД
- 8.4. Оптическая реализация
- 8.4.2. Локальная клеточная логика
- 8.4.2.2. Алгоритм перекодированных таблиц и согласованная фильтрация
- 8.4.2.3. Клеточная логика, использующая матрицы согласованных фильтров
- 8.5. Заключение
- Глава 9. ВОЛОКОННО-ОПТИЧЕСКИЕ ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- 9.2. Характеристики волоконно-оптических ПЛМ
- 9.2.2. Рассеиваемая мощность
- 9.2.3. Производительность и возможность изменения масштабов устройства
- 9.2.4. Сравнение возможностей различных методик реализации комбинационной логики
- 9.3. Проблемы создания логических схем для волоконно-оптических систем
- 9.3.2. Роль свойств декодеров высоких порядков
- 9.3.3. Производительность, функциональная сложность и затраты энергии
- 9.4. Перестраиваемые волоконные системы
- 9.4.2. Динамически программируемые логические матрицы
- 9.5. Выводы
- Часть IV. СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- Глава 10. ОПТИКА И СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
- 10.2. Что такое искусственный интеллект?
- 10.2.1. Характеристики знаний
- 10.2.2. Представление знаний
- 10.2.3. Поиск
- 10.2.4. Сравнительные характеристики символьных и цифровых вычислений
- 10.3. Функциональные возможности символьных вычислений
- 10.3.2. Понимание речи
- 10.3.3. Техническое зрение
- 10.3.4. Понимание естественного языка
- 10.3.5. Экспертные системы
- 10.4. Архитектуры символьных вычислений
- 10.4.2. Архитектуры параллельной обработки
- 10.4.3. Оптическая реализация мультипроцессорных архитектур
- 10.4.4. Чисто оптические архитектуры
- 10.4.5. Гибридные оптоэлектрониые системы
- Глоссарий
- Глава 11. ОПТИЧЕСКИЕ МЕЖЭЛЕМЕНТНЫЕ СОЕДИНЕНИЯ ДЛЯ СИМВОЛЬНОЙ И ЦИФРОВОЙ ОБРАБОТКИ И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 11.2. Роль параллелизма и символьной обработки в вычислениях, проводимых в реальном времени
- 11.2.2. Необходимость вычислений в реальном времени
- 11.2.3. Необходимость параллельной обработки
- 11.2.4. Требования, предъявляемые к структуре процессоров
- 11.3. Преимущества перекрестных оптических схем
- 11.3.2. Преимущества оптических межэлементных соединений
- 11.3.3. Возможность реконфигурации сетей с оптическими переключателями
- 11.3.4. Получение запрограммированного потока данных с помощью оптических переключателей
- 11.4. Оптический процессор с перекрестной схемой
- 11.4.2. Описание элементов обработки
- 11.4.3. Оптический перекрестный переключатель и устройства с деформируемыми зеркалами
- 11.4.4. Программирование и функциональные операции
- 11.5. Получение логических выводов с помощью оптического процессора с перекрестной схемой
- 11.5.2. Схема «от фактов к цели» и ее реализация
- 11.5.3. Схема «от цели к фактам» и ее реализация
- 11.6. Цифровая обработка сигналов с помощью оптического мультипроцессора с перекрестной схемой
- 11.6.2. Коррелятор и матрично-векторный умножитель
- 11.6.3. Авторегрессивное моделирование для задачи спектрального анализа
- 11.7. Случай одновременного выполнения символьных и цифровых вычислений, пример речевой системы
- 11.7.2. Символьно-цифровое распознавание речи и система синтаксического анализа
- 11.7.3. Распознавание речи с помощью динамического изменения масштаба времени
- 11.7.4. Синтаксический анализ речи с помощью экспертной системы синтаксического анализа типа «ситуация — действие», «жди и смотри»
- 11.8. Выводы
- ЛИТЕРАТУРА