| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.2. Многозначная пороговая логика
6.2.1. Теоретические основы
Исследования многозначной пороговой логики возникли в начальный период исследований пороговой логики. За важной работой [7] по описанию свойств пороговых (двоичных) функций последовали пионерские работы [8, 9] по троичной пороговой логике. На протяжении последующего десятилетия основное внимание исследователей привлекла именно троичная пороговая логика, что определялось, вероятно, появлением возможности для ее приборной реализации на основе дискретных полупроводниковых компонент. В числе наиболее важных результатов данного периода можно упомянуть работы, посвященные описанию свойств троичных пороговых функций [10, 11], подсчету и классификации всех трехместных троичных пороговых функций [12, 13], откуда следует, что существует 85 629 таких функций (в то время как рядом авторов независимо указывалось на существование 471 двухместных троичных пороговых функций), а также табличный метод реализации троичных пороговых функций с числом переменных, достигающим трех [13, 14].
Первыми публикациями по многозначной пороговой логике (за исключением троичной), по-видимому, являются работы [15—17]. Интересно заметить, что в [15] набор  корней единицы был использован в качестве области определения
корней единицы был использован в качестве области определения  -значных функций, а для исследования пороговых функций использовались методы гармонического анализа функций. Данный подход, однако, не получил дальнейшего развития в последующей литературе. С другой стороны, в [16] в качестве области
-значных функций, а для исследования пороговых функций использовались методы гармонического анализа функций. Данный подход, однако, не получил дальнейшего развития в последующей литературе. С другой стороны, в [16] в качестве области
определения р-значной функции были использованы первые  неотрицательные корня, а также были введены понятия характеристического вектора многозначной пороговой функции и даны необходимые и достаточные условия того, что
неотрицательные корня, а также были введены понятия характеристического вектора многозначной пороговой функции и даны необходимые и достаточные условия того, что  -значная функция являлась пороговой функцией.
-значная функция являлась пороговой функцией.
Следующее определение представляет собой упрощенный вариант материала, изложенного в работе [17].
Определение 6.1
Пусть  Функция
Функция  является
является  -местной
-местной  -значной пороговой функцией, если только существуют действительный вектор
-значной пороговой функцией, если только существуют действительный вектор  называемый весовым вектором, и действительный вектор
называемый весовым вектором, и действительный вектор  называемый пороговым вектором, такие что
называемый пороговым вектором, такие что

где  обозначает внутреннее произведение
обозначает внутреннее произведение  и X.
и X.
Становится ясно, что, если система (6.1) имеет решение, тогда она имеет бесконечно много решений. Большая их часть удовлетворяет более жесткой системе неравенств со знаком  вместо
вместо 
Следует отметить, что определение не требует, чтобы функция устанавливала фактически многооднозначное соответствие. Если  не принимает заданного значения
не принимает заданного значения  в V, это только означает, что в
в V, это только означает, что в  существуют X, такие что
существуют X, такие что  и в (6.1) выражение
и в (6.1) выражение  все еще является формально правильным, но не имеет решений. (Функция
все еще является формально правильным, но не имеет решений. (Функция  устанавливает нестрогое многооднозначное соответствие, если для любого
устанавливает нестрогое многооднозначное соответствие, если для любого  существует по крайней мере одно
существует по крайней мере одно  такое что
такое что 
Определение 6.2
Пусть  Тогда
Тогда  является пороговой функцией, если только существует набор
является пороговой функцией, если только существует набор  -мерных параллельных гиперплоскостей в
-мерных параллельных гиперплоскостей в  разделяющих
разделяющих  от 1).
от 1).
Рассмотрим пример троичной пороговой функции на рис. 6.1. Введем следующее обозначение. Если  — пороговая функция с весовым вектором
— пороговая функция с весовым вектором  и пороговым вектором Т, то запишем
и пороговым вектором Т, то запишем  и назовем
и назовем  структурой
структурой  Отсюда для примера на рис. 6.1 получим, что
Отсюда для примера на рис. 6.1 получим, что 
Лемма 6.1
Пусть  является пороговой функцией со структурой
является пороговой функцией со структурой  . Тогда
. Тогда  справедливо в случаях, где масштабный множитель
справедливо в случаях, где масштабный множитель  является целым положительным числом.
является целым положительным числом.
Доказательство: Следует непосредственно из уравнения (6.1).
Лемма 6.2
Для всех  положим
положим  Более того, определим
Более того, определим  Пусть
Пусть  является пороговой функцией со структурой
является пороговой функцией со структурой  . Функция от функции
. Функция от функции  по любому а также является пороговой функцией и имеет структуру
по любому а также является пороговой функцией и имеет структуру  где да
где да 
Доказательство: Пусть  Тогда
Тогда  Пусть
Пусть  будет таким, что
будет таким, что  для всех
для всех  Отсюда следует, что
Отсюда следует, что


Рис. 6.1, Пример двуместной четырехуровневой пороговой функции.
Отсюда получаем

Положим в данном случае  Так как
Так как  то можно записать
то можно записать

но

Определим  Тогда
Тогда

Отсюда следует

На рис. 6.2 показана функция от функции  где
где  является функцией, ранее изображенной на рис. 6.1.
является функцией, ранее изображенной на рис. 6.1.
Следствие 6.1
Пусть  является пороговой функцией со структурой
является пороговой функцией со структурой  . Более того, предположим, что некоторые
. Более того, предположим, что некоторые  имеют отрицательные значения, например
имеют отрицательные значения, например  где
где  Тогда
Тогда  реализуется в виде пороговой функции с положительными весовыми коэффициентами, которую вычисляют, находя дополнения
реализуется в виде пороговой функции с положительными весовыми коэффициентами, которую вычисляют, находя дополнения

Рис. 6.2. Четырехуровневая пороговая функция, полученная из функции, заданной на рис. 6.1 путем замены второго аргумента на его дополнение.
к соответствующим аргументам  и увеличив все пороги на величину
и увеличив все пороги на величину
Лемма 6.3
Пусть  является пороговой функцией со структурой
является пороговой функцией со структурой  . Тогда
. Тогда  также является пороговой функцией и имеет структуру
также является пороговой функцией и имеет структуру  где
где 
Доказательство:

Умножая на  получим
получим

Пусть  Более того, прибавим
Более того, прибавим  к обеим частям второго члена приведенного выше выражения. Это приводит к
к обеим частям второго члена приведенного выше выражения. Это приводит к

Пример
Пусть  — функция, представленная на рис. 6.1. Тогда справедливо следующее:
— функция, представленная на рис. 6.1. Тогда справедливо следующее:

Следствие 6.2
Пусть  является пороговой функцией со структурой
является пороговой функцией со структурой  . Двойственная функция, заданная как
. Двойственная функция, заданная как  также является пороговой функцией и имеет структуру
также является пороговой функцией и имеет структуру  где для всех
где для всех  таких, что
таких, что  справедливо равенство
справедливо равенство

Доказательство
Следует непосредственно из лемм 6.2 и 6.3. Пример представлен на рис. 6.3.
Лемма 6.4
Пусть  является пороговой функцией. Ее структура
является пороговой функцией. Ее структура  при этом удовлетворяет строгому варианту уравнения (6.1). Пусть
при этом удовлетворяет строгому варианту уравнения (6.1). Пусть  так что
так что  если
если  для всех
для всех  принадлежащих V. Тогда
принадлежащих V. Тогда  справедливо для если
справедливо для если  и
и
 положительная бесконечно малая величина)
положительная бесконечно малая величина) 
Доказательство: Из определения  и строгого неравенства для
и строгого неравенства для  становится ясно, что
становится ясно, что

Другими словами:
Не существует X такого, что 
Для всех X, таких что  или
или  Иначе
Иначе 
Если заменить элементы Т на соответствующие элементы Т и  на
на  в уравнении (6.1), то изменяется все выражения, кроме двух, а именно
в уравнении (6.1), то изменяется все выражения, кроме двух, а именно

Первое из них не имеет решений, так как по определению не существует X, таких что  Левая сторона второго выражения соответствует
Левая сторона второго выражения соответствует  и включает в себя все X, такие что
и включает в себя все X, такие что  или
или  но таковыми являются в точности все X, такие что
но таковыми являются в точности все X, такие что  Отсюда следует, что второе выражение является справедливым, что завершает доказательство.
Отсюда следует, что второе выражение является справедливым, что завершает доказательство.

Рис. 6.3. Двойственная функция, полученная из функции, показанной на рис,  и ее пороговая структура,
и ее пороговая структура,
Следствие 6.3
Пусть  является таким, как указано в лемме 6.4. Пусть
является таким, как указано в лемме 6.4. Пусть  обладает тем свойством, что
обладает тем свойством, что  если
если  для всех других
для всех других  принадлежащих V. Тогда
принадлежащих V. Тогда  во всех случаях, где
во всех случаях, где  если
если 
Лемма 6.5
Пусть  является
является  -значной пороговой функцией. При этом пусть
-значной пороговой функцией. При этом пусть  является взаимнооднозначным соответствием. Тогда
является взаимнооднозначным соответствием. Тогда  также является пороговой функцией со структурой
также является пороговой функцией со структурой  , где
, где  является весовым вектором, полученным путем перестановки весовых коэффициентов в
является весовым вектором, полученным путем перестановки весовых коэффициентов в  таким же способом, как элементы X переставляются под
таким же способом, как элементы X переставляются под 
Доказательство: Следует непосредственно из уравнения (1) и свойства коммутативности суммы в 
В качестве заключительного замечания к данному теоретическому основанию следует напомнить, что авторы [18] доказали функциональную полноту многозначной пороговой логики. Это означает, что любая многозначная система может быть реализована только с помощью пороговых функций. Однако это не означает, что многозначные системы следует реализовывать именно с помощью пороговых функций.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ПРОСТРАНСТВЕННЫЕ МОДУЛЯТОРЫ СВЕТА
- Глава 1. МАГНИТООПТИЧЕСКИЕ МОДУЛЯТОРЫ СВЕТА
- 1.2. Принцип действия магнитооптических модуляторов
- 1.3. Магнитные свойства ферримагнитных гранатов и механизмы переключения
- 1.3.2. Формирование магнитных доменов
- 1.3.3. Подвод внешнего магнитного поля и петля гистерезиса
- 1.4. Оптические свойства магнитооптических гранатовых пленок
- 1.4.2. Спектральная зависимость коэффициента пропускания
- 1.4.3. Практические ограничения полной эффективности
- 1.4.4. Ограничения величины контраста
- 1.5. Конструкция магнитооптических модуляторов
- 1.5.2. Модуляторы с термомагнитным переключением
- 1.5.3. Модулятор света «лайтмод» с магнитной адресацией
- 1.5.4. Способ переключения с помощью магнитного поля смещения
- 1.6. Обсуждение результатов и перспектив
- Глава 2. ОПТИЧЕСКИЕ БИСТАБИЛЬНЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 2.2. Принципы работы бистабильных устройств
- 2.3. Требования к характеристикам нелинейных устройств и материалам
- 2.4. Причины возникновения нелинейных оптических эффектов в полупроводниках
- 2.5. Современное состояние работ по оптическим бистабильным устройствам
- 2.6. Оптические логические элементы Фабри — Перо (ОЛЭФП)
- 2.7. Устройства на собственном электрооптическом эффекте (СЭОУ)
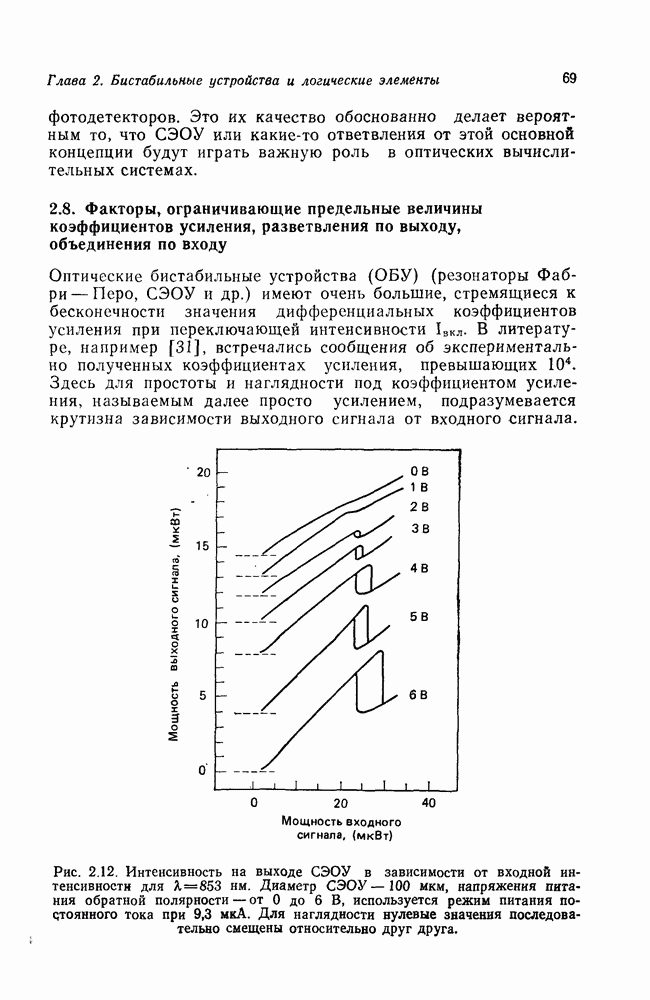
- 2.8. Факторы, ограничивающие предельные величины коэффициентов усиления, разветвления по выходу, объединения по входу
- 2.9. Концепции архитектуры
- 2.10. Предельные параметры и вычислительные возможности ОБУ
- 2.11. Три-стабильность и многозначная логика
- 2.12. Выводы
- Глава 3. КОМПОНЕНТЫ ОПТИЧЕСКОГО ПРОЦЕССОРА НА ОСНОВЕ ПРИБОРОВ С ЗАРЯДОВОЙ СВЯЗЬЮ (ПЗС)
- 3.2. Примеры электрооптической обработки сигналов (ЭООС)
- 3.3. Принципы работы ПЗС
- 3.3.1. Обсуждение конструкций с высоким быстродействием
- 3.4. Применение ПЗС в качестве выходных устройств ЭООС
- 3.5. Адресуемые ПЗС-пространственные модуляторы света (ПЗС-ПМС)
- 3.5.2. Устройство и характеристики ПЗС-модулятора
- 3.5.3. Эффект выбеливания
- 3.5.4. Эффект электропоглощения в квантовых ямах
- 3.6. Выводы
- Часть II. МНОГОЗНАЧНАЯ И ПОРОГОВАЯ ЛОГИКА
- Глава 4. МНОГОЗНАЧНАЯ ЛОГИКА В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 4.2. Проблема полноты в двоичной логике
- 4.3. Многозначные логические схемы, основанные на системе счисления в остаточных классах (ССОК)
- 4.4. Оптические многозначные логические ССОК-процессоры
- 4.5. Проблема полноты в многозначной логике
- 4.6. Краткое изложение и выводы
- Глава 5. ПОРОГОВОЕ КОДИРОВАНИЕ И ВЗВЕШИВАНИЕ В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 5.1.2. Определения взвешивания и порогового кодирования
- 5.1.3. Стандартная и нестандартная пороговые логики
- 5.2. Устройства с внешним пороговым кодированием
- 5.2.2. Пример 2-разрядного перестраиваемого устройства
- 5.3. Устройства с внутренним пороговым кодированием
- 5.4. Заключение
- Глава 6. МНОГОЗНАЧНАЯ ПОРОГОВАЯ ЛОГИКА
- 6.2. Многозначная пороговая логика
- 6.2.2. Критические оценки возможностей
- 6.2.3. Многозначная пороговая логика и электрооптические устройства
- 6.3. Мультилинейные разделяющиеся функции
- 6.4. Перспективные разработки
- ЧАСТЬ III. СИСТОЛИЧЕСКИЕ ПРОЦЕССОРЫ И ОПТИЧЕСКИЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 7. ОПТИЧЕСКОЕ УМНОЖЕНИЕ МАТРИЦ
- 7.2. Цифровая оптика
- 7.2.2. Оптические устройства, выполняющие свертку при операциях умножения
- 7.2.2.2. Временная свертка
- 7.3. Рабочие характеристики
- 7.3.1. Быстродействие процессора
- 7.3.2. Проблемы разработки систем и возможности их приборной реализации
- 7.4. Заключение
- Глава 8. АРХИТЕКТУРЫ КЛЕТОЧНОЙ ЛОГИКИ
- 8.2. Клеточная логика
- 8.2.1. Клеточные компьютеры
- 8.2.2. Структуры матриц
- 8.2.3. Клеточный автомат
- 8.2.4. Клеточная матрица Минника и синтез логических функций
- 8.2.5. Перестраиваемые матрицы
- 8.2.6. Классификация методов обработки данных
- 8.3. Оптическая двоичная логика и архитектура МКМД
- 8.4. Оптическая реализация
- 8.4.2. Локальная клеточная логика
- 8.4.2.2. Алгоритм перекодированных таблиц и согласованная фильтрация
- 8.4.2.3. Клеточная логика, использующая матрицы согласованных фильтров
- 8.5. Заключение
- Глава 9. ВОЛОКОННО-ОПТИЧЕСКИЕ ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- 9.2. Характеристики волоконно-оптических ПЛМ
- 9.2.2. Рассеиваемая мощность
- 9.2.3. Производительность и возможность изменения масштабов устройства
- 9.2.4. Сравнение возможностей различных методик реализации комбинационной логики
- 9.3. Проблемы создания логических схем для волоконно-оптических систем
- 9.3.2. Роль свойств декодеров высоких порядков
- 9.3.3. Производительность, функциональная сложность и затраты энергии
- 9.4. Перестраиваемые волоконные системы
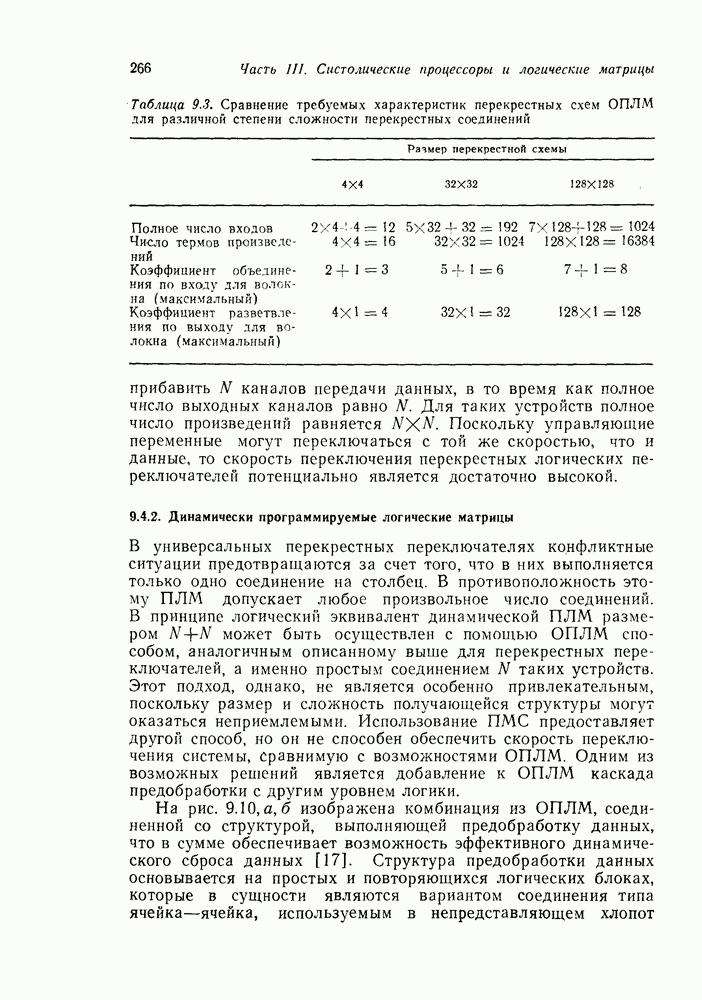
- 9.4.2. Динамически программируемые логические матрицы
- 9.5. Выводы
- Часть IV. СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- Глава 10. ОПТИКА И СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
- 10.2. Что такое искусственный интеллект?
- 10.2.1. Характеристики знаний
- 10.2.2. Представление знаний
- 10.2.3. Поиск
- 10.2.4. Сравнительные характеристики символьных и цифровых вычислений
- 10.3. Функциональные возможности символьных вычислений
- 10.3.2. Понимание речи
- 10.3.3. Техническое зрение
- 10.3.4. Понимание естественного языка
- 10.3.5. Экспертные системы
- 10.4. Архитектуры символьных вычислений
- 10.4.2. Архитектуры параллельной обработки
- 10.4.3. Оптическая реализация мультипроцессорных архитектур
- 10.4.4. Чисто оптические архитектуры
- 10.4.5. Гибридные оптоэлектрониые системы
- Глоссарий
- Глава 11. ОПТИЧЕСКИЕ МЕЖЭЛЕМЕНТНЫЕ СОЕДИНЕНИЯ ДЛЯ СИМВОЛЬНОЙ И ЦИФРОВОЙ ОБРАБОТКИ И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 11.2. Роль параллелизма и символьной обработки в вычислениях, проводимых в реальном времени
- 11.2.2. Необходимость вычислений в реальном времени
- 11.2.3. Необходимость параллельной обработки
- 11.2.4. Требования, предъявляемые к структуре процессоров
- 11.3. Преимущества перекрестных оптических схем
- 11.3.2. Преимущества оптических межэлементных соединений
- 11.3.3. Возможность реконфигурации сетей с оптическими переключателями
- 11.3.4. Получение запрограммированного потока данных с помощью оптических переключателей
- 11.4. Оптический процессор с перекрестной схемой
- 11.4.2. Описание элементов обработки
- 11.4.3. Оптический перекрестный переключатель и устройства с деформируемыми зеркалами
- 11.4.4. Программирование и функциональные операции
- 11.5. Получение логических выводов с помощью оптического процессора с перекрестной схемой
- 11.5.2. Схема «от фактов к цели» и ее реализация
- 11.5.3. Схема «от цели к фактам» и ее реализация
- 11.6. Цифровая обработка сигналов с помощью оптического мультипроцессора с перекрестной схемой
- 11.6.2. Коррелятор и матрично-векторный умножитель
- 11.6.3. Авторегрессивное моделирование для задачи спектрального анализа
- 11.7. Случай одновременного выполнения символьных и цифровых вычислений, пример речевой системы
- 11.7.2. Символьно-цифровое распознавание речи и система синтаксического анализа
- 11.7.3. Распознавание речи с помощью динамического изменения масштаба времени
- 11.7.4. Синтаксический анализ речи с помощью экспертной системы синтаксического анализа типа «ситуация — действие», «жди и смотри»
- 11.8. Выводы
- ЛИТЕРАТУРА