| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.2.2. Пример 2-разрядного перестраиваемого устройства
Взвешивание и соединение, осуществляемые оптически с помощью компьютерно синтезированных голограмм, обычно требуют знания дифракционных картин голограммы. При этом голограммы, изменяющие амплитуды и фазы, позволяют получить корректную таблицу истинности, описывающую соотношение входного-выходного сигналов с максимальным весовым коэффициентом и отклонением порога. В случае геометрической оптической схемы 2-разрядного умножителя, показанного на рис. 5.3, были легко получены выражения, определяющие поведение соотношения входного-выходного сигналов. Данная благоприятная ситуация может являться исключением при конструировании систем с внешним пороговым кодированием, как правило, имеющих меньшие размеры, большую эффективность и т. д., для которых приближение геометрической оптики не применимо.
Рассмотрим, например, получение восьми голограмм дальнего поля (каждая из них для тех же параметров, что у двух указанных выше разработок), которые осуществляют в системе с внешним пороговым кодированием восемь функций двух булевых переменных, имеющих положительный порог (например, восемь из тех шестнадцати функций, для которых два нулевых входных сигнала порождают нулевой выходной сигнал). На рис. 5.5 показана простая оптическая схема, состоящая из экрана с двумя маленькими отверстиями, разнесенными на расстояние у. Одно из отверстий покрыто пленкой 0, изменяющей фазу; имеется детектор 4 и верхний и нижний взаимно когерентные точечные источники  . В приближении дальнего поля расстояния
. В приближении дальнего поля расстояния  и у, а также длина волны
и у, а также длина волны  должны быть малы по сравнению с расстоянием
должны быть малы по сравнению с расстоянием  . В рамках данного приближения и при фиксированном
. В рамках данного приближения и при фиксированном  задача сводится к нахождению величин у и 0, таких, что продетектированный сигнал
задача сводится к нахождению величин у и 0, таких, что продетектированный сигнал  только для включенного источника I, сигнал
только для включенного источника I, сигнал  полученный только при включенном источнике к, и сигнал
полученный только при включенном источнике к, и сигнал  полученный при обоих включенных источниках, имеют все шесть
полученный при обоих включенных источниках, имеют все шесть
возможных неравенств. Обращаясь за определениями к рис. 5.5, получаем следующие приближенные соотношения:

где  На рис. 5.6 показаны графики [6] приближенных выражений для
На рис. 5.6 показаны графики [6] приближенных выражений для  в зависимости
в зависимости

Рис. 5.5. Схема получения голограмм дальнего поля, реализующих все восемь положительных пороговых функций двух булевых переменных в системе с внешним пороговым кодированием.

Рис. 5.6. Графики приближенных зависимостей  от х при
от х при  .
.
от х для  . Заметим, что четыре из шести неравенств могут быть удовлетворены при указанных значениях; два других соотношения могут быть удовлетворены для других величин
. Заметим, что четыре из шести неравенств могут быть удовлетворены при указанных значениях; два других соотношения могут быть удовлетворены для других величин  .
.
Пример уравнения (5.6) в целом демонстрирует возможную сложность задачи внешнего порогового кодирования (в рамках физической оптики). Большую часть трудностей можно было бы предсказать, если удовлетворить условиям дифракции Фраунгофера и если таблицы истинности, описывающие соотношение входного-выходного сигналов имеют большое число возможных корректных вариантов. Один из подходов к проблемам такого синтеза состоит в выполнении дополнительной обработки после фотодетектирования и использования методик логического упрощения и арифметики ССОК с целью уменьшения объема информации, которая должна быть накоплена для голографической перекодировки [22]. Более общий подход заключается в поиске возможных условий перехода в ССОК и обратно и способов дополнительной чисто электронной обработки.
Данный подход позволял использовать (а) получение, как правило, больших систем нелинейных кодирующих неравенств, полностью описывающих требуемую систему внешнего порогового кодирования; (б) нахождение оптимальных решений для этих систем, по возможности относительно отклонений весового коэффициента и порога, используя методики нелинейного программирования [26];  идентификацию оптических систем (возможно основанных на компьютерно-синтезированных голограммах), реализующих решения. В случае оптически записанных голограмм недавняя публикация [27] показывает, что управление относительными фазами таблицы истинности кодирующих предметных пучков является весьма важным для получения избирательного восстановления без интерференции (от неселективного восстановления). В другой недавней работе было показано, что такая интерференция может быть уменьшена при использовании методик, где применяется сравнение усиления сигнала в нелинейных оптических резонаторах, содержащих, например, искажающие фазу зеркала
идентификацию оптических систем (возможно основанных на компьютерно-синтезированных голограммах), реализующих решения. В случае оптически записанных голограмм недавняя публикация [27] показывает, что управление относительными фазами таблицы истинности кодирующих предметных пучков является весьма важным для получения избирательного восстановления без интерференции (от неселективного восстановления). В другой недавней работе было показано, что такая интерференция может быть уменьшена при использовании методик, где применяется сравнение усиления сигнала в нелинейных оптических резонаторах, содержащих, например, искажающие фазу зеркала  Указанные методики явно используют оптическую процедуру принятия решения и, таким образом, относятся к категориям устройств с внутренним пороговым кодированием.
Указанные методики явно используют оптическую процедуру принятия решения и, таким образом, относятся к категориям устройств с внутренним пороговым кодированием.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ПРОСТРАНСТВЕННЫЕ МОДУЛЯТОРЫ СВЕТА
- Глава 1. МАГНИТООПТИЧЕСКИЕ МОДУЛЯТОРЫ СВЕТА
- 1.2. Принцип действия магнитооптических модуляторов
- 1.3. Магнитные свойства ферримагнитных гранатов и механизмы переключения
- 1.3.2. Формирование магнитных доменов
- 1.3.3. Подвод внешнего магнитного поля и петля гистерезиса
- 1.4. Оптические свойства магнитооптических гранатовых пленок
- 1.4.2. Спектральная зависимость коэффициента пропускания
- 1.4.3. Практические ограничения полной эффективности
- 1.4.4. Ограничения величины контраста
- 1.5. Конструкция магнитооптических модуляторов
- 1.5.2. Модуляторы с термомагнитным переключением
- 1.5.3. Модулятор света «лайтмод» с магнитной адресацией
- 1.5.4. Способ переключения с помощью магнитного поля смещения
- 1.6. Обсуждение результатов и перспектив
- Глава 2. ОПТИЧЕСКИЕ БИСТАБИЛЬНЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 2.2. Принципы работы бистабильных устройств
- 2.3. Требования к характеристикам нелинейных устройств и материалам
- 2.4. Причины возникновения нелинейных оптических эффектов в полупроводниках
- 2.5. Современное состояние работ по оптическим бистабильным устройствам
- 2.6. Оптические логические элементы Фабри — Перо (ОЛЭФП)
- 2.7. Устройства на собственном электрооптическом эффекте (СЭОУ)
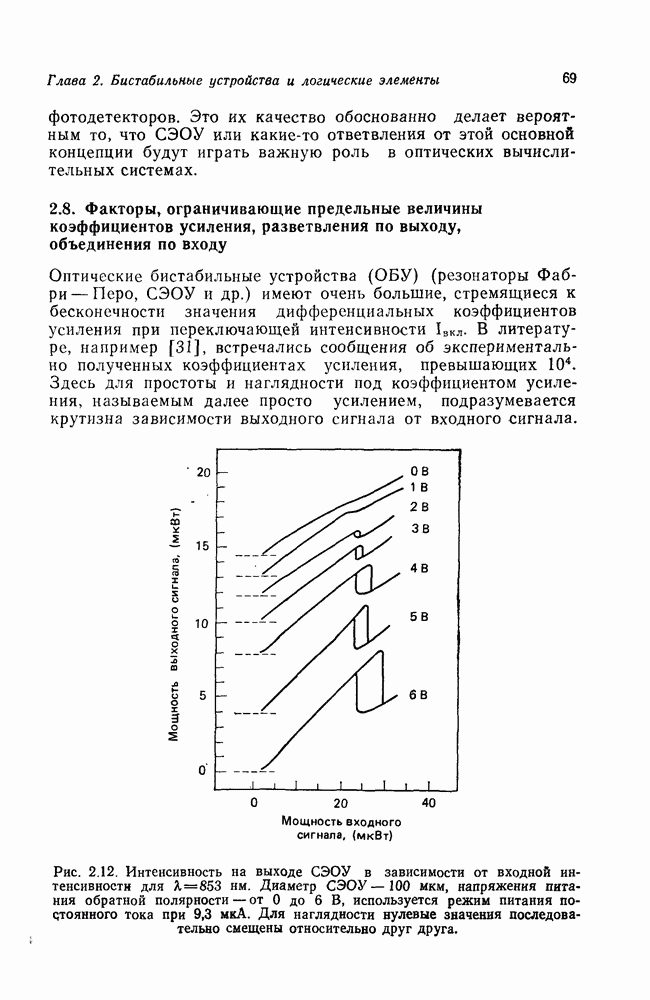
- 2.8. Факторы, ограничивающие предельные величины коэффициентов усиления, разветвления по выходу, объединения по входу
- 2.9. Концепции архитектуры
- 2.10. Предельные параметры и вычислительные возможности ОБУ
- 2.11. Три-стабильность и многозначная логика
- 2.12. Выводы
- Глава 3. КОМПОНЕНТЫ ОПТИЧЕСКОГО ПРОЦЕССОРА НА ОСНОВЕ ПРИБОРОВ С ЗАРЯДОВОЙ СВЯЗЬЮ (ПЗС)
- 3.2. Примеры электрооптической обработки сигналов (ЭООС)
- 3.3. Принципы работы ПЗС
- 3.3.1. Обсуждение конструкций с высоким быстродействием
- 3.4. Применение ПЗС в качестве выходных устройств ЭООС
- 3.5. Адресуемые ПЗС-пространственные модуляторы света (ПЗС-ПМС)
- 3.5.2. Устройство и характеристики ПЗС-модулятора
- 3.5.3. Эффект выбеливания
- 3.5.4. Эффект электропоглощения в квантовых ямах
- 3.6. Выводы
- Часть II. МНОГОЗНАЧНАЯ И ПОРОГОВАЯ ЛОГИКА
- Глава 4. МНОГОЗНАЧНАЯ ЛОГИКА В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 4.2. Проблема полноты в двоичной логике
- 4.3. Многозначные логические схемы, основанные на системе счисления в остаточных классах (ССОК)
- 4.4. Оптические многозначные логические ССОК-процессоры
- 4.5. Проблема полноты в многозначной логике
- 4.6. Краткое изложение и выводы
- Глава 5. ПОРОГОВОЕ КОДИРОВАНИЕ И ВЗВЕШИВАНИЕ В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 5.1.2. Определения взвешивания и порогового кодирования
- 5.1.3. Стандартная и нестандартная пороговые логики
- 5.2. Устройства с внешним пороговым кодированием
- 5.2.2. Пример 2-разрядного перестраиваемого устройства
- 5.3. Устройства с внутренним пороговым кодированием
- 5.4. Заключение
- Глава 6. МНОГОЗНАЧНАЯ ПОРОГОВАЯ ЛОГИКА
- 6.2. Многозначная пороговая логика
- 6.2.2. Критические оценки возможностей
- 6.2.3. Многозначная пороговая логика и электрооптические устройства
- 6.3. Мультилинейные разделяющиеся функции
- 6.4. Перспективные разработки
- ЧАСТЬ III. СИСТОЛИЧЕСКИЕ ПРОЦЕССОРЫ И ОПТИЧЕСКИЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 7. ОПТИЧЕСКОЕ УМНОЖЕНИЕ МАТРИЦ
- 7.2. Цифровая оптика
- 7.2.2. Оптические устройства, выполняющие свертку при операциях умножения
- 7.2.2.2. Временная свертка
- 7.3. Рабочие характеристики
- 7.3.1. Быстродействие процессора
- 7.3.2. Проблемы разработки систем и возможности их приборной реализации
- 7.4. Заключение
- Глава 8. АРХИТЕКТУРЫ КЛЕТОЧНОЙ ЛОГИКИ
- 8.2. Клеточная логика
- 8.2.1. Клеточные компьютеры
- 8.2.2. Структуры матриц
- 8.2.3. Клеточный автомат
- 8.2.4. Клеточная матрица Минника и синтез логических функций
- 8.2.5. Перестраиваемые матрицы
- 8.2.6. Классификация методов обработки данных
- 8.3. Оптическая двоичная логика и архитектура МКМД
- 8.4. Оптическая реализация
- 8.4.2. Локальная клеточная логика
- 8.4.2.2. Алгоритм перекодированных таблиц и согласованная фильтрация
- 8.4.2.3. Клеточная логика, использующая матрицы согласованных фильтров
- 8.5. Заключение
- Глава 9. ВОЛОКОННО-ОПТИЧЕСКИЕ ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- 9.2. Характеристики волоконно-оптических ПЛМ
- 9.2.2. Рассеиваемая мощность
- 9.2.3. Производительность и возможность изменения масштабов устройства
- 9.2.4. Сравнение возможностей различных методик реализации комбинационной логики
- 9.3. Проблемы создания логических схем для волоконно-оптических систем
- 9.3.2. Роль свойств декодеров высоких порядков
- 9.3.3. Производительность, функциональная сложность и затраты энергии
- 9.4. Перестраиваемые волоконные системы
- 9.4.2. Динамически программируемые логические матрицы
- 9.5. Выводы
- Часть IV. СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- Глава 10. ОПТИКА И СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
- 10.2. Что такое искусственный интеллект?
- 10.2.1. Характеристики знаний
- 10.2.2. Представление знаний
- 10.2.3. Поиск
- 10.2.4. Сравнительные характеристики символьных и цифровых вычислений
- 10.3. Функциональные возможности символьных вычислений
- 10.3.2. Понимание речи
- 10.3.3. Техническое зрение
- 10.3.4. Понимание естественного языка
- 10.3.5. Экспертные системы
- 10.4. Архитектуры символьных вычислений
- 10.4.2. Архитектуры параллельной обработки
- 10.4.3. Оптическая реализация мультипроцессорных архитектур
- 10.4.4. Чисто оптические архитектуры
- 10.4.5. Гибридные оптоэлектрониые системы
- Глоссарий
- Глава 11. ОПТИЧЕСКИЕ МЕЖЭЛЕМЕНТНЫЕ СОЕДИНЕНИЯ ДЛЯ СИМВОЛЬНОЙ И ЦИФРОВОЙ ОБРАБОТКИ И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 11.2. Роль параллелизма и символьной обработки в вычислениях, проводимых в реальном времени
- 11.2.2. Необходимость вычислений в реальном времени
- 11.2.3. Необходимость параллельной обработки
- 11.2.4. Требования, предъявляемые к структуре процессоров
- 11.3. Преимущества перекрестных оптических схем
- 11.3.2. Преимущества оптических межэлементных соединений
- 11.3.3. Возможность реконфигурации сетей с оптическими переключателями
- 11.3.4. Получение запрограммированного потока данных с помощью оптических переключателей
- 11.4. Оптический процессор с перекрестной схемой
- 11.4.2. Описание элементов обработки
- 11.4.3. Оптический перекрестный переключатель и устройства с деформируемыми зеркалами
- 11.4.4. Программирование и функциональные операции
- 11.5. Получение логических выводов с помощью оптического процессора с перекрестной схемой
- 11.5.2. Схема «от фактов к цели» и ее реализация
- 11.5.3. Схема «от цели к фактам» и ее реализация
- 11.6. Цифровая обработка сигналов с помощью оптического мультипроцессора с перекрестной схемой
- 11.6.2. Коррелятор и матрично-векторный умножитель
- 11.6.3. Авторегрессивное моделирование для задачи спектрального анализа
- 11.7. Случай одновременного выполнения символьных и цифровых вычислений, пример речевой системы
- 11.7.2. Символьно-цифровое распознавание речи и система синтаксического анализа
- 11.7.3. Распознавание речи с помощью динамического изменения масштаба времени
- 11.7.4. Синтаксический анализ речи с помощью экспертной системы синтаксического анализа типа «ситуация — действие», «жди и смотри»
- 11.8. Выводы
- ЛИТЕРАТУРА