| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
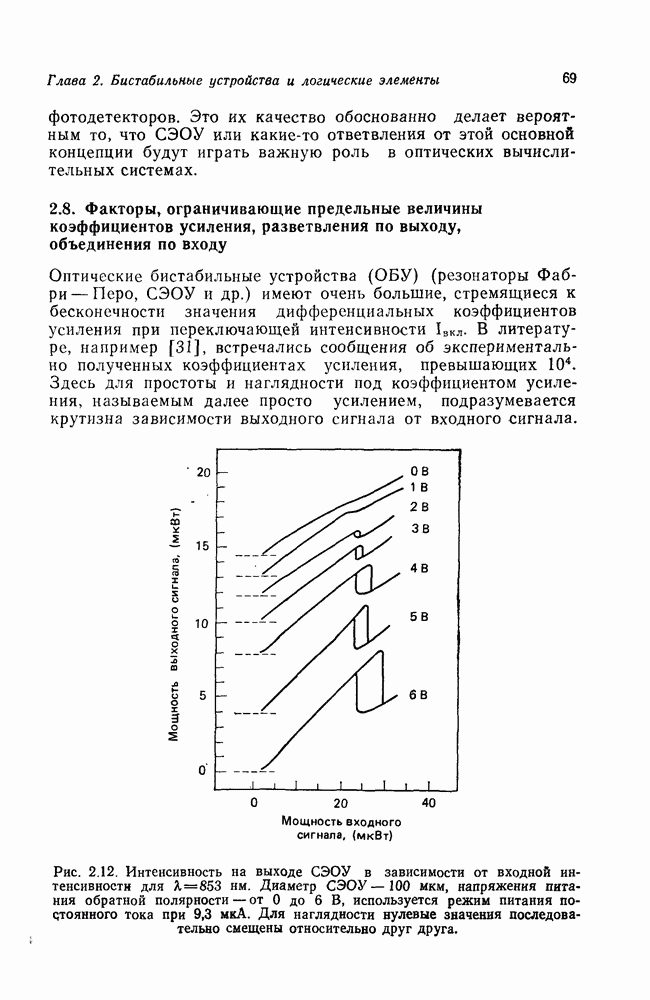
7.3. Рабочие характеристики
В предыдущих разделах описан ряд схем умножителей матрицы на вектор и матрицы на матрицу. Ниже представлен список этих умножителей, где каждая из схем получила специальное обозначение, используемое ниже в таблицах с 7.1 по 7.4.
Умножители матрицы на вектор
1М ПИ — одномерный с пространственным интегрированием
1МВИ(1) - одномерный с временным интегрированием
1М ВИ(П) - одномерный с временным интегрированием [13] 2МПИ — двумерный с пространственным интегрированием
2М ВИ (I) — двумерный с временным интегрированием
2МВЩП) - двумерный с временным интегрированием [16]
1МВП — вычисляющий внешнее произведение с помощью одномерных модуляторов
2МВП — вычисляющий внешнее произведение с помощью двумерных модуляторов

(кликните для просмотра скана)
Таблица 7.2. Рабочие характеристики умножителей матрицы на матрицу

Таблица 7.3. Отношение Псалтиса для умножителей матрицы на вектор

Таблица 7.4. Отношение Псалтиса для умножителей матрицы на матрицу

Умножитель матрицы на матрицу
ПИ — с пространственным интегрированием
ВИ (I) — с временным интегрированием
ВИ (II) — с временным интегрированием [15]
ВИ (III) — с временным интегрированием [16]
1МВП - вычисляющий внешнее произведение с помощью одномерных модуляторов
2М ВМ — вычисляющий внешнее произведение с помощью двумерных модуляторов
Цель данного раздела состоит в сравнении всех этих архитектур с определенных общих позиций. Чтобы сделать это, требуется дать определение целому ряду параметров, однако всегда имеется опасность сделать это слишком формальным, отдаленным от практики способом. С другой стороны, следует избегать опасности заняться научными «спекуляциями», аккуратно подгоняя сами параметры с целью демонстрации идеальных характеристик для любой из архитектур. Спорным является также и вопрос о том, может ли какая-либо из этих архитектур при определенных условиях работать лучше, чем указано в представленных ниже таблицах. Во всяком случае условия, при которых осуществляется такое улучшение, должны быть описаны очень тщательно.
Представленные здесь таблицы наиболее полезны для сравнительных оценок архитектур. Так как сравнение производится в общем виде, ни одной из архитектур не может быть приписано преимущество над другими. Тем не менее читателям, интересующимся возможностью использования тех или иных архитектур для конкретных задач, можно рекомендовать ознакомиться здесь с основными характеристиками и в дальнейшем расширить свои знания уже применительно к своим собственным потребностям.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ПРОСТРАНСТВЕННЫЕ МОДУЛЯТОРЫ СВЕТА
- Глава 1. МАГНИТООПТИЧЕСКИЕ МОДУЛЯТОРЫ СВЕТА
- 1.2. Принцип действия магнитооптических модуляторов
- 1.3. Магнитные свойства ферримагнитных гранатов и механизмы переключения
- 1.3.2. Формирование магнитных доменов
- 1.3.3. Подвод внешнего магнитного поля и петля гистерезиса
- 1.4. Оптические свойства магнитооптических гранатовых пленок
- 1.4.2. Спектральная зависимость коэффициента пропускания
- 1.4.3. Практические ограничения полной эффективности
- 1.4.4. Ограничения величины контраста
- 1.5. Конструкция магнитооптических модуляторов
- 1.5.2. Модуляторы с термомагнитным переключением
- 1.5.3. Модулятор света «лайтмод» с магнитной адресацией
- 1.5.4. Способ переключения с помощью магнитного поля смещения
- 1.6. Обсуждение результатов и перспектив
- Глава 2. ОПТИЧЕСКИЕ БИСТАБИЛЬНЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 2.2. Принципы работы бистабильных устройств
- 2.3. Требования к характеристикам нелинейных устройств и материалам
- 2.4. Причины возникновения нелинейных оптических эффектов в полупроводниках
- 2.5. Современное состояние работ по оптическим бистабильным устройствам
- 2.6. Оптические логические элементы Фабри — Перо (ОЛЭФП)
- 2.7. Устройства на собственном электрооптическом эффекте (СЭОУ)
- 2.8. Факторы, ограничивающие предельные величины коэффициентов усиления, разветвления по выходу, объединения по входу
- 2.9. Концепции архитектуры
- 2.10. Предельные параметры и вычислительные возможности ОБУ
- 2.11. Три-стабильность и многозначная логика
- 2.12. Выводы
- Глава 3. КОМПОНЕНТЫ ОПТИЧЕСКОГО ПРОЦЕССОРА НА ОСНОВЕ ПРИБОРОВ С ЗАРЯДОВОЙ СВЯЗЬЮ (ПЗС)
- 3.2. Примеры электрооптической обработки сигналов (ЭООС)
- 3.3. Принципы работы ПЗС
- 3.3.1. Обсуждение конструкций с высоким быстродействием
- 3.4. Применение ПЗС в качестве выходных устройств ЭООС
- 3.5. Адресуемые ПЗС-пространственные модуляторы света (ПЗС-ПМС)
- 3.5.2. Устройство и характеристики ПЗС-модулятора
- 3.5.3. Эффект выбеливания
- 3.5.4. Эффект электропоглощения в квантовых ямах
- 3.6. Выводы
- Часть II. МНОГОЗНАЧНАЯ И ПОРОГОВАЯ ЛОГИКА
- Глава 4. МНОГОЗНАЧНАЯ ЛОГИКА В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 4.2. Проблема полноты в двоичной логике
- 4.3. Многозначные логические схемы, основанные на системе счисления в остаточных классах (ССОК)
- 4.4. Оптические многозначные логические ССОК-процессоры
- 4.5. Проблема полноты в многозначной логике
- 4.6. Краткое изложение и выводы
- Глава 5. ПОРОГОВОЕ КОДИРОВАНИЕ И ВЗВЕШИВАНИЕ В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 5.1.2. Определения взвешивания и порогового кодирования
- 5.1.3. Стандартная и нестандартная пороговые логики
- 5.2. Устройства с внешним пороговым кодированием
- 5.2.2. Пример 2-разрядного перестраиваемого устройства
- 5.3. Устройства с внутренним пороговым кодированием
- 5.4. Заключение
- Глава 6. МНОГОЗНАЧНАЯ ПОРОГОВАЯ ЛОГИКА
- 6.2. Многозначная пороговая логика
- 6.2.2. Критические оценки возможностей
- 6.2.3. Многозначная пороговая логика и электрооптические устройства
- 6.3. Мультилинейные разделяющиеся функции
- 6.4. Перспективные разработки
- ЧАСТЬ III. СИСТОЛИЧЕСКИЕ ПРОЦЕССОРЫ И ОПТИЧЕСКИЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 7. ОПТИЧЕСКОЕ УМНОЖЕНИЕ МАТРИЦ
- 7.2. Цифровая оптика
- 7.2.2. Оптические устройства, выполняющие свертку при операциях умножения
- 7.2.2.2. Временная свертка
- 7.3. Рабочие характеристики
- 7.3.1. Быстродействие процессора
- 7.3.2. Проблемы разработки систем и возможности их приборной реализации
- 7.4. Заключение
- Глава 8. АРХИТЕКТУРЫ КЛЕТОЧНОЙ ЛОГИКИ
- 8.2. Клеточная логика
- 8.2.1. Клеточные компьютеры
- 8.2.2. Структуры матриц
- 8.2.3. Клеточный автомат
- 8.2.4. Клеточная матрица Минника и синтез логических функций
- 8.2.5. Перестраиваемые матрицы
- 8.2.6. Классификация методов обработки данных
- 8.3. Оптическая двоичная логика и архитектура МКМД
- 8.4. Оптическая реализация
- 8.4.2. Локальная клеточная логика
- 8.4.2.2. Алгоритм перекодированных таблиц и согласованная фильтрация
- 8.4.2.3. Клеточная логика, использующая матрицы согласованных фильтров
- 8.5. Заключение
- Глава 9. ВОЛОКОННО-ОПТИЧЕСКИЕ ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- 9.2. Характеристики волоконно-оптических ПЛМ
- 9.2.2. Рассеиваемая мощность
- 9.2.3. Производительность и возможность изменения масштабов устройства
- 9.2.4. Сравнение возможностей различных методик реализации комбинационной логики
- 9.3. Проблемы создания логических схем для волоконно-оптических систем
- 9.3.2. Роль свойств декодеров высоких порядков
- 9.3.3. Производительность, функциональная сложность и затраты энергии
- 9.4. Перестраиваемые волоконные системы
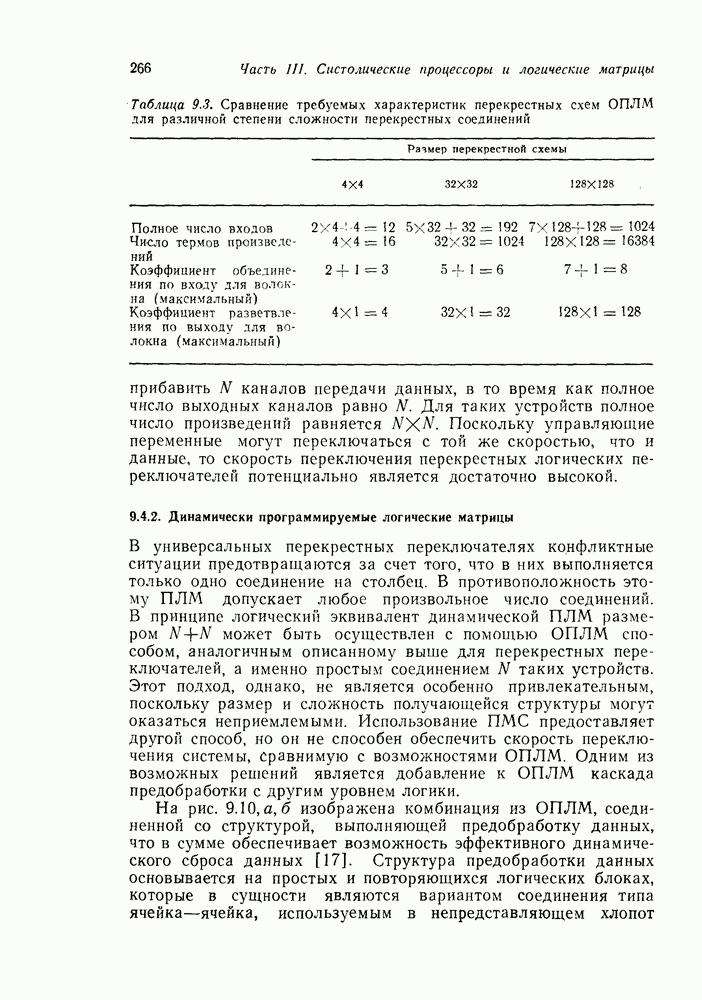
- 9.4.2. Динамически программируемые логические матрицы
- 9.5. Выводы
- Часть IV. СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- Глава 10. ОПТИКА И СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
- 10.2. Что такое искусственный интеллект?
- 10.2.1. Характеристики знаний
- 10.2.2. Представление знаний
- 10.2.3. Поиск
- 10.2.4. Сравнительные характеристики символьных и цифровых вычислений
- 10.3. Функциональные возможности символьных вычислений
- 10.3.2. Понимание речи
- 10.3.3. Техническое зрение
- 10.3.4. Понимание естественного языка
- 10.3.5. Экспертные системы
- 10.4. Архитектуры символьных вычислений
- 10.4.2. Архитектуры параллельной обработки
- 10.4.3. Оптическая реализация мультипроцессорных архитектур
- 10.4.4. Чисто оптические архитектуры
- 10.4.5. Гибридные оптоэлектрониые системы
- Глоссарий
- Глава 11. ОПТИЧЕСКИЕ МЕЖЭЛЕМЕНТНЫЕ СОЕДИНЕНИЯ ДЛЯ СИМВОЛЬНОЙ И ЦИФРОВОЙ ОБРАБОТКИ И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 11.2. Роль параллелизма и символьной обработки в вычислениях, проводимых в реальном времени
- 11.2.2. Необходимость вычислений в реальном времени
- 11.2.3. Необходимость параллельной обработки
- 11.2.4. Требования, предъявляемые к структуре процессоров
- 11.3. Преимущества перекрестных оптических схем
- 11.3.2. Преимущества оптических межэлементных соединений
- 11.3.3. Возможность реконфигурации сетей с оптическими переключателями
- 11.3.4. Получение запрограммированного потока данных с помощью оптических переключателей
- 11.4. Оптический процессор с перекрестной схемой
- 11.4.2. Описание элементов обработки
- 11.4.3. Оптический перекрестный переключатель и устройства с деформируемыми зеркалами
- 11.4.4. Программирование и функциональные операции
- 11.5. Получение логических выводов с помощью оптического процессора с перекрестной схемой
- 11.5.2. Схема «от фактов к цели» и ее реализация
- 11.5.3. Схема «от цели к фактам» и ее реализация
- 11.6. Цифровая обработка сигналов с помощью оптического мультипроцессора с перекрестной схемой
- 11.6.2. Коррелятор и матрично-векторный умножитель
- 11.6.3. Авторегрессивное моделирование для задачи спектрального анализа
- 11.7. Случай одновременного выполнения символьных и цифровых вычислений, пример речевой системы
- 11.7.2. Символьно-цифровое распознавание речи и система синтаксического анализа
- 11.7.3. Распознавание речи с помощью динамического изменения масштаба времени
- 11.7.4. Синтаксический анализ речи с помощью экспертной системы синтаксического анализа типа «ситуация — действие», «жди и смотри»
- 11.8. Выводы
- ЛИТЕРАТУРА