| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.2.2.2. Временная свертка
Альтернативой частотной свертке является операция свертки, выполняемая по временному аргументу. В обычной методике вычисления свертки преобразованная функция с обратной зависимостью от времени поддерживается постоянной, а относительно нее изменяется вторая функция. Их произведение во всех точках образует свертку. Временная свертка особенно привлекательна для оптических вычислений по двум причинам. Данная методика может выполняться на акустооптических брегговских ячейках, являющихся доступными, надежными и (относительно) недорогими. Может быть также использован ряд других подходов, включая интегральную оптику. Временная свертка также совместима с концепцией систолических процессоров [10]. В систолическом процессоре данные поступают в обрабатывающую ячейку, умножаются, суммируются и перемещаются в следующую обрабатывающую ячейку. Для получения общего результата вычислений складывают результаты из всех ячеек. Далее будет показано, что это именно тот способ, согласно которому работает устройство, выполняющее временную свертку.
На рис. 7.2 показаны два основных типа устройств, выполняющих временную свертку. В схеме с пространственным интегрированием (рис. 7.2, а) функция  вводится в устройство в виде пространственно изменяющейся функции (возможно, с помощью фиксированной маски или матрицы
вводится в устройство в виде пространственно изменяющейся функции (возможно, с помощью фиксированной маски или матрицы

Рис. 7.2. Схемы выполнения свертки по области временной координаты: а — с пространственным интегрированием; б — с временным интегрированием.
светодиодов), а само устройство работает как сдвиговый регистр. В качестве такого устройства могут применяться акустооптическая ячейка, устройство на поверхностных акустических волнах или даже ПЗСсдвиговый регистр, выполняющий дискретный сдвиг функции. Функция  поддерживается постоянной, в то время как
поддерживается постоянной, в то время как  сдвигается относительно нее. Свет, выходящий из сдвигового регистра, суммируется по пространству с помощью линз (изображенных скобками) на одном приемнике. Тогда временная зависимость
сдвигается относительно нее. Свет, выходящий из сдвигового регистра, суммируется по пространству с помощью линз (изображенных скобками) на одном приемнике. Тогда временная зависимость  сигнала, выходящего из детектора, представляет собой функцию
сигнала, выходящего из детектора, представляет собой функцию

являющуюся сверткой  и
и  На рис. 7.2, б показана схема временного интегрирования. Одна из функций,
На рис. 7.2, б показана схема временного интегрирования. Одна из функций,  подается в качестве зависящего от времени сигнала на источник света, например светодиод или полупроводниковый лазер. Другая функция,
подается в качестве зависящего от времени сигнала на источник света, например светодиод или полупроводниковый лазер. Другая функция,  подается на сдвиговый регистр. Функция
подается на сдвиговый регистр. Функция  равномерно «распределяется» по сдвиговому регистру с помощью линзы (снова изображенной скобками), в то время как
равномерно «распределяется» по сдвиговому регистру с помощью линзы (снова изображенной скобками), в то время как  сдвигается относительно нее. Свет, выходящий из сдвигового регистра, суммируется по времени дискретными элементами или матрицей фотодетекторов. Сигнал в матрице фотодетекторов можно представить в виде
сдвигается относительно нее. Свет, выходящий из сдвигового регистра, суммируется по времени дискретными элементами или матрицей фотодетекторов. Сигнал в матрице фотодетекторов можно представить в виде

где  — скорость сдвига функции
— скорость сдвига функции  в сдвиговом регистре. Сигнал
в сдвиговом регистре. Сигнал  представляет вариант пространственной выборки операций свертки от
представляет вариант пространственной выборки операций свертки от  и
и 
При рассмотрении рис. 7.2 становится очевидным, что устройства, производящие пространственную и временную свертки, являются зеркальными образцами друг друга, где выходной и входной сигналы поменялись ролями. Для умножения двух чисел может быть использована любая из конфигураций, при этом функции  и
и  представляют в виде последовательностей цифр, описывающих соответствующие числа. Свертка должна выполняться дискретно; данные фотодетекторов могут считываться только тогда, когда цифры, представляющие
представляют в виде последовательностей цифр, описывающих соответствующие числа. Свертка должна выполняться дискретно; данные фотодетекторов могут считываться только тогда, когда цифры, представляющие  синхронизированы с цифрами, описывающими
синхронизированы с цифрами, описывающими  Это требует импульсного режима работы источника света или детектора. Для наглядности представим сдвиговые регистры как строки из клеточек, по которым перемещаются цифры, пробегающие по одной клеточке за тактовый цикл. Все входные и выходные функции будут записаны аналогичным образом, чтобы показать, каким образом данные должны быть форматированы.
Это требует импульсного режима работы источника света или детектора. Для наглядности представим сдвиговые регистры как строки из клеточек, по которым перемещаются цифры, пробегающие по одной клеточке за тактовый цикл. Все входные и выходные функции будут записаны аналогичным образом, чтобы показать, каким образом данные должны быть форматированы.
Ниже снова будет рассмотрен пример умножения десятичных чисел 
На рис. 7.3 показана схема вычисления свертки с пространственным и временным интегрированием для выполнения операции умножения. В схеме с пространственным интегрированием (рис. 7.3, а) сдвиговый регистр состоит из трех ячеек (так как в данном примере  Число
Число  передвигается по регистру синхронно с цифрами числа
передвигается по регистру синхронно с цифрами числа  по регистру. Если цифра вводится в систему источником света, то она сохраняется в ней в течение трех циклов, в то время пока другое число перемещают относительно него. Для числа
по регистру. Если цифра вводится в систему источником света, то она сохраняется в ней в течение трех циклов, в то время пока другое число перемещают относительно него. Для числа  требуются пять циклов, чтобы полностью очистить сдвиговый регистр и освободить место для умножения следующего числа. Таким образом, за этим числом должны последовать два буферных нуля, которые также оказываются включенными в последовательность цифр выходного сигнала (следует обратить внимание на смешанный формат выходного сигнала). Эти два буферных «пространства» рассчитаны на случай переполнения, которое может возникнуть после преобразования результата в обычный, несмешанный формат представления числа. В течение соответствующего буферного интервала времени источники входного светового сигнала могут быть выключены на период, составляющий два тактовых цикла. Этот интервал времени может быть использован для медленного переключения входного сигнала от светодиодов из одного значения в другое. В этом случае источник света может иметь гораздо большее время срабатывания, чем тактовый цикл. Фотодетекторы, однако, должны реагировать на каждый тактовый цикл.
требуются пять циклов, чтобы полностью очистить сдвиговый регистр и освободить место для умножения следующего числа. Таким образом, за этим числом должны последовать два буферных нуля, которые также оказываются включенными в последовательность цифр выходного сигнала (следует обратить внимание на смешанный формат выходного сигнала). Эти два буферных «пространства» рассчитаны на случай переполнения, которое может возникнуть после преобразования результата в обычный, несмешанный формат представления числа. В течение соответствующего буферного интервала времени источники входного светового сигнала могут быть выключены на период, составляющий два тактовых цикла. Этот интервал времени может быть использован для медленного переключения входного сигнала от светодиодов из одного значения в другое. В этом случае источник света может иметь гораздо большее время срабатывания, чем тактовый цикл. Фотодетекторы, однако, должны реагировать на каждый тактовый цикл.
В случае временного интегрирования (рис. 7.3, б) для вычисления полной свертки требуется наличие пяти ячеек в сдвиговом регистре. Теперь для очистки регистра от числа  требуется семь тактовых циклов. Следует заметить, что цифры
требуется семь тактовых циклов. Следует заметить, что цифры  вводятся в обратном порядке по сравнению со случаем
вводятся в обратном порядке по сравнению со случаем

Рис. 7.3. Схема умножения  выполняемого с помощью операции дискретной свертки цифр: а — с пространственным интегрированием; б - с временным интегрированием.
выполняемого с помощью операции дискретной свертки цифр: а — с пространственным интегрированием; б - с временным интегрированием.
пространственного интегрирования. Число должно быть полностью загружено в регистр до начала выполнения операции свертки, так что числу  должны предшествовать два буферных нуля (показанные в выходном сигнале). За числом
должны предшествовать два буферных нуля (показанные в выходном сигнале). За числом  также должны следовать два буферных нуля (также показанные в выходном сигнале). Входной источник света должен отслеживать каждый тактовый импульс, что требует от источника высокого быстродействия. Фотодетектор интегрирует сигнал на протяжении трех циклов. Результат интегрирования периодически выводится на матрицу фотодетекторов. Это позволяет также периодически производить считывание данных с детекторов за то время, пока выполняется умножение. В другом варианте архитектуры с временным интегрированием сдвиг обоих чисел относительно друг друга производится в противоположных направлениях, что дает сокращение времени, вдвое затрачиваемого на выполнение свертки. Такая архитектура является совместимой с методами интегральной оптики [8], однако она не пригодна для применения в систолических системах и далее не будет обсуждаться.
также должны следовать два буферных нуля (также показанные в выходном сигнале). Входной источник света должен отслеживать каждый тактовый импульс, что требует от источника высокого быстродействия. Фотодетектор интегрирует сигнал на протяжении трех циклов. Результат интегрирования периодически выводится на матрицу фотодетекторов. Это позволяет также периодически производить считывание данных с детекторов за то время, пока выполняется умножение. В другом варианте архитектуры с временным интегрированием сдвиг обоих чисел относительно друг друга производится в противоположных направлениях, что дает сокращение времени, вдвое затрачиваемого на выполнение свертки. Такая архитектура является совместимой с методами интегральной оптики [8], однако она не пригодна для применения в систолических системах и далее не будет обсуждаться.
Два основных блока умножителей, показанные на рис. 7.3, могут использоваться в различных сочетаниях при формировании систолических процессоров. Процессоры данного типа ранее были описаны в  и ниже это описание просто изложено повторно. Блоки умножителей могут соединяться как последовательно, так и параллельно. В первом случае имеется один входной сигнал
и ниже это описание просто изложено повторно. Блоки умножителей могут соединяться как последовательно, так и параллельно. В первом случае имеется один входной сигнал  и несколько входных сигналов
и несколько входных сигналов  Соответственно в случае умножения матрицы на вектор элементы вектора представляют собой входной сигнал
Соответственно в случае умножения матрицы на вектор элементы вектора представляют собой входной сигнал  а элементы каждой строки матрицы являются входными сигналами
а элементы каждой строки матрицы являются входными сигналами  Эта схема требует сдвига только в одном измерении и будет далее именоваться одномерной архитектурой.
Эта схема требует сдвига только в одном измерении и будет далее именоваться одномерной архитектурой.
Если блоки умножителя размещаются параллельно, то тогда имеется лишь один входной сигнал  который необходимо перемещать относительно нескольких входов
который необходимо перемещать относительно нескольких входов  . Соответственно
. Соответственно  представляет входной вектор,
представляет входной вектор,  строки матрицы. Поскольку требуется сдвиг в двух измерениях, то далее такая архитектура называется двумерной.
строки матрицы. Поскольку требуется сдвиг в двух измерениях, то далее такая архитектура называется двумерной.
Ниже представлены примеры выполнения свертки каждым из типов архитектур, рассмотренных для одной и той же задачи. Для большей убедительности взят случай умножения матрицы на вектор. Задача выглядит следующим образом.

Хотя в приведенном примере не используется смешанный формат, но в результате выполнения задачи возникает
переполнение. Кроме того, в приведенной задаче используются лишь целые числа. Однако, как показал опыт, полученный при эксплуатации ЭВМ, двоичное представление с успехом может быть использовано для обозначения различных знаков, дробей и даже комплексных чисел (хотя и за счет необходимости использования дополнительных разрядов). В процессе проверки того, как каждый процессор выполняет указанную задачу, имеется возможность сделать общие выводы о требованиях, предъявляемых к интерфейсным устройствам и скорости обработки.
Одномерная архитектура.
Сперва рассмотрим одномерную архитектуру с пространственным интегрированием (рис. 7.4). Ранее эта архитектура была описана в [12] и получила известность как схема оптического систолического матричного процессора (ОСМП). Для умножения матрицы  на вектор
на вектор  с точностью в I цифр ОСМП должен иметь один вход для ввода вектора,
с точностью в I цифр ОСМП должен иметь один вход для ввода вектора,  входов для ввода матричных элементов и
входов для ввода матричных элементов и  детекторов выходного сигнала. Элементы с, представляющие собой изменяющиеся по времени сигналы от
детекторов выходного сигнала. Элементы с, представляющие собой изменяющиеся по времени сигналы от  детекторов, подаются параллельно. Для решения задачи эти сигналы требуется просуммировать и перезаписать в смешанном формате. Последующий сигнал показывает, что ОСМП использует
детекторов, подаются параллельно. Для решения задачи эти сигналы требуется просуммировать и перезаписать в смешанном формате. Последующий сигнал показывает, что ОСМП использует  тактовых цикла для выполнения операции умножения.
тактовых цикла для выполнения операции умножения.
На рис. 7.5 показана одномерная архитектура с временным интегрированием. Как для элементов А, так и для элементов  требуются буферные разряды. В схеме имеется
требуются буферные разряды. В схеме имеется  входов для матричных элементов и один вход для ввода вектора. Для
входов для матричных элементов и один вход для ввода вектора. Для

Рис. 7.4. Схема одномерного умножителя матрицы на вектор с пространственным интегрированием.

(кликните для просмотра скана)
регистрации выходного сигнала требуется  фотодетекторов. Выходной сигнал может быть представлен в виде последовательности определенных сигналов путем соответствующего переключения детекторов, относящихся к заданным элементам вектора выходного вектора. Получающаяся последовательная серия сигналов может передаваться в соответствующую схему для выполнения суммирования и преобразования результата из смешанного формата в обычный. Процессор указанного вида требует использования
фотодетекторов. Выходной сигнал может быть представлен в виде последовательности определенных сигналов путем соответствующего переключения детекторов, относящихся к заданным элементам вектора выходного вектора. Получающаяся последовательная серия сигналов может передаваться в соответствующую схему для выполнения суммирования и преобразования результата из смешанного формата в обычный. Процессор указанного вида требует использования  таких же параллельных схем, как в случае ОСМП. Для выполнения процедуры умножения матрицы на вектор требуется
таких же параллельных схем, как в случае ОСМП. Для выполнения процедуры умножения матрицы на вектор требуется  тактовых циклов.
тактовых циклов.
В [13] описан вариант одномерной архитектуры с временным интегрированием, позволяющий резко увеличить скорость вычисления. Это достигается путем увеличения числа входов до величины  и сдвига буферных нулей между входными сигналами. Эта процедура также предусматривает сдвиг цифр, возникающих при переполнении, от выходного сигнала (рис. 7.6). Теперь для завершения процедуры матрично-векторного умножения требуется лишь
и сдвига буферных нулей между входными сигналами. Эта процедура также предусматривает сдвиг цифр, возникающих при переполнении, от выходного сигнала (рис. 7.6). Теперь для завершения процедуры матрично-векторного умножения требуется лишь  тактовых циклов.
тактовых циклов.
Двумерная архитектура.
В [14] описана двумерная архитектура с пространственным интегрированием и рассмотрен случай систолического акустооптического двоичного процессора выполнения свертки (САОДПС). Как показано на рис. 7.7, для САОДПС требуется I входов для ввода вектора и  входов для ввода матрицы. Имеется
входов для ввода матрицы. Имеется  детекторов выходного сигнала. САОДПС должен иметь два набора сдвиговых регистров; один набор быстро сдвигает матричные элементы относительно элементов вектора, в то время как другой набор регистров медленно передвигает вектор последовательно по всем строкам матрицы. Вектор выходного сигнала представляет собой
детекторов выходного сигнала. САОДПС должен иметь два набора сдвиговых регистров; один набор быстро сдвигает матричные элементы относительно элементов вектора, в то время как другой набор регистров медленно передвигает вектор последовательно по всем строкам матрицы. Вектор выходного сигнала представляет собой  последовательных серий, которые требуется просуммировать и преобразовать. Процесс умножения занимает время, равное
последовательных серий, которые требуется просуммировать и преобразовать. Процесс умножения занимает время, равное  тактовых циклов. Последний из обсуждаемых умножителей матриц на вектор, показанный на рис. 7.8, представляет двумерную архитектуру с временным интегрированием. Имеется один вход для вектора, который требуется развернуть и переместить относительно
тактовых циклов. Последний из обсуждаемых умножителей матриц на вектор, показанный на рис. 7.8, представляет двумерную архитектуру с временным интегрированием. Имеется один вход для вектора, который требуется развернуть и переместить относительно  входов матрицы. Выходной сигнал требует
входов матрицы. Выходной сигнал требует  фотодетекторов, которые должны быть синхронизированы с целью параллельного вывода выходных сигналов. Затраты времени составят в этом случае
фотодетекторов, которые должны быть синхронизированы с целью параллельного вывода выходных сигналов. Затраты времени составят в этом случае  тактовых циклов.
тактовых циклов.
Умножитель матрицы на матрицу.
На основе описанного выше умножителя на вектор может быть создан умножитель матрицы на матрицу. Например,  одномерных умножителей с пространственным интегрированием могут быть размещены параллельно для умножения матрицы
одномерных умножителей с пространственным интегрированием могут быть размещены параллельно для умножения матрицы  на матрицу
на матрицу 
Аналогичная конфигурация возникает при последовательном размещении двумерных умножителей с пространственным интегрированием. Очевидно, что при таком методе конструирования могут быть получены только два вида умножителей матрицы на матрицу, а именно варианты с пространственным и временным интегрированием. Оба они показаны ниже, но для простоты изображены лишь входные сигналы. Выходные

Рис. 7.6. Схема одномерного умножителя матрицы на вектор с временным интегрированием, обладающего повышенным быстродействием [13].

Рис. 7.7, Схема двумерного умножителя матрицы на вектор с пространственным интегрированием [14].

(кликните для просмотра скана)
сигналы могут быть получены с помощью соответствующих схем умножителей матрицы на вектор.
На рис. 7.9 показан вариант с пространственным интегрированием, где матричное произведение есть  при
при  Имеется
Имеется  входов для одной матрицы и
входов для одной матрицы и  входов для другой. Для выходной матрицы имеется
входов для другой. Для выходной матрицы имеется  фотодетекторов. Вид входных сигналов позволяет заключить, что выполнение всей процедуры потребует
фотодетекторов. Вид входных сигналов позволяет заключить, что выполнение всей процедуры потребует  тактовых циклов. Показанный на рис. 7.10 вариант схемы с временным интегрированием требует наличия
тактовых циклов. Показанный на рис. 7.10 вариант схемы с временным интегрированием требует наличия  входов для одной матрицы и
входов для одной матрицы и  входов для другой. Имеется
входов для другой. Имеется  синхронизируемых выходов. Операция умножения занимает лишь
синхронизируемых выходов. Операция умножения занимает лишь  тактовых циклов. Соответственно архитектура с временным интегрированием допускает большую степень параллелизма при умножении матрицы на матрицу.
тактовых циклов. Соответственно архитектура с временным интегрированием допускает большую степень параллелизма при умножении матрицы на матрицу.
Более совершенные характеристики были достигнуты для устройства, названного его создателем «быстродействующим биполярным некогерентным вычислительным устройством на светоделительном кубе, работающим без подачи напряжения», или сокращенно RUBIC cube [15] (рис. 7.11). Как и ранее, улучшение было достигнуто за счет увеличения числа

Рис. 7.9. Схема умножителя матрицы на матрицу с пространственным интегрированием,

Рис. 7.10. Схема умножителя матрицы на матрицу с временным интегрированием.

(кликните для просмотра скана)
входов и исключения возможностей возникновения с переполнением регистров. Дляг одной матрицы требуется  входов, для другой
входов, для другой  входов. Имеется
входов. Имеется  выходов. Полное время операции вычисления составляет лишь
выходов. Полное время операции вычисления составляет лишь  тактовых циклов.
тактовых циклов.
Разновидности основной архитектуры.
Сообщалось и о других способах преобразования схем вычисления свертки в схемы умножителей матрицы на матрицу. В [16] для получения промежуточного произведения при вычислении внутреннего произведения двух векторов используется основная схема вычисления свертки с интегрированием по времени. Все промежуточные произведения вычисляются параллельно на независимых друг от друга умножителях и суммируются с помощью цилиндрической линзы. Таким образом, для перемножения двух векторов, состоящих из  элементов, с точностью в
элементов, с точностью в  знаков требуется
знаков требуется  входов для каждого вектора,
входов для каждого вектора,  фотодетекторных элементов и
фотодетекторных элементов и  тактовых циклов. При выполнении суммирования с помощью линз максимальное значение на детектирующем элементе составляет
тактовых циклов. При выполнении суммирования с помощью линз максимальное значение на детектирующем элементе составляет  Матрично-векторный умножитель схематично показан на рис. 7.12. Следует заметить, что буферные нули в данном случае не требуются, поскольку элементы вводятся параллельно. Для построения матрично-векторного умножителя для перемножения матрицы
Матрично-векторный умножитель схематично показан на рис. 7.12. Следует заметить, что буферные нули в данном случае не требуются, поскольку элементы вводятся параллельно. Для построения матрично-векторного умножителя для перемножения матрицы  и вектора
и вектора  все
все  умножителей векторов размещаются параллельно. Теперь каждый элемент матрицы а имеет вход (при общем числе входов
умножителей векторов размещаются параллельно. Теперь каждый элемент матрицы а имеет вход (при общем числе входов  а элементы вектора
а элементы вектора  сдвигаются относительно этих входов. Умножение выполняется за интервал времени, составляющий
сдвигаются относительно этих входов. Умножение выполняется за интервал времени, составляющий  циклов; при этом
циклов; при этом  используется
используется  детекторов выходного сигнала. Возможности процессора удается расширить до операции умножения матрицы на матрицу с помощью временного разделения каналов для ввода элементов
детекторов выходного сигнала. Возможности процессора удается расширить до операции умножения матрицы на матрицу с помощью временного разделения каналов для ввода элементов  при условии построчной загрузки матрицы по соответствующим буферам. В схеме имеется также
при условии построчной загрузки матрицы по соответствующим буферам. В схеме имеется также  входов для одной матрицы и
входов для одной матрицы и  входов для другой, а также
входов для другой, а также  детекторов выходного сигнала. Затраты времени на вычисления составляют
детекторов выходного сигнала. Затраты времени на вычисления составляют  тактовых циклов.
тактовых циклов.
В работе [17] описан матрично-векторный умножитель с улучшенными возможностями, в котором используется частотное разделение каналов в акустооптической ячейке. Как указано в  данная архитектура не может быть незамедлительно приспособлена для цифровых вычислений, но ее можно несколько модифицировать для обработки цифровых данных. Вначале рассмотрим схему умножителя вектора на вектор, выполняющего свертку с пространственным интегрированием. Для достижения точности вычислений в I цифр при размерности вектора
данная архитектура не может быть незамедлительно приспособлена для цифровых вычислений, но ее можно несколько модифицировать для обработки цифровых данных. Вначале рассмотрим схему умножителя вектора на вектор, выполняющего свертку с пространственным интегрированием. Для достижения точности вычислений в I цифр при размерности вектора  необходимо использовать I входов для ввода одного вектора и один вход для ввода другого вектора, а обрабатывающая
необходимо использовать I входов для ввода одного вектора и один вход для ввода другого вектора, а обрабатывающая
ячейка должна иметь I разрядов. В схеме имеется один фотодетектор выходного сигнала; для вычисления внутреннего произведения требуется  тактовых циклов. Если в качестве входного сигнала в акустооптической ячейке рассматривается одна строка матрицы А, то все строки А могут быть введены одновременно путем использования различных несущих частот для каждой из строк. Следовательно, все элементы матрицы выходного сигнала появляются в выходной плоскости одновременно (рис. 7.13). Различные элементы с несколько смещены на рисунке, поскольку линза преобразует частоту входного сигнала в координату выходного сигнала. В данном случае элементы вектора
тактовых циклов. Если в качестве входного сигнала в акустооптической ячейке рассматривается одна строка матрицы А, то все строки А могут быть введены одновременно путем использования различных несущих частот для каждой из строк. Следовательно, все элементы матрицы выходного сигнала появляются в выходной плоскости одновременно (рис. 7.13). Различные элементы с несколько смещены на рисунке, поскольку линза преобразует частоту входного сигнала в координату выходного сигнала. В данном случае элементы вектора  все еще требуют наличия I входов, в схеме также имеется
все еще требуют наличия I входов, в схеме также имеется  детекторов выходного сигнала.
детекторов выходного сигнала.

Рис. 7.13. Умножитель матрицы на вектор с частотным разделением каналов [17].
Процедура матрично-векторного умножения производится за  тактовых цикла. Длительность тактового цикла не зависит от
тактовых цикла. Длительность тактового цикла не зависит от  но величина
но величина  ограничена возможностями акустооптической ячейки (см. разд. 7.3.2).
ограничена возможностями акустооптической ячейки (см. разд. 7.3.2).
7.2.2.3. Способы определения внешнего произведения методом вычисления свертки
Все обсуждавшиеся до сих пор методы позволяют умножать две матрицы или матрицу на вектор путем выполнения операции внутреннего произведения между строками одной матрицы и столбцами другой. Согласно [18], произведение матриц может также быть найдено с помощью вычисления внешнего
произведения. Внешнее произведение определяется выражением  где
где  -мерный вектор,
-мерный вектор,  -мерный вектор, а с — матрица
-мерный вектор, а с — матрица  Для частного случая с
Для частного случая с  получаем
получаем

Если элементы с суммируются вдоль противоположных диагоналей, то может быть получен новый вектор с, компоненты которого

представляют собой не что иное, как свертку а и Ь. Отсюда следует, что если  являются цифровыми представлениями чисел, то можно определить результат их перемножения.
являются цифровыми представлениями чисел, то можно определить результат их перемножения.
Матрично-векторное произведение выполняется путем вычисления внешнего произведения первого столбца матрицы и первого элемента вектора, сложения с результатом внешнего произведения второго столбца и второго элемента и т. д. Например, произведение

в двоичной записи выглядит так;

Если две подматрицы соответствующей матрицы суммируются вдоль противодиагоналей, то в результате получим

Возможности умножителя могут быть легко расширены для случая умножения матрицы на матрицу.
Для больших матриц, разделенных на подматрицы, процедура суммирования вдоль противодиагоналей может оказаться весьма тяжелой задачей. В работе [19] было предложено выполнять суммирование вдоль противодиагоналей оригинальным
способом, записывая вектор в виде матрицы следующим образом:

Правильный результат получают уже в смешанном формате, путем умножения исходной матрицы на дополненный вектор. Эта процедура может быть выполнена с помощью любого из обсуждавшихся выше вариантов умножения матрицы на матрицу. Ценой этого будет служить увеличение объема памяти, необходимое для записи вектора, и задача класса умножение матрицы на вектор оказывается «отданной в уплату» за задачу класса матрица — матрица. В целом же кажется более выгодным использовать оптические методы для выполнения суммирования вдоль противодиагоналей. В число возможных оптических способов решения такой задачи входит сегментация цилиндрических линз, сегментация голографических линз или применение матриц оптических волокон, соединяющих соответствующие элементы с детекторами, на которых происходит суммирование.
В работе [20] предложены две возможные схемы построения процессоров внешнего произведения. В первом случае используется перекрестное включение одномерных входных модуляторов (рис. 7.14). Для умножения матрицы на вектор в один из модуляторов вводят целый столбец матрицы, а элементы вектора размещаются в другом модуляторе. Матричный модулятор должен обладать  разрядами, а модулятор для ввода вектора должен иметь I разрядов. Когда оба модулятора загружены, то от источника света подается импульс света и перекрестное произведение записывается на матрице
разрядами, а модулятор для ввода вектора должен иметь I разрядов. Когда оба модулятора загружены, то от источника света подается импульс света и перекрестное произведение записывается на матрице  интегрирующих по времени детекторов. Если суммирование осуществляется оптически, необходимо только
интегрирующих по времени детекторов. Если суммирование осуществляется оптически, необходимо только  детекторов. Каждое промежуточное произведение может быть «накоплено» на детекторе за время загрузки входного сигнала в модулятор, которое полагаем равным
детекторов. Каждое промежуточное произведение может быть «накоплено» на детекторе за время загрузки входного сигнала в модулятор, которое полагаем равным  Полное число тактовых импульсов для операции умножения матрицы на вектор составляет
Полное число тактовых импульсов для операции умножения матрицы на вектор составляет  Для умножения матрицы на матрицу требуется
Для умножения матрицы на матрицу требуется  детекторов, при этом необходимое число тактовых циклов составляет лишь
детекторов, при этом необходимое число тактовых циклов составляет лишь  (если
(если 
Во втором методе используется один двумерный пространственный модулятор света, адресация которого проводится с
Таблица 7.1. Рабочие характеристики умножителей матрицы на вектор

помощью специальной перекрестной матрицы согласно данным, показанным на рис. 7.15. Если предположить, что возможна параллельная адресация всех перекрещивающихся электродов, тогда адресация всей матрицы может быть осуществлена за один тактовый цикл. В этом случае за время другого тактового цикла можно включить источник света и произвести запись набора величин промежуточных произведений. Для умножения матрицы на вектор необходимо  модуляторов,
модуляторов,  фотодетекторов, процедура занимает
фотодетекторов, процедура занимает  тактовых циклов. Для умножения матрицы на матрицу требуется
тактовых циклов. Для умножения матрицы на матрицу требуется  модуляторов,
модуляторов,  фотодетекторов, затраты времени составляют лишь
фотодетекторов, затраты времени составляют лишь  тактовых циклов.
тактовых циклов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ПРОСТРАНСТВЕННЫЕ МОДУЛЯТОРЫ СВЕТА
- Глава 1. МАГНИТООПТИЧЕСКИЕ МОДУЛЯТОРЫ СВЕТА
- 1.2. Принцип действия магнитооптических модуляторов
- 1.3. Магнитные свойства ферримагнитных гранатов и механизмы переключения
- 1.3.2. Формирование магнитных доменов
- 1.3.3. Подвод внешнего магнитного поля и петля гистерезиса
- 1.4. Оптические свойства магнитооптических гранатовых пленок
- 1.4.2. Спектральная зависимость коэффициента пропускания
- 1.4.3. Практические ограничения полной эффективности
- 1.4.4. Ограничения величины контраста
- 1.5. Конструкция магнитооптических модуляторов
- 1.5.2. Модуляторы с термомагнитным переключением
- 1.5.3. Модулятор света «лайтмод» с магнитной адресацией
- 1.5.4. Способ переключения с помощью магнитного поля смещения
- 1.6. Обсуждение результатов и перспектив
- Глава 2. ОПТИЧЕСКИЕ БИСТАБИЛЬНЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 2.2. Принципы работы бистабильных устройств
- 2.3. Требования к характеристикам нелинейных устройств и материалам
- 2.4. Причины возникновения нелинейных оптических эффектов в полупроводниках
- 2.5. Современное состояние работ по оптическим бистабильным устройствам
- 2.6. Оптические логические элементы Фабри — Перо (ОЛЭФП)
- 2.7. Устройства на собственном электрооптическом эффекте (СЭОУ)
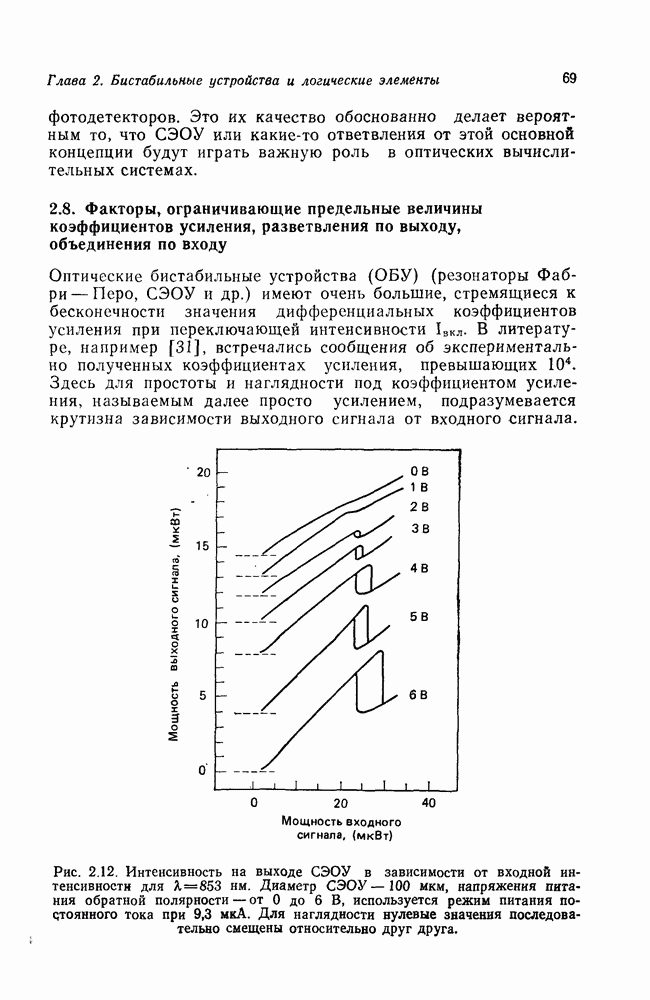
- 2.8. Факторы, ограничивающие предельные величины коэффициентов усиления, разветвления по выходу, объединения по входу
- 2.9. Концепции архитектуры
- 2.10. Предельные параметры и вычислительные возможности ОБУ
- 2.11. Три-стабильность и многозначная логика
- 2.12. Выводы
- Глава 3. КОМПОНЕНТЫ ОПТИЧЕСКОГО ПРОЦЕССОРА НА ОСНОВЕ ПРИБОРОВ С ЗАРЯДОВОЙ СВЯЗЬЮ (ПЗС)
- 3.2. Примеры электрооптической обработки сигналов (ЭООС)
- 3.3. Принципы работы ПЗС
- 3.3.1. Обсуждение конструкций с высоким быстродействием
- 3.4. Применение ПЗС в качестве выходных устройств ЭООС
- 3.5. Адресуемые ПЗС-пространственные модуляторы света (ПЗС-ПМС)
- 3.5.2. Устройство и характеристики ПЗС-модулятора
- 3.5.3. Эффект выбеливания
- 3.5.4. Эффект электропоглощения в квантовых ямах
- 3.6. Выводы
- Часть II. МНОГОЗНАЧНАЯ И ПОРОГОВАЯ ЛОГИКА
- Глава 4. МНОГОЗНАЧНАЯ ЛОГИКА В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 4.2. Проблема полноты в двоичной логике
- 4.3. Многозначные логические схемы, основанные на системе счисления в остаточных классах (ССОК)
- 4.4. Оптические многозначные логические ССОК-процессоры
- 4.5. Проблема полноты в многозначной логике
- 4.6. Краткое изложение и выводы
- Глава 5. ПОРОГОВОЕ КОДИРОВАНИЕ И ВЗВЕШИВАНИЕ В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 5.1.2. Определения взвешивания и порогового кодирования
- 5.1.3. Стандартная и нестандартная пороговые логики
- 5.2. Устройства с внешним пороговым кодированием
- 5.2.2. Пример 2-разрядного перестраиваемого устройства
- 5.3. Устройства с внутренним пороговым кодированием
- 5.4. Заключение
- Глава 6. МНОГОЗНАЧНАЯ ПОРОГОВАЯ ЛОГИКА
- 6.2. Многозначная пороговая логика
- 6.2.2. Критические оценки возможностей
- 6.2.3. Многозначная пороговая логика и электрооптические устройства
- 6.3. Мультилинейные разделяющиеся функции
- 6.4. Перспективные разработки
- ЧАСТЬ III. СИСТОЛИЧЕСКИЕ ПРОЦЕССОРЫ И ОПТИЧЕСКИЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 7. ОПТИЧЕСКОЕ УМНОЖЕНИЕ МАТРИЦ
- 7.2. Цифровая оптика
- 7.2.2. Оптические устройства, выполняющие свертку при операциях умножения
- 7.2.2.2. Временная свертка
- 7.3. Рабочие характеристики
- 7.3.1. Быстродействие процессора
- 7.3.2. Проблемы разработки систем и возможности их приборной реализации
- 7.4. Заключение
- Глава 8. АРХИТЕКТУРЫ КЛЕТОЧНОЙ ЛОГИКИ
- 8.2. Клеточная логика
- 8.2.1. Клеточные компьютеры
- 8.2.2. Структуры матриц
- 8.2.3. Клеточный автомат
- 8.2.4. Клеточная матрица Минника и синтез логических функций
- 8.2.5. Перестраиваемые матрицы
- 8.2.6. Классификация методов обработки данных
- 8.3. Оптическая двоичная логика и архитектура МКМД
- 8.4. Оптическая реализация
- 8.4.2. Локальная клеточная логика
- 8.4.2.2. Алгоритм перекодированных таблиц и согласованная фильтрация
- 8.4.2.3. Клеточная логика, использующая матрицы согласованных фильтров
- 8.5. Заключение
- Глава 9. ВОЛОКОННО-ОПТИЧЕСКИЕ ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- 9.2. Характеристики волоконно-оптических ПЛМ
- 9.2.2. Рассеиваемая мощность
- 9.2.3. Производительность и возможность изменения масштабов устройства
- 9.2.4. Сравнение возможностей различных методик реализации комбинационной логики
- 9.3. Проблемы создания логических схем для волоконно-оптических систем
- 9.3.2. Роль свойств декодеров высоких порядков
- 9.3.3. Производительность, функциональная сложность и затраты энергии
- 9.4. Перестраиваемые волоконные системы
- 9.4.2. Динамически программируемые логические матрицы
- 9.5. Выводы
- Часть IV. СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- Глава 10. ОПТИКА И СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
- 10.2. Что такое искусственный интеллект?
- 10.2.1. Характеристики знаний
- 10.2.2. Представление знаний
- 10.2.3. Поиск
- 10.2.4. Сравнительные характеристики символьных и цифровых вычислений
- 10.3. Функциональные возможности символьных вычислений
- 10.3.2. Понимание речи
- 10.3.3. Техническое зрение
- 10.3.4. Понимание естественного языка
- 10.3.5. Экспертные системы
- 10.4. Архитектуры символьных вычислений
- 10.4.2. Архитектуры параллельной обработки
- 10.4.3. Оптическая реализация мультипроцессорных архитектур
- 10.4.4. Чисто оптические архитектуры
- 10.4.5. Гибридные оптоэлектрониые системы
- Глоссарий
- Глава 11. ОПТИЧЕСКИЕ МЕЖЭЛЕМЕНТНЫЕ СОЕДИНЕНИЯ ДЛЯ СИМВОЛЬНОЙ И ЦИФРОВОЙ ОБРАБОТКИ И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 11.2. Роль параллелизма и символьной обработки в вычислениях, проводимых в реальном времени
- 11.2.2. Необходимость вычислений в реальном времени
- 11.2.3. Необходимость параллельной обработки
- 11.2.4. Требования, предъявляемые к структуре процессоров
- 11.3. Преимущества перекрестных оптических схем
- 11.3.2. Преимущества оптических межэлементных соединений
- 11.3.3. Возможность реконфигурации сетей с оптическими переключателями
- 11.3.4. Получение запрограммированного потока данных с помощью оптических переключателей
- 11.4. Оптический процессор с перекрестной схемой
- 11.4.2. Описание элементов обработки
- 11.4.3. Оптический перекрестный переключатель и устройства с деформируемыми зеркалами
- 11.4.4. Программирование и функциональные операции
- 11.5. Получение логических выводов с помощью оптического процессора с перекрестной схемой
- 11.5.2. Схема «от фактов к цели» и ее реализация
- 11.5.3. Схема «от цели к фактам» и ее реализация
- 11.6. Цифровая обработка сигналов с помощью оптического мультипроцессора с перекрестной схемой
- 11.6.2. Коррелятор и матрично-векторный умножитель
- 11.6.3. Авторегрессивное моделирование для задачи спектрального анализа
- 11.7. Случай одновременного выполнения символьных и цифровых вычислений, пример речевой системы
- 11.7.2. Символьно-цифровое распознавание речи и система синтаксического анализа
- 11.7.3. Распознавание речи с помощью динамического изменения масштаба времени
- 11.7.4. Синтаксический анализ речи с помощью экспертной системы синтаксического анализа типа «ситуация — действие», «жди и смотри»
- 11.8. Выводы
- ЛИТЕРАТУРА