| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.2.3. Поиск
Большие размеры баз знаний и пространства состояний, необходимые для решения практических символьных задач, обусловливают обязательное применение стратегии поиска либо так называемых релевантных фактов, содержащихся в базе знаний, либо путей решения в пространстве состояний задачи. На рис. 10.6 изображены различные виды поиска, включая чисто случайный поиск и весьма специфический эвристический поиск (эвристика предполагает использование знаний по определенной проблеме с целью придать поиску направленный характер). Хотя на этой упрощенной диаграмме стратегии поиска разделены на конкретные категории, однако фактически такого четкого разграничения провести невозможно. Чем менее направленным является поиск, тем большее время требуется для достижения цели. С другой стороны, чем более целенаправленным

Рис. 10.5. Элементы исчисления предикатов.
является поиск, тем более сложными оказываются процедуры управления. В предельном, наиболее сложном случае средства управления включали бы в себя такой объем знаний о процессе поиска, что сама необходимость поиска исключалась бы; т. е. средства управления направили бы решение непосредственно на цель. Поскольку оба крайних случая практически не реальны, то обычно делают попытки найти некоторую компромиссную стратегию, являющуюся наилучшей для конкретной задачи. Фактически многие системы ИИ используют комбинацию схем общего и частного назначения, что позволяет видоизменить общую стратегию поиска цели после его осуществления, согласно изменяющейся структуре пространства состояний.
К методикам поиска относят несколько общих стратегий, которые могли бы выполнять роль более или менее целенаправленных процедур в зависимости от той степени, в которой проблемная область и информация о цели применяются при выборе путей поиска. Некоторые из этих стратегий будут рассматриваться ниже. При этом будут сравниваться между собой древовидная структура и направленный граф, метод обхода дерева «перебором в глубину» и метод «перебора в ширину», а также методика вывода «от фактов к цели» и методика «от цели к фактам».
Процесс поиска может быть осуществлен путем следования либо по структуре направленного графа, изображенного на рис. 10.7, а, либо по соответствующей древовидной структуре, показанной на рис. 10.7, б. Поиск методом направленного графа позволяет вернуться к одной из ранее пройденных вершин графа и продолжить поиск по другому маршруту. С другой стороны, дерево поиска может совершить повторы при реализации стратегий. Например, при поиске устойчивых решений узел  может быть пройден повторно (например, через вершины А С F...), если первая попытка (через
может быть пройден повторно (например, через вершины А С F...), если первая попытка (через  не позволила достичь цели. Очевидным недостатком древовидной структуры
не позволила достичь цели. Очевидным недостатком древовидной структуры

Рис. 10.6. Иерархия стратегий поиска,
является избыточность числа проходов, а одним из преимуществ — использование намного меньшего объема памяти из-за того, что запоминать предыдущую стратегию в данном случае не требуется. Выбор древовидной структуры или графа часто определяется характером решаемой задачи, т. е. тем, насколько велика вероятность возникновения повторения ситуаций. Ресурсы памяти будут также являться решающим фактором.
Схемы поиска также могут отличаться порядком поиска вершин. Строго последовательный поиск, известный как перебор в глубину, следует заданной стратегии (например, ветви или дереву) до тех пор, пока стратегия не приведет к успеху в достижении цели, или не будет выявлено, что пора прекратить безуспешный поиск. В последнем случае происходит возврат к последней пройденной вершине, имеющей еще непроверенные ветви. Такая процедура поиска экономит ресурсы памяти, поскольку оказавшиеся бесполезными ветви исключаются из рассмотрения, однако, если проблемная область характеризуется длинными процедурами поисков, то перебор в глубину может потребовать слишком больших затрат времени. Приведенный на рис. 10.7, б пример поиска перебором в глубине осуществляется по узлам ABDBECACFC...
С другой стороны, в методе поиска перебором в ширину все состояния, связанные с начальным, проверяются на соответствие поставленной цели, и лишь после этого осуществляется переход на более глубокий уровень дерева или графа. Если цель не была достигнута, тогда эти состояния (или вершины) на первом уровне расширяют, т. е. генерируют и тестируют все возможные связанные с ними состояния. Например, поиск в ширину, осуществляемый по дереву целей, изображенному на рис. 10.7,б, происходит в порядке прохождения вершин,  до тех пор, пока не будет достигнуто состояние цели. Данный тип поиска может оказаться очень полезным в
до тех пор, пока не будет достигнуто состояние цели. Данный тип поиска может оказаться очень полезным в

Рис. 10.7, а — поиск с помощью направленного графа; 6 — дерево поиска,
системах параллельной обработки, которые будут обсуждаться в разд. 10.4.
До этого места в изложении процедуру решения проблемы и процесс проведения рассуждений представляли как последовательность событий, выполняемую из начального состояния в направлении состояния (состояний) цели. Другой способ, которым иногда пользуются, исходит из заданной цели и выполняется в обратном порядке, при этом стараются удовлетворить начальным условиям. В обратной процедуре проведения рассуждений, известной среди специалистов по ИИ как способ рассуждений «от цели к фактам», сначала находят одно или более состояний, которые могут привести к определению цели, и проверить, достигнуто ли соответствие с начальным состоянием (состояниями). Если нет, то поиск продолжается. Для систем продукций это означает, что в этом случае части «тогда» согласуются между собой и соответственно части «если» запускаются в действие (например, если часть «тогда» используется для нахождения более отдаленной вершины). Конкретно выбор либо процедуры от «цели к фактам», либо процедуры «от фактов к цели» определяется прежде всего двумя факторами — соотношением случаев ветвления с переходом назад по телу программы и случаев ветвления с переходом вперед, а также соотношением числа состояний цели и числа начальных состояний. Другими словами, если сформированное дерево поиска в конкретной проблемной области разветвляется в значительно большей степени при прямой процедуре поиска, чем при обратной процедуре поиска, то в этом случае процедура «от цели к фактам» будет более целесообразной. Если разветвление в обоих направлениях приблизительно одинаково, решающее значение приобретат число состояний. Процедура «от цели к фактам» выглядит более привлекательной при решении задач синтеза сложных объектов, когда существует широкий спектр исходных объектов, на основе которых приводится синтез. Примером служит задача определения того, какие характеристики материала необходимы для оптимального изготовления конкретного устройства. Здесь лучше было бы начать процедуру поиска с состояния цели (требований к устройству), чем с поисков наборов характеристик для всех возможных материалов.
С другой стороны, в шахматах проведение рассуждений никогда не может быть проведено «от цели к фактам» вследствие исключительно большого числа путей, ведущих к победе.
Для многих практических задач пространство состояний является настолько большим, что обычно жертвуют поиском гарантированных оптимальных решений в пользу применения специальных стратегий и тактики ограничения процесса поиска и удовлетворяются хорошим решением, отказываясь от наилучшего решения. Процесс поиска в шахматных задачах является
прекрасным примером этого; в противном случае шахматные задачи не могли бы решаться с помощью компьютеров. Как упомянуто выше, варьирование объемами информации может быть использовано для продуманного управления выше обсуждавшимися схемами поиска. Такие методики, как индексация, факторизация, сопоставление с образцом относят к категории эвристических методов общего назначения; однако их роль в ограничении сложных процедур поиска сравнительно невелика, тем более что они часто делают необходимым использование существенно более сложных эвристических методов, по сравнению с указанными выше методиками общего назначения. При индексировании используются заранее установленные схемы присвоения индексов, описывающих состояние задачи, а также задающих процесс запоминания правил, применяемых к каждому из состояний задачи (при этом требуется, чтобы эти правила могли быть связаны с индексом данного состояния). Из области хранения данных об определенном состоянии задачи впоследствии можно вызвать индекс этого состояния, что в свою очередь позволяет вызвать все правила, которые могли быть использованы. Более привлекательной выглядит операция факторизации. Если база знаний может быть разделена на большие множества данных, мало пересекающиеся между собой, то при рассмотрении соответствующей информации о проблемной области целые секции могут быть исключены. Например, если рассматриваемый вопрос связан с диагностикой легочных заболеваний, то для системы не требуется поиск части ее базы знаний, связанной с процедурами при проведении реальных хирургических операций на легком. Ограничение поиска также может быть достигнуто с помощью метода сопоставления с образцом, аналогичного традиционным задачам сравнения, где операция сопоставления используется для проверки того, что были найдены правильная форма, слово и т. д. Сопоставление с образцом часто используется в задачах распознавания речи, понимания естественного языка, распознавания образов; все они будут обсуждаться в разд. 10.3.
Можно ввести количественные коэффициенты, описывающие процесс ограничения поиска, с этой целью используют эвристические или оценочные функции определенных видов. Как показано на рис. 10.6, этот случай относят к классу эвристики частного назначения. Эвристическая функция дает значения весового или стоимостного коэффициента для каждой из вершин, что служит в определенной степени мерой «качества» пути достижения решения вплоть до данной вершины. Для различных проблемных областей будут иметься разные возможности для реализации таких функций, отсюда и появляется термин «частного назначения». Наиболее часто применяются концепции измерения качества пути, основанные на метрических

Рис. 10.8. Поиск «наилучшего первого».
представлениях расстояния до вершины или степени трудности поиска цели, а также выражаемые разностью путей между текущей вершиной и вершиной цели. Как уже упомянуто выше, в любом случае приходится искать компромисс между возможной экономией времени поиска, достигаемой за счет применения эвристических функций, и затратами времени на вычисления самих функций; т. е. сложные функции могут обеспечить прекрасное управление процессом поиска, но время, необходимое для их вычисления, может быть больше, чем время, которое потребовалось бы для реализации случайной процедуры поиска.
Если задана функция меры качества, описывающая пути поиска решения, то процесс поиска может проводиться по методу «первого наилучшего». Согласно данной методике, в качестве вершин, из которых предстоит расширить поиск цели, выбирают вершины, обладающие наилучшей мерой качества. Например, можно считать, что числа, записанные рядом с каждой из вершин на рис. 10.8, представляют собой значения эвристической функции, так что чем меньше соответствующее число, тем целесообразнее продолжить поиск именно из этой вершины. Соответственно поиск по методу «первого наилучшего» будет происходить следующим образом:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ПРОСТРАНСТВЕННЫЕ МОДУЛЯТОРЫ СВЕТА
- Глава 1. МАГНИТООПТИЧЕСКИЕ МОДУЛЯТОРЫ СВЕТА
- 1.2. Принцип действия магнитооптических модуляторов
- 1.3. Магнитные свойства ферримагнитных гранатов и механизмы переключения
- 1.3.2. Формирование магнитных доменов
- 1.3.3. Подвод внешнего магнитного поля и петля гистерезиса
- 1.4. Оптические свойства магнитооптических гранатовых пленок
- 1.4.2. Спектральная зависимость коэффициента пропускания
- 1.4.3. Практические ограничения полной эффективности
- 1.4.4. Ограничения величины контраста
- 1.5. Конструкция магнитооптических модуляторов
- 1.5.2. Модуляторы с термомагнитным переключением
- 1.5.3. Модулятор света «лайтмод» с магнитной адресацией
- 1.5.4. Способ переключения с помощью магнитного поля смещения
- 1.6. Обсуждение результатов и перспектив
- Глава 2. ОПТИЧЕСКИЕ БИСТАБИЛЬНЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 2.2. Принципы работы бистабильных устройств
- 2.3. Требования к характеристикам нелинейных устройств и материалам
- 2.4. Причины возникновения нелинейных оптических эффектов в полупроводниках
- 2.5. Современное состояние работ по оптическим бистабильным устройствам
- 2.6. Оптические логические элементы Фабри — Перо (ОЛЭФП)
- 2.7. Устройства на собственном электрооптическом эффекте (СЭОУ)
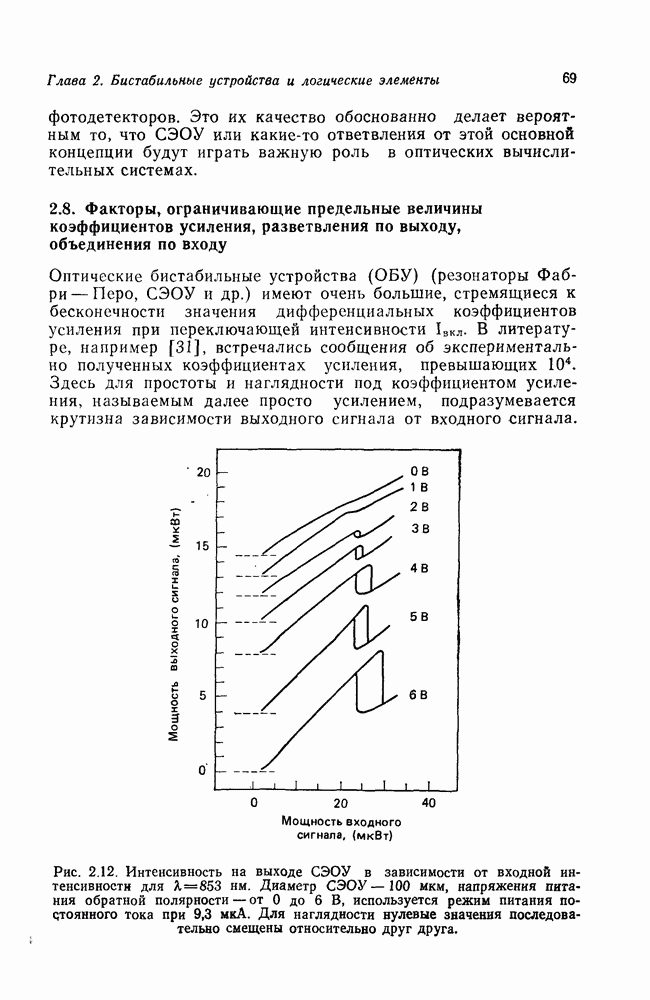
- 2.8. Факторы, ограничивающие предельные величины коэффициентов усиления, разветвления по выходу, объединения по входу
- 2.9. Концепции архитектуры
- 2.10. Предельные параметры и вычислительные возможности ОБУ
- 2.11. Три-стабильность и многозначная логика
- 2.12. Выводы
- Глава 3. КОМПОНЕНТЫ ОПТИЧЕСКОГО ПРОЦЕССОРА НА ОСНОВЕ ПРИБОРОВ С ЗАРЯДОВОЙ СВЯЗЬЮ (ПЗС)
- 3.2. Примеры электрооптической обработки сигналов (ЭООС)
- 3.3. Принципы работы ПЗС
- 3.3.1. Обсуждение конструкций с высоким быстродействием
- 3.4. Применение ПЗС в качестве выходных устройств ЭООС
- 3.5. Адресуемые ПЗС-пространственные модуляторы света (ПЗС-ПМС)
- 3.5.2. Устройство и характеристики ПЗС-модулятора
- 3.5.3. Эффект выбеливания
- 3.5.4. Эффект электропоглощения в квантовых ямах
- 3.6. Выводы
- Часть II. МНОГОЗНАЧНАЯ И ПОРОГОВАЯ ЛОГИКА
- Глава 4. МНОГОЗНАЧНАЯ ЛОГИКА В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 4.2. Проблема полноты в двоичной логике
- 4.3. Многозначные логические схемы, основанные на системе счисления в остаточных классах (ССОК)
- 4.4. Оптические многозначные логические ССОК-процессоры
- 4.5. Проблема полноты в многозначной логике
- 4.6. Краткое изложение и выводы
- Глава 5. ПОРОГОВОЕ КОДИРОВАНИЕ И ВЗВЕШИВАНИЕ В ОПТИЧЕСКИХ ВЫЧИСЛЕНИЯХ
- 5.1.2. Определения взвешивания и порогового кодирования
- 5.1.3. Стандартная и нестандартная пороговые логики
- 5.2. Устройства с внешним пороговым кодированием
- 5.2.2. Пример 2-разрядного перестраиваемого устройства
- 5.3. Устройства с внутренним пороговым кодированием
- 5.4. Заключение
- Глава 6. МНОГОЗНАЧНАЯ ПОРОГОВАЯ ЛОГИКА
- 6.2. Многозначная пороговая логика
- 6.2.2. Критические оценки возможностей
- 6.2.3. Многозначная пороговая логика и электрооптические устройства
- 6.3. Мультилинейные разделяющиеся функции
- 6.4. Перспективные разработки
- ЧАСТЬ III. СИСТОЛИЧЕСКИЕ ПРОЦЕССОРЫ И ОПТИЧЕСКИЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 7. ОПТИЧЕСКОЕ УМНОЖЕНИЕ МАТРИЦ
- 7.2. Цифровая оптика
- 7.2.2. Оптические устройства, выполняющие свертку при операциях умножения
- 7.2.2.2. Временная свертка
- 7.3. Рабочие характеристики
- 7.3.1. Быстродействие процессора
- 7.3.2. Проблемы разработки систем и возможности их приборной реализации
- 7.4. Заключение
- Глава 8. АРХИТЕКТУРЫ КЛЕТОЧНОЙ ЛОГИКИ
- 8.2. Клеточная логика
- 8.2.1. Клеточные компьютеры
- 8.2.2. Структуры матриц
- 8.2.3. Клеточный автомат
- 8.2.4. Клеточная матрица Минника и синтез логических функций
- 8.2.5. Перестраиваемые матрицы
- 8.2.6. Классификация методов обработки данных
- 8.3. Оптическая двоичная логика и архитектура МКМД
- 8.4. Оптическая реализация
- 8.4.2. Локальная клеточная логика
- 8.4.2.2. Алгоритм перекодированных таблиц и согласованная фильтрация
- 8.4.2.3. Клеточная логика, использующая матрицы согласованных фильтров
- 8.5. Заключение
- Глава 9. ВОЛОКОННО-ОПТИЧЕСКИЕ ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- 9.2. Характеристики волоконно-оптических ПЛМ
- 9.2.2. Рассеиваемая мощность
- 9.2.3. Производительность и возможность изменения масштабов устройства
- 9.2.4. Сравнение возможностей различных методик реализации комбинационной логики
- 9.3. Проблемы создания логических схем для волоконно-оптических систем
- 9.3.2. Роль свойств декодеров высоких порядков
- 9.3.3. Производительность, функциональная сложность и затраты энергии
- 9.4. Перестраиваемые волоконные системы
- 9.4.2. Динамически программируемые логические матрицы
- 9.5. Выводы
- Часть IV. СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ И ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
- Глава 10. ОПТИКА И СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
- 10.2. Что такое искусственный интеллект?
- 10.2.1. Характеристики знаний
- 10.2.2. Представление знаний
- 10.2.3. Поиск
- 10.2.4. Сравнительные характеристики символьных и цифровых вычислений
- 10.3. Функциональные возможности символьных вычислений
- 10.3.2. Понимание речи
- 10.3.3. Техническое зрение
- 10.3.4. Понимание естественного языка
- 10.3.5. Экспертные системы
- 10.4. Архитектуры символьных вычислений
- 10.4.2. Архитектуры параллельной обработки
- 10.4.3. Оптическая реализация мультипроцессорных архитектур
- 10.4.4. Чисто оптические архитектуры
- 10.4.5. Гибридные оптоэлектрониые системы
- Глоссарий
- Глава 11. ОПТИЧЕСКИЕ МЕЖЭЛЕМЕНТНЫЕ СОЕДИНЕНИЯ ДЛЯ СИМВОЛЬНОЙ И ЦИФРОВОЙ ОБРАБОТКИ И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 11.2. Роль параллелизма и символьной обработки в вычислениях, проводимых в реальном времени
- 11.2.2. Необходимость вычислений в реальном времени
- 11.2.3. Необходимость параллельной обработки
- 11.2.4. Требования, предъявляемые к структуре процессоров
- 11.3. Преимущества перекрестных оптических схем
- 11.3.2. Преимущества оптических межэлементных соединений
- 11.3.3. Возможность реконфигурации сетей с оптическими переключателями
- 11.3.4. Получение запрограммированного потока данных с помощью оптических переключателей
- 11.4. Оптический процессор с перекрестной схемой
- 11.4.2. Описание элементов обработки
- 11.4.3. Оптический перекрестный переключатель и устройства с деформируемыми зеркалами
- 11.4.4. Программирование и функциональные операции
- 11.5. Получение логических выводов с помощью оптического процессора с перекрестной схемой
- 11.5.2. Схема «от фактов к цели» и ее реализация
- 11.5.3. Схема «от цели к фактам» и ее реализация
- 11.6. Цифровая обработка сигналов с помощью оптического мультипроцессора с перекрестной схемой
- 11.6.2. Коррелятор и матрично-векторный умножитель
- 11.6.3. Авторегрессивное моделирование для задачи спектрального анализа
- 11.7. Случай одновременного выполнения символьных и цифровых вычислений, пример речевой системы
- 11.7.2. Символьно-цифровое распознавание речи и система синтаксического анализа
- 11.7.3. Распознавание речи с помощью динамического изменения масштаба времени
- 11.7.4. Синтаксический анализ речи с помощью экспертной системы синтаксического анализа типа «ситуация — действие», «жди и смотри»
- 11.8. Выводы
- ЛИТЕРАТУРА