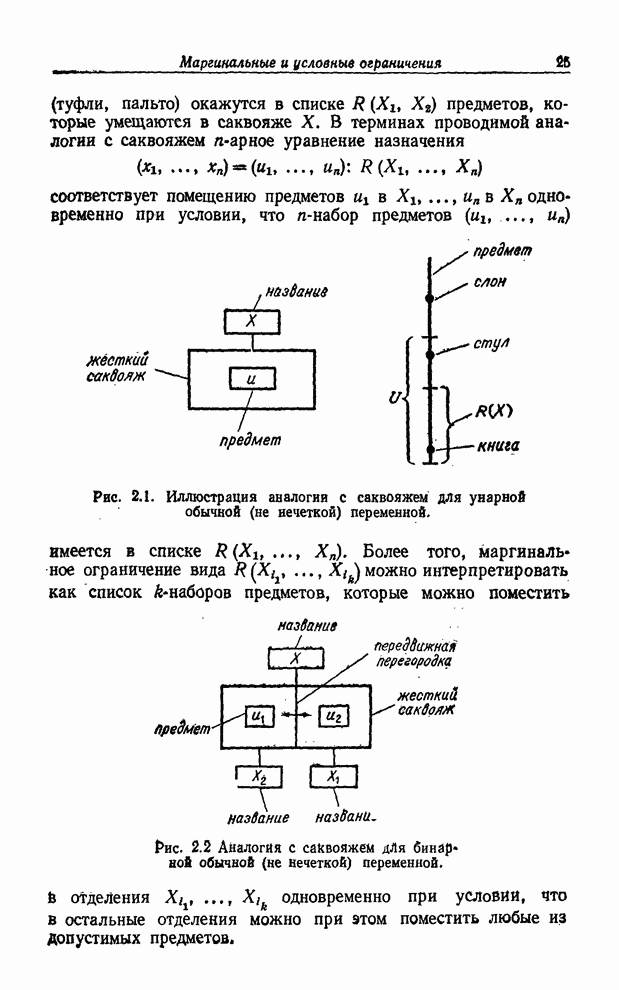
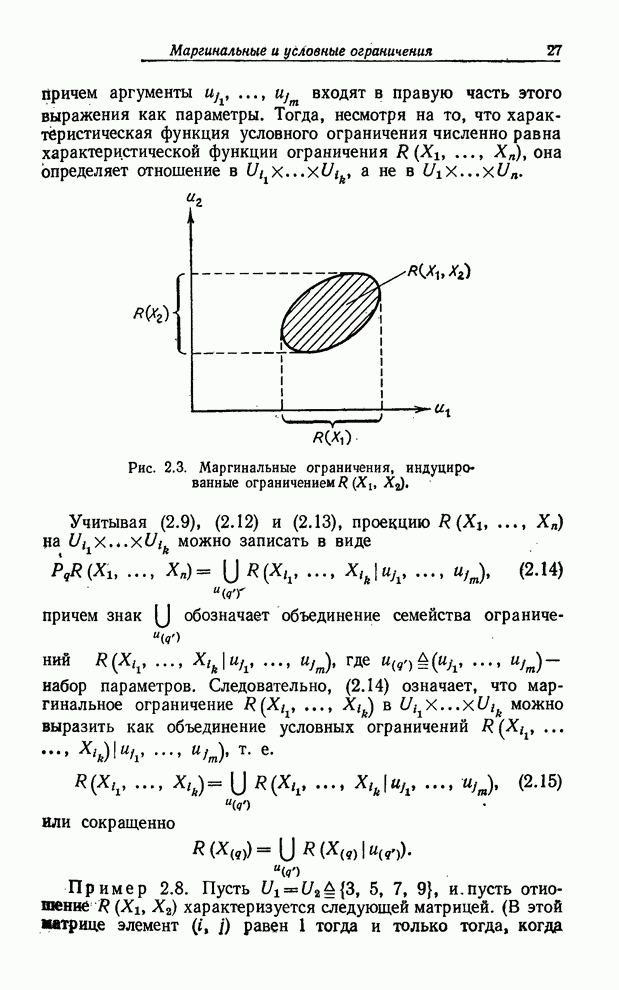
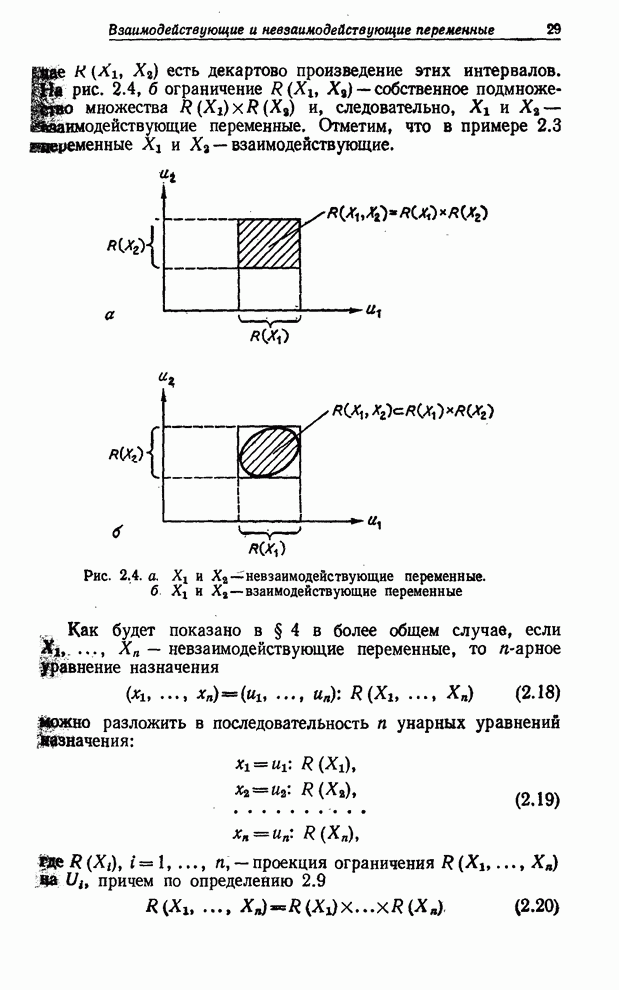
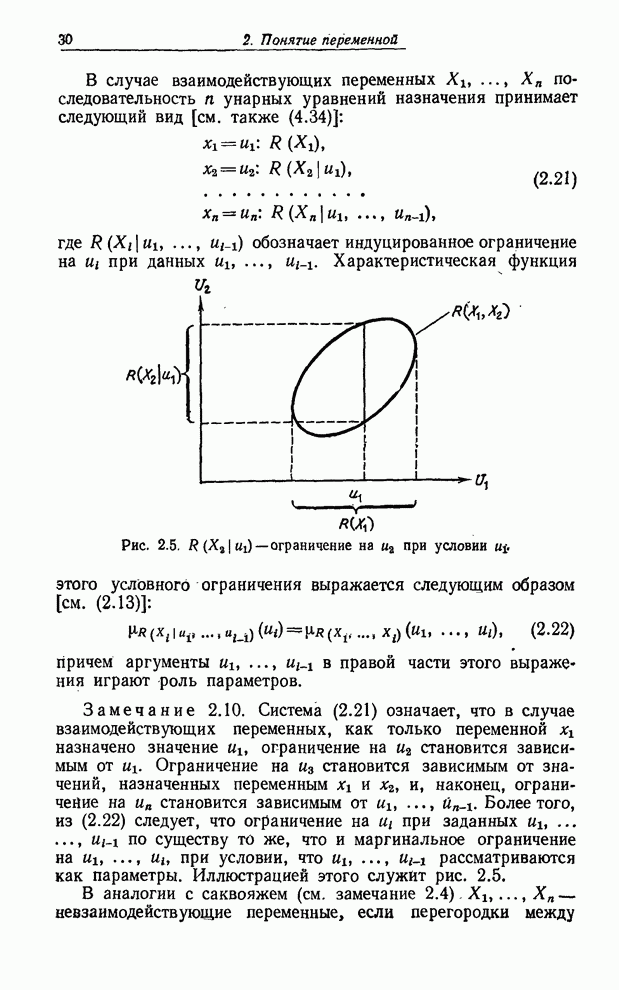
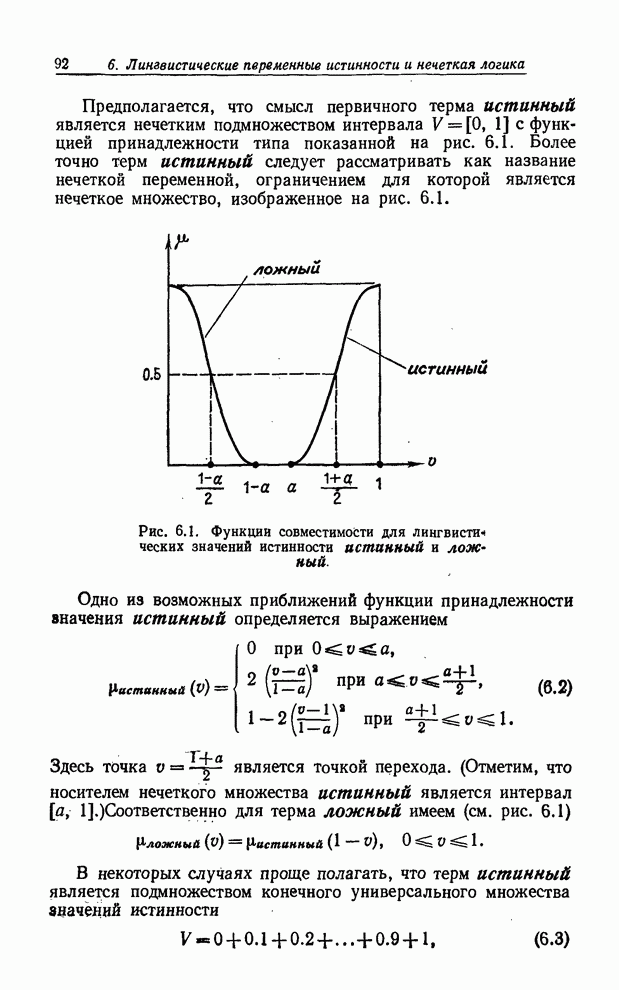
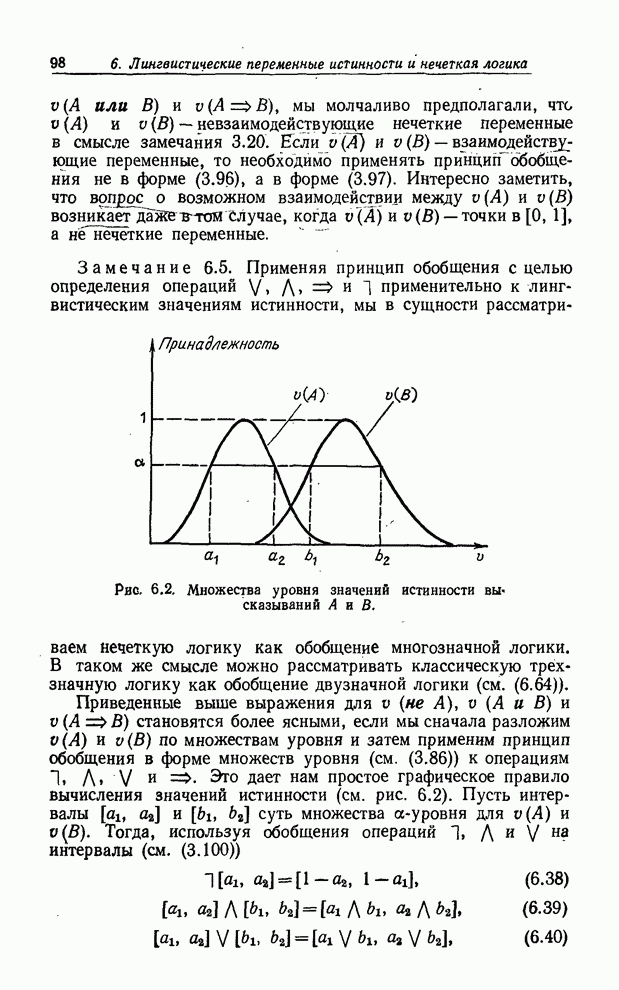
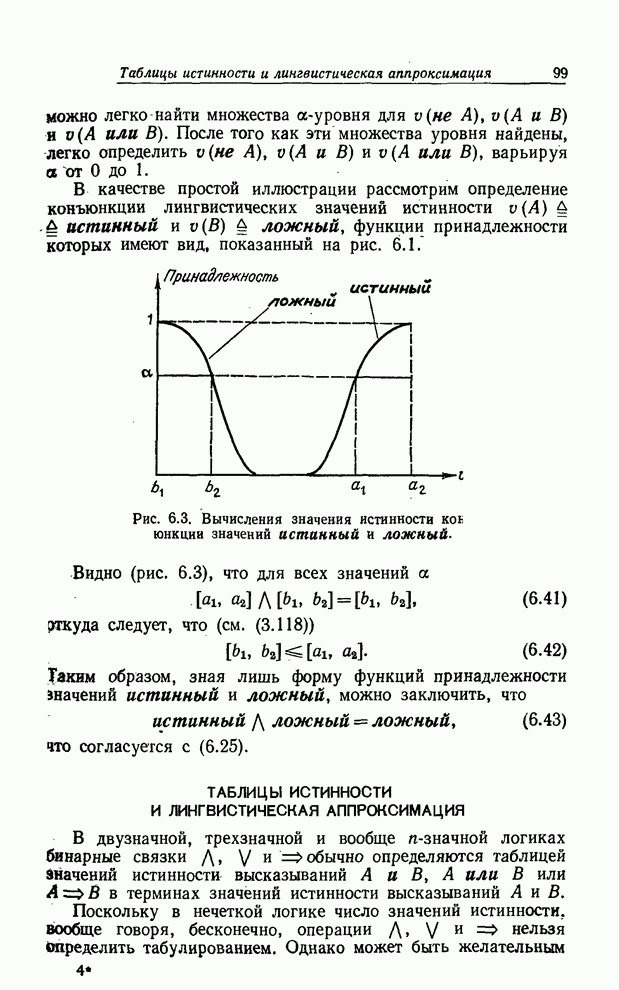
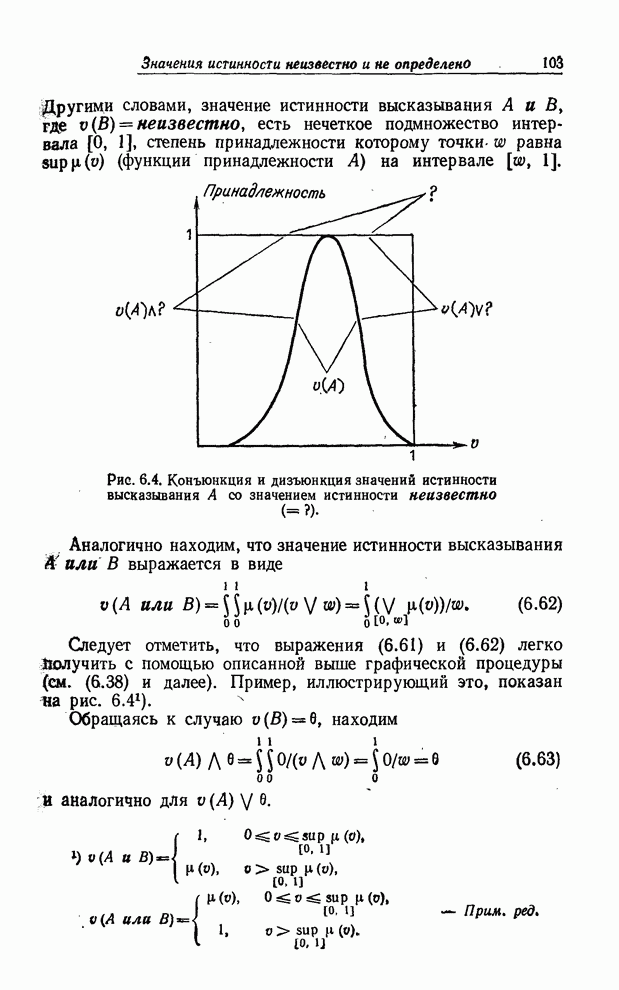
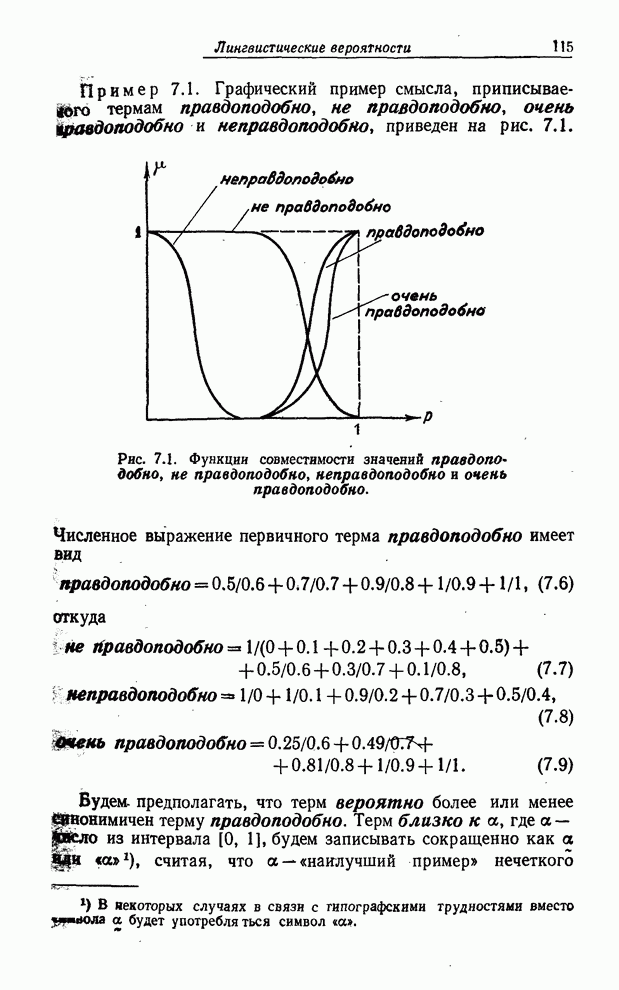
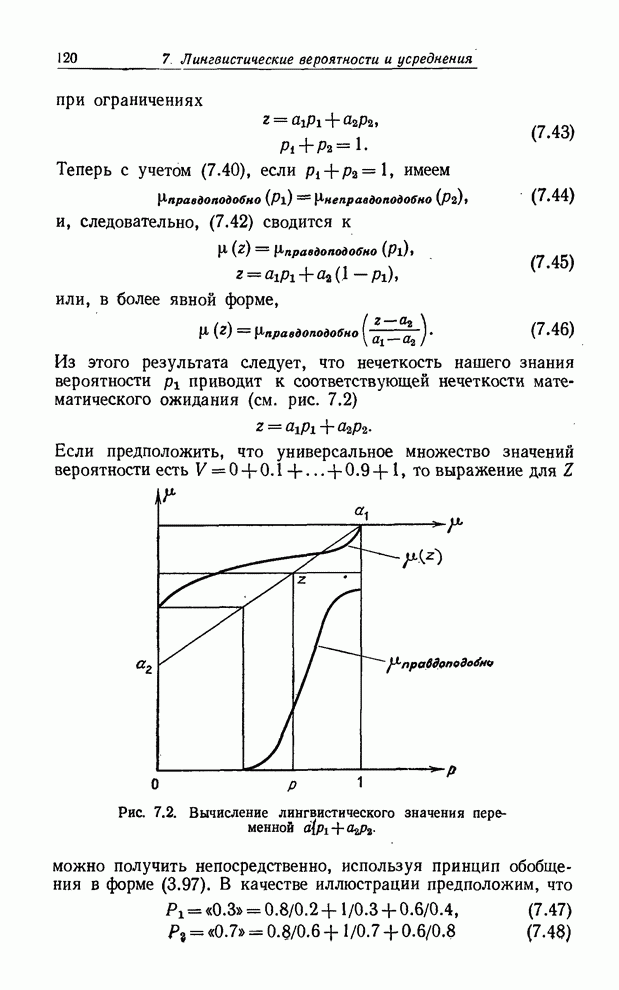
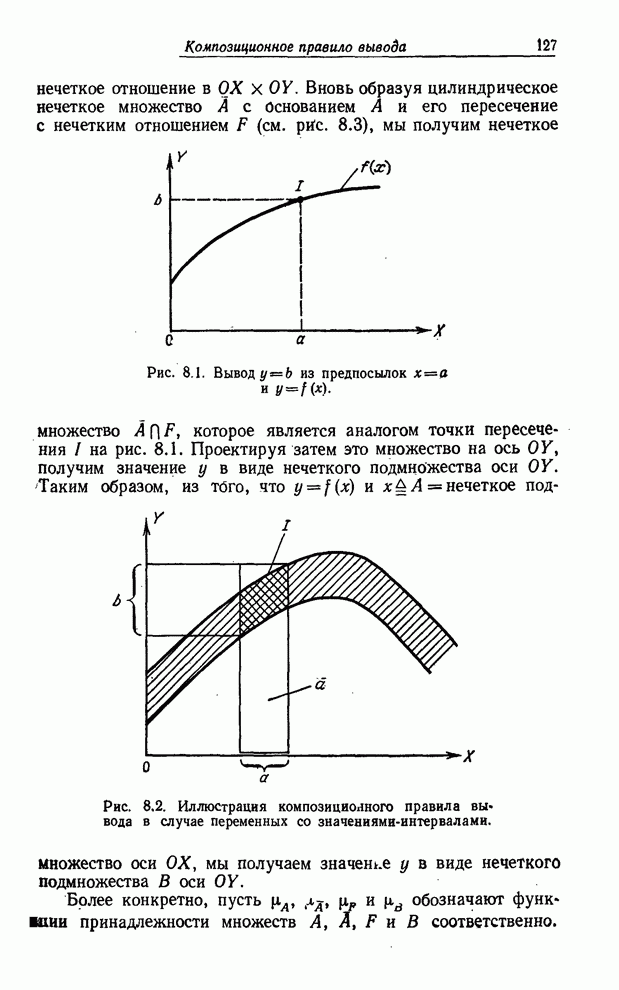
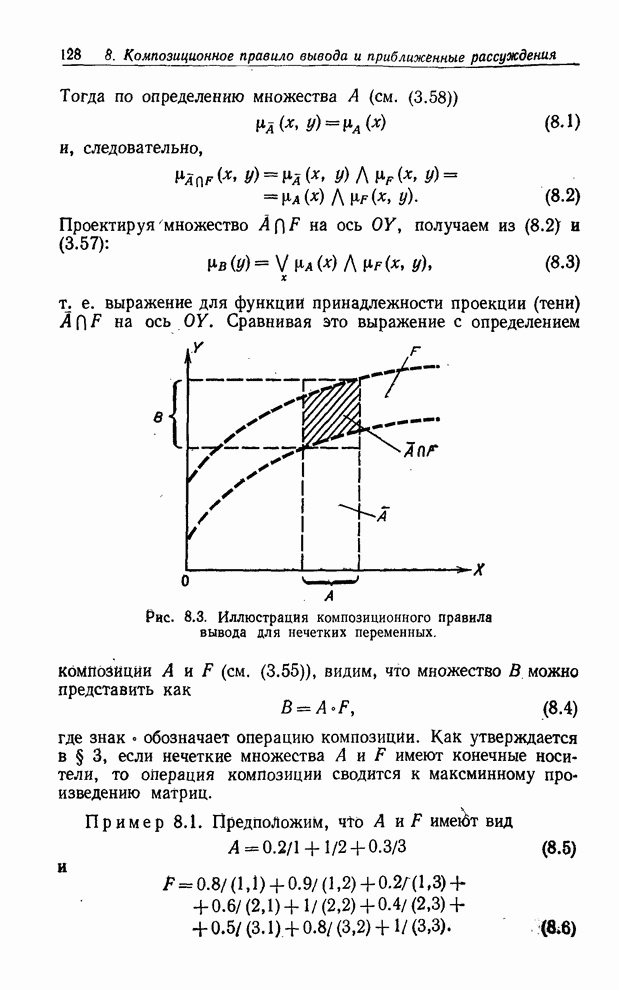
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
Если ![]() есть
есть ![]() -арное
нечеткое отношение в
-арное
нечеткое отношение в ![]() , то его проекция (тень)
на
, то его проекция (тень)
на ![]() есть
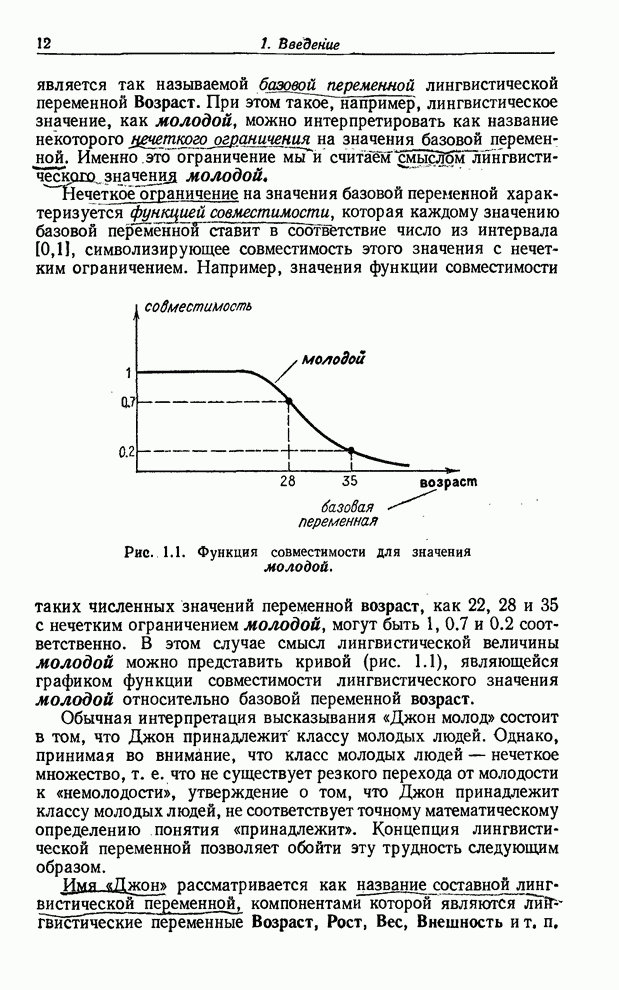
есть ![]() -арное
нечеткое отношение
-арное
нечеткое отношение ![]() в
в ![]() ,
которое определяется следующим образом (ср. с (2.12)):
,
которое определяется следующим образом (ср. с (2.12)):
 (3.57)
(3.57)
где
![]() — последовательность индексов
— последовательность индексов ![]() ;
; ![]() ;
; ![]() — дополнение
— дополнение ![]() ;
а
;
а
![]()
где
верхняя грань берется по значениям всех тех ![]() ,
которые входят в
,
которые входят в ![]() . Следует отметить, что если
. Следует отметить, что если ![]() — обычное (не нечеткое) отношение, то
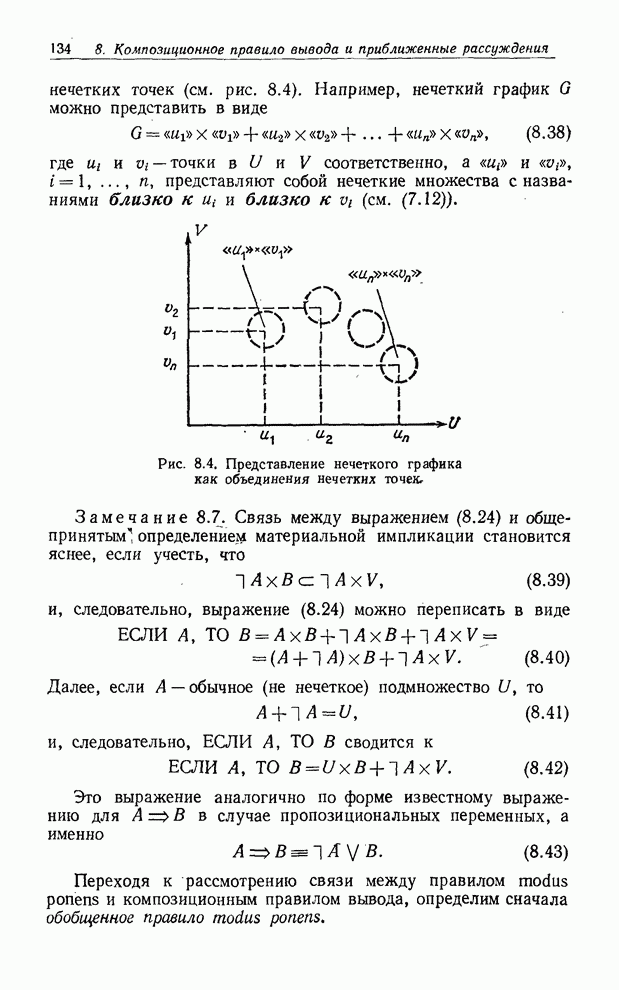
(3.57) сводится к (2.9).
— обычное (не нечеткое) отношение, то
(3.57) сводится к (2.9).
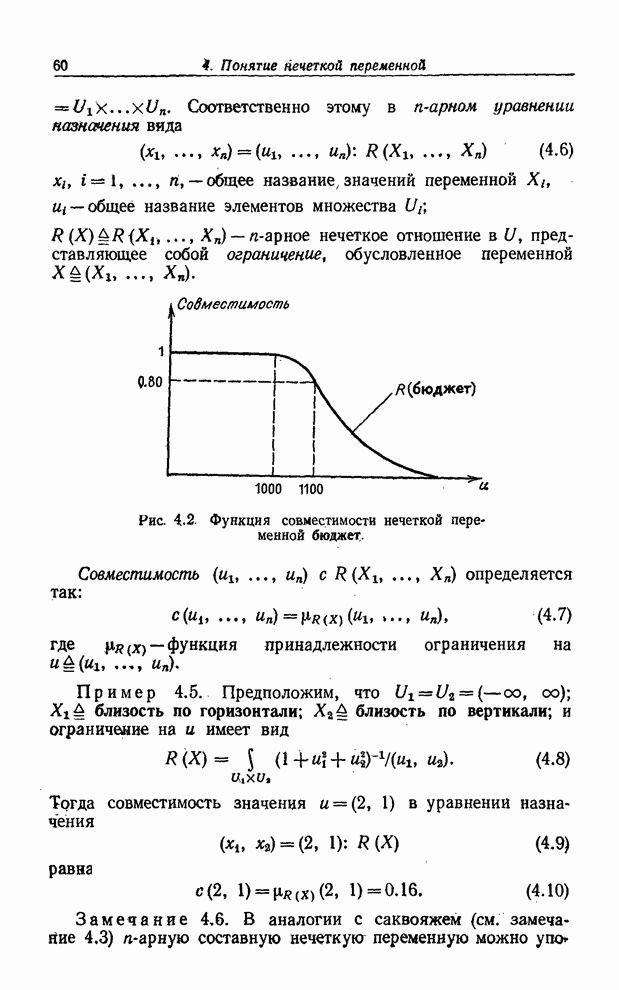
Пример 3.11. Для нечеткого отношения, определенного матрицей отношения (3.54), имеем
![]()
и
![]()
Ясно,
что различные нечеткие отношения в ![]() могут иметь
идентичные проекции на
могут иметь
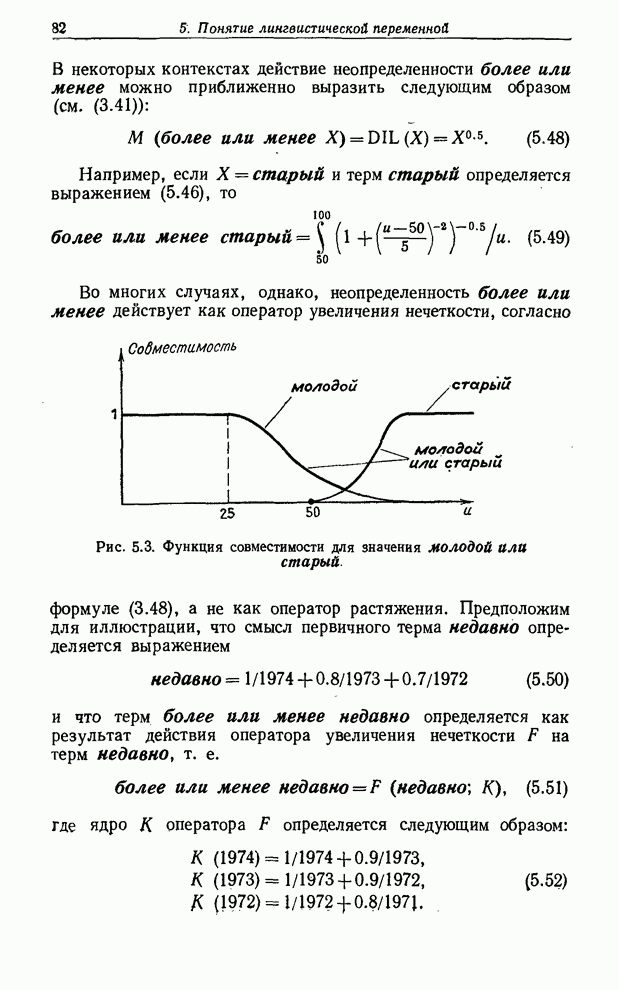
идентичные проекции на ![]() . Однако для данного
нечеткого отношения
. Однако для данного
нечеткого отношения ![]() в
в ![]() существует
единственное наибольшее отношение
существует
единственное наибольшее отношение ![]() в
в ![]() , проекция которого на
, проекция которого на ![]() есть
есть ![]() . Из
(3.57) следует, что функция принадлежности отношения
. Из
(3.57) следует, что функция принадлежности отношения ![]() имеет
вид
имеет
вид
![]() (3.58)
(3.58)
при
этом следует учитывать, что равенство (3.58) справедливо для всех ![]() , таких, что
, таких, что ![]() -й,
…,
-й,
…, ![]() -й аргументы
-й аргументы ![]() равны
соответственно первому, второму...
равны
соответственно первому, второму... ![]() -му аргументу
-му аргументу ![]() . Отсюда следует, что значение функции
. Отсюда следует, что значение функции ![]() в точке
в точке ![]() равно значению
этой функции в точке
равно значению
этой функции в точке ![]() , если только
, если только ![]() . Исходя из этого будем называть
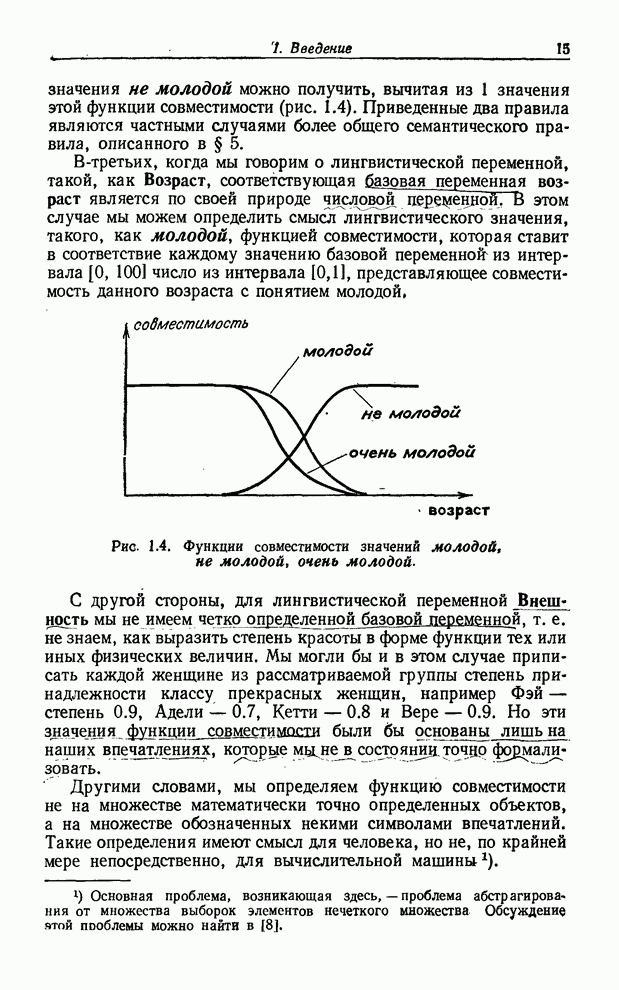
отношение
. Исходя из этого будем называть
отношение ![]() цилиндрическим продолжением отношения
цилиндрическим продолжением отношения
![]() , причем само
, причем само ![]() является
основанием отношения
является
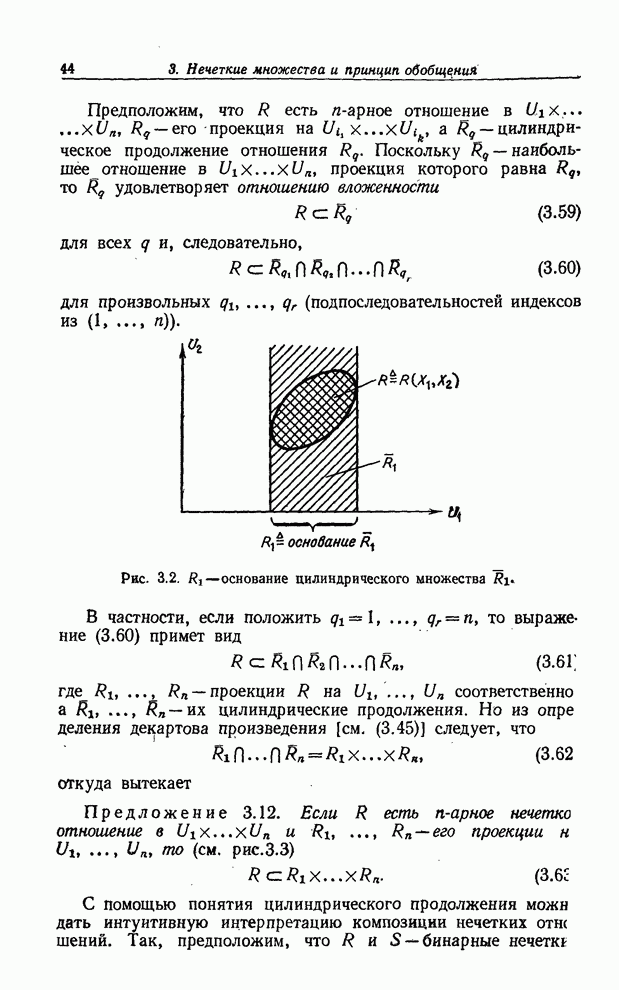
основанием отношения ![]() (см. рис. 3.2).
(см. рис. 3.2).
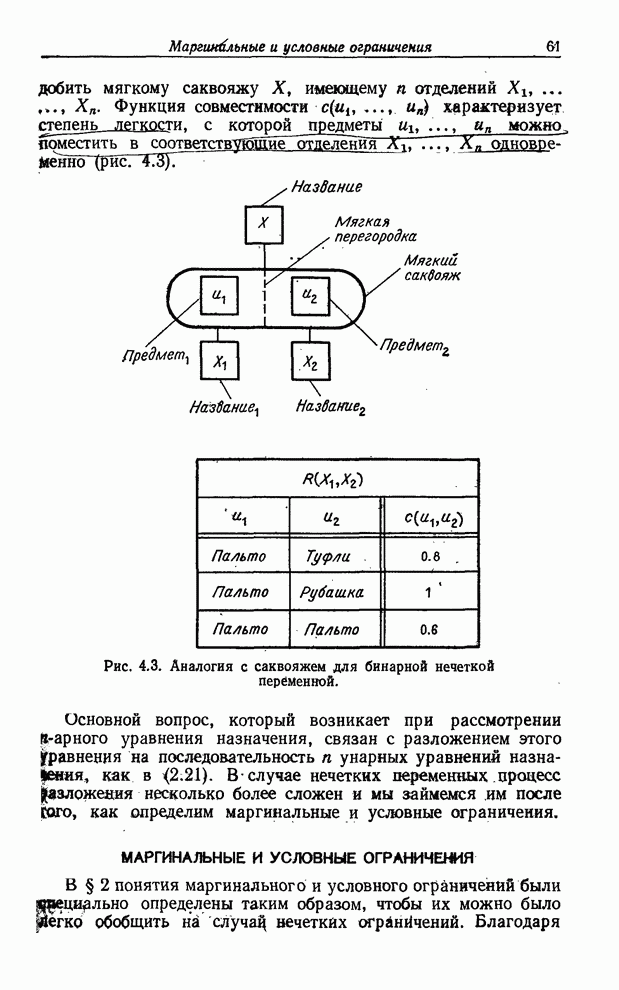
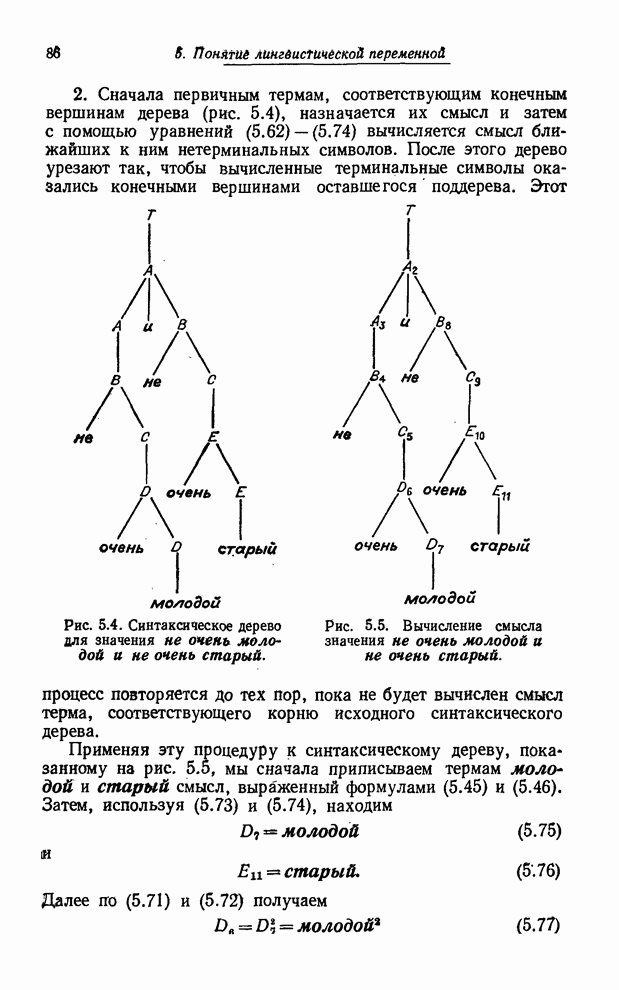
Предположим,
что ![]() есть
есть ![]() -арное
отношение в
-арное
отношение в ![]() ,
, ![]() — его
проекция на
— его
проекция на ![]() , а
, а ![]() —
цилиндрическое продолжение отношения
—
цилиндрическое продолжение отношения ![]() . Поскольку
. Поскольку ![]() —наибольшее отношение в
—наибольшее отношение в ![]() , проекция которого равна
, проекция которого равна ![]() , то
, то ![]() удовлетворяет
отношению вложенности
удовлетворяет
отношению вложенности
![]() (3.59)
(3.59)
для
всех ![]() и, следовательно,
и, следовательно,
![]() (3.60)
(3.60)
для
произвольных ![]() (подпоследовательностей индексов из
(подпоследовательностей индексов из ![]() ).
).
Рис. 3.2. ![]() — основание
цилиндрического множества
— основание
цилиндрического множества ![]() .
.
В
частности, если положить ![]() , то выражение
(3.60) примет вид
, то выражение
(3.60) примет вид
![]() (3.61)
(3.61)
где
![]() — проекции
— проекции ![]() на
на ![]() соответственно, a
соответственно, a ![]() — их цилиндрические продолжения. Но из
определения декартова произведения [см. (3.45)] следует, что
— их цилиндрические продолжения. Но из
определения декартова произведения [см. (3.45)] следует, что
![]() (3.62)
(3.62)
откуда вытекает
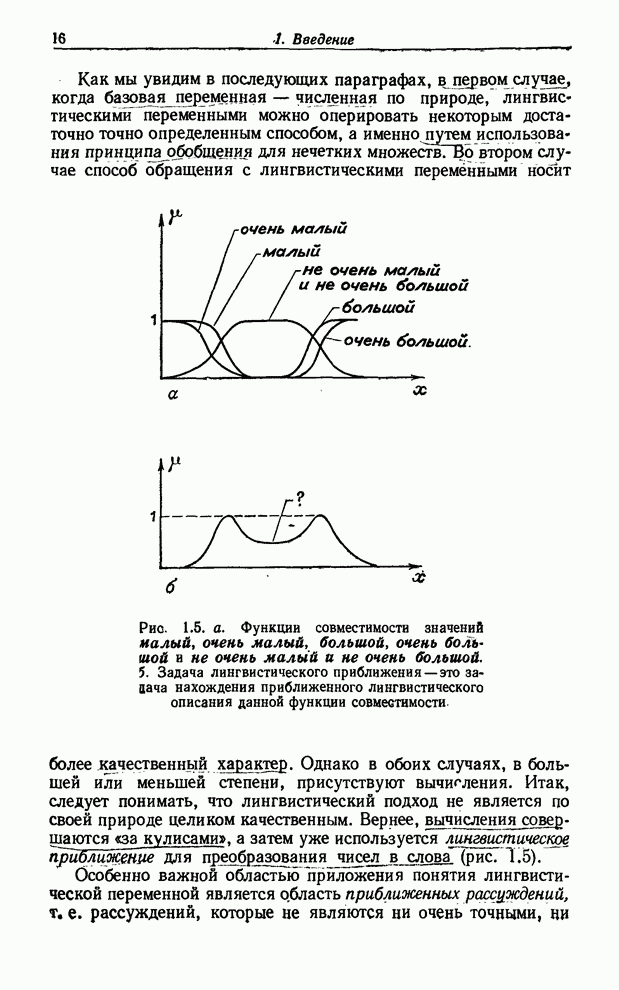
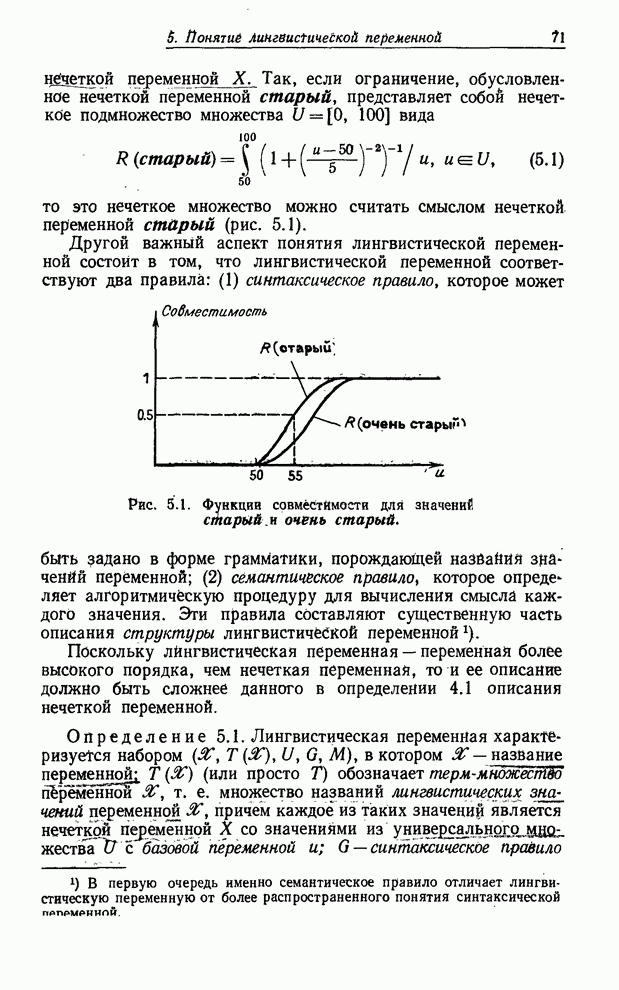
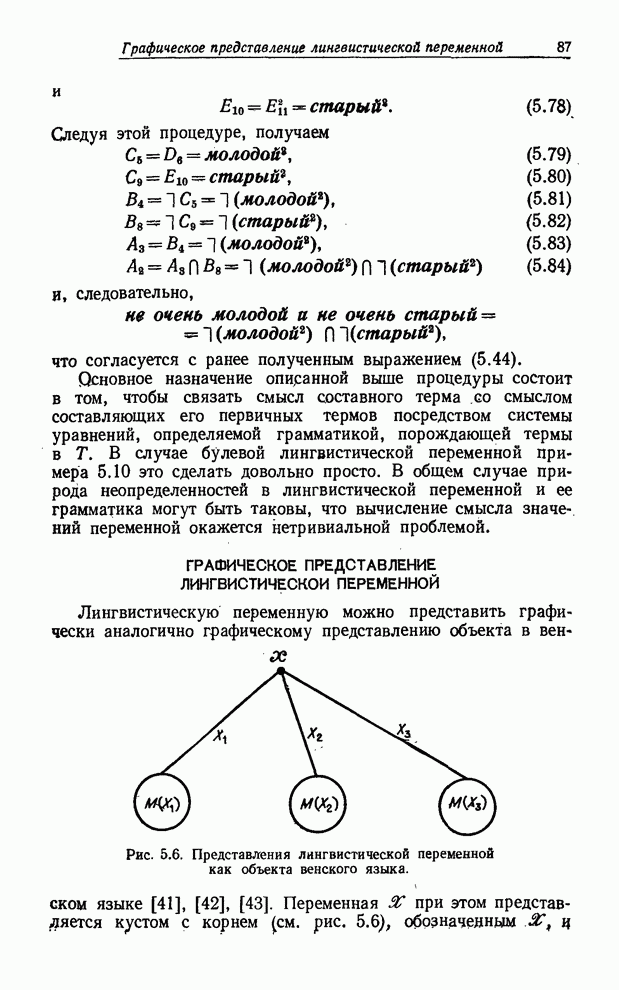
Предложение
3.12.
Если ![]() есть
есть ![]() -арнoе
нечеткое отношение в
-арнoе
нечеткое отношение в ![]() и
и ![]() — его проекции на
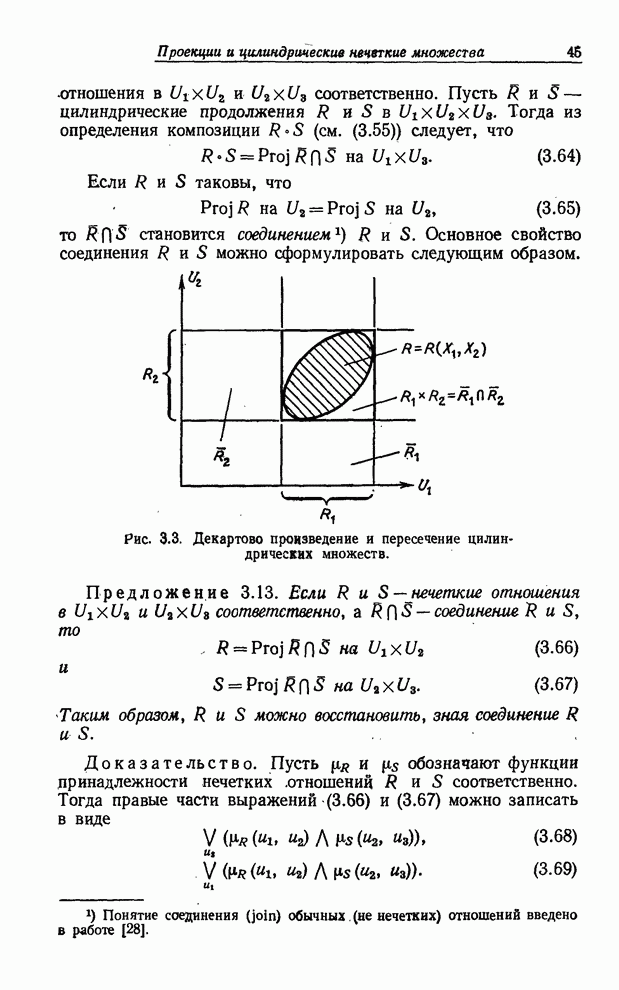
— его проекции на ![]() , то (см. рис.3.3)
, то (см. рис.3.3)
![]() (3.63)
(3.63)
С
помощью понятия цилиндрического продолжения можно дать интуитивную
интерпретацию композиции нечетких отношений. Так, предположим, что ![]() и
и ![]() —
бинарные нечеткие отношения в
—
бинарные нечеткие отношения в ![]() и
и ![]() соответственно. Пусть
соответственно. Пусть ![]() и
и ![]() —
цилиндрические продолжения
—
цилиндрические продолжения ![]() и
и ![]() в
в ![]() . Тогда
из определения композиции
. Тогда
из определения композиции ![]() (см. (3.55))
следует, что
(см. (3.55))
следует, что
![]() на
на ![]() .
(3.64)
.
(3.64)
Если
![]() и
и ![]() таковы,
что
таковы,
что
![]() на
на ![]() на
на ![]() , (3.65)
, (3.65)
то
![]() становится соединением
становится соединением ![]() и
и ![]() .
Основное свойство соединения
.
Основное свойство соединения ![]() и
и ![]() можно сформулировать следующим
образом.
можно сформулировать следующим
образом.

Рис. 3.3. Декартово произведение и пересечение цилиндрических множеств.
Предложение
3.13.
Если ![]() и
и ![]() —
нечеткие отношения в
—
нечеткие отношения в ![]() и
и ![]() соответственно, а
соответственно, а ![]() — соединение
— соединение ![]() и
и ![]() ,
то
,
то
![]() на
на ![]() ,
(3.66)
,
(3.66)
и
![]() на
на ![]() .
(3.67)
.
(3.67)
Таким
образом, ![]() и
и ![]() можно
восстановить, зная соединение
можно
восстановить, зная соединение ![]() и
и ![]() .
.
Доказательство.
Пусть ![]() и
и ![]() обозначают
функции принадлежности нечетких отношений
обозначают
функции принадлежности нечетких отношений ![]() и
и ![]() соответственно. Тогда правые части
выражений (3.66) и (3.67) можно записать в виде
соответственно. Тогда правые части
выражений (3.66) и (3.67) можно записать в виде
![]() (3.68)
(3.68)
![]() (3.69)
(3.69)
В
силу дистрибутивности и коммутативности операций ![]() и
и ![]() (3.68) и (3.69) можно переписать в
виде
(3.68) и (3.69) можно переписать в
виде
 (3.70)
(3.70)
и
 (3.71)
(3.71)
Более того, из определения соединения следует равенство (3.65) и, значит,
![]() (3.72)
(3.72)
Из
этого равенства и определения операции ![]() получаем
получаем
![]() (3.73)
(3.73)
и
![]() . (3.74)
. (3.74)
Следовательно,
 (3.75)
(3.75)
и
 (3.76)
(3.76)
что и означает выполнение (3.66) и (3.67). Предложение доказано.
Основное свойство проекций, которое нам понадобится в § 4, следующее.
Предложение
3.14.
Если ![]() — нормальное отношение (см.
(3.23)), то и каждая из его проекций — нормальное отношение.
— нормальное отношение (см.
(3.23)), то и каждая из его проекций — нормальное отношение.
Доказательство.
Пусть ![]() есть
есть ![]() -арное
отношение в
-арное
отношение в ![]() , и пусть
, и пусть ![]() — его
проекция (тень) на
— его
проекция (тень) на ![]() , где
, где ![]() .
Поскольку
.
Поскольку ![]() нормально, то, согласно (3.23),
имеем
нормально, то, согласно (3.23),
имеем
![]() , (3.77)
, (3.77)
или в сокращенной записи
![]()
С
другой стороны, по определению ![]() [см. (3.57)]
[см. (3.57)]
![]()
или
![]()
и,
следовательно, высота ![]() равна
равна
![]() (3.78)
(3.78)
Предложение доказано.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
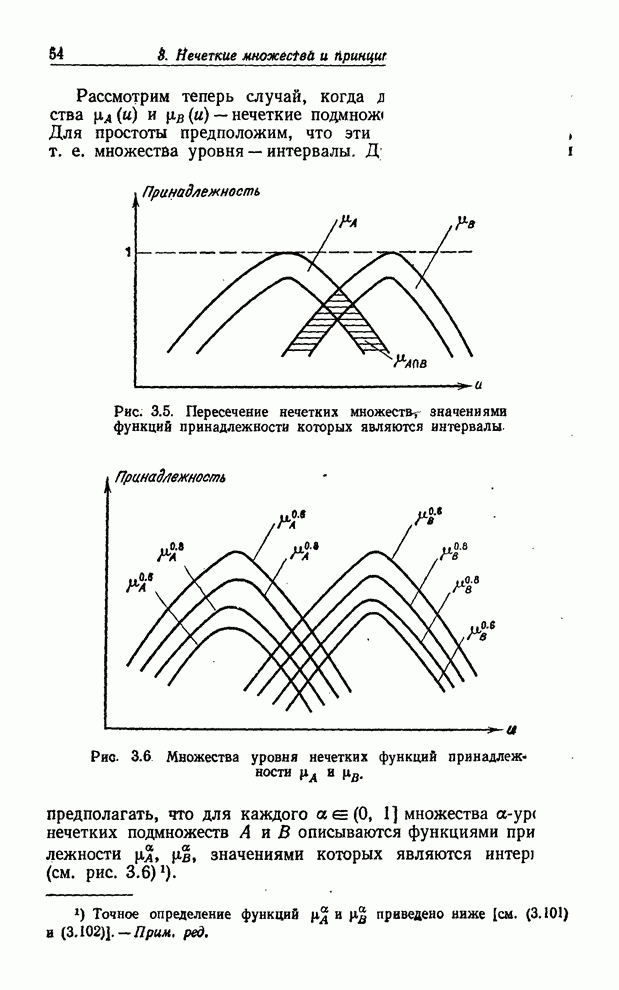
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
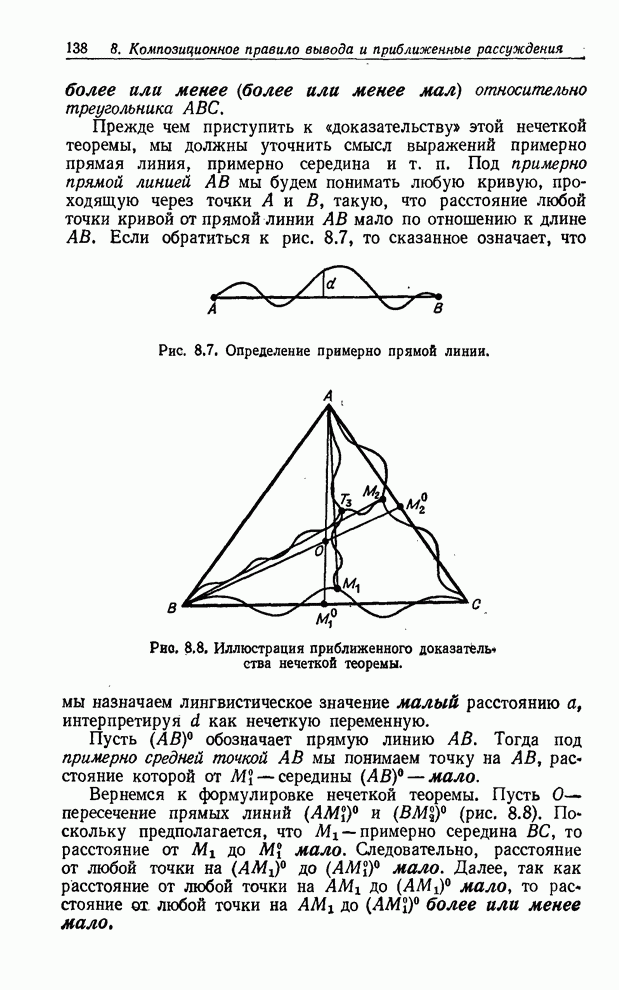
- НЕЧЕТКИЕ ТЕОРЕМЫ
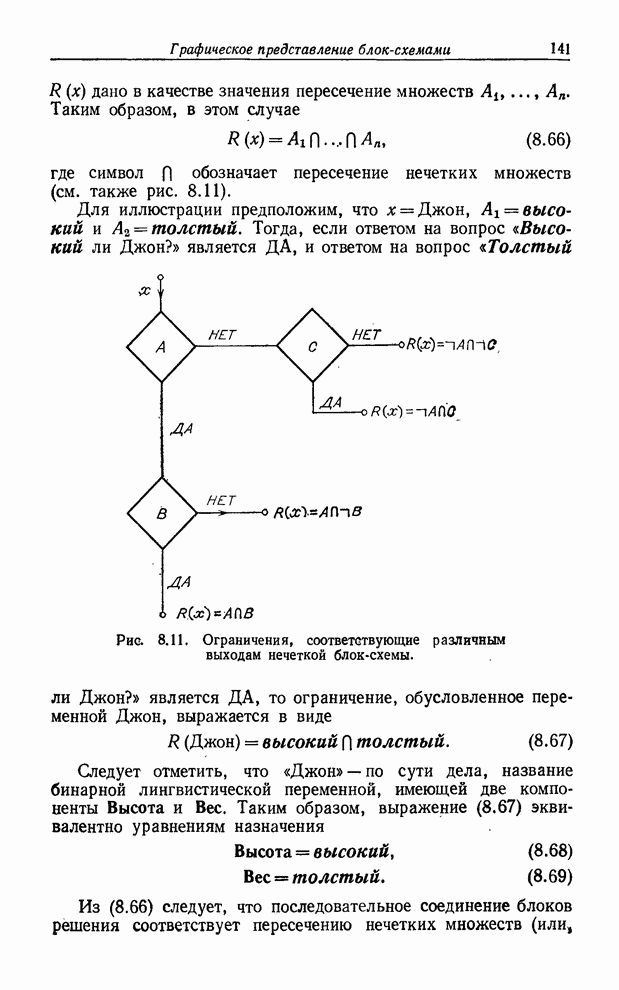
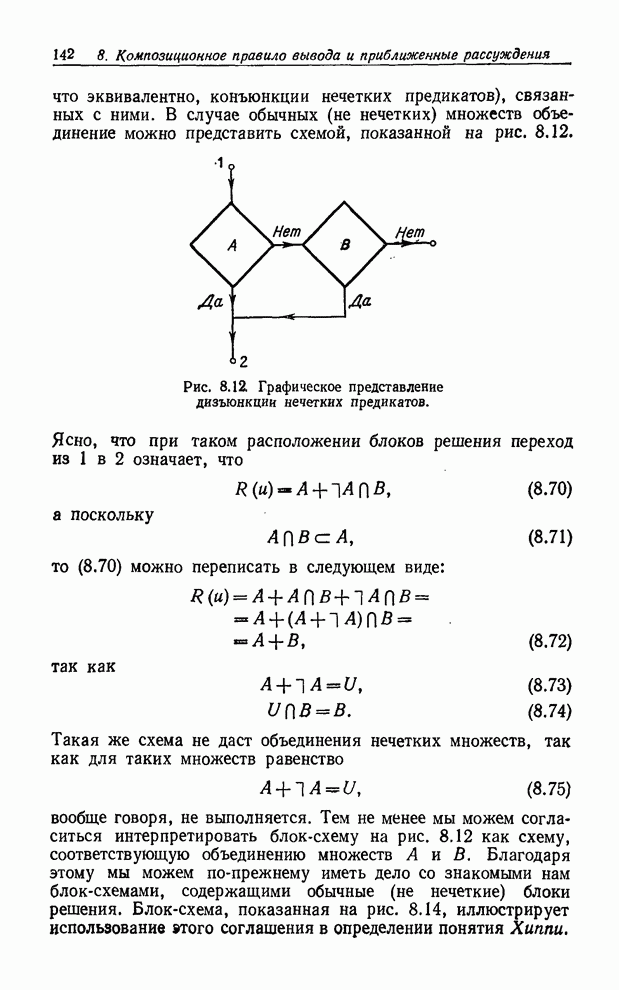
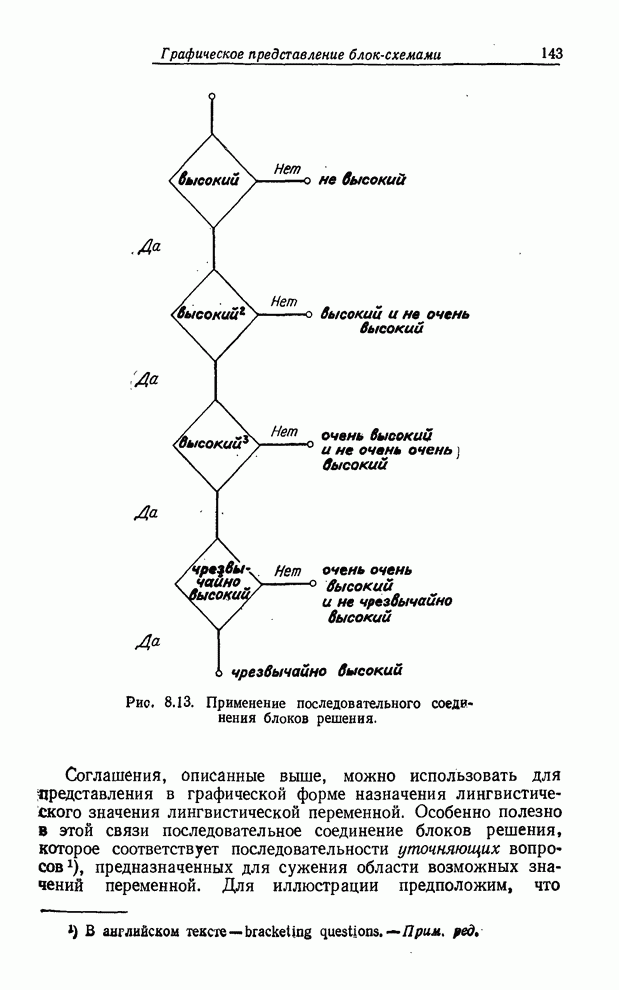
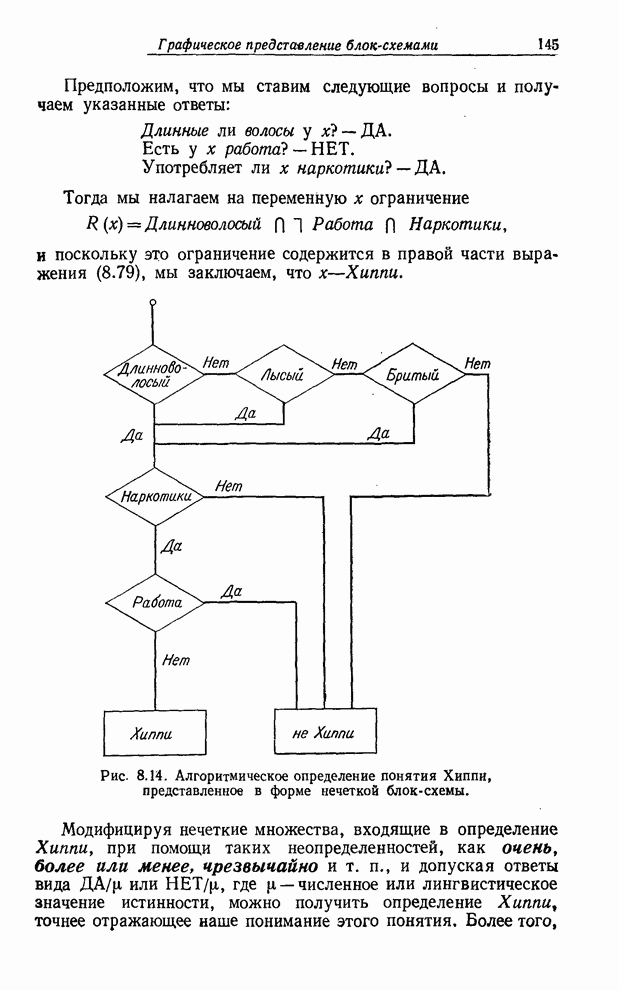
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ