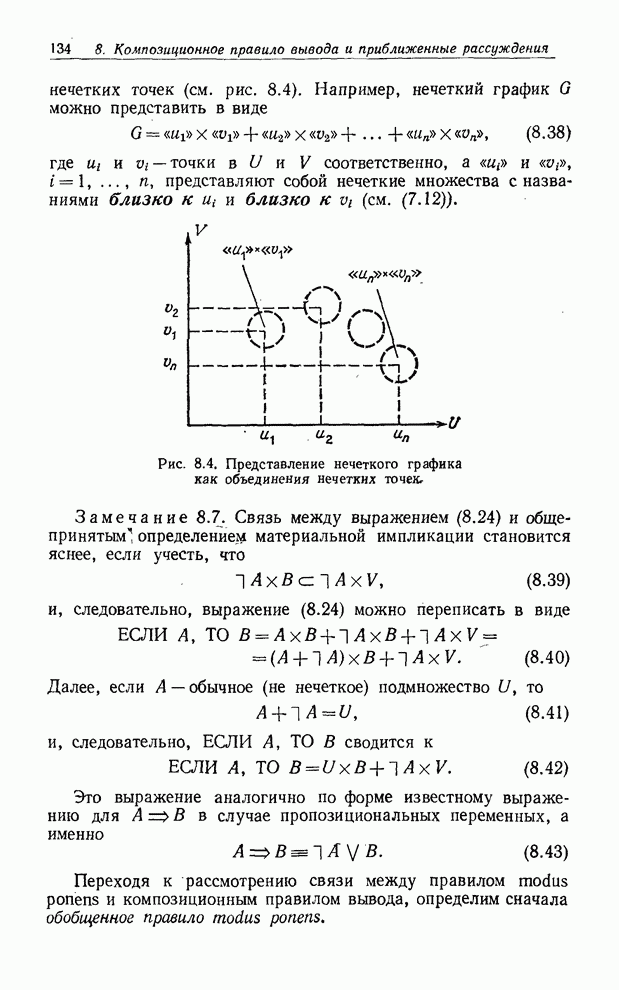
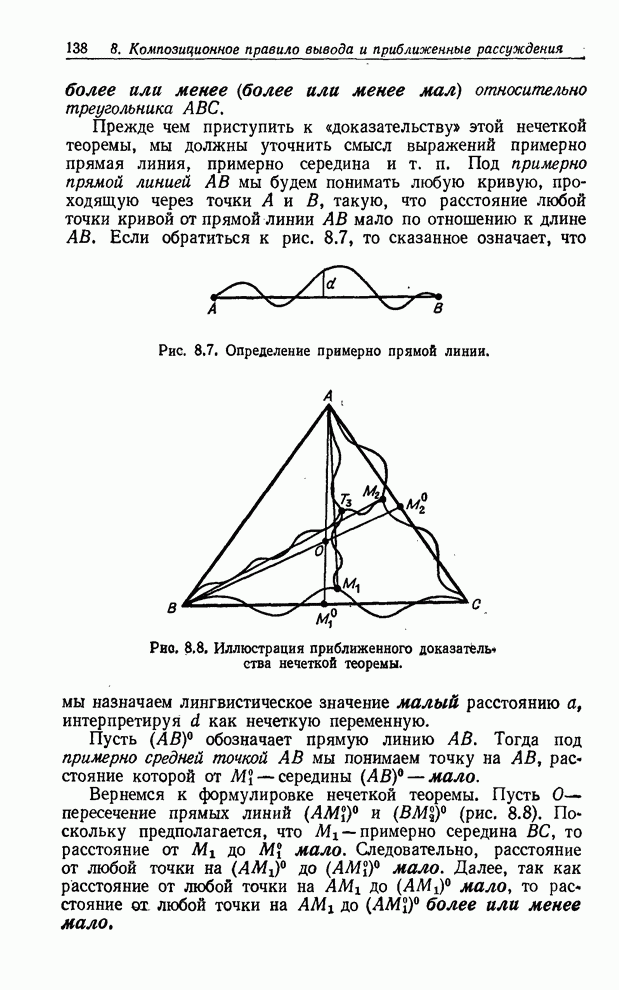
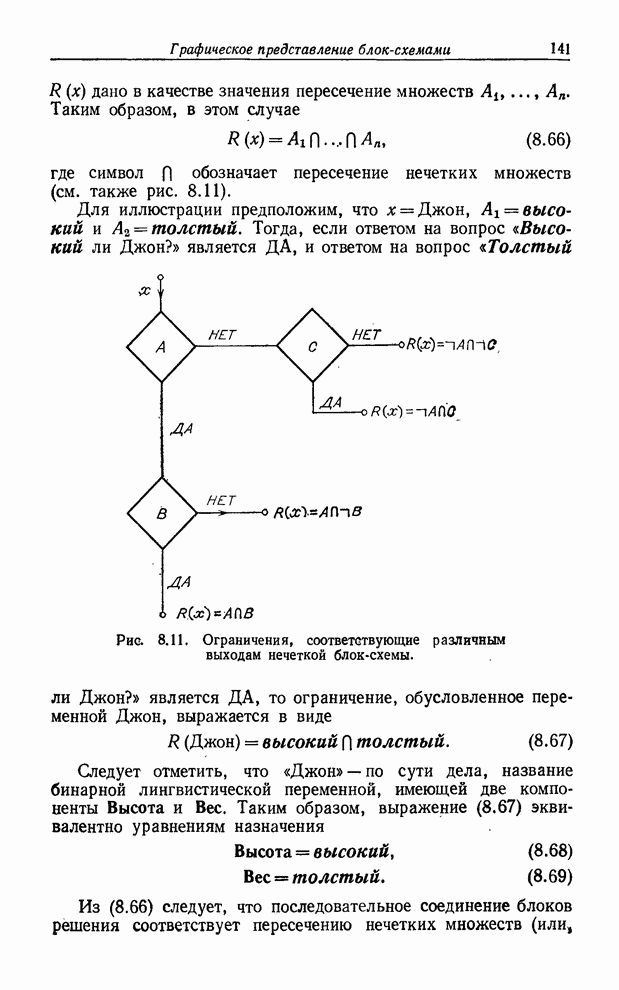
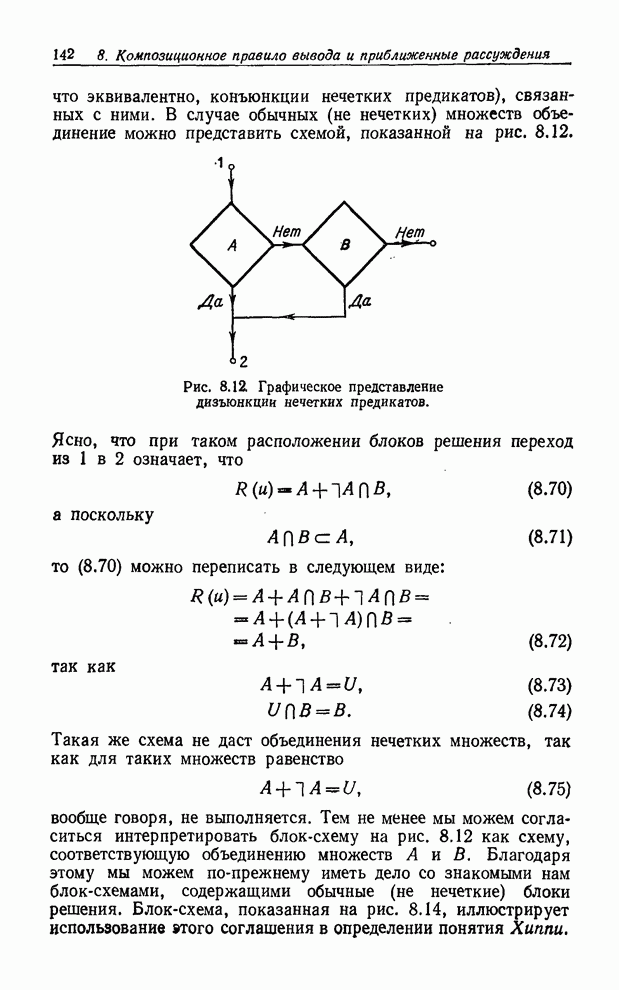
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. ПОНЯТИЕ ПЕРЕМЕННОЙ
Обсуждение понятия лингвистической переменной в предыдущем параграфе носило неформальный характер. Чтобы подготовить почву для формального определения, сконцентрируем внимание в этом параграфе на понятии обычной (не нечеткой) переменной. После этого в § 3 мы обобщим понятие переменной на случай нечеткой переменной и определим лингвистическую переменную как переменную, значениями которой являются нечеткие переменные. Хотя понятие обычной (не нечеткой) переменной элементарно по сути, оно ни в коем случае не тривиально.
В дальнейшем нам будет удобно пользоваться следующей формализацией понятия обычной переменной.
Определение
2.1. Обычная (не нечеткая) переменная характеризуется тройкой ![]() , где
, где
![]() -
название переменной,
-
название переменной,
![]() -
универсальное множество (конечное или бесконечное),
-
универсальное множество (конечное или бесконечное),
![]() -
общее название элементов множества
-
общее название элементов множества ![]() ,
,
![]() -
подмножество множества
-
подмножество множества ![]() , представляющее собой ограничение на
значения элементов
, представляющее собой ограничение на
значения элементов ![]() ,
обусловленное названием
,
обусловленное названием ![]() .
.
Для
удобства будем вместо ![]() писать сокращенно
писать сокращенно ![]() ,
, ![]() или
или ![]() , где
, где ![]() обозначает общее название значений
переменной
обозначает общее название значений
переменной ![]() ,
и называть
,
и называть ![]() просто
ограничением на
просто
ограничением на ![]() или
ограничением, обусловленным переменной
или
ограничением, обусловленным переменной ![]() .
.
Кроме того, переменной соответствует уравнение назначения
![]() , (2.1)
, (2.1)
или, что эквивалентно,
![]() ,
,
![]() . (2.2)
. (2.2)
Это
уравнение отражает тот факт, что переменной ![]() назначено значение
назначено значение ![]() с учетом ограничения
с учетом ограничения ![]() . Таким образом,
уравнение назначения удовлетворяется тогда и только тогда, когда
. Таким образом,
уравнение назначения удовлетворяется тогда и только тогда, когда ![]() .
.
Пример
2.2. Проиллюстрируем сказанное на примере переменной возраст. В этом случае в
качестве ![]() можно
взять множество целых чисел 0, 1, 2, 3, …, a
можно
взять множество целых чисел 0, 1, 2, 3, …, a ![]() может быть подмножеством 0, 1, 2, …,
100.
может быть подмножеством 0, 1, 2, …,
100.
Вообще
пусть ![]() - переменные
с соответствующими универсальными множествами
- переменные
с соответствующими универсальными множествами ![]() . Упорядоченный набор
. Упорядоченный набор ![]() будем называть
будем называть ![]() -арной составной
переменной. Универсальным множеством для
-арной составной
переменной. Универсальным множеством для ![]() является декартово произведение
является декартово произведение
![]() ,
(2.3)
,
(2.3)
а
ограничением ![]() является
является
![]() -арное
отношение в
-арное
отношение в ![]() .
Это отношение можно определить характеристической функцией (функцией
принадлежности)
.
Это отношение можно определить характеристической функцией (функцией
принадлежности) ![]() ,
причем
,
причем
 (2.4)
(2.4)
а
![]() - общее
название элементов множества
- общее
название элементов множества ![]() ,
, ![]() . Соответственно этому
. Соответственно этому ![]() -арное уравнение
назначения имеет вид
-арное уравнение
назначения имеет вид
![]() ,
(2.5)
,
(2.5)
которое следует понимать как
![]() ,
,
![]() , (2.6)
, (2.6)
при
ограничении ![]() ,
где
,
где ![]() ,
, ![]() - общее название
значений переменной
- общее название
значений переменной ![]() .
.
Пример
2.3. Предположим, что ![]() возраст отца,
возраст отца, ![]() возраст сына, и
возраст сына, и ![]() . Далее предположим,
что
. Далее предположим,
что ![]() (
(![]() и
и ![]() - общие названия значений
переменных
- общие названия значений
переменных ![]() и
и
![]() ). Тогда
). Тогда ![]() можно определить так:
можно определить так:
 (2.7)
(2.7)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ