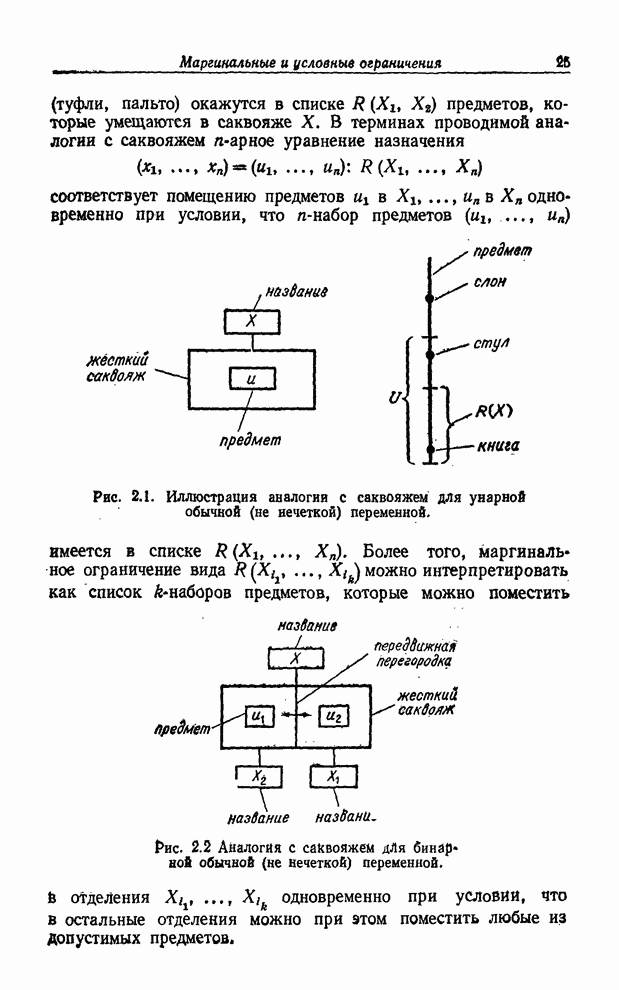
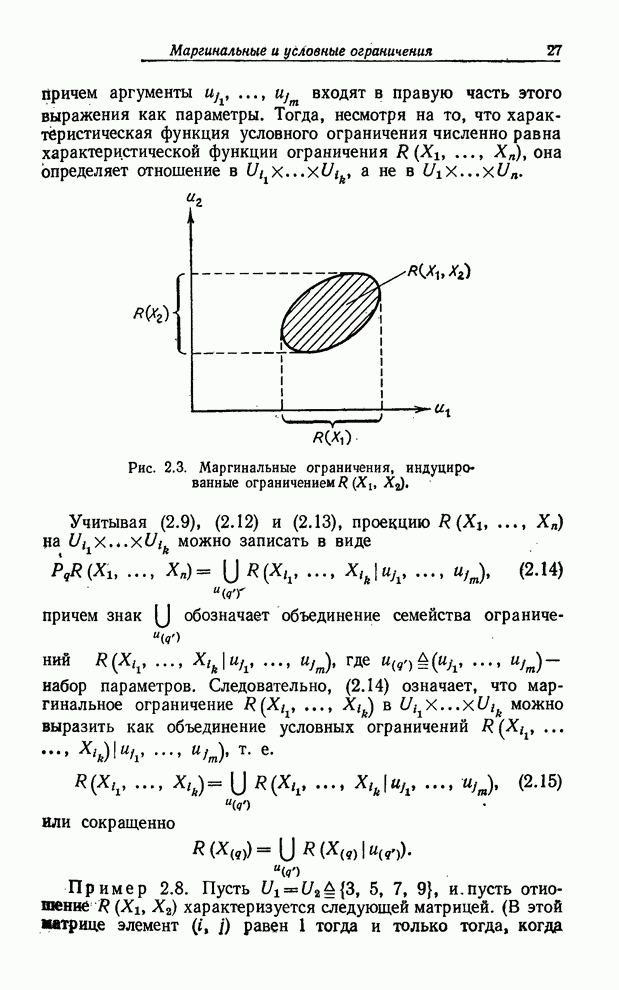
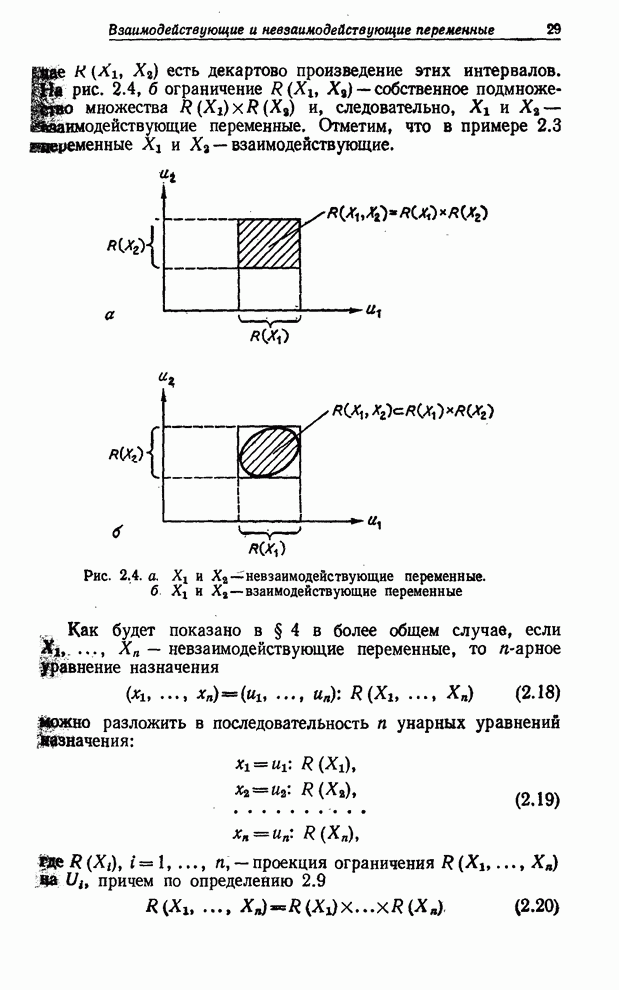
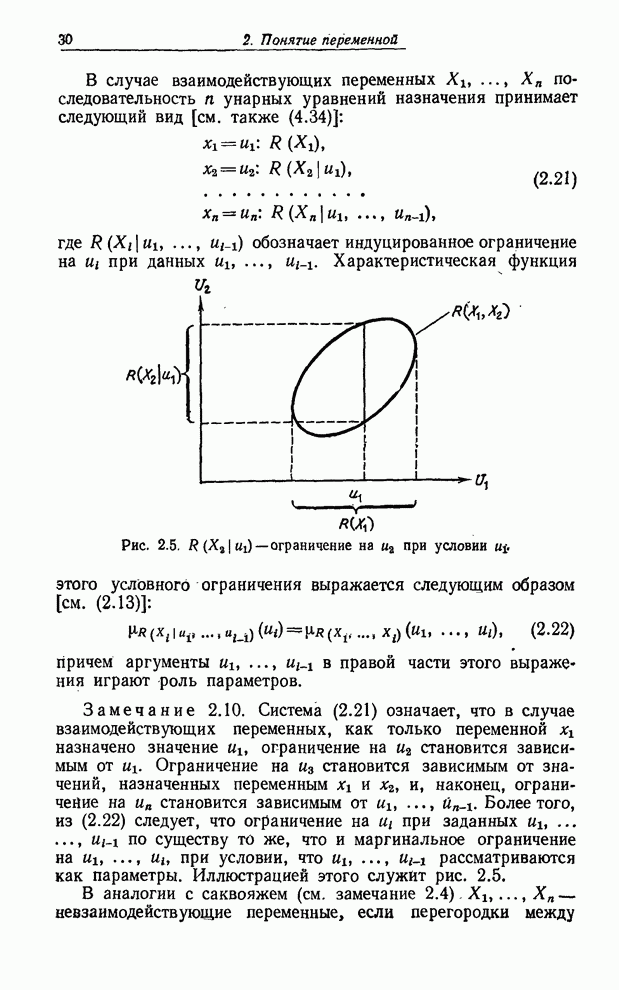
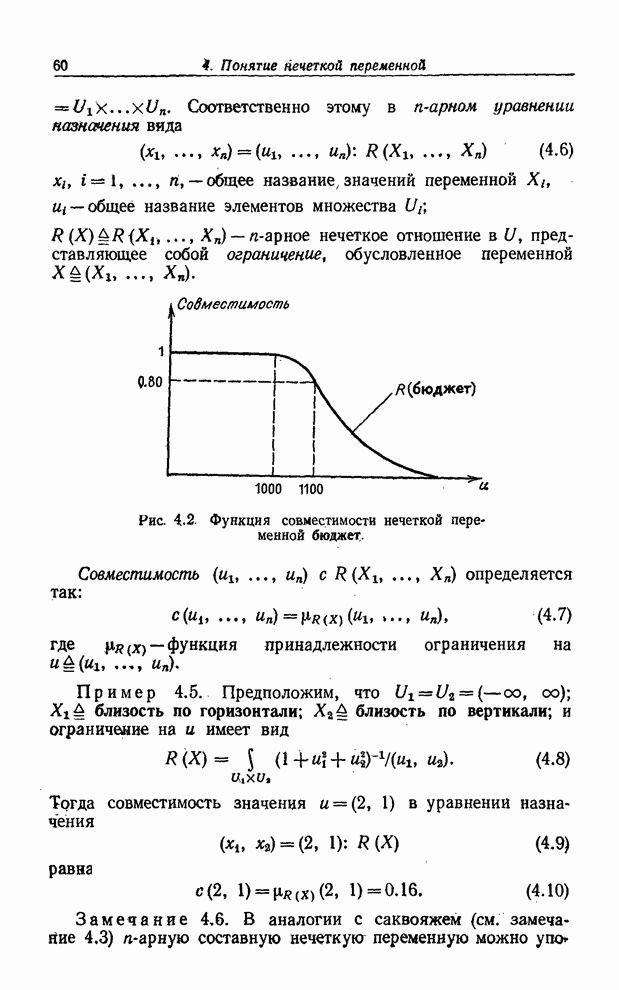
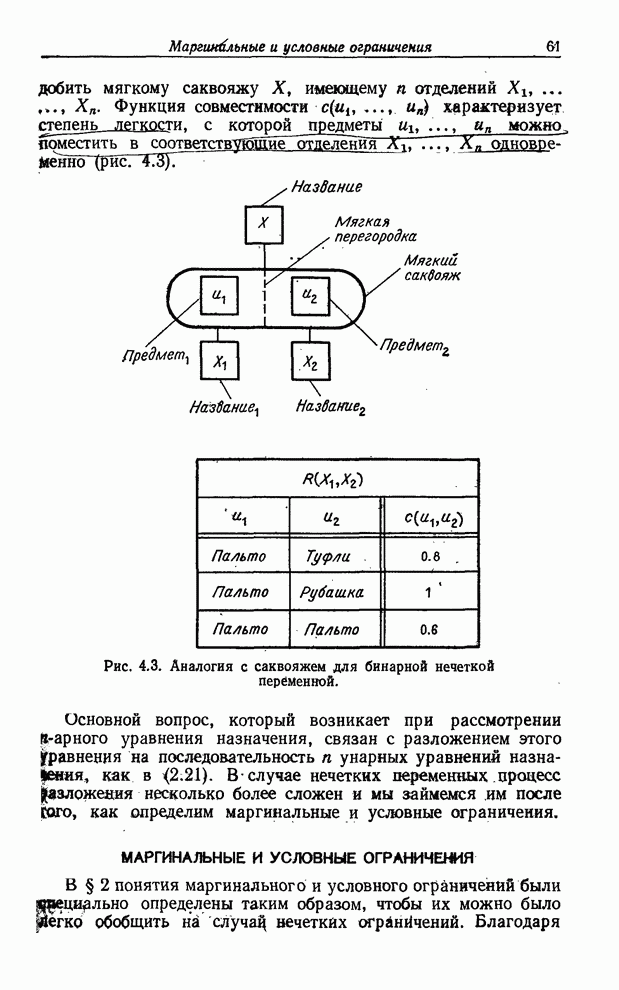
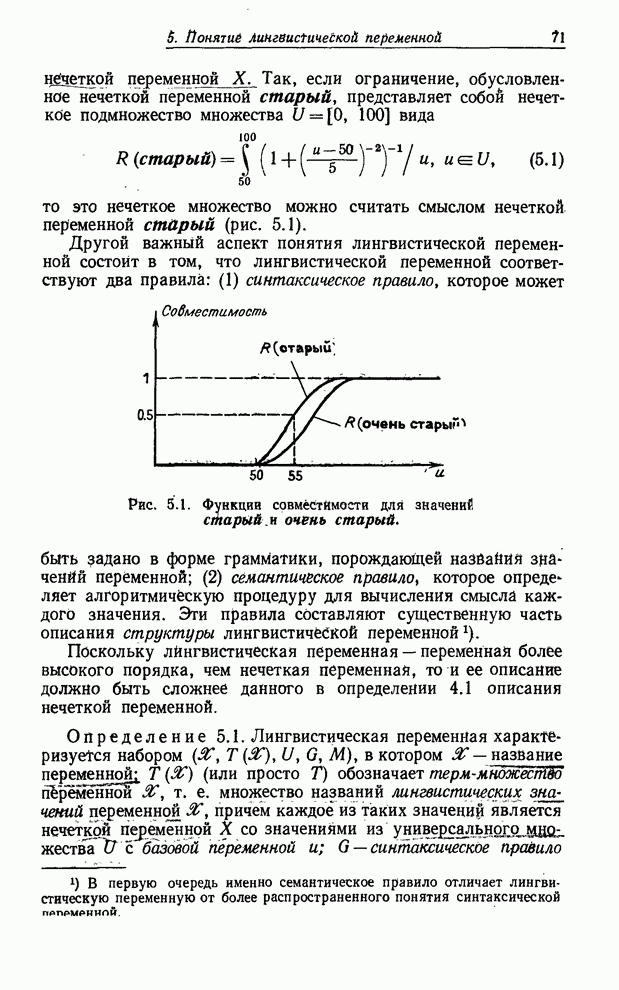
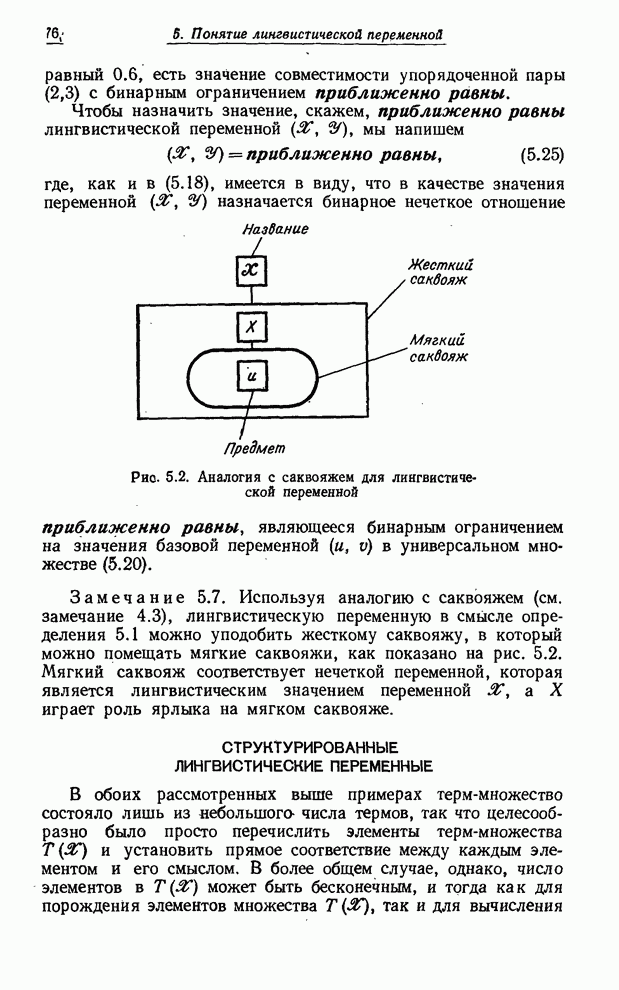
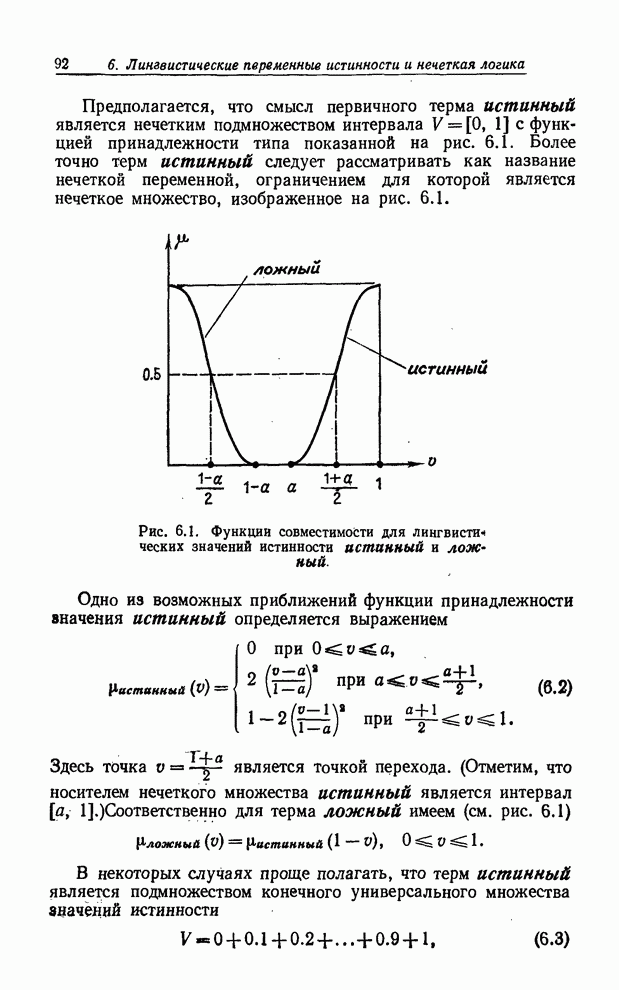
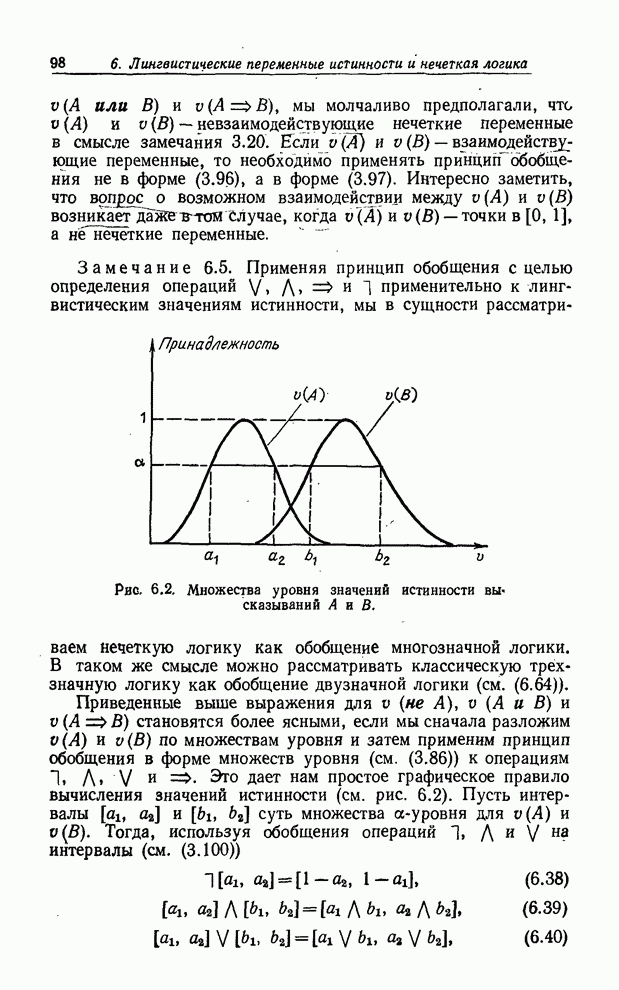
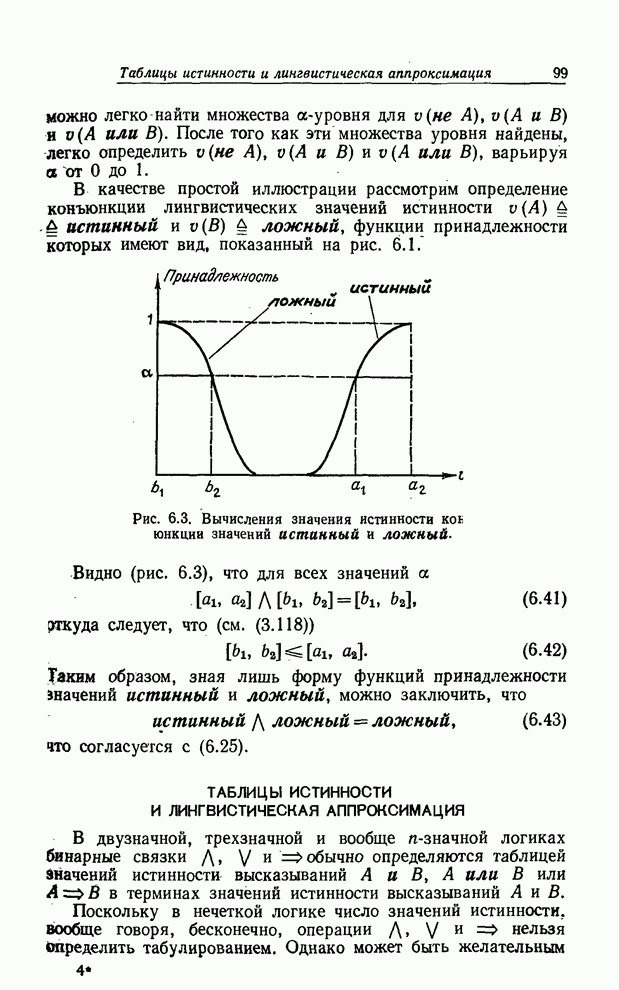
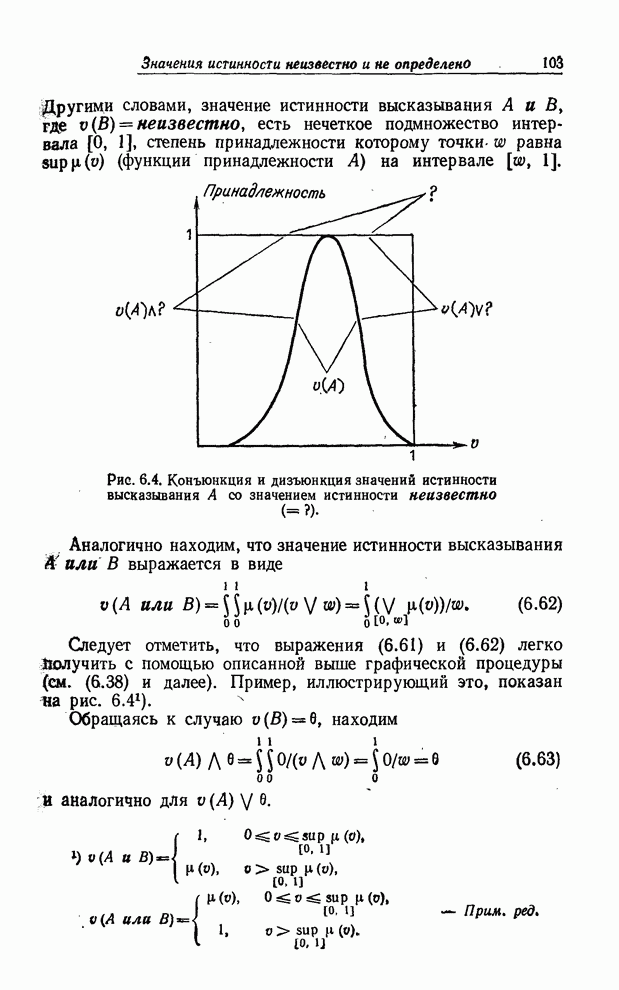
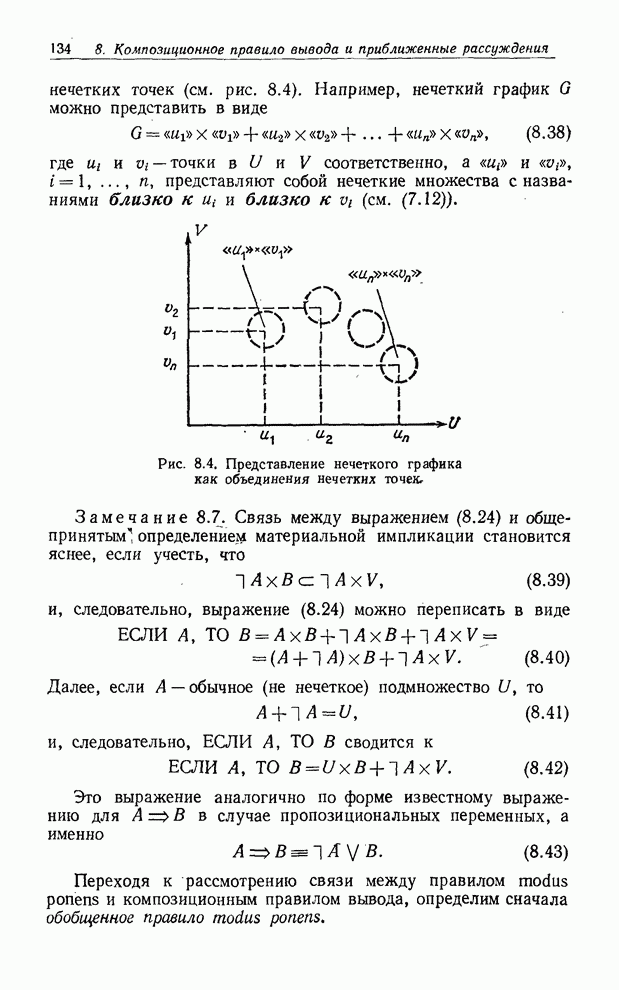
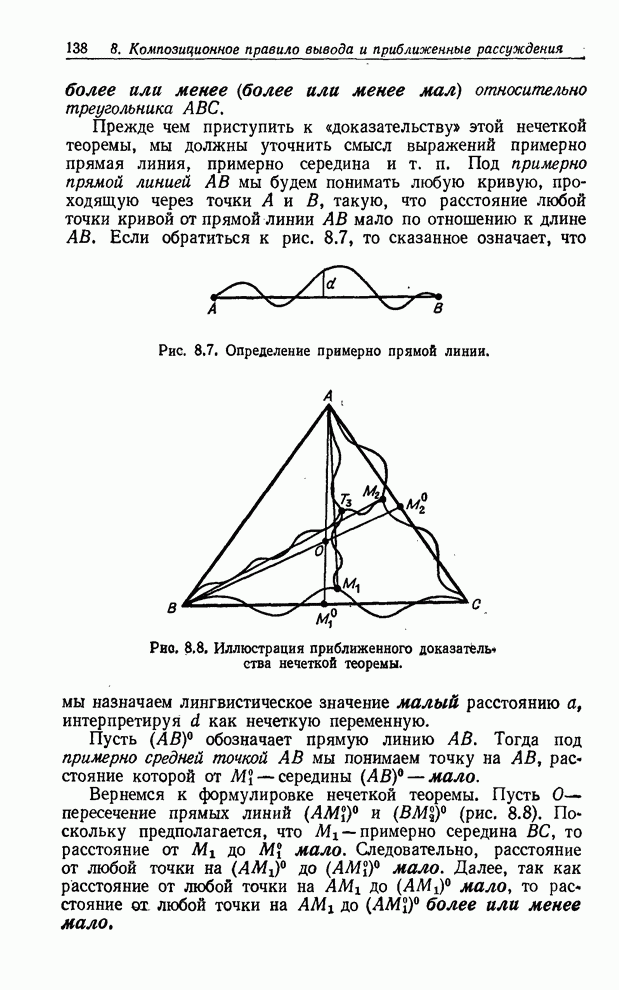
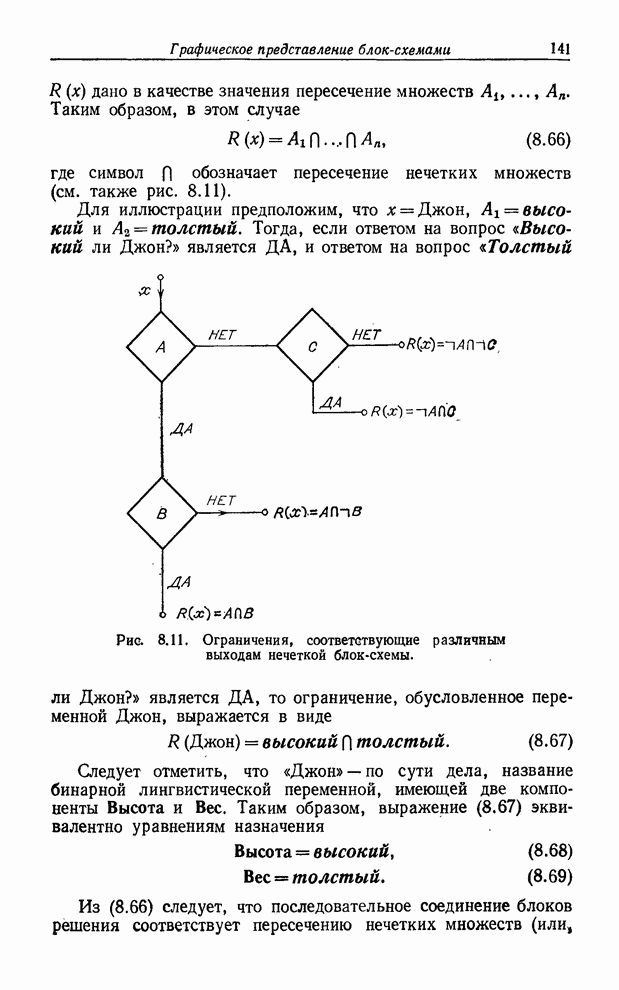
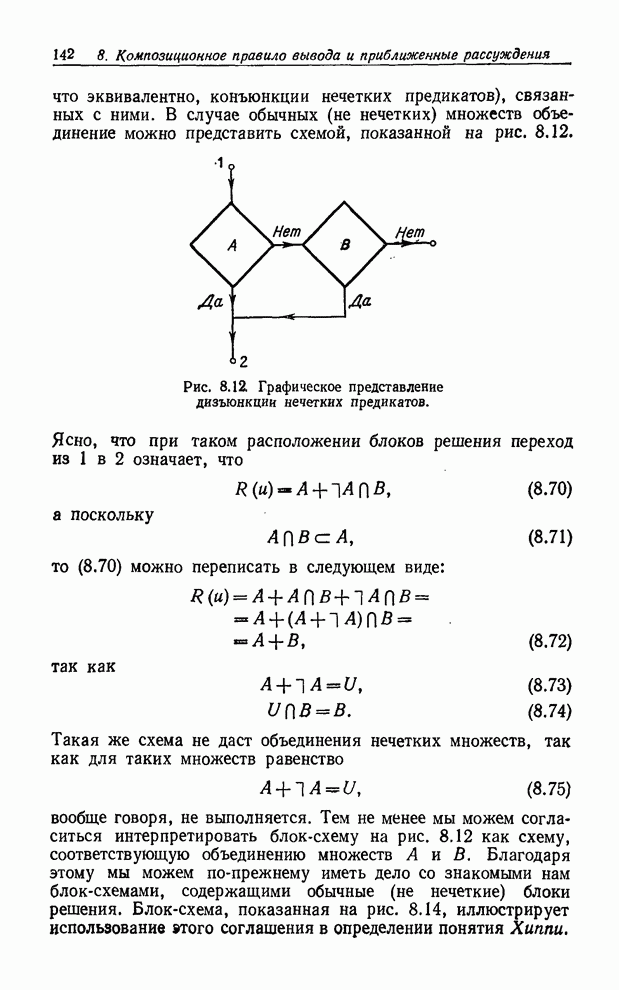
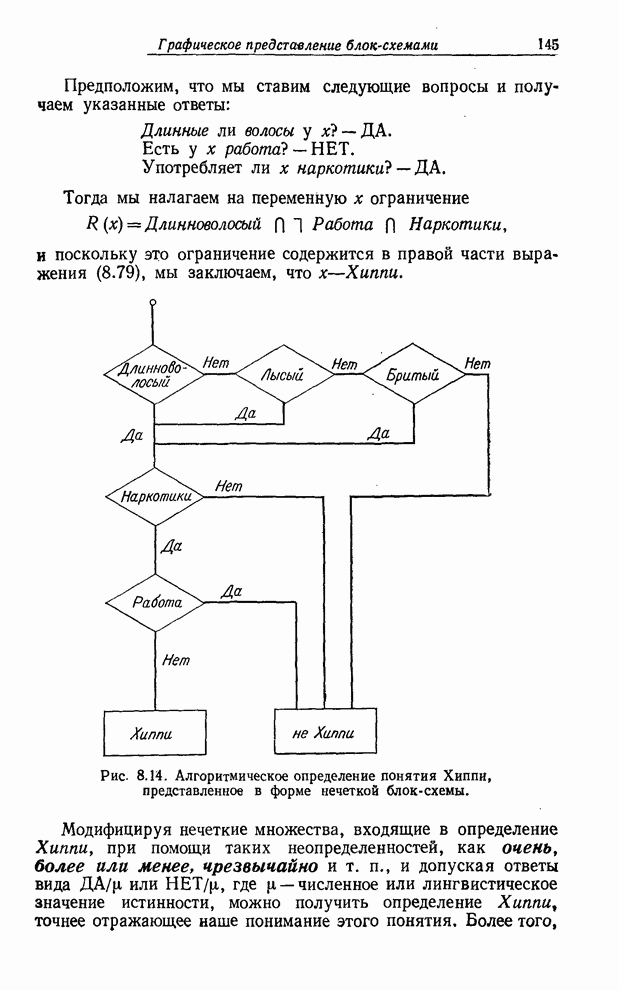
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
Ниже приведены некоторые из основных операций, которые можно осуществлять над нечеткими множествами.
1.
Дополнение
нечеткого множества ![]() обозначается
символом
обозначается
символом ![]() (или
иногда
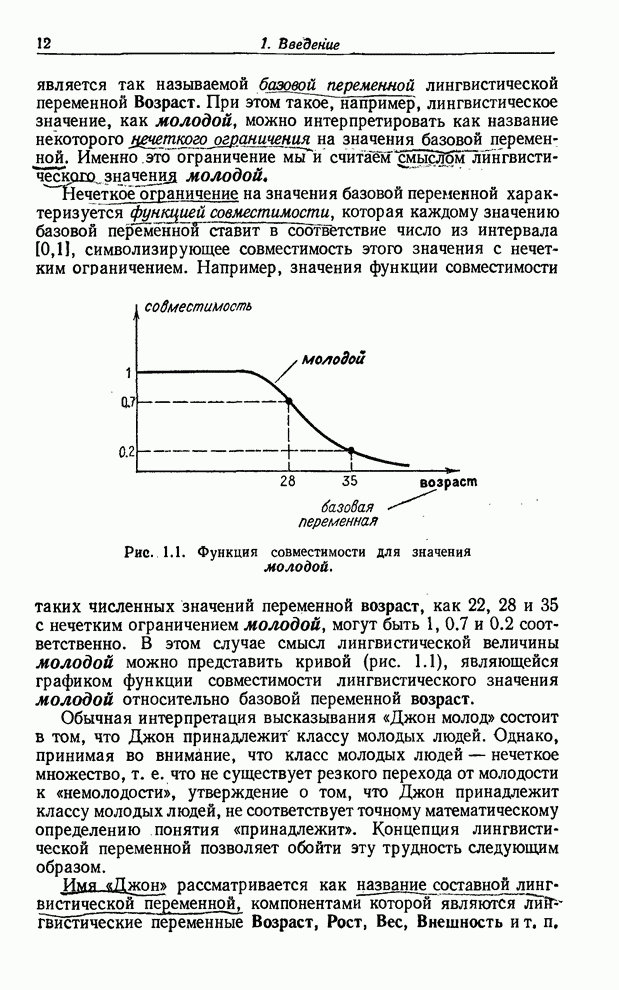
(или
иногда ![]() ) и определяется
следующим образом:
) и определяется
следующим образом:
![]() (3.33)
(3.33)
Операция
дополнения соответствует логическому отрицанию. Так, например, если ![]() — название
нечеткого множества, то «не
— название
нечеткого множества, то «не ![]() » понимается как
» понимается как ![]() (см. пример 3.8).
(см. пример 3.8).
2.
Объединение
нечетких множеств ![]() и
и
![]() обозначается
обозначается
![]() (или, что
более привычно,
(или, что
более привычно, ![]() )
и определяется следующим образом:
)
и определяется следующим образом:
![]() (3.34)
(3.34)
Объединение
соответствует логической связке «или». Так, если, например, ![]() и
и ![]() — названия нечетких
множеств, то запись «
— названия нечетких
множеств, то запись «![]() или
или ![]() » понимается как
» понимается как ![]() .
.
3.
Пересечение ![]() и
и ![]() обозначается
обозначается ![]() и
определяется следующим образом:
и
определяется следующим образом:
![]() (3.35)
(3.35)
Пересечение соответствует логической связке «и», т. е.
![]() (3.36)
(3.36)
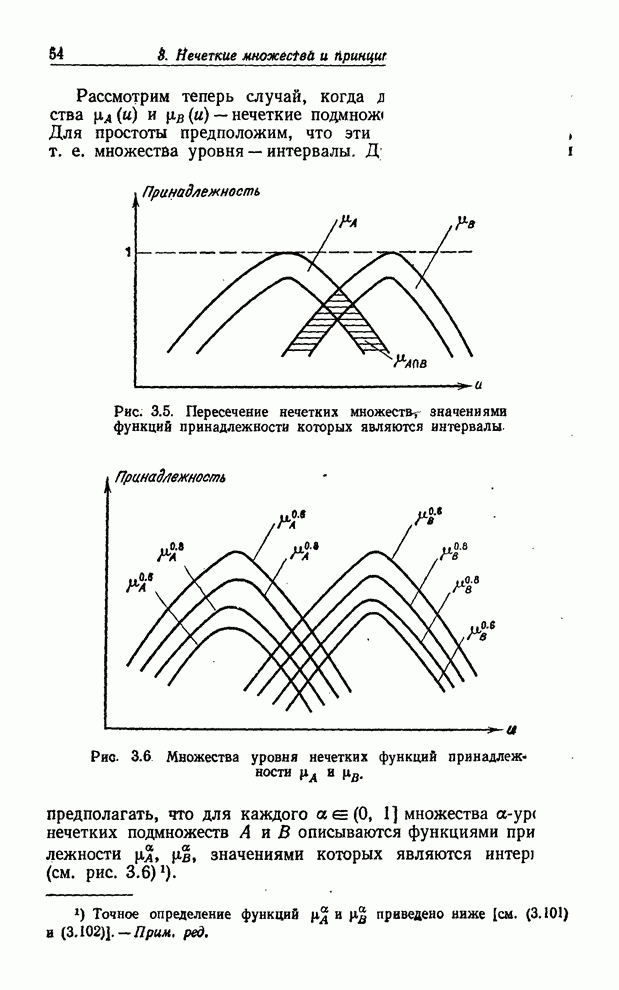
Замечание 3.7. Следует иметь в виду, что
![]() и
и ![]()
— не единственные операции, посредством которых можно определить операции объединения и пересечения (по этому вопросу см. [25] и [26]). В связи с этим важно отметить, что если операция «и» определяется с помощью операции min, как в (3.36), то она является «жесткой» в том смысле, что в ней недостаточно учитываются функции принадлежности обоих множеств. В противоположность этому операция «и», определяемая с помощью арифметического произведения, как в (3.37), является «мягкой». Какое из этих двух, а возможно, и других определений является наиболее подходящим, зависит от смысла, вкладываемого в эту операцию в каждом конкретном случае.
4.
Произведение
![]() и
и ![]() обозначается
обозначается
![]() и
определяется формулой
и
определяется формулой
![]() (3.37)
(3.37)
Таким
образом, любое нечеткое множество ![]() , где
, где ![]() — положительное число,
следует понимать так:
— положительное число,
следует понимать так:
![]() (3.38)
(3.38)
Аналогично,
если ![]() —
любое неотрицательное число, такое, что
—
любое неотрицательное число, такое, что ![]() , то
, то
![]() (3.39)
(3.39)
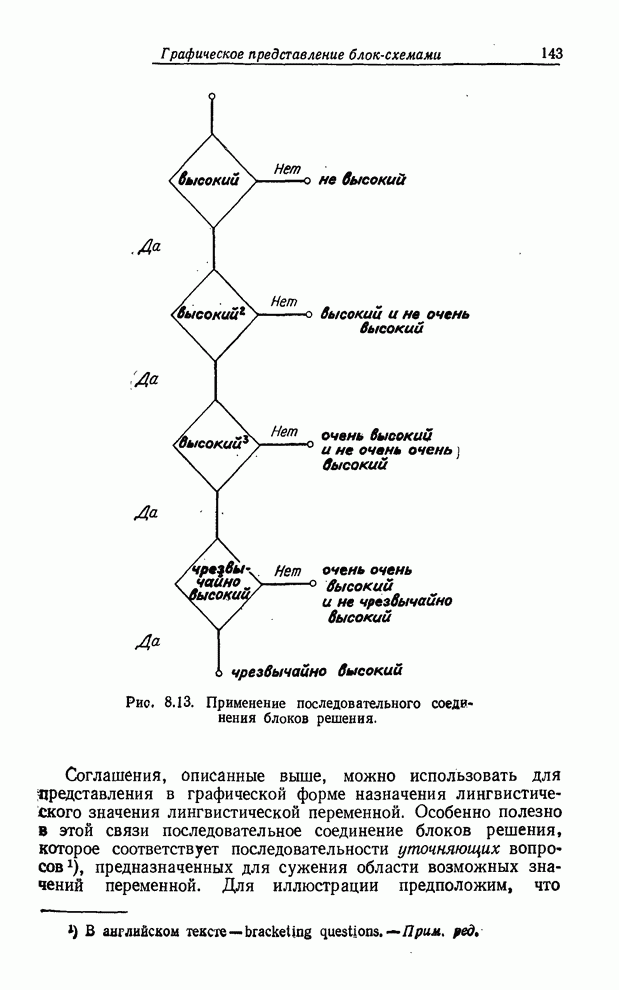
Частными случаями операции возведения в степень [см. (3.35)] являются операция концентрирования, определяемая следующим образом
![]() (3.40)
(3.40)
и операция растяжения
![]() (3.41)
(3.41)
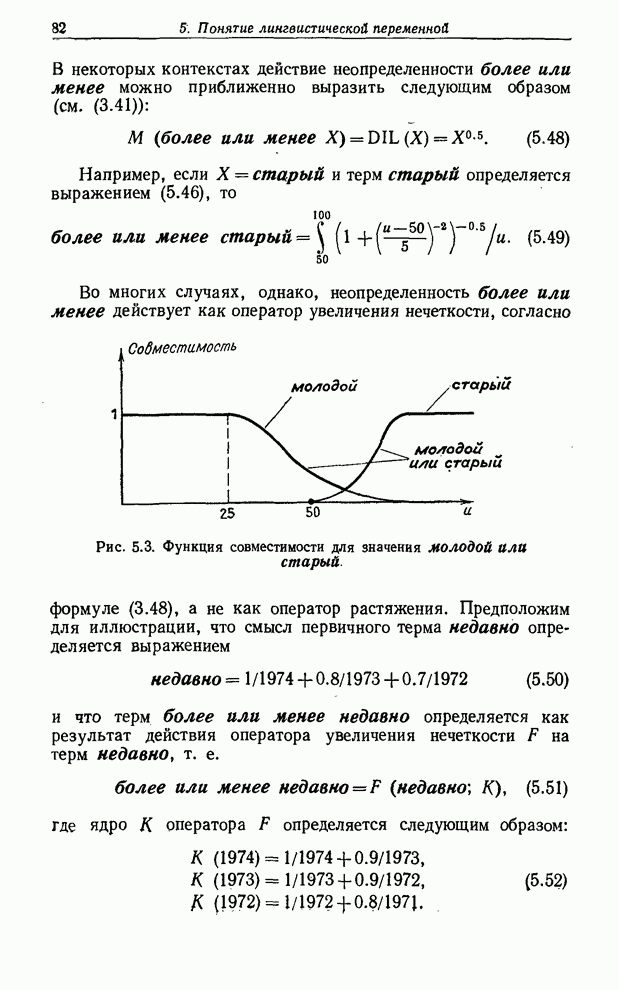
Как будет показано в §6, операции концентрирования и растяжения полезны в представлении лингвистических неопределенностей.
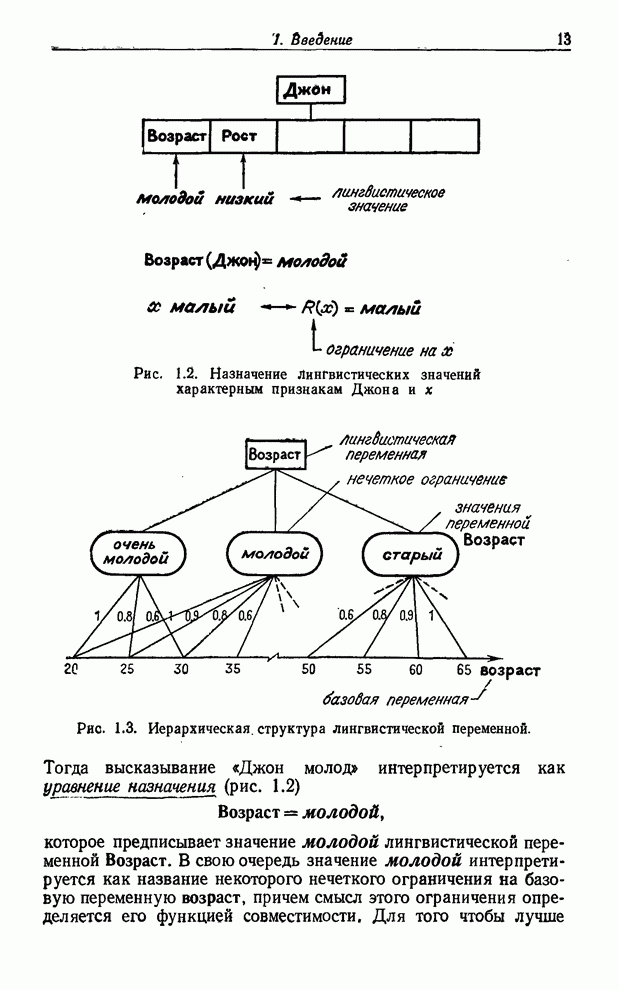
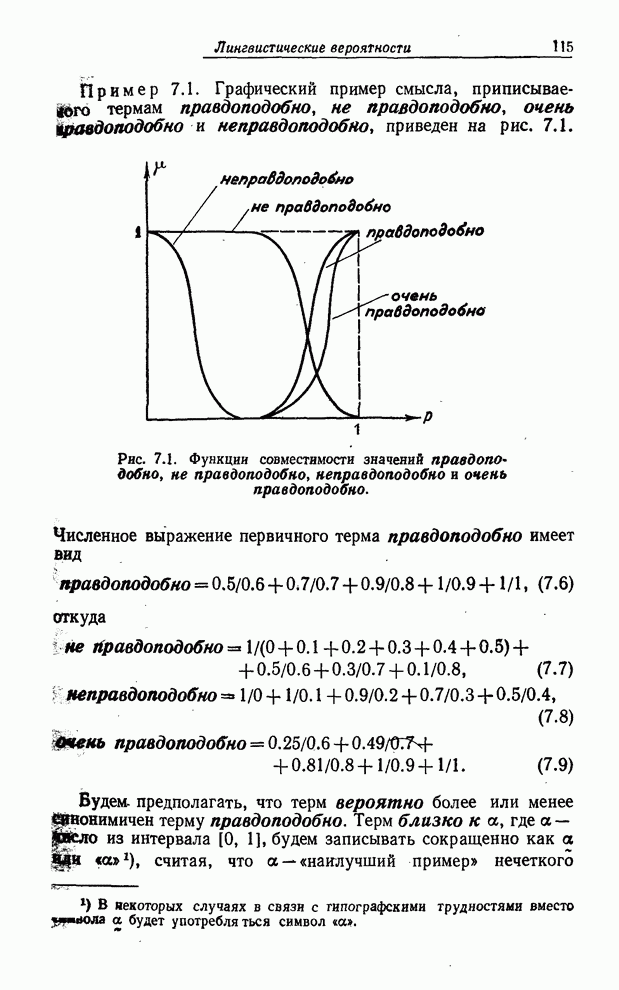
Пример 3.8. Если
 (3.42)
(3.42)
 (3.43)
(3.43)
5.
Если ![]() —
нечеткие подмножества универсального множества
—
нечеткие подмножества универсального множества ![]() , а
, а ![]() — неотрицательные весовые коэффициенты,
сумма которых равна 1, то выпуклой комбинацией нечетких множеств
— неотрицательные весовые коэффициенты,
сумма которых равна 1, то выпуклой комбинацией нечетких множеств ![]() называется нечеткое множество
называется нечеткое множество
![]() с функцией
принадлежности вида
с функцией
принадлежности вида
![]() (3.44)
(3.44)
где знак + означает арифметическое суммирование. Понятие выпуклой комбинации полезно в представлении таких лингвистических неопределенностей, как существенно, типично и т. п. [27].
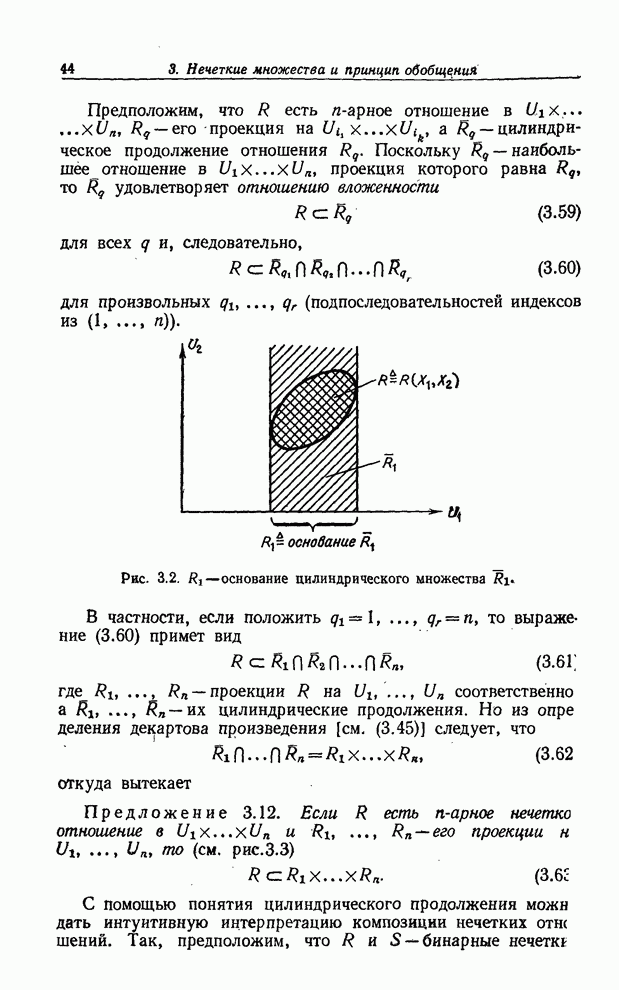
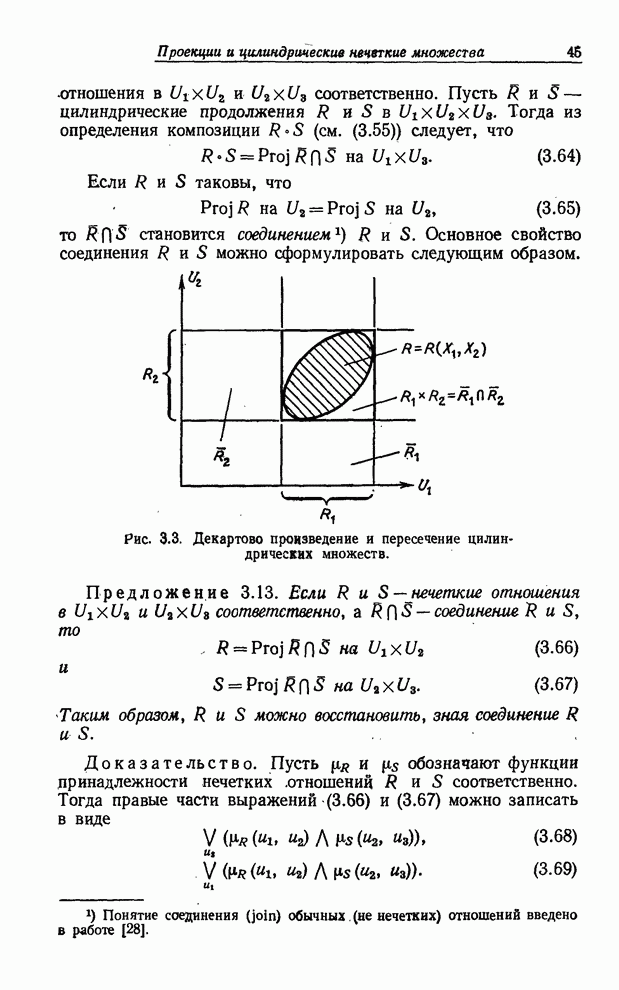
6.
Пусть ![]() —
нечеткие подмножества универсальных множеств
—
нечеткие подмножества универсальных множеств ![]() соответственно. Декартово произведение
этих подмножеств обозначается
соответственно. Декартово произведение
этих подмножеств обозначается ![]() и определяется как нечеткое подмножество
множества
и определяется как нечеткое подмножество
множества ![]() с
функцией принадлежности
с
функцией принадлежности
![]() . (3.45)
. (3.45)
Таким образом [см. (3.52)],
![]() (3.46)
(3.46)
Пример
3.9. Если
![]() ,
, ![]() и
и ![]() , то
, то
![]() (3.47)
(3.47)
7.
Оператор увеличения нечеткости используется обычно для преобразования
обычного (не нечеткого) множества в нечеткое или для увеличения нечеткости
нечеткого множества. Так, результатом действия оператора увеличения нечеткости ![]() на
нечеткое подмножество
на
нечеткое подмножество ![]() множества
множества ![]() является нечеткое
подмножество
является нечеткое
подмножество ![]() вида
вида
![]() (3.48)
(3.48)
где
нечеткое множество ![]() является
ядром оператора
является
ядром оператора ![]() ,
т. е. результатом действия оператора
,
т. е. результатом действия оператора ![]() на одноточечное множество
на одноточечное множество ![]() :
:
![]() (3.49)
(3.49)
![]() — произведение (в смысле определения
(3.39)) числа
— произведение (в смысле определения
(3.39)) числа ![]() и
нечеткого множества
и
нечеткого множества ![]() ,
a
,
a ![]() — знак объединения семейства
нечетких множеств
— знак объединения семейства
нечетких множеств ![]() ,
,
![]() . В
сущности, выражение (3.48) аналогично интегральному представлению линейного
оператора, в котором
. В
сущности, выражение (3.48) аналогично интегральному представлению линейного
оператора, в котором ![]() играет роль импульсной
переходной функции.
играет роль импульсной
переходной функции.
Пример
3.10.
Пусть ![]() ,
, ![]() и
и ![]() определены
следующий образом:
определены
следующий образом:
 (3.50)
(3.50)
Тогда
![]() (3.51)
(3.51)
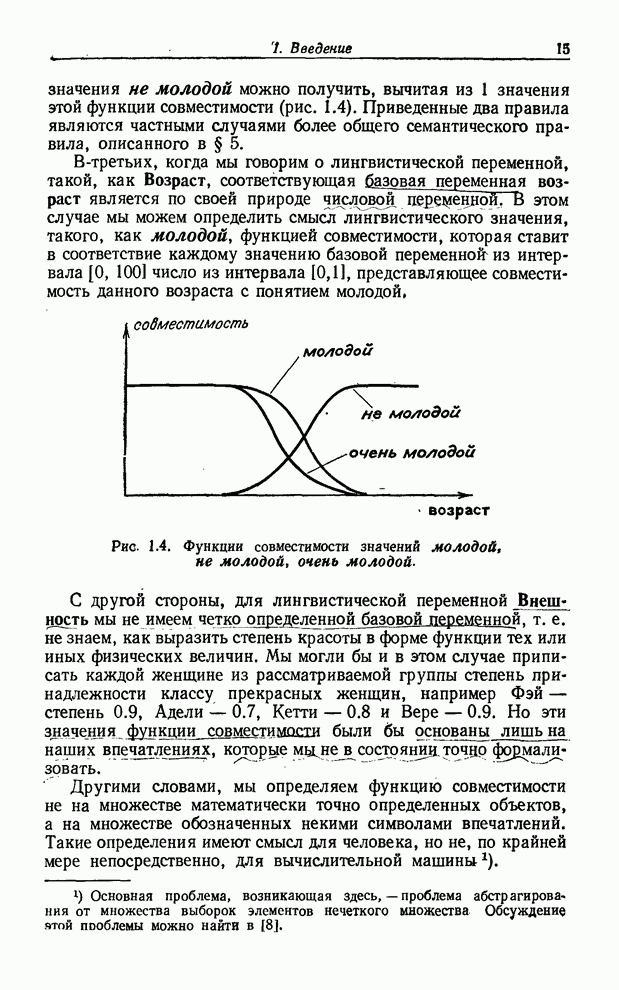
Операция
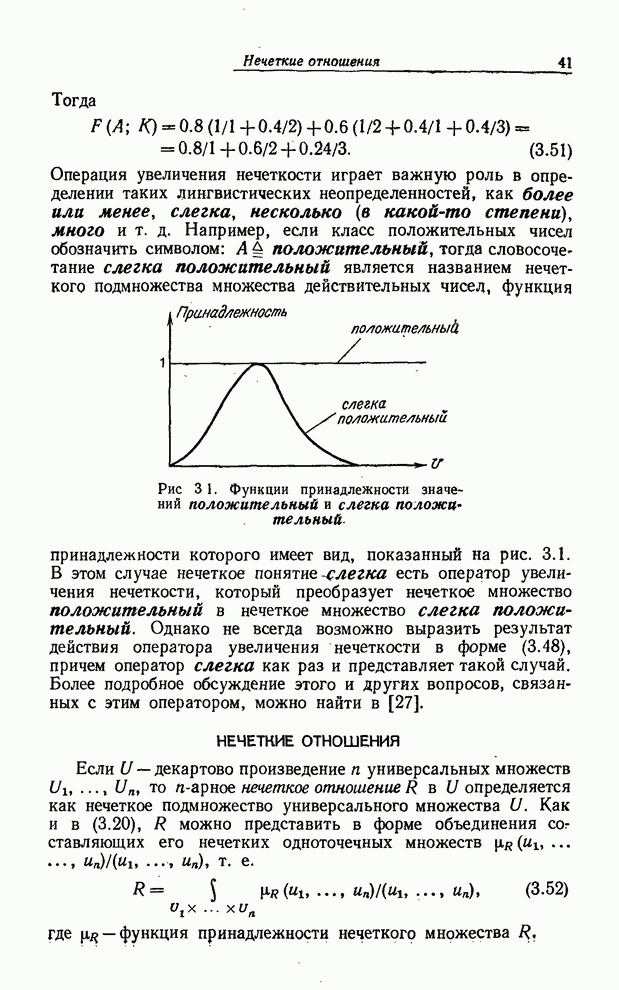
увеличения нечеткости играет важную роль в определении таких лингвистических неопределенностей,
как более или менее, слегка, несколько (в какой-то
степени), много и т. д. Например, если класс положительных чисел
обозначить символом: ![]() положительный, тогда
словосочетание слегка положительный является названием нечеткого
подмножества множества действительных чисел, функция принадлежности которого
имеет вид, показанный на рис. 3.1. В этом случае нечеткое понятие слегка есть
оператор увеличения нечеткости, который преобразует нечеткое множество положительный
в нечеткое множество слегка положительный. Однако не всегда
возможно выразить результат действия оператора увеличения нечеткости в форме
(3.48), причем оператор слегка как раз и представляет такой
случай. Более подробное обсуждение этого и других вопросов, связанных с этим
оператором, можно найти в [27].
положительный, тогда
словосочетание слегка положительный является названием нечеткого
подмножества множества действительных чисел, функция принадлежности которого
имеет вид, показанный на рис. 3.1. В этом случае нечеткое понятие слегка есть
оператор увеличения нечеткости, который преобразует нечеткое множество положительный
в нечеткое множество слегка положительный. Однако не всегда
возможно выразить результат действия оператора увеличения нечеткости в форме
(3.48), причем оператор слегка как раз и представляет такой
случай. Более подробное обсуждение этого и других вопросов, связанных с этим
оператором, можно найти в [27].

Рис. 3.1. Функции принадлежности значений положительный и слегка положительный
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ПОНЯТИЕ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- ВЗАИМОДЕЙСТВУЮЩИЕ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 3. НЕЧЁТКИЕ МНОЖЕСТВА И ПРИНЦИП ОБОБЩЕНИЯ
- МНОЖЕСТВА УРОВНЯ НЕЧЕТКОГО ПОДМНОЖЕСТВА УНИВЕРСАЛЬНОГО МНОЖЕСТВА
- ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
- НЕЧЕТКИЕ ОТНОШЕНИЯ
- ПРОЕКЦИИ И ЦИЛИНДРИЧЕСКИЕ НЕЧЕТКИЕ МНОЖЕСТВА
- ПРИНЦИП ОБОБЩЕНИЯ
- НЕЧЕТКИЕ МНОЖЕСТВА С НЕЧЕТКИМИ ФУНКЦИЯМИ ПРИНАДЛЕЖНОСТИ
- 4. ПОНЯТИЕ НЕЧЕТКОЙ ПЕРЕМЕННОЙ
- МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ ОГРАНИЧЕНИЯ
- СЕПАРАБЕЛЬНОСТЬ И НЕВЗАИМОДЕЙСТВУЮЩИЕ ПЕРЕМЕННЫЕ
- 5. ПОНЯТИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- СТРУКТУРИРОВАННЫЕ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- БУЛЕВЫ ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЛИНГВИСТИЧЕСКОЙ ПЕРЕМЕННОЙ
- 6. ЛИНГВИСТИЧЕСКИЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И НЕЧЕТКАЯ ЛОГИКА
- ЛОГИЧЕСКИЕ СВЯЗКИ В НЕЧЕТКОЙ ЛОГИКЕ
- ТАБЛИЦЫ ИСТИННОСТИ И ЛИНГВИСТИЧЕСКАЯ АППРОКСИМАЦИЯ
- ЗНАЧЕНИЯ ИСТИННОСТИ
- СОСТАВНЫЕ ПЕРЕМЕННЫЕ ИСТИННОСТИ И РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ИСТИННОСТИ
- 7. ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ И УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- ЛИНГВИСТИЧЕСКИЕ ВЕРОЯТНОСТИ
- ВЫЧИСЛЕНИЯ С ЛИНГВИСТИЧЕСКИМИ ВЕРОЯТНОСТЯМИ
- УСРЕДНЕНИЯ ПО НЕЧЕТКИМ МНОЖЕСТВАМ
- 8. КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА И ПРИБЛИЖЕННЫЕ РАССУЖДЕНИЯ
- КОМПОЗИЦИОННОЕ ПРАВИЛО ВЫВОДА
- Правило modus ponens как частный случай композиционного правила вывода
- НЕЧЕТКИЕ ТЕОРЕМЫ
- ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЛОК-СХЕМАМИ
- Заключительные замечания
- СПИСОК ЛИТЕРАТУРЫ